Entanglement-Based CV-QKD with Information Reconciliation over Entanglement-Assisted Link
Abstract
:1. Introduction
2. Proposed Entanglement-Based CV-QKD with Information Reconciliation over Entanglement-Assisted Links
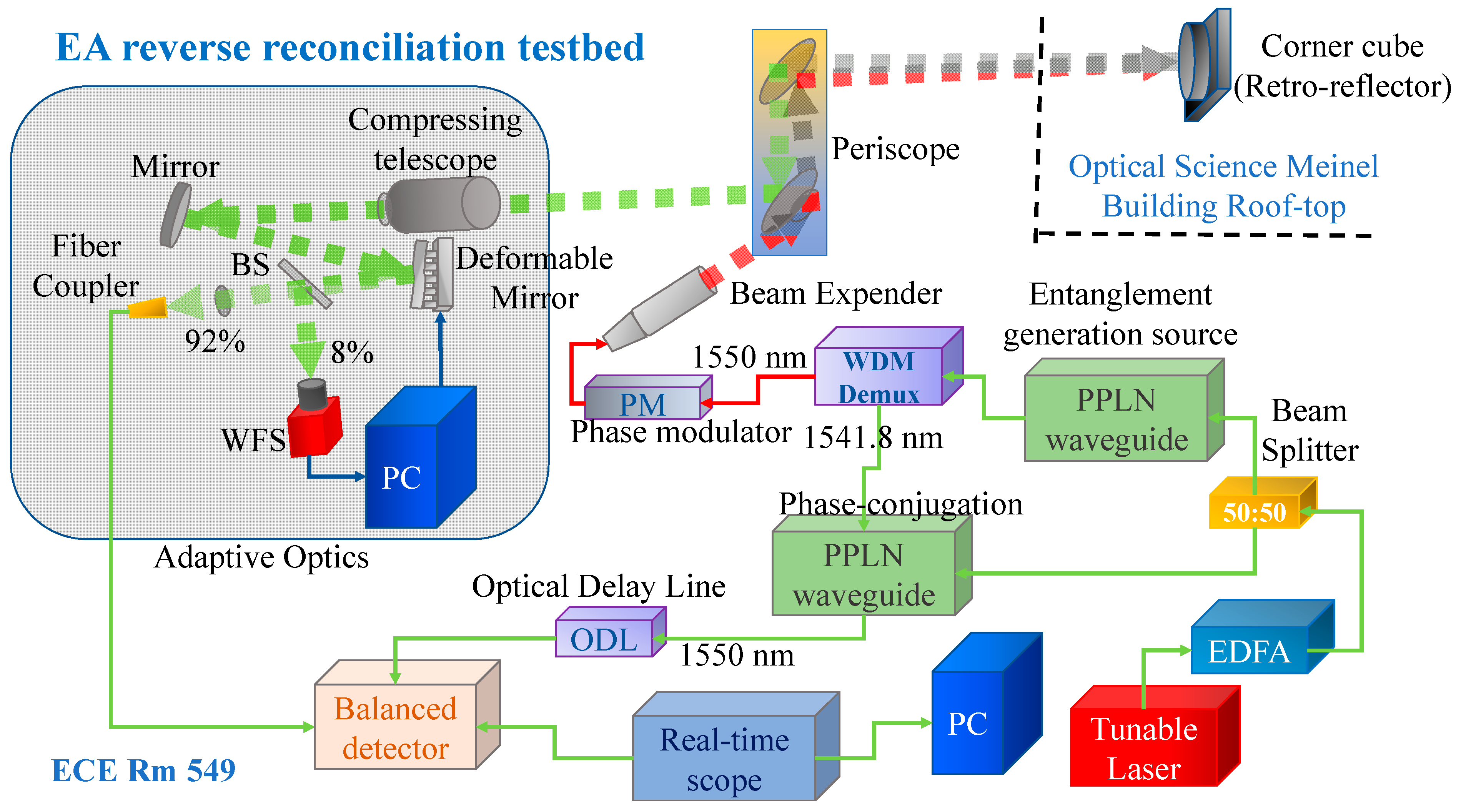
3. Description of Terrestrial Free-Space Optical (FSO) Testbed to Study the Proposed Entanglement-Based CV-QKD Scheme
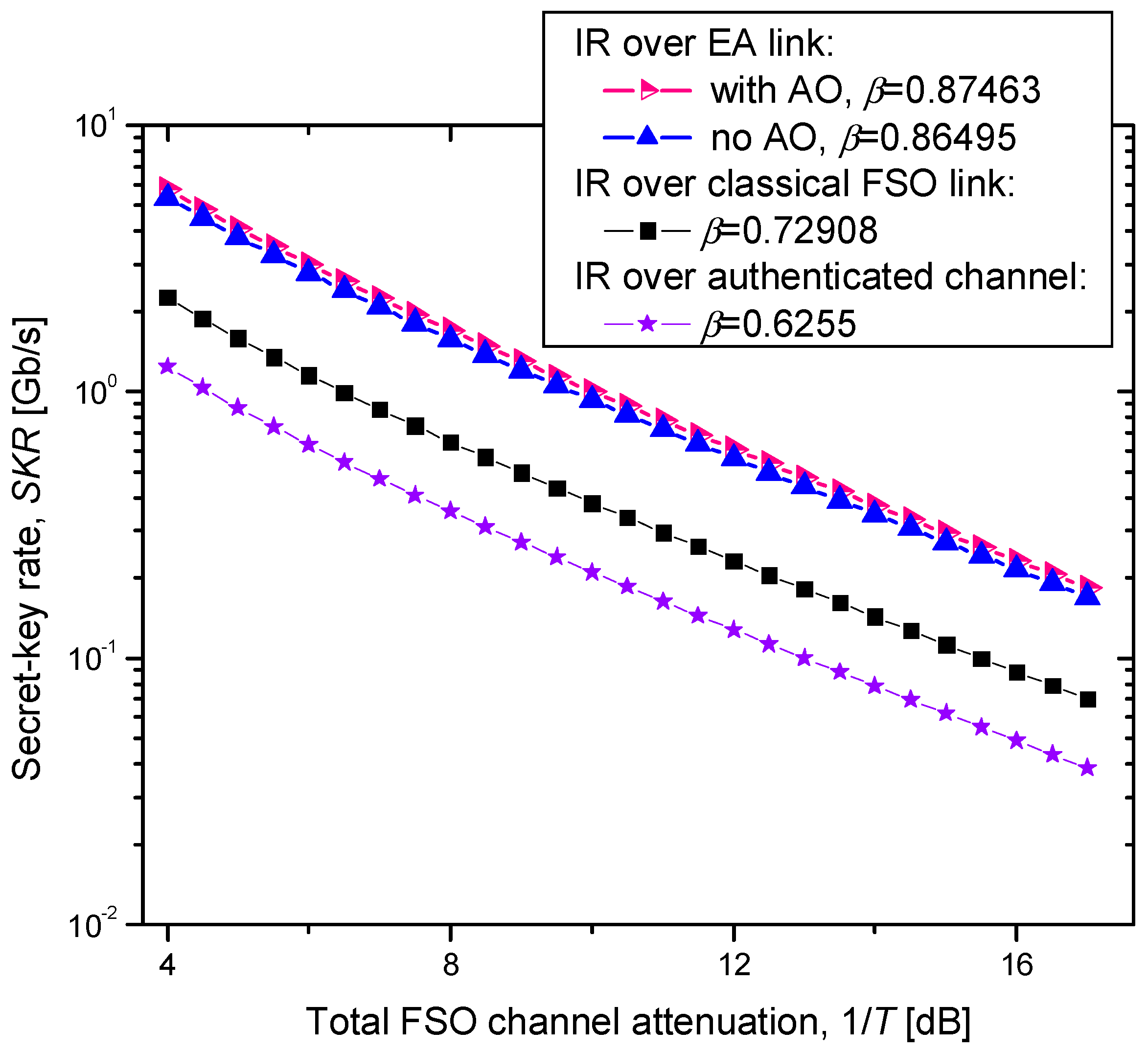
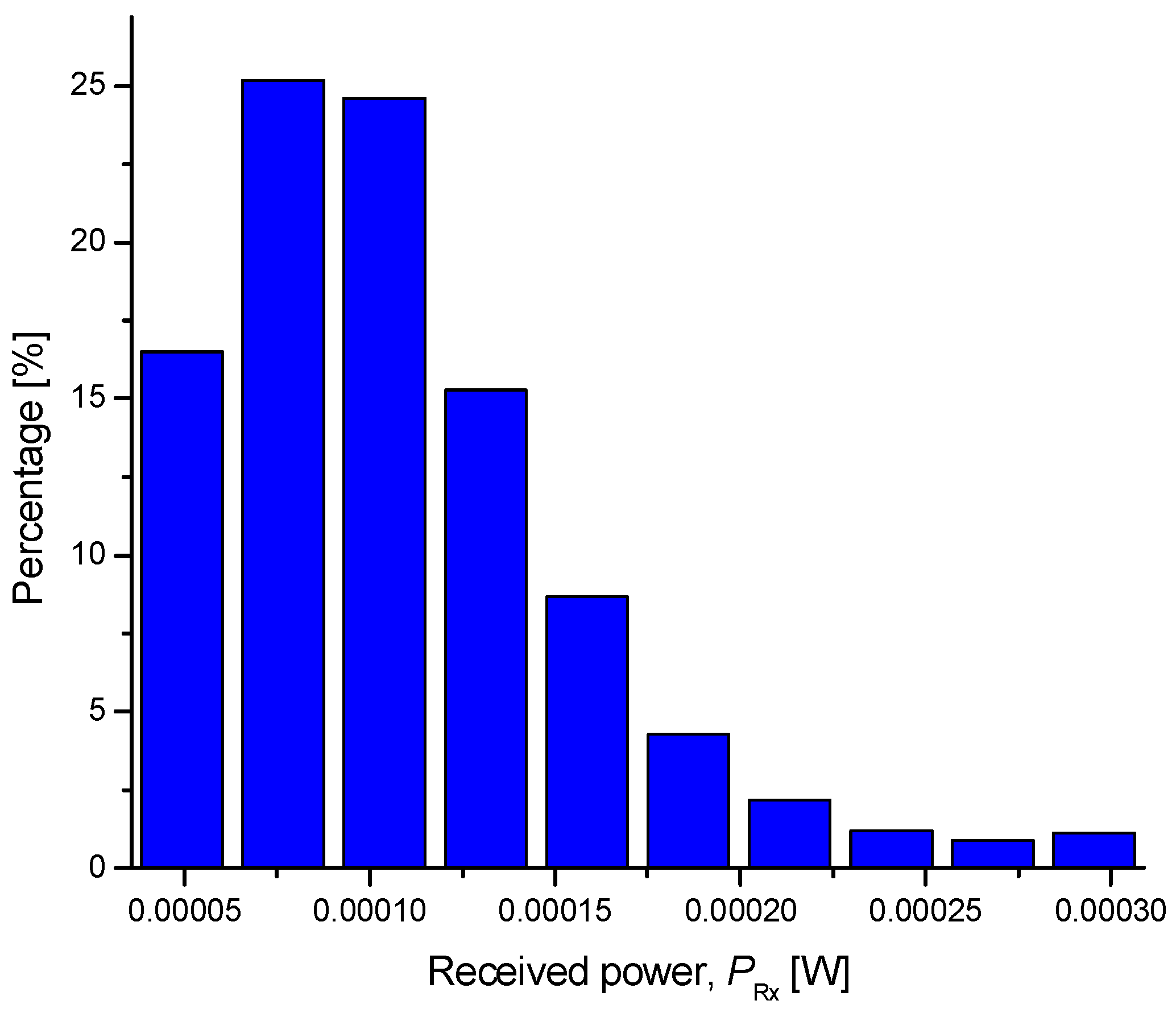
4. Experimental Results
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Djordjevic, I.B. Quantum Communication, Quantum Networks, and Quantum Sensing; Elsevier/Academic Press: London, UK; San Diego, CA, USA, 2022. [Google Scholar]
- Cariolaro, G. Quantum Communications; Springer International Publishing AG: Cham, Switzerland; Heidelberg, Germany, 2015. [Google Scholar]
- Djordjevic, I.B. Physical-Layer Security and Quantum Key Distribution; Springer International Publishing AG: Cham, Switzerland; Heidelberg, Germany, 2019. [Google Scholar]
- Hao, S.; Shi, H.; Gagatsos, C.N.; Mishra, M.; Bash, B.; Djordjevic, I.; Guha, S.; Zhuang, Q.; Zhang, Z. Demonstration of entanglement-enhanced covert sensing. Phys. Rev. Lett. 2022, 129, 010501. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, I.B. Quantum Information Processing, Quantum Computing, and Quantum Error Correction: An Engineering Approach, 2nd ed.; Elsevier/Academic Press: London, UK; San Diego, CA, USA, 2021. [Google Scholar]
- Liao, S.-K.; Cai, W.Q.; Liu, W.Y.; Zhang, L.; Li, Y.; Ren, J.G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Djordjevic, I.B. Four-dimensionally multiplexed eight-state continuous-variable quantum key distribution over turbulent channels. IEEE Photonics J. 2017, 9, 7600408. [Google Scholar] [CrossRef]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Villing, A.; Tualle-Brouri, R.; Grangier, P. Field test of a continuous-variable quantum key distribution prototype. New J. Phys. 2009, 11, 045023. [Google Scholar] [CrossRef]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Tualle-Brouri, R.; Grangier, P. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. B 2009, 42, 114014. [Google Scholar] [CrossRef]
- Djordjevic, I.B. On entanglement assisted classical optical communication with transmitter side optical phase-conjugation. IEEE Access 2021, 9, 168930–168936. [Google Scholar] [CrossRef]
- Nafria, V.; Djordjevic, I.B. Entanglement Assisted Communication over the Free-Space Optical Link with Azimuthal Phase Correction for Atmospheric Turbulence by Adaptive Optics. Opt. Express 2023, 31, 39906–39916. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, I.B.; Nafria, V. Entanglement Based Detection, Networking, Sensing, and Radars. IEEE Photonics J. 2024, 16, 7300610. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Seth, L. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Ralph, T.C. Continuous variable quantum cryptography. Phys. Rev. A 1999, 61, 010303. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous Variable Quantum Cryptography Using Coherent States. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- Silberhorn, C.; Ralph, T.C.; Lütkenhaus, N.; Leuchs, G. Continuous variable quantum cryptography: Beating the 3 dB Loss Limit. Phys. Rev. A 2002, 89, 167901. [Google Scholar] [CrossRef] [PubMed]
- Grosshans, F. Communication et Cryptographie Quantiques avec des Variables Continues. Ph.D. Thesis, Université Paris XI, Bière-sur-Yvette, France, 2002. [Google Scholar]
- Grosshans, F.; Cerf, N.J. Continuous-Variable Quantum Cryptography is Secure against Non-Gaussian Attacks. Phys. Rev. Lett. 2004, 92, 047905. [Google Scholar] [CrossRef] [PubMed]
- Grosshans, F.; Grangier, P. Reverse reconciliation protocols for quantum cryptography with continuous variables. arXiv 2022. [Google Scholar] [CrossRef]
- Grosshans, F.; Van Assche, G.; Wenger, J.; Tualle-Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using Gaussian-modulated coherent states. Nature 2003, 421, 238. [Google Scholar] [CrossRef] [PubMed]
- Grosshans, F. Collective attacks and unconditional security in continuous variable quantum key distribution. Phys. Rev. Lett. 2005, 94, 020504. [Google Scholar] [CrossRef] [PubMed]
- Heid, M.; Lütkenhaus, N. Efficiency of coherent-state quantum cryptography in the presence of loss: Influence of realistic error correction. Phys. Rev. A 2006, 73, 052316. [Google Scholar] [CrossRef]
- García-Patrón, R.; Cerf, N.J. Unconditional Optimality of Gaussian Attacks against Continuous-Variable Quantum Key Distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar] [CrossRef] [PubMed]
- Navascués, M.; Grosshans, F.; Acín, A. Optimality of Gaussian Attacks in Continuous-Variable Quantum Cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar] [CrossRef]
- Leverrier, A.; Grangier, P. Unconditional security proof of long-distance continuous-variable quantum key distribution with discrete modulation. Phys. Rev. Lett. 2009, 102, 180504. [Google Scholar] [CrossRef] [PubMed]
- Xuan, Q.; Zhang, Z.; Voss, P.L. A 24 km fiber-based discretely signaled continuous variable quantum key distribution system. Opt. Express 2009, 17, 24244–24249. [Google Scholar] [CrossRef] [PubMed]
- Becir, A.; El-Orany, F.A.A.; Wahiddin, M.R.B. Continuous-variable quantum key distribution protocols with eight-state discrete modulation. Int. J. Quantum Inform. 2012, 10, 1250004. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.; Zeng, G. Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 2016, 6, 19201. [Google Scholar] [CrossRef] [PubMed]
- Patel, K.A.; Dynes, J.F.; Choi, I.; Sharpe, A.W.; Dixon, A.R.; Yuan, Z.L.; Penty, R.V.; Shields, J. Coexistence of high-bit-rate quantum key distribution and data on optical fiber. Phys. Rev. X 2012, 2, 041010. [Google Scholar] [CrossRef]
- Nitin, J.; Chin, H.-M.; Mani, H.; Lupo, C.; Nikolic, D.S.; Kordts, A.; Pirandola, S.; Pedersen, T.B.; Kolb, M.; Ömer, B.; et al. Practical continuous-variable quantum key distribution with composable security. Nat. Commun. 2022, 13, 4740. [Google Scholar]
- Van Assche, G. Quantum Cryptography and Secret-Key Distillation; Cambridge University Press: Cambridge, NY, USA, 2006. [Google Scholar]
- Andrews, L.C.; Phillips, R.L.; Young, C.Y. Laser Beam Scintillation with Applications; SPIE Publications: Bellingham, WA, USA, 2001. [Google Scholar]
- Djordjevic, I.B. Advanced Optical and Wireless Communications Systems, 2nd ed.; Springer Nature Switzerland AG: Cham, Switzerland, 2022. [Google Scholar]
- Tyson, R.H. Principles of Adaptive Optics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lukin, V.P.; Fortes, B.V. Adaptive Beaming and Imaging in the Turbulent Atmosphere; SPIE Press: Bellingham, WA, USA, 2002. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djordjevic, I.B.; Nafria, V. Entanglement-Based CV-QKD with Information Reconciliation over Entanglement-Assisted Link. Entropy 2024, 26, 305. https://doi.org/10.3390/e26040305
Djordjevic IB, Nafria V. Entanglement-Based CV-QKD with Information Reconciliation over Entanglement-Assisted Link. Entropy. 2024; 26(4):305. https://doi.org/10.3390/e26040305
Chicago/Turabian StyleDjordjevic, Ivan B., and Vijay Nafria. 2024. "Entanglement-Based CV-QKD with Information Reconciliation over Entanglement-Assisted Link" Entropy 26, no. 4: 305. https://doi.org/10.3390/e26040305
APA StyleDjordjevic, I. B., & Nafria, V. (2024). Entanglement-Based CV-QKD with Information Reconciliation over Entanglement-Assisted Link. Entropy, 26(4), 305. https://doi.org/10.3390/e26040305






