Efficient Constant Envelope Precoding for Massive MU-MIMO Downlink via Majorization-Minimization Method
Abstract
:1. Introduction
- One of the main challenges in solving the CE precoding problem is the interdependence between the CE precoded signal and the precoding factor. To address this problem, we employ a two-stage iterative procedure involving an alternating minimization (AltMin) framework. When addressing the CE precoded signal, the CE constraint is simplified and transformed into unit modulus constraints by introducing an auxiliary variable. Additionally, the unit modulus constraint is converted to continuous by adding a penalty term to the objective function.
- The optimal precoded signal is obtained using the majorization-minimization (MM) framework. In the MM framework, the key is how to construct the surrogate function. We exploit the channel characteristics of massive MU-MIMO systems and combine them with a second-order Taylor expansion to obtain an efficient surrogate function. Unlike the one-step GEMM method described in [14], we obtain the precise values of the auxiliary variables through multiple iterations. In addition, we derive the L-Lipschiz constant and analyze the exact property, convergence, and computational complexity of the proposed algorithm.
- The proposed method is extended to DCE precoding schemes that have finite phase resolution. At first, we manipulate the continuous phase of the CE signal to align with the PSK constellation by performing a straightforward rotation. Then, we employ algebraic knowledge to derive the DCE precoded signal by making secondary decisions.
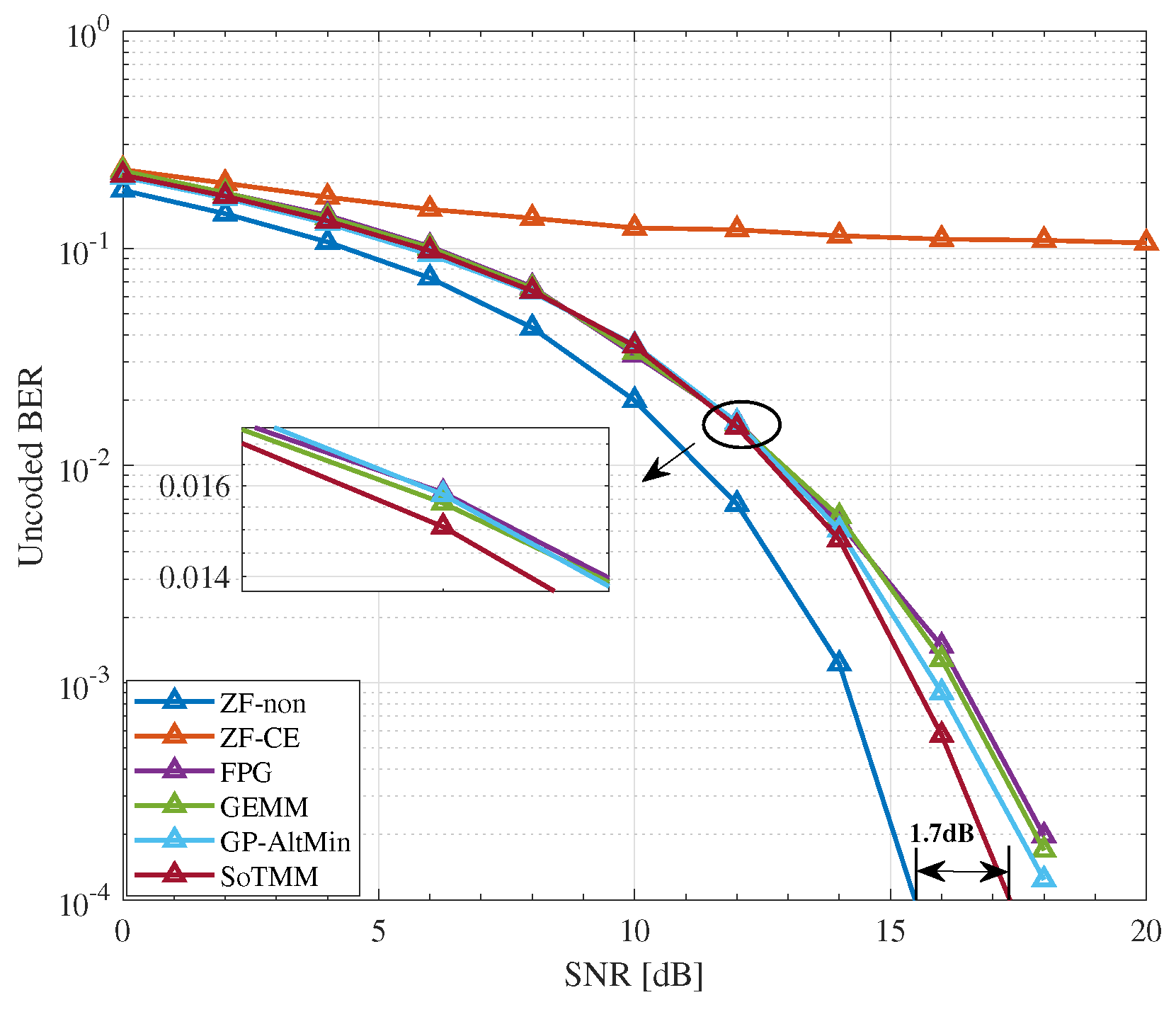
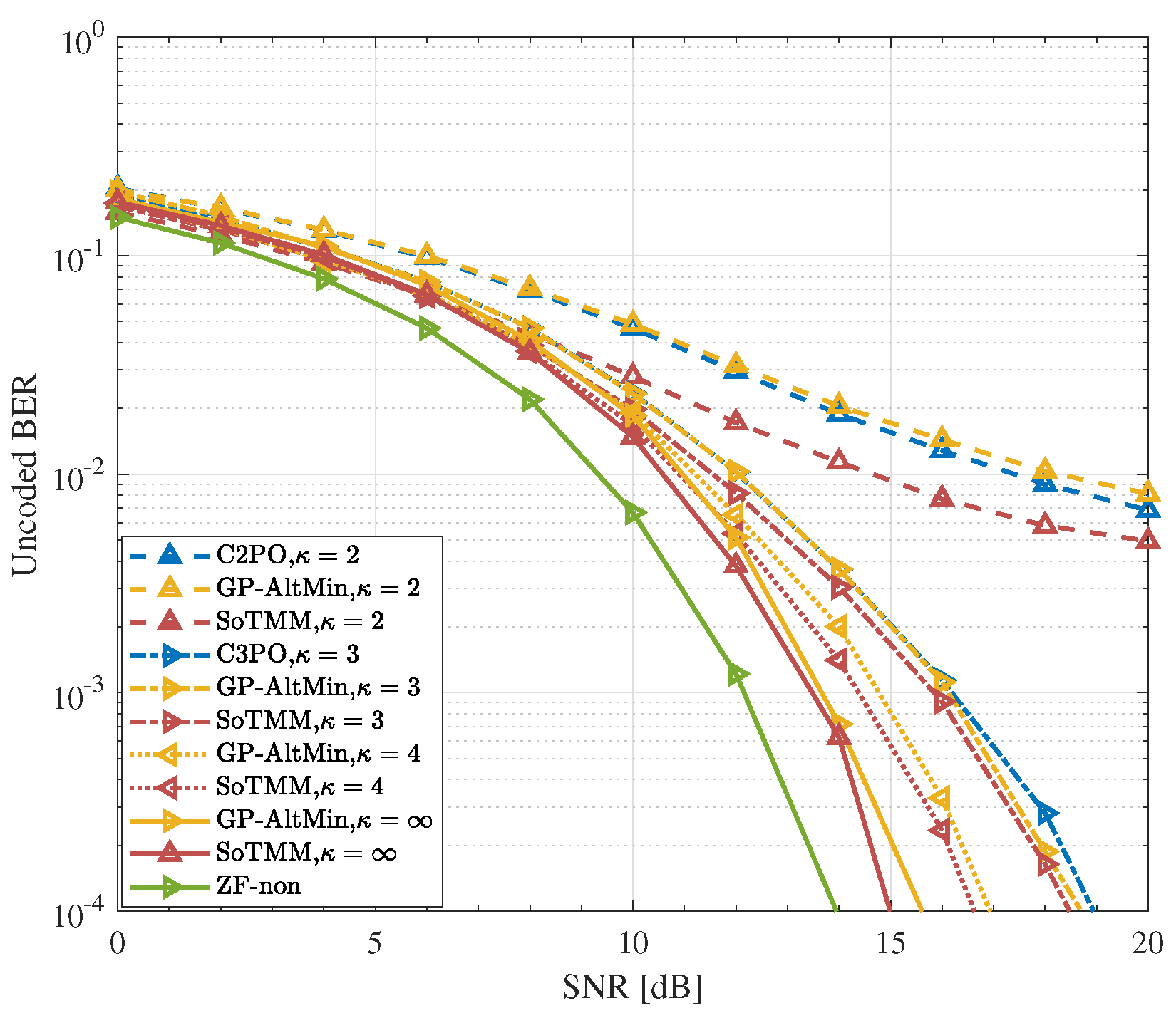
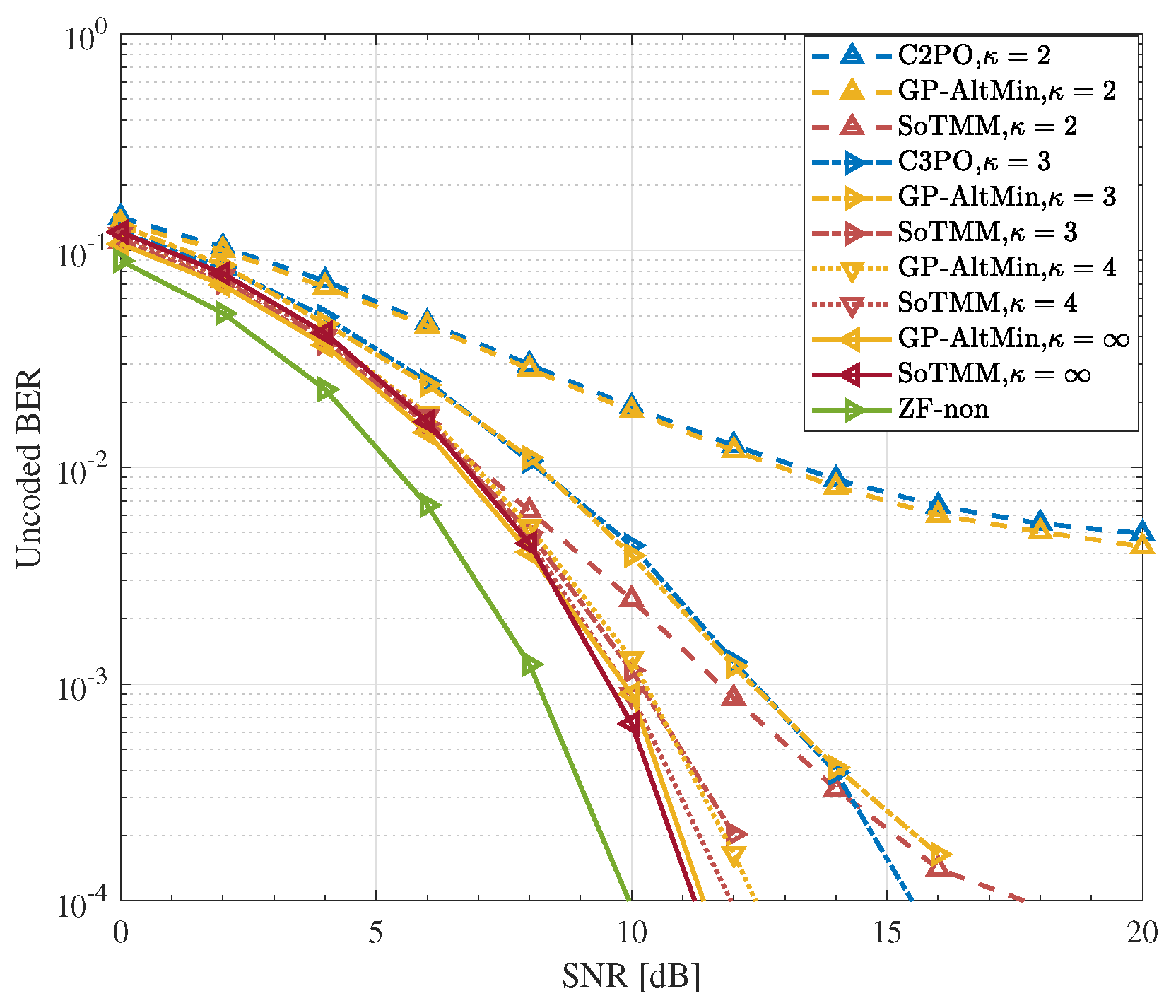
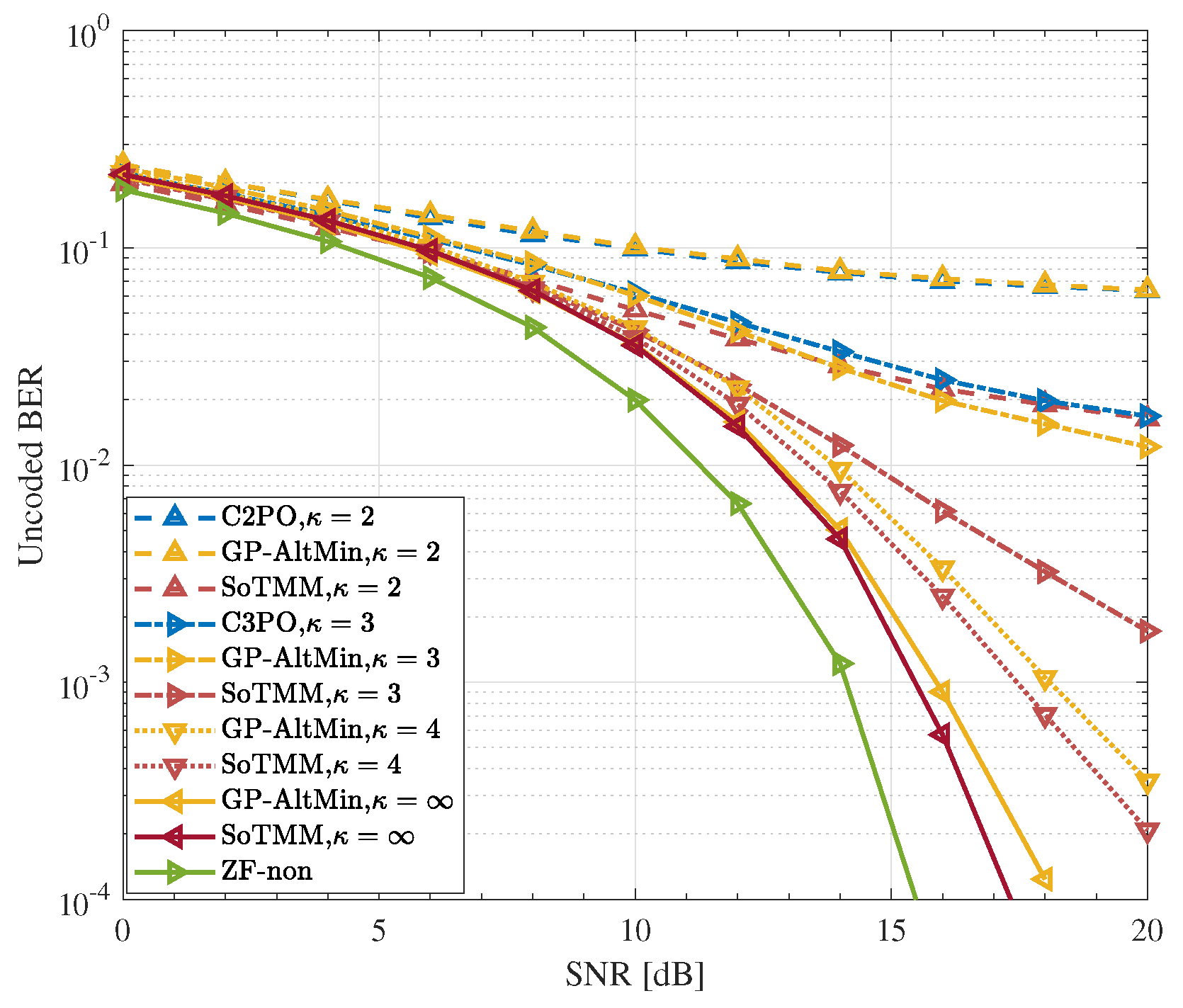
- Simulation results demonstrate that in the CE precoding case, the proposed algorithm exhibits superior uncoded BER performance and a lower computational complexity when compared to existing approaches. In both PSK modulation and QAM modulation, the suggested CE precoding method can achieve a performance gain of about . In the 3-phase case, the proposed algorithm also has better performance.
2. System Model and Problem Formulation
2.1. System Model
2.2. Problem Formulation
3. Majorization-Minimization Method for Constant Envelope Precoding
3.1. Surrogate Function Using Second-Order Taylor Expansion
3.2. MM Method for Solving CE Precoding
| Algorithm 1 SoTMM method for solving problem (5) |
|
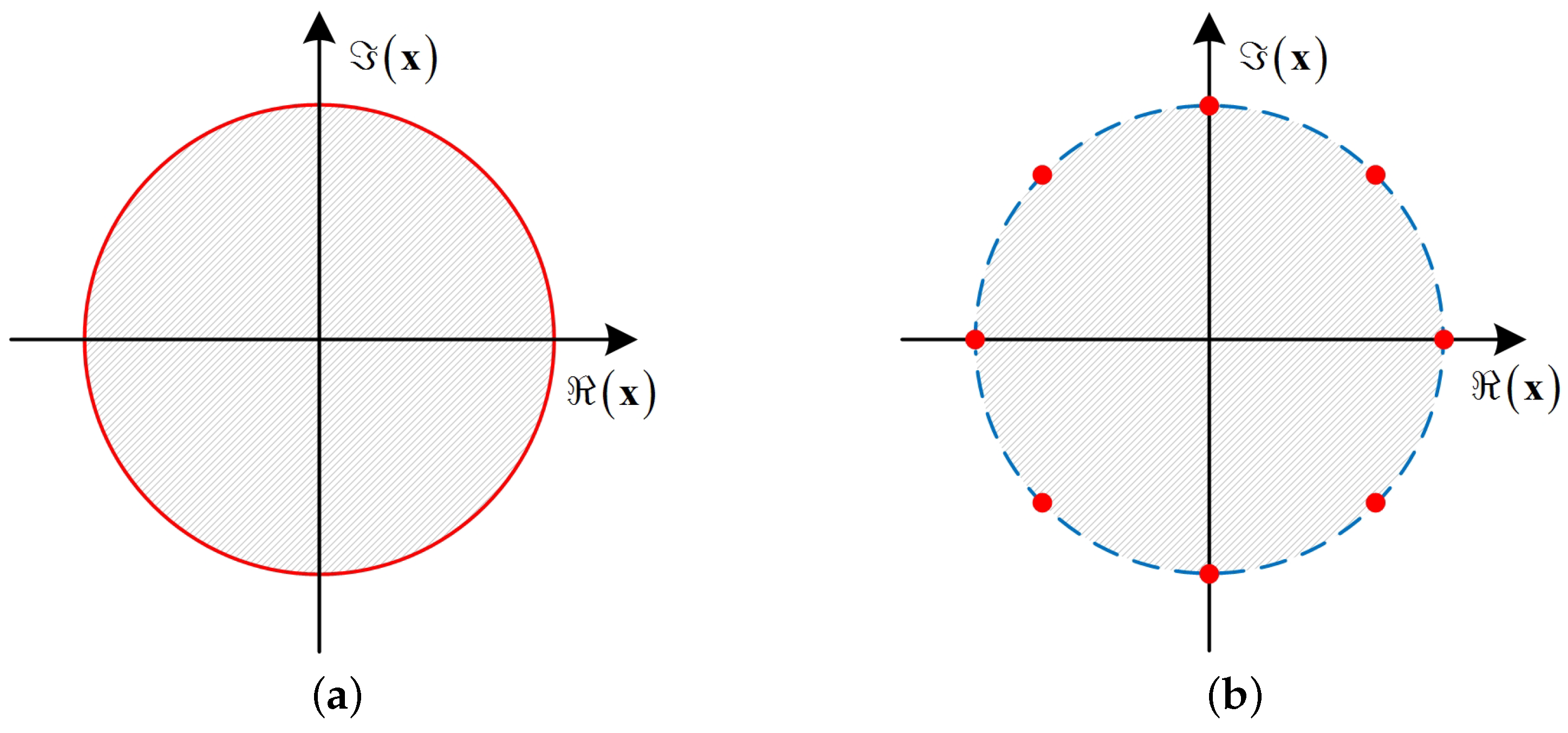
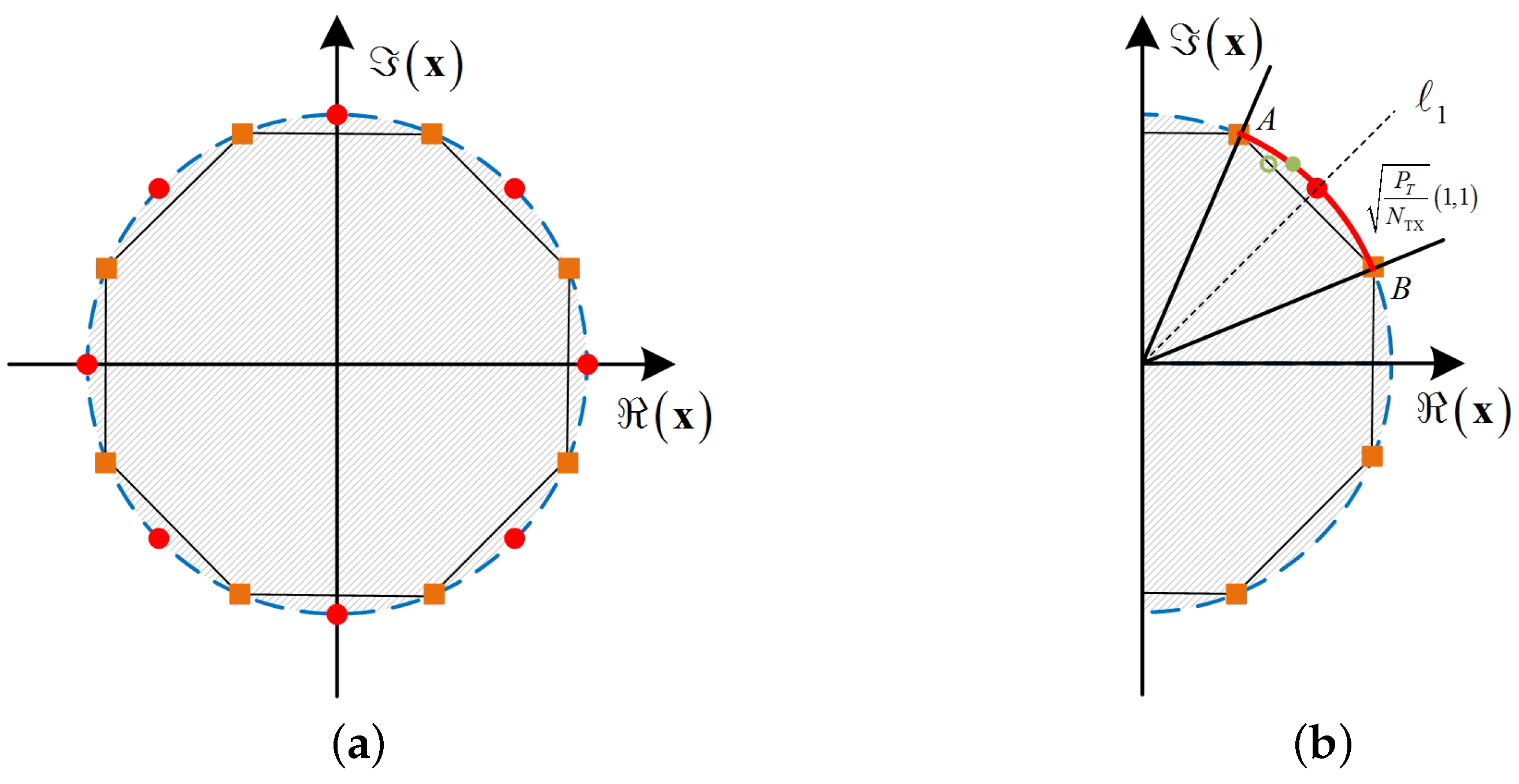
3.3. DCE Precoding
4. Performance Analysis
4.1. The Exact Property of Problem (10)
4.2. Convergence Analysis
4.3. Complexity Analysis
5. Simulation Results and Discussions
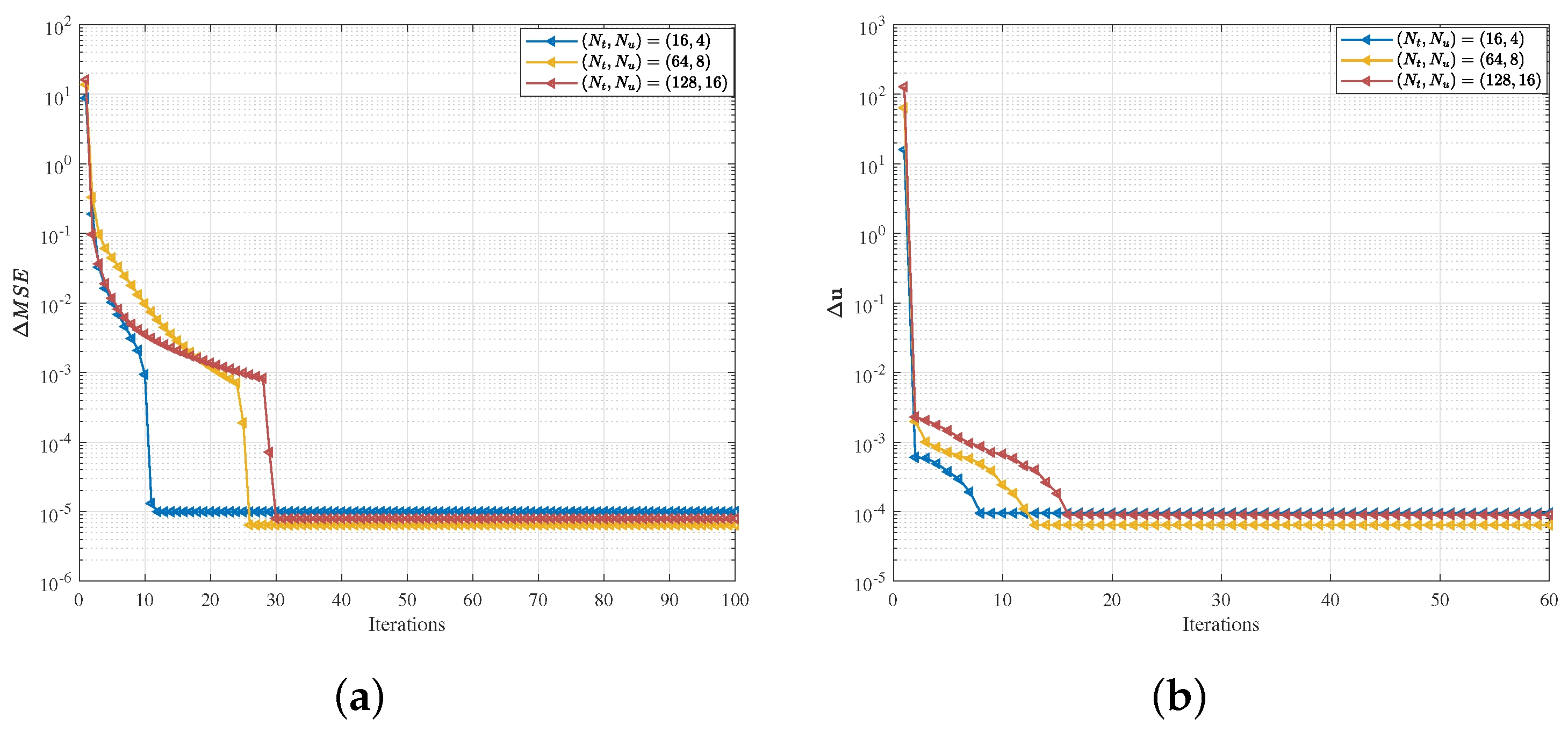
5.1. Convergence Analysis
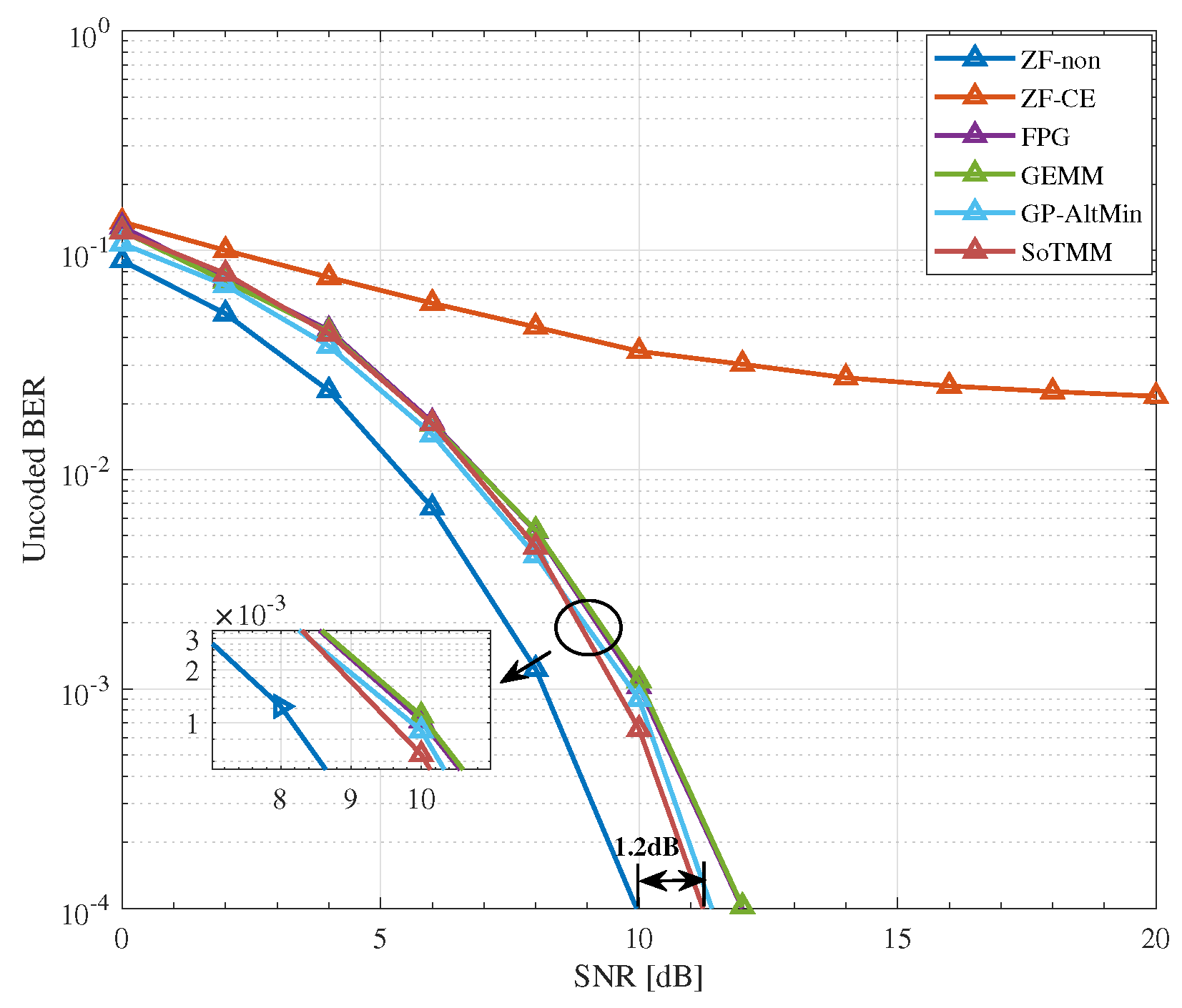
5.2. CE Precoding
5.3. DCE Precoding
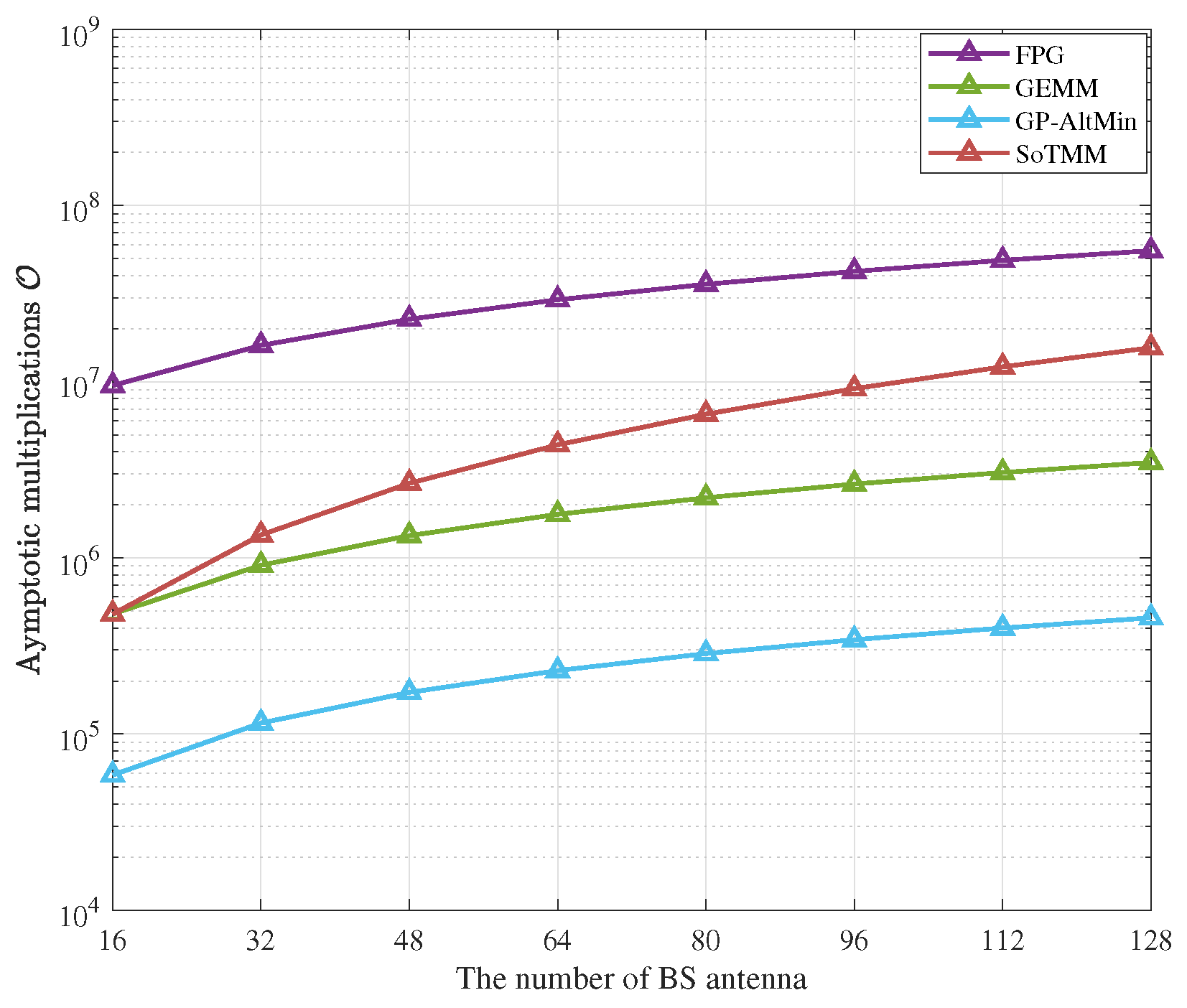
5.4. Complexity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 2
Appendix B. Proof of Theorem 2
References
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.Y.; Swindlehurst, A.L.; Ashikhmin, A.; Zhang, R. An overview of massive MIMO: Benefits and challenges. IEEE J. Sel. Top. Signal Process. 2014, 8, 742–758. [Google Scholar] [CrossRef]
- Rezaei, F.; Tadaion, A. Multi-layer beamforming in uplink/downlink massive MIMO systems with multi-antenna users. Signal Process. 2019, 164, 58–66. [Google Scholar] [CrossRef]
- Li, A.; Spano, D.; Krivochiza, J.; Domouchtsidis, S.; Tsinos, C.G.; Masouros, C.; Chatzinotas, S.; Li, Y.; Vucetic, B.; Ottersten, B. A tutorial on interference exploitation via symbol-level precoding: Overview, state-of-the-art and future directions. IEEE Commun. Surv. Tutor. 2020, 22, 796–839. [Google Scholar] [CrossRef]
- Mohammed, S.K.; Larsson, E.G. Single-user beamforming in large-scale MISO systems with per-antenna constant-envelope constraints: The doughnut channel. IEEE Trans. Wirel. Commun. 2012, 11, 3992–4005. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R.; Lim, T.J. MISO multicasting with constant envelope precoding. IEEE Wirel. Commun. Lett. 2016, 5, 588–591. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R.; Lim, T.J. Constant envelope precoding for MIMO systems. IEEE Trans. Commun. 2018, 66, 149–162. [Google Scholar] [CrossRef]
- Mohammed, S.K.; Larsson, E.G. Per-antenna constant envelope precoding for large multi-user MIMO systems. IEEE Trans. Commun. 2013, 61, 1059–1071. [Google Scholar] [CrossRef]
- Chen, J.C.; Wen, C.K.; Wong, K.K. Improved constant envelope multiuser precoding for massive MIMO systems. IEEE Commun. Lett. 2014, 18, 1311–1314. [Google Scholar] [CrossRef]
- Chen, J.C. Efficient constant envelope precoding with quantized phases for massive MU-MIMO downlink systems. IEEE Trans. Veh. Technol. 2019, 68, 4059–4063. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R.; Lim, T.J. Constant envelope precoding with adaptive receiver constellation in MISO fading channel. IEEE Trans. Wirel. Commun. 2016, 15, 6871–6882. [Google Scholar] [CrossRef]
- Shao, M.; Li, Q.; Ma, W.K.; So, A.M.C. Minimum symbol error rate-based constant envelope precoding for multiuser massive MISO downlink. In Proceedings of the IEEE Statistical Signal Processing Workshop, SSP, Freiburg im Breisgau, Germany, 10–13 June 2018; pp. 727–731. [Google Scholar]
- Shao, M.; Li, Q.; Ma, W.K.; So, A.M.C. A framework for one-bit and constant-envelope precoding over multiuser massive MISO channels. IEEE Trans. Signal Process. 2019, 67, 5309–5324. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, N.; Liu, F.; Li, A.; Zhou, J.; Masouros, C. Constant Envelope Precoding With Extended Degrees of Freedom Through Per-User Symbol Scaling. IEEE Commun. Lett. 2021, 25, 1620–1624. [Google Scholar] [CrossRef]
- Amadori, P.V.; Masouros, C. Constant envelope precoding by interference exploitation in phase shift keying-modulated multiuser transmission. IEEE Trans. Wirel. Commun. 2017, 16, 538–550. [Google Scholar] [CrossRef]
- Amadori, P.V.; Masouros, C. Constructive interference based constant envelope precoding. In Proceedings of the 2016 IEEE 17th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Edinburgh, UK, 3–6 July 2016; pp. 1–5. [Google Scholar]
- Liu, F.; Masouros, C.; Amadori, P.V.; Sun, H. An efficient manifold algorithm for constructive interference based constant envelope precoding. IEEE Signal Process. Lett. 2017, 24, 1542–1546. [Google Scholar] [CrossRef]
- Noll, A.; Jedda, H.; Nossek, J. PSK precoding in multi-user MISO systems. In Proceedings of the 1th IWSA—International ITG Workshop Smart Antennas, Berlin, Germany, 15–17 March 2017; pp. 1–7. [Google Scholar]
- Nedelcu, A.; Steiner, F.; Staudacher, M.; Kramer, G.; Zirwas, W.; Ganesan, R.S.; Baracca, P.; Wesemann, S. Quantized precoding for multi-antenna downlink channels with MAGIQ. In Proceedings of the WSA 2018; 22nd International ITG Workshop on Smart Antennas, Bochum, Germany, 14–16 March 2018; pp. 1–8. [Google Scholar]
- Jedda, H.; Mezghani, A.; Swindlehurst, A.L.; Nossek, J.A. Quantized constant envelope precoding with PSK and QAM signaling. IEEE Trans. Wirel. Commun. 2018, 17, 8022–8034. [Google Scholar] [CrossRef]
- Jacobsson, S.; Durisi, G.; Coldrey, M.; Goldstein, T.; Studer, C. Quantized precoding for massive MU-MIMO. IEEE Trans. Commun. 2017, 65, 4670–4684. [Google Scholar] [CrossRef]
- Jacobsson, S.; Durisi, G.; Coldrey, M.; Goldstein, T.; Studer, C. Nonlinear 1-bit precoding for massive MU-MIMO with higher-order modulation. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 763–767. [Google Scholar]
- Castañeda, O.; Jacobsson, S.; Durisi, G.; Coldrey, M.; Goldstein, T.; Studer, C. 1-bit massive MU-MIMO precoding in VLSI. IEEE J. Emer. Select. Top. Circu. Syste. 2017, 7, 508–522. [Google Scholar] [CrossRef]
- Waldspurger, I.; d’Aspremont, A.; Mallat, S. Phase recovery, maxcut and complex semidefinite programming. Math. Program. 2015, 149, 47–81. [Google Scholar] [CrossRef]
- So, A.M.C.; Zhang, J.; Ye, Y. On approximating complex quadratic optimization problems via semidefinite programming relaxations. Math. Program. 2007, 110, 93–110. [Google Scholar] [CrossRef]
- Luo, Z.Q.; Ma, W.K.; So, A.M.C.; Ye, Y.; Zhang, S. Semidefinite relaxation of quadratic optimization problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Shao, M.; Dai, Q.; Ma, W.K. Extreme-Point Pursuit for Unit-Modulus Optimization. In Proceedings of the ICASSP IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 23–27 May 2022; pp. 5548–5552. [Google Scholar]
- Tranter, J.; Sidiropoulos, N.D.; Fu, X.; Swami, A. Fast unit-modulus least squares with applications in beamforming. IEEE Trans. Signal Process. 2017, 65, 2875–2887. [Google Scholar] [CrossRef]
- Fan, J.; Han, F.; Liu, H. Challenges of big data analysis. Natl. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Babu, P.; Palomar, D.P. Majorization-minimization algorithms in signal processing, communications, and machine learning. IEEE Trans. Signal Process. 2016, 65, 794–816. [Google Scholar] [CrossRef]
- Hunter, D.R.; Lange, K. A tutorial on MM algorithms. Am. Stat. 2004, 58, 30–37. [Google Scholar] [CrossRef]
- Lange, K. MM Optimization Algorithms; SIAM: Philadelphia, PA, USA, 2016. [Google Scholar]
- Song, J.; Babu, P.; Palomar, D.P. Optimization methods for designing sequences with low autocorrelation sidelobes. IEEE Trans. Signal Process. 2015, 63, 3998–4009. [Google Scholar] [CrossRef]
- Arora, A.; Tsinos, C.G.; Rao, B.S.M.R.; Chatzinotas, S.; Ottersten, B. Hybrid transceivers design for large-scale antenna arrays using majorization-minimization algorithms. IEEE Trans. Signal Process. 2019, 68, 701–714. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Haqiqatnejad, A.; Kayhan, F.; ShahbazPanahi, S.; Ottersten, B. Finite-Alphabet Symbol-Level Multiuser Precoding for Massive MU-MIMO Downlink. IEEE Trans. Signal Process. 2021, 69, 5595–5610. [Google Scholar] [CrossRef]
- Pedregal, P. Introduction to Optimization; Springer: Berlin/Heidelberg, Germany, 2004; Volume 46. [Google Scholar]
- Martinet, B. Regularisation d’inequations variationelles par approximations successives. Rev. Fr. D’informatique Rech. Oper. 1970, 4, 154–159. [Google Scholar]
- Xu, Y.; Yin, W. A block coordinate descent method for regularized multiconvex optimization with applications to nonnegative tensor factorization and completion. SIAM J. Imaging Sci. 2013, 6, 1758–1789. [Google Scholar] [CrossRef]


| Methods | Maximum Iterations | Computational Complexity |
|---|---|---|
| FPG | ||
| GEMM | ||
| GP-AltMin | , | |
| SoTMM | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, R.; Li, H.; Dong, Y.; Xue, G. Efficient Constant Envelope Precoding for Massive MU-MIMO Downlink via Majorization-Minimization Method. Entropy 2024, 26, 349. https://doi.org/10.3390/e26040349
Liang R, Li H, Dong Y, Xue G. Efficient Constant Envelope Precoding for Massive MU-MIMO Downlink via Majorization-Minimization Method. Entropy. 2024; 26(4):349. https://doi.org/10.3390/e26040349
Chicago/Turabian StyleLiang, Rui, Hui Li, Yingli Dong, and Guodong Xue. 2024. "Efficient Constant Envelope Precoding for Massive MU-MIMO Downlink via Majorization-Minimization Method" Entropy 26, no. 4: 349. https://doi.org/10.3390/e26040349
APA StyleLiang, R., Li, H., Dong, Y., & Xue, G. (2024). Efficient Constant Envelope Precoding for Massive MU-MIMO Downlink via Majorization-Minimization Method. Entropy, 26(4), 349. https://doi.org/10.3390/e26040349





