Elicitation of Rank Correlations with Probabilities of Concordance: Method and Application to Building Management
Abstract
:1. Introduction
2. Material and Methods
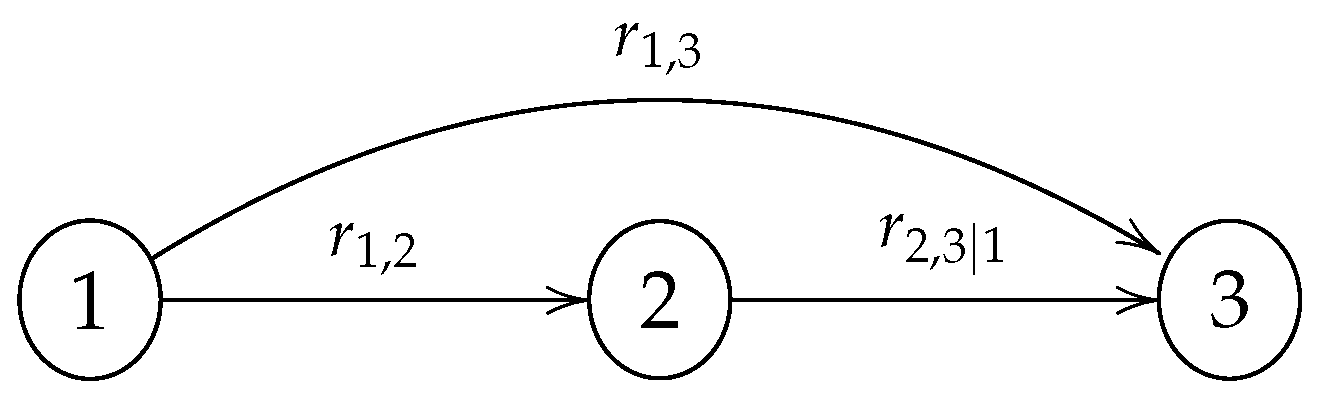
2.1. Gaussian Copula-Based Bayesian Networks
- 1.
- A directed acyclic graph (DAG) with n nodes specifying conditional independence relationships in a BBN;
- 2.
- n variables , assigned to the nodes, with continuous invertible distribution functions;
- 3.
- The specification (2), i = 1, …, n, of conditional rank correlations on the arcs of the BBN;
- 4.
- A copula realizing all correlations [−1, 1] for which correlation 0 entails independence.
2.2. Dependence Assessment
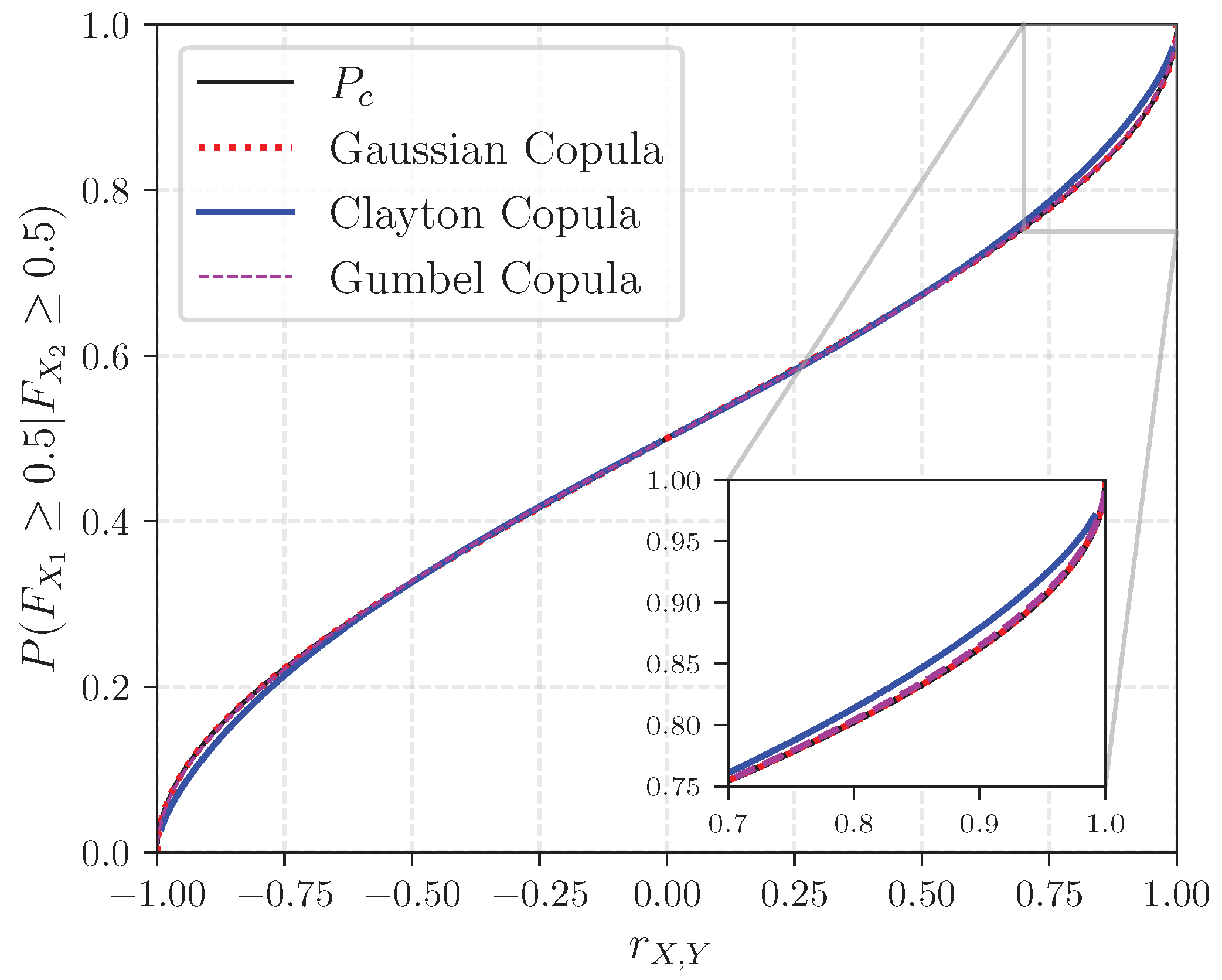
2.2.1. Concordance Probabilities
“Two individuals A and B are randomly selected among Dutch males between 18 and 50 years old. Given that B is taller than A , what is the probability that B weighs more than A ?”
- The expert assesses the probability of concordance ;
- is converted to an unconditional rank correlation using Equations (5)–(7);
- The correlation coefficient is logged into Matlatzinca. If the respondent’s answer is mathematically acceptable, move to the next question and go back to step 1;
- Else, the expert is given the mathematically valid range for . Because this range is directly affected by their answers to the previous questions, the experts may review and modify previous answers accordingly.
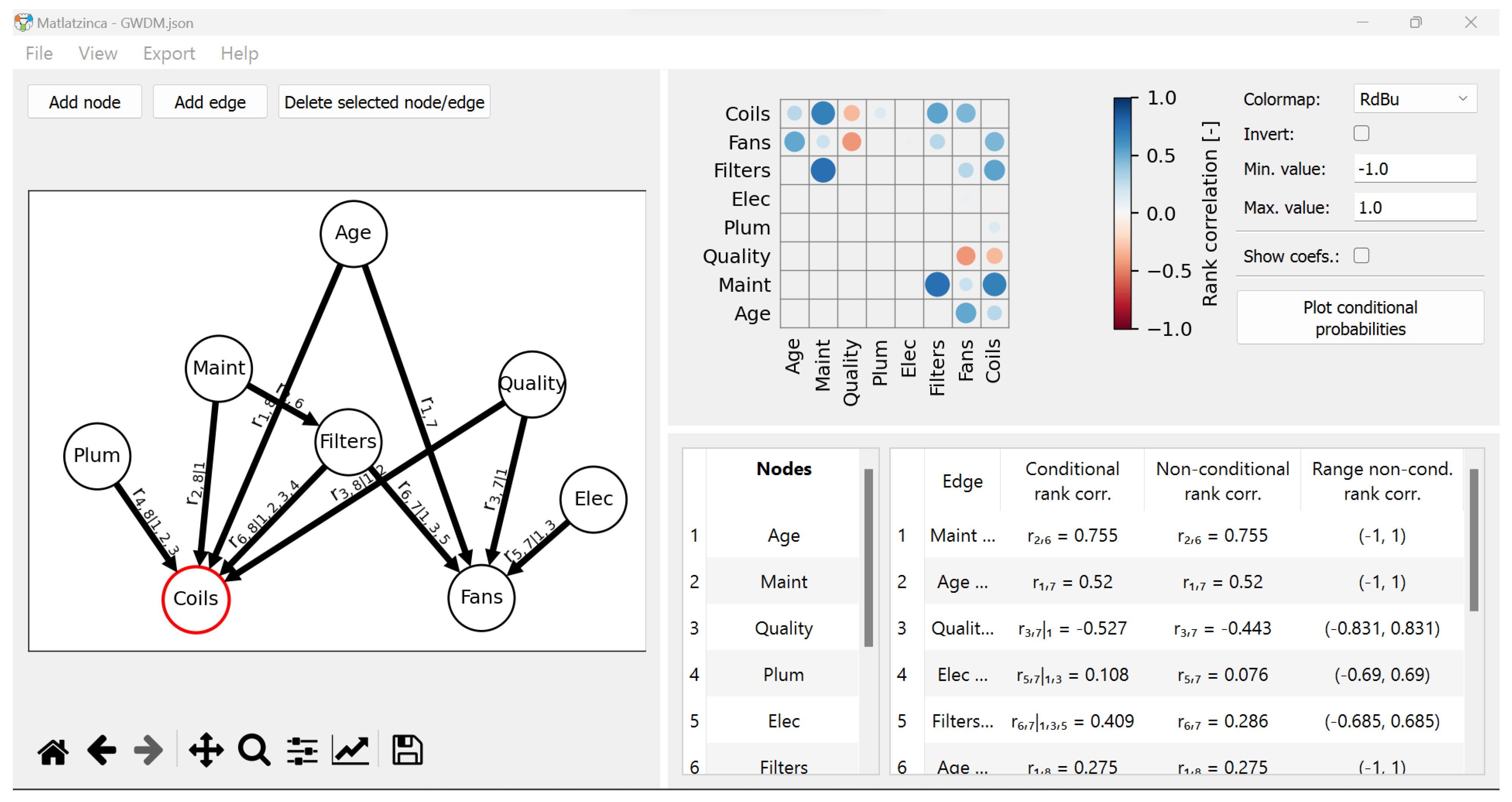
2.2.2. Software
- The drawing panel. This is where the DAG representing the dependence structure of the BN is drawn. Notice that, as discussed in Section 2.1, the arcs provide information regarding the ordering of parents in the DAG.
- The input panel. It contains, on the left-hand side, the labels of the Nodes displayed in the drawing panel, which can be edited by the user. On the right-hand side, it presents the Edges and related measures of dependence. For the quantification of the arcs, users have two input options: Spearman’s conditional rank correlations (Conditional rank corr.) as well as unconditional rank correlations (Non-conditional rank corr.). The last column indicates the range of acceptable unconditional rank correlations, briefly discussed at the end of the previous section, which depends on the structure of the DAG and other values of the correlations. This column is updated as users provide values of (un)conditional rank correlations.
- The correlation matrix panel. In addition to their numerical value, each correlation coefficient is displayed with a circle whose diameter is proportional to its absolute value, and a colormap indicating the position of the coefficient on the [−1, 1] scale.
2.3. Dependence Calibration
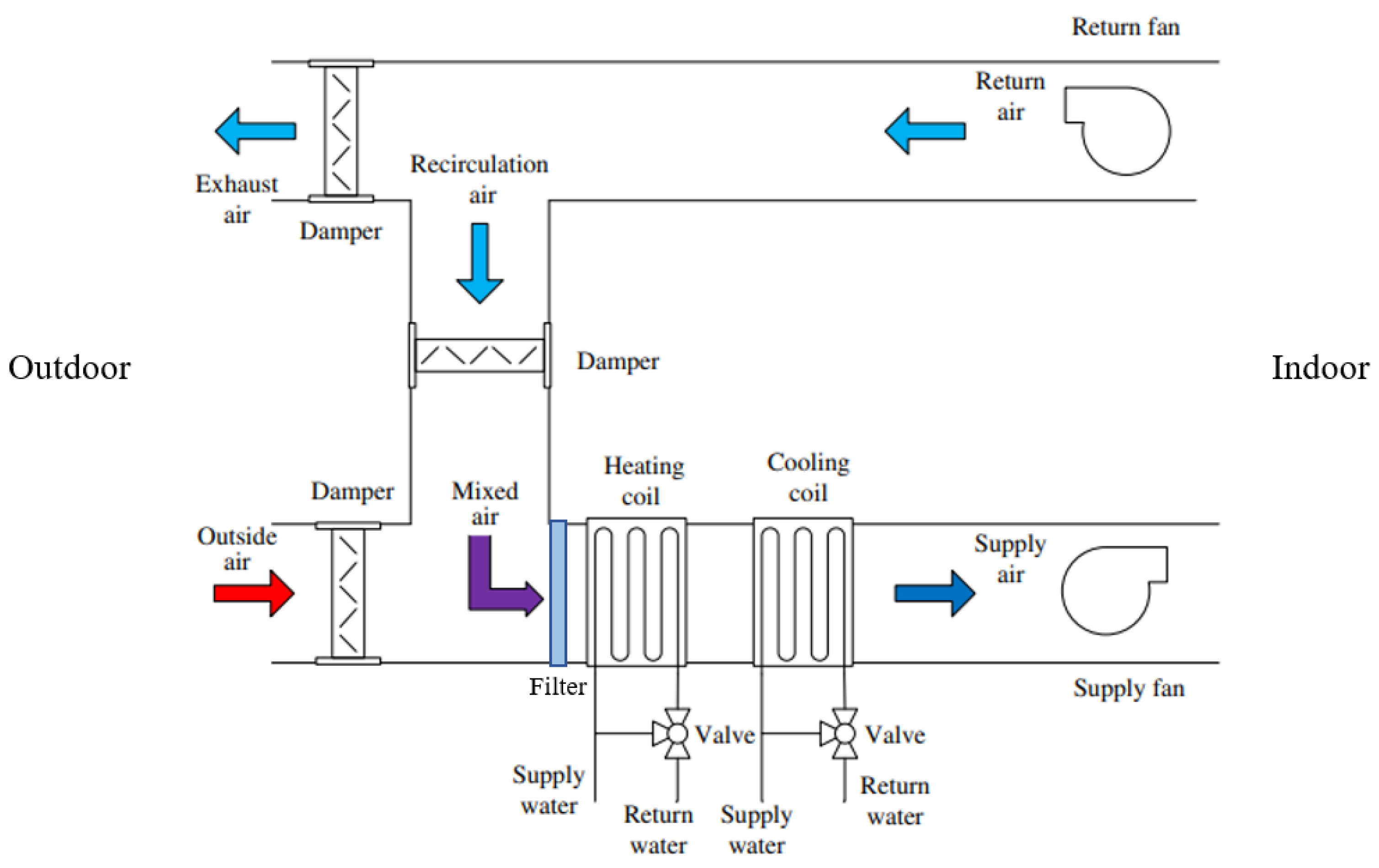
3. Case Study
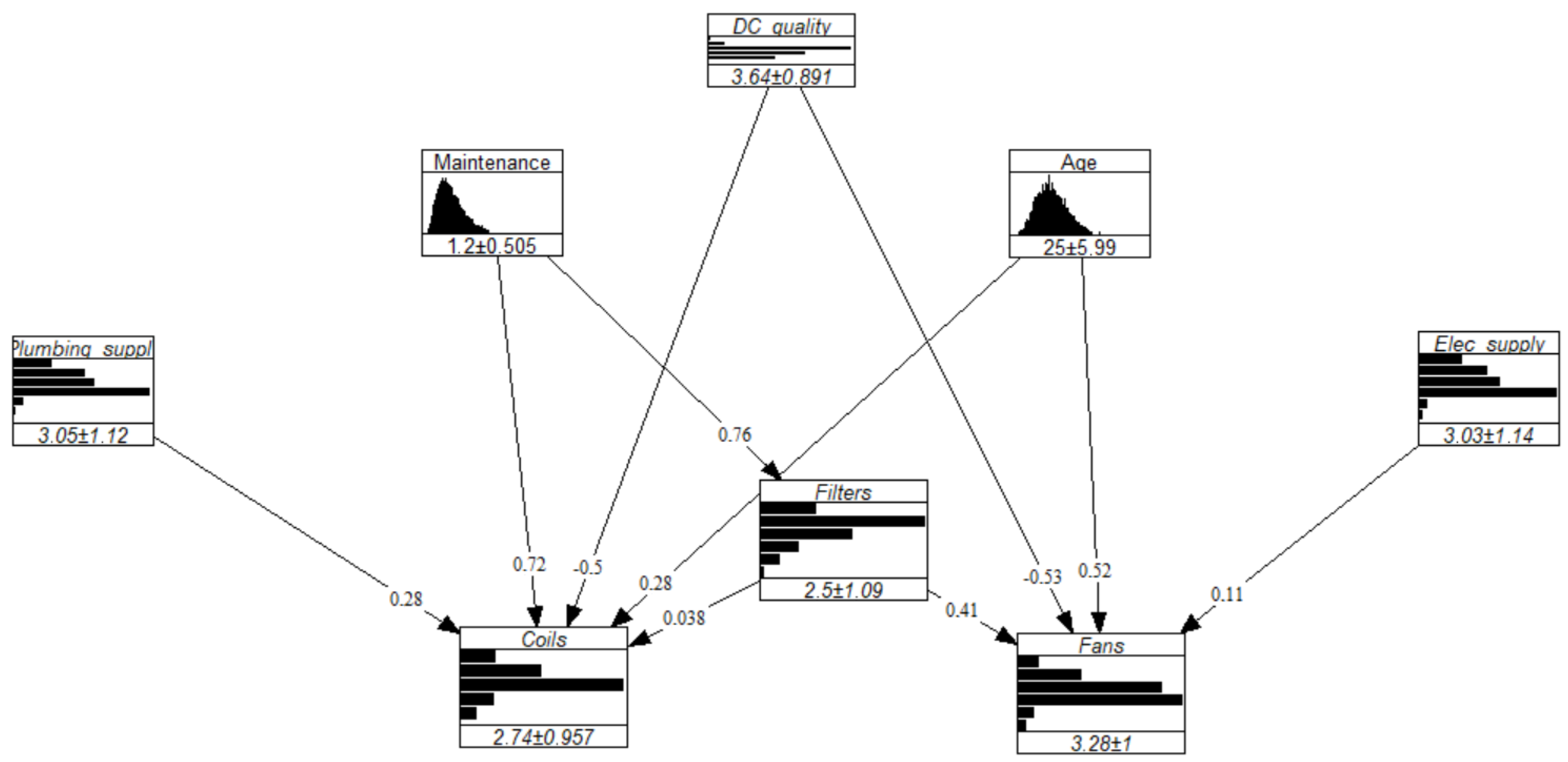
3.1. Graph Structure
- Because of their comparatively short lifespan, the condition of the filters and the coils are exclusively affected by the maintenance interval, i.e., Maintenance interval → Filters and Maintenance interval → Coils.
- The condition of the plumbing supply system (boiler, chiller) affects the coils as these elements are functionally interdependent: the warm or chilled water (or other fluid) from the plumbing system supplies the coils, i.e., Plumbing supply → Coils. Likewise, the electrical supply system exclusively interacts with the fans, i.e., Electrical supply→ Fans.
- Since the filters are responsible for reducing the number of particles entering the AHU, their failure allows for the accumulation of particles on the coils and thus speeds up their deterioration by corrosion, i.e., Filters → Coils.
- The condition of the fans can be impacted by the filters in at least two ways. First, polluted filters oblige the fans to exert more power to maintain the same perceived airflow. Secondly, particles that enter the AHU partially flow through the ducts where they accumulate, thus leading to reduced airflow and additional stress on the fans. Clearly, then, these components are interdependent, i.e., Filters → Fans.
- The AHU’s age and the Design & Construction quality of the installation both directly affect the coils and fans, i.e., AHU Age → Coils, AHU Age → Fans, Design & Construction quality → Coils, and Design & Construction quality → Fans.
3.2. Quantification: Experts’ Judgments
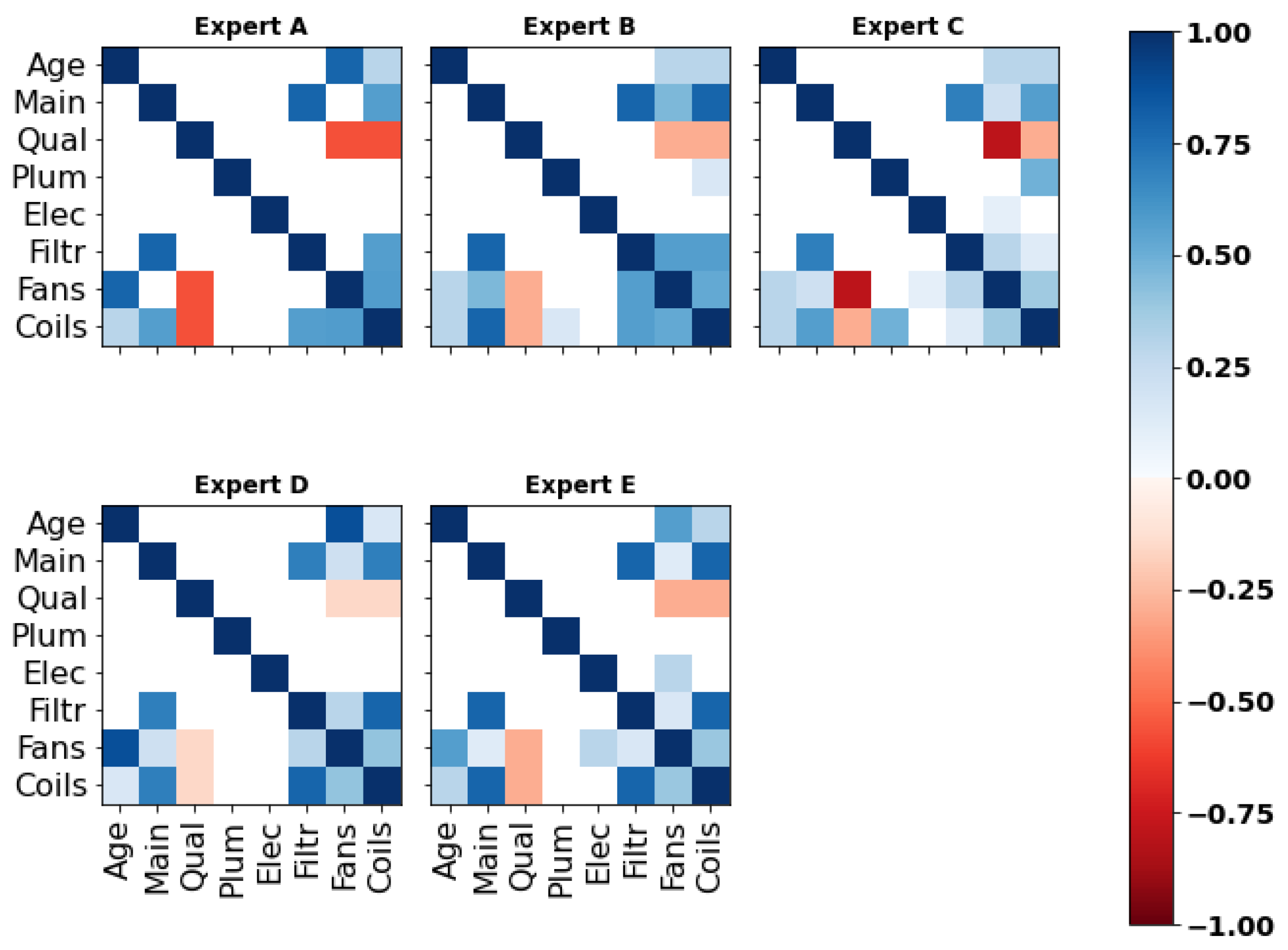
3.2.1. Individual Assessments
“Two buildings A and B are randomly selected among all non-residential buildings in the Netherlands. Given that the air handling unit in building A is more recent than in building B , what is the probability that the fans are in better condition in building A than in building B ?”
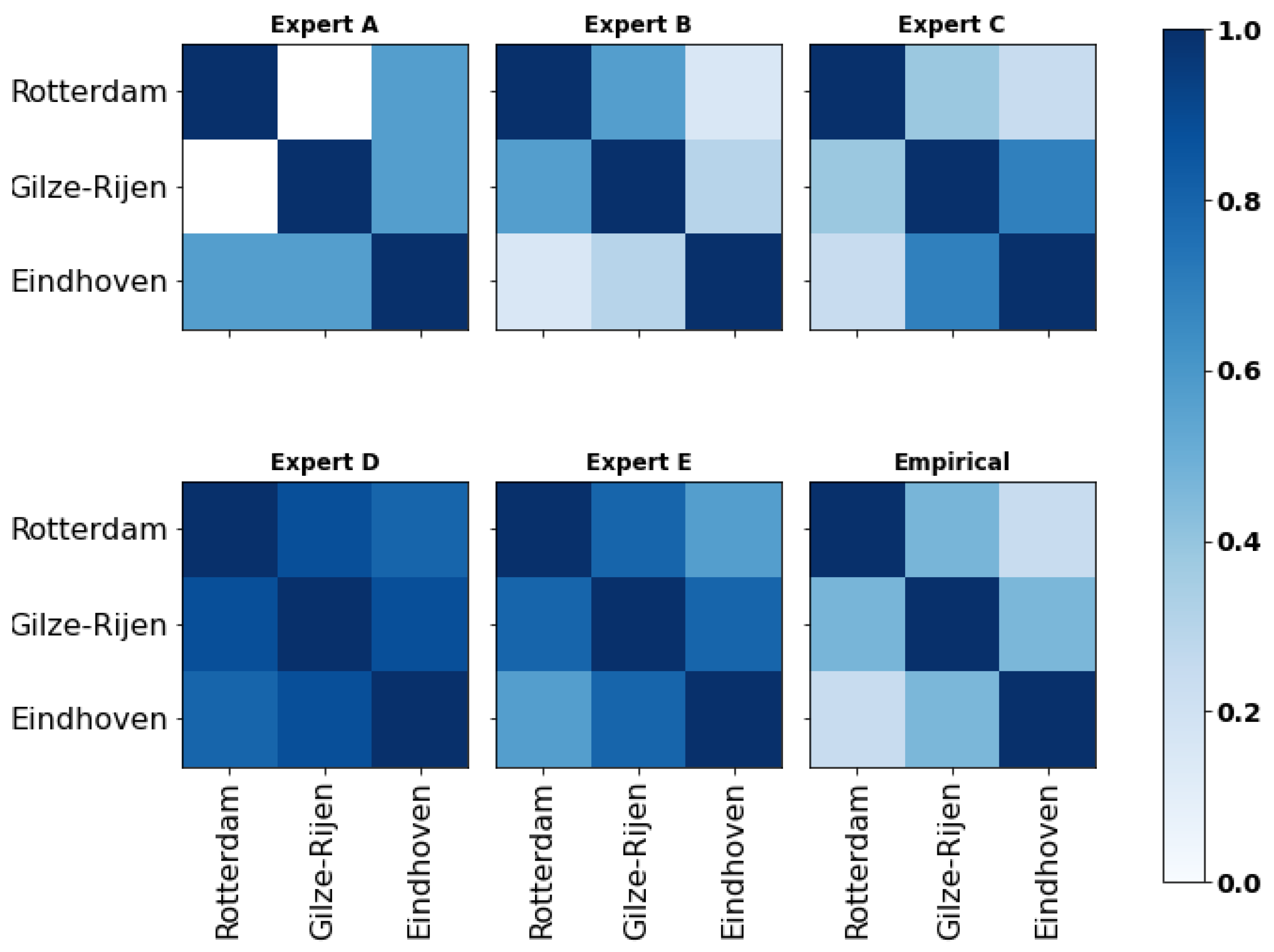
3.2.2. Aggregation
“Two moments H1 and H2 (defined by the hour) are taken randomly between the 1 January 2023 and the 18 June 2023. Given that the hourly precipitation is higher at H2 than at H1 in Gilze-Rijen, what is the probability that the hourly precipitation is also higher at H2 than at H1 in Rotterdam?”
3.2.3. Marginal Distributions
4. Results
4.1. Dependence Structure
4.1.1. Individual Assessments
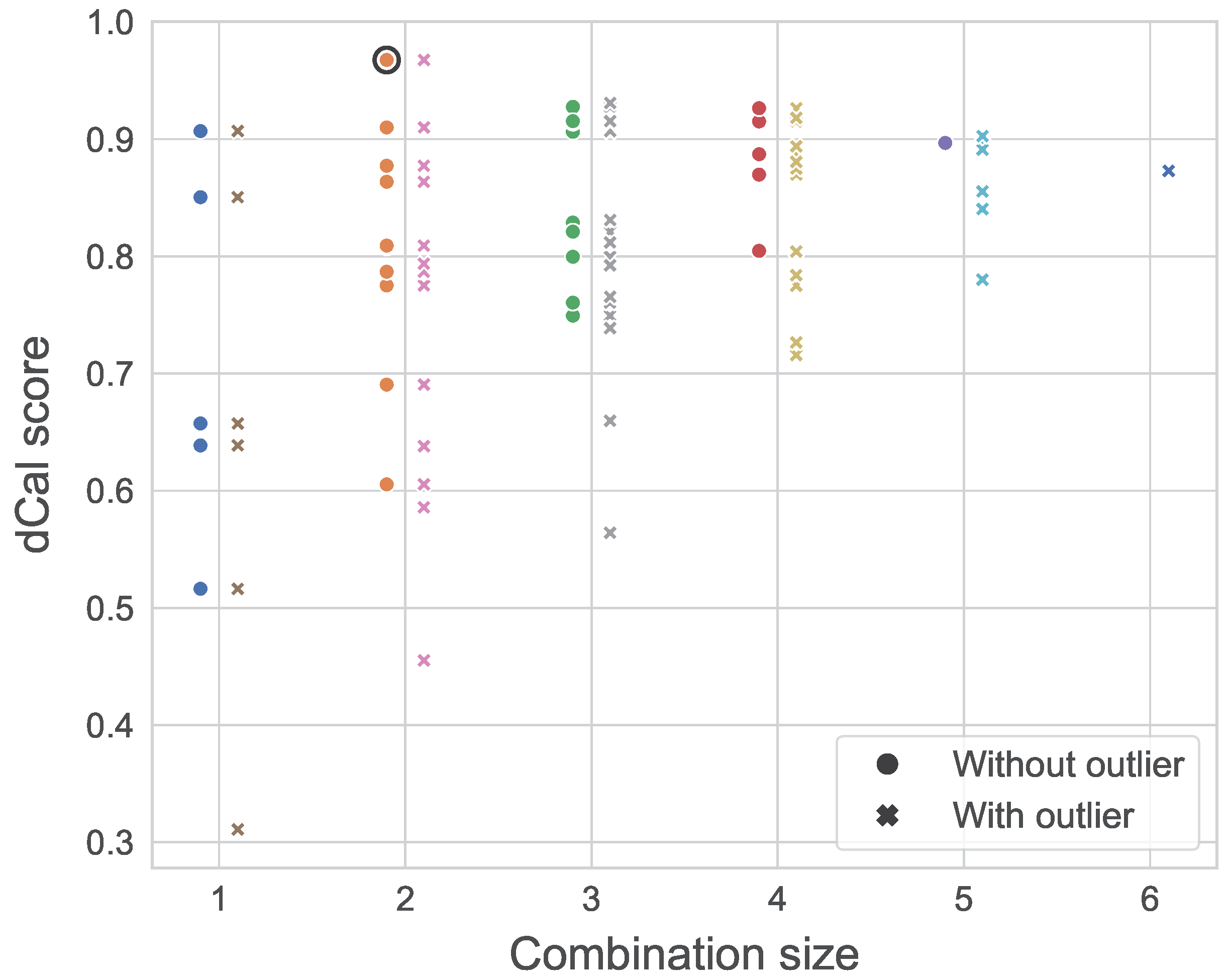
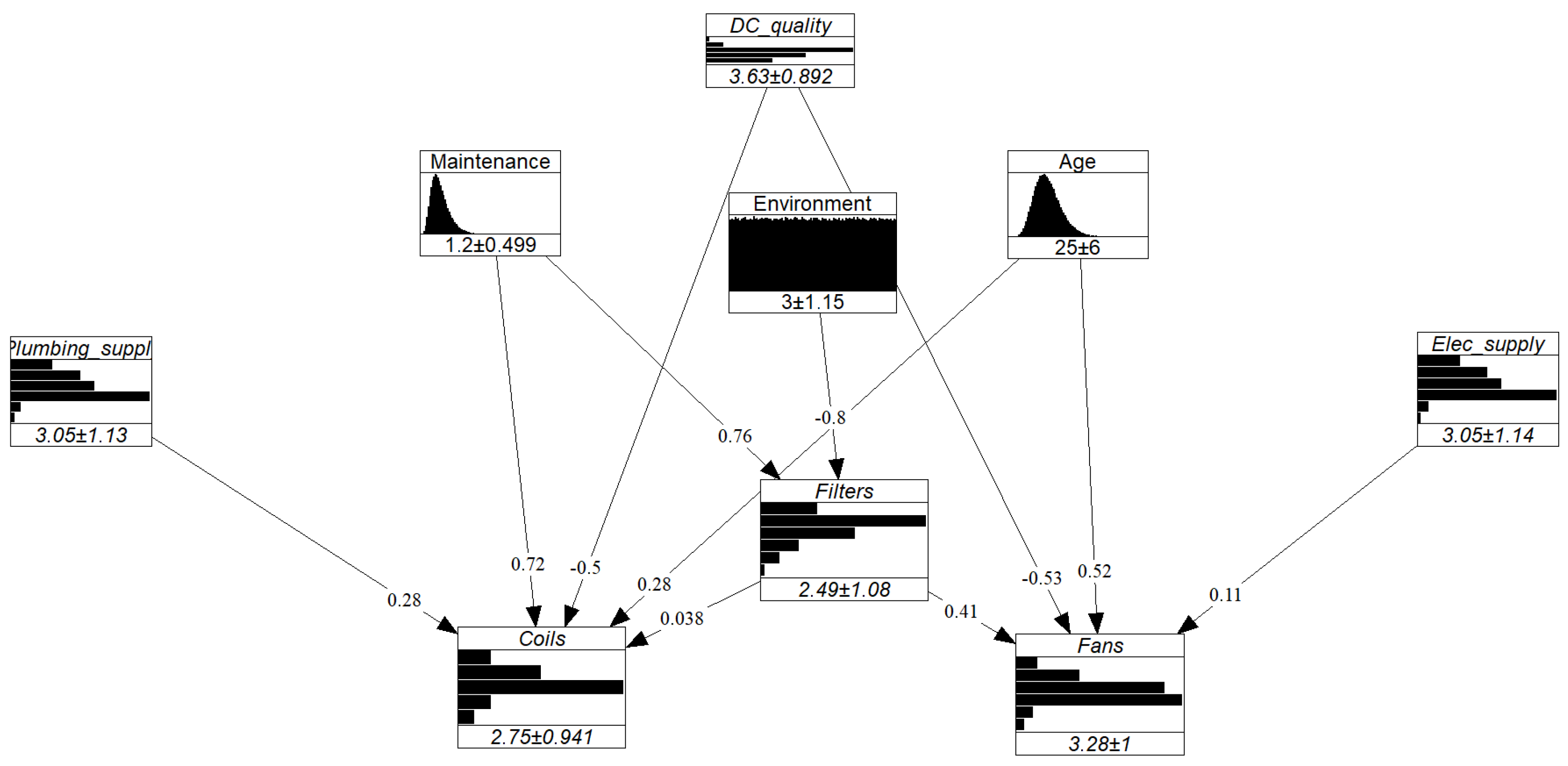
4.1.2. Dependence Calibration
4.1.3. Decision Makers
4.2. Marginal Distributions
- ‘AHU Age’: continuous. Defined on .
- ‘Maintenance interval’: continuous. Defined on .
- ‘Design & Construction quality’: discrete. Takes values between 1 (very poor) and 5 (excellent).
- ‘Filters’, ‘Fans’, ‘Coils’, ‘Plumbing supply elements’ and ‘Electrical supply elements’: discrete. Assessed on the 1–6 scale defined in NEN 2767 [9].
5. Discussion
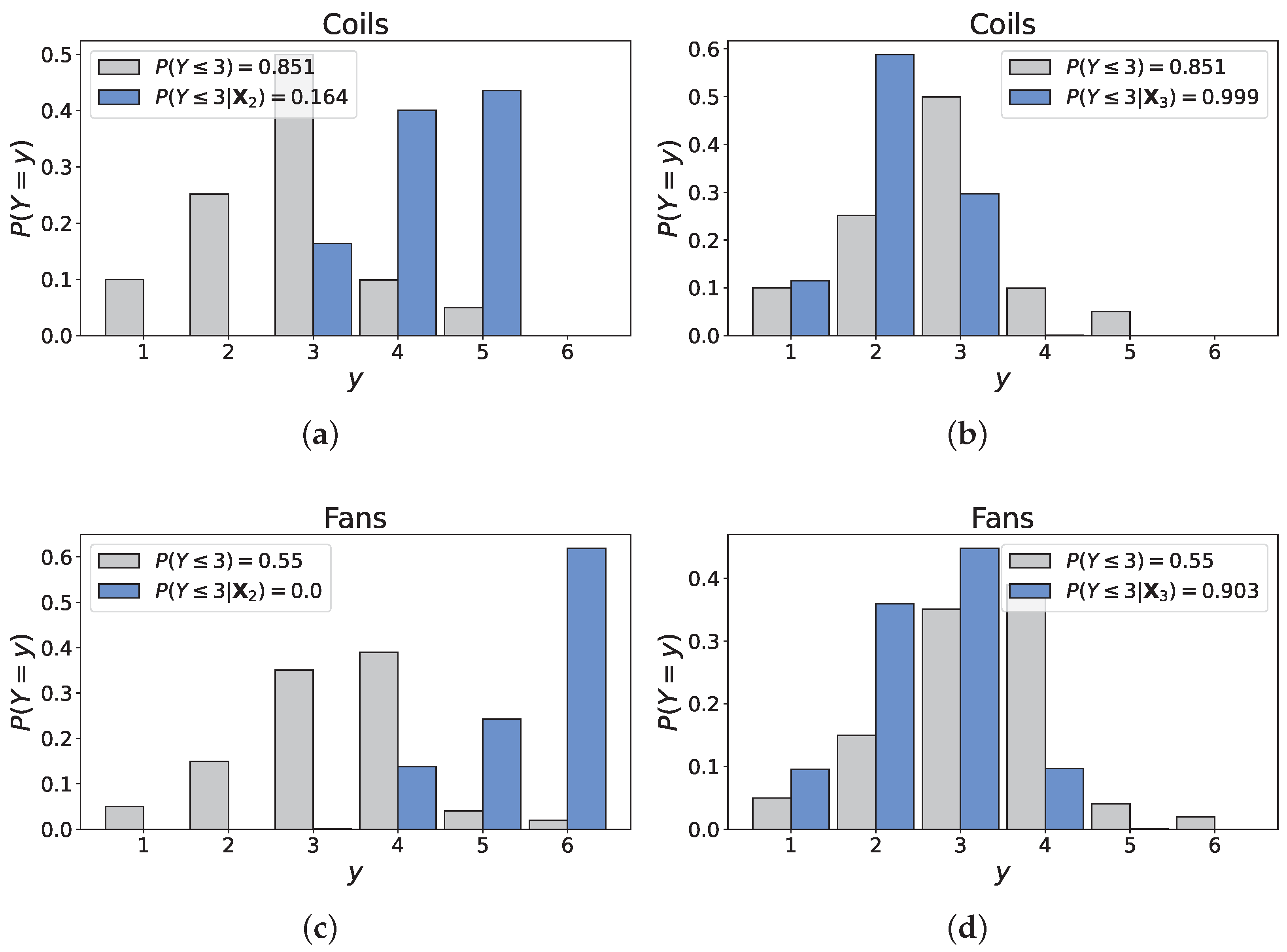
- Scenario 1: old AHU, frequent maintenance;
- Scenarios 2/3: excellent Design & Construction quality, recent/old AHU.
- •
- ‘AHU age’: 40 years,
- •
- ‘Maintenance interval’: 6 months,
- •
- ‘Design & Construction quality’: 3.63 (mean value),
- ⇒
- .
- •
- ‘AHU age’: 40 years,
- •
- ‘Maintenance interval’: 1.20 (mean value),
- •
- ‘Design & Construction quality’: 1 (very poor, Scen. 2)/5 (excellent, Scen. 3),
- ⇒
- ; .
- •
- ‘AHU age’: 40 years,
- •
- ‘Maintenance interval’: 6 months,
- •
- ‘Design & Construction quality’: 3.63 (mean value),
- •
- ‘Environmental conditions’: 1 (very unfavorable),
- ⇒
- .
6. Conclusions
“Two buildings A and B are randomly selected among all non-residential buildings in the Netherlands. Given that the AHUs in buildings A and B are both z years old, and that the AHU in building A is maintained more regularly than in building B (), what is the probability that the coils are in better condition in building A than building B ()?”
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHU | Air Handling Unit |
| BN | Bayesian Network |
| CBM | Condition-Based Maintenance |
| CDF | Cumulative Distribution Function |
| DAG | Directed Acyclic Graph |
| GCBN | Gaussian Copula-based Bayesian Network |
| GUI | Graphical User Interface |
| MEP | Mechanical, Electrical, and Plumbing |
| NPBN | Non-Parametric Bayesian Network |
| PM | Preventive Maintenance |
| SEJ | Structured Expert Judgment |
Appendix A. Probability of Concordance, Probability of Exceedance and Rank Correlation
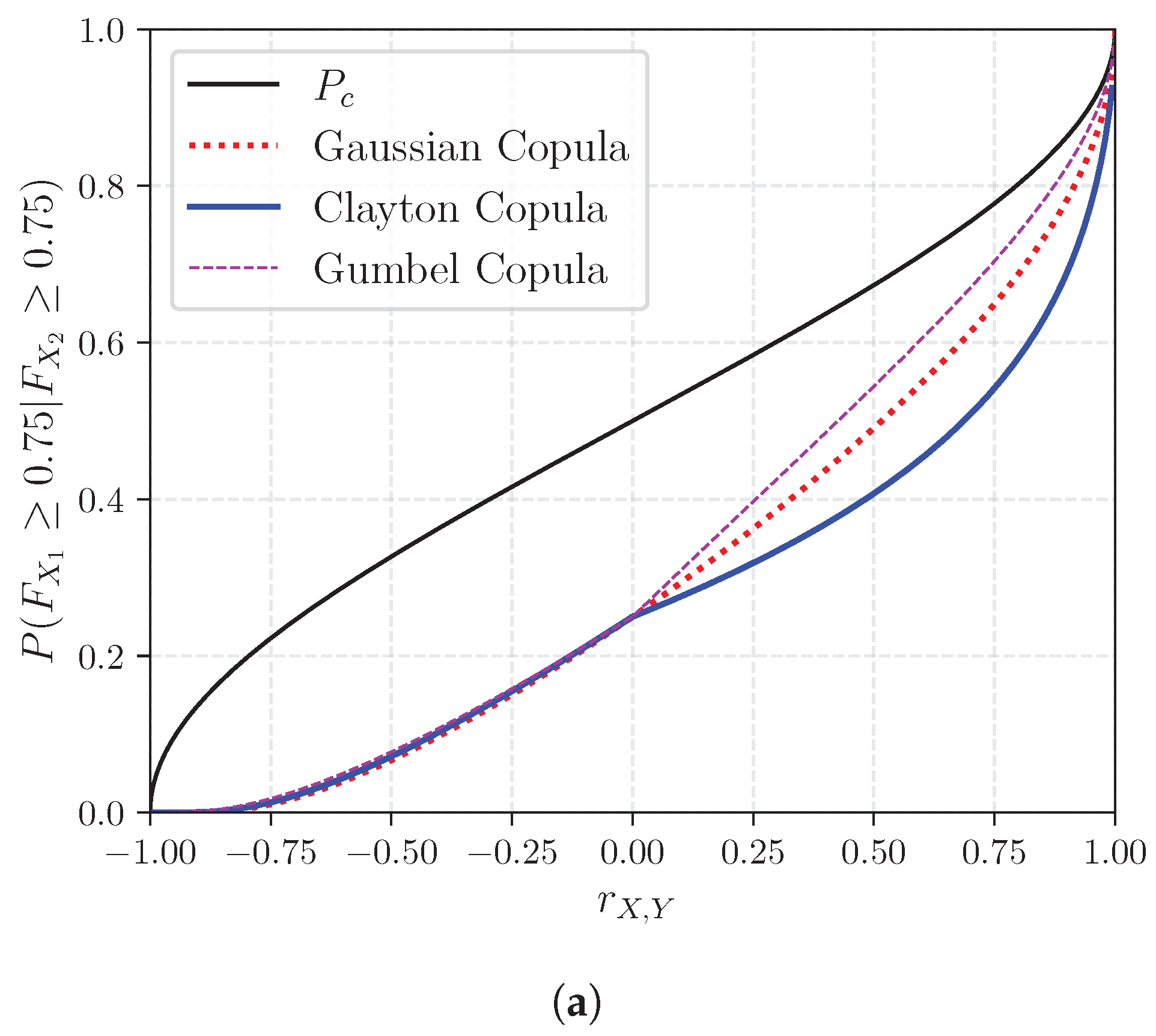
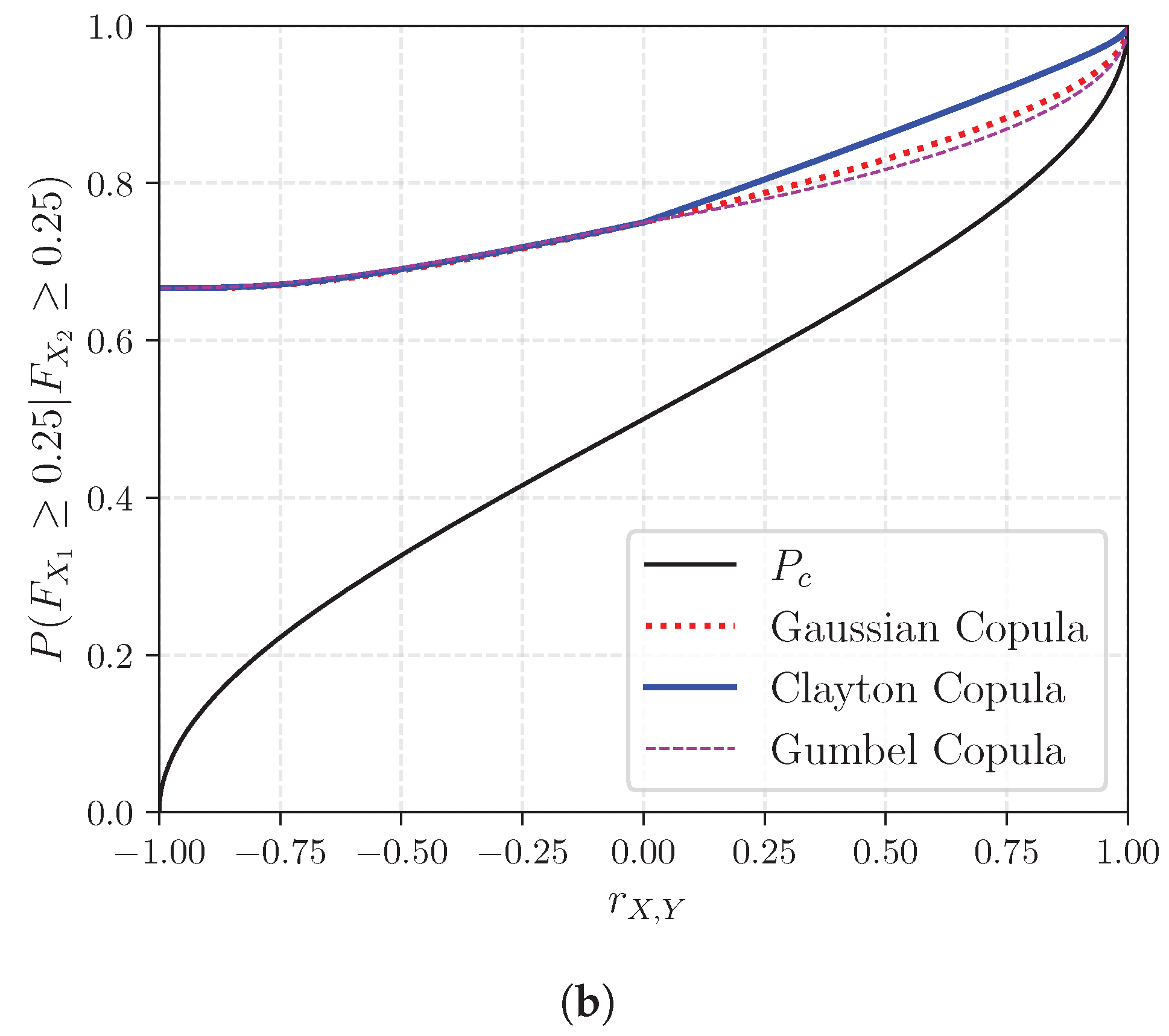
Appendix B. List of Questionnaire Respondents
| Name | Role | Organization | Experience (Years) |
|---|---|---|---|
| Boris Hadzisejdic | Maintenance specialist | TU Delft | 1.5 |
| Marcel Klok | Maintenance engineer | TU Delft | 43 |
| Frans Strik | Installations advisor | Van Dorp | 25 |
| Arie Taal | Lecturer (indoor climate, energy transition) | De Haagse Hogeschool | 40 |
| Ziao Wang | PhD candidate | TU Delft | 3 |
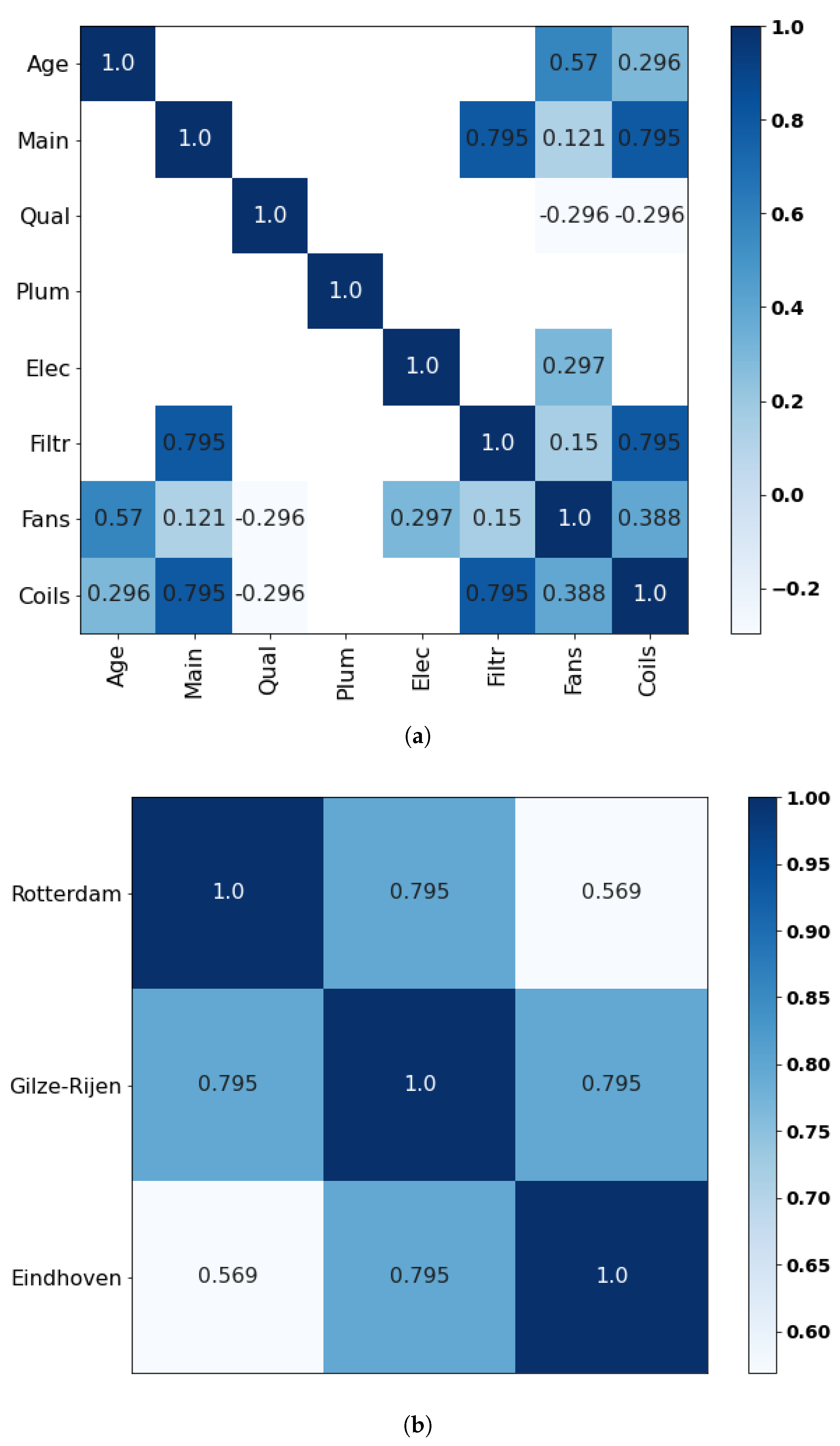
Appendix C. Correlation Matrices
Appendix C.1. Expert A

Appendix C.2. Expert B

Appendix C.3. Expert C
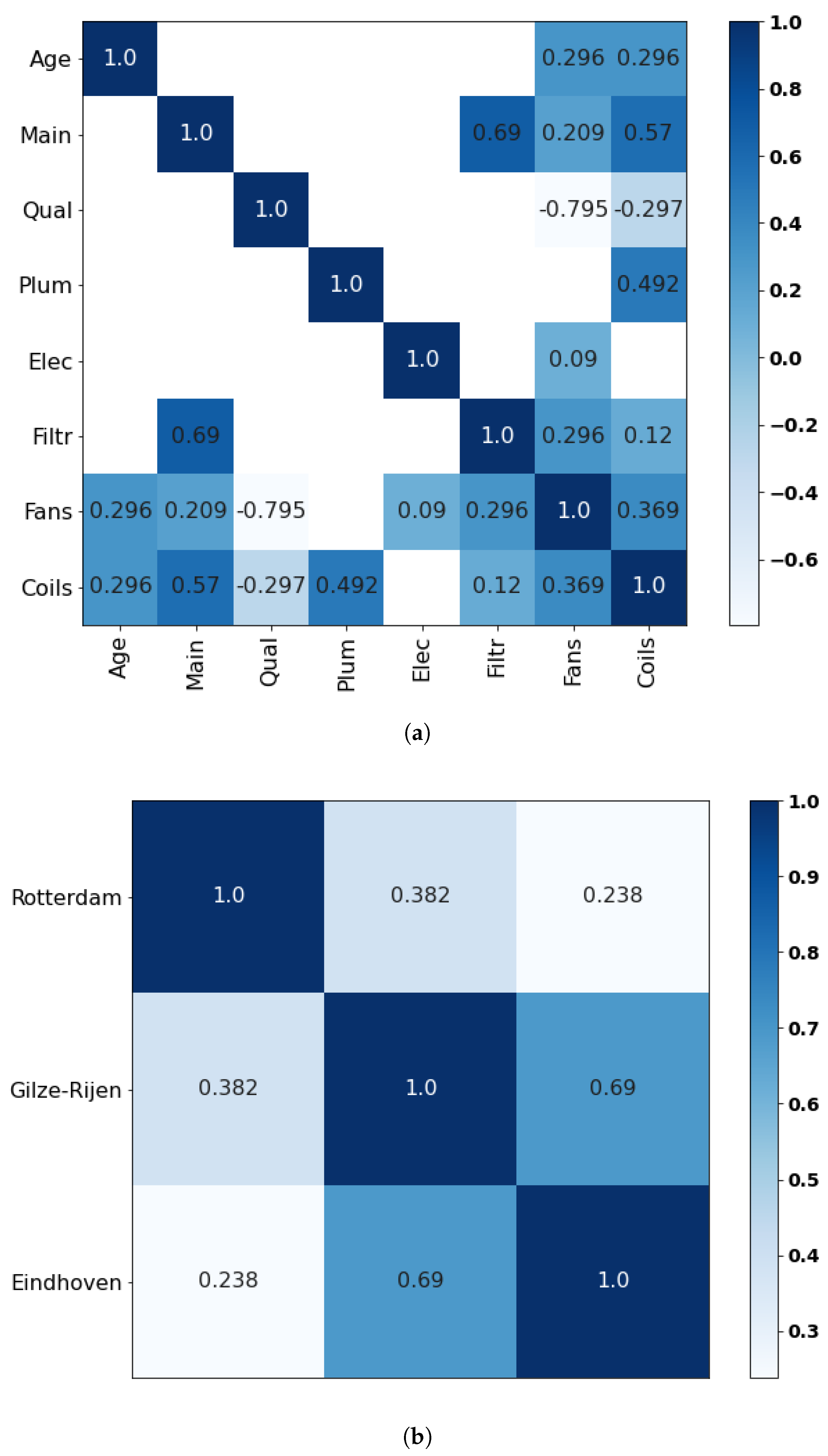
Appendix C.4. Expert D
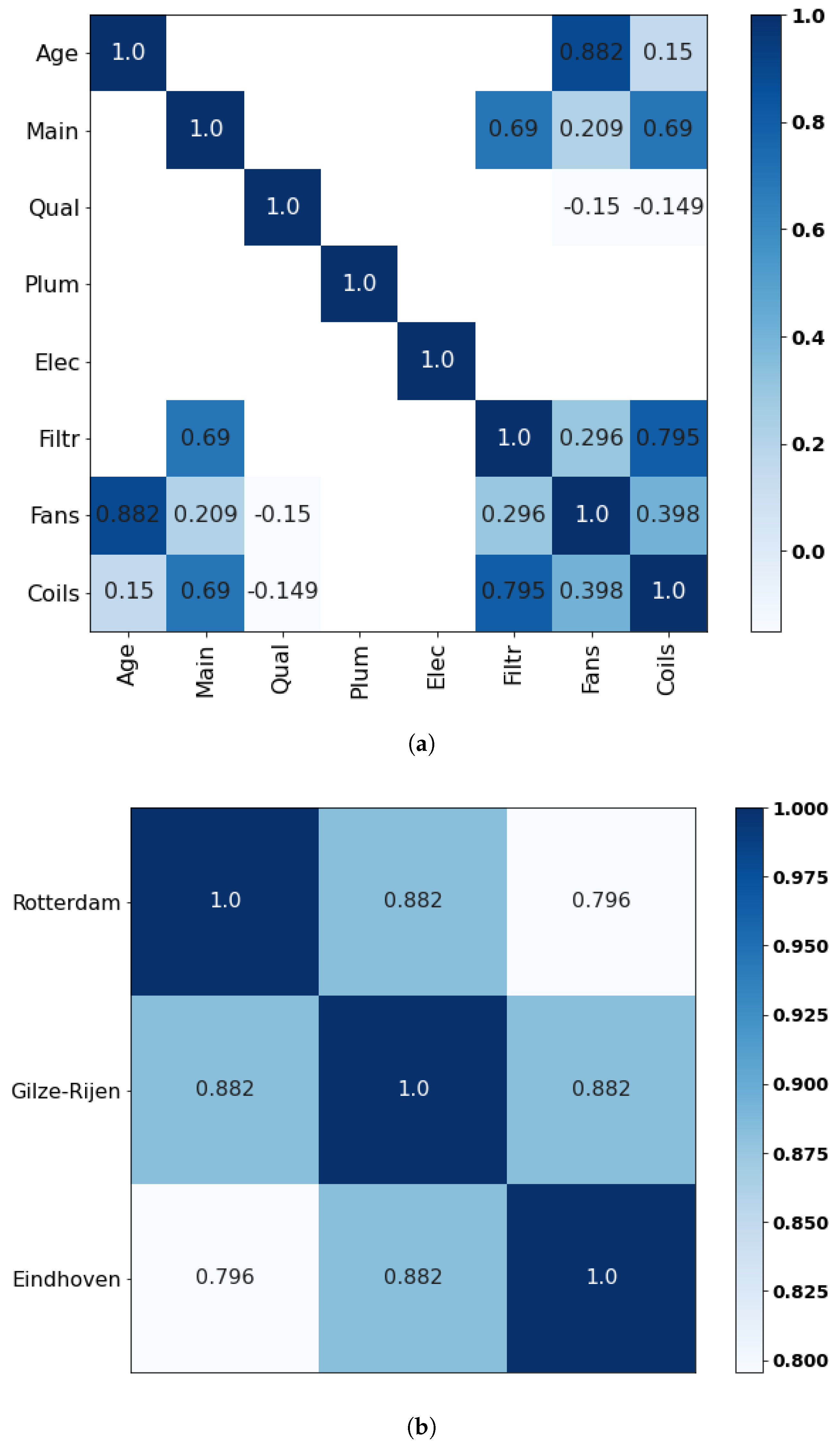
Appendix C.5. Expert E
Appendix D. Demonstration of the Relations to Compute Spearman’s Rank Correlation from a Probability of Concordance
References
- Bortolini, R.; Forcada, N. A probabilistic performance evaluation for buildings and constructed assets. Build. Res. Inf. 2020, 48, 838–855. [Google Scholar] [CrossRef]
- CEN. Maintenance. Maintenance Terminology; OCLC: 9521555828; CEN: Oak Brook, IL, USA, 2010. [Google Scholar]
- Sullivan, G.; Pugh, R.; Melendez, A.P.; Hunt, W.D. Operations & Maintenance Best Practices—A Guide to Achieving Operational Efficiency (Release 3); Technical Report PNNL-19634, 1034595; Pacific Northwest National Lab.(PNNL): Richland, WA, USA, 2010. [CrossRef]
- Straub, A. Maintenance and Repair. In International Encyclopedia of Housing and Home; Elsevier: San Diego, CA, USA, 2012; pp. 186–194. [Google Scholar] [CrossRef]
- Endrenyi, J.; Aboresheid, S.; Allan, R.; Anders, G.; Asgarpoor, S.; Billinton, R.; Chowdhury, N.; Dialynas, E.; Fipper, M.; Fletcher, R.; et al. The present status of maintenance strategies and the impact of maintenance on reliability. IEEE Trans. Power Syst. 2001, 16, 638–646. [Google Scholar] [CrossRef]
- Lee, H.; Cha, J.H. New stochastic models for preventive maintenance and maintenance optimization. Eur. J. Oper. Res. 2016, 255, 80–90. [Google Scholar] [CrossRef]
- Lind, H.; Muyingo, H. Building maintenance strategies: Planning under uncertainty. Prop. Manag. 2012, 30, 14–28. [Google Scholar] [CrossRef]
- Lupășteanu, V.; Lupășteanu, R.; Chingălată, C. Condition assessment of buildings in Romania: A proposed method and case study. J. Build. Eng. 2022, 47, 103814. [Google Scholar] [CrossRef]
- NEN. NEN 2767 Conditiemeting van bouw- en Installatiedelen—Deel 1: Methodiek (Condition Assessment of Building and Installation Components—Part 1: Methodology); NEN: Delft, The Netherlands, 2006. [Google Scholar]
- Weeks, D.J.; Leite, F. Facility Defect and Cost Reduction by Incorporating Maintainability Knowledge Transfer Using Maintenance Management System Data. J. Perform. Constr. Facil. 2021, 35, 04021004. [Google Scholar] [CrossRef]
- Zalejska, J.A.; Hungria, G.R. Defects in newly constructed residential buildings: Owners’ perspective. Int. J. Build. Pathol. Adapt. 2019, 37, 163–185. [Google Scholar] [CrossRef]
- Waddicor, D.A.; Fuentes, E.; Sisó, L.; Salom, J.; Favre, B.; Jiménez, C.; Azar, M. Climate change and building ageing impact on building energy performance and mitigation measures application: A case study in Turin, northern Italy. Build. Environ. 2016, 102, 13–25. [Google Scholar] [CrossRef]
- Bortolini, R.; Forcada, N. A probabilistic-based approach to support the comfort performance assessment of existing buildings. J. Clean. Prod. 2019, 237, 117720. [Google Scholar] [CrossRef]
- Islam, R.; Nazifa, T.H.; Mohamed, S.F. Factors Influencing Facilities Management Cost Performance in Building Projects. J. Perform. Constr. Facil. 2019, 33, 04019036. [Google Scholar] [CrossRef]
- Uusitalo, L. Advantages and challenges of Bayesian networks in environmental modelling. Ecol. Model. 2007, 203, 312–318. [Google Scholar] [CrossRef]
- Phan, T.D.; Smart, J.C.R.; Capon, S.J.; Hadwen, W.L.; Sahin, O. Applications of Bayesian belief networks in water resource management: A systematic review. Environ. Model. Softw. 2016, 85, 98–111. [Google Scholar] [CrossRef]
- Kaikkonen, L.; Parviainen, T.; Rahikainen, M.; Uusitalo, L.; Lehikoinen, A. Bayesian Networks in Environmental Risk Assessment: A Review. Integr. Environ. Assess. Manag. 2021, 17, 62–78. [Google Scholar] [CrossRef] [PubMed]
- Morales-Nápoles, O.; Kurowicka, D.; Roelen, A. Eliciting conditional and unconditional rank correlations from conditional probabilities. Reliab. Eng. Syst. Saf. 2008, 93, 699–710. [Google Scholar] [CrossRef]
- Morales-Nápoles, O.; Hanea, A.M.; Worm, D.T. Experimental results about the assessments of conditional rank correlations by experts: Example with air pollution estimates. In Safety, Reliability and Risk Analysis: Beyond the Horizon, Proceedings of the European Safety and Reliability Conference, ESREL 2013, Amsterdam, The Netherlands, 29 September–2 October 2013; CRC Press: London, UK, 2014. [Google Scholar]
- Nogal, M.; Morales Nápoles, O.; O’Connor, A. Structured expert judgement to understand the intrinsic vulnerability of traffic networks. Transp. Res. Part A Policy Pract. 2019, 127, 136–152. [Google Scholar] [CrossRef]
- Morales-Nápoles, O.; Delgado-Hernández, D.J.; De-León-Escobedo, D.; Arteaga-Arcos, J.C. A continuous Bayesian network for earth dams’ risk assessment: Methodology and quantification. Struct. Infrastruct. Eng. 2014, 10, 589–603. [Google Scholar] [CrossRef]
- Hanea, D.; Jagtman, H.; Ale, B. Analysis of the Schiphol Cell Complex fire using a Bayesian belief net based model. Reliab. Eng. Syst. Saf. 2012, 100, 115–124. [Google Scholar] [CrossRef]
- Neil, M.; Fenton, N.; Nielson, L. Building large-scale Bayesian networks. Knowl. Eng. Rev. 2000, 15, 257–284. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de répartition à N dimensions et leurs marges. In Annales de l’ISUP; ISUP: Paris, France, 1959. [Google Scholar]
- Nešlehová, J. On rank correlation measures for non-continuous random variables. J. Multivar. Anal. 2007, 98, 544–567. [Google Scholar] [CrossRef]
- Hanea, A.M.; Morales-Nápoles, O.; Ababei, D. Non-parametric Bayesian networks: Improving theory and reviewing applications. Reliab. Eng. Syst. Saf. 2015, 144, 265–284. [Google Scholar] [CrossRef]
- Hanea, A.M.; Kurowicka, D.; Cooke, R.M. Hybrid Method for Quantifying and Analyzing Bayesian Belief Nets. Qual. Reliab. Eng. Int. 2006, 22, 709–729. [Google Scholar] [CrossRef]
- Cooke, R.M.; Goossens, L.L. TU Delft expert judgment data base. Reliab. Eng. Syst. Saf. 2008, 93, 657–674. [Google Scholar] [CrossRef]
- Clemen, R.T.; Reilly, T. Correlations and Copulas for Decision and Risk Analysis. Manag. Sci. 1999, 45, 208–224. [Google Scholar] [CrossRef]
- Werner, C.; Bedford, T.; Cooke, R.M.; Hanea, A.M.; Morales-Nápoles, O. Expert judgement for dependence in probabilistic modelling: A systematic literature review and future research directions. Eur. J. Oper. Res. 2017, 258, 801–819. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Clemen, R.T.; Fischer, G.W.; Winkler, R.L. Assessing Dependence: Some Experimental Results. Manag. Sci. 2000, 46, 1100–1115. [Google Scholar] [CrossRef]
- Derumigny, A.; Fermanian, J.D. A classification point-of-view about conditional Kendall’s tau. Comput. Stat. Data Anal. 2019, 135, 70–94. [Google Scholar] [CrossRef]
- Fang, H.B.; Fang, K.T.; Kotz, S. The Meta-elliptical Distributions with Given Marginals. J. Multivar. Anal. 2002, 82, 1–16. [Google Scholar] [CrossRef]
- Kurowicka, D.; Cooke, R.M. Uncertainty Analysis with High Dimensional Dependence Modelling; Google-Books-ID: DRVGNYU7RskC; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Rongen, G.; Morales-Nápoles, O. Matlatzinca: A PyBANSHEE-based graphical user interface for elicitation of non-parametric Bayesian networks from experts. SoftwareX 2024, 26, 101693. [Google Scholar] [CrossRef]
- Paprotny, D.; Morales-Nápoles, O.; Worm, D.T.; Ragno, E. BANSHEE–A MATLAB toolbox for non-parametric Bayesian networks. SoftwareX 2020, 12, 100588. [Google Scholar] [CrossRef]
- Koot, P.; Mendoza-Lugo, M.A.; Paprotny, D.; Morales-Nápoles, O.; Ragno, E.; Worm, D.T. PyBanshee version (1.0): A Python implementation of the MATLAB toolbox BANSHEE for Non-Parametric Bayesian Networks with updated features. SoftwareX 2023, 21, 101279. [Google Scholar] [CrossRef]
- Mendoza-Lugo, M.A.; Morales-Nápoles, O. Version 1.3-BANSHEE—A MATLAB toolbox for Non-Parametric Bayesian Networks. SoftwareX 2023, 23, 101479. [Google Scholar] [CrossRef]
- Paprotny, D.; Kreibich, H.; Morales-Nápoles, O.; Wagenaar, D.; Castellarin, A.; Carisi, F.; Bertin, X.; Merz, B.; Schröter, K. A probabilistic approach to estimating residential losses from different flood types. Nat. Hazards 2021, 105, 2569–2601. [Google Scholar] [CrossRef]
- Mendoza-Lugo, M.A.; Morales-Nápoles, O.; Delgado-Hernández, D.J. A Non-parametric Bayesian Network for multivariate probabilistic modelling of Weigh-in-Motion System Data. Transp. Res. Interdiscip. Perspect. 2022, 13, 100552. [Google Scholar] [CrossRef]
- Clemen, R.T.; Winkler, R. Combining probability distributions from experts in risk analysis. Risk Anal. 1999, 19, 187–203. [Google Scholar] [CrossRef]
- French, S. Aggregating expert judgement. Rev. De La Real Acad. De Cienc. Exactas Fis. Y Naturales. Ser. A Mat. 2011, 105, 181–206. [Google Scholar] [CrossRef]
- Cooke, R.M. Experts in Uncertainty: Opinion and Subjective Probability in Science; Oxford University Press: New York, NY, USA, 1991; p. 321. [Google Scholar]
- Morales-Nápoles, O.; Paprotny, D.; Worm, D.; Abspoel-Bukman, L.; Courage, W. Characterization of precipitation through copulas and expert judgement for risk assessment of infrastructure. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 04017012. [Google Scholar] [CrossRef]
- Rongen, G.; Morales-Nápoles, O.; Kok, M. Structured expert elicitation of dependence between river tributaries using Non-Parametric Bayesian Networks. 2023; Unpublished work. [Google Scholar]
- Kusiak, A.; Li, M. Cooling output optimization of an air handling unit. Appl. Energy 2010, 87, 901–909. [Google Scholar] [CrossRef]
- Ramousse, B. Development of a Framework to Estimate the Condition of Mechanical, Electrical and Plumbing Systems with Bayesian Networks. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2023. [Google Scholar]
- Yan, Y.; Cai, J.; Li, T.; Zhang, W.; Sun, L. Fault prognosis of HVAC air handling unit and its components using hidden-semi Markov model and statistical process control. Energy Build. 2021, 240, 110875. [Google Scholar] [CrossRef]
- Straub, A. Dutch standard for condition assessment of buildings. Struct. Surv. 2009, 27, 23–35. [Google Scholar] [CrossRef]
- Hanea, A.M.; Hemming, V.; Nane, G.F. Uncertainty Quantification with Experts: Present Status and Research Needs. Risk Anal. 2022, 42, 254–263. [Google Scholar] [CrossRef] [PubMed]
- Bolger, F.; Rowe, G. The Aggregation of Expert Judgment: Do Good Things Come to Those Who Weight? Risk Anal. 2015, 35, 5–11. [Google Scholar] [CrossRef] [PubMed]
- Brooker, P. Experts, Bayesian Belief Networks, rare events and aviation risk estimates. Saf. Sci. 2011, 49, 1142–1155. [Google Scholar] [CrossRef]
- Pollino, C.A.; Woodberry, O.; Nicholson, A.; Korb, K.; Hart, B.T. Parameterisation and evaluation of a Bayesian network for use in an ecological risk assessment. Environ. Model. Softw. 2007, 22, 1140–1152. [Google Scholar] [CrossRef]
- Chen, S.H.; Pollino, C.A. Good practice in Bayesian network modelling. Environ. Model. Softw. 2012, 37, 134–145. [Google Scholar] [CrossRef]
- Pitchforth, J.; Mengersen, K. A proposed validation framework for expert elicited Bayesian Networks. Expert Syst. Appl. 2013, 40, 162–167. [Google Scholar] [CrossRef]
- Wang, F.; Li, H.; Dong, C.; Ding, L. Knowledge representation using non-parametric Bayesian networks for tunneling risk analysis. Reliab. Eng. Syst. Saf. 2019, 191, 106529. [Google Scholar] [CrossRef]





| Very Poor | Poor | Medium | Good | Excellent |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| Decision Maker | D-Calibration | Perceived Comfort |
|---|---|---|
| Expert A | 0.639 | 4 |
| Expert B | 0.907 | 4 |
| Expert C | 0.85 | 4 |
| Expert D | 0.516 | 2 |
| Expert E | 0.657 | 2 |
| EWDM | 0.869 | - |
| GWDM | 0.897 | - |
| optDM | 0.968 | - |
| Strongly | Disagree | Neither Agree or Disagree | Agree | Strongly Agree |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| Decision Maker | Without Outlier | With Outlier |
|---|---|---|
| Expert D | 0.516 | - |
| Outlier | - | 0.311 |
| EW DM | 0.869 | 0.818 |
| GW DM | 0.897 | 0.873 |
| optDM | 0.968 | - |
| Variable | Distribution | (Mean, std *) |
|---|---|---|
| Age | (24.98, 6.00) | |
| Maintenance interval | (1.20, 0.50) | |
| D&C quality | [0.01, 0.05, 0.44, 0.3, 0.2] | (3.63, 0.89) |
| Filters | [0.15, 0.44, 0.25, 0.1, 0.05, 0.01] | (2.49, 1.08) |
| Fans | [0.05, 0.15, 0.35, 0.39, 0.04, 0.02] | (3.28, 1.00) |
| Coils | [0.1, 0.25, 0.5, 0.1, 0.05, 0] | (2.75, 0.94) |
| Plumbing supply elts | [0.12, 0.2, 0.24, 0.4, 0.03, 0.01] | (3.05, 1.14) |
| Electrical supply elts | [0.12, 0.2, 0.24, 0.4, 0.03, 0.01] | (3.05, 1.14) |
| Very Unfavorable | Unfavorable | Medium | Favorable | Very Favorable |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramousse, B.; Mendoza-Lugo, M.A.; Rongen, G.; Morales-Nápoles, O. Elicitation of Rank Correlations with Probabilities of Concordance: Method and Application to Building Management. Entropy 2024, 26, 360. https://doi.org/10.3390/e26050360
Ramousse B, Mendoza-Lugo MA, Rongen G, Morales-Nápoles O. Elicitation of Rank Correlations with Probabilities of Concordance: Method and Application to Building Management. Entropy. 2024; 26(5):360. https://doi.org/10.3390/e26050360
Chicago/Turabian StyleRamousse, Benjamin, Miguel Angel Mendoza-Lugo, Guus Rongen, and Oswaldo Morales-Nápoles. 2024. "Elicitation of Rank Correlations with Probabilities of Concordance: Method and Application to Building Management" Entropy 26, no. 5: 360. https://doi.org/10.3390/e26050360
APA StyleRamousse, B., Mendoza-Lugo, M. A., Rongen, G., & Morales-Nápoles, O. (2024). Elicitation of Rank Correlations with Probabilities of Concordance: Method and Application to Building Management. Entropy, 26(5), 360. https://doi.org/10.3390/e26050360






