A Comparative Analysis of Discrete Entropy Estimators for Large-Alphabet Problems
Abstract
1. Introduction
2. Preliminaries
3. Entropy Estimators
3.1. Overview of Entropy Estimators
3.2. Past Research on Comparison of Entropy Estimators
4. Experimental Methods and Materials
4.1. Experimental Settings
4.2. The Implementation of the Entropy Estimators
5. Results
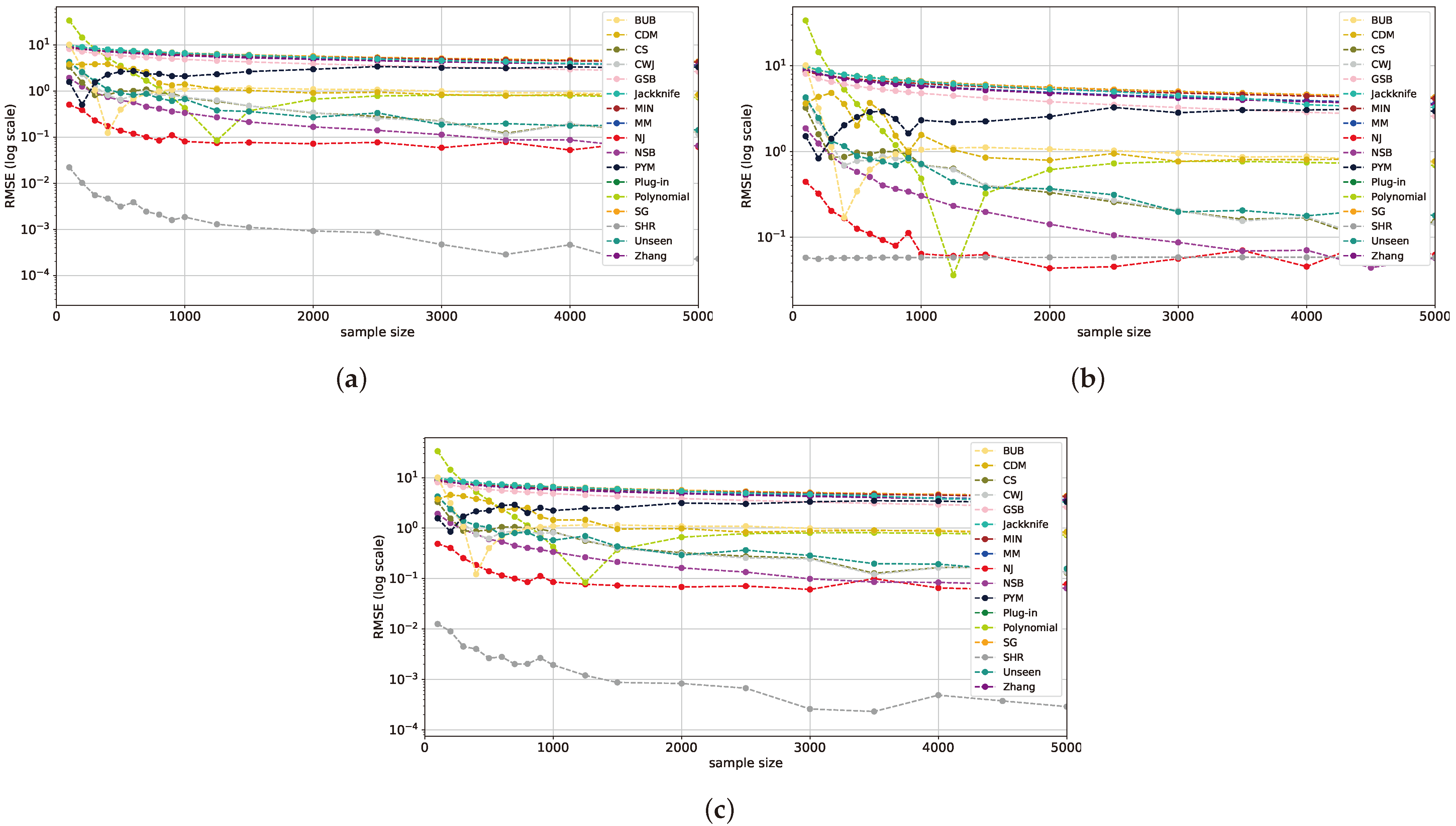
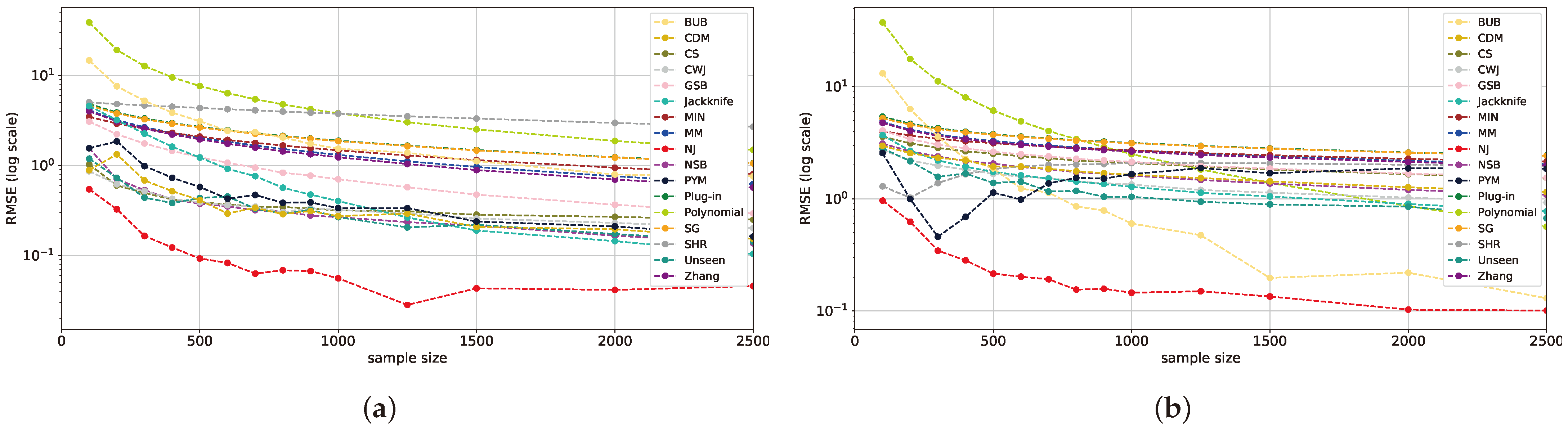
5.1. Varying Sample Size with Fixed Alphabet Size
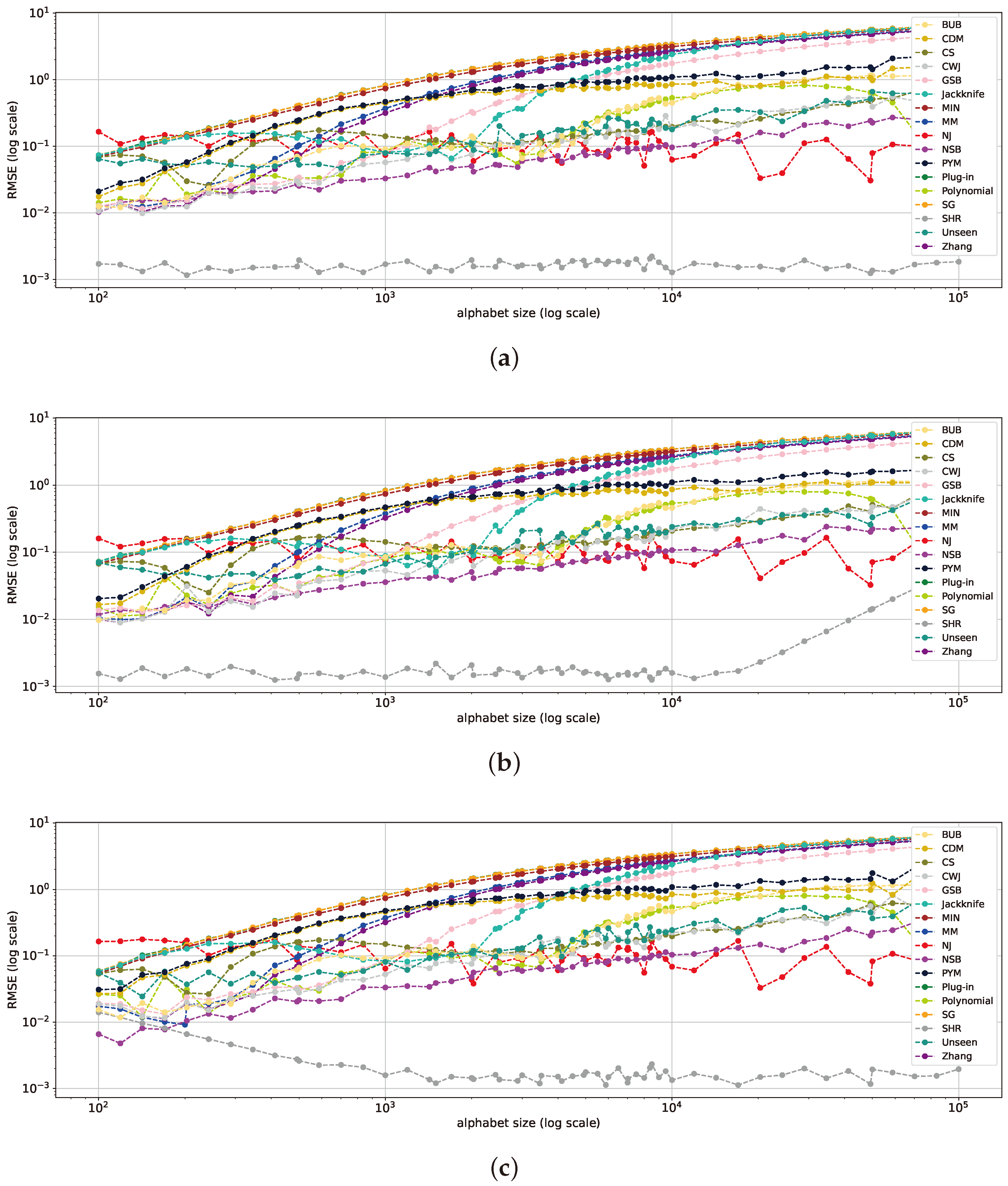
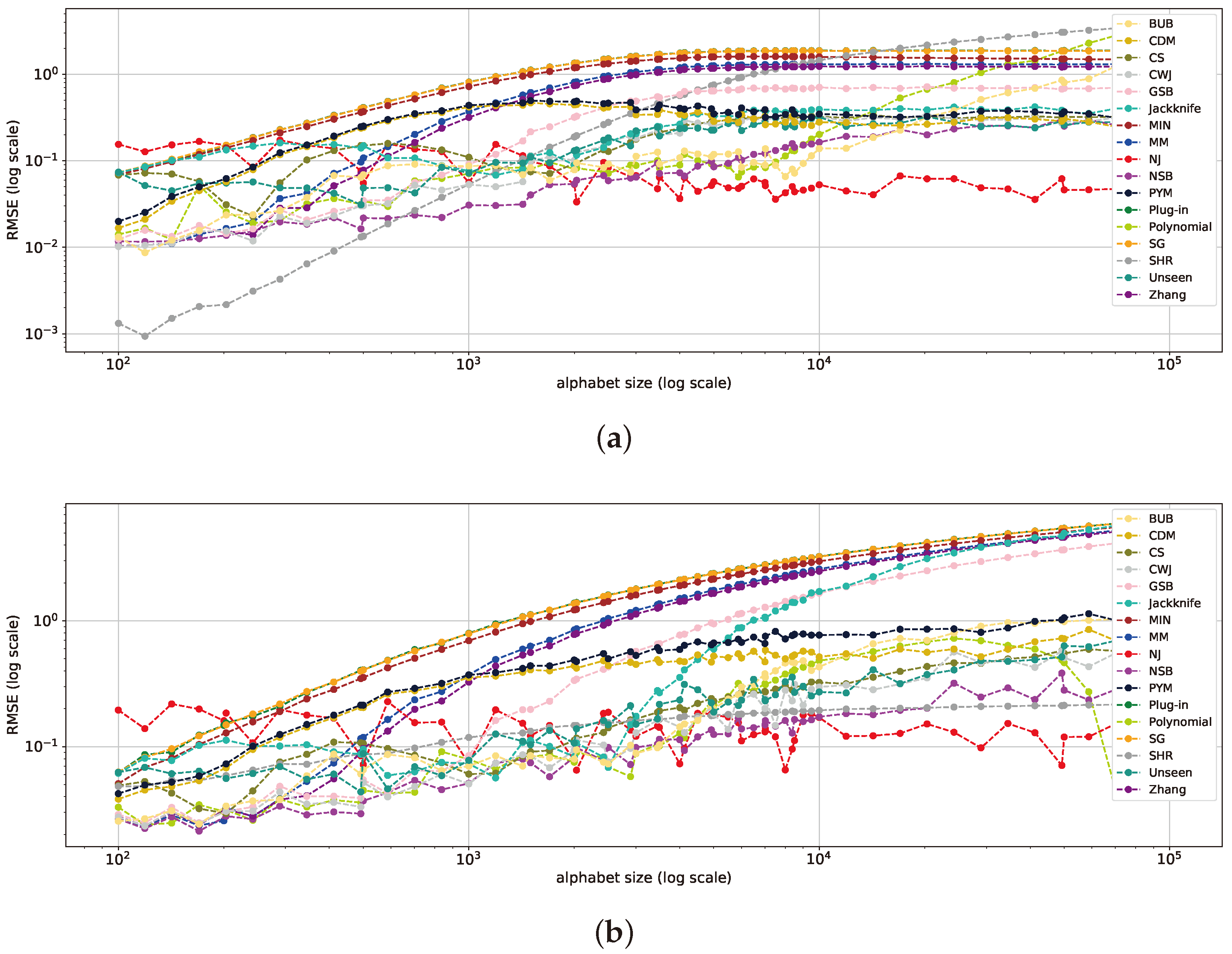
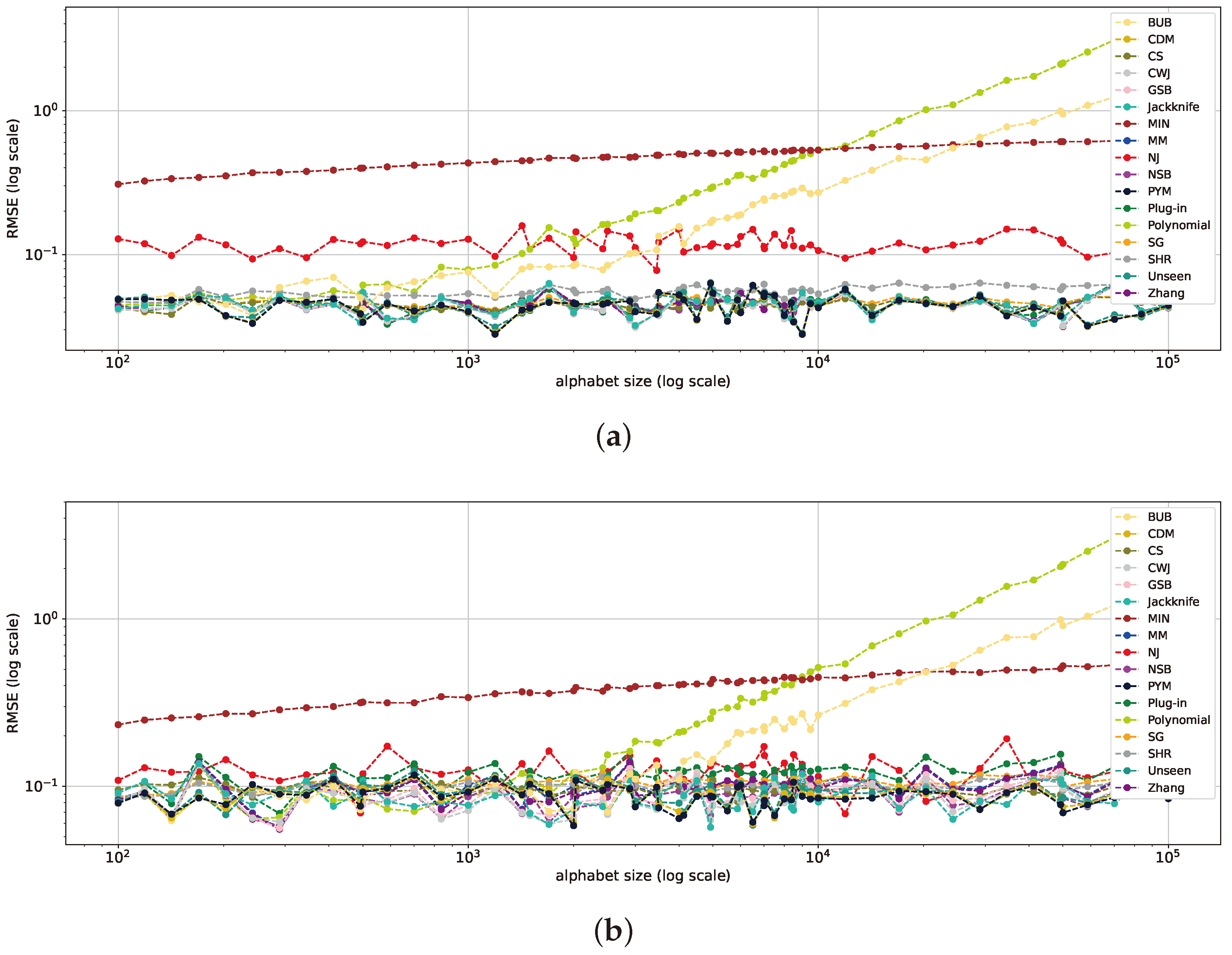
5.2. Varying Alphabet Size with Fixed Sample Size
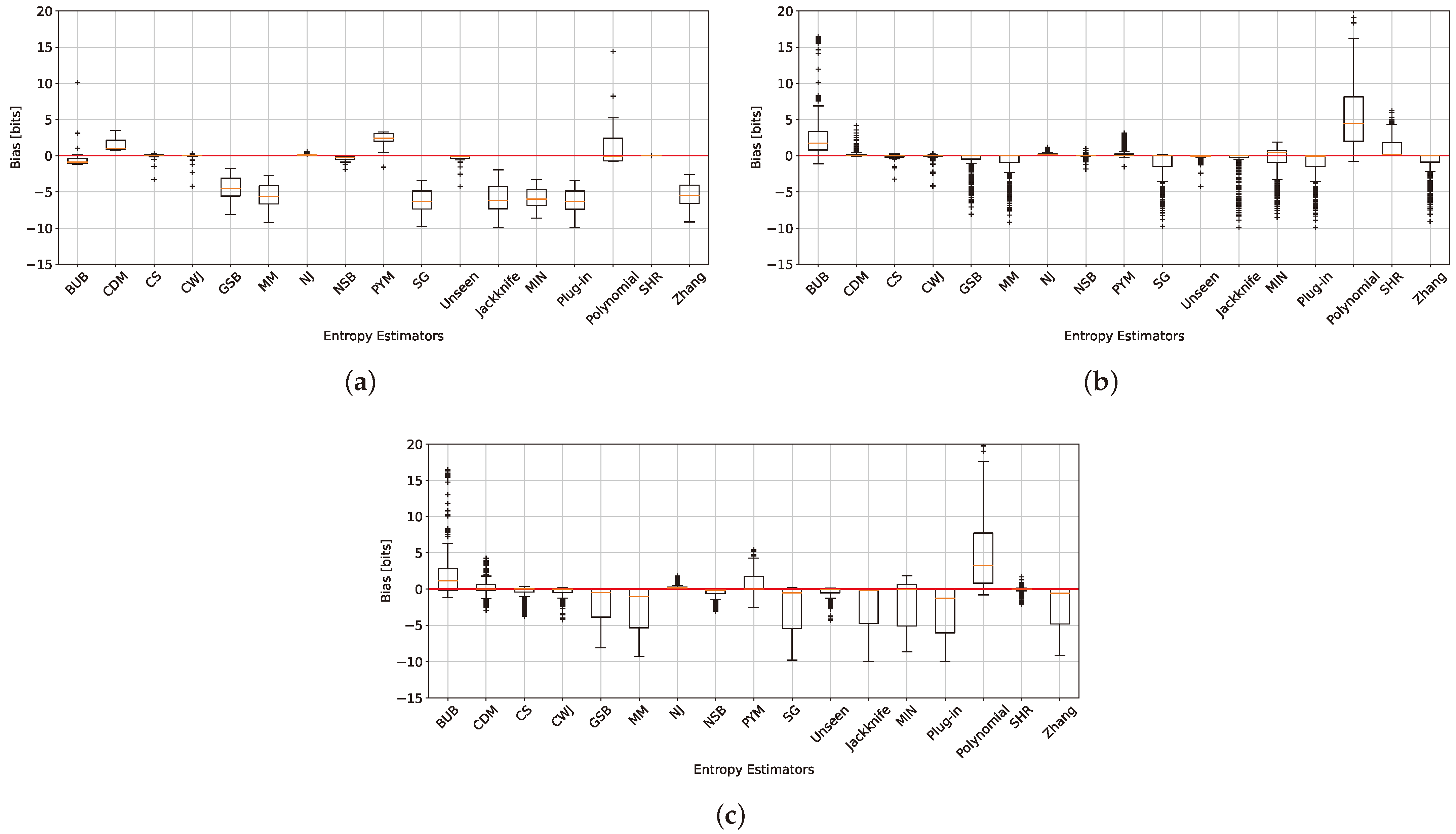
5.3. Bias Analysis
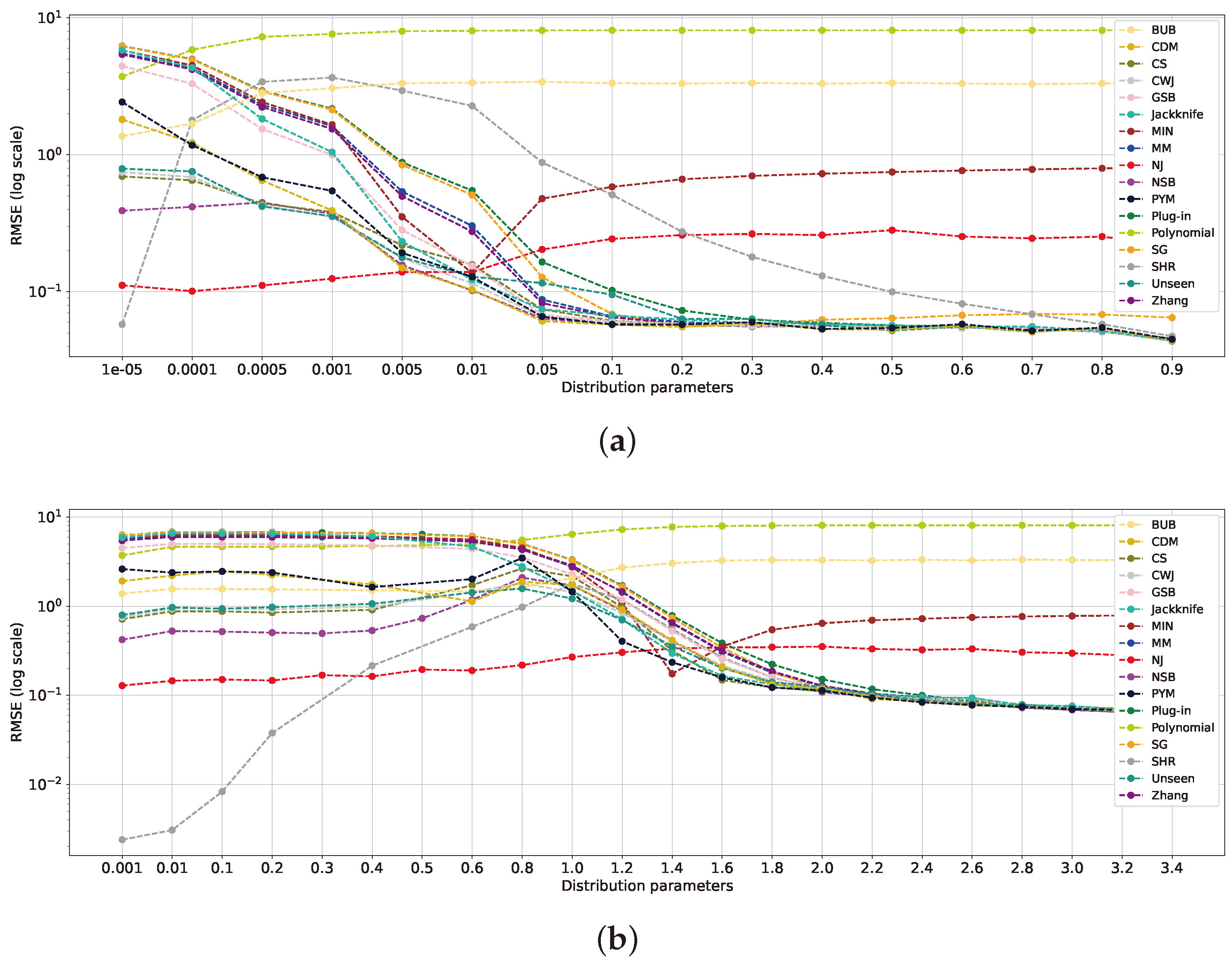
5.4. Distributions According to Parameter Analysis
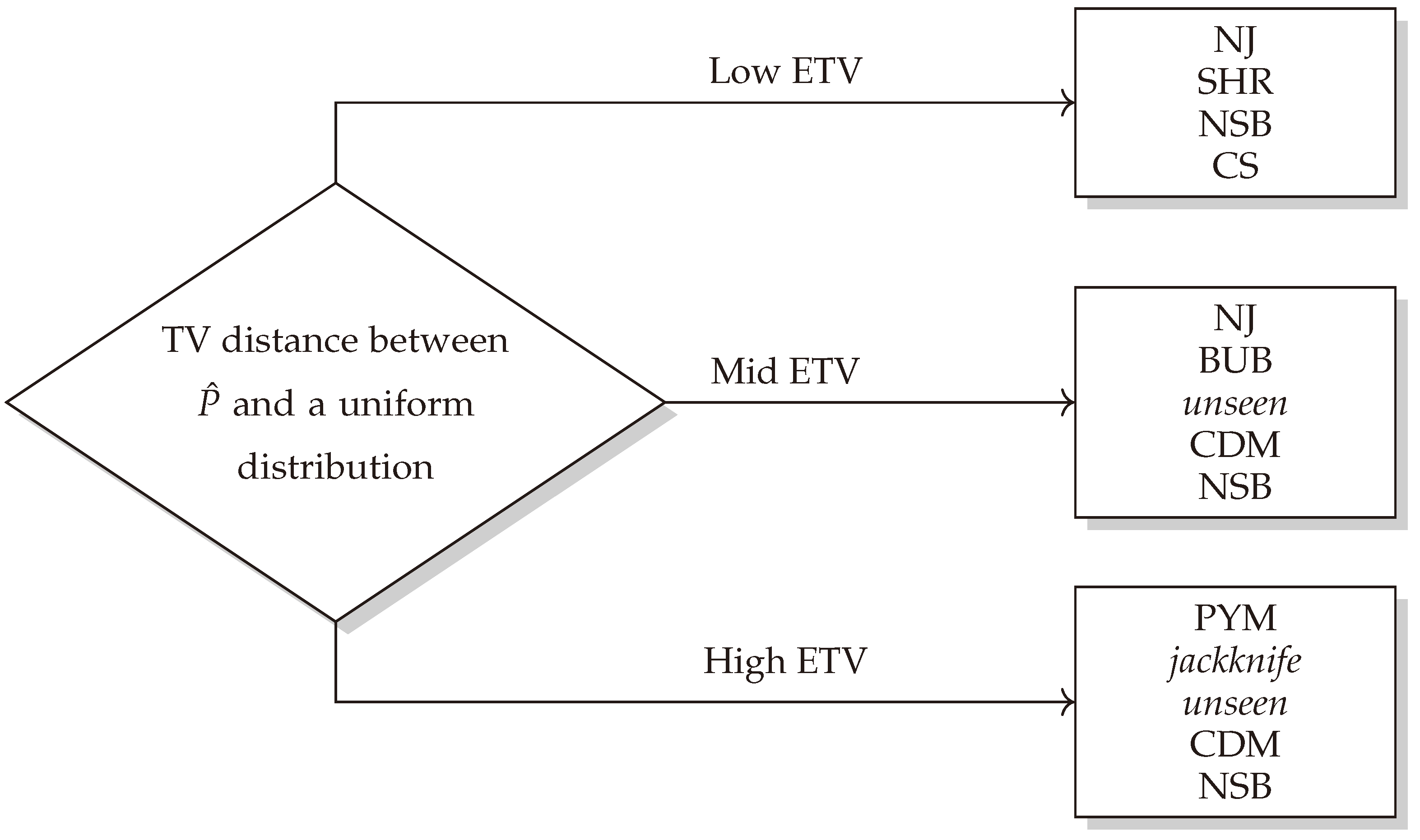
5.5. Analysis of Total Variation Distance from Uniform Distribution
5.6. Choosing the Most Favorable Entropy Estimator
5.7. Real-World Experiments
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Entropy Estimator Definitions
| Estimator | Notation | Description |
|---|---|---|
| Maximum likelihood [20] | plug-in | . |
| Miller–Madow correction [15] | MM | , where n is the sample size, is the observed frequency of x, and m is the number of such that . |
| Jackknife [16] | jackknife | , where is the entropy of the sample, excluding the i-th symbol. |
| Best Upper Bound [2] | BUB | , where , and is calculated using an algorithm proposed in [2] that minimizes a “regularized least squares” problem. |
| Grassberger [10] | GSB | , where is the digamma function. |
| Schürmann [21] | SHU | . |
| Chao–Shen * [22,23] | CS | , where . |
| James–Stein [9] | SHR | , where , with and . |
| Bonachela [25] | BN | . |
| Zhang [12] | Zhang | , where . |
| Chao–Wang–Jost [14] | CWJ | , with where is the number of singletons, and is the number of doubletons in the sample. |
| Schürmann–Grassberger [32] | SG | , where . |
| Minimax prior [33] | MIN | with and . |
| Jeffrey [29] | JEF | with and . |
| Laplace [31] | LAP | with and . |
| NSB [11] | NSB | , where , with , and is the expectation value of the m-th entropy moment for fixed . The explicit expression for is in [50]. |
| CDM [34] | CDM | , where . |
| PYM [35] | PYM | , where is the expected posterior entropy for a given , which determines the prior, and . |
| polynomial [19] | polynomial | , where , where L is the polynomial degree, , is an approximate polynomial coefficient, , denotes the observed frequencies of the equally split sample, and are constants specified in [19]. |
| unseen [13] | unseen | Algorithmic calculation based on linear programming. |
| Neural joint entropy estimator [18] | NJ | Neural network estimator based on minimizing the cross-entropy loss. |
References
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Paninski, L. Estimation of Entropy and Mutual Information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Antos, A.; Kontoyiannis, I. Convergence properties of functional estimates for discrete distributions. Random Struct. Algorithms 2001, 19, 163–193. [Google Scholar] [CrossRef]
- Sechidis, K.; Azzimonti, L.; Pocock, A.; Corani, G.; Weatherall, J.; Brown, G. Efficient feature selection using shrinkage estimators. Mach. Learn. 2019, 108, 1261–1286. [Google Scholar] [CrossRef]
- Capó, E.J.M.; Cuellar, O.J.; Pérez, C.M.L.; Gómez, G.S. Evaluation of input—Output statistical dependence PRNGs by SAC. In Proceedings of the IEEE 2016 International Conference on Software Process Improvement (CIMPS), Aguascalientes, Mexico, 12–14 October 2016; pp. 1–6. [Google Scholar]
- Madarro-Capó, E.J.; Legón-Pérez, C.M.; Rojas, O.; Sosa-Gómez, G.; Socorro-Llanes, R. Bit independence criterion extended to stream ciphers. Appl. Sci. 2020, 10, 7668. [Google Scholar] [CrossRef]
- Li, L.; Titov, I.; Sporleder, C. Improved Estimation of Entropy for Evaluation of Word Sense Induction. Comput. Linguist. 2014, 40, 671–685. [Google Scholar] [CrossRef]
- YAVUZ, Z.K.; Aydin, N.; ALTAY, G. Comprehensive review of association estimators for the inference of gene networks. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 695–718. [Google Scholar]
- Hausser, J.; Strimmer, K. Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks. J. Mach. Learn. Res. 2009, 10, 1469–1484. [Google Scholar]
- Grassberger, P. Entropy estimates from insufficient samplings. arXiv 2003, arXiv:physics/0307138. [Google Scholar]
- Nemenman, I.; Shafee, F.; Bialek, W. Entropy and inference, revisited. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; Volume 14. [Google Scholar]
- Zhang, Z. Entropy estimation in Turing’s perspective. Neural Comput. 2012, 24, 1368–1389. [Google Scholar] [CrossRef]
- Valiant, P.; Valiant, G. Estimating the Unseen: Improved Estimators for Entropy and other Properties. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; Burges, C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K., Eds.; Curran Associates Inc.: Glasgow, UK, 2013; Volume 26. [Google Scholar]
- Chao, A.; Wang, Y.; Jost, L. Entropy and the species accumulation curve: A novel entropy estimator via discovery rates of new species. Methods Ecol. Evol. 2013, 4, 1091–1100. [Google Scholar] [CrossRef]
- Miller, G. Note on the bias of information estimates. In Information Theory in Psychology: Problems and Methods; Free Press: Washington, DC, USA, 1955. [Google Scholar]
- Burnham, K.P.; Overton, W.S. Estimation of the size of a closed population when capture probabilities vary among animals. Biometrika 1978, 65, 625–633. [Google Scholar] [CrossRef]
- Contreras Rodríguez, L.; Madarro-Capó, E.J.; Legón-Pérez, C.M.; Rojas, O.; Sosa-Gómez, G. Selecting an effective entropy estimator for short sequences of bits and bytes with maximum entropy. Entropy 2021, 23, 561. [Google Scholar] [CrossRef]
- Shalev, Y.; Painsky, A.; Ben-Gal, I. Neural joint entropy estimation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5488–5500. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, P. Minimax Rates of Entropy Estimation on Large Alphabets via Best Polynomial Approximation. IEEE Trans. Inf. Theory 2016, 62, 3702–3720. [Google Scholar] [CrossRef]
- Strong, S.P.; Koberle, R.; Van Steveninck, R.R.D.R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197. [Google Scholar] [CrossRef]
- Schürmann, T. Bias analysis in entropy estimation. J. Phys. A Math. Gen. 2004, 37, L295. [Google Scholar] [CrossRef]
- Chao, A.; Shen, T.J. Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Environ. Ecol. Stat. 2003, 10, 429–443. [Google Scholar] [CrossRef]
- Vu, V.Q.; Yu, B.; Kass, R.E. Coverage-adjusted entropy estimation. Stat. Med. 2007, 26, 4039–4060. [Google Scholar] [CrossRef] [PubMed]
- Horvitz, D.G.; Thompson, D.J. A generalization of sampling without replacement from a finite universe. J. Am. Stat. Assoc. 1952, 47, 663–685. [Google Scholar] [CrossRef]
- Bonachela, J.A.; Hinrichsen, H.; Munoz, M.A. Entropy estimates of small data sets. J. Phys. A Math. Theor. 2008, 41, 202001. [Google Scholar] [CrossRef]
- Good, I.J. The population frequencies of species and the estimation of population parameters. Biometrika 1953, 40, 237–264. [Google Scholar] [CrossRef]
- Painsky, A. Convergence guarantees for the Good-Turing estimator. J. Mach. Learn. Res. 2022, 23, 1–37. [Google Scholar]
- Zhang, Z.; Grabchak, M. Bias adjustment for a nonparametric entropy estimator. Entropy 2013, 15, 1999–2011. [Google Scholar] [CrossRef]
- Krichevsky, R.; Trofimov, V. The performance of universal encoding. IEEE Trans. Inf. Theory 1981, 27, 199–207. [Google Scholar] [CrossRef]
- Clarke, B.S.; Barron, A.R. Jeffreys’ prior is asymptotically least favorable under entropy risk. J. Stat. Plan. Inference 1994, 41, 37–60. [Google Scholar] [CrossRef]
- Holste, D.; Grosse, I.; Herzel, H. Bayes’ estimators of generalized entropies. J. Phys. Math. Gen. 1998, 31, 2551. [Google Scholar] [CrossRef]
- Schürmann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos: Interdiscip. J. Nonlinear Sci. 1996, 6, 414–427. [Google Scholar] [CrossRef] [PubMed]
- Trybula, S. Some problems of simultaneous minimax estimation. Ann. Math. Stat. 1958, 29, 245–253. [Google Scholar] [CrossRef]
- Archer, E.W.; Park, I.M.; Pillow, J.W. Bayesian entropy estimation for binary spike train data using parametric prior knowledge. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; Volume 26. [Google Scholar]
- Archer, E.; Park, I.M.; Pillow, J.W. Bayesian Entropy Estimation for Countable Discrete Distributions. J. Mach. Learn. Res. 2014, 15, 2833–2868. [Google Scholar]
- Kozachenko, L.F.; Leonenko, N.N. Sample estimate of the entropy of a random vector. Probl. Peredachi Informatsii 1987, 23, 9–16. [Google Scholar]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinform. 2006, 7, S7. [Google Scholar] [CrossRef] [PubMed]
- Daub, C.O.; Steuer, R.; Selbig, J.; Kloska, S. Estimating mutual information using B-spline functions–an improved similarity measure for analysing gene expression data. BMC Bioinform. 2004, 5, 118. [Google Scholar] [CrossRef] [PubMed]
- Hulle, M.M.V. Edgeworth approximation of multivariate differential entropy. Neural Comput. 2005, 17, 1903–1910. [Google Scholar] [CrossRef]
- Belghazi, M.I.; Baratin, A.; Rajeswar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, R.D. Mine: Mutual information neural estimation. arXiv 2018, arXiv:1801.04062. [Google Scholar]
- Poole, B.; Ozair, S.; Van Den Oord, A.; Alemi, A.; Tucker, G. On variational bounds of mutual information. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: New York, NY, USA, 2019; pp. 5171–5180. [Google Scholar]
- Song, J.; Ermon, S. Understanding the limitations of variational mutual information estimators. arXiv 2019, arXiv:1910.06222. [Google Scholar]
- Hausser, J.; Strimmer, K. Entropy: Estimation of Entropy, Mutual Information and Related Quantities; R Package: Vienna, Austria, 2021. [Google Scholar]
- Cao, L.; Grabchak, M. EntropyEstimation: Estimation of Entropy and Related Quantities; R Package: Vienna, Austria, 2015. [Google Scholar]
- Eric Marcon, B.H. Entropart: Entropy Partitioning to Measure Diversity; R Package: Vienna, Austria, 2023. [Google Scholar]
- Archer, E.; Park, M., II; Pillow, J.W. GitHub—Pillowlab/CDMentropy: Centered Dirichlet Mixture Entropy Estimator for Binary Data; GitHub: San Francisco, CA, USA, 2015. [Google Scholar]
- Archer, E.; Park, M., II; Pillow, J.W. GitHub—Pillowlab/PYMentropy: Discrete Entropy Estimator Using the Pitman-Yor Mixture (PYM) Prior; GitHub: San Francisco, CA, USA, 2020. [Google Scholar]
- Shalev, Y. GitHub—YuvalShalev/NJEE: Neural Joint Entropy Estimiator, Based on Corss-Entropy Loss; GitHub: San Francisco, CA, USA, 2023. [Google Scholar]
- Archer, E.; Park, M., II; Pillow, J.W. GitHub—Simomarsili/ndd: Bayesian Entropy Estimation in Python—Via the Nemenman-Schafee-Bialek Algorithm; GitHub: San Francisco, CA, USA, 2021. [Google Scholar]
- Wolpert, D.H.; Wolf, D.R. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841–6854. [Google Scholar] [CrossRef]



| Distribution Range | Estimators |
|---|---|
| Near-uniform | SHR NJ NSB |
| Mid-uniform | NJ NSB unseen jackknife BUB SHR |
| Near-deterministic (far-uniform) | Zhang PYM MM SG SHR NSB GSB unseen jackknife CWJ plug-in CS CDM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinchas, A.; Ben-Gal, I.; Painsky, A. A Comparative Analysis of Discrete Entropy Estimators for Large-Alphabet Problems. Entropy 2024, 26, 369. https://doi.org/10.3390/e26050369
Pinchas A, Ben-Gal I, Painsky A. A Comparative Analysis of Discrete Entropy Estimators for Large-Alphabet Problems. Entropy. 2024; 26(5):369. https://doi.org/10.3390/e26050369
Chicago/Turabian StylePinchas, Assaf, Irad Ben-Gal, and Amichai Painsky. 2024. "A Comparative Analysis of Discrete Entropy Estimators for Large-Alphabet Problems" Entropy 26, no. 5: 369. https://doi.org/10.3390/e26050369
APA StylePinchas, A., Ben-Gal, I., & Painsky, A. (2024). A Comparative Analysis of Discrete Entropy Estimators for Large-Alphabet Problems. Entropy, 26(5), 369. https://doi.org/10.3390/e26050369






