Entropy-Aided Meshing-Order Modulation Analysis for Wind Turbine Planetary Gear Weak Fault Detection under Variable Rotational Speed
Abstract
:1. Introduction
- (1)
- The strategy of the EMOM-based analysis is first expanded to the time-varying operational condition via the proposed novel EMOM analysis method.
- (2)
- The TFR, using the scaling basis, is refined using the local reassignment strategy, and a new SLRCT is constructed to realize accurate instantaneous rotational frequency extraction.
- (3)
- To identify the meshing modulation area under a time-varying rotational frequency, an EMOM indicator is designed, and an entropy-aided meshing-order gram (EMOMgram) is then constructed. Based on the EMOMgram, the frequency band with the highest indicator can be considered as the most sensitive, and the features of the weak gear fault can be located in the envelope order spectrum of the corresponding filtered result. With the help of information entropy, the selected optimal frequency band is relatively stable under different fault levels and operational modes.
- (4)
- We compare the proposed entropy-aided meshing modulation-based algorithm with the traditional Kurtogram-based algorithm for a planetary gearbox with three different fault levels on the sun gear. With the proposed method, fault-related features can be located not only in the lower orders, but also in the order representing the meshing frequency. This indicates that more features can be detected using the proposed algorithm. Furthermore, the proposed algorithm can locate the fault features of three different fault levels; however, the conventional method could only recognize severe gear faults of a missing tooth.
2. Entropy-Aided Meshing-Order Modulation Method
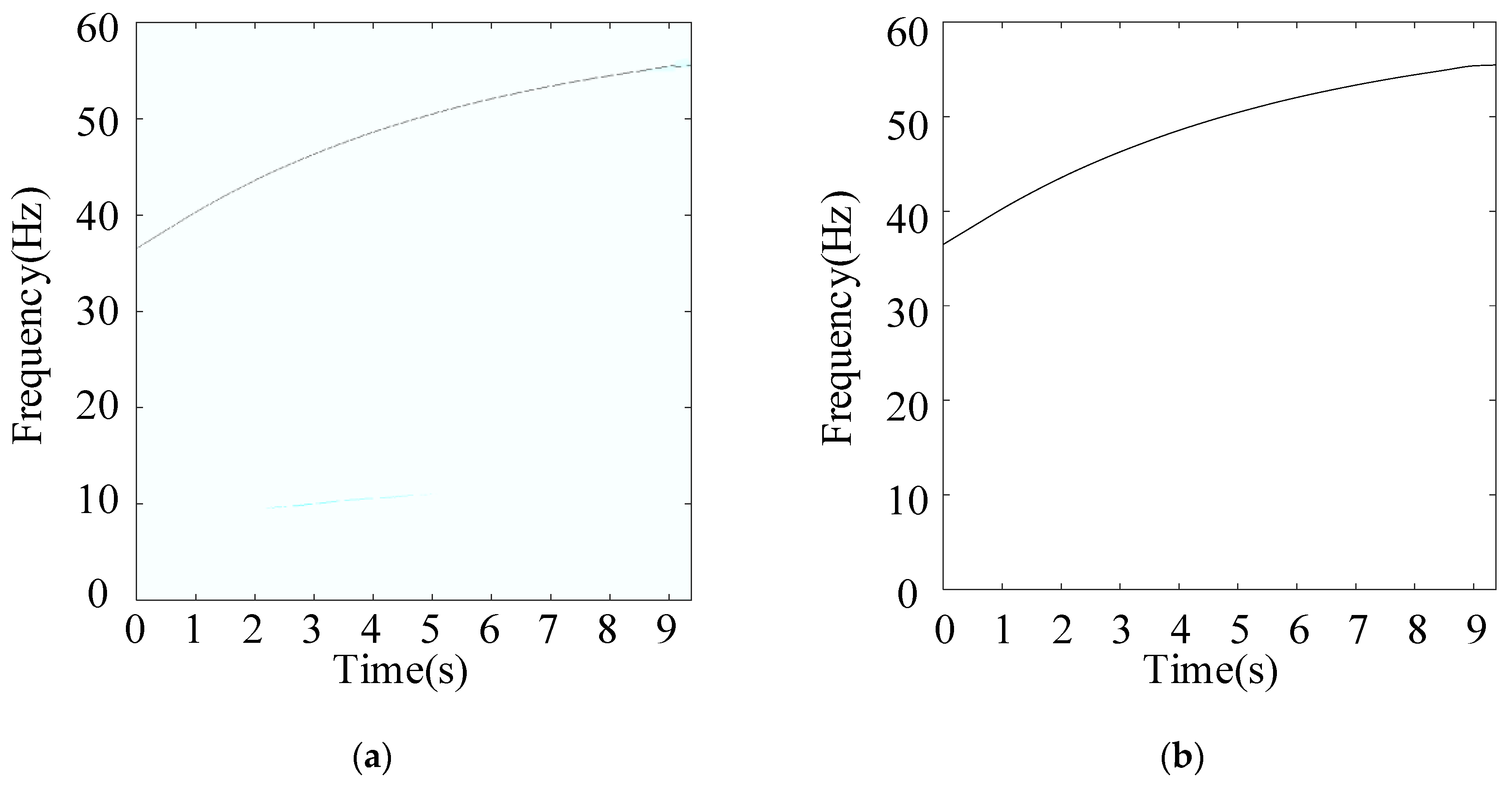
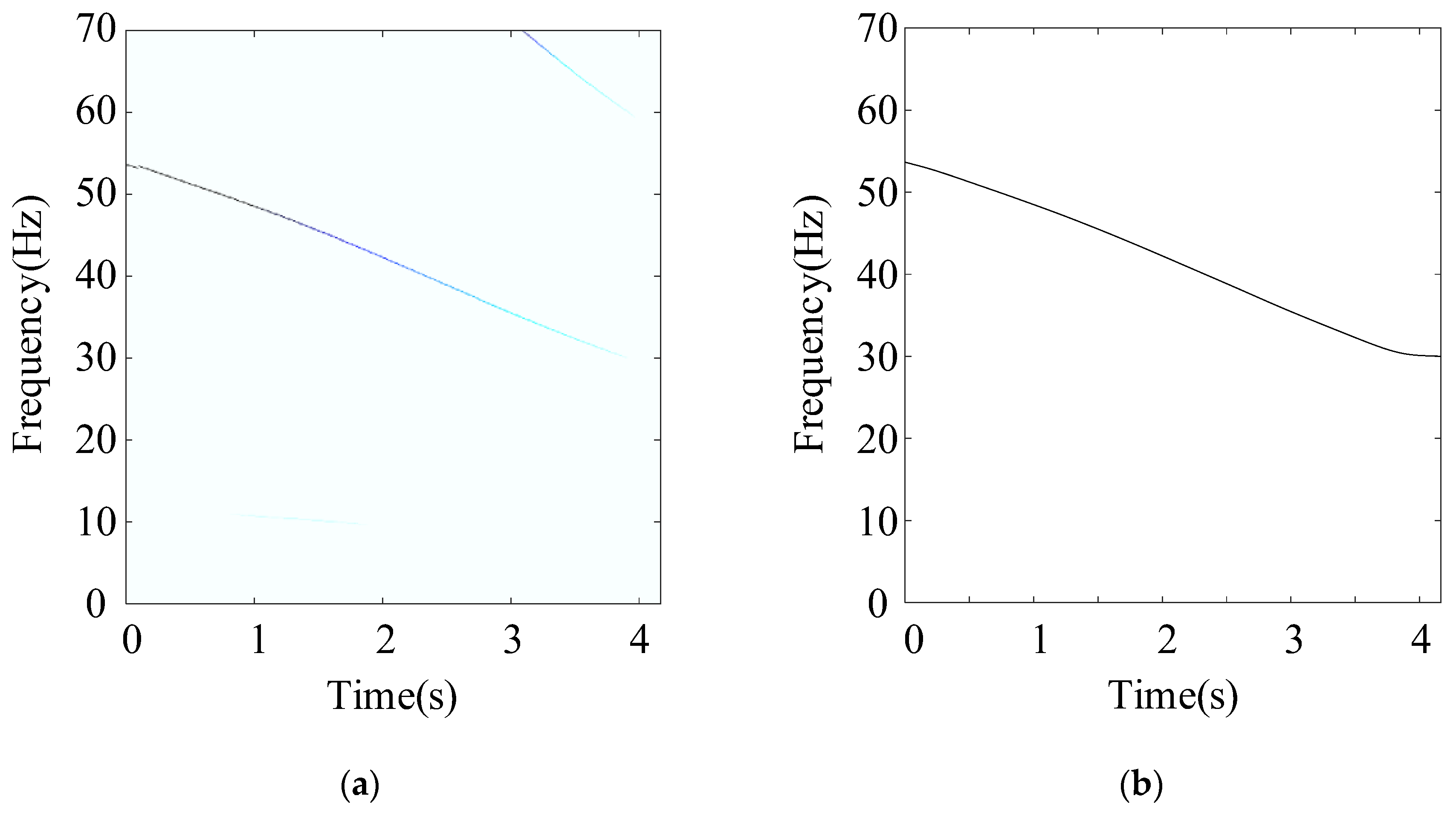
2.1. Instantaneous Rotational Frequency Extraction via Scaling-Basis Local Reassigning Chirplet Transform
2.2. Meshing Modulation Area Determination Using Entropy-Aided Meshing-Order Modulation Analysis
2.2.1. Signal Decomposition
- STEP 1: Filter banks in a binary tree structure containing multiple levels are first constructed by setting a low-pass prototype filter, and then designing quasi-analytic low-pass and high-pass filters using (11) based on the prototype in the following pyramidal manner:
- STEP 2: The current filtered result is further expanded for higher resolution in a 1/3-binary manner.
2.2.2. Entropy-Aided Meshing-Order Modulation Indicator
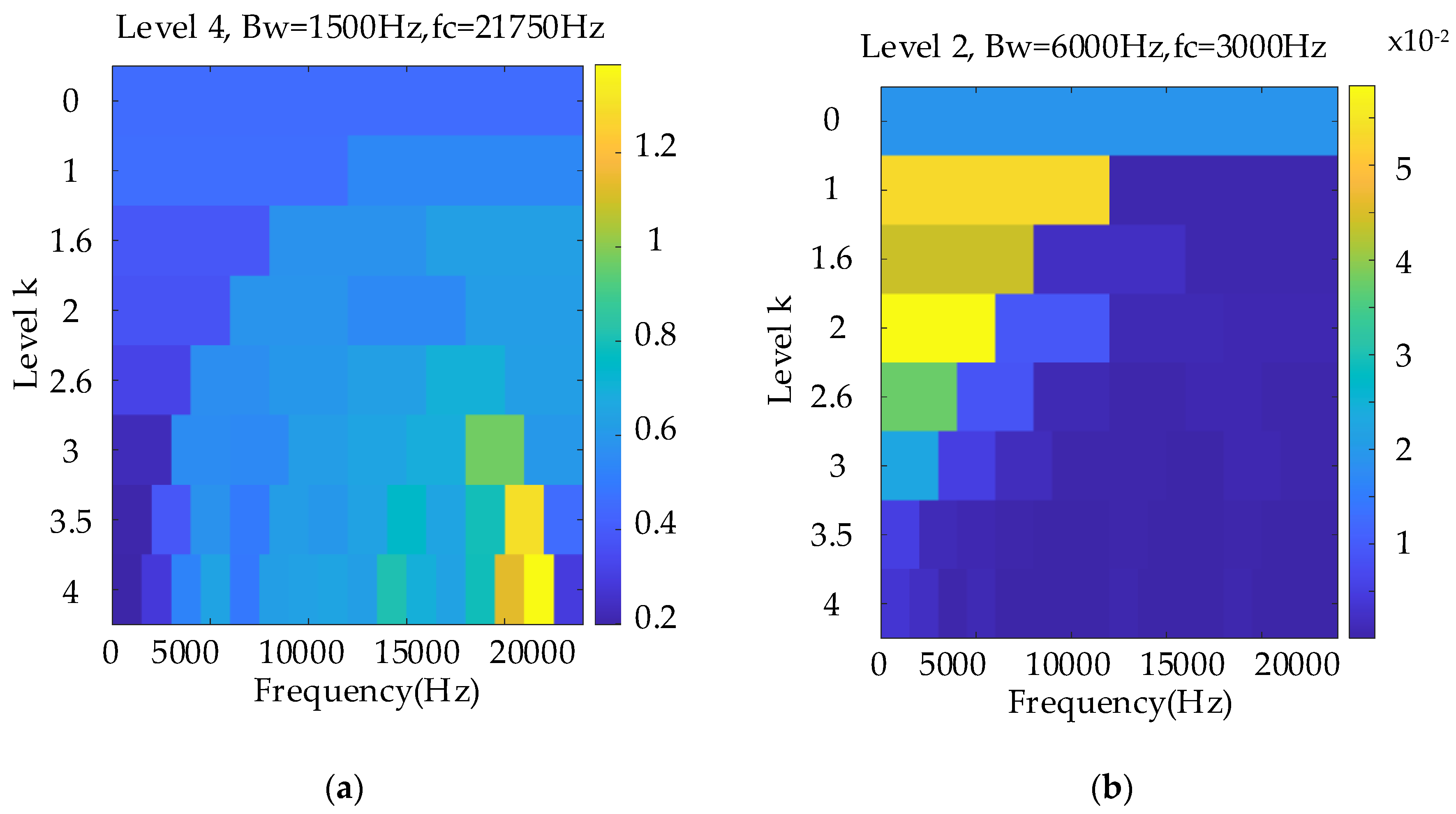
2.2.3. Entropy-Aided Meshing Modulation Area Determination via EMOMgram
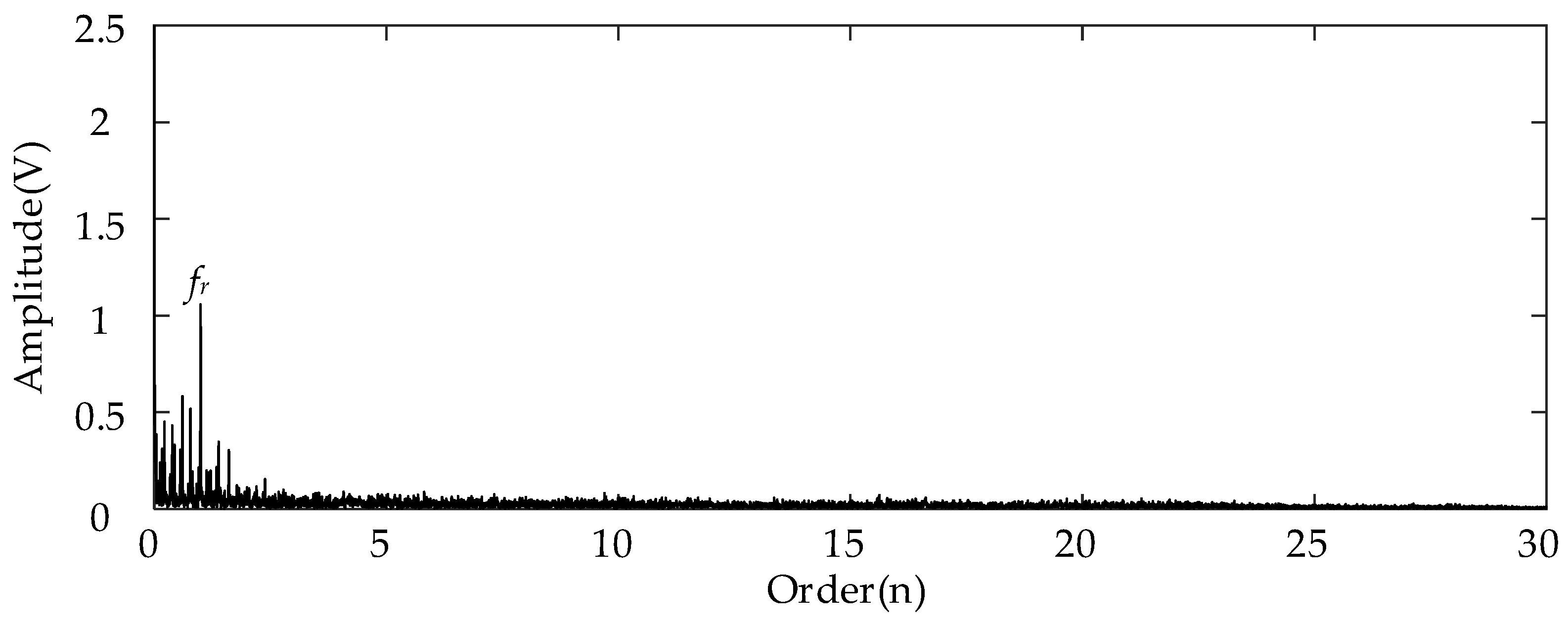
2.3. Gear Weak Fault Detection Based on Filtered Order Spectrum
3. Experimental Tests
3.1. Experimental Test Setup
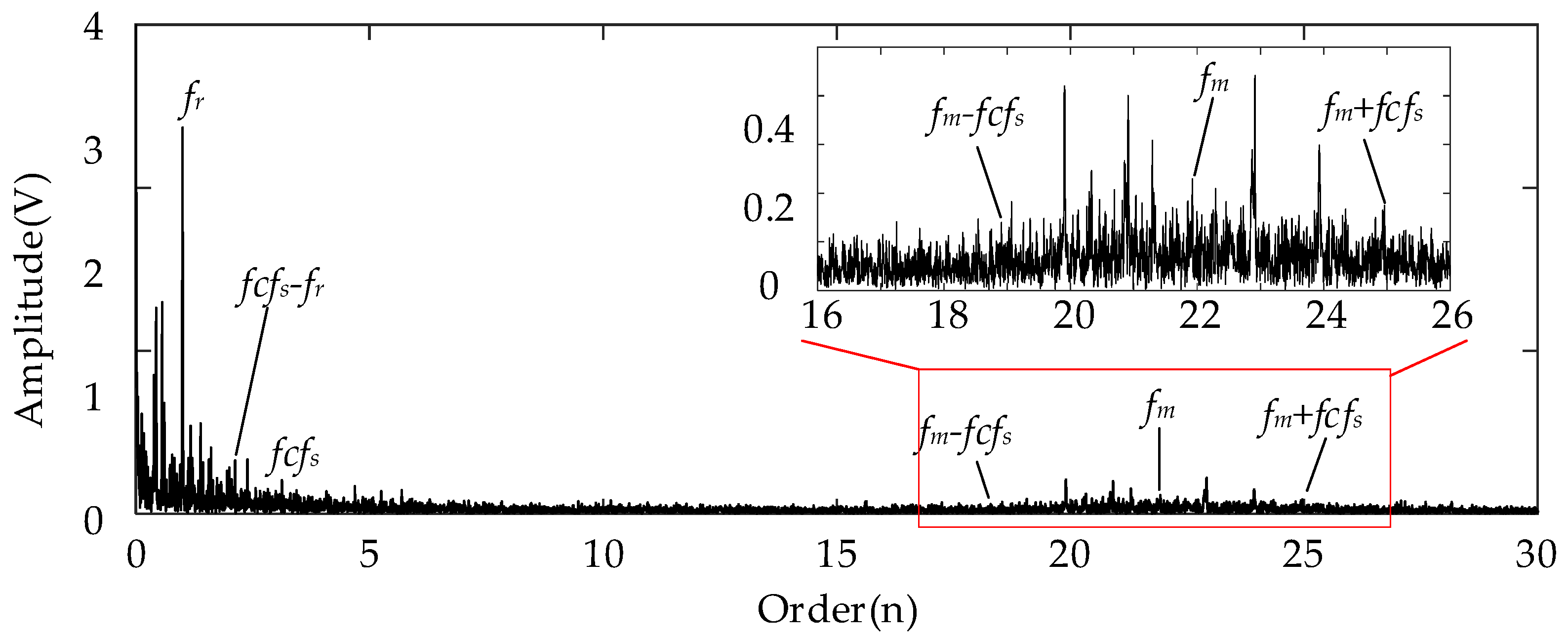
3.2. Fault Detection Results
3.2.1. Missing Tooth Fault
3.2.2. Tooth Break Fault
3.2.3. Tooth Root Crack Fault
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| SLRCT | Scaling-basis local reassigning chirplet transform |
| EMOM | Entropy-aided meshing-order modulation |
| TFR | Time–frequency representation |
| IF | Instantaneous frequency |
| EMOMgram | Entropy-aided meshing-order gram |
| FCF | Fault characteristic frequency |
References
- Feng, Z.; Zuo, M.J. Vibration Signal Models for Fault Diagnosis of Planetary Gearboxes. J. Sound Vib. 2012, 331, 4919–4939. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Li, W.; Li, Y. Frequency Response Model and Mechanism for Wind Turbine Planetary Gear Train Vibration Analysis. IET Renew. Power Gener. 2017, 11, 425–432. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Hoseini, M.R. Understanding Vibration Properties of a Planetary Gear Set for Fault Detection. In Proceedings of the 2014 International Conference on Prognostics and Health Management, PHM 2014, Cheney, WA, USA, 22–25 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Zuo, J.; Miao, Y.; Zhang, B.; Lin, J. Cyclostationary Feature Mode Decomposition and Its Application in Fault Diagnosis of Planetary Gearboxes via Built-in Information. IEEE Sens. J. 2023, 24, 1129–1139. [Google Scholar] [CrossRef]
- Sun, B.; Li, H.; Wang, C.; Zhang, K.; Chen, S. Current-Aided Dynamic Time Warping for Planetary Gearbox Fault Detection at Time-Varying Speeds. IEEE Sens. J. 2023, 24, 390–402. [Google Scholar] [CrossRef]
- McFadden, P.D.; Howard, I.M. The Detection of Seeded Faults in an Epicyclic Gearbox by Signal Averaging of the Vibration; Aeronautical Research Laboratories: Melbourne, Australia, 1990. [Google Scholar]
- Chen, B.; Song, D.; Cheng, Y.; Zhang, W.; Huang, B.; Muhamedsalih, Y. IGIgram: An Improved Gini Index-Based Envelope Analysis for Rolling Bearing Fault Diagnosis. J. Dyn. Monit. Diagn. 2022, 1, 111–124. [Google Scholar] [CrossRef]
- Inalpolat, M.; Kahraman, A. A Theoretical and Experimental Investigation of Modulation Sidebands of Planetary Gear Sets. J. Sound Vib. 2009, 323, 677–696. [Google Scholar] [CrossRef]
- McFadden, P.D. Window Functions for the Calculation of the Time Domain Averages of the Vibration of the Individual Planet Gears and Sun Gear in an Epicyclic Gearbox. J. Vib. Acoust. Trans. ASME 1994, 116, 179–187. [Google Scholar] [CrossRef]
- Samuel, P.D.; Pines, D.J. Vibration Separation Methodology for Planetary Gear Health Monitoring. In Smart Structures and Materials 2000: Smart Structures and Integrated Systems; SPIE: Bellingham, WA, USA, 2000; Volume 3985, pp. 250–260. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Y.; Wu, X.; Na, J. Localized Fault Detection of Sun Gears Based on Windowed Synchronous Averaging in the Angular Domain. Adv. Mech. Eng. 2017, 9, 1687814017696412. [Google Scholar] [CrossRef]
- Barszcz, T.; Randall, R.B. Application of Spectral Kurtosis for Detection of a Tooth Crack in the Planetary Gear of a Wind Turbine. Mech. Syst. Signal Process. 2009, 23, 1352–1365. [Google Scholar] [CrossRef]
- Fan, Z.; Li, H. A Hybrid Approach for Fault Diagnosis of Planetary Bearings Using an Internal Vibration Sensor. Meas. J. Int. Meas. Confed. 2015, 64, 71–80. [Google Scholar] [CrossRef]
- Lei, Y.; Han, D.; Lin, J.; He, Z. Planetary Gearbox Fault Diagnosis Using an Adaptive Stochastic Resonance Method. Mech. Syst. Signal Process. 2013, 38, 113–124. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J.; Hao, R.; Chu, F.; Lee, J. Ensemble Empirical Mode Decomposition-Based Teager Energy Spectrum for Bearing Fault Diagnosis. J. Vib. Acoust. 2013, 135, 1–21. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J.; Qu, J.; Tian, T.; Liu, Z. Joint Amplitude and Frequency Demodulation Analysis Based on Local Mean Decomposition for Fault Diagnosis of Planetary Gearboxes. Mech. Syst. Signal Process. 2013, 40, 56–75. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, D.; Zuo, M. Planetary Gearbox Fault Diagnosis via Joint Amplitude and Frequency Demodulation Analysis Based on Variational Mode Decomposition. Appl. Sci. 2017, 7, 775. [Google Scholar] [CrossRef]
- Wang, T.; Chu, F.; Feng, Z. Meshing Frequency Modulation (MFM) Index-Based Kurtogram for Planet Bearing Fault Detection. J. Sound Vib. 2018, 432, 437–453. [Google Scholar] [CrossRef]
- Wang, T.; Chu, F.; Han, Q. Fault Diagnosis for Wind Turbine Planetary Ring Gear via a Meshing Resonance Based Fi Ltering Algorithm. ISA Trans. 2017, 67, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Yan, R.; Liu, Y.; Wang, Q. Tacholess Speed Estimation in Order Tracking: A Review with Application to Rotating Machine Fault Diagnosis. IEEE Trans. Instrum. Meas. 2019, 68, 2315–2332. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, H.; Cui, L. Frequency-Chirprate Synchrosqueezing-Based Scaling Chirplet Transform for Wind Turbine Nonstationary Fault Feature Time–Frequency Representation. Mech. Syst. Signal Process. 2024, 209, 111112. [Google Scholar] [CrossRef]
- Shi, J.; Liang, M.; Necsulescu, D.-S.; Guan, Y. Generalized Stepwise Demodulation Transform and Synchrosqueezing for Time-Frequency Analysis and Bearing Fault Diagnosis. J. Sound Vib. 2016, 368, 202–222. [Google Scholar] [CrossRef]
- Liu, D.; Cui, L.; Cheng, W. A Review on Deep Learning in Planetary Gearbox Health State Recognition: Methods, Applications, and Dataset Publication. Meas. Sci. Technol. 2024, 35, 012002. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Wang, H.; Bai, Y.; Mao, J.X.; Chang, X.Y.; Wang, L. Bin Switching Bayesian Dynamic Linear Model for Condition Assessment of Bridge Expansion Joints Using Structural Health Monitoring Data. Mech. Syst. Signal Process. 2021, 160, 107879. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep Neural Networks: A Promising Tool for Fault Characteristic Mining and Intelligent Diagnosis of Rotating Machinery with Massive Data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Han, D.; Guo, X.; Shi, P. An Intelligent Fault Diagnosis Method of Variable Condition Gearbox Based on Improved DBN Combined with WPEE and MPE. IEEE Access 2020, 8, 131299–131309. [Google Scholar] [CrossRef]
- Han, Y.; Tang, B.; Deng, L. An Enhanced Convolutional Neural Network with Enlarged Receptive Fields for Fault Diagnosis of Planetary Gearboxes. Comput. Ind. 2019, 107, 50–58. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Wang, Y. An Intelligent Diagnosis Scheme Based on Generative Adversarial Learning Deep Neural Networks and Its Application to Planetary Gearbox Fault Pattern Recognition. Neurocomputing 2018, 310, 213–222. [Google Scholar] [CrossRef]
- Yu, X.; Tang, B.; Zhang, K. Fault Diagnosis of Wind Turbine Gearbox Using a Novel Method of Fast Deep Graph Convolutional Networks. IEEE Trans. Instrum. Meas. 2021, 70, 6502714. [Google Scholar] [CrossRef]
- Li, M.; Wang, T.; Chu, F.; Han, Q.; Qin, Z.; Zuo, M.J. Scaling-Basis Chirplet Transform. IEEE Trans. Ind. Electron. 2021, 68, 8777–8788. [Google Scholar] [CrossRef]
- Guan, Y.; Liang, M.; Necsulescu, D.S. Velocity Synchronous Linear Chirplet Transform. IEEE Trans. Ind. Electron. 2019, 66, 6270–6280. [Google Scholar] [CrossRef]
- Yu, G.; Wang, Z.; Zhao, P.; Li, Z. Local Maximum Synchrosqueezing Transform: An Energy-Concentrated Time-Frequency Analysis Tool. Mech. Syst. Signal Process. 2019, 117, 537–552. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. Second-Order Synchrosqueezing Transform or Invertible Reassignment? Towards Ideal Time-Frequency Representations. IEEE Trans. Signal Process. 2015, 63, 1335–1344. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Huang, Z.; Xia, Y. An Improved Multi-Taper S-Transform Method to Estimate Evolutionary Spectrum and Time-Varying Coherence of Nonstationary Processes. Mech. Syst. Signal Process. 2023, 198, 110386. [Google Scholar] [CrossRef]
- Antoni, J. Fast Computation of the Kurtogram for the Detection of Transient Faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]


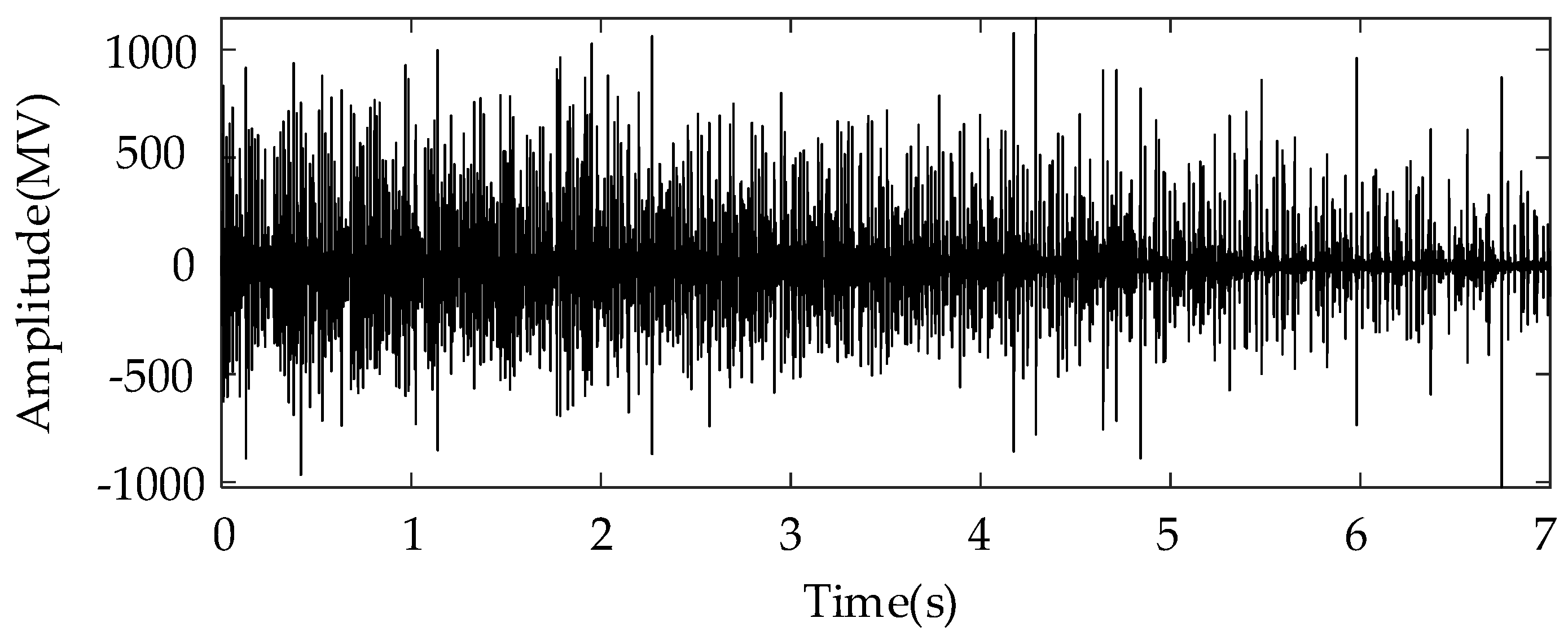
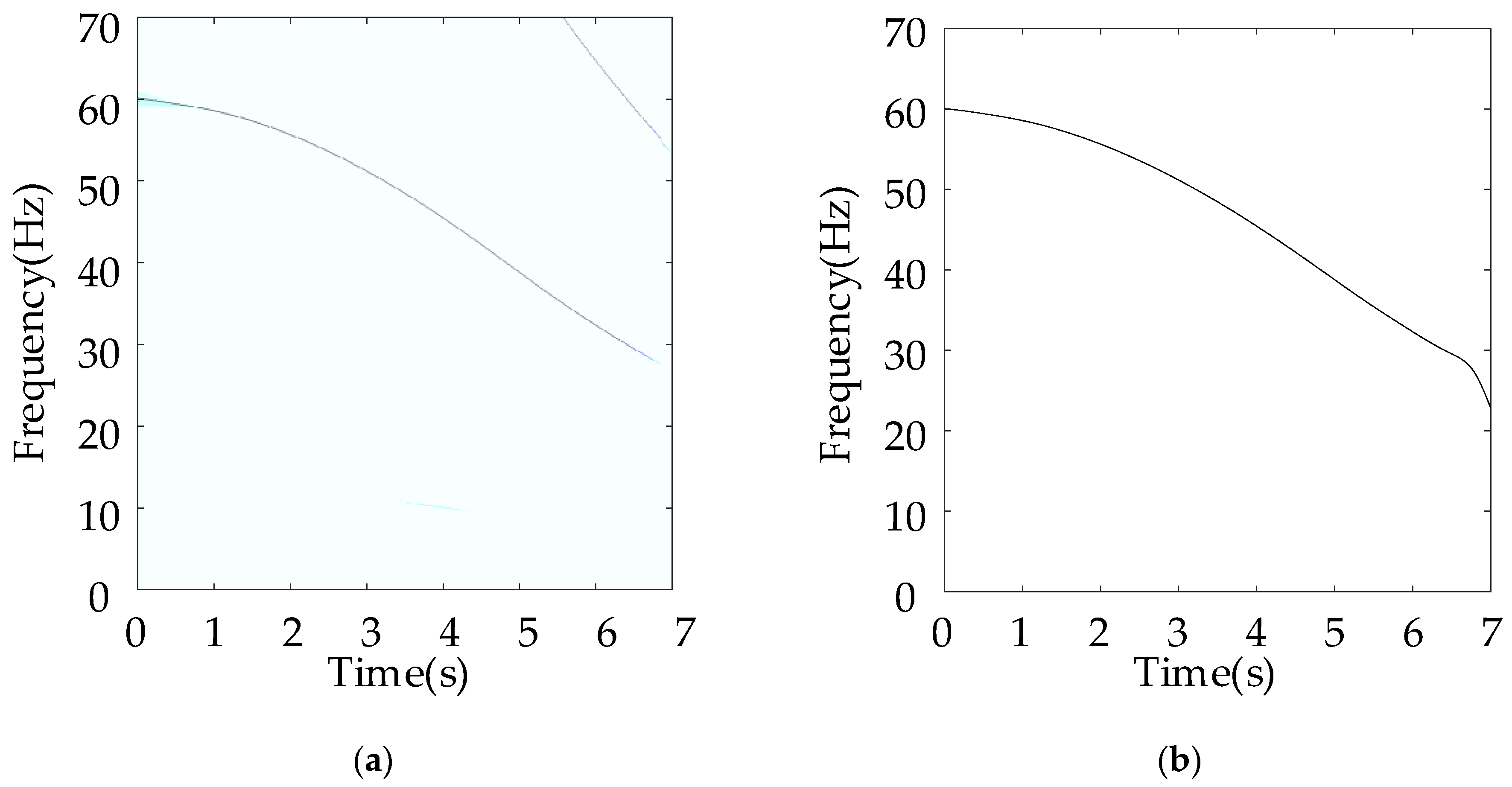

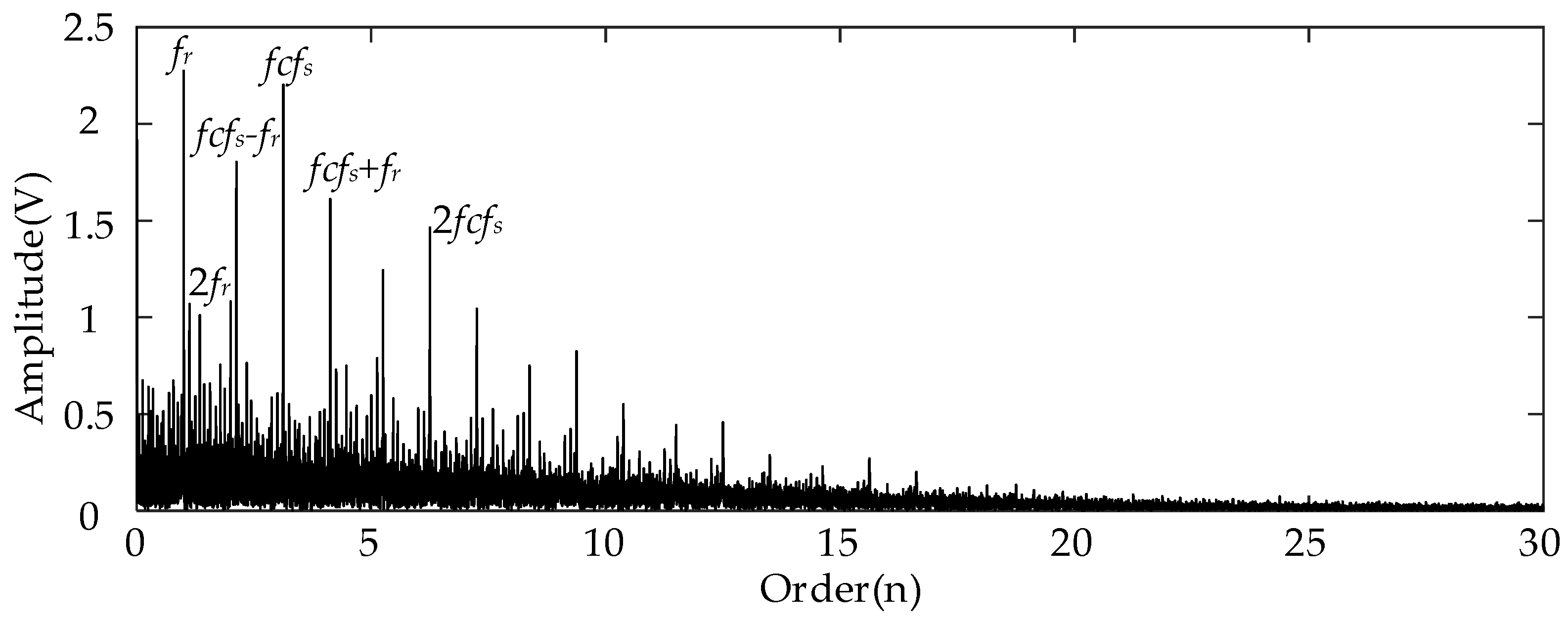
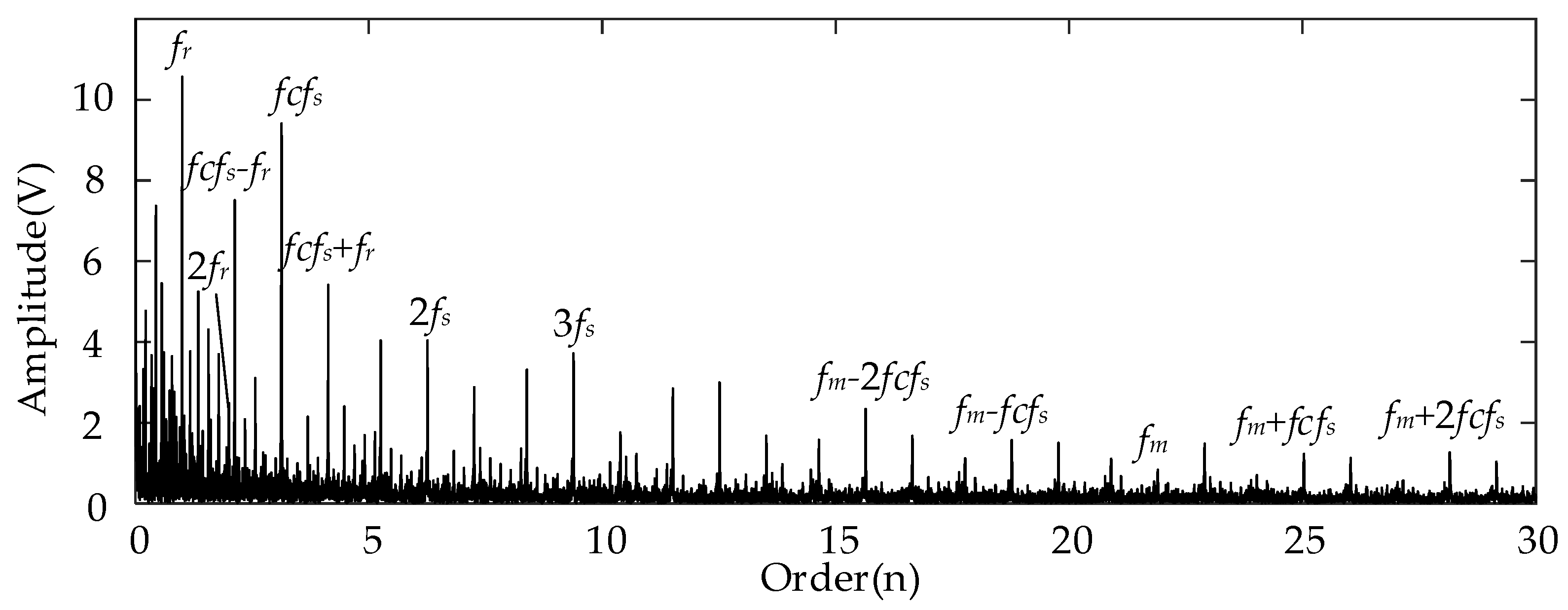





| Title 1 | First Level | Second Level | Third Level | ||||
|---|---|---|---|---|---|---|---|
| Gear | Sun gear Zs | Planetary gear Zp | Ring gear Zr | Low speed Z2l | High speed Z2h | Low speed Z3l | High speed Z3h |
| Tooth number | 28 | 36 (4) | 100 | 100 | 29 | 90 | 36 |
| Ratio | 5.647 | 3.44 | 2.5 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, S.; Wu, H.; Shen, H.; Wang, T.; Fu, H. Entropy-Aided Meshing-Order Modulation Analysis for Wind Turbine Planetary Gear Weak Fault Detection under Variable Rotational Speed. Entropy 2024, 26, 409. https://doi.org/10.3390/e26050409
Zhi S, Wu H, Shen H, Wang T, Fu H. Entropy-Aided Meshing-Order Modulation Analysis for Wind Turbine Planetary Gear Weak Fault Detection under Variable Rotational Speed. Entropy. 2024; 26(5):409. https://doi.org/10.3390/e26050409
Chicago/Turabian StyleZhi, Shaodan, Hengshan Wu, Haikuo Shen, Tianyang Wang, and Hongfei Fu. 2024. "Entropy-Aided Meshing-Order Modulation Analysis for Wind Turbine Planetary Gear Weak Fault Detection under Variable Rotational Speed" Entropy 26, no. 5: 409. https://doi.org/10.3390/e26050409
APA StyleZhi, S., Wu, H., Shen, H., Wang, T., & Fu, H. (2024). Entropy-Aided Meshing-Order Modulation Analysis for Wind Turbine Planetary Gear Weak Fault Detection under Variable Rotational Speed. Entropy, 26(5), 409. https://doi.org/10.3390/e26050409






