A Direct Entropic Approach to the Thermal Balance of Spontaneous Chemical Reactions
Abstract
:1. Introduction
1.1. Foundations
1.2. Qualitative Description of an Exothermic Reaction
1.3. The Model to Be Discussed in This Paper: Assumptions and Limitations
1.4. Teaching Thermodynamics and Thermochemistry
2. Conceptual Background
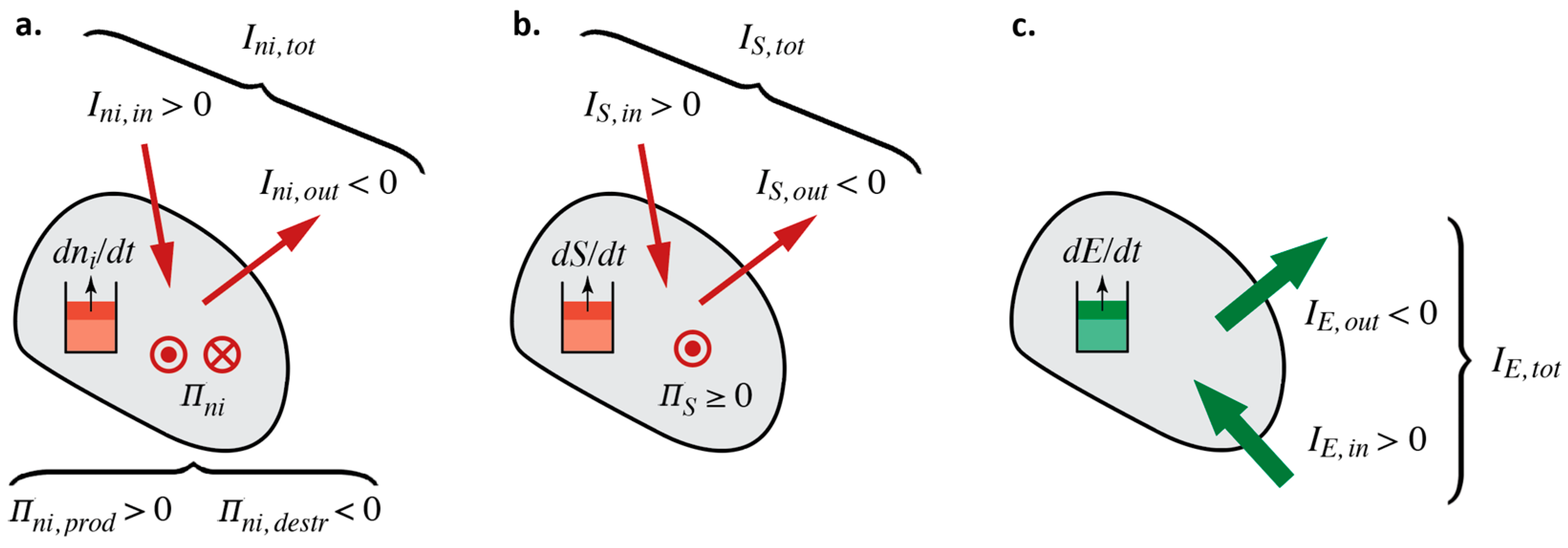
2.1. Spatially Uniform Processes and Consequences of Steady-State Operation
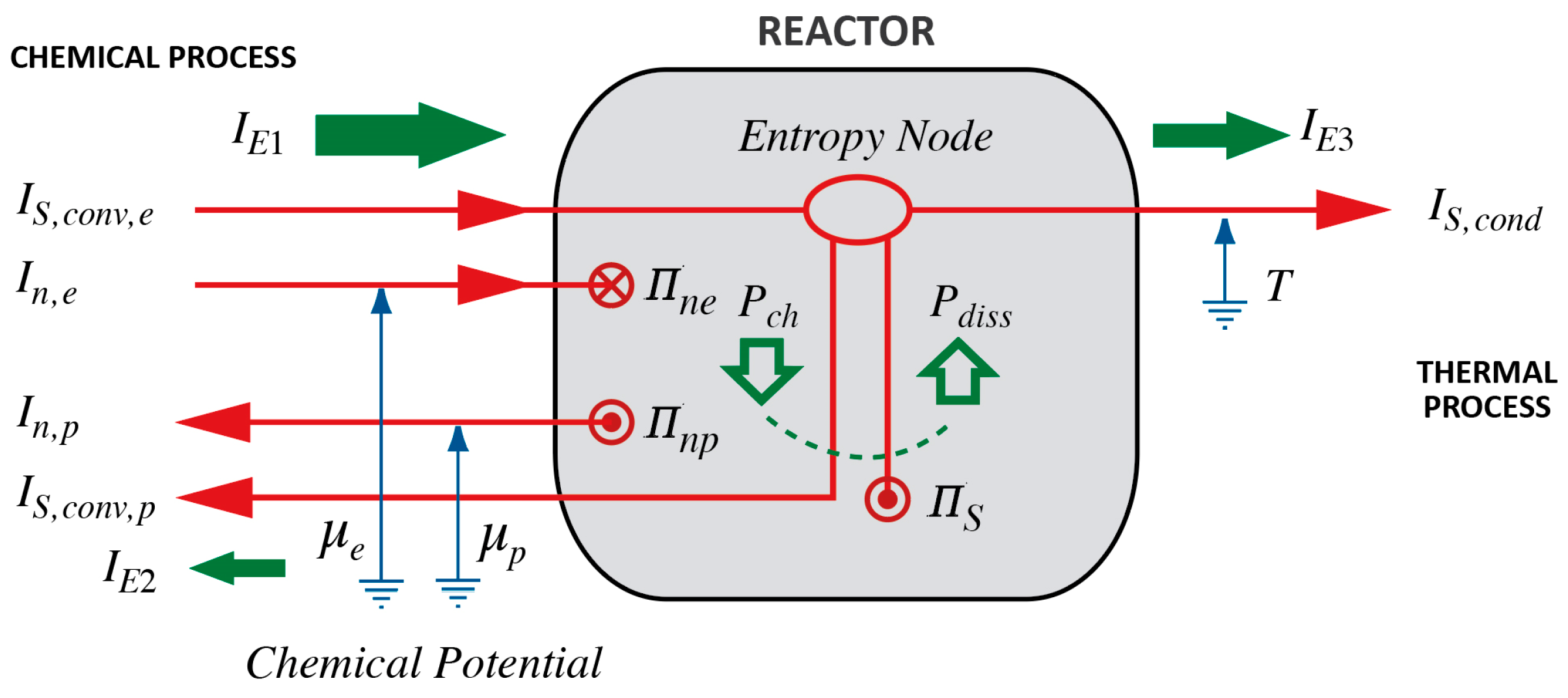
2.2. The General Balances of Amount of Substance, Entropy, and Energy
2.3. Stoichiometry, Individual Production/Destruction Rates, and Overall Reaction Rate
2.4. The Entropy of Substances and Convective Entropy Currents
2.5. Power and Energy Currents of Chemical and Thermal Processes
3. A Model of Exothermic and Endothermic Chemical Reactions
3.1. Basing the Model upon the Primitive Concepts of Chemical and Thermal Processes
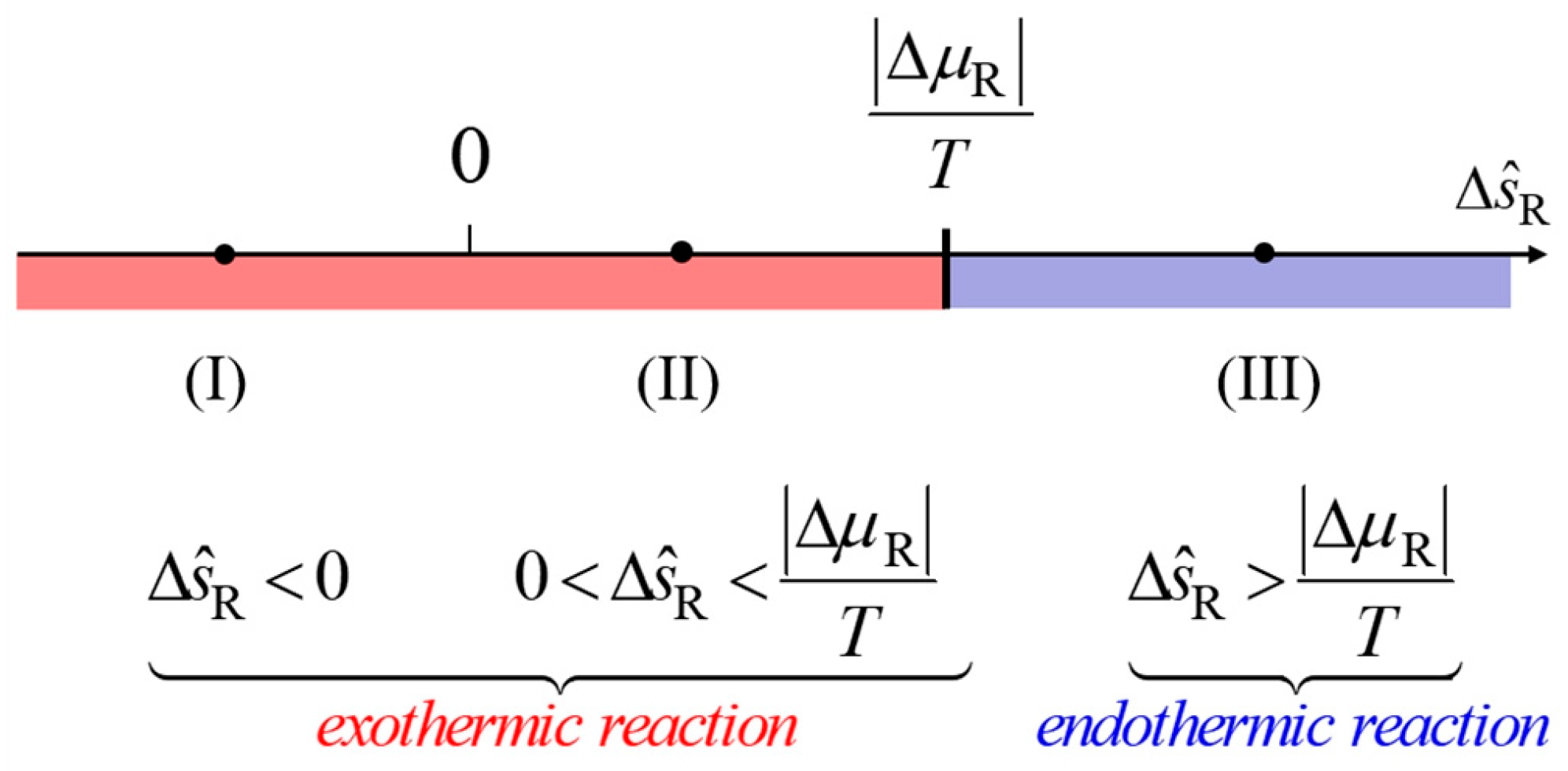
3.2. Interpreting the Conditions for Heating/Cooling
4. Examples of Spontaneous Steady-State Exothermic and Endothermic Reactions
4.1. Example I: Methane Combustion—Exothermic Process
4.2. Example II: Decomposition of Hydrogen Peroxide—Exothermic Process
4.3. Example III: Reaction of Barium Hydroxide and Ammonium Nitrate—Endothermic Process
5. Some Didactic Considerations
5.1. Preparing Learners for a Direct Approach to Thermal and Chemical Dynamics
5.2. Energy Exchanged in Heating/Cooling and Thermodynamic Potentials
5.3. The Power of a Direct Approach to Experiential Primitives
5.4. The Power of a Dynamical Systems Approach to Processes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Fuchs, H.U. A Direct Entropic Approach to Uniform and Spatially Continuous Dynamical Models of Thermoelectric Devices. Energy Harvest. Syst. 2014, 1, 253–265. [Google Scholar] [CrossRef]
- Fuchs, H.U. The Dynamics of Heat, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Fuchs, H.U.; D’Anna, M.; Corni, F. Entropy and the experience of heat. Entropy 2022, 24, 646–682. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A. Advanced Engineering Thermodynamics; John Wiley & Sons: New York, NY, USA, 1988. [Google Scholar]
- Bejan, A. Entropy Generation Minimization. The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- De Vos, A. Thermodynamics of Solar Energy Conversion; Wiley-VCH Verlag: New York, NY, USA, 2008. [Google Scholar]
- Sieniutycz, S.; De Vos, A. (Eds.) Thermodynamics of Energy Conversion and Transport; Springer: New York, NY, USA, 2000. [Google Scholar]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics. In Encyclopedia of Physics; Flügge, S., Ed.; v. III/3; Springer: Berlin/Heidelberg, Germany, 1965. [Google Scholar]
- Truesdell, C.; Toupin, R.A. The Classical Field Theories. In Encyclopedia of Physics; Flügge, S., Ed.; v. III/1; Springer: Berlin/Heidelberg, Germany, 1960. [Google Scholar]
- Truesdell, C.A. Rational Thermodynamics, 2nd ed.; Springer: New York, NY, USA, 1984. [Google Scholar]
- Müller, I. Thermodynamics; Pitman: Boston, MA, USA, 1985. [Google Scholar]
- Jou, D.; Casas-Vázqzez, J.; Lebon, G. Extended Irreversible Thermodynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Gentner, D. Structure-mapping: A theoretical framework for analogy. Cogn. Sci. 1983, 7, 155–170. [Google Scholar]
- Fuchs, H.U. From image schemas to dynamical models in fluids, electricity, heat, and motion Examples, Practical Experience, and Philosophy. In Proceedings of the 2006 GIREP Conference, Modeling in Physics and Physics Education, Amsterdam, The Netherlands, 20–25 August 2006; van den Berg, E., Ellermeijer, T., Slooten, O., Eds.; GIREP: Reims, France; pp. 166–187. [Google Scholar]
- Herrmann, F.; Wu, G.; Pohlig, M.; Fuchs, H.U.; D’Anna, M.; Rosenberg, J. Analogies: A key to understanding physics. In Proceedings of the Selected Papers of the GIREP-ICPE-MPTL International Conference-Reims, Reims, France, 22–27 August 2010; Kaminski, W., Michelini, M., Eds.; GIREP: Reims, France; pp. 145–163. [Google Scholar]
- Corni, F.; Fuchs, H.U.; Dumont, E. Conceptual metaphor in physics education: Roots of analogy, visual metaphors, and a primary physics course for student teachers. J. Phys. Conf. Ser. 2019, 1286, 012059. [Google Scholar] [CrossRef]
- D’Anna, M.; Fuchs, H.U.; Lubini, P. System Dynamics Modeling: From Mechanics to Chemistry. A Dynamical Model of Mutarotation of Glucose. In Selected Papers of the Girep Conference, Physics Curriculum Design, Development and Validation; University of Cyprus: Nicosia, Cyprus, 2008. [Google Scholar]
- Fuchs, H.U. Introductory Chemical Dynamics—Using the Chemical Potential from the Start. Rev. Cub. Fis. 2010, 27 Pt 2A, 119–124. [Google Scholar]
- Lubini, P.; D’Anna, M. Adopting the Chemical Potential in the High School Curriculum: Why not? CHIMIA Int. J. Chem. 2018, 72, 32–35. [Google Scholar] [CrossRef] [PubMed]
- Carnot, S. Réflexions Sur la Puissance Motrice du Feu et Sur Les Machines Propres à Développer Cette Puissance; Bachelier: Paris, France, 1824. [Google Scholar]
- Klotz, I.M.; Rosenberg, R.M. Chemical Thermodynamics: Basic Theories and Methods; The Benjamin/Cummings Publishing Company, Inc.: Melo Park, CA, USA, 1986. [Google Scholar]
- Atkins, P.; de Paula, J.; Keeler, J. Atkins’ Physical Chemistry, 12th ed.; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
- Haynie, D.T. Biological Thermodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Bain, K.; Moon, A.; Mack, R.; Towns, M.H. A review of research on the teaching and learning of thermodynamics at the university level. Chem. Educ. Res. Pract. 2014, 15, 320–335. [Google Scholar] [CrossRef]
- Tsaparlis, G. Teaching and learning physical chemistry: A review of educational research. In Advances in Teaching Physical Chemistry; Ellison, M.D., Schoolcraft, T.A., Eds.; American Chemical Society: Washington, DC, USA, 2007; pp. 75–112. [Google Scholar]
- Kibirige, I.; Masemola, M.A. Grade 12 Learners’ Understanding of Chemical Reactions. Mediterr. J. Soc. Sci. 2014, 5, 290–295. [Google Scholar] [CrossRef]
- MacWood, G.; Verhoek, F.H. How Can You Tell Whether a Reaction Will Occur? J. Chem. Educ. 1961, 38, 334–337. [Google Scholar] [CrossRef]
- Carson, E.M.; Watson, J.R. Undergraduate students’ understandings of entropy and Gibbs free energy. Univ. Chem. Educ. 2002, 6, 4–12. [Google Scholar]
- Bain, K.; Towns, M.H. Investigation of Undergraduate and Graduate Chemistry Students’ Understanding of Thermodynamic Driving Forces in Chemical Reactions and Dissolution. J. Chem. Educ. 2018, 95, 512–520. [Google Scholar] [CrossRef]
- Ochs, R.S. Thermodynamics and Spontaneity. J. Chem. Educ. 1996, 73, 952–954. [Google Scholar] [CrossRef]
- Tarsitani, C.; Vicentini, M. Scientific Mental Representations of Thermodynamics. Sci. Educ. 1996, 5, 51–68. [Google Scholar] [CrossRef]
- Banerjee, A. Teaching Chemical Equilibrium and Thermodynamics in Undergraduate General Chemistry Classes. J. Chem. Educ. 1995, 72, 879–881. [Google Scholar] [CrossRef]
- Job, G.; Rüffler, R. Physical Chemistry from a Different Angle; Springer: New York, NY, USA, 2016. [Google Scholar]
- Keenan, J.H. Availability and Irreversibility in Thermodynamics. Br. J. Appl. Phys. 1951, 2, 183–192. [Google Scholar] [CrossRef]
- Corning, P.A.; Kline, S.J. Thermodynamics, Information and Life Revisited, Part I: ‘To Be or Entropy’. Syst. Res. 1998, 15, 273–295. [Google Scholar] [CrossRef]
- Corni, F.; Fuchs, H.U. Primary Physical Science for Student Teachers at Kindergarten and Primary School Levels: Part I—Foundations of an Imaginative Approach to Physical Science. Interchange 2020, 51, 315–343. [Google Scholar] [CrossRef]
- Tyreus, B. Dominant Variables for Partial Control. 1. A Thermodynamic Method for their Identification. Ind. Eng. Chem. Res. 1999, 38, 1432–1443. [Google Scholar] [CrossRef]
- Falk, G.; Herrmann, F.; Schmid, G.B. Energy forms or energy carriers? Am. J. Phys. 1983, 51, 1074–1077. [Google Scholar] [CrossRef]
- Arcak, M. On spatially uniform behavior in reaction-diffusion PDE and coupled ODE systems. arXiv 2018, arXiv:0908.2614. [Google Scholar]
- Brenig, L. 2018 Reducing nonlinear dynamical systems to canonical forms. Phil. Trans. R. Soc. A 2018, 376, 20170384. [Google Scholar] [CrossRef] [PubMed]
- Lumped Parameter Model for the Cardiovascular System. Available online: https://en.wikipedia.org/wiki/Lumped_parameter_model_for_the_cardiovascular_system (accessed on 22 April 2024).
- Herrmann, F. Comencemos con la entropia. Rev. Cub. Fis. 2010, 27 Pt 2A, 113–118. [Google Scholar]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatics; Wiley: New York, NY, USA, 1985; p. 318. [Google Scholar]
- Job, G.; Herrmann, F. Chemical potential—A quantity in search of recognition. Eur. J. Phys. 2006, 27, 353–371. [Google Scholar] [CrossRef]
- Job, G. Table of Chemical Potentials. Available online: https://www.job-stiftung.de/index7dbf.html?data-collection (accessed on 8 February 2024).
- Fuchs, H.U.; Corni, F. Primary Physical Science Education. An Imaginative Approach to Encounters with Nature; Springer: Cham, Switzerland, 2023. [Google Scholar]
- The Engineering Toolbox: Standard State and Enthalpy of Formation, Gibbs Free Energy of Formation, Entropy and Heat Capacity. Available online: https://www.engineeringtoolbox.com/standard-state-enthalpy-formation-definition-value-Gibbs-free-energy-entropy-molar-heat-capacity-d_1978.html (accessed on 9 February 2024).
- The Engineering Toolbox: Standard Enthalpy of Formation, Gibbs Energy of Formation, Entropy and Molar Heat Capacity of Organic Substances. Available online: https://www.engineeringtoolbox.com/standard-enthalpy-formation-value-Gibbs-free-energy-entropy-heat-capacity-organic-d_1979.html (accessed on 9 February 2024).
- Raff, L.M. Spontaneity and Equilibrium: Why “ΔG < 0 Denotes a Spontaneous Process” and “ΔG = 0 Means the System Is at Equilibrium” Are Incorrect. J. Chem. Educ. 2014, 72, 879. [Google Scholar]
- Glasser, L. Correct Use of Physique, une présentation dynamique. Helmholtz and Gibbs Function Differences, ΔA and ΔG: The van’t Hoff Reaction Box. J. Chem. Educ. 2016, 93, 978–980. [Google Scholar] [CrossRef]
- Glass, S.V.; DeKock, R.L. A Mechanical Analogue for Chemical Potential, Extent of Reaction, and the Gibbs Energy. J. Chem. Educ. 2016, 75, 190–193. [Google Scholar] [CrossRef]
- Prigogine, I.; Kondepudi, D. Modern Thermodynamics—From Heat Engines to Dissipative Structures; Wiley: Chichester, UK, 1998; pp. 103–118. [Google Scholar]
- De Donder, T. L’Affinité; Gauthier-Villars: Paris, France, 1936; p. 18. [Google Scholar]
- Lambert, F.L. Disorder—A Cracked Crutch for Supporting Entropy Discussions. J. Chem. Educ. 2002, 79, 187–192. [Google Scholar] [CrossRef]
- Gerhart, F.J. The A+B C of Chemical Thermodynamics. J. Chem. Educ. 1994, 71, 539–548. [Google Scholar] [CrossRef]
| CH4 + 2O2 |  | CO2 + 2H2O | ||||
| −0.25 | ||||||
| −2.74 | ||||||
| −2.99 | ||||||
| (a) | (b) | |||||
| 2 H2O2 |  | 2 H2O + O2 | ||||
| +0.125 | ||||||
| −0.784 | ||||||
| −0.659 | ||||||
| (a) | (b) | |||||
| Ba(OH)2·8H2O + 2NH4NO3 |  | 2NH3 + 10 H2O + Ba(NO3)2 | ||||
| +0.57 | ||||||
| −0.12 | ||||||
| +0.45 | ||||||
| (a) | (b) | |||||
| Example I | Combustion of methane | −73.1 | −818.0 | −891.1 < 0 | Exothermic reaction |
| Example II | Decomposition of hydrogen peroxide | 37.4 | −233.8 | −196.4 < 0 | Exothermic reaction |
| Example III | Reaction between barium hydroxide and ammonium nitrate | 169.4 | −36.0 | 133.4 > 0 | Endothermic reaction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Anna, M.; Lubini, P.; Fuchs, H.U.; Corni, F. A Direct Entropic Approach to the Thermal Balance of Spontaneous Chemical Reactions. Entropy 2024, 26, 450. https://doi.org/10.3390/e26060450
D’Anna M, Lubini P, Fuchs HU, Corni F. A Direct Entropic Approach to the Thermal Balance of Spontaneous Chemical Reactions. Entropy. 2024; 26(6):450. https://doi.org/10.3390/e26060450
Chicago/Turabian StyleD’Anna, Michele, Paolo Lubini, Hans U. Fuchs, and Federico Corni. 2024. "A Direct Entropic Approach to the Thermal Balance of Spontaneous Chemical Reactions" Entropy 26, no. 6: 450. https://doi.org/10.3390/e26060450






