Extended Regression Analysis for Debye–Einstein Models Describing Low Temperature Heat Capacity Data of Solids
Abstract
:1. Introduction
2. Literature Data and Theory
2.1. Debye–Einstein Integral
2.2. Bayesian Framework and MCMC Regression
3. Results and Discussion
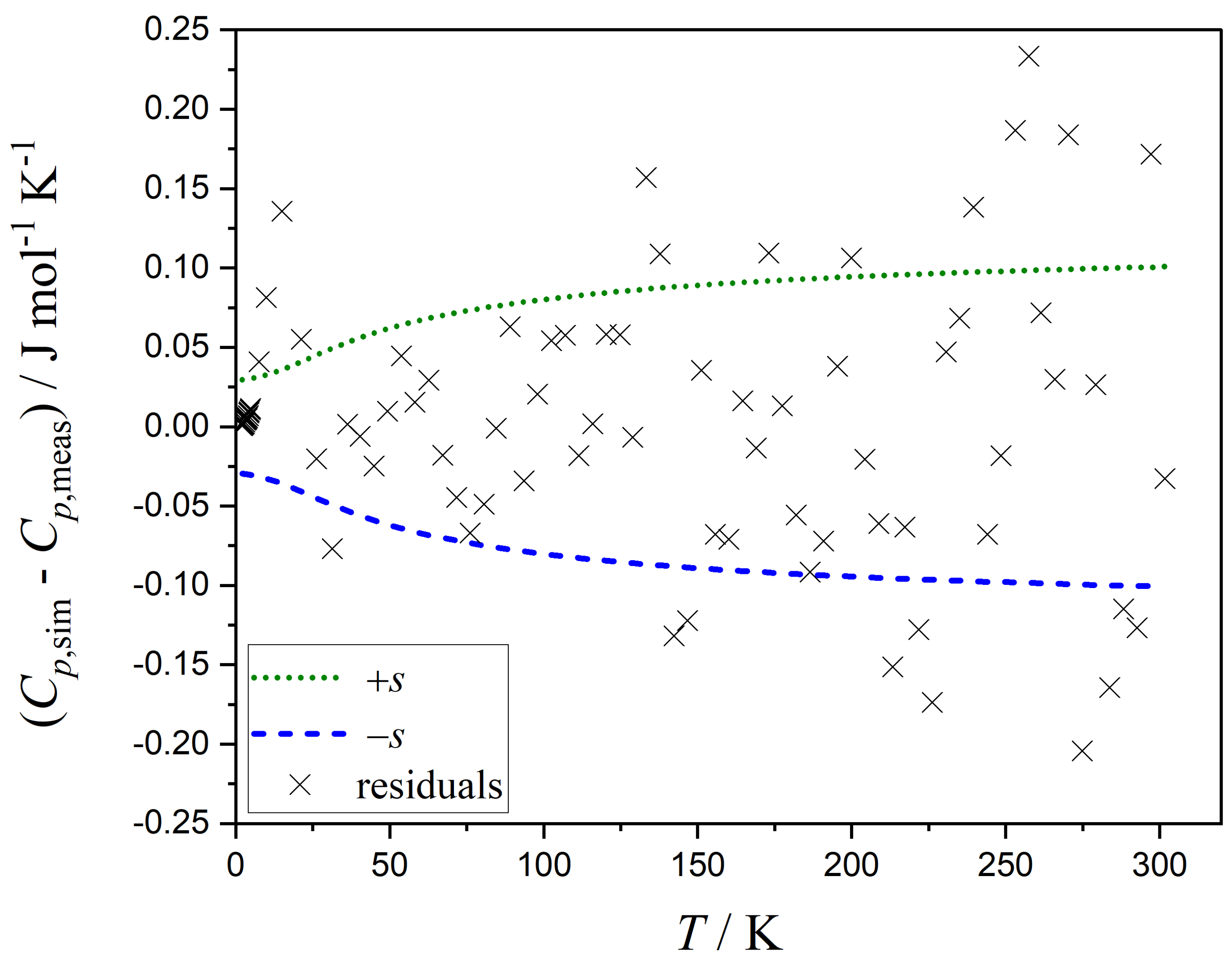
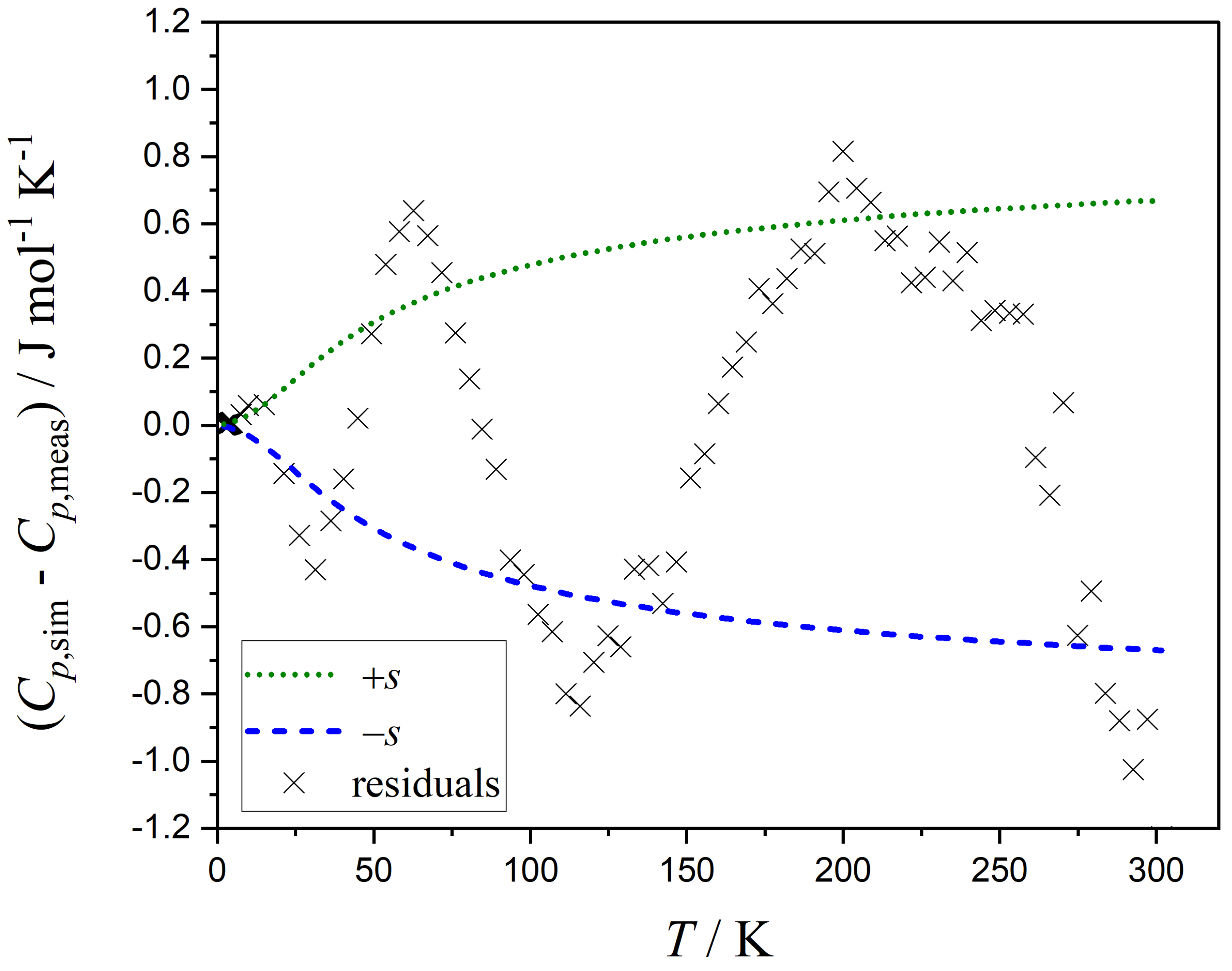
3.1. Estimating the Uncertainties of Each Measurement Point
- The temperature dependency of the residuals should adequately describe the temperature dependency of the standard errors and vice versa, e.g., as the residuals increase with increasing heat capacities, the standard errors should also increase with increasing heat capacities.
- The correlations between the parameters in the function for the standard errors should not be excessively high (e.g., above 90 percent), as this indicates the potential for using a simpler standard error function without significant data loss.
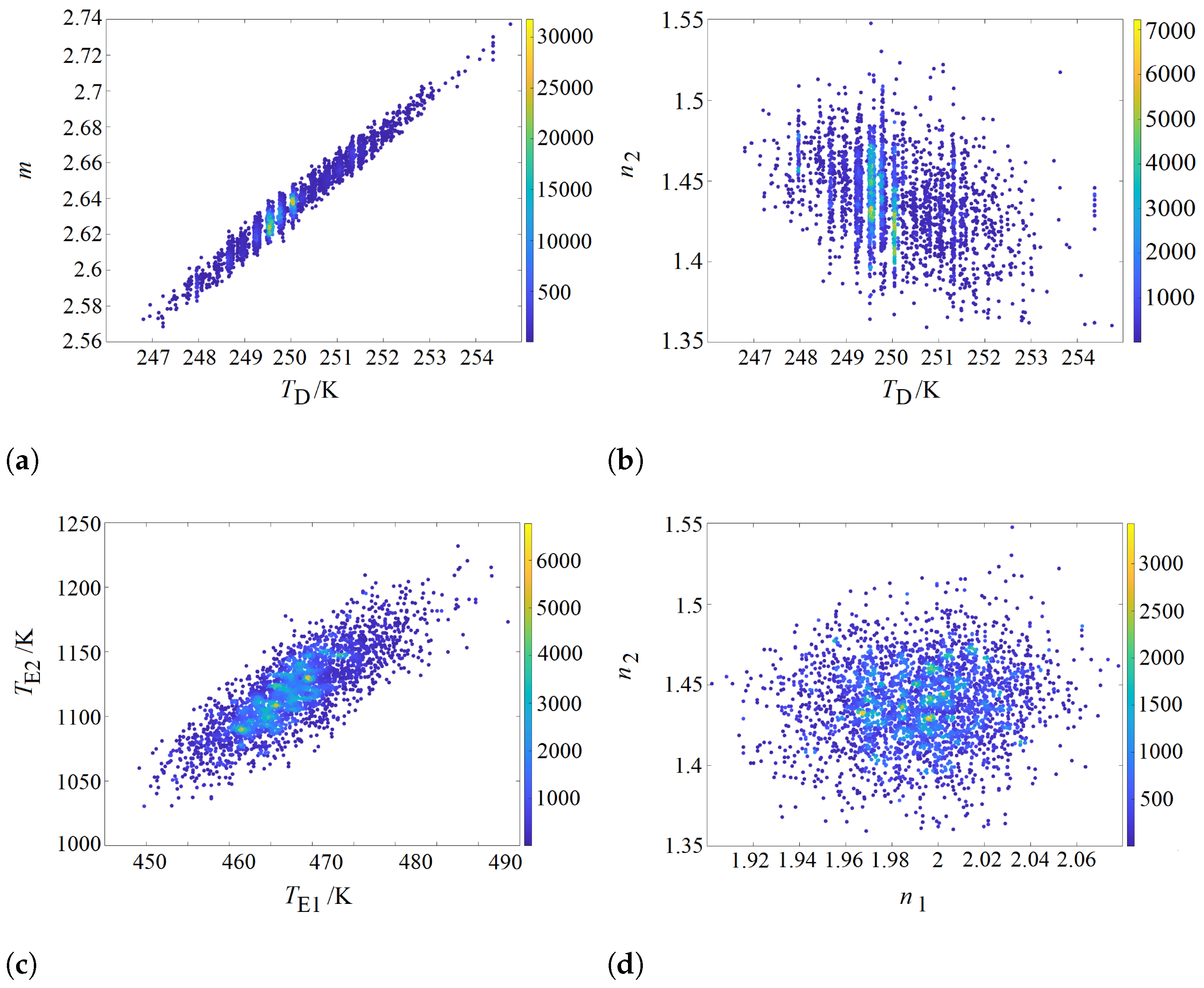
3.2. Determining the Correlation between Parameters
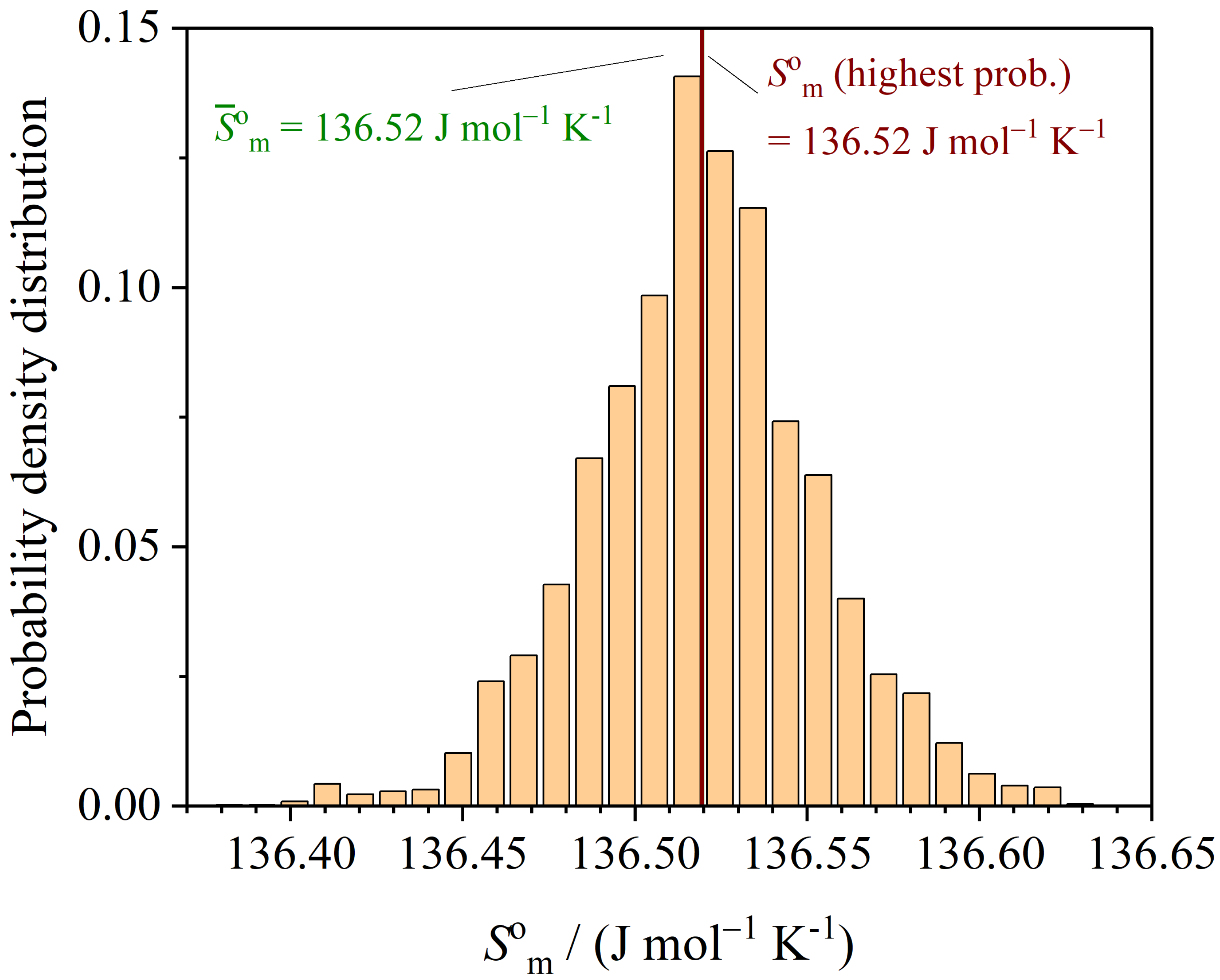
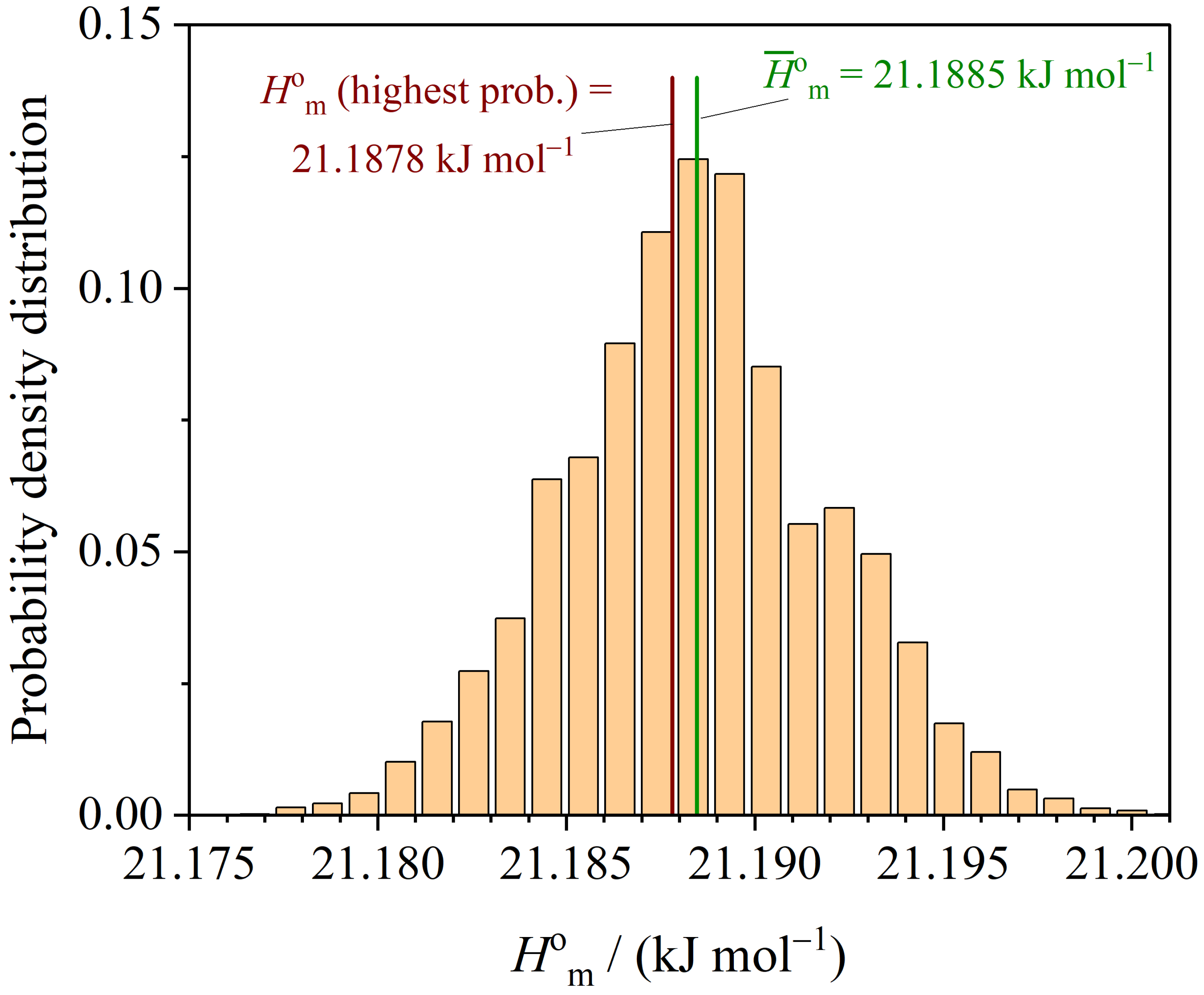
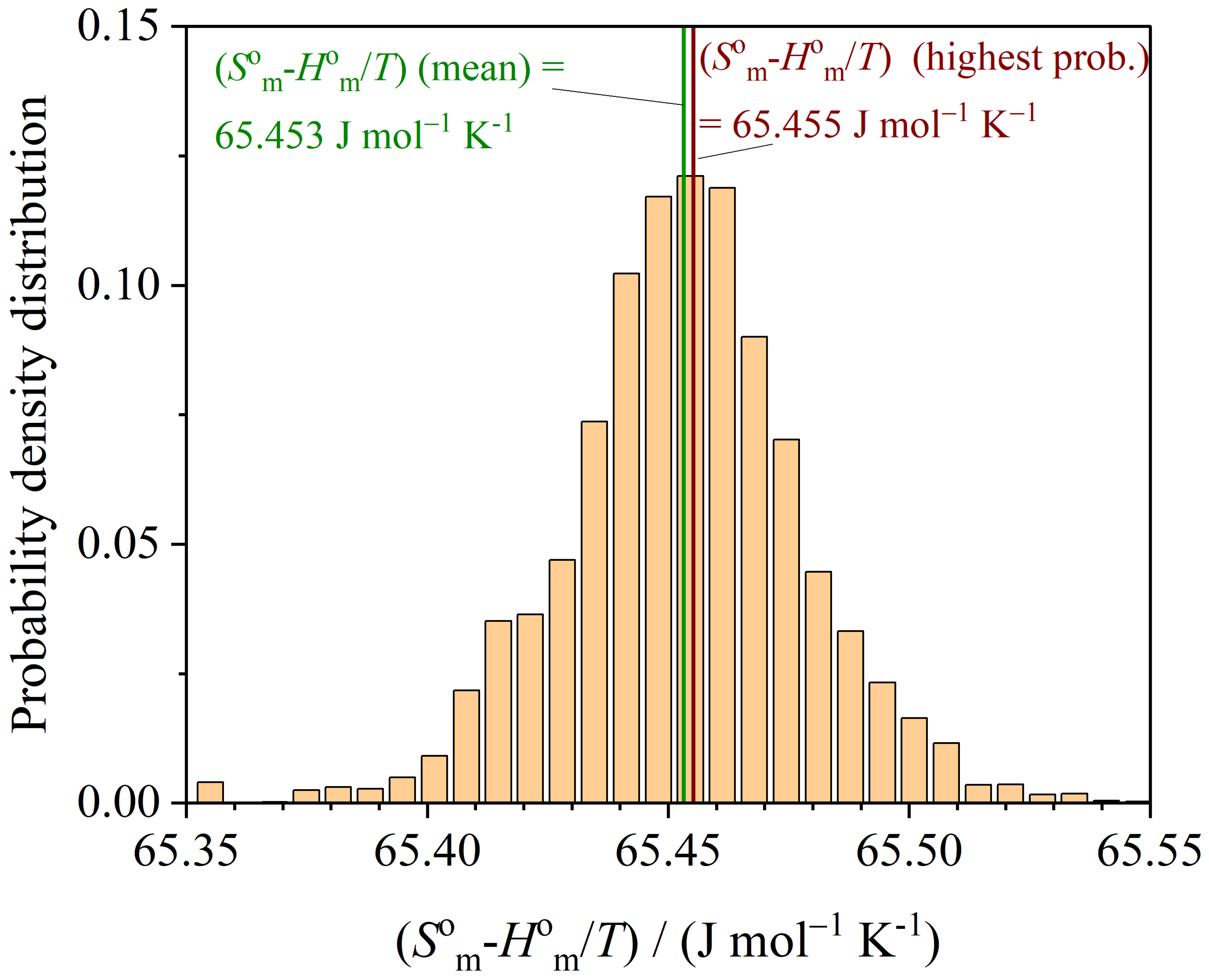
3.3. Thermodynamic Functions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ditmars, D.A.; Ishihara, S.; Chang, S.S.; Bernstein, G.; West, E.D. Enthalpy and Heat-Capacity Standard Reference Material: Synthetic Sapphire (Alpha-Al2O3) From 10 to 2250 K. J. Res. Natl. Bur. Stand. 1982, 87, 159–163. [Google Scholar] [CrossRef] [PubMed]
- Bissengaliyeva, M.R.; Bekturganov, N.S.; Gogol, D.B.; Taimassova, S. Low-temperature heat capacity and thermodynamic functions of natural chalcanthite. J. Chem. Thermodyn. 2017, 111, 199–206. [Google Scholar] [CrossRef]
- Bissengaliyeva, M.R.; Knyazev, A.V.; Bespyatov, M.A.; Gogol, D.B.; Taimassova, S.T.; Zhakupov, R.M.; Sadyrbekov, D.T. Low-temperature heat capacity and thermodynamic functions of thulium and lutetium titanates and Schottky anomaly in Tm2Ti2O7. J. Chem. Thermodyn. 2022, 165, 106646. [Google Scholar] [CrossRef]
- Smith, A.L.; Griveau, J.C.; Colineau, E.; Raison, P.E.; Konings, R. Low temperature heat capacity of α-Na2NpO4. Thermochim. Acta 2015, 617, 129–135. [Google Scholar] [CrossRef]
- Kelley, K.K.; King, E.G. Contributions to the Data on Theoretical Metallurgy. XIV. Entropies of the Elements and Inorganic Compounds; US Government Printing Office: Washington, DC, USA, 1961; p. 149.
- Chen, Q.; Sundman, B. Modeling of thermodynamic properties for Bcc, Fcc, liquid, and amorphous iron. J. Phase. Equilib. 2001, 22, 631–644. [Google Scholar] [CrossRef]
- Musikhin, A.; Naumov, V.; Bespyatov, M.; Ivannikova, N. The heat capacity of Li2MoO4 in the temperature range 6–310 K. J. Alloys Compd. 2015, 639, 145–148. [Google Scholar] [CrossRef]
- Roslyakova, I.; Sundman, B.; Dette, H.; Zhang, L.; Steinbach, I. Modeling of Gibbs energies of pure elements down to 0 K using segmented regression. Calphad 2016, 55, 165–180. [Google Scholar] [CrossRef]
- Gamsjäger, E.; Morishita, M.; Gamsjäger, H. Calculating entropies of alkaline earth metal molybdates. Monatshefte für Chemie Chem. Mon. 2016, 147, 263–267. [Google Scholar] [CrossRef]
- Wu, L.; Schliesser, J.M.; Woodfield, B.F.; Xu, H.; Navrotsky, A. Heat capacities, standard entropies and Gibbs energies of Sr-, Rb- and Cs-substituted barium aluminotitanate hollandites. J. Chem. Thermodyn. 2016, 93, 1–7. [Google Scholar] [CrossRef]
- Morishita, M.; Kinoshita, Y.; Houshiyama, H.; Nozaki, A.; Yamamoto, H. Thermodynamic properties for calcium molybdate, molybdenum tri-oxide and aqueous molybdate ion. J. Chem. Thermodyn. 2017, 114, 30–43. [Google Scholar] [CrossRef]
- Gamsjäger, E.; Wiessner, M. Low temperature heat capacities and thermodynamic functions described by Debye-Einstein integrals. Monatshefte für Chemie Chem. Mon. 2018, 149, 357–368. [Google Scholar] [CrossRef]
- Shumway, S.G.; Wilson, J.; Lilova, K.; Subramani, T.; Navrotsky, A.; Woodfield, B.F. The low-temperature heat capacity and thermodynamic properties of greigite (Fe3S4). J. Chem. Thermodyn. 2022, 173, 106836. [Google Scholar] [CrossRef]
- Gabriel, J.J.; Paulson, N.H.; Duong, T.C.; Becker, C.A.; Tavazza, F.; Kattner, U.R.; Stan, M. Bayesian automated weighting of aggregated DFT, MD, and experimental data for candidate thermodynamic models of aluminum with uncertainty quantification. Materialia 2021, 20, 101216. [Google Scholar] [CrossRef]
- Honarmandi, P.; Duong, T.C.; Ghoreishi, S.F.; Allaire, D.; Arroyave, R. Bayesian uncertainty quantification and information fusion in CALPHAD-based thermodynamic modeling. Acta Mater. 2019, 164, 636–647. [Google Scholar] [CrossRef]
- Paulson, N.H.; Bocklund, B.J.; Otis, R.A.; Liu, Z.K.; Stan, M. Quantified uncertainty in thermodynamic modeling for materials design. Acta Mater. 2019, 174, 9–15. [Google Scholar] [CrossRef]
- Malakhov, D.V. Confidence intervals of calculated phase boundaries. Calphad 1997, 21, 391–400. [Google Scholar] [CrossRef]
- Königsberger, E.; Gamsjäger, H. Analysis of phase diagrams employing Bayesian excess parameter estimation. Monatshefte für Chemie Chem. Mon. 1990, 121, 119–127. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F. DREAM_(D): An adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems. Hydrol. Earth Syst. Sci. 2011, 15, 3701–3713. [Google Scholar] [CrossRef]
- Gagin, A.; Levin, I. Accounting for unknown systematic errors in Rietveld refinements: A Bayesian statistics approach. J. Appl. Crystallogr. 2015, 48, 1201–1211. [Google Scholar] [CrossRef]
- Box, G.E.P. Science and Statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- Boerio-Goates, J.; Stevens, R.; Hom, B.K.; Woodfield, B.F.; Piccione, P.M.; Davis, M.E.; Navrotsky, A. Heat capacities, third-law entropies and thermodynamic functions of SiO2 molecular sieves from T = 0 K to 400 K. J. Chem. Thermodyn. 2002, 34, 205–227. [Google Scholar] [CrossRef]
- Dachs, E.; Benisek, A. A sample-saving method for heat capacity measurements on powders using relaxation calorimetry. Cryogenics 2011, 51, 460–464. [Google Scholar] [CrossRef]
- Bissengaliyeva, M.R.; Gogol, D.B.; Taimassova, S.; Bekturganov, N.S. Experimental determination of thermodynamic characteristics of smithsonite. J. Chem. Thermodyn. 2012, 51, 31–36. [Google Scholar] [CrossRef]
- Bissengaliyeva, M.R.; Gogol, D.B.; Taimassova, S.T.; Bekturganov, N.S. The heat capacity and thermodynamic functions of cerussite. J. Chem. Thermodyn. 2012, 47, 197–202. [Google Scholar] [CrossRef]
- Morishita, M.; Houshiyama, H. The Third Law Entropy of Strontium Molybdates. Mater. Trans. 2015, 56, 545–549. [Google Scholar] [CrossRef]
- Quantum Design (Ed.) Quantum Design: Physical Property Measurement System: Heat Capacity Option User’s Manual; Quantum Design: San Diego, CA, USA, 2004. [Google Scholar]
- Dachs, E.; Bertoldi, C. Precision and accuracy of the heat-pulse calorimetric technique: Lowtemperature heat capacities of milligram-sized synthetic mineral samples. Eur. J. Mineral. 2005, 17, 251–259. [Google Scholar] [CrossRef]
- Ogris, D.M.; Gamsjäger, E. Heat capacities and standard entropies and enthalpies of some compounds essential for steelmaking and refractory design approximated by Debye-Einstein integrals. Calphad 2021, 75, 102345. [Google Scholar] [CrossRef]
- Sivia, D.S. Data Analysis: A Bayesian Tutorial; for Scientists and Engineers, 2nd ed.; Oxford science publications, Oxford Univ. Press: Oxford, UK, 2006. [Google Scholar]
- Braak, C.J.F.T. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Wiessner, M.; Angerer, P.; van der Zwaag, S.; Gamsjäger, E. Transient phase fraction and dislocation density estimation from in-situ X-ray diffraction data with a low signal-to-noise ratio using a Bayesian approach to the Rietveld analysis. Mater. Charact. 2021, 172, 110860. [Google Scholar] [CrossRef]
- OriginLab Corporation. OriginPro, Version 2022b; OriginLab Corporation: Northampton, MA, USA, 2022. [Google Scholar]
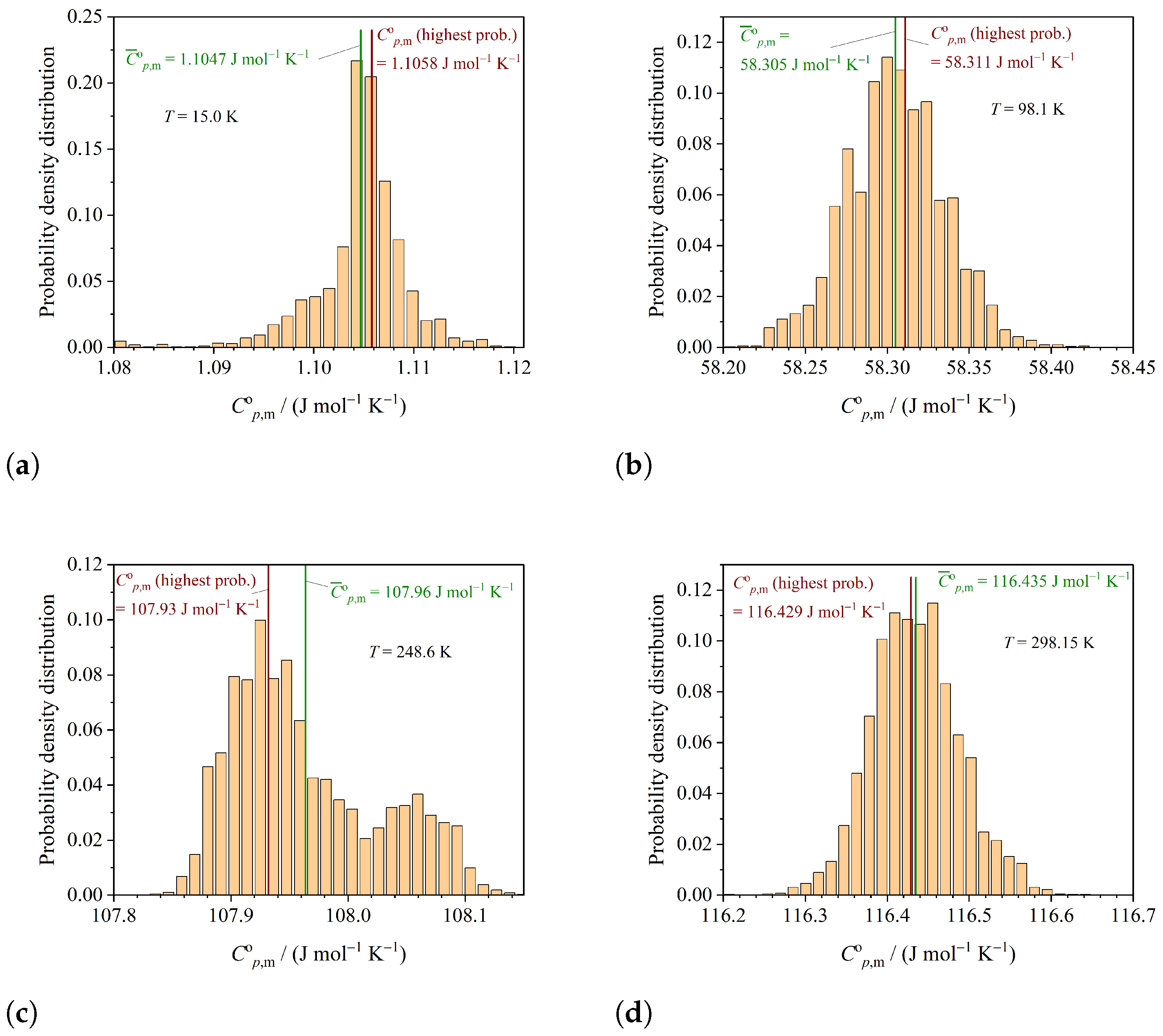
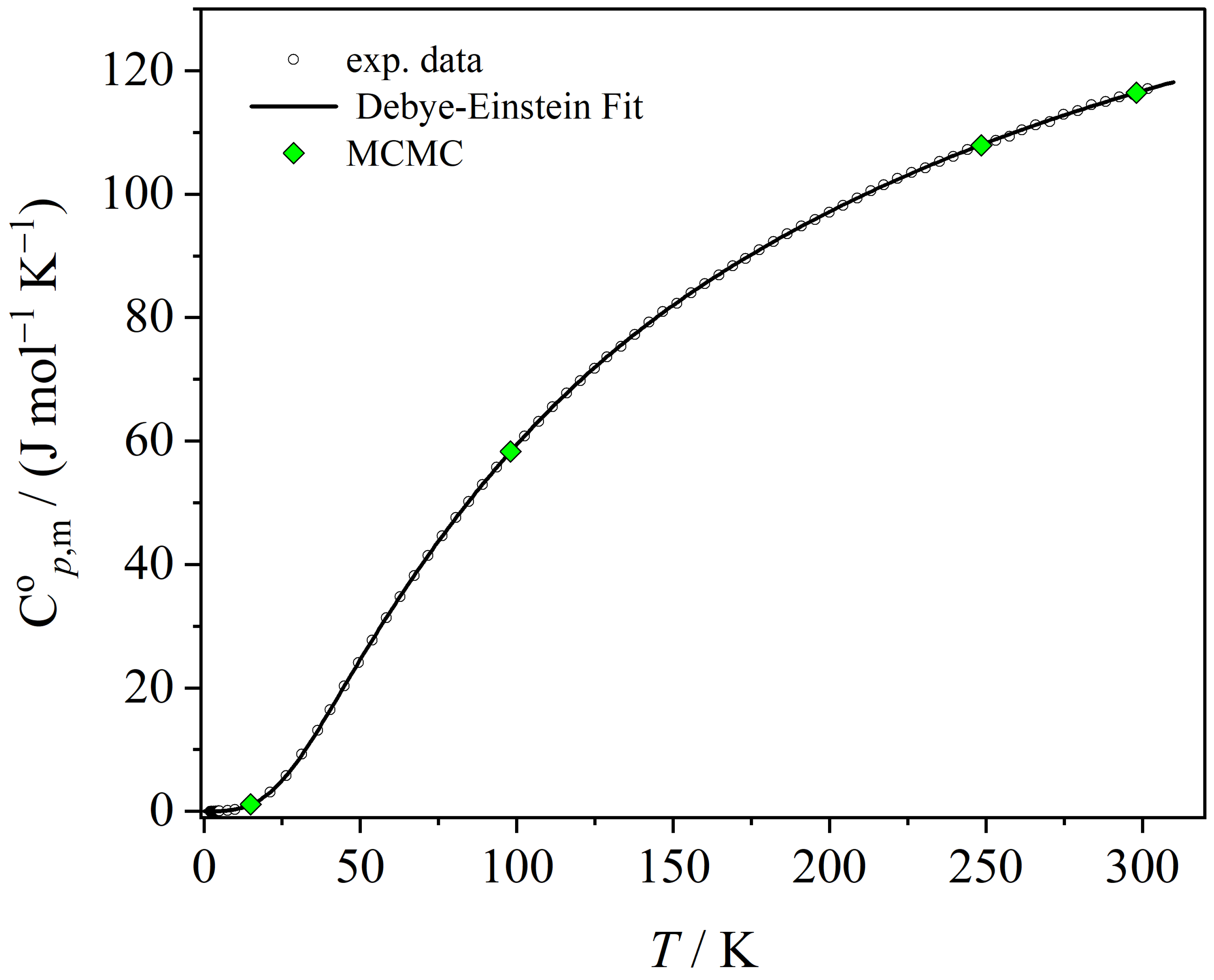
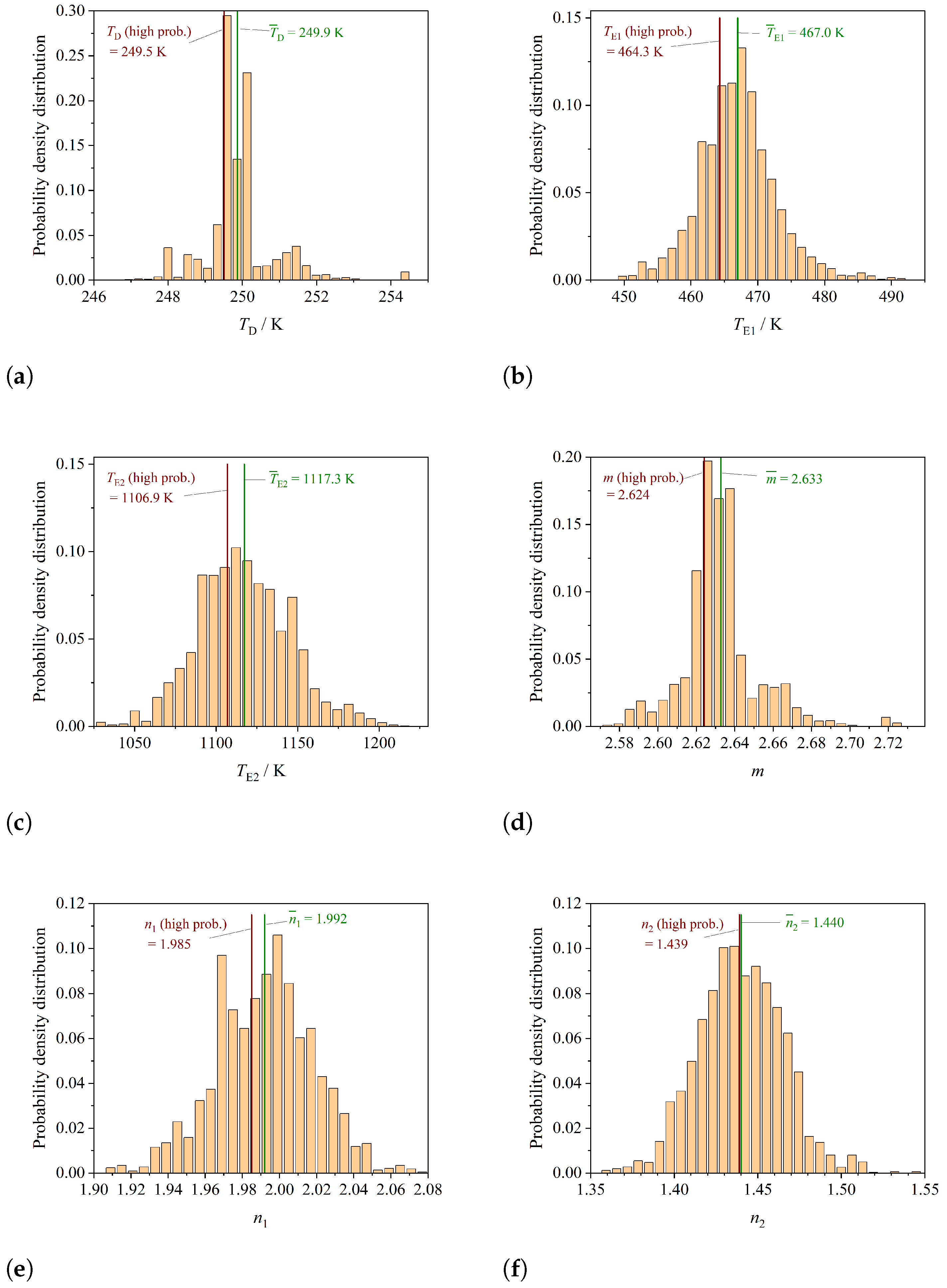
| Method | m | |||||
|---|---|---|---|---|---|---|
| LSQ | ||||||
| MCMC (highest prob.) | ||||||
| MCMC (mean) |
| Method | / | / |
|---|---|---|
| MCMC (highest prob.) | ||
| MCMC (mean) | 0.030 |
| m | ||||||||
|---|---|---|---|---|---|---|---|---|
| m | 1.0 | 0.31 | −0.33 | 0.98 | 0.91 | 0.61 | 0.00 | 0.09 |
| 1.0 | 0.09 | 0.19 | 0.67 | 0.9 | 0.04 | −0.05 | ||
| 1.0 | −0.31 | −0.26 | 0.21 | −0.01 | 0.00 | |||
| 1.0 | 0.83 | 0.52 | −0.03 | 0.12 | ||||
| 1.0 | 0.83 | 0.02 | 0.04 | |||||
| 1.0 | 0.02 | 0.01 | ||||||
| 1.0 | −0.62 | |||||||
| 1.0 |
| Source | () | ||
|---|---|---|---|
| From [26] | 21.14 | 65.32 | |
| LM (least squares) | 136.51 | 21.188 | 65.45 |
| MCMC (highest prob.) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamsjäger, E.; Wiessner, M. Extended Regression Analysis for Debye–Einstein Models Describing Low Temperature Heat Capacity Data of Solids. Entropy 2024, 26, 452. https://doi.org/10.3390/e26060452
Gamsjäger E, Wiessner M. Extended Regression Analysis for Debye–Einstein Models Describing Low Temperature Heat Capacity Data of Solids. Entropy. 2024; 26(6):452. https://doi.org/10.3390/e26060452
Chicago/Turabian StyleGamsjäger, Ernst, and Manfred Wiessner. 2024. "Extended Regression Analysis for Debye–Einstein Models Describing Low Temperature Heat Capacity Data of Solids" Entropy 26, no. 6: 452. https://doi.org/10.3390/e26060452
APA StyleGamsjäger, E., & Wiessner, M. (2024). Extended Regression Analysis for Debye–Einstein Models Describing Low Temperature Heat Capacity Data of Solids. Entropy, 26(6), 452. https://doi.org/10.3390/e26060452







