The Interplay between Tunneling and Parity Violation in Chiral Molecules
Abstract
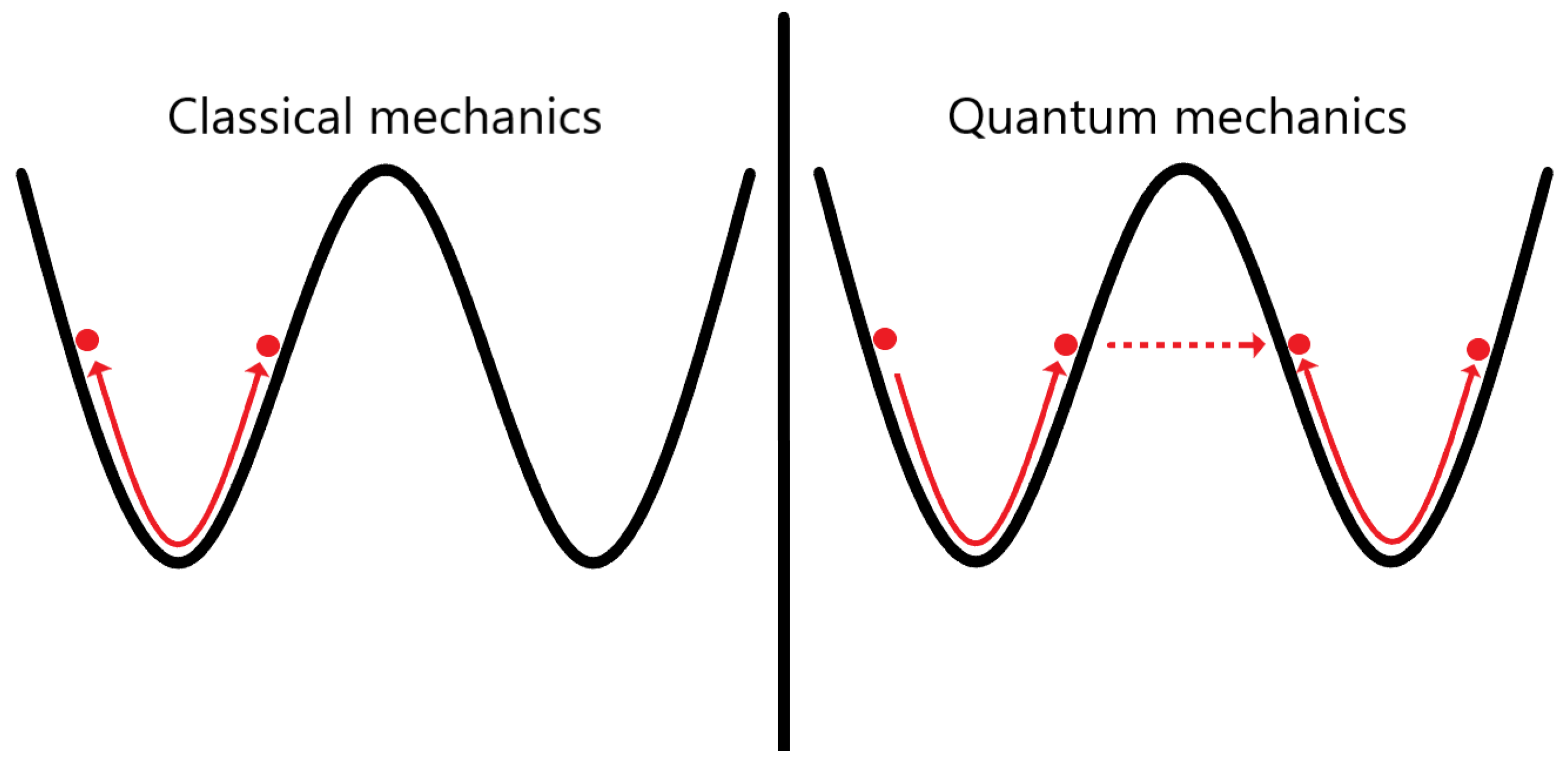
1. Introduction
2. Introduction to Molecular Chirality
3. Parity Violation
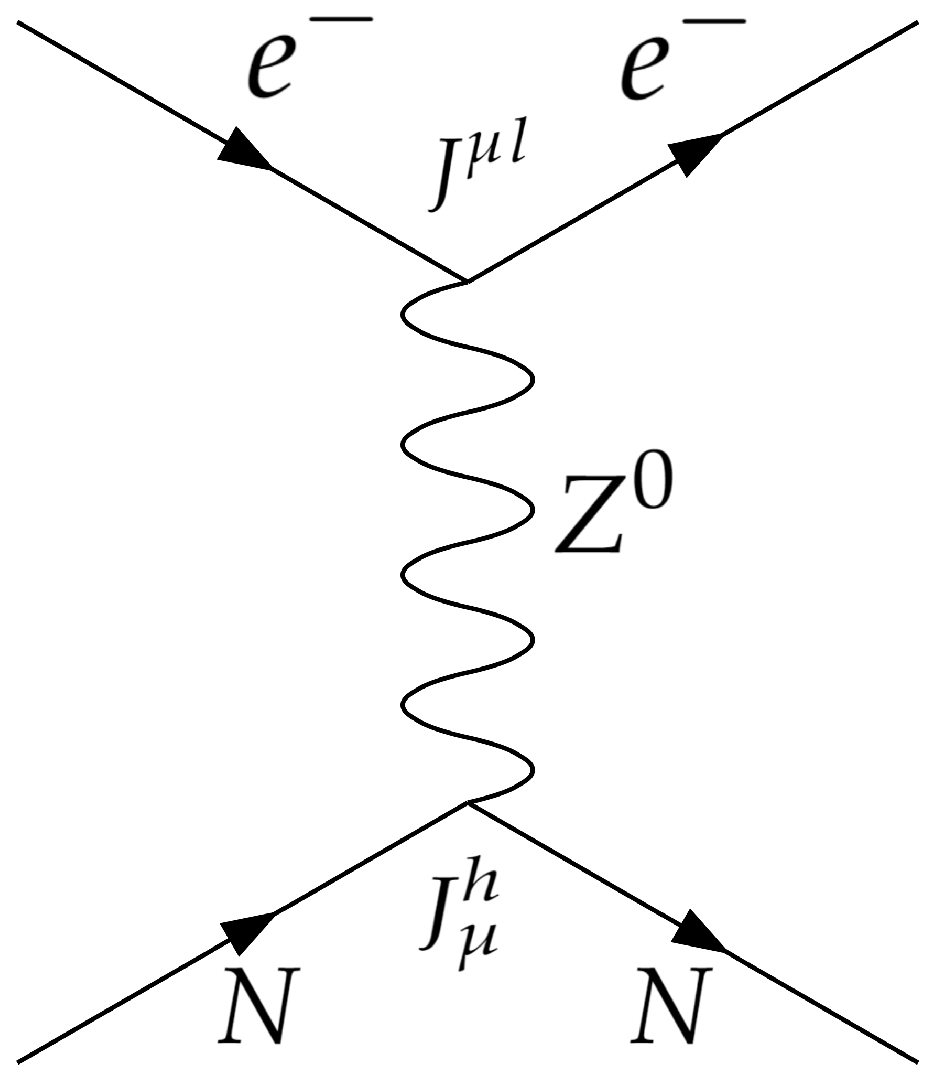
4. Parity-Violating Interactions
Electroweak Interaction
5. Calculations of PVED
6. Experiments Searching the PVED
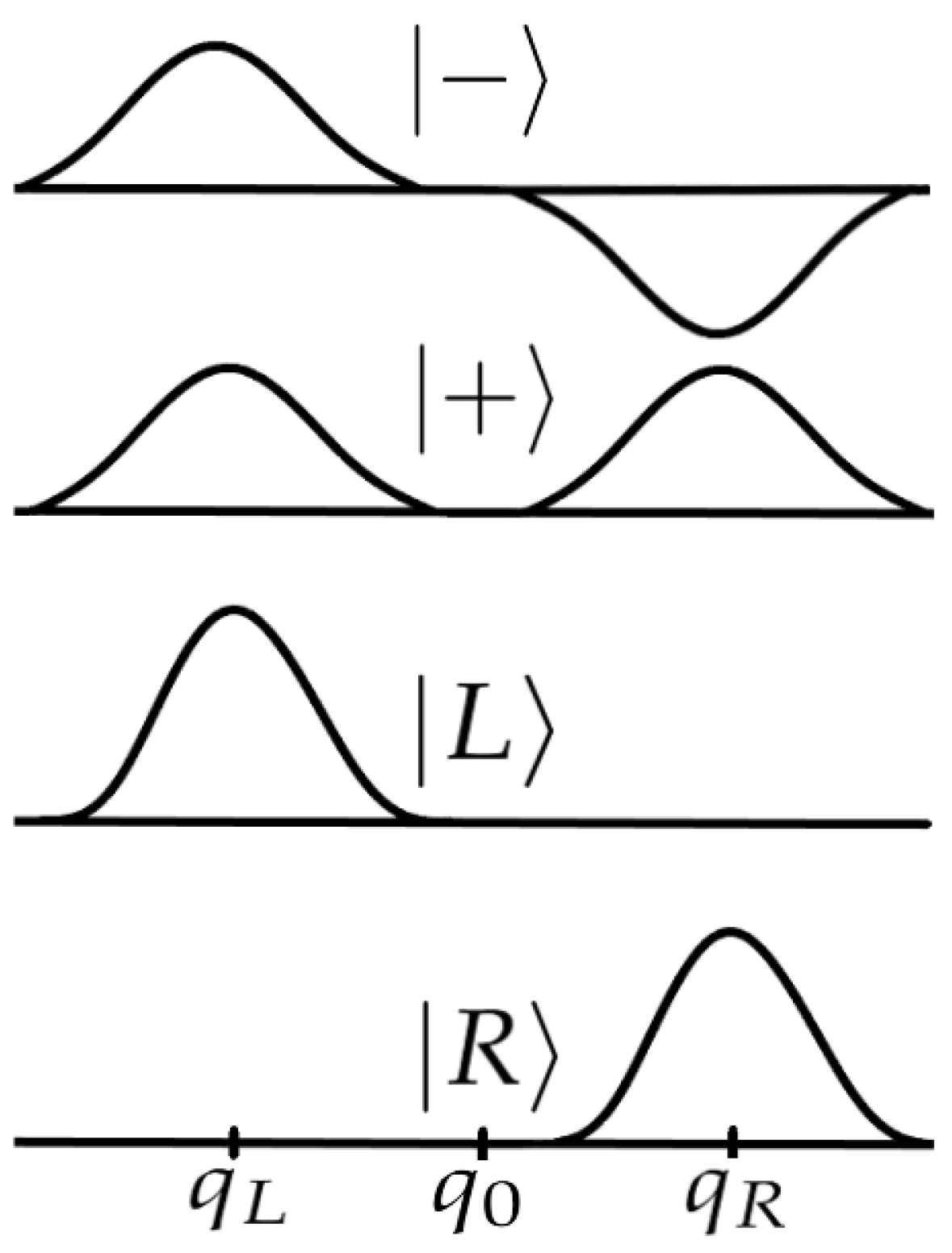
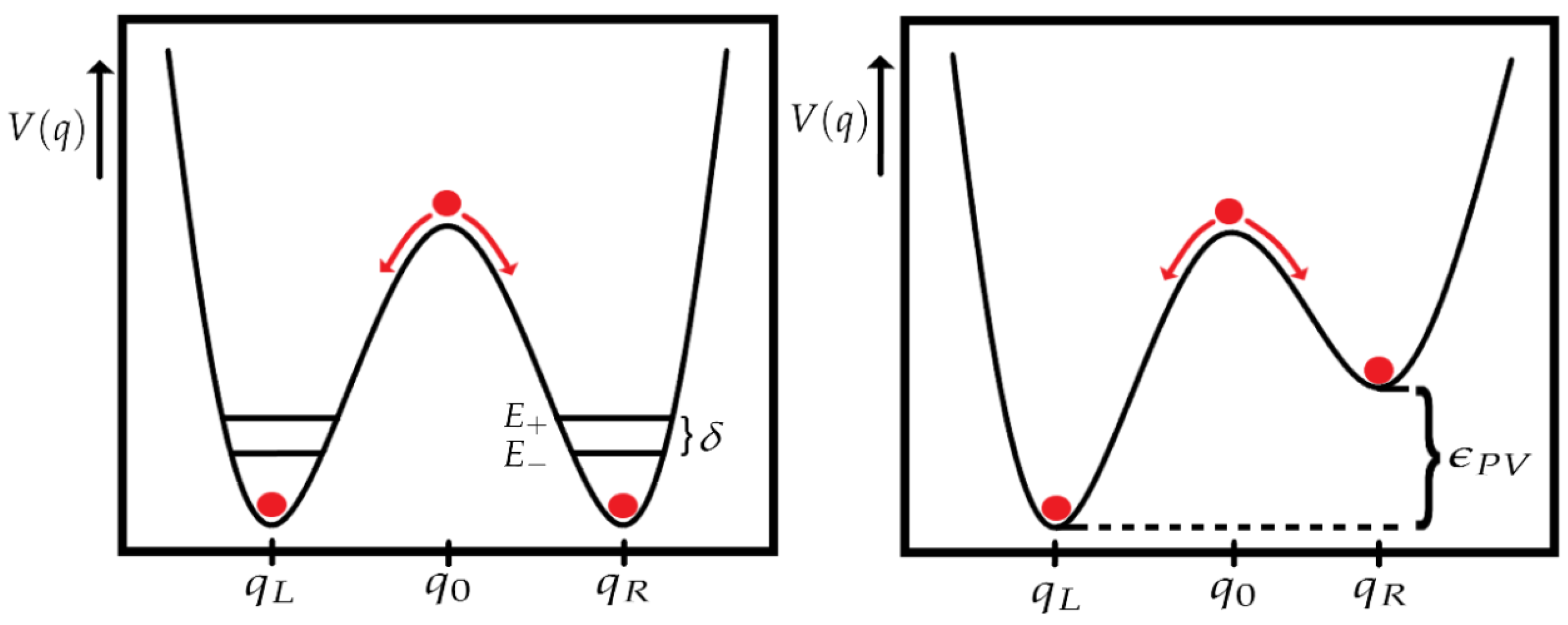
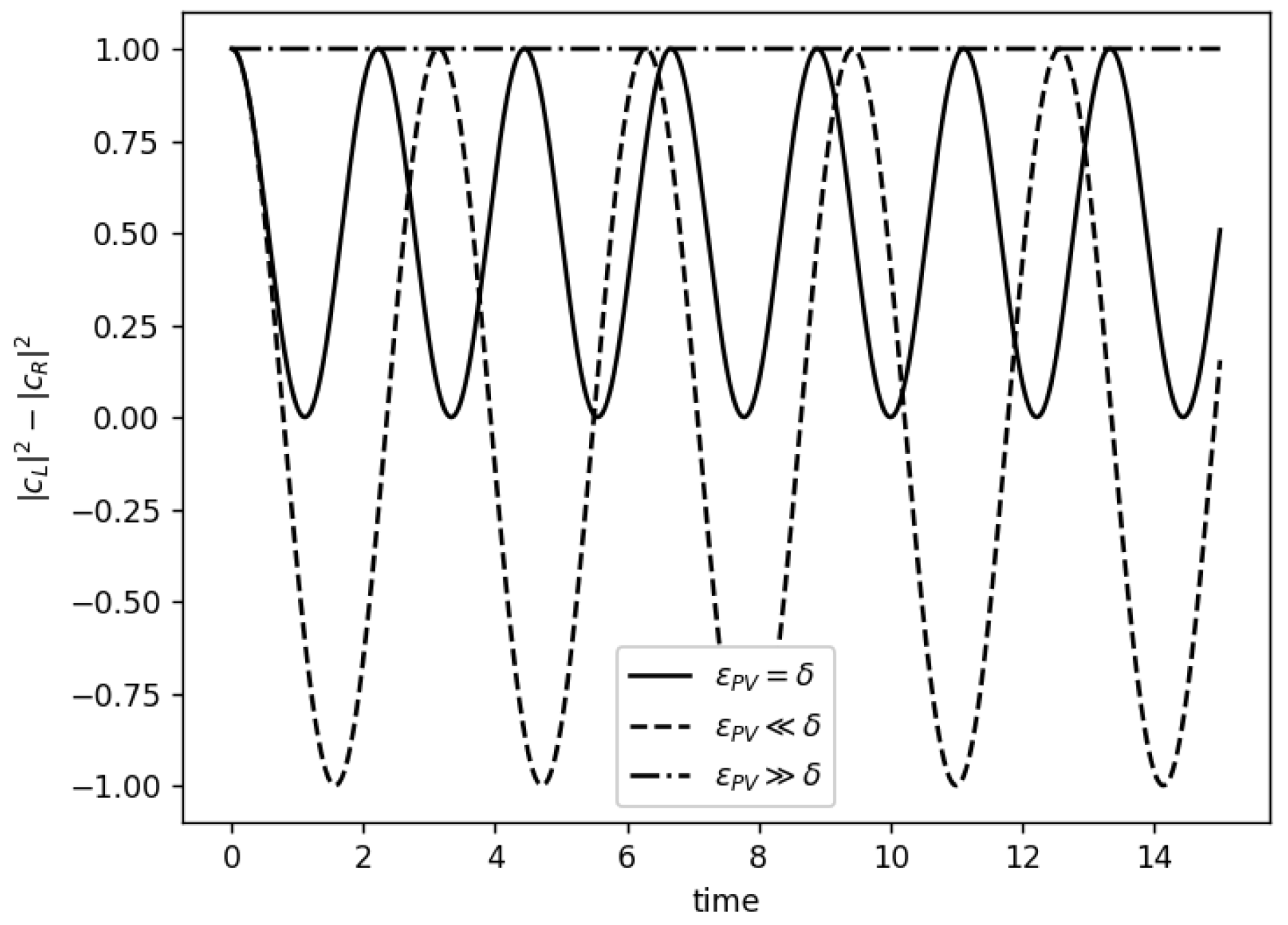
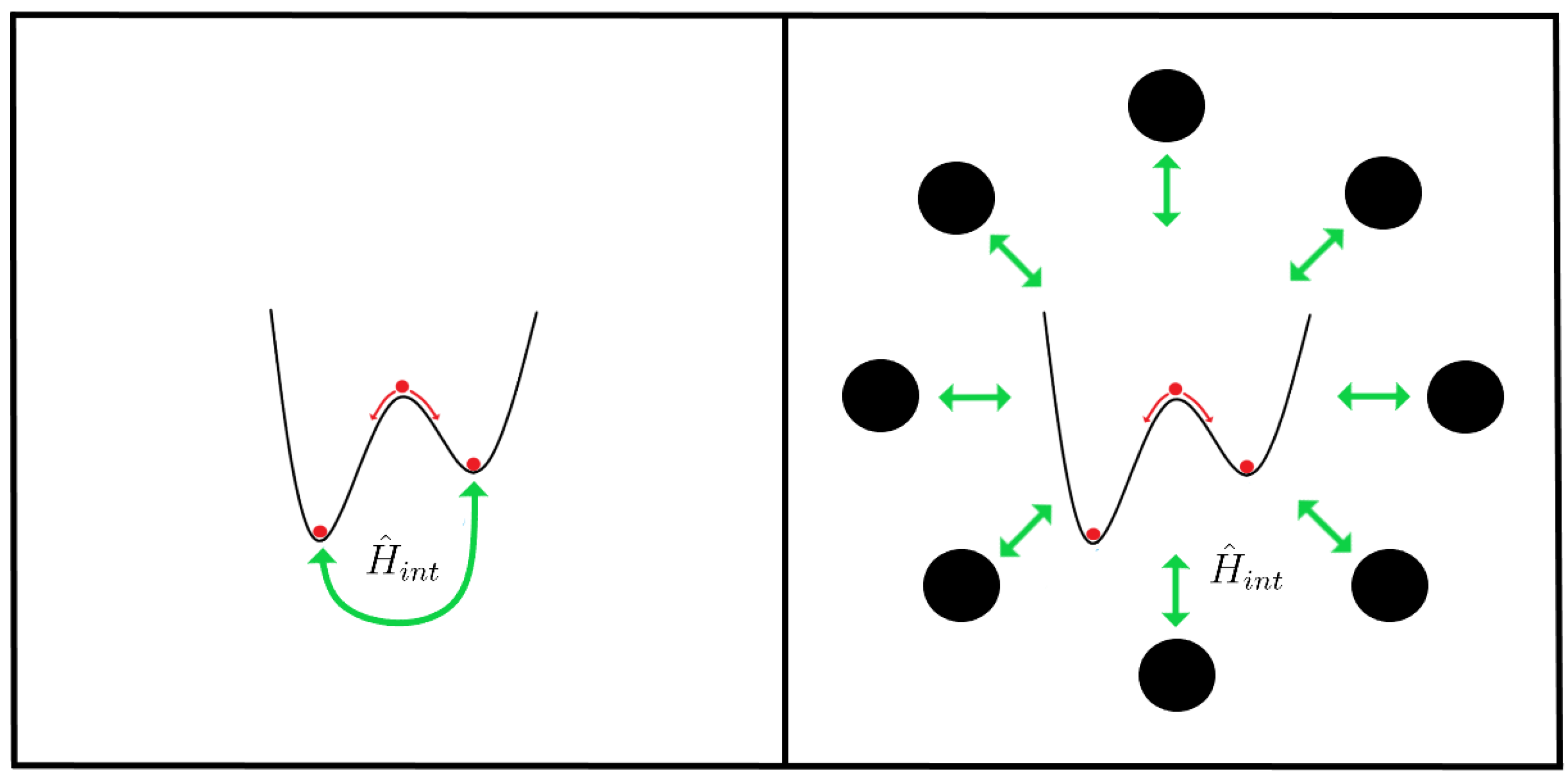
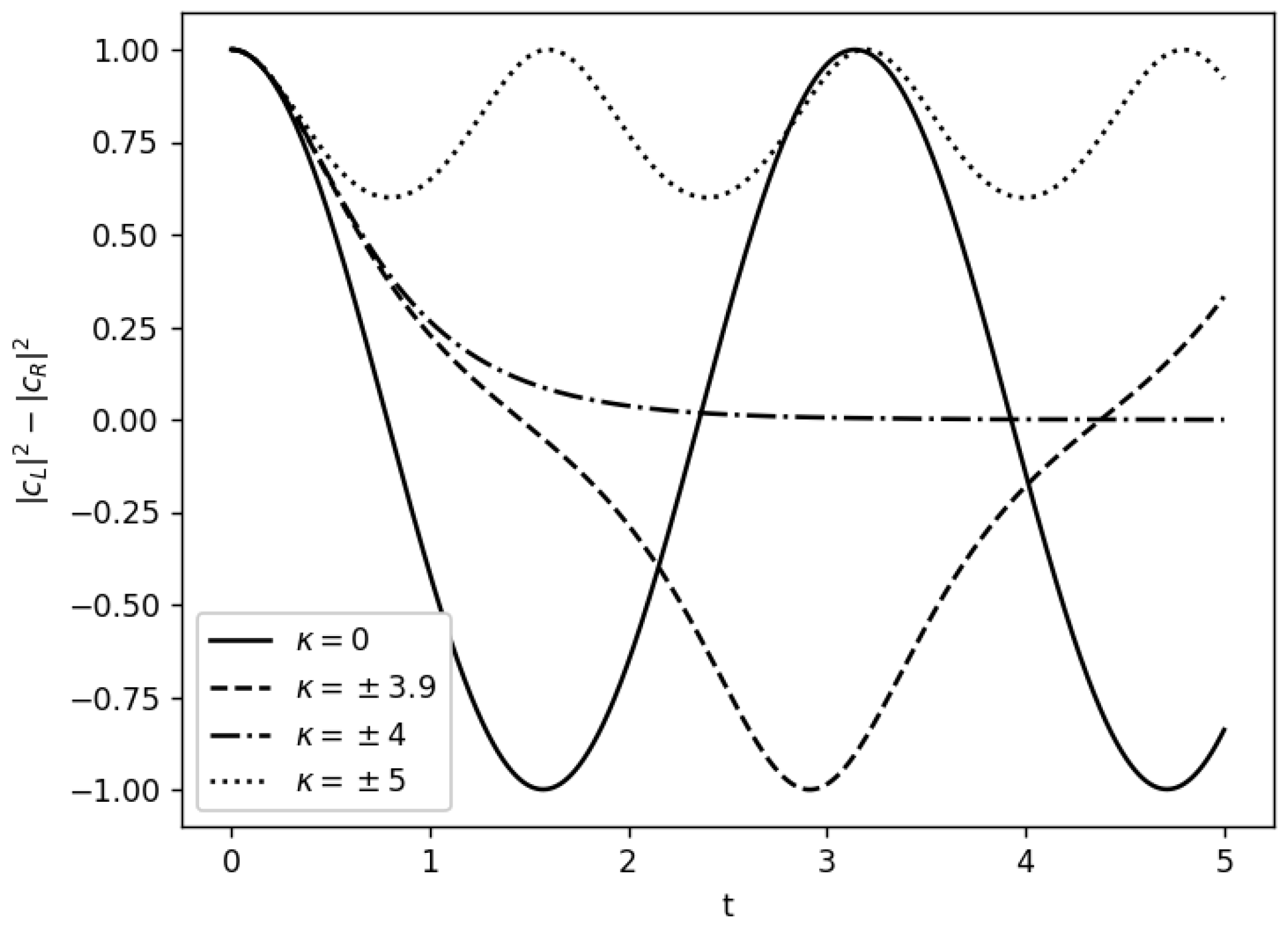
7. Solutions to Hund’s Paradox
7.1. Mean-Field Theory
7.2. Decoherence
8. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Newton, I. Philosophiae Naturalis Principia Mathematica; Apud Guil. & Joh. Innys: London, UK, 1687. [Google Scholar]
- Klein, M. Max Planck and the Beginnings of the Quantum Theory. Arch. Hist. Exact Sci. 1962, 1, 459–479. [Google Scholar] [CrossRef]
- Schrödinger, E. An Undulatory Theory of the Mechanics of Atoms and Molecules. Phys. Rev. 1926, 28, 1049–1070. [Google Scholar] [CrossRef]
- Mehra, J. The Historical Development of Quantum Theory 1–6; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Razavy, M. Quantum Theory of Tunneling; World Scientific: Singapore, 2003. [Google Scholar]
- Hund, F. Zur Deutung der Molekelspektren II. Z. Phys. 1927, 42, 93–120. [Google Scholar] [CrossRef]
- Hund, F. Zur Deutung der Molekelspektren III. Bemerkungen über das Schwingungs- und Rotationsspektrum bei Molekeln mit mehr als zwei Kernen. J. Phys. Chem. Lett. 1927, 43, 805–826. [Google Scholar]
- Kelvin, W.T. The Molecular Tactics of a Crystal; Clarendon Press: Oxford, UK, 1984. [Google Scholar]
- Barron, L.D. Parity and Optical Activity. Nature 1972, 238, 7–19. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.D.; Yang, C.N. Question of Parity Conservation in Weak Interactions. Phys. Rev. 1956, 104, 1371. [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayward, R.; Hoppes, D.; Hudson, R. An experimental test of parity conservation in beta decay. Phys. Rev. 1957, 105, 1413–1415. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C. Parity violation induced by weak neutral currents in atomic physics. J. Phys. 1974, 35, 899–927. [Google Scholar] [CrossRef]
- Barkov, L.; Zolotorev, M. Parity violation in atomic bismuth. Phys. Lett. B 1979, 85, 308–313. [Google Scholar] [CrossRef]
- Wood, C.S.; Bennet, S.C.; Cho, D.; Masterson, B.P.; Roberts, J.L.; Tanner, C.E.; Wiemann, C.E. Measurement of Parity Nonconservation and an Anapole Moment in Cesium. Science 1997, 275, 1759–1763. [Google Scholar] [CrossRef]
- Quack, M. How important is parity violation for molecular and biomolecular chirality? Angew. Chem. Int. Ed. 2002, 41, 4618–4630. [Google Scholar] [CrossRef] [PubMed]
- Berger, R. Chapter 4—Parity-Violation Effects in Molecules. In Relativistic Electronic Structure Theory; Theoretical and Computational, Chemistry; Schwerdtfeger, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2004; Volume 14, pp. 188–288. [Google Scholar]
- Quack, M.; Stohner, J. Parity violation in chiral molecules. Chimia 2005, 59, 530–538. [Google Scholar] [CrossRef]
- Crassous, J.; Chardonnet, C.; Saue, T.; Schwerdtfeger, P. Recent experimental and theoretical developments towards the observation of parity violation (PV) effects in molecules by spectroscopy. Org. Biomol. Chem. 2005, 3, 2218–2224. [Google Scholar] [CrossRef] [PubMed]
- Quack, M.; Stohner, J.; Willeke, M. High-Resolution Spectroscopic Studies and Theory of Parity Violation in Chiral Molecules. Annu. Rev. Phys. Chem. 2008, 59, 741–769. [Google Scholar] [CrossRef] [PubMed]
- Schwerdtfeger, P. The Search for Parity Violation in Chiral Molecules. In Computational Spectroscopy; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; Chapter 7; pp. 201–221. [Google Scholar]
- Berger, R.; Stohner, J. Parity violation. WIREs Comput. Mol. Sci. 2019, 9, e1396. [Google Scholar] [CrossRef]
- Quack, M.; Seyfang, G.; Wichmann, G. Chapter Three—Fundamental and approximate symmetries, parity violation and tunneling in chiral and achiral molecules. In Chemical Physics and Quantum Chemistry; Advances in Quantum Chemistry; Ruud, K., Brändas, E.J., Eds.; Academic Press: Cambridge, MA, USA, 2020; Volume 81, pp. 51–104. [Google Scholar]
- Quack, M. On the measurement of the parity violating energy difference between enantiomers. Chem. Phys. Lett. 1986, 132, 147–153. [Google Scholar] [CrossRef]
- Quack, M. Structure and Dynamics of Chiral Molecules. Angew. Chem. Int. Ed. Engl. 1989, 28, 571–586. [Google Scholar] [CrossRef]
- Quack, M.; Seyfang, G.; Wichmann, G. Perspectives on parity violation in chiral molecules: Theory, spectroscopic experiment and biomolecular homochirality. Chem. Sci. 2022, 13, 10598–10643. [Google Scholar] [CrossRef] [PubMed]
- Harris, R.; Stodolsky, L. Quantum beats in optical activity and weak interactions. Phys. Lett. B 1978, 78, 313–317. [Google Scholar] [CrossRef]
- Bargueño, P.; Gonzalo, I.; de Tudela, R.P. Detection of parity violation in chiral molecules by external tuning of electroweak optical activity. Phys. Rev. A 2009, 80, 012110. [Google Scholar] [CrossRef]
- Bargueño, P.; Gonzalo, I.; de Tudela, R.P.; Miret, S. Parity violation and critical temperature of non-interacting chiral molecules. Chem. Phys. Lett. 2009, 483, 204–208. [Google Scholar] [CrossRef]
- Sahu, N.; Richardson, J.; Berger, R. Instanton calculations of tunneling splittings in chiral molecules. J. Comput. Chem. 2021, 42, 210–221. [Google Scholar] [CrossRef] [PubMed]
- Jones, N. Frontier experiments: Tough science. Nature 2012, 481, 14–17. [Google Scholar] [CrossRef]
- Luzio, L.D.; Giannotti, M.; Nardi, E.; Visinelli, L. The landscape of QCD axion models. Phys. Rep. 2020, 870, 1–117. [Google Scholar] [CrossRef]
- Moody, J.E.; Wilczek, F. New macroscopic forces? Phys. Rev. D 1984, 30, 130–138. [Google Scholar] [CrossRef]
- Gaul, K.; Kozlov, M.G.; Isaev, T.A.; Berger, R. Parity-nonconserving interactions of electrons in chiral molecules with cosmic fields. Phys. Rev. A 2020, 102, 032816. [Google Scholar] [CrossRef]
- Dortra-Urra, A.; Bargueño, P. Homochirality: A Perspective from Fundamental Physics. Symmetry 2019, 11, 661. [Google Scholar] [CrossRef]
- Leitner, J.; Okubo, S. Parity, Charge Conjugation, and Time Reversal in the Gravitational Interaction. Phys. Rev. 1964, 136, B1542–B1546. [Google Scholar] [CrossRef]
- Dass, N.D.H. Test for C, P, and T Nonconservation in Gravitation. Phys. Rev. Lett. 1976, 36, 393–395. [Google Scholar] [CrossRef]
- Alexander, S.; Yunes, N. Chern–Simons modified general relativity. Phys. Rep. 2009, 480, 1–55. [Google Scholar] [CrossRef]
- Jackiw, R.; Pi, S.Y. Chern-Simons modification of general relativity. Phys. Rev. D 2003, 68, 104012. [Google Scholar] [CrossRef]
- Bargueño, P. Chirality and Gravitational Parity Violation. Chirality 2015, 27, 375–381. [Google Scholar] [CrossRef]
- Bargueño, P.; de Tudela, R.P. Constraining long-range parity violation in gravitation using high resolution spectroscopy of chiral molecules. Phys. Rev. D 2008, 78, 102004. [Google Scholar] [CrossRef]
- Gaul, K.; Kozlov, M.G.; Isaev, T.A.; Berger, R. Chiral Molecules as Sensitive Probes for Direct Detection of P-Odd Cosmic Fields. Phys. Rev. Lett. 2020, 125, 123004. [Google Scholar] [CrossRef] [PubMed]
- Glashow, S.L. Partial-symmetries of weak interactions. Nucl. Phys. 1961, 22, 579–588. [Google Scholar] [CrossRef]
- Weinberg, S. A Model of Leptons. Phys. Rev. Lett. 1967, 19, 1264–1266. [Google Scholar] [CrossRef]
- Salam, A. Weak and electromagnetic interactions. Conf. Proc. C 1961, 22, 579–588. [Google Scholar]
- Zel’dovich, Y.B. Parity Nonconservation in the First Order in the Weak-Interaction Constant in Electron Scattering and Other Effects. J. Exp. Theor. Phys. JETP 1959, 9, 682. [Google Scholar]
- Ginges, J.; Flambaum, V. Violations of fundamental symmetries in atoms and tests of unification theories of elementary particles. Phys. Rep. 2004, 397, 63–154. [Google Scholar] [CrossRef]
- Barron, L. Fundamental symmetry aspects of optical activity. Chem. Phys. Lett. 1981, 79, 392–394. [Google Scholar] [CrossRef]
- Barron, L. True and false chirality and parity violation. Chem. Phys. Lett. 1986, 123, 423–427. [Google Scholar] [CrossRef]
- Barron, L.D. False Chirality, Absolute Enantioselection and CP Violation: Pierre Curie’s Legacy. Magnetochemistry 2020, 6, 5. [Google Scholar] [CrossRef]
- Martínez-Gil, D.; Bargueño, P.; Miret-Artés, S. On the role of true and false chirality in producing parity violating energy differences. Proc. R. Soc. Math. Phys. Eng. Sci. 2023. under review. [Google Scholar]
- Laerdahl, J.K.; Schwerdtfeger, P. Fully relativistic ab initio calculations of the energies of chiral molecules including parity-violating weak interactions. Phys. Rev. A 1999, 60, 4439–4453. [Google Scholar] [CrossRef]
- Berger, R.; Quack, M. Multiconfiguration linear response approach to the calculation of parity violating potentials in polyatomic molecules. J. Chem. Phys. 2000, 112, 3148–3158. [Google Scholar] [CrossRef]
- Hegstrom, R.; Rein, D.W.; Sandars, P.G.H. Calculation of the parity nonconserving energy difference between mirror-image molecules. J. Chem. Phys. 1980, 73, 2329–2341. [Google Scholar] [CrossRef]
- Zel’dovich, B.Y.; Saakyan, D.; Sobel’man, I. Energy difference between right-hand and left-hand molecules, due to parity nonconservation in weak interactions of electrons with nuclei. JETP Lett. 1977, 25, 106. [Google Scholar]
- Rein, D.; Hegstrom, R.; Sandars, P. Parity non-conserving energy difference between mirror image molecules. Phys. Lett. A 1979, 71, 499–502. [Google Scholar] [CrossRef]
- Bakasov, A.; Ha, T.-K.; Quack, M. Ab Initio Calculation of Molecular Energies Including Parity Violating Interactions. In Chemical Evolution: Physics of the Origin and Evolution of Life: Proceedings of the Fourth Trieste Conference on Chemical Evolution, Trieste, Italy, 4–8 September 1995; Chela-Flores, J., Raulin, F., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1996; pp. 287–296. [Google Scholar]
- Bakasov, A.; Ha, T.-K.; Quack, M. Ab initio calculation of molecular energies including parity violating interactions. J. Chem. Phys. 1998, 109, 7263–7285. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Zanasi, R. On the calculation of parity-violating energies in hydrogen peroxide and hydrogen disulphide molecules within the random-phase approximation. Chem. Phys. Lett. 1997, 279, 349–354. [Google Scholar] [CrossRef]
- Hennum, A.C.; Helgaker, T.; Klopper, W. Parity-violating interaction in H2O2 calculated from density-functional theory. Chem. Phys. Lett. 2002, 354, 274–282. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Saue, T.; van Stralen, J.; Visscher, L. Relativistic second-order many-body and density-functional theory for the parity-violation contribution to the C-F stretching mode in CHFClBr. Phys. Rev. A 2005, 71, 012103. [Google Scholar] [CrossRef]
- Berger, R. Breit interaction contribution to parity violating potentials in chiral molecules containing light nuclei. J. Chem. Phys. 2008, 129, 154105. [Google Scholar] [CrossRef] [PubMed]
- Laerdahl, J.; Schwerdtfeger, P.; Quiney, H. Theoretical analysis of parity-violating energy differences between the enantiomers of chiral molecules. Phys. Rev. Lett. 2000, 84, 3811–3814. [Google Scholar] [CrossRef] [PubMed]
- Berger, R.; Langermann, N.; van Wüllen, C. Zeroth-order regular approximation approach to molecular parity violation. Phys. Rev. A 2005, 71, 042105. [Google Scholar] [CrossRef]
- Berger, R.; van Wüller, C. Density functional calculations of molecular parity-violating effects within the zeroth-order regular approximation. J. Chem. Phys. 2005, 122, 134316. [Google Scholar] [CrossRef] [PubMed]
- Nesse, F.; Wolf, A.; Fleig, T.; Reiher, M.; Hess, B. Calculation of electric-field gradients based on higher-order generalized Douglas–Kroll transformations. J. Chem. Phys. 2005, 122, 204107. [Google Scholar] [CrossRef] [PubMed]
- Figgen, D.; Koers, A.; Schwerdtfeger, P. NWHClI: A Small and Compact Chiral Molecule with Large Parity-Violation Effects in the Vibrational Spectrum. Angew. Chem. Int. Ed. 2010, 49, 2941–2943. [Google Scholar] [CrossRef] [PubMed]
- Daussy, C.; Marrel, T.; Amy-Klein, A.; Nguyen, C.T.; Bordé, C.J.; Chardonnet, C. Limit on the Parity Nonconserving Energy Difference between the Enantiomers of a Chiral Molecule by Laser Spectroscopy. Phys. Rev. Lett. 1999, 83, 1554–1557. [Google Scholar] [CrossRef]
- Fujiki, M. Experimental Tests of Parity Violation at Helical Polysilylene Level. Macromol. Rapid Commun. 2001, 22, 669–674. [Google Scholar] [CrossRef]
- Fujiki, M. Mirror Symmetry Breaking in Helical Polysilanes: Preference between Left and Right of Chemical and Physical Origin. Symmetry 2010, 2, 1625–1652. [Google Scholar] [CrossRef]
- Fujiki, M.; Koe, J.; Mori, T.; Kimura, Y. Questions of Mirror Symmetry at the Photoexcited and Ground States of Non-Rigid Luminophores Raised by Circularly Polarized Luminescence and Circular Dichroism Spectroscopy: Part 1. Oligofluorenes, Oligophenylenes, Binaphthyls and Fused Aromatics. Molecules 2018, 23, 2606. [Google Scholar] [CrossRef] [PubMed]
- Ledbetter, M.; Crawford, C.; Pines, A.; Wemmer, D.; Knappe, S.; Kitching, J.; Budker, D. Optical detection of NMR J-spectra at zero magnetic field. J. Magn. Reson. 2009, 199, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Darquié, B.; Stoeffler, C.; Shelovnikov, A.; Daussy, C.; Amy-Klein, A.; Chardonnet, C.; Zrig, S.; Guy, L.; Crassous, J.; Soulard, P.; et al. Progress toward the first observation of parity violation in chiral molecules by high-resolution laser spectroscopy. Chirality 2010, 22, 870–884. [Google Scholar] [CrossRef] [PubMed]
- MacDermott, A.; Hegstrom, R. Optical rotation of molecules in beams: The magic angle. Chem. Phys. 2004, 305, 47–53. [Google Scholar] [CrossRef]
- MacDermott, A.; Hegstrom, R. A proposed experiment to measure the parity-violating energy difference between enantiomers from the optical rotation of chiral ammonia-like “cat” molecules. Chem. Phys. 2004, 305, 55–68. [Google Scholar] [CrossRef]
- Schnell, M.; Meijer, G. Cold Molecules: Preparation, Applications, and Challenges. Angew. Chem. Int. Ed. 2009, 48, 6010–6031. [Google Scholar] [CrossRef] [PubMed]
- Lahamer, A.; Mahurin, S.; Compton, R.; House, D.; Laerdahl, J.; Lein, M.; Schwerdtfeger, P. Search for a Parity-Violating Energy Difference between Enantiomers of a Chiral Iron Complex. Phys. Rev. Lett. 2000, 85, 4470–4473. [Google Scholar] [CrossRef] [PubMed]
- Arimondo, E.; Glorieux, P.; Oka, T. Observation of inverted infrared lamb dips in separated optical isomers. Opt. Commun. 1977, 23, 369–372. [Google Scholar] [CrossRef]
- Ziskind, M.; Daussy, C.; Marrel, T.; Chardonnet, C. Improved sensitivity in the search for a parity-violating energy difference in the vibrational spectrum of the enantiomers of CHFClBr. Eur. Phys. J. D 2002, 20, 219–225. [Google Scholar] [CrossRef]
- Quack, M. Fundamental Symmetries and Symmetry Violations from High Resolution Spectroscopy. In Handbook of High-Resolution Spectroscopy; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; Chapter 18; pp. 659–722. [Google Scholar]
- Eills, J.; Blanchard, J.W.; Bougas, L.; Kozlov, M.G.; Pines, A.; Budker, D. Measuring molecular parity nonconservation using nuclear-magnetic-resonance spectroscopy. Phys. Rev. A 2017, 96, 042119. [Google Scholar] [CrossRef]
- Cournol, A.; Manceau, M.; Pierens, M.; Lecordier, L.; Tran, D.B.A.; Santagata, R.; Darquié, B. A new experiment to test parity symmetry in cold chiral molecules using vibrational spectroscopy. Quantum Electron. 2019, 49, 288. [Google Scholar] [CrossRef]
- Stickler, B.A.; Diekmann, M.; Berger, R.; Wang, D. Enantiomer Superpositions from Matter-Wave Interference of Chiral Molecules. Phys. Rev. X 2021, 11, 031056. [Google Scholar] [CrossRef]
- Satterthwaite, L.; Koumarianou, G.; Sorensen, D.; Patterson, D. Sub-Hz Differential Rotational Spectroscopy of Enantiomers. Symmetry 2022, 1, 28. [Google Scholar] [CrossRef]
- Erez, I.; Wallach, E.R.; Shagam, Y. Simultaneous Enantiomer-Resolved Ramsey Spectroscopy Scheme for Chiral Molecules. Phys. Rev. X 2023, 13, 041025. [Google Scholar] [CrossRef]
- Sahu, N.; Gaul, K.; Wilm, A.; Schnell, M.; Berger, R. Towards detection of molecular parity violation by microwave spectroscopy of CpRe(CH3)(CO)(NO). arXiv 2023, arXiv:2303.08263. [Google Scholar]
- Dietiker, P.; Miloglyadov, E.; Quack, M.; Schneider, A.; Seyfang, G. Infrared laser induced population transfer and parity selection in 14NH3: A proof of principle experiment towards detecting parity violation in chiral molecules. J. Chem. Phys. 2015, 143, 244305. [Google Scholar] [CrossRef] [PubMed]
- Berger, R.; Gottselig, M.; Quack, M.; Willeke, M. Parity Violation Dominates the Dynamics of Chirality in Dichlorodisulfane. Angew. Chem. Int. Ed. Engl. 2001, 10, 4195–4198. [Google Scholar] [CrossRef]
- Prentner, R.; Quack, M.; Stohner, J.; Willeke, M. Wavepacket Dynamics of the Axially Chiral Molecule Cl-O-O-Cl under Coherent Radiative Excitation and Including Electroweak Parity Violation. Phys. Chem. A 2015, 119, 12805–12822. [Google Scholar] [CrossRef]
- Quantum beats in electric field optical activity and parity non-conservation. Chem. Phys. Lett. 2002, 365, 343–346. [CrossRef]
- Harris, R.A.; Shi, Y.; Cina, J.A. On the measurement of superpositions of chiral amplitudes by polarized light scattering. J. Chem. Phys. 1994, 105, 3459. [Google Scholar] [CrossRef]
- Cina, J.A.; Harris, R.A. On the preparation and measurement of superpositions of chiral amplitudes. J. Chem. Phys. 1994, 100, 2531–2536. [Google Scholar] [CrossRef]
- Cina, J.A.; Harris, R.A. Superpositions of Handed Wave Functions. Science 1995, 267, 832–833. [Google Scholar] [CrossRef]
- Letokhov, V. On difference of energy levels of le and right molecules due to weak interactions. Phys. Lett. A 1975, 53, 275–276. [Google Scholar] [CrossRef]
- Kompanets, O.N.; Kukudzhanov, A.R.; Letokhov, V.S.; Gervits, L.L. Narrow resonances of saturated absorption of asymmetrical molecule CHFClBr and possibility of weak current detection in molecular physics. Opt. Commun. 1976, 19, 414–416. [Google Scholar] [CrossRef]
- Fiechter, M.R.; Haase, P.A.B.; Saleh, N.; Soulard, P.; Tremblay, B.; Havenith, R.W.A.; Timmermans, R.G.E.; Schwerdtfeger, P.; Crassous, J.; Darquié, B.; et al. Toward Detection of the Molecular Parity Violation in Chiral Ru(acac)3 and Os(acac)3. J. Phys. Chem. Lett. 2022, 13, 10011–10017. [Google Scholar] [CrossRef]
- Landau, A.; Eduardus; Behar, D.; Wallach, E.; Pasteka, L.; Faraji, S.; Borschevsky, A.; Shagam, Y. Chiral molecule candidates for trapped ion spectroscopy by ab initio calculations: From state preparation to parity violation. J. Chem. Phys. 2023, 159, 114307. [Google Scholar] [CrossRef]
- Eduardus; Shagam, Y.; Landau, A.; Faraji, S.; Schwerdtfeger, P.; Borschevsky, A.; Pašteka, L.F. Large vibrationally induced parity violation effects in CHDBrI+. Chem. Commun. 2023, 59, 14579–14582. [Google Scholar] [CrossRef]
- Lee, J.; Abdiha, E.; Sartakov, B.; Meijer, G.; Eibenberger-Arias, S. Full quantum state control of chiral molecules. arXiv 2024, arXiv:2402.17308. [Google Scholar]
- Vardi, A. On the role of intermolecular interactions in establishing chiral stability. J. Chem. Phys. 2000, 112, 8743–8746. [Google Scholar] [CrossRef]
- Jona-Lasinio, G.; Presilla, C.; Toninelli, C. Interaction Induced Localization in a Gas of Pyramidal Molecules. Phys. Rev. Lett. 2002, 88, 123001. [Google Scholar] [CrossRef]
- Grecchi, V.; Sacchetti, A. Critical conditions for a stable molecular structure. J. Phys. A Math. Gen. 2004, 37, 3527. [Google Scholar] [CrossRef]
- Simonius, M. Spontaneous Symmetry Breaking and Blocking of Metastable States. Phys. Rev. Lett. 1978, 40, 980–983. [Google Scholar] [CrossRef]
- Harris, R.; Stodolsky, L. On the time dependence of optical activity. J. Chem. Phys. 1981, 74, 2145–2155. [Google Scholar] [CrossRef]
- Silbey, R.; Harris, R.A. Variational calculation of the dynamics of a two level system interacting with a bath. J. Chem. Phys. 1984, 80, 2615–2617. [Google Scholar] [CrossRef]
- Silbey, R.; Harris, R.A. Tunneling of molecules in low-temperature media: An elementary description. J. Phys. Chem. 1989, 93, 7062–7071. [Google Scholar] [CrossRef]
- Trost, J.; Hornberger, K. Hund’s Paradox and the Collisional Stabilization of Chiral Molecules. Phys. Rev. Lett. 2009, 103, 023202. [Google Scholar] [CrossRef]
- Athalye, V.; Kumar, A. Decoherence of superposition of molecular chiral states due to Rayleigh scattering. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 2633. [Google Scholar] [CrossRef]
- Berlin, Y.A.; Burin, A.; Goldanskii, V. The Hund paradox and stabilization of molecular chiral states. Z. Phys. D Atoms Mol. Clust. 1996, 37, 1996. [Google Scholar] [CrossRef]
- Bahrami, M.; Shafiee, A.; Bassi, A. Decoherence effects on superpositions of chiral states in a chiral molecule. Phys. Chem. Chem. Phys. 2012, 14, 9214–9218. [Google Scholar] [CrossRef]
- Bargueño, P.; Peñate-Rodríguez, H.C.; Gonzalo, I.; Sols, F.; Miret-Artés, S. Friction-induced enhancement in the optical activity of interacting chiral molecules. Chem. Phys. Lett. 2011, 516, 29–34. [Google Scholar] [CrossRef]
- Peñate-Rodríguez, H.C.; Dorta-Urra, A.; Bargueño, P.; Rojas-Lorenzo, G.; Miret-Artés, S. A Langevin Canonical Approach to the Dynamics of Chiral Systems: Populations and Coherences. Chirality 2013, 25, 514–520. [Google Scholar] [CrossRef]
- Peñate-Rodríguez, H.C.; Dorta-Urra, A.; Bargueño, P.; Rojas-Lorenzo, G.; Miret-Artés, S. A Langevin Canonical Approach to the Dynamics of Chiral Systems: Thermal Averages and Heat Capacity. Chirality 2014, 26, 319–325. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Caldeira, A.; Leggett, A. Path integral approach to quantum Brownian motion. Phys. A Stat. Mech. Its Appl. 1983, 121, 587–616. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Influence of Dissipation on Quantum Tunneling in Macroscopic Systems. Phys. Rev. Lett. 1981, 46, 211–214. [Google Scholar] [CrossRef]
- Caldeira, A.; Leggett, A. Quantum tunnelling in a dissipative system. Ann. Phys. 1983, 149, 374–456. [Google Scholar] [CrossRef]
- Weiss, U. Quantum Dissipative Systems; Series in Modern Condensed Matter Physics; World Scientific: Singapore, 1999. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Gil, D.; Bargueño, P.; Miret-Artés, S. The Interplay between Tunneling and Parity Violation in Chiral Molecules. Entropy 2024, 26, 456. https://doi.org/10.3390/e26060456
Martínez-Gil D, Bargueño P, Miret-Artés S. The Interplay between Tunneling and Parity Violation in Chiral Molecules. Entropy. 2024; 26(6):456. https://doi.org/10.3390/e26060456
Chicago/Turabian StyleMartínez-Gil, Daniel, Pedro Bargueño, and Salvador Miret-Artés. 2024. "The Interplay between Tunneling and Parity Violation in Chiral Molecules" Entropy 26, no. 6: 456. https://doi.org/10.3390/e26060456
APA StyleMartínez-Gil, D., Bargueño, P., & Miret-Artés, S. (2024). The Interplay between Tunneling and Parity Violation in Chiral Molecules. Entropy, 26(6), 456. https://doi.org/10.3390/e26060456








