A Circular-Linear Probabilistic Model Based on Nonparametric Copula with Applications to Directional Wind Energy Assessment
Abstract
1. Introduction
2. Nonparametric Probabilistic Model
2.1. Marginal Probability Density Function of Wind Speed
2.2. Marginal Probability Density Function of Wind Direction
2.3. Metrics for Model Evaluation
2.4. Joint Probability Density Function Estimation of Wind Speed and Direction
3. Wind Data
4. Results and Discussions
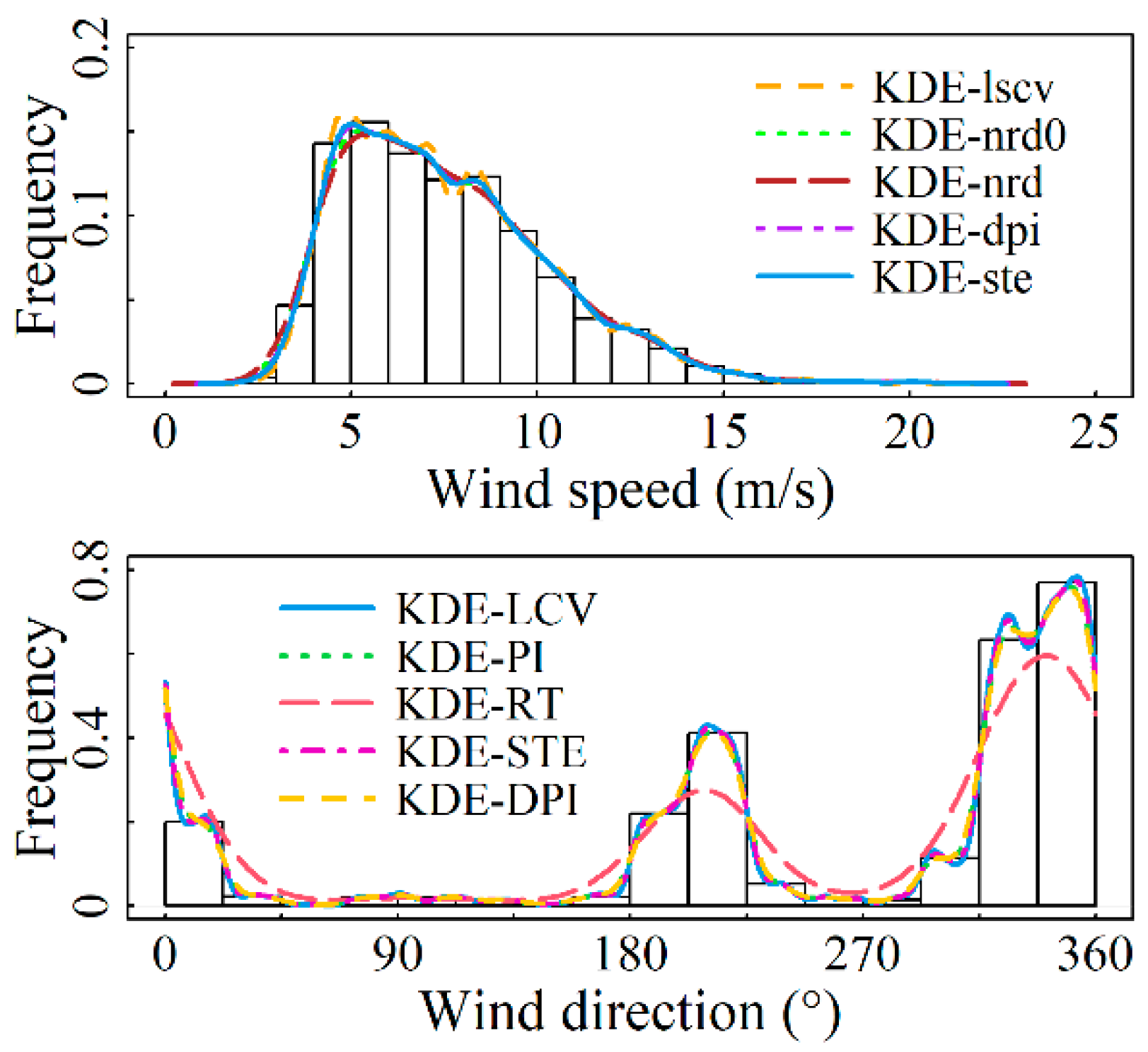
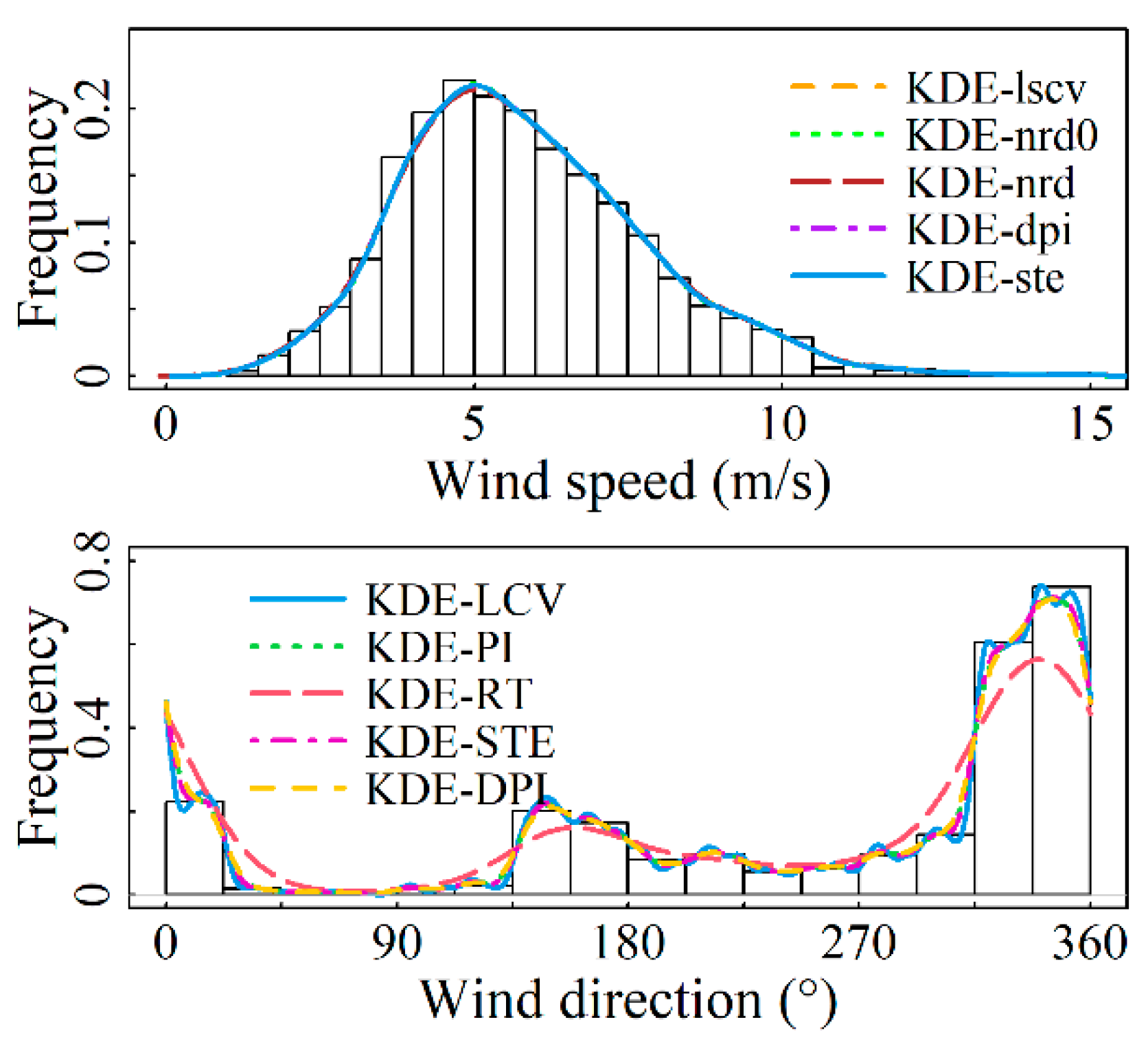
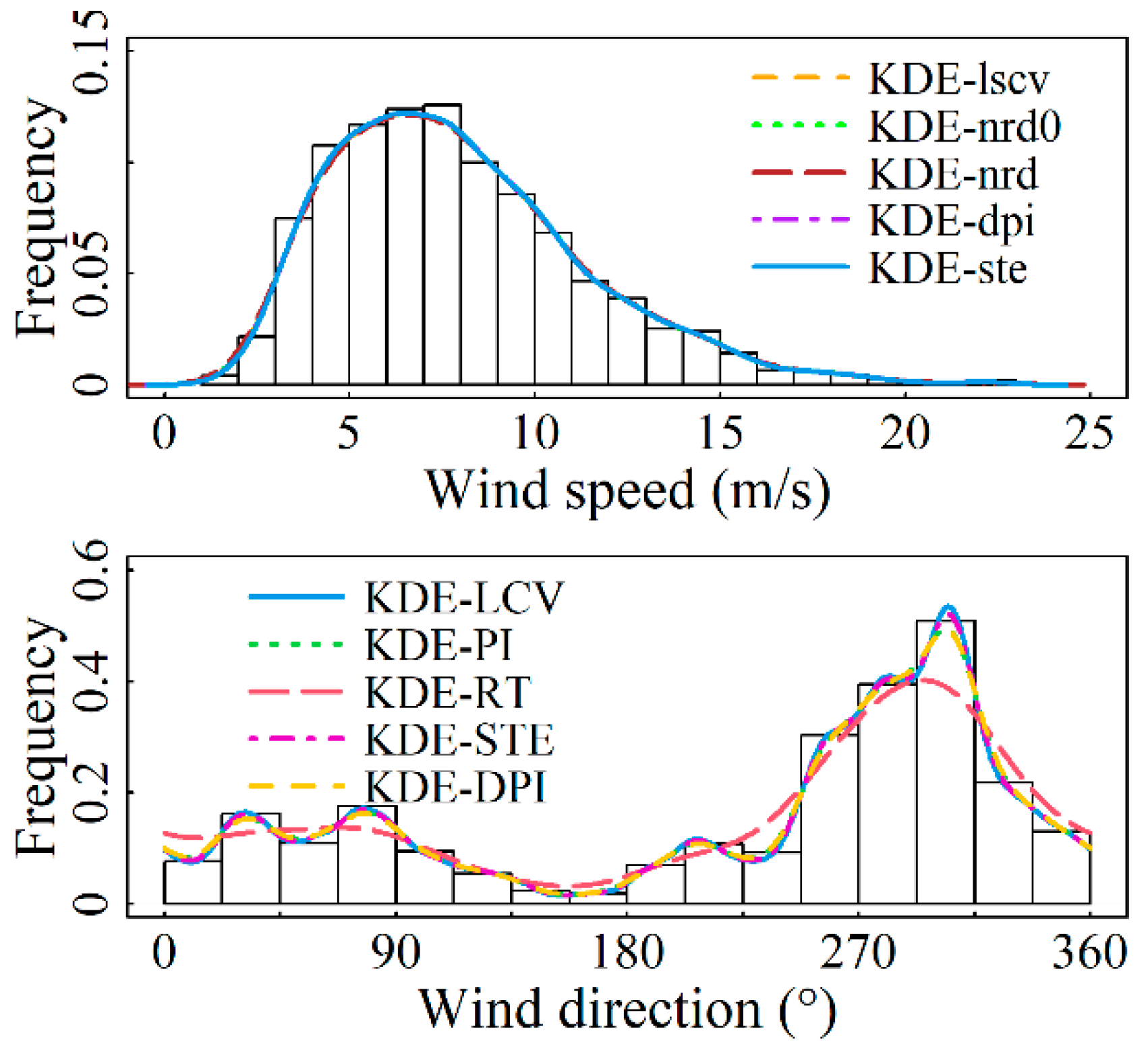
4.1. Fitting Results for Marginal Distributions
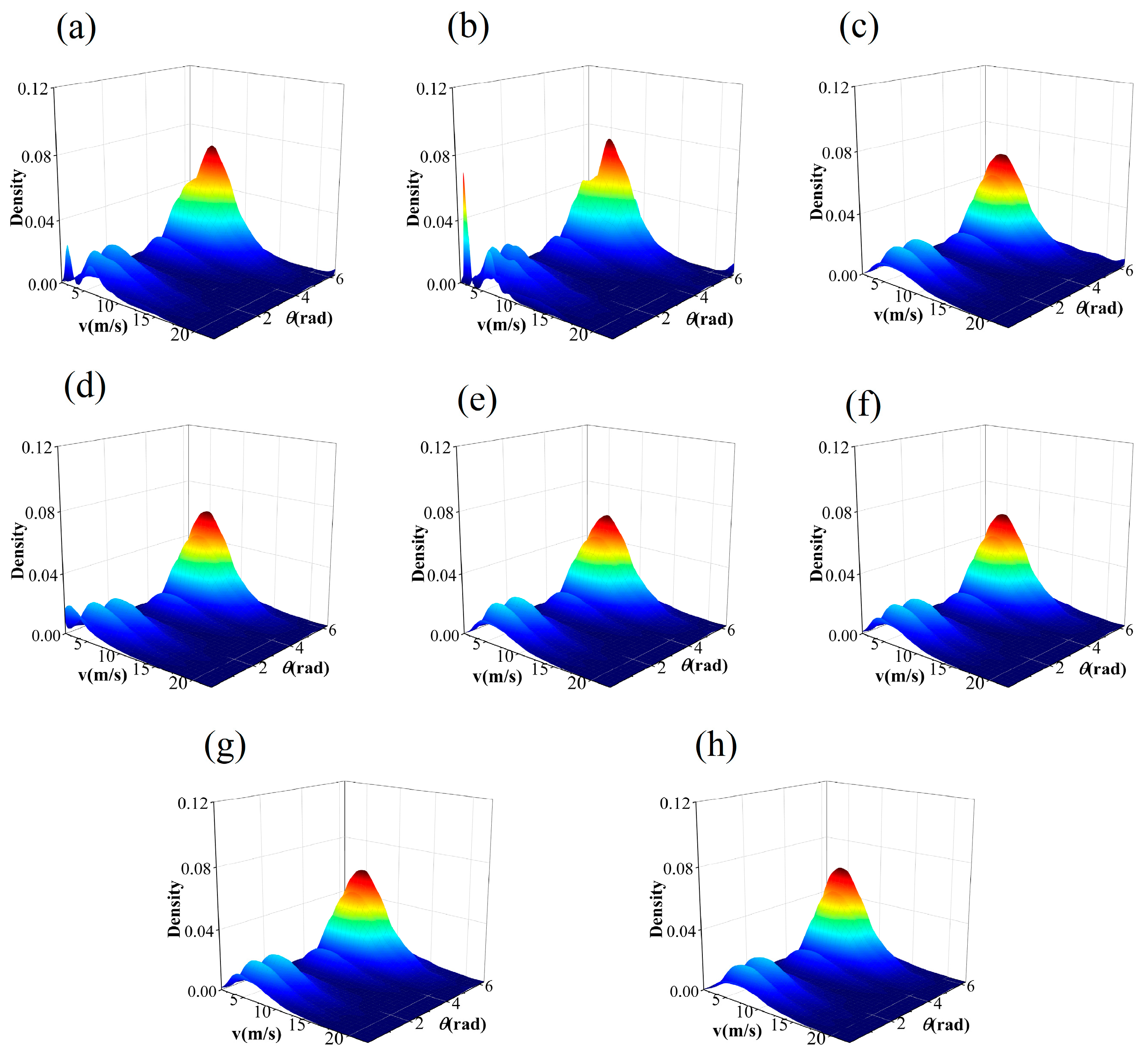
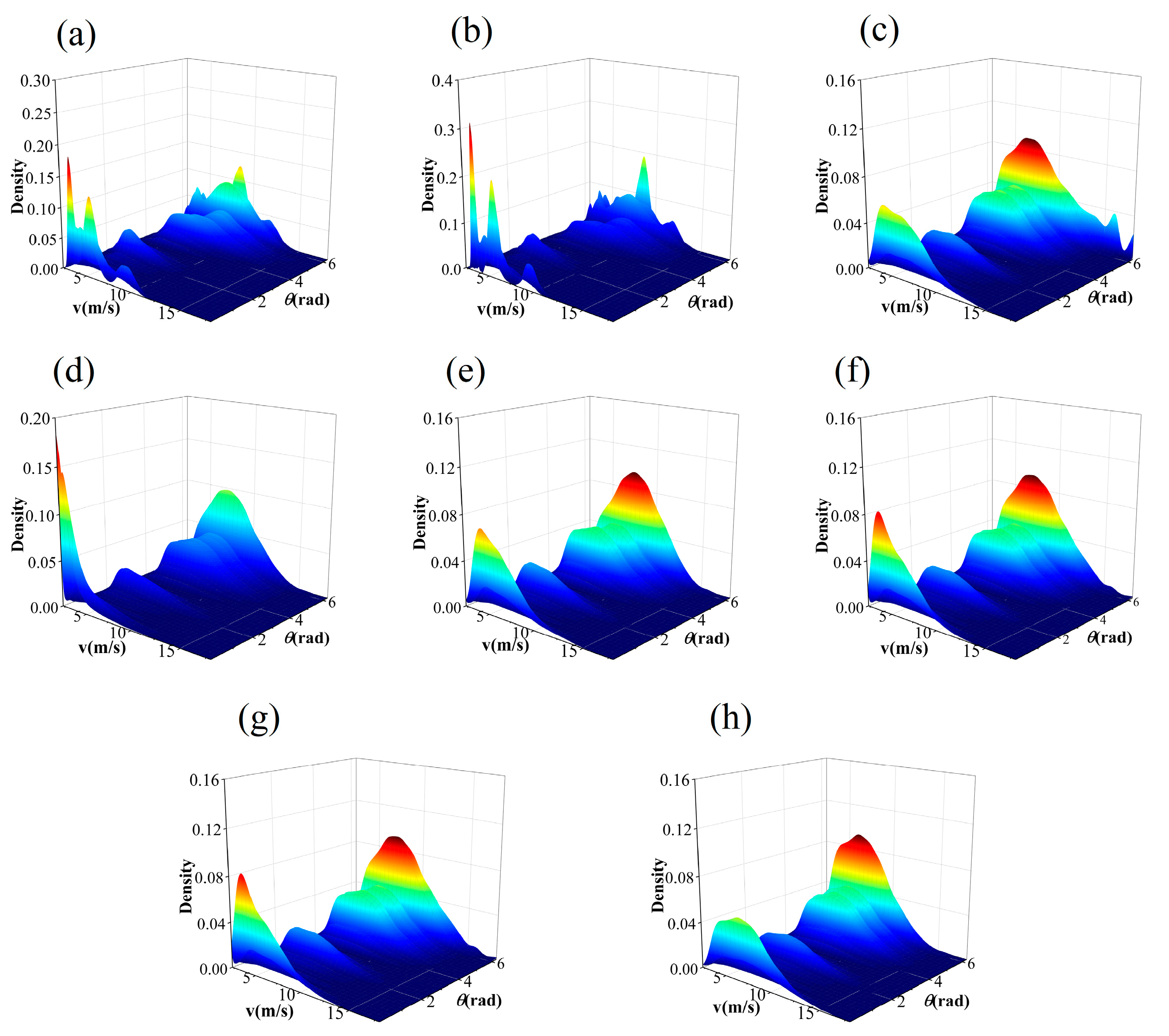
4.2. Results of Fitting the Joint Probability Density Function
5. Directional Wind Energy Assessment
6. Conclusions
- (1)
- For the wind speed component, the Gaussian kernel density function and five bandwidth algorithms were used to compare fitting results, with the KDE-ste model showing the best performance. For the wind direction component, the von Mises kernel density function and five circular data bandwidth algorithms were employed, with the KDE-LCV model demonstrating superior fitting accuracy.
- (2)
- The ranking results of the two evaluating metrics suggest that the performance of the two non-parametric copula models surpasses that of the parametric copulas. Among them, KDE-COP-CV outperforms KDE-COP-PI, indicating the optimum performance of the KDE-COP-CV model in modeling the JPDF of wind speed and wind direction.
- (3)
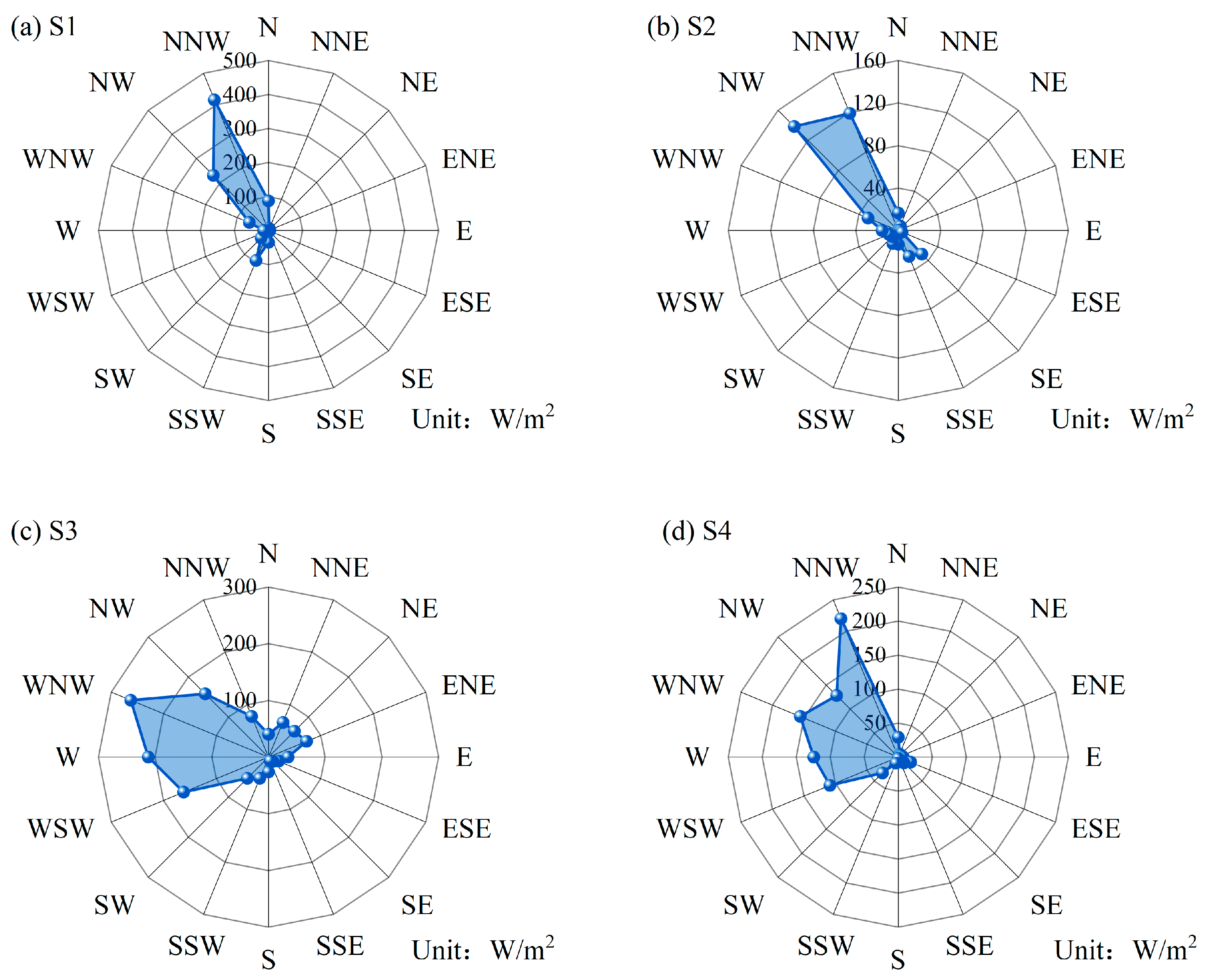
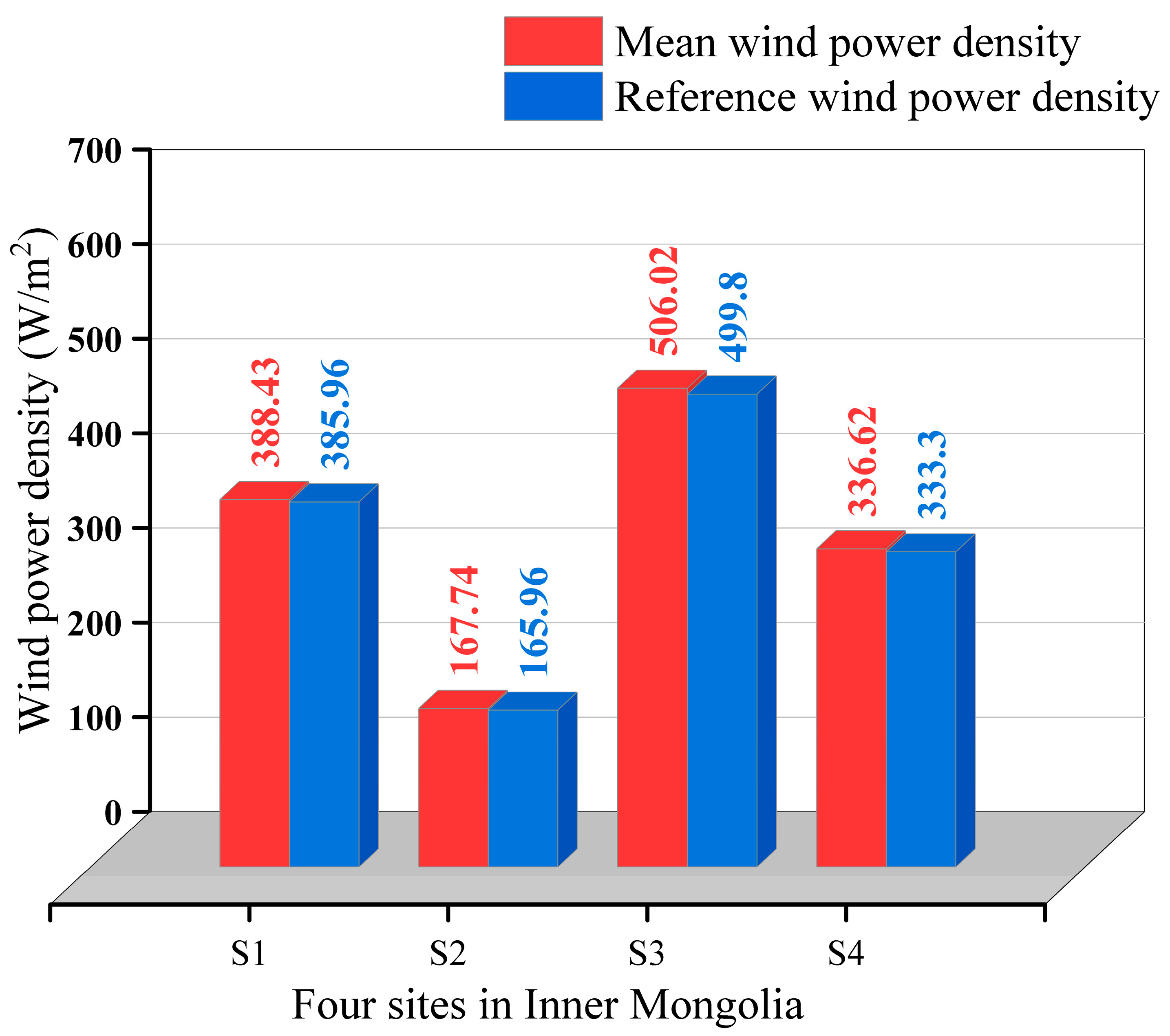
- Based on the KDE-COP-CV model, the WPD distribution of four sites was investigated. The findings reveal that all four sites possess abundant wind resources, especially the sites located in Hohhot city (S1) and Xilin Gol League (S3). Additionally, by intuitively and accurately analyzing the change of WPD relative to the wind direction, this paper identifies that the wind energy is more substantial in the north-east and west directions. In contrast, the wind energy is considerably lower in the southeast direction. These observations highlight deviations from expected patterns when not considering dependence between wind speed and direction. The concentration range of wind energy density varies across different locations, while the directional shifts in wind energy underscore the essential need for a joint analysis involving the two variables of the bivariate wind vector.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, Y.; Bréon, F.-M. Wind Power Potential and Intermittency Issues in the Context of Climate Change. Energy Convers. Manag. 2021, 240, 114276. [Google Scholar] [CrossRef]
- Ji, X.; Zou, J.; Cheng, Z.; Huang, G.; Zhao, Y.-G. Generalized Bivariate Mixture Model of Directional Wind Speed in Mixed Wind Climates. Alex. Eng. J. 2024, 89, 98–109. [Google Scholar] [CrossRef]
- Masoudi, S.M.; Baneshi, M. Layout Optimization of a Wind Farm Considering Grids of Various Resolutions, Wake Effect, and Realistic Wind Speed and Wind Direction Data: A Techno-Economic Assessment. Energy 2022, 244, 123188. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X. Assessing Probabilistic Wind Load Effects via a Multivariate Extreme Wind Speed Model: A Unified Framework to Consider Directionality and Uncertainty. J. Wind Eng. Ind. Aerodyn. 2015, 147, 30–42. [Google Scholar] [CrossRef]
- Roga, S.; Bardhan, S.; Kumar, Y.; Dubey, S.K. Recent Technology and Challenges of Wind Energy Generation: A Review. Sustain. Energy Technol. Assess. 2022, 52, 102239. [Google Scholar] [CrossRef]
- Pishgar-Komleh, S.H.; Keyhani, A.; Sefeedpari, P. Wind Speed and Power Density Analysis Based on Weibull and Rayleigh Distributions (a Case Study: Firouzkooh County of Iran). Renew. Sustain. Energy Rev. 2015, 42, 313–322. [Google Scholar] [CrossRef]
- Baran, S.; Lerch, S. Log-Normal Distribution Based Ensemble Model Output Statistics Models for Probabilistic Wind-Speed Forecasting. Q. J. R. Meteorol. Soc. 2015, 141, 2289–2299. [Google Scholar] [CrossRef]
- Kollu, R.; Rayapudi, S.R.; Narasimham, S.; Pakkurthi, K.M. Mixture Probability Distribution Functions to Model Wind Speed Distributions. Int. J. Energy Environ. Eng. 2012, 3, 27. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F.; Prattico, F. First and Second Order Semi-Markov Chains for Wind Speed Modeling. Phys. A Stat. Mech. Appl. 2013, 392, 1194–1201. [Google Scholar] [CrossRef]
- Aljeddani, S.M.; Mohammed, M.A. An Extensive Mathematical Approach for Wind Speed Evaluation Using Inverse Weibull Distribution. Alex. Eng. J. 2023, 76, 775–786. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C. On the Mixture of Wind Speed Distribution in a Nordic Region. Energy Convers. Manag. 2018, 174, 33–44. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zou, R.; Song, D. Bayesian Infinite Mixture Models for Wind Speed Distribution Estimation. Energy Convers. Manag. 2021, 236, 113946. [Google Scholar] [CrossRef]
- Jia, J.; Yan, Z.; Peng, X.; An, X. A New Distribution for Modeling the Wind Speed Data in Inner Mongolia of China. Renew. Energy 2020, 162, 1979–1991. [Google Scholar] [CrossRef]
- Pan, Y.; Qin, J. A Novel Probabilistic Modeling Framework for Wind Speed with Highlight of Extremes under Data Discrepancy and Uncertainty. Appl. Energy 2022, 326, 119938. [Google Scholar] [CrossRef]
- Wahbah, M.; Feng, S.F.; EL-Fouly, T.H.M.; Zahawi, B. Wind Speed Probability Density Estimation Using Root-Transformed Local Linear Regression. Energy Convers. Manag. 2019, 199, 111889. [Google Scholar] [CrossRef]
- Han, Q.; Ma, S.; Wang, T.; Chu, F. Kernel Density Estimation Model for Wind Speed Probability Distribution with Applicability to Wind Energy Assessment in China. Renew. Sustain. Energy Rev. 2019, 115, 109387. [Google Scholar] [CrossRef]
- Wahbah, M.; Mohandes, B.; EL-Fouly, T.H.M.; El Moursi, M.S. Unbiased Cross-Validation Kernel Density Estimation for Wind and PV Probabilistic Modelling. Energy Convers. Manag. 2022, 266, 115811. [Google Scholar] [CrossRef]
- Alharthi, A.S. A New Probabilistic Model with Applications to the Wind Speed Energy Data Sets. Alex. Eng. J. 2024, 86, 67–78. [Google Scholar] [CrossRef]
- Hirata, Y.; Mandic, D.P.; Suzuki, H.; Aihara, K. Wind Direction Modelling Using Multiple Observation Points. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 591–607. [Google Scholar] [CrossRef]
- Coles, S.G.; Walshaw, D. Directional Modelling of Extreme Wind Speeds. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1994, 43, 139–157. [Google Scholar] [CrossRef]
- Carta, J.A.; Bueno, C.; Ramírez, P. Statistical Modelling of Directional Wind Speeds Using Mixtures of von Mises Distributions: Case Study. Energy Convers. Manag. 2008, 49, 897–907. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wehrly, T.E. Some Angular-Linear Distributions and Related Regression Models. J. Am. Stat. Assoc. 1978, 73, 602–606. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P.; Bueno, C. A Joint Probability Density Function of Wind Speed and Direction for Wind Energy Analysis. Energy Convers. Manag. 2008, 49, 1309–1320. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. Comparison of bivariate distribution construction approaches for analysing wind speed and direction data. Wind Energy 2011, 14, 27–41. [Google Scholar] [CrossRef]
- Han, Q.; Hao, Z.; Hu, T.; Chu, F. Non-Parametric Models for Joint Probabilistic Distributions of Wind Speed and Direction Data. Renew. Energy 2018, 126, 1032–1042. [Google Scholar] [CrossRef]
- Yan, J. Enjoy the Joy of Copulas: With a Package Copula. J. Stat. Softw. 2007, 21, 1–21. [Google Scholar] [CrossRef]
- Qu, X.; Shi, J. Bivariate Modeling of Wind Speed and Air Density Distribution for Long-Term Wind Energy Estimation. Int. J. Green. Energy 2010, 7, 21–37. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Ji, T.Y.; Li, M.S.; Wu, Q.H. Quasi-Monte Carlo Based Probabilistic Optimal Power Flow Considering the Correlation of Wind Speeds Using Copula Function. IEEE Trans. Power Syst. 2018, 33, 2239–2247. [Google Scholar] [CrossRef]
- Han, Q.; Wang, T.; Chu, F. Nonparametric Copula Modeling of Wind Speed-Wind Shear for the Assessment of Height-Dependent Wind Energy in China. Renew. Sustain. Energy Rev. 2022, 161, 112319. [Google Scholar] [CrossRef]
- Schindler, D.; Jung, C. Copula-Based Estimation of Directional Wind Energy Yield: A Case Study from Germany. Energy Convers. Manag. 2018, 169, 359–370. [Google Scholar] [CrossRef]
- Li, H.-N.; Zheng, X.-W.; Li, C. Copula-Based Joint Distribution Analysis of Wind Speed and Direction. J. Eng. Mech. 2019, 145, 04019024. [Google Scholar] [CrossRef]
- Huang, S.; Li, Q.; Shu, Z.; Chan, P.W. Copula-Based Joint Distribution Analysis of Wind Speed and Wind Direction: Wind Energy Development for Hong Kong. Wind Energy 2023, 26, 900–922. [Google Scholar] [CrossRef]
- Charpentier, A.; Fermanian, J.D.; Scaillet, O. The Estimation of Copulas: Theory and Practice. In Copulas: From Theory to Application in Finance; Risk Books: London, UK, 2007. [Google Scholar]
- Geenens, G.; Charpentier, A.; Paindaveine, D. Probit Transformation for Nonparametric Kernel Estimation of the Copula Density. Bernoulli 2017, 23, 1848–1873. [Google Scholar] [CrossRef]
- Han, Q.; Chu, F. Directional Wind Energy Assessment of China Based on Nonparametric Copula Models. Renew. Energy 2021, 164, 1334–1349. [Google Scholar] [CrossRef]
- Carnicero, J.A.; Ausín, M.C.; Wiper, M.P. Non-Parametric Copulas for Circular–Linear and Circular–Circular Data: An Application to Wind Directions. Stoch. Environ. Res. Risk Assess. 2013, 27, 1991–2002. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, T.; Gou, H.; Pu, Q.; Bao, Y. Joint Distribution of Wind Speed and Direction over Complex Terrains Based on Nonparametric Copula Models. J. Wind Eng. Ind. Aerodyn. 2023, 241, 105509. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Chi, D. Wind Energy Potential Assessment for the Site of Inner Mongolia in China. Renew. Sustain. Energy Rev. 2013, 21, 215–228. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, J.; Dong, Y.; Lu, H. Comprehensive Assessment of Wind Resources and the Low-Carbon Economy: An Empirical Study in the Alxa and Xilin Gol Leagues of Inner Mongolia, China. Renew. Sustain. Energy Rev. 2015, 50, 1304–1319. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK, 1986. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation; Wiley and Kegan Paul: New York, NY, USA, 1992. [Google Scholar]
- Wang, Z.; Zhang, W.; Zhang, Y.; Liu, Z. Circular-Linear-Linear Probabilistic Model Based on Vine Copulas: An Application to the Joint Distribution of Wind Direction, Wind Speed, and Air Temperature. J. Wind Eng. Ind. Aerodyn. 2021, 215, 104704. [Google Scholar] [CrossRef]
- Taylor, C.C. Automatic Bandwidth Selection for Circular Density Estimation. Comput. Stat. Data Anal. 2008, 52, 3493–3500. [Google Scholar] [CrossRef]
- Oliveira, M.; Crujeiras, R.M.; Rodríguez-Casal, A. A Plug-in Rule for Bandwidth Selection in Circular Density Estimation. Comput. Stat. Data Anal. 2012, 56, 3898–3908. [Google Scholar] [CrossRef]
- Ameijeiras-Alonso, J. A Reliable Data-Based Smoothing Parameter Selection Method for Circular Kernel Estimation. Stat. Comput. 2024, 34, 73. [Google Scholar] [CrossRef]
- Genest, C.; Okhrin, O.; Bodnar, T. Copula Modeling from Abe Sklar to the Present Day. J. Multivar. Anal. 2023, 201, 105278. [Google Scholar] [CrossRef]
- Wen, K.; Wu, X. Transformation-Kernel Estimation of Copula Densities. J. Bus. Econ. Stat. 2018, 38, 148–164. [Google Scholar] [CrossRef]
- Al-Duais, F.S.; Al-Sharpi, R.S. A Unique Markov Chain Monte Carlo Method for Forecasting Wind Power Utilizing Time Series Model. Alex. Eng. J. 2023, 74, 51–63. [Google Scholar] [CrossRef]
- Zhai, S.; Li, W.; Qiu, Z.; Zhang, X.; Hou, S. An Improved Deep Reinforcement Learning Method for Dispatch Optimization Strategy of Modern Power Systems. Entropy 2023, 25, 546. [Google Scholar] [CrossRef]
- Wang, J.; Qian, Y.; Zhang, L.; Wang, K.; Zhang, H. A Novel Wind Power Forecasting System Integrating Time Series Refining, Nonlinear Multi-Objective Optimized Deep Learning and Linear Error Correction. Energy Convers. Manag. 2024, 299, 117818. [Google Scholar] [CrossRef]




| Metrics | Formulas |
|---|---|
| Station | Affiliated League | Longitude (E) | Latitude (N) | Elevation (m) |
|---|---|---|---|---|
| Hohhot | Hohhot City | 40°86′ | 1153.5 | |
| Arxan | Hinggan League | 47°18′ | 997.0 | |
| Abag Banner | Xilin Gol League | 1147.7 | ||
| Linxi County | Chifeng City | 825.0 |
| S1 | 0.25306 | 0.56485 | 0.66527 | 0.45095 | 0.42104 | |
| 0.99995 | 0.99957 | 0.99929 | 0.99978 | 0.99981 | ||
| 0.00206 | 0.00599 | 0.00768 | 0.00433 | 0.00393 | ||
| 0.00167 | 0.00434 | 0.00554 | 0.00322 | 0.00296 | ||
| S2 | 0.42174 | 0.39584 | 0.46621 | 0.40870 | 0.40729 | |
| 0.99966 | 0.99972 | 0.99952 | 0.99952 | 0.99969 | ||
| 0.00534 | 0.00483 | 0.00629 | 0.00508 | 0.00505 | ||
| 0.00447 | 0.00398 | 0.00538 | 0.00422 | 0.00419 | ||
| S3 | 0.70073 | 0.68510 | 0.80690 | 0.66153 | 0.65195 | |
| 0.99968 | 0.99970 | 0.99950 | 0.99973 | 0.99974 | ||
| 0.00519 | 0.00502 | 0.00647 | 0.00477 | 0.00467 | ||
| 0.00431 | 0.00417 | 0.00536 | 0.00397 | 0.00388 | ||
| S4 | 0.53944 | 0.52687 | 0.62053 | 0.51423 | 0.49787 | |
| 0.99979 | 0.99980 | 0.99966 | 0.99982 | 0.99983 | ||
| 0.00421 | 0.00406 | 0.00529 | 0.00391 | 0.00372 | ||
| 0.00328 | 0.00317 | 0.00412 | 0.00306 | 0.00292 |
| S1 | 301.5840 | 11.6319 | 135.9957 | 119.4548 | 209.1291 | |
| 0.9966 | 0.9274 | 0.9931 | 0.9922 | 0.9953 | ||
| 0.01686 | 0.07772 | 0.02402 | 0.02549 | 0.01980 | ||
| 0.01657 | 0.07169 | 0.02345 | 0.02483 | 0.01941 | ||
| S2 | 352.1935 | 10.4348 | 110.5933 | 89.7135 | 135.5769 | |
| 0.9981 | 0.9378 | 0.9943 | 0.9930 | 0.9953 | ||
| 0.01242 | 0.07198 | 0.02174 | 0.02406 | 0.01970 | ||
| 0.01212 | 0.06634 | 0.02110 | 0.02331 | 0.01915 | ||
| S3 | 96.7885 | 8.8751 | 51.0091 | 49.2768 | 77.9118 | |
| 0.9999 | 0.9964 | 0.9997 | 0.9996 | 0.9998 | ||
| 0.00347 | 0.01741 | 0.00534 | 0.00546 | 0.00402 | ||
| 0.00257 | 0.01464 | 0.00404 | 0.00414 | 0.00299 | ||
| S4 | 334.0411 | 12.8692 | 257.1817 | 102.3456 | 168.9882 | |
| 0.9987 | 0.9593 | 0.9982 | 0.9952 | 0.9972 | ||
| 0.01053 | 0.05817 | 0.01217 | 0.02000 | 0.01528 | ||
| 0.01027 | 0.05530 | 0.01186 | 0.01939 | 0.01487 |
| S1 | S2 | S3 | S4 | |||||
| Model | ||||||||
| KDE–COP–PI | 0.00822 | 0.99976 | 0.00587 | 0.99982 | 0.00531 | 0.99987 | 0.00594 | 0.99983 |
| KDE–COP–CV | 0.00787 | 0.99978 | 0.0056 | 0.99984 | 0.00513 | 0.99988 | 0.00531 | 0.99987 |
| Gumbel | 0.01648 | 0.99901 | 0.01351 | 0.99907 | 0.0122 | 0.99931 | 0.02222 | 0.99772 |
| Clayton | 0.02289 | 0.99802 | 0.01096 | 0.99938 | 0.01008 | 0.99952 | 0.01463 | 0.99898 |
| Frank | 0.01734 | 0.99888 | 0.01141 | 0.99933 | 0.00823 | 0.99968 | 0.0157 | 0.99885 |
| Gaussian | 0.0176 | 0.99885 | 0.01157 | 0.99932 | 0.00983 | 0.99955 | 0.01782 | 0.99852 |
| Student t | 0.01762 | 0.99885 | 0.01153 | 0.99932 | 0.00983 | 0.99955 | 0.01771 | 0.99854 |
| Range | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| N | 87.32 | 16.48 | 40.68 | 29.01 |
| NNE | 6.36 | 4.61 | 66.43 | 4.56 |
| NE | 0.84 | 0.85 | 64.68 | 3.89 |
| ENE | 4.18 | 0.60 | 72.74 | 4.81 |
| E | 3.88 | 2.18 | 34.35 | 7.23 |
| ESE | 2.63 | 3.85 | 19.29 | 19.68 |
| SE | 1.11 | 31.42 | 10.59 | 11.87 |
| SSE | 3.58 | 26.55 | 7.39 | 3.87 |
| S | 34.70 | 12.83 | 26.31 | 2.09 |
| SSW | 95.06 | 13.37 | 40.47 | 9.58 |
| SW | 30.31 | 8.22 | 52.78 | 32.95 |
| WSW | 7.69 | 9.51 | 161.85 | 108.57 |
| W | 13.83 | 15.28 | 211.99 | 124.44 |
| WNW | 61.24 | 30.70 | 263.00 | 156.13 |
| NW | 229.69 | 138.39 | 157.67 | 127.80 |
| NNW | 416.15 | 119.37 | 77.84 | 220.47 |
| 388.43 | 167.74 | 506.02 | 336.62 | |
| WPD | 385.96 | 165.96 | 499.80 | 333.295 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yan, Z. A Circular-Linear Probabilistic Model Based on Nonparametric Copula with Applications to Directional Wind Energy Assessment. Entropy 2024, 26, 487. https://doi.org/10.3390/e26060487
Liu J, Yan Z. A Circular-Linear Probabilistic Model Based on Nonparametric Copula with Applications to Directional Wind Energy Assessment. Entropy. 2024; 26(6):487. https://doi.org/10.3390/e26060487
Chicago/Turabian StyleLiu, Jie, and Zaizai Yan. 2024. "A Circular-Linear Probabilistic Model Based on Nonparametric Copula with Applications to Directional Wind Energy Assessment" Entropy 26, no. 6: 487. https://doi.org/10.3390/e26060487
APA StyleLiu, J., & Yan, Z. (2024). A Circular-Linear Probabilistic Model Based on Nonparametric Copula with Applications to Directional Wind Energy Assessment. Entropy, 26(6), 487. https://doi.org/10.3390/e26060487





