A Semiparametric Bayesian Approach to Heterogeneous Spatial Autoregressive Models
Abstract
1. Introduction
2. Heterogeneous Semiparametric Spatial Autoregressive Models
3. Bayesian Inference
3.1. B-Splines for the Nonparametric Function
3.2. Prior Selection of Parameters
3.3. Posterior Inference
- Sampling from the conditional distribution below:
- Sampling from the conditional distribution below:where and
- Sampling from the conditional distribution below:where and
- Sampling from the conditional distribution below:where
- Sampling from the conditional distribution below:where
4. Simulation Study
5. Real Data Analysis
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cliff, A.; Ord, J.K. Spatial Autocorrelation; Pion: London, UK, 1973. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Anselin, L.; Bera, A.K. Spatial Dependence in Linear Regression Models with an Introduction to Spatial Econometrics; Ullah, A., Giles, D.E.A., Eds.; Handbook of Applied Economics Statistics; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Jin, F.; Lee, L.F. GEL estimation and tests of spatial autoregressive models. J. Econom. 2019, 208, 585–612. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.B.; Cheng, S.L. A penalized quasi-maximum likelihood method for variable selection in the spatial autoregressive model. Spat. Stat. 2018, 25, 86–104. [Google Scholar] [CrossRef]
- Xie, L.; Wang, X.R.; Cheng, W.H.; Tang, T. Variable selection for spatial autoregressive models. Commun. Stat. Theory Methods 2021, 50, 1325–1340. [Google Scholar] [CrossRef]
- Xie, T.F.; Cao, R.Y.; Du, J. Variable selection for spatial autoregressive models with a diverging number of parameters. Stat. Pap. 2020, 61, 1125–1145. [Google Scholar] [CrossRef]
- Su, L.J.; Jin, S.N. Profile quasi-maximum likelihood estimation of partially linear spatial autoregressive models. J. Econom. 2010, 157, 18–33. [Google Scholar] [CrossRef]
- Du, J.; Sun, X.Q.; Cao, R.Y.; Zhang, Z.Z. Statistical inference for partially linear additive spatial autoregressive models. Spat. Stat. 2018, 25, 52–67. [Google Scholar] [CrossRef]
- Cheng, S.L.; Chen, J.B. Estimation of partially linear single-index spatial autoregressive model. Stat. Pap. 2021, 62, 485–531. [Google Scholar] [CrossRef]
- Wei, C.H.; Guo, S.; Zhai, S.F. Statistical inference of partially linear varying coefficient spatial autoregressive models. Econ. Model. 2017, 64, 553–559. [Google Scholar] [CrossRef]
- Hu, Y.P.; Wu, S.Y.; Feng, S.Y.; Jin, J.L. Estimation in Partial Functional Linear Spatial Autoregressive Model. Mathematics 2020, 8, 1680. [Google Scholar] [CrossRef]
- Lin, X.; Lee, L.F. GMM estimation of spatial autoregressive models with unknown heteroskedasticity. J. Econom. 2010, 157, 34–52. [Google Scholar] [CrossRef]
- Dai, X.W.; Jin, L.B.; Tian, M.Z.; Shi, L. Bayesian Local Influence for Spatial Autoregressive Models with Heteroscedasticity. Stat. Pap. 2019, 60, 1423–1446. [Google Scholar] [CrossRef]
- Tang, N.S.; Duan, X.D. A semiparametric Bayesian approach to generalized partial linear mixed models for longitudinal data. Comput. Stat. Data Anal. 2012, 56, 4348–4365. [Google Scholar] [CrossRef]
- Xu, D.K.; Zhang, Z.Z. A semiparametric Bayesian approach to joint mean and variance models. Stat. Probab. Lett. 2013, 83, 1624–1631. [Google Scholar] [CrossRef]
- Ju, Y.Y.; Tang, N.S.; Li, X.X. Bayesian local influence analysis of skew-normal spatial dynamic panel data models. J. Stat. Comput. Simul. 2018, 88, 2342–2364. [Google Scholar] [CrossRef]
- Pfarrhofer, M.; Piribauer, P. Flexible shrinkage in high-dimensional Bayesian spatial autoregressive models. Spat. Stat. 2019, 29, 109–128. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Tang, N.S. Bayesian Quantile Regression with Mixed Discrete and Nonignorable Missing Covariates. Bayesian Anal. 2020, 15, 579–604. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Chen, J.B. Bayesian analysis of partially linear, single-index, spatial autoregressive models. Comput. Stat. 2022, 37, 327–353. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, L.C.; Ye, K.Y.; Wang, M. Bayesian quantile semiparametric mixed-effects double regression models. Stat. Theory Relat. Fields 2021, 5, 303–315. [Google Scholar] [CrossRef]
- Gelman, A.; Roberts, G.O.; Gilks, W.R. Efficient metropolis jumping rules. In Bayesian Statistics; Oxford University Press: New York, NY, USA, 1996; Volume 5. [Google Scholar]
- Geyer, C.J. Practical Markov Chain Monte Carlo. Stat. Sci. 1992, 7, 473–511. [Google Scholar] [CrossRef]
- Lee, L.F. Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica 2004, 72, 1899–1925. [Google Scholar] [CrossRef]
- Gelman, A. Inference and Monitoring Convergence in Markov Chain Monte Carlo in Practice; Chapman and Hall: London, UK, 1996. [Google Scholar]
- Pace, R.K.; Gilley, O.W. Using the spatial configuration of the data to improve estimation. J. Real Estate Financ. Econ. 1997, 14, 330–340. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Y.; Huang, J.Z. Estimation of a semiparametric varying-coefficient mixed regressive spatial autoregressive model. Econom. Stat. 2019, 9, 140–155. [Google Scholar] [CrossRef]
- Luo, G.; Wu, M. Variable selection for semiparametric varying-coefficient spatial autoregressive models with a diverging number of parameters. Commun. Stat. Theory Methods 2021, 50, 2062–2079. [Google Scholar] [CrossRef]
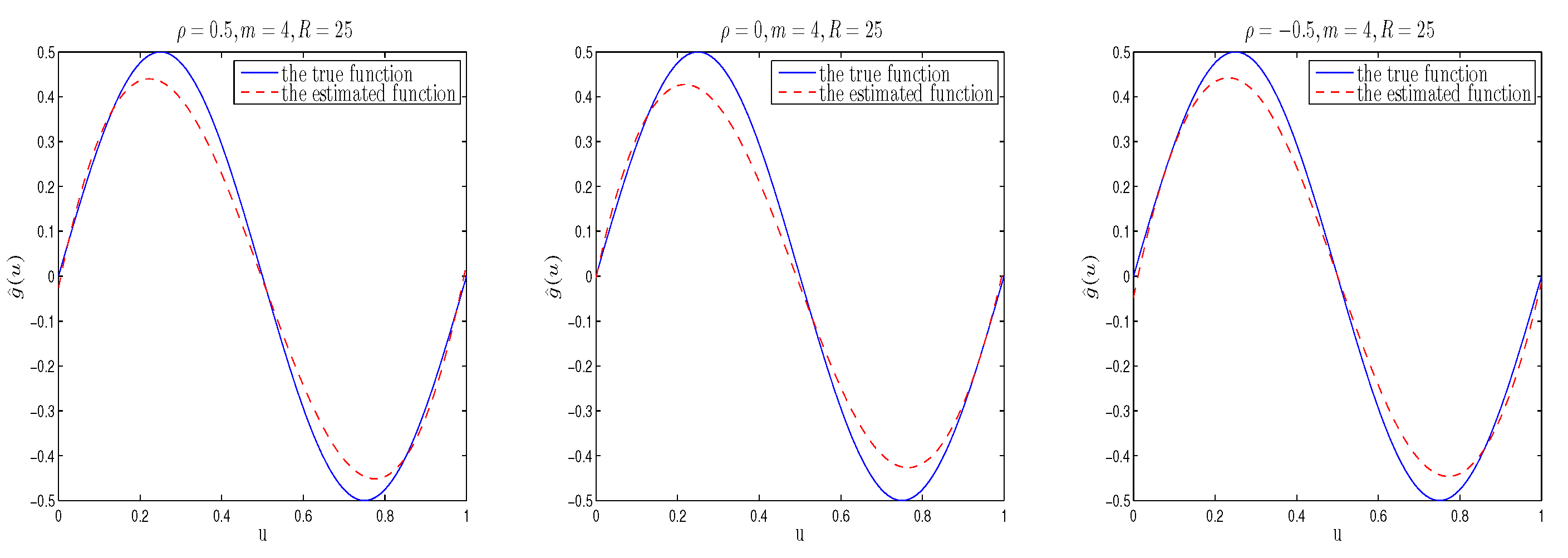

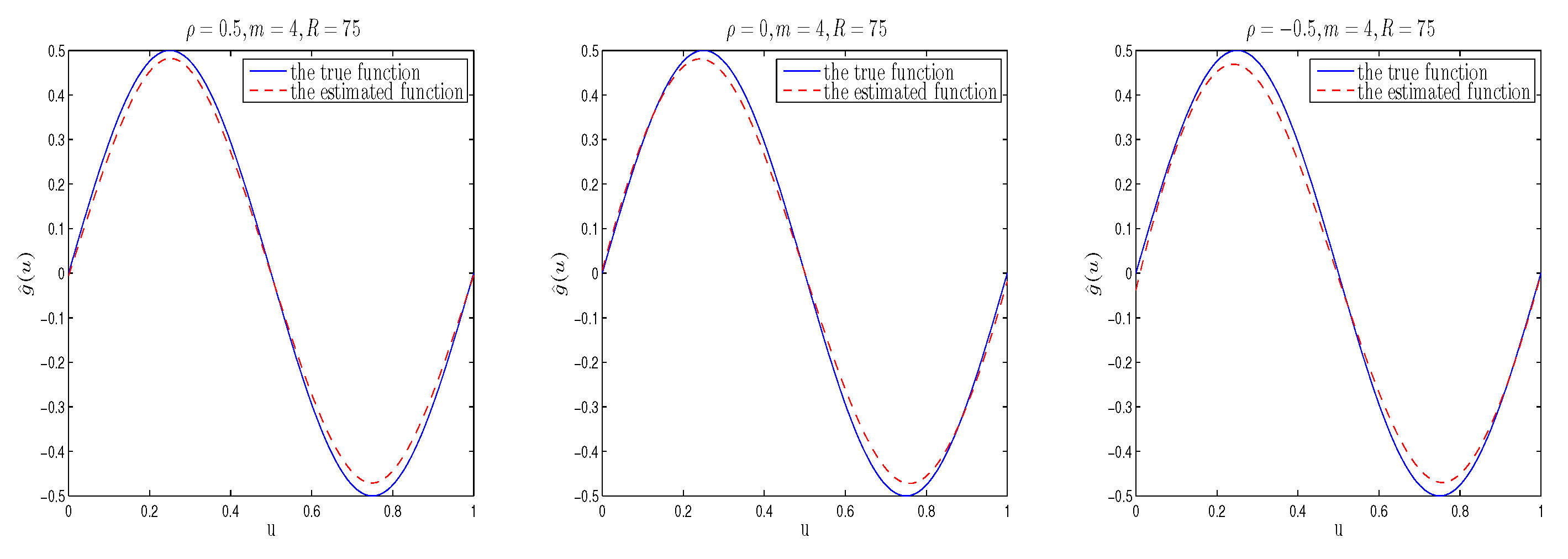



| n | Para. | Bias | RMS | SD | |
|---|---|---|---|---|---|
| I | 100 | 0.0045 | 0.0911 | 0.0910 | |
| 0.0084 | 0.1004 | 0.1000 | |||
| 0.0079 | 0.0926 | 0.0922 | |||
| 0.0053 | 0.1480 | 0.1480 | |||
| 0.0126 | 0.1459 | 0.1454 | |||
| 0.0215 | 0.1540 | 0.1524 | |||
| 0.0633 | 0.0975 | 0.0741 | |||
| 200 | 0.0031 | 0.0710 | 0.0709 | ||
| 0.0062 | 0.0674 | 0.0672 | |||
| 0.0014 | 0.0696 | 0.0695 | |||
| 0.0252 | 0.1215 | 0.1188 | |||
| 0.0093 | 0.1294 | 0.1290 | |||
| 0.0075 | 0.1080 | 0.1078 | |||
| 0.0149 | 0.0557 | 0.0536 | |||
| 300 | 0.0073 | 0.0554 | 0.0550 | ||
| 0.0075 | 0.0568 | 0.0563 | |||
| 0.0091 | 0.0597 | 0.0590 | |||
| 0.0049 | 0.0841 | 0.0840 | |||
| 0.0051 | 0.1074 | 0.1073 | |||
| 0.0047 | 0.0885 | 0.0884 | |||
| 0.0090 | 0.0448 | 0.0439 | |||
| II | 100 | 0.0153 | 0.0987 | 0.0975 | |
| 0.0284 | 0.1122 | 0.1085 | |||
| 0.0282 | 0.1083 | 0.1045 | |||
| 0.0223 | 0.1719 | 0.1704 | |||
| 0.0656 | 0.1866 | 0.1747 | |||
| 0.0540 | 0.1864 | 0.1784 | |||
| 0.0532 | 0.0979 | 0.0822 | |||
| 200 | 0.0057 | 0.0685 | 0.0683 | ||
| 0.0025 | 0.0768 | 0.0768 | |||
| 0.0022 | 0.0727 | 0.0727 | |||
| 0.0004 | 0.1174 | 0.1174 | |||
| 0.0122 | 0.1401 | 0.1396 | |||
| 0.0008 | 0.1202 | 0.1202 | |||
| 0.0320 | 0.0622 | 0.0533 | |||
| 300 | 0.0010 | 0.0658 | 0.0658 | ||
| 0.0036 | 0.0625 | 0.0624 | |||
| 0.0042 | 0.0593 | 0.0591 | |||
| 0.0018 | 0.1085 | 0.1085 | |||
| 0.0077 | 0.1170 | 0.1167 | |||
| 0.0083 | 0.0864 | 0.0860 | |||
| 0.0158 | 0.0439 | 0.0409 | |||
| III | 100 | 0.0001 | 0.0994 | 0.0994 | |
| 0.0117 | 0.1106 | 0.1099 | |||
| 0.0200 | 0.1073 | 0.1054 | |||
| 0.0330 | 0.1788 | 0.1758 | |||
| 0.0059 | 0.1855 | 0.1854 | |||
| 0.0218 | 0.1882 | 0.1869 | |||
| 0.0553 | 0.0986 | 0.0816 | |||
| 200 | 0.0013 | 0.0686 | 0.0686 | ||
| 0.0100 | 0.0780 | 0.0773 | |||
| 0.0062 | 0.0731 | 0.0729 | |||
| 0.0217 | 0.1208 | 0.1189 | |||
| 0.0367 | 0.1465 | 0.1418 | |||
| 0.0135 | 0.1246 | 0.1238 | |||
| 0.0329 | 0.0624 | 0.0531 | |||
| 300 | 0.0052 | 0.0663 | 0.0661 | ||
| 0.0014 | 0.0627 | 0.0627 | |||
| 0.0014 | 0.0593 | 0.0593 | |||
| 0.0121 | 0.1109 | 0.1102 | |||
| 0.0233 | 0.1205 | 0.1182 | |||
| 0.0160 | 0.0878 | 0.0863 | |||
| 0.0160 | 0.0440 | 0.0410 |
| Type | n | Para. | Bias | RMS | SD |
|---|---|---|---|---|---|
| I | 100 | 0.0017 | 0.1025 | 0.1025 | |
| 0.0065 | 0.1031 | 0.1029 | |||
| 0.0192 | 0.0955 | 0.0936 | |||
| 0.0114 | 0.1689 | 0.1685 | |||
| 0.0089 | 0.1785 | 0.1783 | |||
| 0.0020 | 0.1573 | 0.1573 | |||
| 0.0092 | 0.0934 | 0.0929 | |||
| 200 | 0.0074 | 0.0623 | 0.0618 | ||
| 0.0002 | 0.0833 | 0.0833 | |||
| 0.0042 | 0.0665 | 0.0663 | |||
| 0.0001 | 0.0995 | 0.0995 | |||
| 0.0050 | 0.1196 | 0.1195 | |||
| 0.0177 | 0.1082 | 0.1067 | |||
| 0.0043 | 0.0702 | 0.0701 | |||
| 300 | 0.0038 | 0.0551 | 0.0549 | ||
| 0.0093 | 0.0590 | 0.0582 | |||
| 0.0102 | 0.0442 | 0.0430 | |||
| 0.0004 | 0.0904 | 0.0904 | |||
| 0.0061 | 0.1070 | 0.1068 | |||
| 0.0031 | 0.0977 | 0.0977 | |||
| 0.0004 | 0.0540 | 0.0540 | |||
| II | 100 | 0.0180 | 0.1001 | 0.0985 | |
| 0.0027 | 0.1205 | 0.1205 | |||
| 0.0111 | 0.1139 | 0.1134 | |||
| 0.0456 | 0.1827 | 0.1770 | |||
| 0.0596 | 0.2049 | 0.1960 | |||
| 0.0397 | 0.1852 | 0.1809 | |||
| 0.0125 | 0.0975 | 0.0967 | |||
| 200 | 0.0000 | 0.0567 | 0.0567 | ||
| 0.0041 | 0.0763 | 0.0762 | |||
| 0.0044 | 0.0598 | 0.0597 | |||
| 0.0101 | 0.1219 | 0.1215 | |||
| 0.0028 | 0.1599 | 0.1598 | |||
| 0.0041 | 0.1352 | 0.1351 | |||
| 0.0012 | 0.0680 | 0.0680 | |||
| 300 | 0.0043 | 0.0525 | 0.0523 | ||
| 0.0004 | 0.0601 | 0.0601 | |||
| 0.0018 | 0.0503 | 0.0503 | |||
| 0.0079 | 0.0910 | 0.0907 | |||
| 0.0019 | 0.1130 | 0.1130 | |||
| 0.0021 | 0.1001 | 0.1000 | |||
| 0.0032 | 0.0663 | 0.0662 | |||
| III | 100 | 0.0016 | 0.0991 | 0.0991 | |
| 0.0157 | 0.1237 | 0.1227 | |||
| 0.0013 | 0.1135 | 0.1135 | |||
| 0.0091 | 0.1838 | 0.1836 | |||
| 0.0025 | 0.2074 | 0.2074 | |||
| 0.0044 | 0.1888 | 0.1888 | |||
| 0.0117 | 0.0964 | 0.0957 | |||
| 200 | 0.0070 | 0.0573 | 0.0569 | ||
| 0.0033 | 0.0768 | 0.0767 | |||
| 0.0003 | 0.0604 | 0.0604 | |||
| 0.0142 | 0.1229 | 0.1220 | |||
| 0.0281 | 0.1658 | 0.1634 | |||
| 0.0096 | 0.1387 | 0.1384 | |||
| 0.0017 | 0.0679 | 0.0679 | |||
| 300 | 0.0002 | 0.0523 | 0.0523 | ||
| 0.0053 | 0.0605 | 0.0603 | |||
| 0.0044 | 0.0506 | 0.0504 | |||
| 0.0067 | 0.0923 | 0.0921 | |||
| 0.0179 | 0.1156 | 0.1142 | |||
| 0.0071 | 0.1021 | 0.1018 | |||
| 0.0035 | 0.0659 | 0.0658 |
| Type | n | Para. | Bias | RMS | SD |
|---|---|---|---|---|---|
| I | 100 | 0.0184 | 0.1006 | 0.0989 | |
| 0.0087 | 0.1127 | 0.1123 | |||
| 0.0051 | 0.1000 | 0.0999 | |||
| 0.0018 | 0.1711 | 0.1710 | |||
| 0.0183 | 0.1643 | 0.1633 | |||
| 0.0107 | 0.1699 | 0.1695 | |||
| 0.0364 | 0.1197 | 0.1141 | |||
| 200 | 0.0124 | 0.0743 | 0.0733 | ||
| 0.0184 | 0.0786 | 0.0764 | |||
| 0.0022 | 0.0774 | 0.0773 | |||
| 0.0182 | 0.1269 | 0.1256 | |||
| 0.0091 | 0.1236 | 0.1233 | |||
| 0.0024 | 0.1247 | 0.1247 | |||
| 0.0077 | 0.0707 | 0.0703 | |||
| 300 | 0.0078 | 0.0592 | 0.0587 | ||
| 0.0067 | 0.0618 | 0.0614 | |||
| 0.0016 | 0.0549 | 0.0549 | |||
| 0.0026 | 0.1008 | 0.1008 | |||
| 0.0074 | 0.1121 | 0.1119 | |||
| 0.0021 | 0.1044 | 0.1044 | |||
| 0.0099 | 0.0596 | 0.0588 | |||
| II | 100 | 0.0023 | 0.1156 | 0.1156 | |
| 0.0072 | 0.1083 | 0.1080 | |||
| 0.0073 | 0.0958 | 0.0955 | |||
| 0.0519 | 0.1788 | 0.1711 | |||
| 0.0447 | 0.1885 | 0.1831 | |||
| 0.0173 | 0.1759 | 0.1751 | |||
| 0.0103 | 0.1074 | 0.1069 | |||
| 200 | 0.0013 | 0.0756 | 0.0756 | ||
| 0.0152 | 0.0888 | 0.0875 | |||
| 0.0086 | 0.0740 | 0.0735 | |||
| 0.0296 | 0.1097 | 0.1056 | |||
| 0.0352 | 0.1359 | 0.1313 | |||
| 0.0275 | 0.1190 | 0.1158 | |||
| 0.0039 | 0.0693 | 0.0692 | |||
| 300 | 0.0005 | 0.0520 | 0.0520 | ||
| 0.0082 | 0.0668 | 0.0663 | |||
| 0.0059 | 0.0627 | 0.0625 | |||
| 0.0224 | 0.1046 | 0.1022 | |||
| 0.0230 | 0.1092 | 0.1068 | |||
| 0.0157 | 0.0989 | 0.0977 | |||
| 0.0059 | 0.0662 | 0.0660 | |||
| III | 100 | 0.0143 | 0.1080 | 0.1071 | |
| 0.0106 | 0.1198 | 0.1194 | |||
| 0.0110 | 0.1107 | 0.1101 | |||
| 0.0032 | 0.1955 | 0.1954 | |||
| 0.0074 | 0.2199 | 0.2198 | |||
| 0.0143 | 0.2213 | 0.2208 | |||
| 0.0321 | 0.1208 | 0.1165 | |||
| 200 | 0.0041 | 0.0691 | 0.0690 | ||
| 0.0002 | 0.0824 | 0.0824 | |||
| 0.0016 | 0.0792 | 0.0791 | |||
| 0.0116 | 0.1109 | 0.1103 | |||
| 0.0117 | 0.1396 | 0.1391 | |||
| 0.0075 | 0.1269 | 0.1267 | |||
| 0.0131 | 0.0798 | 0.0787 | |||
| 300 | 0.0123 | 0.0608 | 0.0595 | ||
| 0.0033 | 0.0655 | 0.0654 | |||
| 0.0008 | 0.0553 | 0.0553 | |||
| 0.0055 | 0.0996 | 0.0994 | |||
| 0.0042 | 0.1384 | 0.1383 | |||
| 0.0247 | 0.0988 | 0.0956 | |||
| 0.0037 | 0.0524 | 0.0522 |
| n | ||||
|---|---|---|---|---|
| 0.5 | 100 | 0.0456 | 0.0507 | 0.0490 |
| 200 | 0.0302 | 0.0381 | 0.0379 | |
| 300 | 0.0230 | 0.0206 | 0.0204 | |
| 0 | 100 | 0.0557 | 0.0616 | 0.0608 |
| 200 | 0.0356 | 0.0379 | 0.0378 | |
| 300 | 0.0221 | 0.0251 | 0.0250 | |
| −0.5 | 100 | 0.0429 | 0.0630 | 0.0534 |
| 200 | 0.0342 | 0.0316 | 0.0355 | |
| 300 | 0.0268 | 0.0251 | 0.0214 |
| Related Variables | Detailed Description |
|---|---|
| CRIM | Per capita crime rate by town |
| ZN | Proportion of residential land zoned for lots over 25,000 sq.ft. |
| INDUS | Proportion of non-retail business acres per town |
| CHAS | Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) |
| NOX | Nitric oxide concentration (parts per 10 million) |
| RM | Average number of rooms per dwelling |
| AGE | Proportion of owner-occupied units built prior to 1940 |
| DIS | Weighted distances to five Boston employment centres |
| RAD | Index of accessibility to radial highways |
| TAX | Full-value property-tax rate per $10,000 |
| PTRATIO | Pupil–teacher ratio by town |
| B | where Bk is the proportion of blacks by town |
| LSTAT | % lower status of the population |
| MEDV | Median value of owner-occupied homes in USD 1000’s |
| Parameter | EST | SD | CI |
|---|---|---|---|
| −0.1335 | 0.1098 | (−0.3460, 0.0835) | |
| 0.0386 | 0.0507 | (−0.0614, 0.1397) | |
| −0.0839 | 0.0850 | (−0.2541, 0.0803) | |
| 0.3899 | 0.0931 | (0.2034, 0.5633) | |
| −0.1591 | 0.0693 | (−0.3043, −0.0305) | |
| 0.2403 | 0.1182 | (0.0122, 0.4697) | |
| −0.2143 | 0.0914 | (−0.3908, −0.0346) | |
| −0.1288 | 0.0530 | (−0.2366, −0.0259) | |
| 0.1058 | 0.07521 | (−0.0437, 0.2515) | |
| 0.2132 | 0.1602 | (−0.1234, 0.5461) | |
| −0.3000 | 0.1937 | (−0.7381, 0.0715) | |
| 0.6484 | 0.1974 | (0.2865, 1.0527) | |
| 0.1553 | 0.0910 | (−0.0335, 0.3302) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Xu, D.; Ke, S. A Semiparametric Bayesian Approach to Heterogeneous Spatial Autoregressive Models. Entropy 2024, 26, 498. https://doi.org/10.3390/e26060498
Liu T, Xu D, Ke S. A Semiparametric Bayesian Approach to Heterogeneous Spatial Autoregressive Models. Entropy. 2024; 26(6):498. https://doi.org/10.3390/e26060498
Chicago/Turabian StyleLiu, Ting, Dengke Xu, and Shiqi Ke. 2024. "A Semiparametric Bayesian Approach to Heterogeneous Spatial Autoregressive Models" Entropy 26, no. 6: 498. https://doi.org/10.3390/e26060498
APA StyleLiu, T., Xu, D., & Ke, S. (2024). A Semiparametric Bayesian Approach to Heterogeneous Spatial Autoregressive Models. Entropy, 26(6), 498. https://doi.org/10.3390/e26060498






