A Symmetric Form of the Clausius Statement of the Second Law of Thermodynamics
Abstract
1. Introduction
2. The Second Law of Thermodynamics Claimed by Clausius
3. Another Statement of the Second Law of Thermodynamics
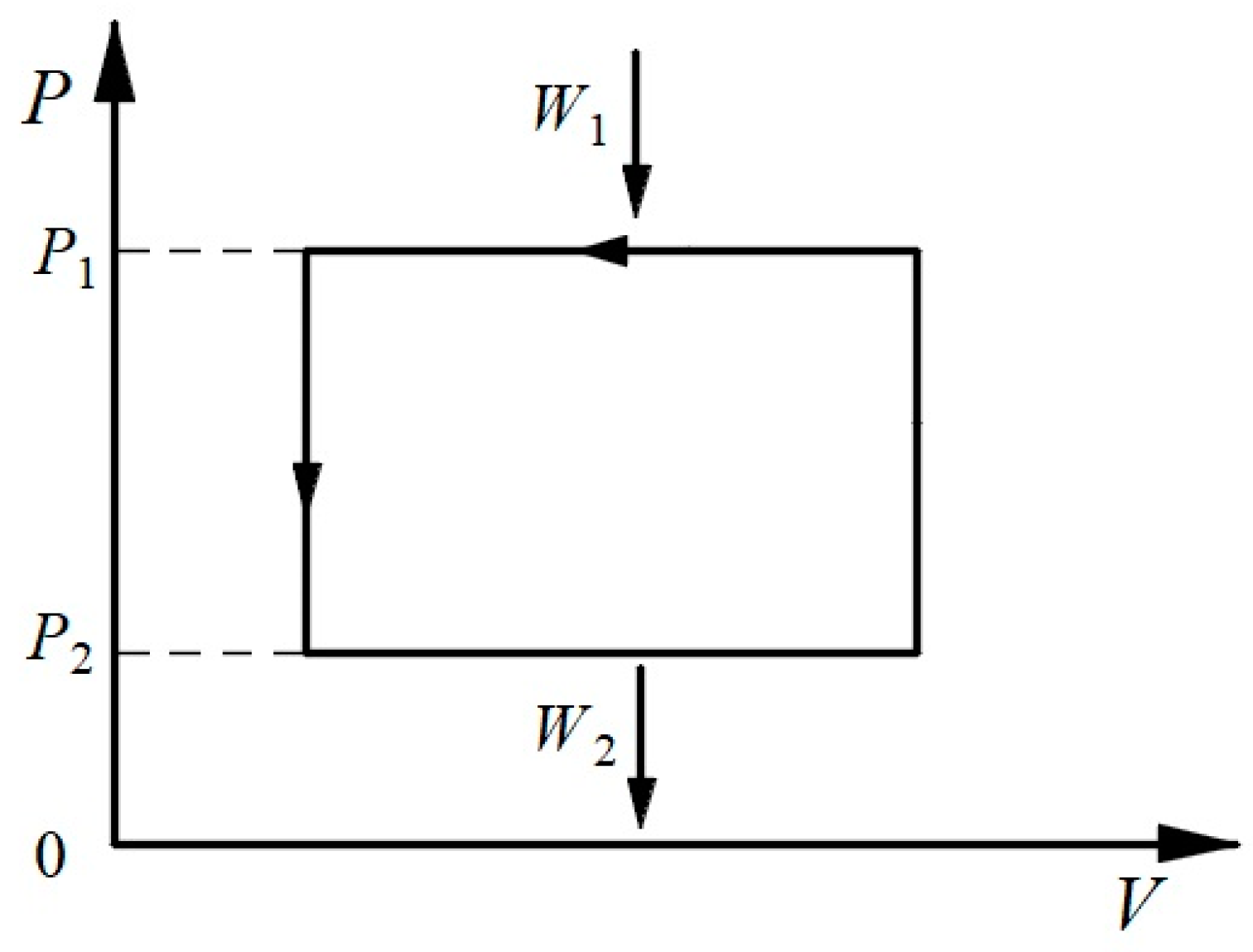
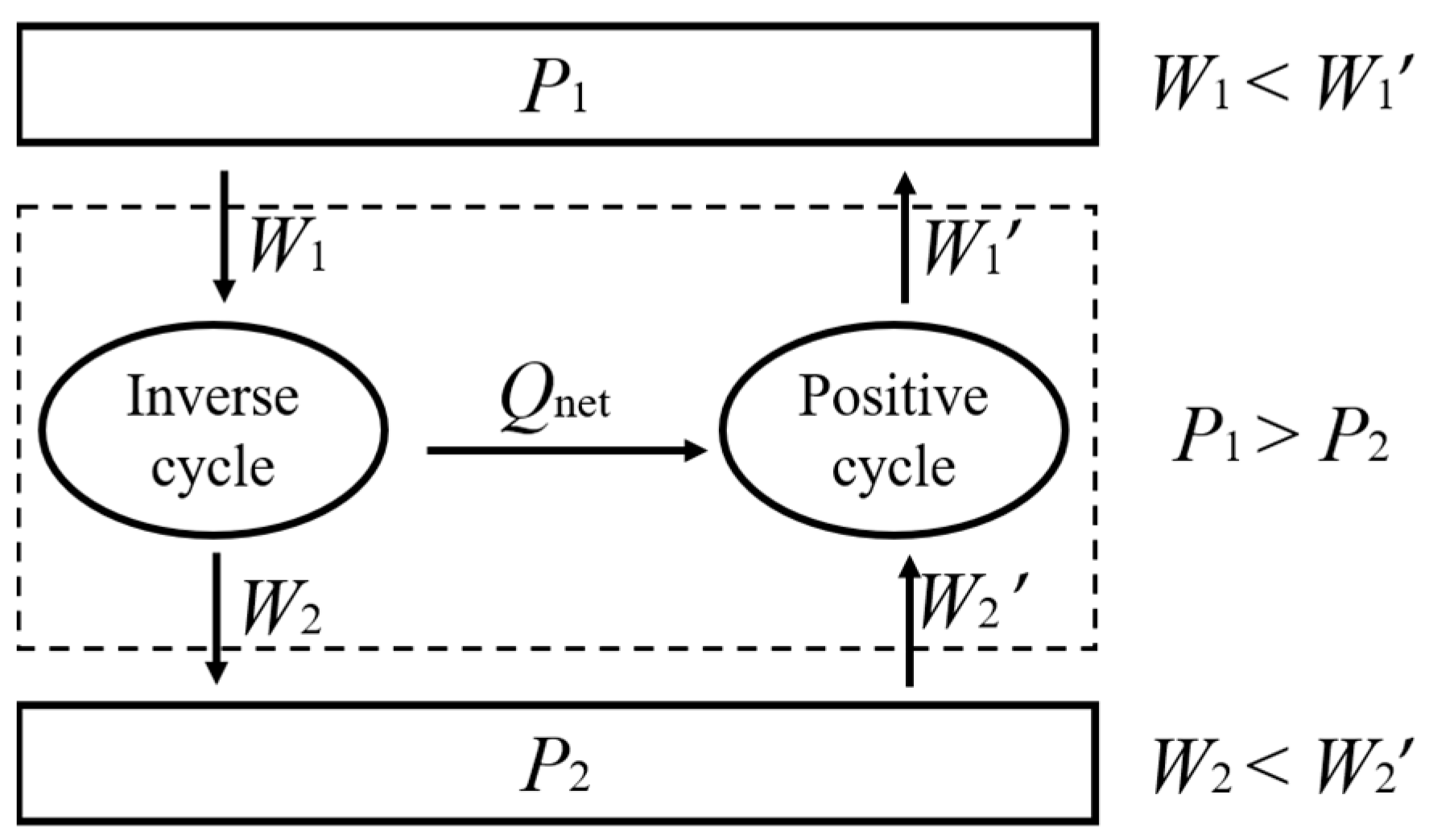
3.1. Thermodynamic Symmetry
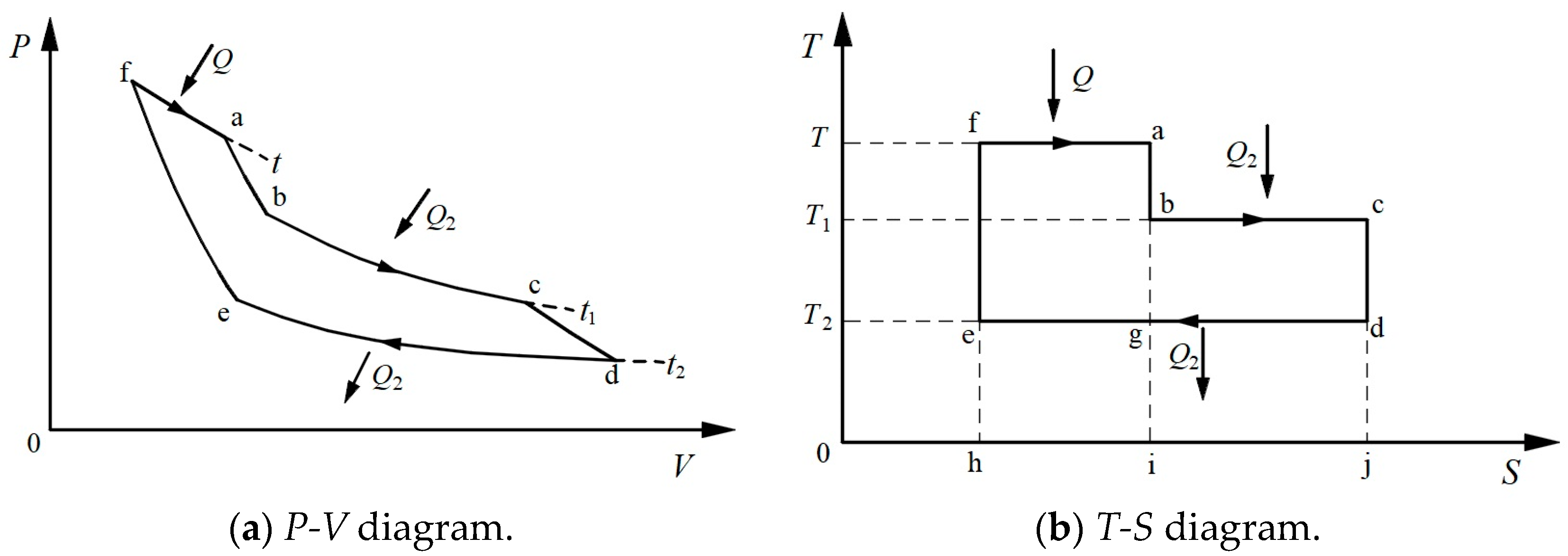
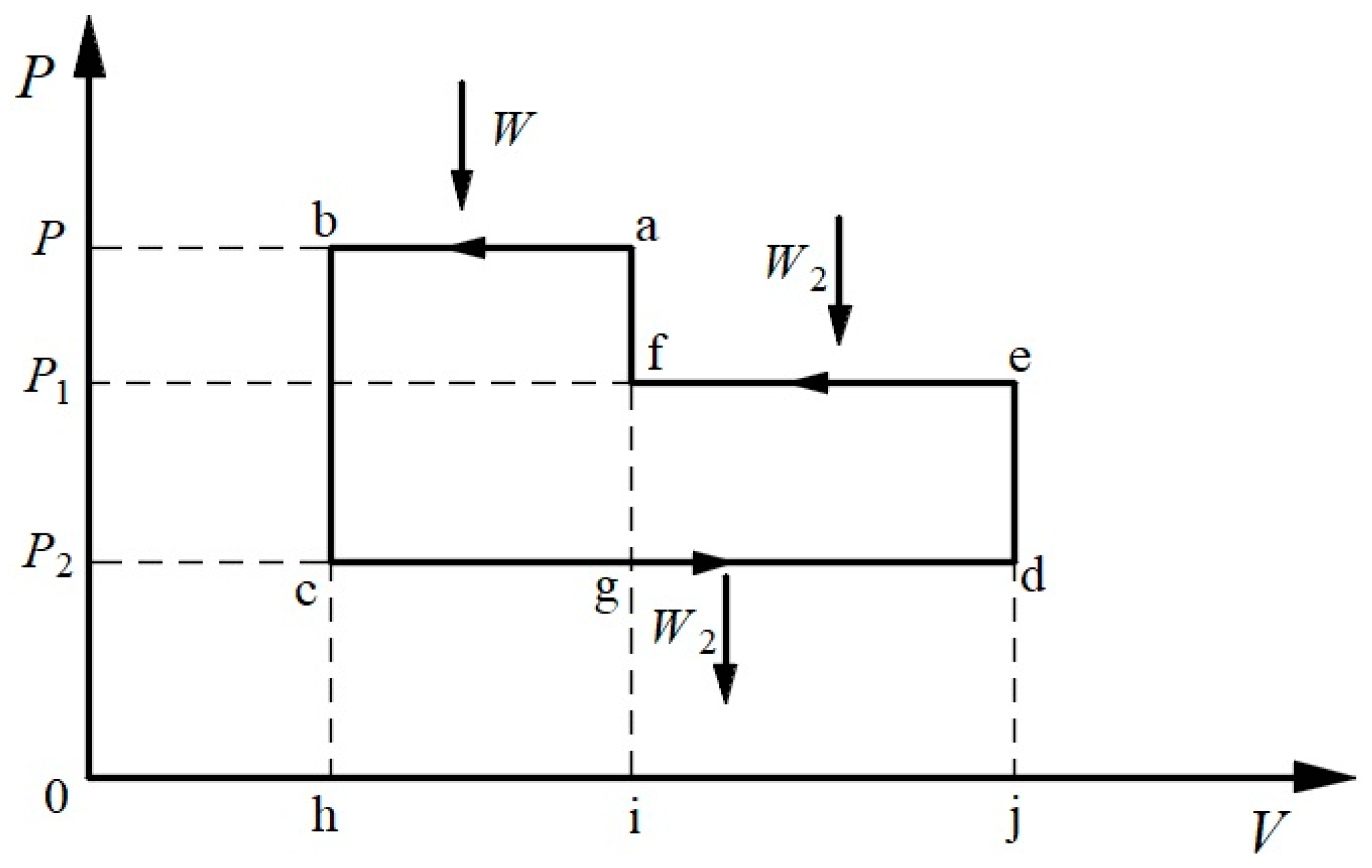
3.2. Symmetric Form of the Carnot Theorem
3.3. Symmetrical Form of Clausius’s TET
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bridgman, P.W. Reflections on thermodynamics. In Proceedings of the American Academy of Arts and Sciences; American Academy of Arts & Sciences: Cambridge, MA, USA, 1953. [Google Scholar]
- Clausius, R.; Hirst, T.A.; Tyndall, J. The Mechanical Theory of Heat, with its Applications to the Steam-engine and to the Physical Properties of Bodies; John van Voorst: London, UK, 1867. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; Walter, R.; Browne, M.A., Translators; Macmillan and Co.: London, UK, 1879. [Google Scholar]
- Xue, T.-W.; Guo, Z.-Y. What is the real Clausius statement of the second law of thermodynamics? Entropy 2019, 21, 926. [Google Scholar] [CrossRef]
- Xue, T.-W.; Guo, Z.-Y. Thermoelectric Cycle and the Second Law of Thermodynamics. Entropy 2023, 25, 155. [Google Scholar] [CrossRef] [PubMed]
- Xue, T.-W.; Guo, Z.-Y. Correspondence of the Symmetry of Thermodynamic Properties of Matter with the Symmetry of Equations of State. Entropy 2023, 25, 1532. [Google Scholar] [CrossRef] [PubMed]
- Bordoni, S. Routes towards an Abstract Thermodynamics in the late nineteenth century. Eur. Phys. J. H 2013, 38, 617–660. [Google Scholar] [CrossRef]
- Cropper, W.H. Rudolf Clausius and the road to entropy. Am. J. Phys. 1998, 54, 1068–1074. [Google Scholar] [CrossRef]
- Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley: New York, NY, USA, 1998. [Google Scholar]
- Helm, G. The Historical Development of Energetics; Springer Science & Business Media: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Bucher, M. Diagram of the second law of thermodynamics. Am. J. Phys. 1993, 61, 462–466. [Google Scholar] [CrossRef]
- Demetrius, L.A.; Wolf, C. Directionality theory and the second law of thermodynamics. Physica A 2022, 598, 127325. [Google Scholar] [CrossRef]
- Coveney, P.V. The second law of thermodynamics: Entropy, irreversibility and dynamics. Nature 1988, 333, 409–415. [Google Scholar] [CrossRef]
- Leaf, B. The principles of thermodynamics. J. Chem. Phys. 1944, 12, 89–98. [Google Scholar] [CrossRef]
- Feidt, M.; Valero-Capilla, A. Advances in Thermodynamics and Circular Thermoeconomics: Fundamentals and Criteria; John Wiley & Sons: Brisbane City, Australia, 2024. [Google Scholar]
- Smith, C. Natural philosophy and thermodynamics: William thomson and ‘the dynamical theory of heat’. Brit. J. Hist. Sci. 1976, 9, 293–319. [Google Scholar] [CrossRef]
- Müller, I. A History of Thermodynamics: The Doctrine of Energy and Entropy; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Leff, H.S. Thermodynamic entropy: The spreading and sharing of energy. Am. J. Phys. 1996, 64, 1261. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Nature of Thermodynamics; Harvard University Press: Cambridge, MA, USA, 1941. [Google Scholar]
- von Oettingen, A.J. Die thermodynamischen Beziehungen antithetisch entwickelt. Mem. Acad. Sci. St. Petersb. 1885, XXXII, 1–70. [Google Scholar]
- Rosenholm, J.B. A rational approach to basic equilibrium thermodynamics. Adv. Colloid Interface Sci. 2021, 294, 102433. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, J. Theorie der Wärme; Neesen, F., Translator; Friedrich Vieweg & Sohn: Braunschweig, Germany, 1878. [Google Scholar]
- Wang, C.; Chen, L.; Ge, Y.; Sun, F. Comparison of air-standard rectangular cycles with different specific heat models. Appl. Therm. Eng. 2016, 109, 507–513. [Google Scholar] [CrossRef]
- da Silva, M.F. Some considerations about thermodynamic cycles. Eur. J. Phys. 2011, 33, 13–42. [Google Scholar] [CrossRef]
- Zhao, T.; Hua, Y.-C.; Guo, Z.-Y. The principle of least action for reversible thermodynamic processes and cycles. Entropy 2018, 20, 542. [Google Scholar] [CrossRef] [PubMed]

| Heat-to-Work | Work-to-Heat | |
|---|---|---|
| Fundamental principle | Heat can never pass from a cold to a warm body without some other change | Volumetric work can never pass from low pressure to high pressure without some other change |
| Second law | Theorem of equivalence between the transformation of work to heat and the transformation of heat from high to low temperatures | Theorem of equivalence between the transformation of heat to work and the transformation of work from high to low pressures |
| Basic cycle | Carnot cycle | Isobaric-isochoric cycle |
| Cycle theorem | The heat efficiency of a reversible Carnot cycle is only dependent on the temperatures of two heat reservoirs (Carnot’s theorem) | The work efficiency of a reversible isobaric-isochoric cycle is only dependent on the pressures of two work reservoirs |
| Maximum efficiency | Carnot heat efficiency: | Work efficiency of a reversible isobaric-isochoric cycle: |
| Characteristic variable | Entropy: | Volume: |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, T.-W.; Zhao, T.; Guo, Z.-Y. A Symmetric Form of the Clausius Statement of the Second Law of Thermodynamics. Entropy 2024, 26, 514. https://doi.org/10.3390/e26060514
Xue T-W, Zhao T, Guo Z-Y. A Symmetric Form of the Clausius Statement of the Second Law of Thermodynamics. Entropy. 2024; 26(6):514. https://doi.org/10.3390/e26060514
Chicago/Turabian StyleXue, Ti-Wei, Tian Zhao, and Zeng-Yuan Guo. 2024. "A Symmetric Form of the Clausius Statement of the Second Law of Thermodynamics" Entropy 26, no. 6: 514. https://doi.org/10.3390/e26060514
APA StyleXue, T.-W., Zhao, T., & Guo, Z.-Y. (2024). A Symmetric Form of the Clausius Statement of the Second Law of Thermodynamics. Entropy, 26(6), 514. https://doi.org/10.3390/e26060514








