Unambiguous Models and Machine Learning Strategies for Anomalous Extreme Events in Turbulent Dynamical System
Abstract
:1. Introduction
Contributions of This Work
2. An Unambiguous Model Framework for the Investigation of Extreme Events
2.1. General Formulation of the Unambiguous Mathematical Models
Topographic Barotropic Model with Large-Scale Mean Flow Interaction and Strong Small-Scale Feedbacks
2.2. Analytical Solutions from the Conditional Gaussian Models
2.2.1. Explicit Solutions to the Topographic Model with Damping and Stochastic Forcing
2.2.2. Statistical Solutions for the Mean and Variance
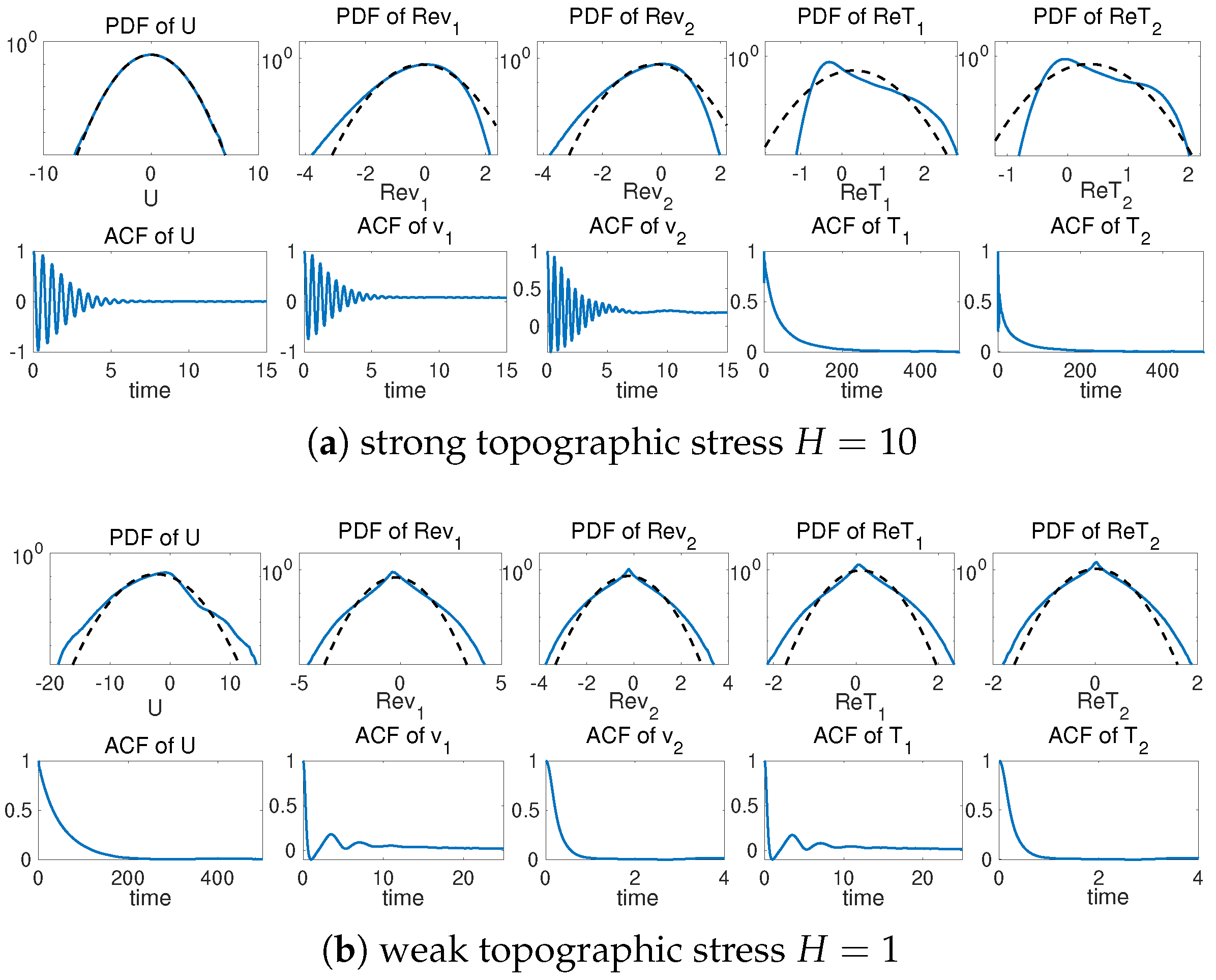
2.3. Different Statistical Regimes of Flow and Tracer Fields in the Two-Mode Model
3. Neural Network Architecture for Correlated Dynamical Processes
3.1. Architecture of the Neural Network Model
3.1.1. Residual Network to Capture the Dynamical Model Update
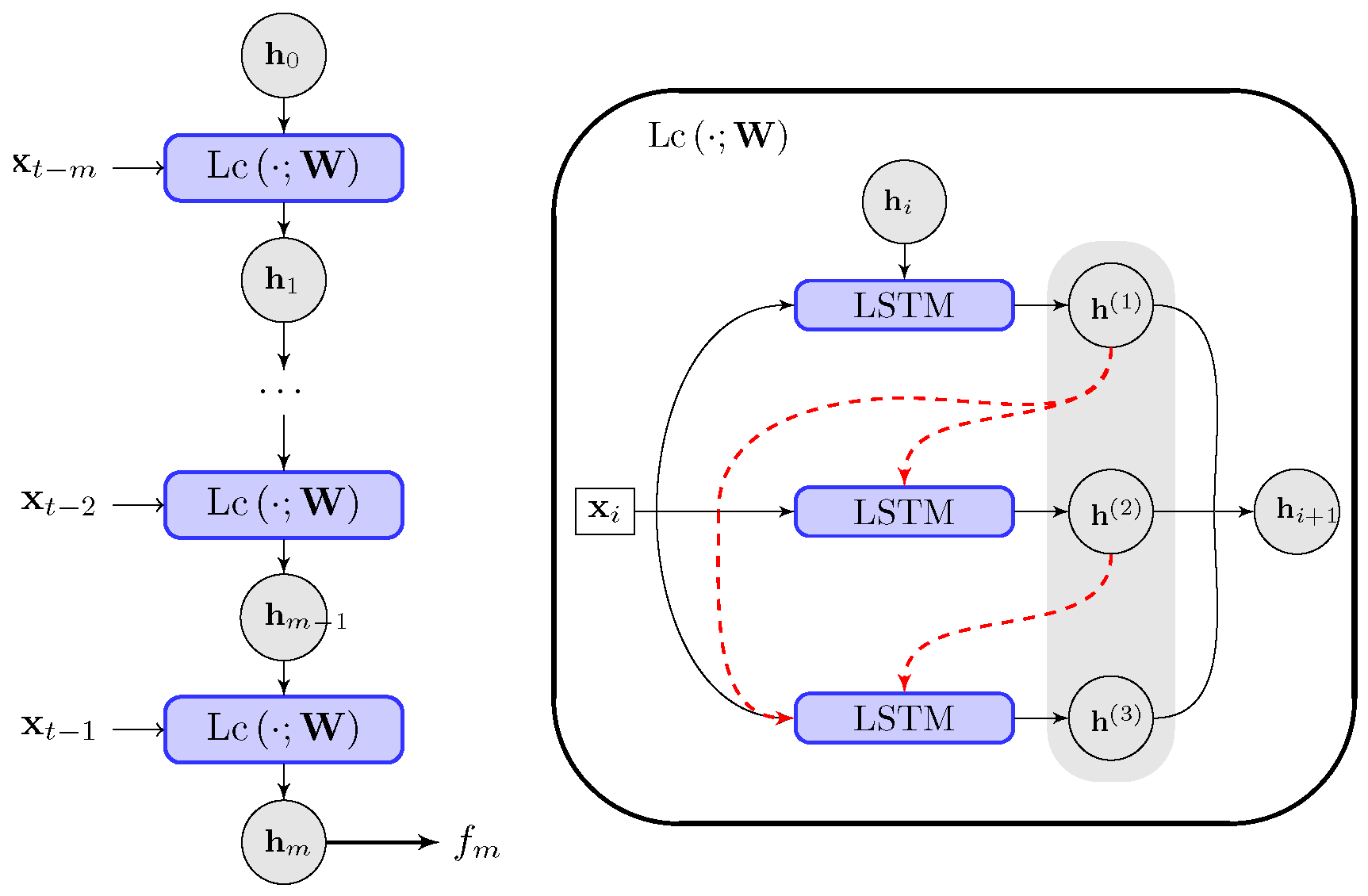
3.1.2. LSTM Network to Approximate Time-Correlated Unresolved Processes
3.1.3. Modified Connections in the LSTM Cell Admitting Dynamical Structures
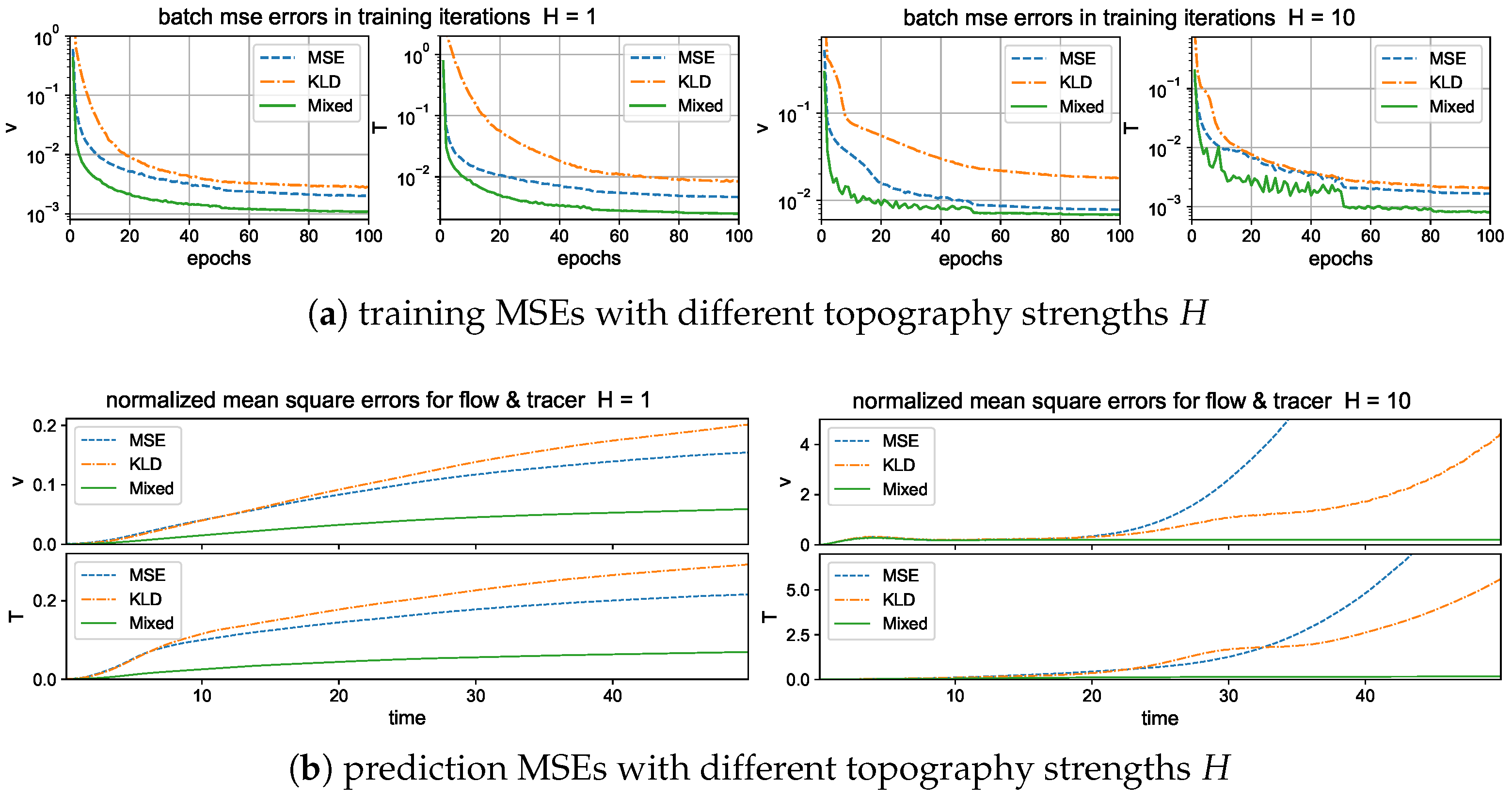
3.2. Different Metrics for Calibrating the Loss Error
- The distance:
- The relative entropy loss:
- Mixed loss by an -relaxation with the relative entropy loss:
4. Learning Multiscale Dynamics Informed of the Physical Model
4.1. General Model Setup and the Neural Network Model
4.1.1. Decoupled Neural Networks for Multiscale Dynamics
4.1.2. Multistep Training Loss Including Time-Dependent Data
4.2. Metrics to Measure the Accuracy in Training and Prediction
5. Predicting Extreme Events and Related Statistics Using the Neural Network Model
- In the training stage, the time trajectory is segmented into batches of short sequences for training the neural network model parameters. Usually, the model is only updated a small number of steps of length (say, in the standard test case) for efficient training.
- In the prediction stage, the optimized model is used for prediction along a long time sequence. The prediction model is iterated recurrently using the previous outputs up to a long-time (say, iterations).
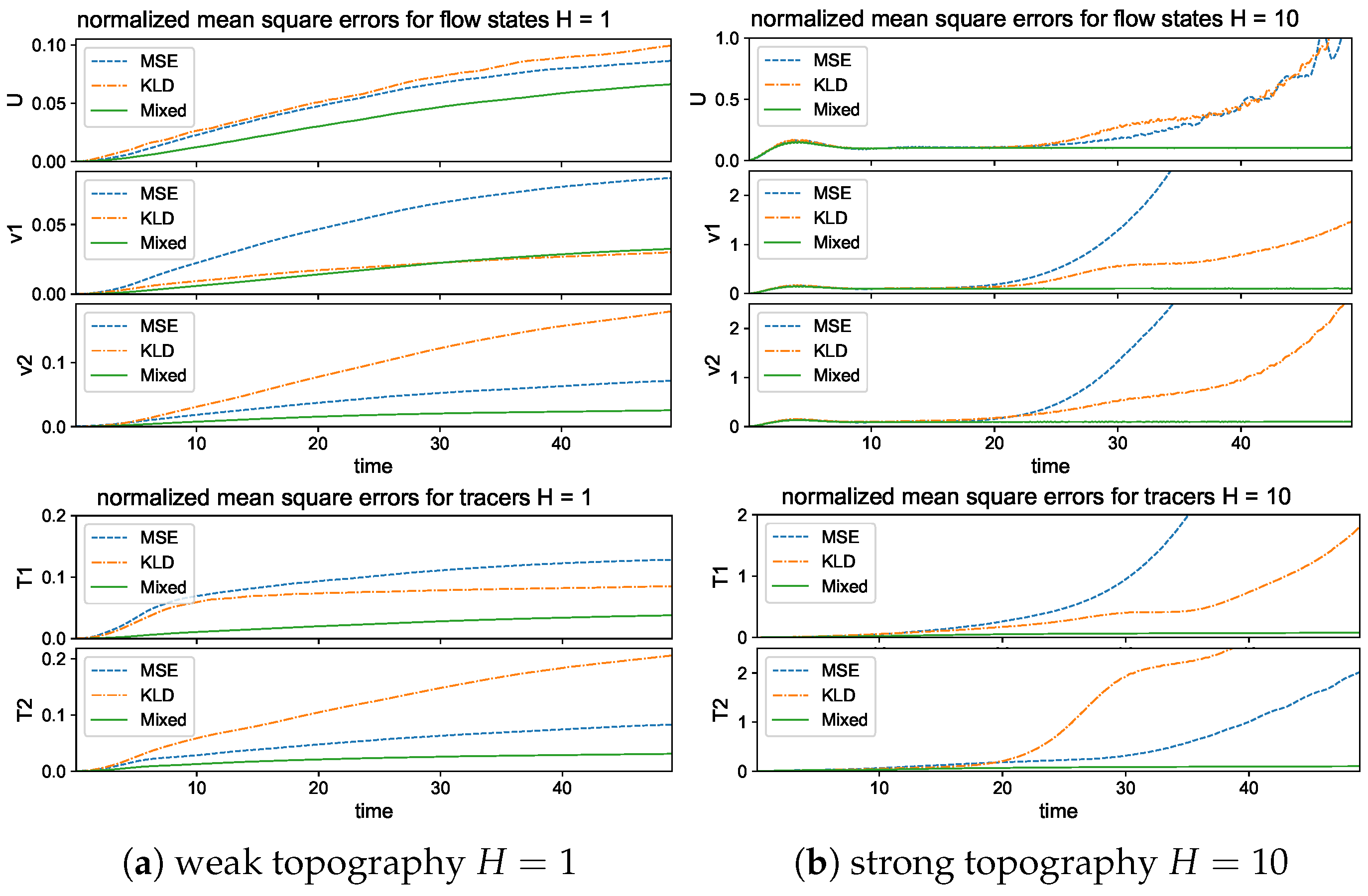
5.1. Training and Prediction with Different Loss Functions
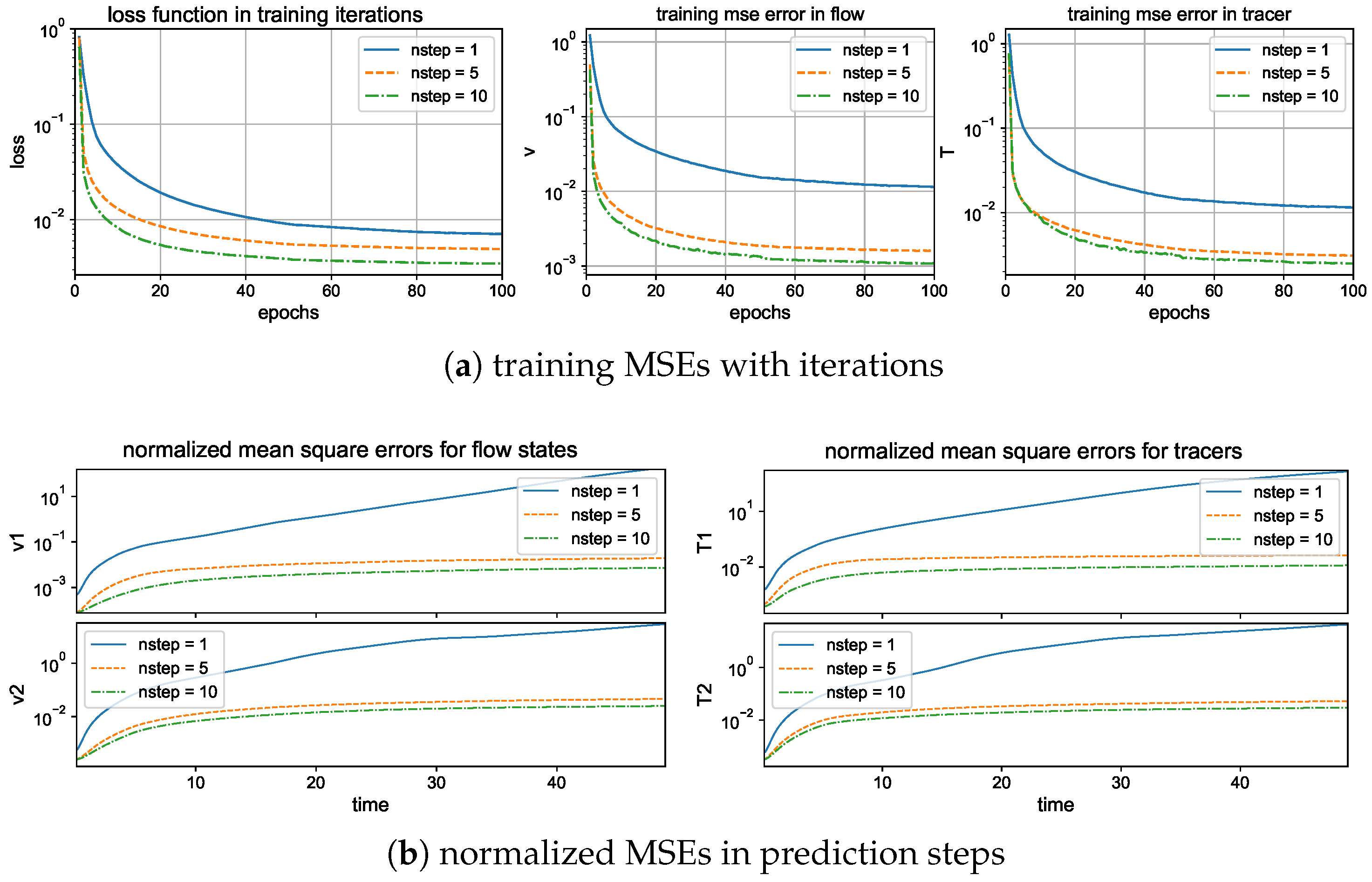
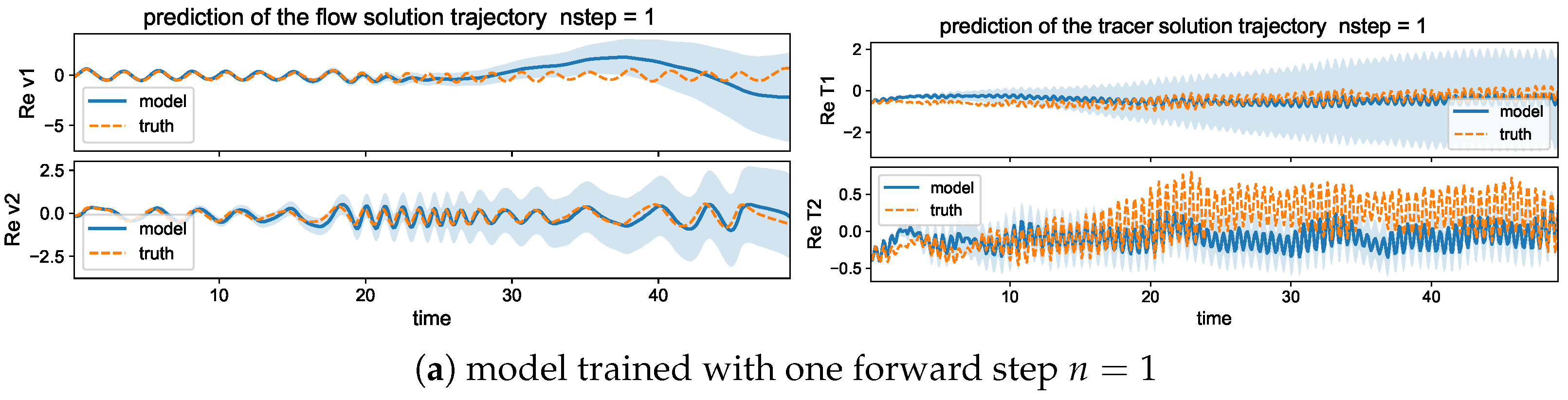
5.2. Maintaining Model Stability by Measuring Multiple Forward Steps
5.2.1. Training and Prediction Errors with Different Forward Time Steps
5.2.2. Trajectory Prediction Including Multiple Time Scales
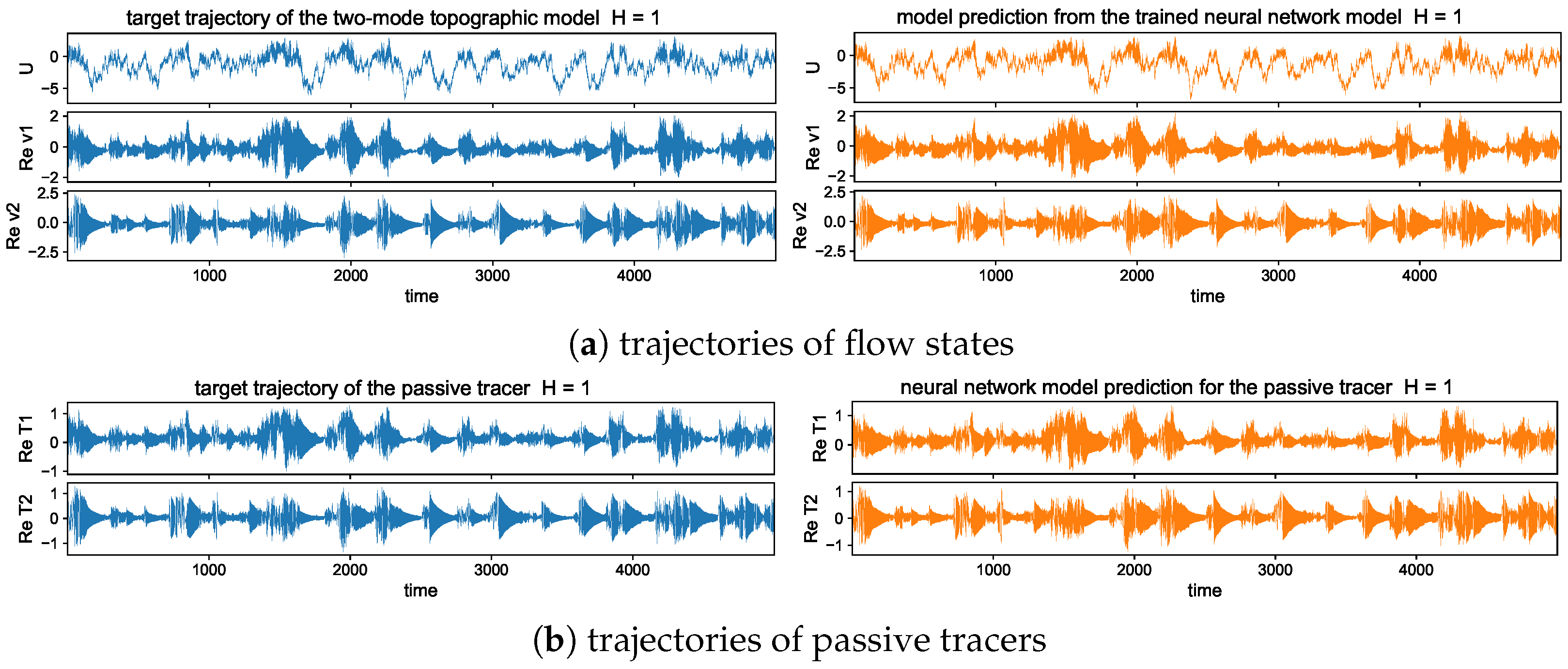
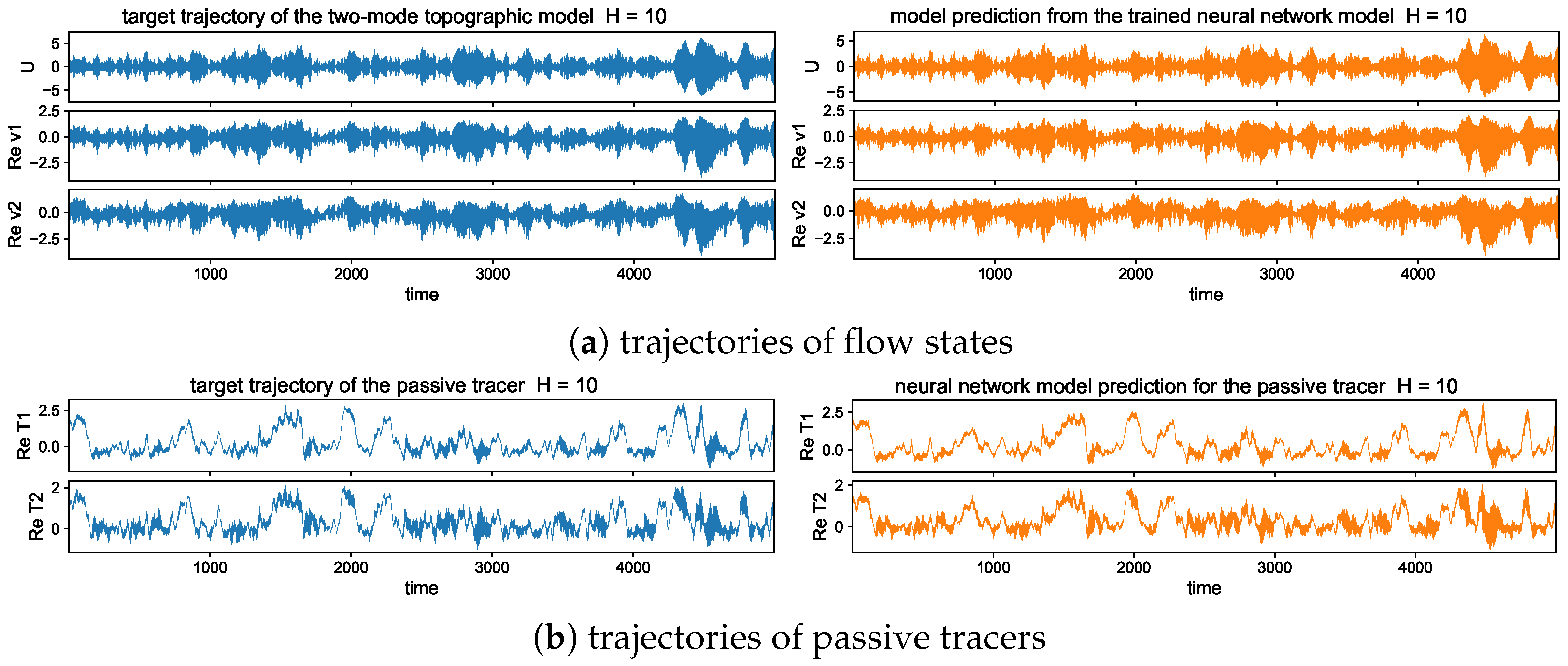
5.3. Long-Time Prediction in Different Dynamical Regimes
- Trajectory prediction: the neural network is used for the pathwise prediction for one trajectory solution from a particular initial state with uncertainties from input value and white noise forcing. Solution trajectories are solved very efficiently with N = 50,000 iterations (with time step size to the final simulation time ).
- Statistical prediction: the neural network is used to recover from data key statistical features in leading-order statistics generated by different white noise forcing amplitudes. Instead of focusing on the pathwise solutions, it is often more useful with practical importance to learn the representative statistical structures directly.
5.3.1. Trajectory Prediction with the Trained Model in Different Dynamical Regimes
5.3.2. Statistical Prediction in Leading Statistics for Different Noise Forcing
6. Summary and Discussion
- The trained neural network model shows uniformly high skill in learning the true dynamics. The improved model architecture enables a faster convergence rate in the training stage, and more accurate and robust predictions under different forcing scenarios. A longer time updating step is permitted allowing data measured at sparse time intervals.
- The choice of a proper loss function for the optimization of model parameters is shown to have a crucial role to improve the accuracy and stability in the final trained neural network. A mixed loss function using the relative entropy loss together with a small loss correction is shown to effectively improve the accuracy in training for complex systems with extreme events.
- A multistep training process, that is, using multiple iterative model outputs in training the loss function, is useful to improve model stability against the accumulated model errors during long-time iterations. The prediction skill of the model can be improved, and training efficiency is maintained by measuring only small update steps during the training procedure.
- The solution trajectory can be tracked by the neural network model with high accuracy and stability in a long time series prediction for the key multiscale structures with extreme events in flow and tracer states.
- Different model statistics in ensemble mean and variance can be predicted with uniform accuracy among different dynamical regimes using the same neural network model trained from a single set of data.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Details about the Derivations for the Flow and Tracer Model Solutions
Appendix A.1. Explicit Statistical Solutions for the Flow Field
Appendix A.2. Explicit Statistical Solutions for the Passive Tracer
Appendix B. More Details about the Neural Network Model Results
Appendix B.1. Details about the Inner Connections in the LSTM Cell
Appendix B.2. Neural Network Algorithm for Training and Prediction in the Two-Mode Model
| Algorithm A1: The improved LSTM network with the fully connected inner structure (16) and (17) is used to learn the small-scale dynamics for : |
|
Appendix B.3. Detailed Training and Prediction Results for Different Model Regimes
Appendix B.4. Trajectory Prediction with Different Levels of Noises
References
- Majda, A.J. Introduction to Turbulent Dynamical Systems in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Mohamad, M.A.; Sapsis, T.P. Sequential sampling strategy for extreme event statistics in nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2018, 115, 11138–11143. [Google Scholar] [CrossRef] [PubMed]
- Dematteis, G.; Grafke, T.; Vanden-Eijnden, E. Rogue waves and large deviations in deep sea. Proc. Natl. Acad. Sci. USA 2018, 115, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Bolles, C.T.; Speer, K.; Moore, M. Anomalous wave statistics induced by abrupt depth change. Phys. Rev. Fluids 2019, 4, 011801. [Google Scholar] [CrossRef]
- Sapsis, T.P. Statistics of Extreme Events in Fluid Flows and Waves. Annu. Rev. Fluid Mech. 2020, 53, 85–111. [Google Scholar] [CrossRef]
- Majda, A.J.; Kramer, P.R. Simplified models for turbulent diffusion: Theory, numerical modelling, and physical phenomena. Phys. Rep. 1999, 314, 237–574. [Google Scholar] [CrossRef]
- Reich, S.; Cotter, C. Probabilistic Forecasting and Bayesian Data Assimilation; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Nazarenko, S.; Lukaschuk, S. Wave turbulence on water surface. Annu. Rev. Condens. Matter Phys. 2016, 7, 61–88. [Google Scholar] [CrossRef]
- Farazmand, M.; Sapsis, T.P. A variational approach to probing extreme events in turbulent dynamical systems. Sci. Adv. 2017, 3, e1701533. [Google Scholar] [CrossRef]
- Tong, S.; Vanden-Eijnden, E.; Stadler, G. Extreme event probability estimation using PDE-constrained optimization and large deviation theory, with application to tsunamis. Commun. Appl. Math. Comput. Sci. 2021, 16, 181–225. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence: The Legacy of an Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Tao, W.K.; Chern, J.D.; Atlas, R.; Randall, D.; Khairoutdinov, M.; Li, J.L.; Waliser, D.E.; Hou, A.; Lin, X.; Peters-Lidard, C. A multiscale modeling system: Developments, applications, and critical issues. Bull. Am. Meteorol. Soc. 2009, 90, 515–534. [Google Scholar] [CrossRef]
- Lucarini, V.; Faranda, D.; de Freitas, J.M.M.; Holland, M.; Kuna, T.; Nicol, M.; Todd, M.; Vaienti, S. Extremes and Recurrence in Dynamical Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Köppen, M. The curse of dimensionality. In Proceedings of the 5th Online World Conference on Soft Computing in Industrial Applications (WSC5), Online, 4–18 September 2000; Volume 1, pp. 4–8. [Google Scholar]
- Daum, F.; Huang, J. Curse of dimensionality and particle filters. In Proceedings of the 2003 IEEE Aerospace Conference Proceedings (Cat. No. 03TH8652), Big Sky, MT, USA, 8–15 March 2003; Volume 4, pp. 4_1979–4_1993. [Google Scholar]
- Rudy, S.H.; Kutz, J.N.; Brunton, S.L. Deep learning of dynamics and signal-noise decomposition with time-stepping constraints. J. Comput. Phys. 2019, 396, 483–506. [Google Scholar] [CrossRef]
- Vlachas, P.R.; Pathak, J.; Hunt, B.R.; Sapsis, T.P.; Girvan, M.; Ott, E.; Koumoutsakos, P. Backpropagation algorithms and reservoir computing in recurrent neural networks for the forecasting of complex spatiotemporal dynamics. Neural Netw. 2020, 126, 191–217. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, A.; Subel, A.; Hassanzadeh, P. Data-driven super-parameterization using deep learning: Experimentation with multiscale Lorenz 96 systems and transfer learning. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002084. [Google Scholar] [CrossRef]
- Harlim, J.; Jiang, S.W.; Liang, S.; Yang, H. Machine learning for prediction with missing dynamics. J. Comput. Phys. 2020, 109922. [Google Scholar] [CrossRef]
- Gamahara, M.; Hattori, Y. Searching for turbulence models by artificial neural network. Phys. Rev. Fluids 2017, 2, 054604. [Google Scholar] [CrossRef]
- Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 2019, 858, 122–144. [Google Scholar] [CrossRef]
- Singh, A.P.; Medida, S.; Duraisamy, K. Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils. AIAA J. 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
- Harlim, J.; Mahdi, A.; Majda, A.J. An ensemble Kalman filter for statistical estimation of physics constrained nonlinear regression models. J. Comput. Phys. 2014, 257, 782–812. [Google Scholar] [CrossRef]
- Majda, A.J.; Qi, D. Strategies for reduced-order models for predicting the statistical responses and uncertainty quantification in complex turbulent dynamical systems. SIAM Rev. 2018, 60, 491–549. [Google Scholar] [CrossRef]
- Bolton, T.; Zanna, L. Applications of deep learning to ocean data inference and subgrid parameterization. J. Adv. Model. Earth Syst. 2019, 11, 376–399. [Google Scholar] [CrossRef]
- Qi, D.; Harlim, J. Machine learning-based statistical closure models for turbulent dynamical systems. Philos. Trans. R. Soc. A 2022, 380, 20210205. [Google Scholar] [CrossRef]
- Qi, D.; Harlim, J. A data-driven statistical-stochastic surrogate modeling strategy for complex nonlinear non-stationary dynamics. J. Comput. Phys. 2023, 485, 112085. [Google Scholar] [CrossRef]
- McDermott, P.L.; Wikle, C.K. An ensemble quadratic echo state network for non-linear spatio-temporal forecasting. Stat 2017, 6, 315–330. [Google Scholar] [CrossRef]
- Qi, D.; Majda, A.J. Predicting extreme events for passive scalar turbulence in two-layer baroclinic flows through reduced-order stochastic models. Commun. Math. Sci. 2018, 16, 17–51. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Qi, D.; Majda, A.J. Using machine learning to predict extreme events in complex systems. Proc. Natl. Acad. Sci. USA 2020, 117, 52–59. [Google Scholar] [CrossRef]
- Chen, N.; Qi, D. A physics-informed data-driven algorithm for ensemble forecast of complex turbulent systems. Appl. Math. Comput. 2024, 466, 128480. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Qi, D.; Majda, A.J. Low-dimensional reduced-order models for statistical response and uncertainty quantification: Barotropic turbulence with topography. Phys. D Nonlinear Phenom. 2017, 343, 7–27. [Google Scholar] [CrossRef]
- Qi, D.; Majda, A.J. Rigorous statistical bounds in uncertainty quantification for one-layer turbulent geophysical flows. J. Nonlinear Sci. 2018, 28, 1709–1761. [Google Scholar] [CrossRef]
- Weeks, E.R.; Tian, Y.; Urbach, J.; Ide, K.; Swinney, H.L.; Ghil, M. Transitions between blocked and zonal flows in a rotating annulus with topography. Science 1997, 278, 1598–1601. [Google Scholar] [CrossRef]
- Majda, A.J.; Moore, M.; Qi, D. Statistical dynamical model to predict extreme events and anomalous features in shallow water waves with abrupt depth change. Proc. Natl. Acad. Sci. USA 2019, 116, 3982–3987. [Google Scholar] [CrossRef]
- Hu, R.; Edwards, T.K.; Smith, L.M.; Stechmann, S.N. Initial investigations of precipitating quasi-geostrophic turbulence with phase changes. Res. Math. Sci. 2021, 8, 6. [Google Scholar] [CrossRef]
- Moore, N.J.; Bolles, C.T.; Majda, A.J.; Qi, D. Anomalous waves triggered by abrupt depth changes: Laboratory experiments and truncated KdV statistical mechanics. J. Nonlinear Sci. 2020, 30, 3235–3263. [Google Scholar] [CrossRef]
- Liptser, R.S.; Shiryaev, A.N. Statistics of Random Processes II: Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 6. [Google Scholar]
- Chen, N.; Majda, A.J. Beating the curse of dimension with accurate statistics for the Fokker–Planck equation in complex turbulent systems. Proc. Natl. Acad. Sci. USA 2017, 114, 12864–12869. [Google Scholar] [CrossRef]
- Chen, N.; Majda, A.J. Conditional Gaussian systems for multiscale nonlinear stochastic systems: Prediction, state estimation and uncertainty quantification. Entropy 2018, 20, 509. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 2342–2350. [Google Scholar]
- Kullback, S. Information Theory and Statistics; Courier Corporation: Chelmsford, MA, USA, 1997. [Google Scholar]
- Majda, A.; Abramov, R.V.; Grote, M.J. Information Theory and Stochastics for Multiscale Nonlinear Systems; American Mathematical Society: Providence, RI, USA, 2005; Volume 25. [Google Scholar]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. An overview and comparative analysis of recurrent neural networks for short term load forecasting. arXiv 2017, arXiv:1705.04378. [Google Scholar]
- Lesieur, M. Turbulence in Fluids: Stochastic and Numerical Modelling; Nijhoff: Boston, MA, USA, 1987; Volume 488. [Google Scholar]
- Ahmed, F.; Neelin, J.D. Explaining scales and statistics of tropical precipitation clusters with a stochastic model. J. Atmos. Sci. 2019, 76, 3063–3087. [Google Scholar] [CrossRef]
- Majda, A.J.; Chen, N. Model error, information barriers, state estimation and prediction in complex multiscale systems. Entropy 2018, 20, 644. [Google Scholar] [CrossRef]
- Majda, A.J.; Gershgorin, B. Elementary models for turbulent diffusion with complex physical features: Eddy diffusivity, spectrum and intermittency. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120184. [Google Scholar] [CrossRef]
- Majda, A.J.; Qi, D. Linear and nonlinear statistical response theories with prototype applications to sensitivity analysis and statistical control of complex turbulent dynamical systems. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 103131. [Google Scholar] [CrossRef]
- Majda, A.J.; Qi, D. Effective control of complex turbulent dynamical systems through statistical functionals. Proc. Natl. Acad. Sci. USA 2017, 114, 5571–5576. [Google Scholar] [CrossRef] [PubMed]
- Müller, P.; Garrett, C.; Osborne, A. Rogue waves. Oceanography 2005, 18, 66. [Google Scholar] [CrossRef]
- Majda, A.J.; Harlim, J. Filtering Complex Turbulent Systems; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Covington, J.; Qi, D.; Chen, N. Effective Statistical Control Strategies for Complex Turbulent Dynamical Systems. Proc. R. Soc. A 2023, 479, 20230546. [Google Scholar] [CrossRef]
- Bach, E.; Colonius, T.; Scherl, I.; Stuart, A. Filtering dynamical systems using observations of statistics. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 033119. [Google Scholar] [CrossRef] [PubMed]



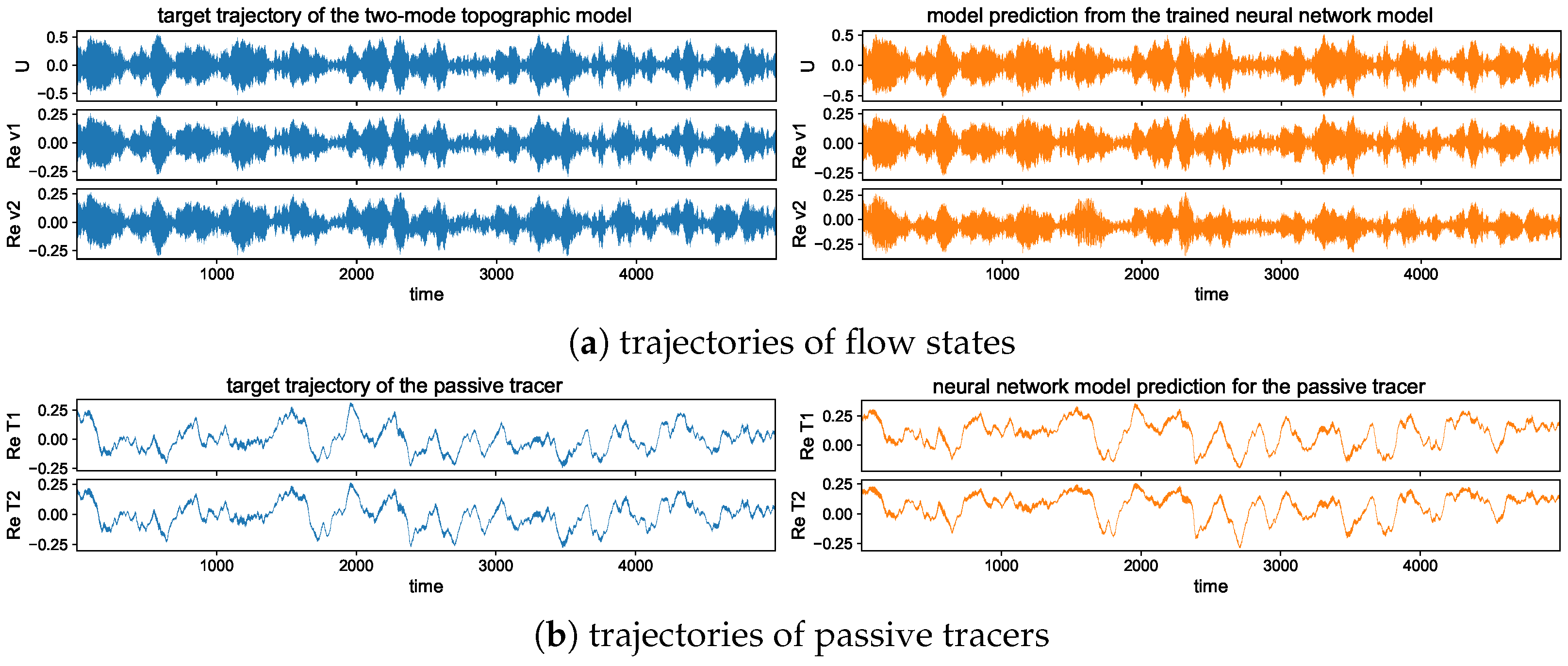
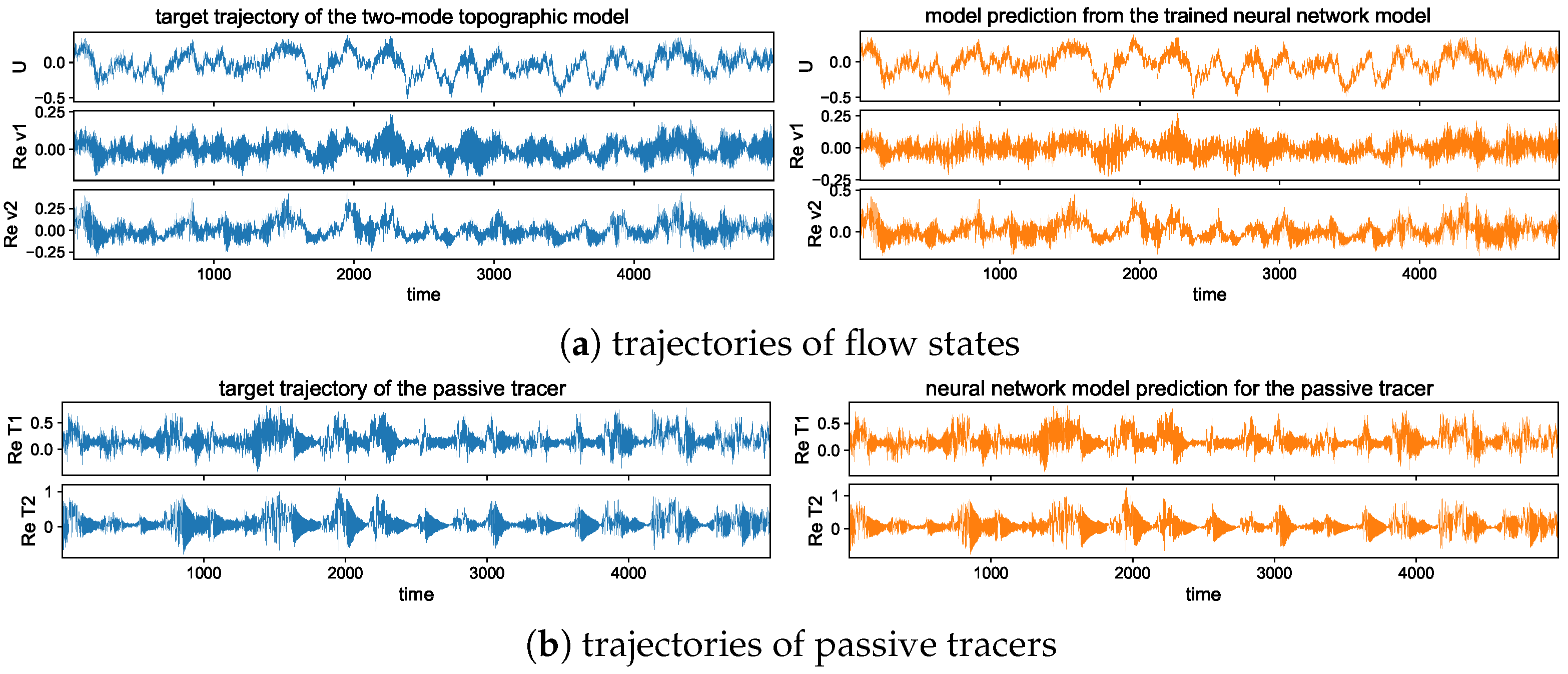
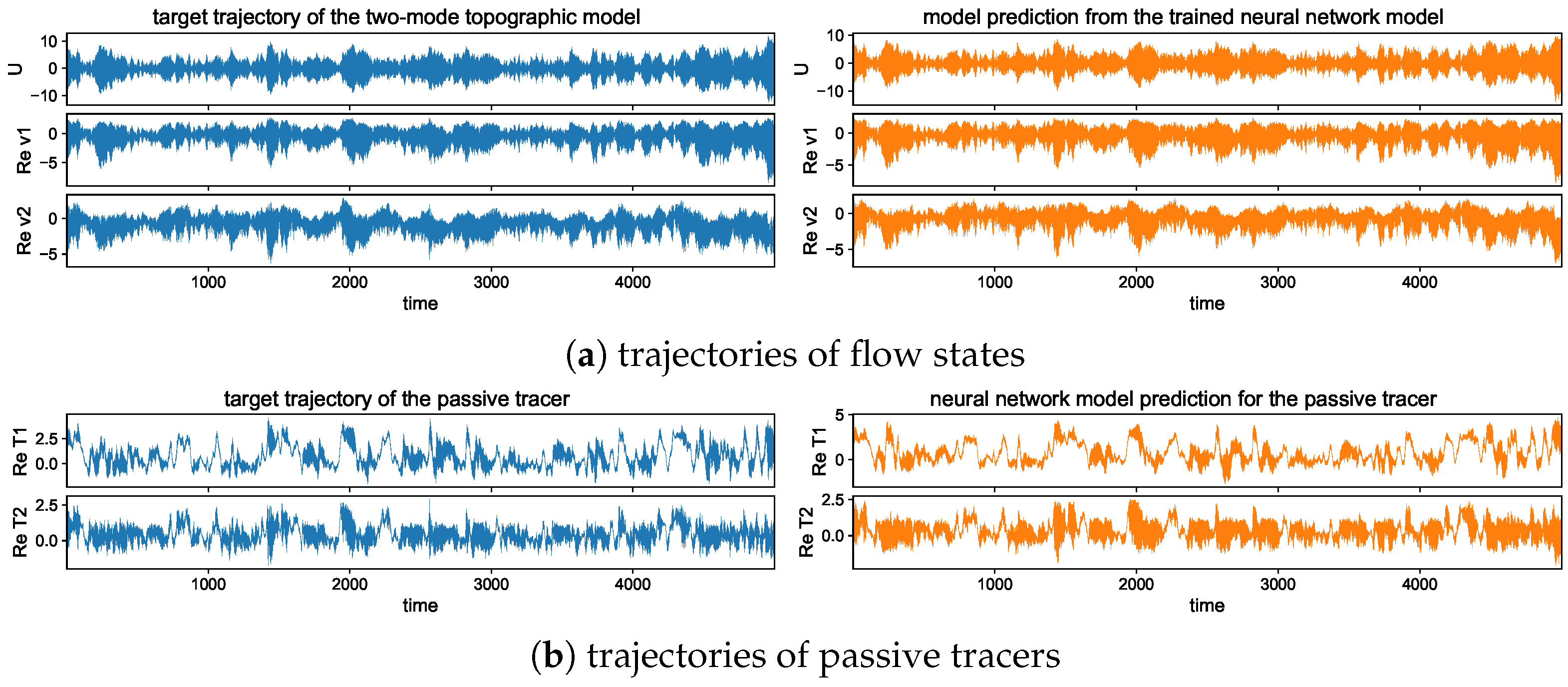

| U | ||||||
| 3.03 × 10−4 | 2.49 × 10−5 | 5.53 × 10−4 | 1.96 × 10−5 | 7.60 × 10−4 | ||
| 7.26 × 10−3 | 6.57 × 10−2 | 3.12 × 10−2 | 7.50 × 10−2 | 3.57 × 10−2 | ||
| 5.34 × 10−4 | 2.87 × 10−4 | 9.16 × 10−4 | 4.29 × 10−2 | 8.05 × 10−2 | ||
| 9.25 × 10−1 | 8.82 × 10−2 | 8.51 × 10−2 | 5.31 × 10−2 | 6.75 × 10−2 | ||
| U | ||||||
| 7.98 × 10−2 | 8.50 × 10−3 | 2.03 × 10−2 | 6.18 × 10−2 | 1.92 × 10−2 | ||
| 1.92 × 10−1 | 2.40 × 10−1 | 2.57 × 10−1 | 2.51 × 10−1 | 2.49 × 10−1 | ||
| 2.84 × 10−5 | 6.77 × 10−2 | 2.53 × 10−1 | 4.60 × 10−2 | 1.44 × 10−2 | ||
| 9.00 × 10−1 | 4.68 × 10−1 | 4.03 × 10−1 | 4.41 × 10−1 | 2.03 × 10−1 | ||
| total training epochs | 100 |
| training batch size | 100 |
| starting learning rate | 0.005 |
| learning rate reduction rate | 0.5 |
| learning rate reduction at iteration step | 50, 80 |
| time step size between two measurements | 0.1 |
| LSTM sequence length m | 100 |
| forward prediction steps in training n | 10 |
| hidden state size h | 50 |
| number of stages in LSTM cell s | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, D. Unambiguous Models and Machine Learning Strategies for Anomalous Extreme Events in Turbulent Dynamical System. Entropy 2024, 26, 522. https://doi.org/10.3390/e26060522
Qi D. Unambiguous Models and Machine Learning Strategies for Anomalous Extreme Events in Turbulent Dynamical System. Entropy. 2024; 26(6):522. https://doi.org/10.3390/e26060522
Chicago/Turabian StyleQi, Di. 2024. "Unambiguous Models and Machine Learning Strategies for Anomalous Extreme Events in Turbulent Dynamical System" Entropy 26, no. 6: 522. https://doi.org/10.3390/e26060522
APA StyleQi, D. (2024). Unambiguous Models and Machine Learning Strategies for Anomalous Extreme Events in Turbulent Dynamical System. Entropy, 26(6), 522. https://doi.org/10.3390/e26060522






