Pedaling Asymmetry Reflected by Bilateral EMG Complexity in Chronic Stroke
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
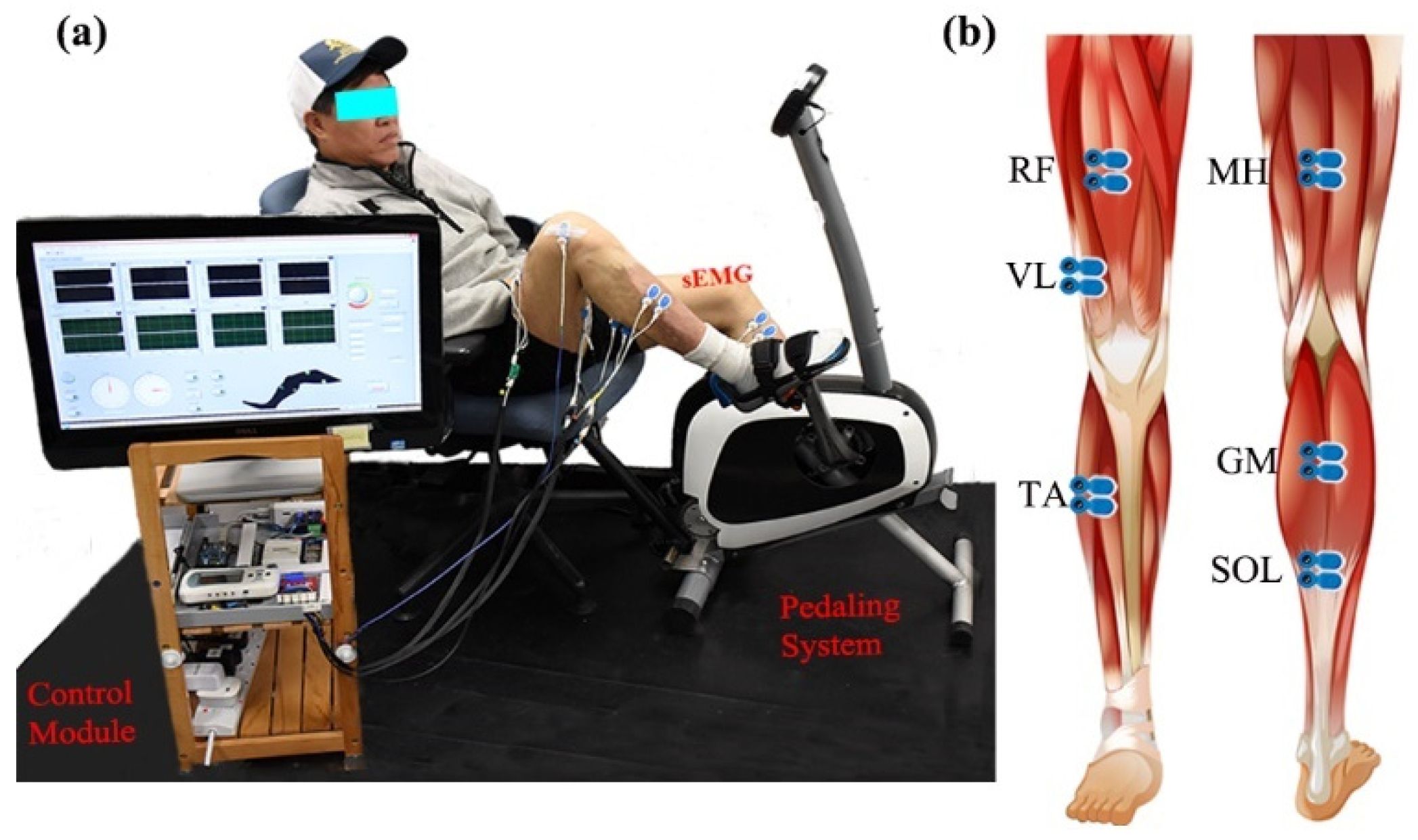
2.2. Study Paradigm
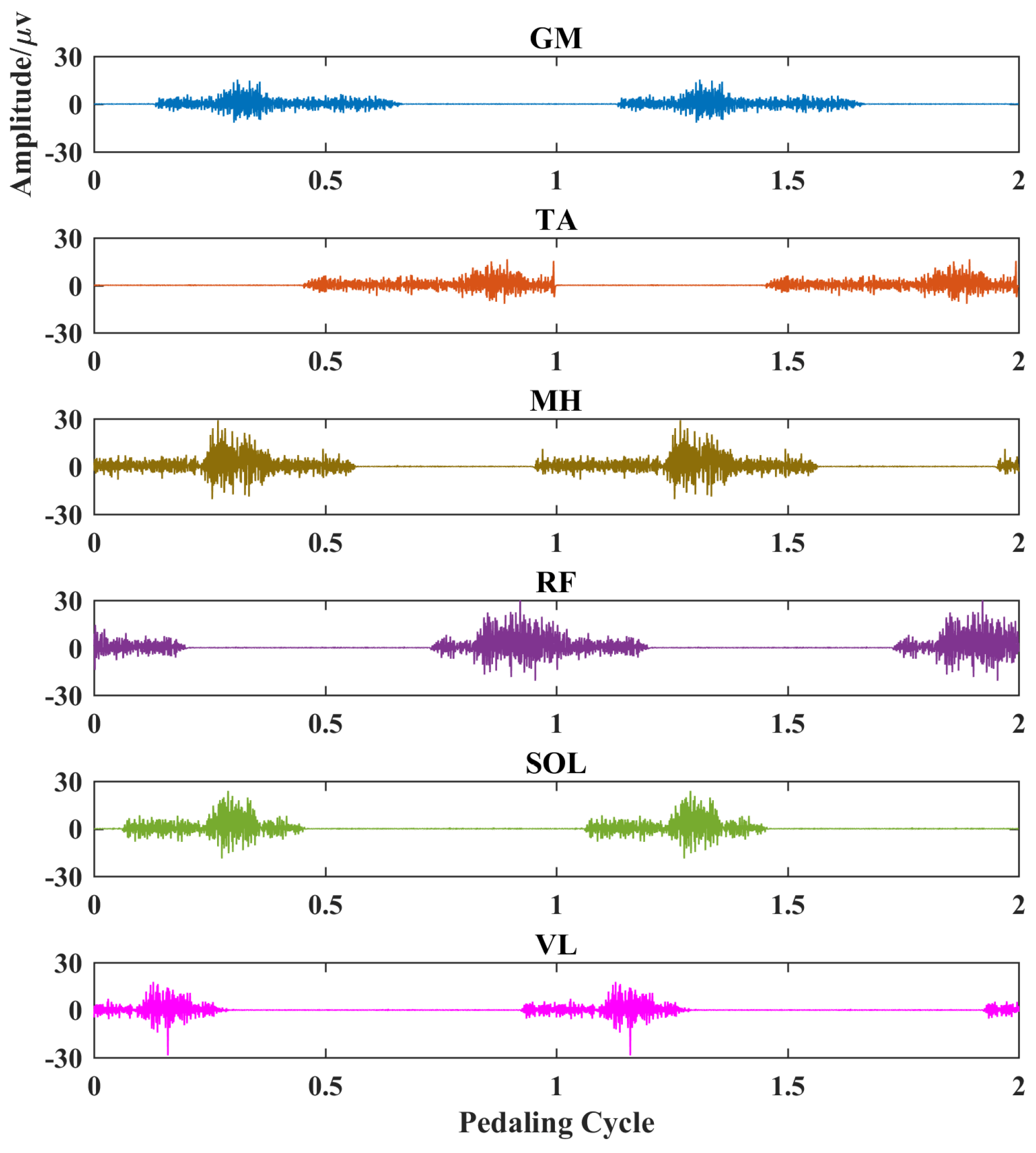
2.3. Data Analysis
2.4. Fuzzy Approximate Entropy and Fuzzy Sample Entropy
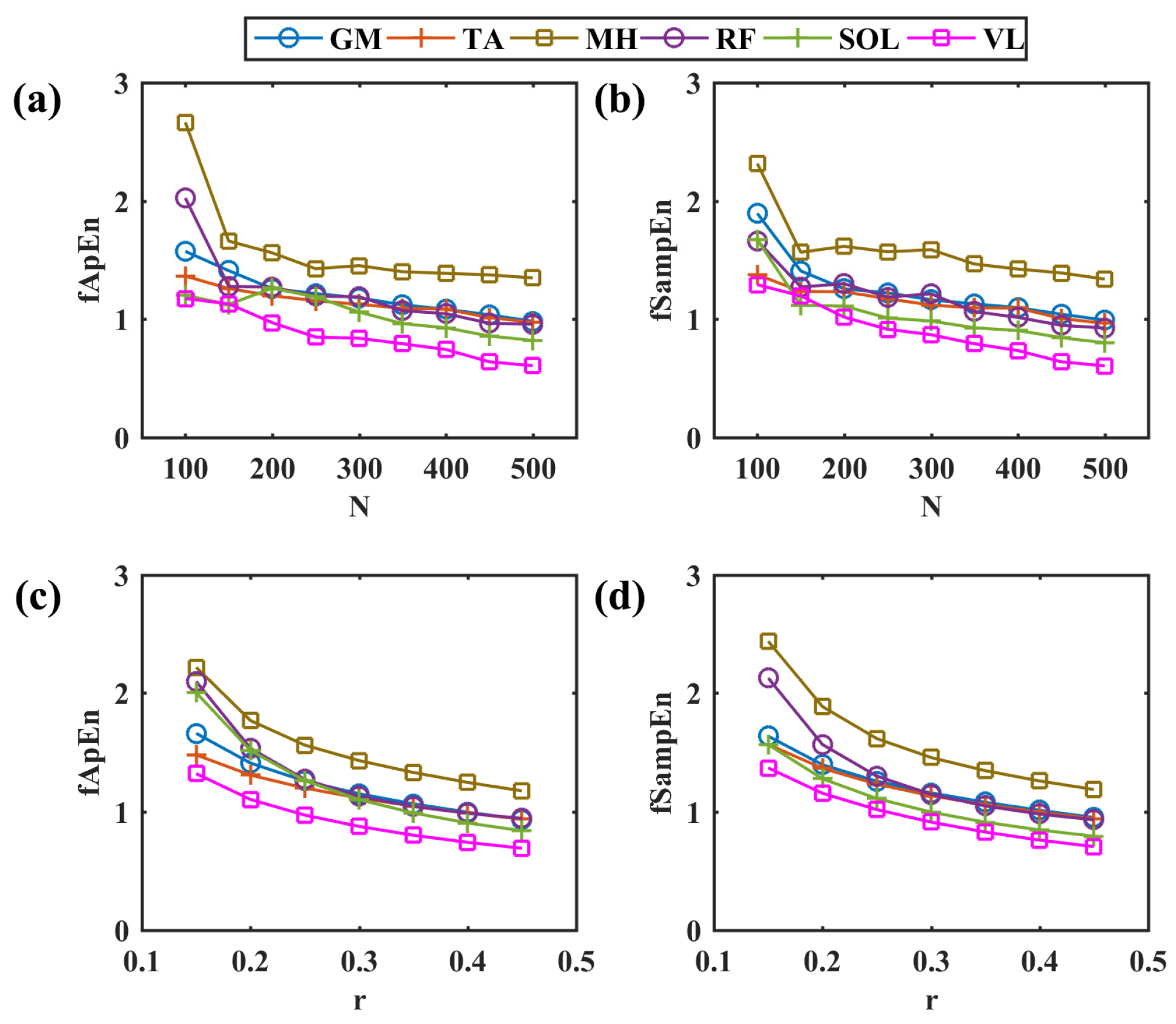
2.5. EMG Simulation and Fuzzy Entropy Parameter Selection
2.6. Statistical Analysis
3. Results
3.1. Simulated EMG and Fuzzy Entropy Parameter Selection
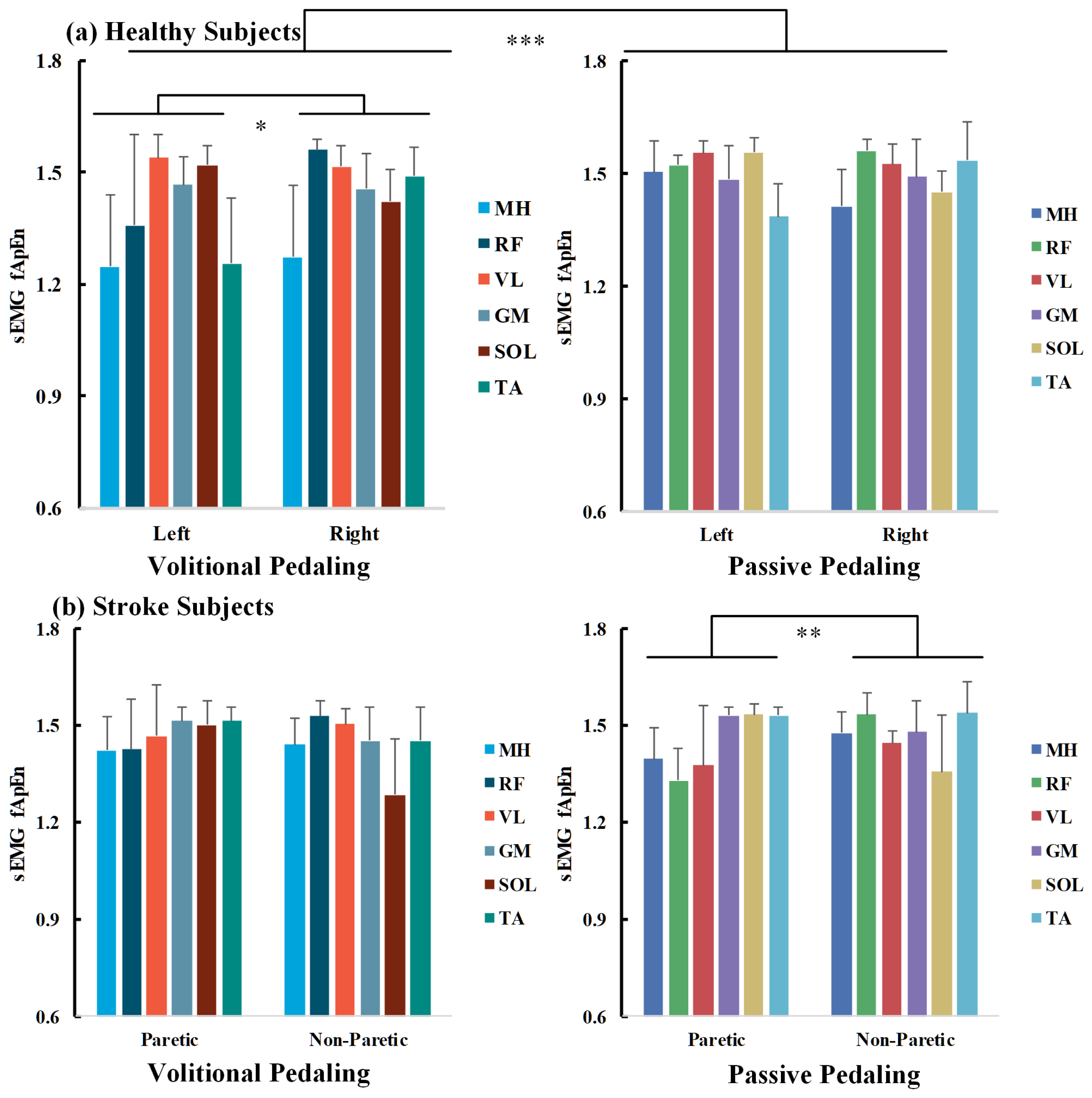
3.2. Comparisons of Kinematics and Conventional EMG Metrics in Pedaling
3.3. Factors Influencing fApEn in Healthy Participants
3.4. Factors Influencing fApEn in Chronic Stroke Participants
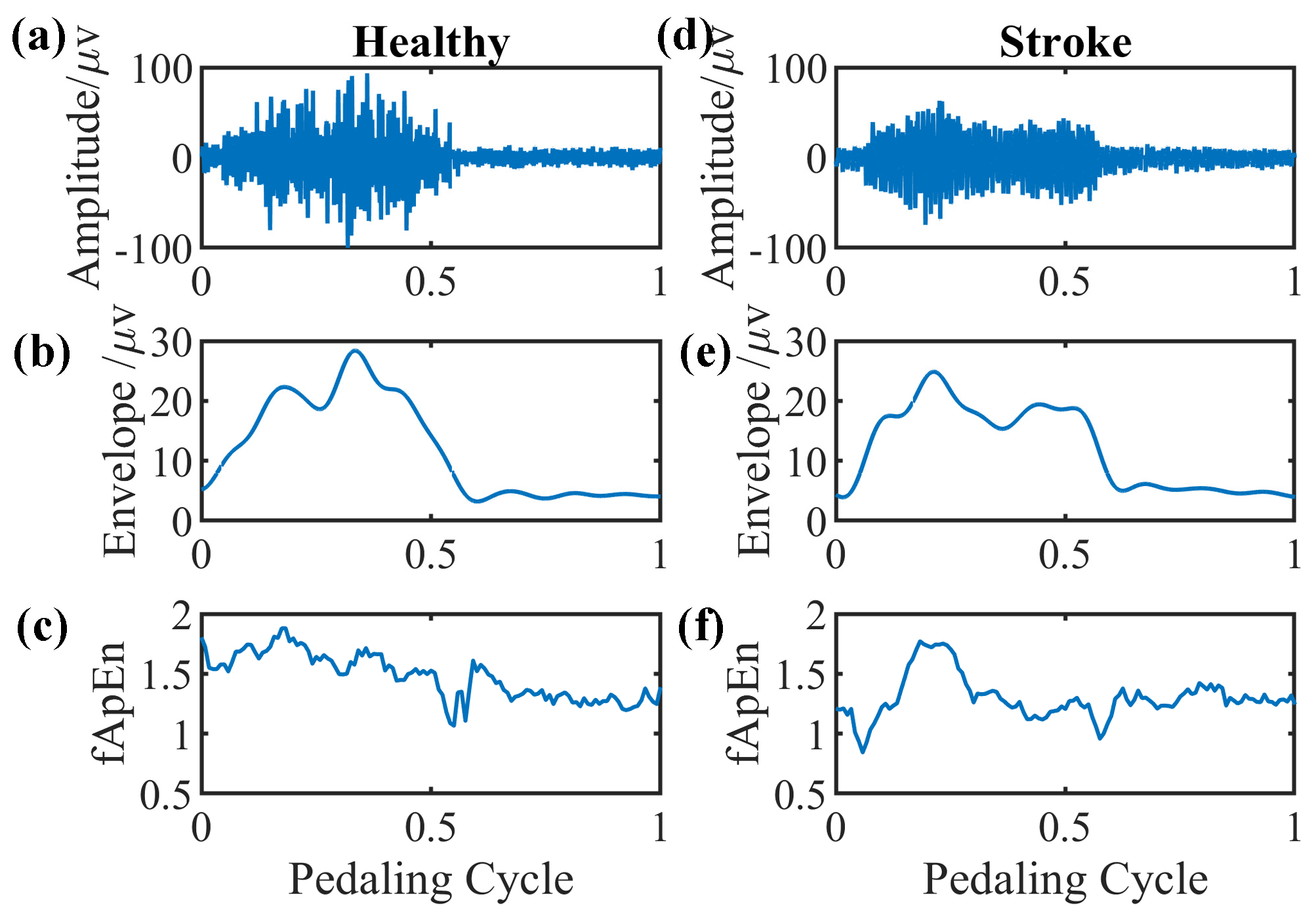
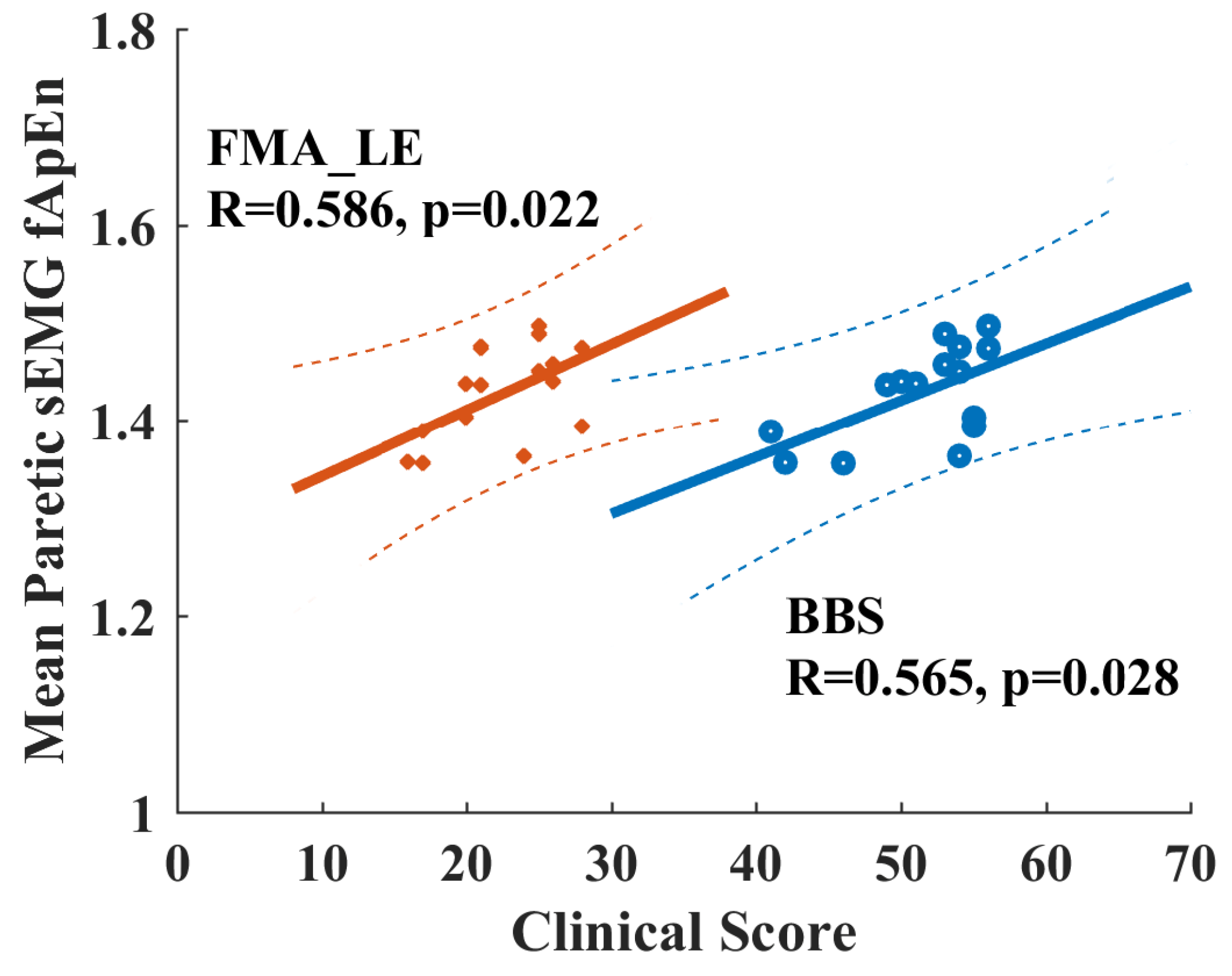
3.5. fApEn and Its Clinical Implications
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Langhorne, P.; Audebert, H.J.; Cadilhac, D.A.; Kim, J.; Lindsay, P. Stroke Systems of Care in High-Income Countries: What Is Optimal? Lancet 2020, 396, 1433–1442. [Google Scholar] [CrossRef]
- Kwakkel, G.; Meskers, C.G.M.; Ward, N.S. Time for the next Stage of Stroke Recovery Trials. Lancet Neurol. 2020, 19, 636–637. [Google Scholar] [CrossRef]
- Park, Y.-H.; Lee, D.-H.; Lee, J.-H. A Comprehensive Review: Robot-Assisted Treatments for Gait Rehabilitation in Stroke Patients. Medicina 2024, 60, 620. [Google Scholar] [CrossRef]
- Penev, Y.P.; Beneke, A.; Root, K.T.; Meisel, E.; Kwak, S.; Diaz, M.; Root, J.; Hosseini, M.R.; Lucke-Wold, B. Therapeutic Effectiveness of Brain Computer Interfaces in Stroke Patients: A Systematic Review. J. Exp. Neurol. 2023, 4, 87–93. [Google Scholar] [CrossRef]
- Bao, S.; Khan, A.; Song, R.; Kai-yu Tong, R. Rewiring the Lesioned Brain: Electrical Stimulation for Post-Stroke Motor Restoration. J. Stroke 2020, 22, 47–63. [Google Scholar] [CrossRef]
- Jaillard, A. Structural or Functional Metrics to Assess Motor Impairment in Chronic Stroke? Stroke 2021, 52, 250–252. [Google Scholar] [CrossRef]
- Wang, C.; Peng, L.; Hou, Z.-G.; Li, J.; Zhang, T.; Zhao, J. Quantitative Assessment of Upper-Limb Motor Function for Post-Stroke Rehabilitation Based on Motor Synergy Analysis and Multi-Modality Fusion. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 943–952. [Google Scholar] [CrossRef]
- Jiang, N.; Falla, D.; d’Avella, A.; Graimann, B.; Farina, D. Myoelectric Control in Neurorehabilitation. Crit. Rev. Biomed. Eng. 2010, 38, 381–391. [Google Scholar] [CrossRef] [PubMed]
- Abdul Halim, H.N.; Azaman, A.; Manaf, H.; Saidin, S.; Zulkapri, I.; Yahya, A. Gait Asymmetry Assessment Using Muscle Activity Signal: A Review of Current Methods. J. Phys. Conf. Ser. 2019, 1372, 012075. [Google Scholar] [CrossRef]
- Wang, J.; Hu, Q.; Wu, C.; Li, S.; Deng, Q.; Tang, R.; Li, K.; Nie, Y.; Shen, B. Gait Asymmetry Variation in Kinematics, Kinetics, and Muscle Force along with the Severity Levels of Knee Osteoarthritis. Orthop. Surg. 2023, 15, 1384. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- de Vries, C.; Staff, R.T.; Waiter, G.D.; Sokunbi, M.O.; Sandu, A.L.; Murray, A.D. Motion during Acquisition Is Associated with fMRI Brain Entropy. IEEE J. Biomed. Health Inform. 2019, 24, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Tian, N.; Chen, Y.; Sun, W.; Liu, H.; Wang, X.; Yan, T.; Song, R. Investigating the Stroke- and Aging-Related Changes in Global and Instantaneous Intermuscular Coupling Using Cross-Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1573–1582. [Google Scholar] [CrossRef]
- Viteckova, S.; Kutilek, P.; Svoboda, Z.; Krupicka, R.; Kauler, J.; Szabo, Z. Gait Symmetry Measures: A Review of Current and Prospective Methods. Biomed. Signal Process. Control 2018, 42, 89–100. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Ao, D.; Sun, R.; Tong, K.; Song, R. Characterization of Stroke- and Aging-Related Changes in the Complexity of EMG Signals during Tracking Tasks. Ann. Biomed. Eng. 2015, 43, 990–1002. [Google Scholar] [CrossRef] [PubMed]
- Yarosh, C.A.; Hoffman, D.S.; Strick, P.L. Deficits in Movements of the Wrist Ipsilateral to a Stroke in Hemiparetic Subjects. J. Neurophysiol. 2004, 92, 3276–3285. [Google Scholar] [CrossRef]
- Sun, R.; Song, R.; Tong, K. Complexity Analysis of EMG Signals for Patients after Stroke during Robot-Aided Rehabilitation Training Using Fuzzy Approximate Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 1013–1019. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, P. Sample Entropy Analysis of Surface EMG for Improved Muscle Activity Onset Detection against Spurious Background Spikes. J. Electromyogr. Kinesiol. 2012, 22, 901–907. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Yu, Z.; Chen, X.; Li, S.; Zhou, P. EMG-Torque Relation in Chronic Stroke: A Novel EMG Complexity Representation with a Linear Electrode Array. IEEE J. Biomed. Health Inform. 2017, 21, 1562–1572. [Google Scholar] [CrossRef]
- Xie, T.; Leng, Y.; Zhi, Y.; Jiang, C.; Tian, N.; Luo, Z.; Yu, H.; Song, R. Increased Muscle Activity Accompanying with Decreased Complexity as Spasticity Appears: High-Density EMG-Based Case Studies on Stroke Patients. Front. Bioeng. Biotechnol. 2020, 8, 589321. [Google Scholar] [CrossRef] [PubMed]
- Damiano, D.L.; Norman, T.; Stanley, C.J.; Park, H.-S. Comparison of Elliptical Training, Stationary Cycling, Treadmill Walking and Overground Walking. Gait Posture 2011, 34, 260–264. [Google Scholar] [CrossRef] [PubMed]
- Tian, R.; Dewald, J.P.A.; Sinha, N.; Yang, Y. Assessing Neural Connectivity and Associated Time Delays of Muscle Responses to Continuous Position Perturbations. Ann. Biomed. Eng. 2021, 49, 432–440. [Google Scholar] [CrossRef] [PubMed]
- Kautz, S.A.; Brown, D.A. Relationships between Timing of Muscle Excitation and Impaired Motor Performance during Cyclical Lower Extremity Movement in Post-Stroke Hemiplegia. Brain 1998, 121, 515–526. [Google Scholar] [CrossRef] [PubMed]
- Cleland, B.T.; Gelting, T.; Arand, B.; Struhar, J.; Schindler-Ivens, S. Impaired Interlimb Coordination Is Related to Asymmetries during Pedaling after Stroke. Clin. Neurophysiol. 2019, 130, 1474–1487. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.; Wang, J.; He, P. Multi-Resolution Entropy Analysis of Gait Symmetry in Neurological Degenerative Diseases and Amyotrophic Lateral Sclerosis. Med. Eng. Phys. 2008, 30, 299–310. [Google Scholar] [CrossRef]
- Bao, S.; Leung, K.W.; Chen, C.; Tong, K. Cortical Contribution during Active and Passive Pedaling: A Preliminary Study. In Proceedings of the 2019 9th International IEEE/EMBS Conference on Neural Engineering (NER), San Francisco, CA, USA, 20–23 March 2019; pp. 1034–1037. [Google Scholar]
- Bao, S.-C.; Leung, W.-C.K.; Cheung, V.C.; Zhou, P.; Tong, K.-Y. Pathway-Specific Modulatory Effects of Neuromuscular Electrical Stimulation during Pedaling in Chronic Stroke Survivors. J. NeuroEngineering Rehabil. 2019, 16, 143. [Google Scholar] [CrossRef]
- Hu, X.-L.; Tong, R.K.; Ho, N.S.K.; Xue, J.; Rong, W.; Li, L.S.W. Wrist Rehabilitation Assisted by an Electromyography-Driven Neuromuscular Electrical Stimulation Robot After Stroke. Neurorehabil. Neural Repair 2015, 29, 767–776. [Google Scholar] [CrossRef] [PubMed]
- Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of Recommendations for SEMG Sensors and Sensor Placement Procedures. J. Electromyogr. Kinesiol. 2000, 10, 361–374. [Google Scholar] [CrossRef]
- Qiu, S.; Yi, W.; Xu, J.; Qi, H.; Du, J.; Wang, C.; He, F.; Ming, D. Event-Related Beta EEG Changes During Active, Passive Movement and Functional Electrical Stimulation of the Lower Limb. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 283–290. [Google Scholar] [CrossRef]
- Sangani, S.G.; Starsky, A.J.; McGuire, J.R.; Schmit, B.D. Multijoint Reflex Responses to Constant-Velocity Volitional Movements of the Stroke Elbow. J. Neurophysiol. 2009, 102, 1398–1410. [Google Scholar] [CrossRef] [PubMed]
- Cleland, B.T.; Schindler-Ivens, S. Brain Activation during Passive and Volitional Pedaling After Stroke. Mot. Control 2019, 23, 52–80. [Google Scholar] [CrossRef]
- De Luca, C.J.; Donald Gilmore, L.; Kuznetsov, M.; Roy, S.H. Filtering the Surface EMG Signal: Movement Artifact and Baseline Noise Contamination. J. Biomech. 2010, 43, 1573–1579. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.E.; Iqbal, K.; White, G.; Holtz, J.K. A Review of EMG Techniques for Detection of Gait Disorders. In Artificial Intelligence-Applications in Medicine and Biology; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Cao, Y.; Cai, L.; Wang, J.; Wang, R.; Yu, H.; Cao, Y.; Liu, J. Characterization of Complexity in the Electroencephalograph Activity of Alzheimer’s Disease Based on Fuzzy Entropy. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 083116. [Google Scholar] [CrossRef]
- Xie, H.-B.; Guo, J.-Y.; Zheng, Y.-P. Fuzzy Approximate Entropy Analysis of Chaotic and Natural Complex Systems: Detecting Muscle Fatigue Using Electromyography Signals. Ann. Biomed. Eng. 2010, 38, 1483–1496. [Google Scholar] [CrossRef] [PubMed]
- Merletti, R.; Lo Conte, L.; Avignone, E.; Guglielminotti, P. Modeling of Surface Myoelectric Signals. I. Model Implementation. IEEE Trans. Biomed. Eng. 1999, 46, 810–820. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; De Stefano, A.; Allen, R. A Simulation Model of the Surface EMG Signal for Analysis of Muscle Activity during the Gait Cycle. Comput. Biol. Med. 2006, 36, 601–618. [Google Scholar] [CrossRef] [PubMed]
- Macintosh, B.R.; Neptune, R.R.; Horton, J.F. Cadence, Power, and Muscle Activation in Cycle Ergometry. Med. Sci. Sports Exerc. 2000, 32, 1281–1287. [Google Scholar] [CrossRef] [PubMed]
- Ryan, M.M.; Gregor, R.J. EMG Profiles of Lower Extremity Muscles during Cycling at Constant Workload and Cadence. J. Electromyogr. Kinesiol. 1992, 2, 69–80. [Google Scholar] [CrossRef]
- Piasecki, M.; Ireland, A.; Coulson, J.; Stashuk, D.W.; Hamilton-Wright, A.; Swiecicka, A.; Rutter, M.K.; McPhee, J.S.; Jones, D.A. Motor Unit Number Estimates and Neuromuscular Transmission in the Tibialis Anterior of Master Athletes: Evidence That Athletic Older People Are Not Spared from Age-related Motor Unit Remodeling. Physiol. Rep. 2016, 4, e12987. [Google Scholar] [CrossRef]
- Tang, A.; Rymer, W.Z. Abnormal Force--EMG Relations in Paretic Limbs of Hemiparetic Human Subjects. J. Neurol. Neurosurg. Psychiatry 1981, 44, 690–698. [Google Scholar] [CrossRef]
- Vlaar, M.P.; Solis-Escalante, T.; Vardy, A.N.; van der Helm, F.C.T.; Schouten, A.C. Quantifying Nonlinear Contributions to Cortical Responses Evoked by Continuous Wrist Manipulation. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 481–491. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Zhang, X.; Tang, X.; Gao, X.; Chen, X. Re-Evaluating Electromyogram–Force Relation in Healthy Biceps Brachii Muscles Using Complexity Measures. Entropy 2017, 19, 624. [Google Scholar] [CrossRef]
- Barański, R.; Wojnicz, W.; Zagrodny, B.; Ludwicki, M.; Sobierajska-Rek, A. Towards Hand Grip Force Assessment by Using EMG Estimators. Measurement 2024, 226, 114137. [Google Scholar] [CrossRef]
- Li, X.; Rymer, W.Z.; Zhou, P. A Simulation-Based Analysis of Motor Unit Number Index (MUNIX) Technique Using Motoneuron Pool and Surface Electromyogram Models. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 297–304. [Google Scholar] [CrossRef]
- Mottram, C.J.; Heckman, C.J.; Powers, R.K.; Rymer, W.Z.; Suresh, N.L. Disturbances of Motor Unit Rate Modulation Are Prevalent in Muscles of Spastic-Paretic Stroke Survivors. J. Neurophysiol. 2014, 111, 2017–2028. [Google Scholar] [CrossRef]
- Dash, A.; Dutta, A.; Lahiri, U. Quantification of Grip Strength with Complexity Analysis of Surface Electromyogram for Hemiplegic Post-Stroke Patients. NeuroRehabilitation 2019, 45, 45–56. [Google Scholar] [CrossRef]
- Kamavuako, E.N.; Farina, D.; Yoshida, K.; Jensen, W. Estimation of Grasping Force from Features of Intramuscular EMG Signals with Mirrored Bilateral Training. Ann. Biomed. Eng. 2012, 40, 648–656. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Zhang, X.; Mu, J.; Wu, M.; Zhu, Z.; Liu, Z.; Wang, Y. Spasticity Measurement Based on the HHT Marginal Spectrum Entropy of sEMG Using a Portable System: A Preliminary Study. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1424–1434. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, X.; Tang, X.; Cao, S.; Gao, X.; Chen, X. Surface Electromyographic Examination of Poststroke Neuromuscular Changes in Proximal and Distal Muscles Using Clustering Index Analysis. Front Neurol 2017, 8, 731. [Google Scholar] [CrossRef]
- Cheung, V.C.K.; Piron, L.; Agostini, M.; Silvoni, S.; Turolla, A.; Bizzi, E. Stability of Muscle Synergies for Voluntary Actions after Cortical Stroke in Humans. Proc. Natl. Acad. Sci. USA 2009, 106, 19563–19568. [Google Scholar] [CrossRef]
- von Carlowitz-Ghori, K.; Bayraktaroglu, Z.; Hohlefeld, F.U.; Losch, F.; Curio, G.; Nikulin, V.V. Corticomuscular Coherence in Acute and Chronic Stroke. Clin. Neurophysiol. 2014, 125, 1182–1191. [Google Scholar] [CrossRef]


| Participant | Age | Gender | TSS | Type | FMA-LE | BBS | Affected Side | Lesion Location |
|---|---|---|---|---|---|---|---|---|
| 1 | 59 | F | 7.3 | H | 24 | 54 | R | Cortical L |
| 2 | 59 | F | 6.3 | H | 20 | 51 | R | Subcortical L |
| 3 | 60 | F | 7.4 | I | 25 | 53 | R | Subcortical L |
| 4 | 54 | F | 14.8 | I | 26 | 53 | L | Cortical R |
| 5 | 69 | M | 10.4 | I | 26 | 50 | L | Cortical R |
| 6 | 37 | M | 4.6 | I | 21 | 49 | R | Cortical L |
| 7 | 72 | F | 5.8 | I | 25 | 56 | R | Cortical L |
| 8 | 63 | M | 2.2 | I | 17 | 41 | L | Cortical R |
| 9 | 57 | M | 2.3 | I | 21 | 54 | L | Cortical R |
| 10 | 72 | F | 4.2 | I | 25 | 54 | L | Cortical R |
| 11 | 61 | M | 9.0 | I | 28 | 55 | L | Subcortical R |
| 12 | 61 | M | 3.4 | H | 28 | 56 | R | Subcortical L |
| 13 | 65 | F | 3.9 | H | 16 | 42 | L | Cortical R |
| 14 | 60 | F | 2.9 | I | 20 | 55 | R | Subcortical L |
| 15 | 36 | F | 2.1 | H | 17 | 46 | R | Cortical L |
| Parameters | Value |
|---|---|
| Muscle axial conductivity | σZ = 0.328Sm−1 |
| Muscle radial conductivity | σY = 0.063Sm−1 |
| Intracellular conductivity | σI = 1.010Sm−1 |
| Fiber diameter | d = 55 ± 10 µm, mean ± SD; Gaussian distribution |
| Single fiber conduction velocity | V = 2.2 + 0.05 × (d − 25), d in µm |
| Muscle radius | Length: mean = 100 mm, SD = 1 mm, Gaussian distribution; position: uniform distribution |
| Motor unit | Circle shape; diameter: range 5–10 mm, lambda = 6 mm, Poisson distribution; position: uniform distribution |
| Motor unit firing rate | Range from 8–90 Hz, maximum contraction, range 70–90 Hz, steady, 8–40 Hz, lambda: 12 Hz, Poisson distribution |
| Pedaling cycle | 2400 ms/cycle (360°) |
| Muscle activation pattern and No. of recruited motor unit | |
| N_MU = 150, range: 45–225°, max: 90–120° |
| N_MU = 150, range: 160–360°, max: 280–320° |
| N_MU = 250, range: 340–190°, max: 80–120° |
| N_MU = 250, range: 260–60°, max: 290–350° |
| N_MU = 200, range: 20–150°, max: 80–110° |
| N_MU = 150, range: 330–80°, max: 30–60° |
| Source | Healthy | Stroke |
|---|---|---|
| Channels | F(5,264) = 15.957, p < 0.001, partial η2 = 0.232 | F(5,336) = 4.674, p < 0.001, partial η2 = 0.065 |
| Tasks | F(1,264) = 31.034, p < 0.001, partial η2 = 0.105 | F(1,336) = 0.665, p = 0.415 |
| Sides | F(1,264) = 3.590, p = 0.059 | F(1,336) = 2.366, p = 0.125 |
| Channels*Tasks | F(5,264) = 4.566, p = 0.001, partial η2 = 0.080 | F(5,336) = 2.654, p = 0.023, partial η2 = 0.038 |
| Channels*Sides | F(5,264) = 11.711, p < 0.001, partial η2 = 0.182 | F(5,336) = 22.910, p < 0.001, partial η2 = 0.254 |
| Tasks*Sides | F(1,264) = 5.594, p = 0.019, partial η2 = 0.021 | F(1,336) = 5.188, p = 0.023, partial η2 = 0.015 |
| Channels*Tasks*Sides | F(5,264) = 1.327, p = 0.253 | F(5,336) = 0.197, p = 0.310 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, S.-C.; Sun, R.; Tong, R.K.-Y. Pedaling Asymmetry Reflected by Bilateral EMG Complexity in Chronic Stroke. Entropy 2024, 26, 538. https://doi.org/10.3390/e26070538
Bao S-C, Sun R, Tong RK-Y. Pedaling Asymmetry Reflected by Bilateral EMG Complexity in Chronic Stroke. Entropy. 2024; 26(7):538. https://doi.org/10.3390/e26070538
Chicago/Turabian StyleBao, Shi-Chun, Rui Sun, and Raymond Kai-Yu Tong. 2024. "Pedaling Asymmetry Reflected by Bilateral EMG Complexity in Chronic Stroke" Entropy 26, no. 7: 538. https://doi.org/10.3390/e26070538
APA StyleBao, S.-C., Sun, R., & Tong, R. K.-Y. (2024). Pedaling Asymmetry Reflected by Bilateral EMG Complexity in Chronic Stroke. Entropy, 26(7), 538. https://doi.org/10.3390/e26070538







