Energy, Exergetic, and Thermoeconomic Analyses of Hydrogen-Fueled 1-kW Proton-Exchange Membrane Fuel Cell
Abstract
:1. Introduction
2. Energy and Exergy Analyses of Thermal Systems
2.1. Energy Conservation
2.2. Exergy Balance Equation and the Second Law of Thermodynamics
2.3. Exergy Cost-Balance Equation
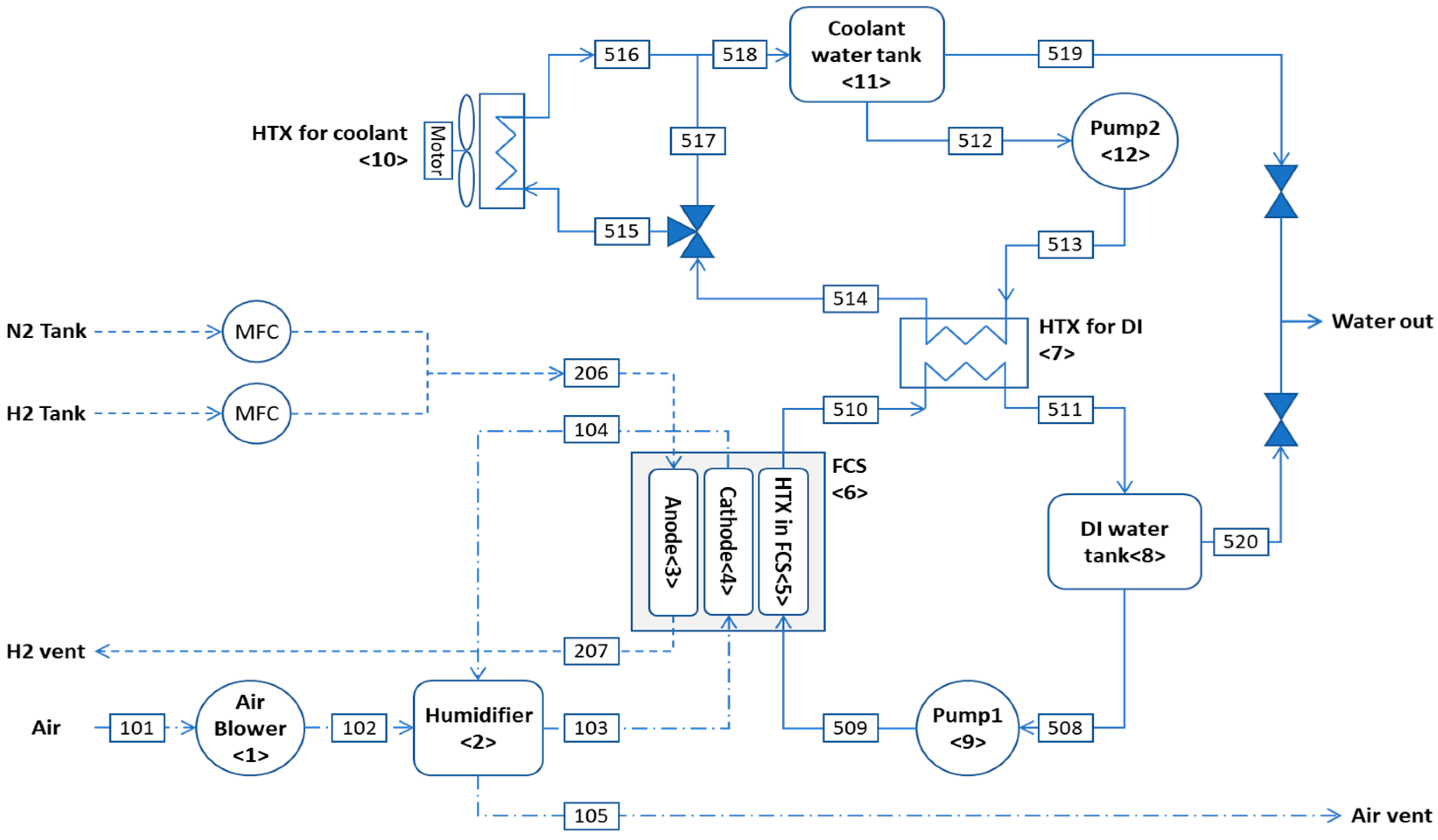
3. Hydrogen-Fueled 1-kW PEMFC System
3.1. Energy Conservation and Exergy Balance and Exergy Cost-Balance Equations for PEMFC System
- Air blowerwhere .
- Humidifier
- Anode
- Cathode
- HTX in the FCS
- FCS
- HTX for DI
- DI water tank
- Pump 1where .
- HTX for coolantwhere .
- Coolant water tank
- Pump 2where .
3.2. Energy Conservation and Exergy Balance of the FCS
3.3. Exergy Cost-Balance Equation for the Overall System
4. Calculation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| unit cost | |
| annualized cost | |
| initial investment cost | |
| unit cost of fuel | |
| exergy per unit mass | |
| exergy flow rate | |
| enthalpy per unit mass | |
| enthalpy flow rate | |
| latent heat of water | |
| electric current | |
| irreversibility rate | |
| mass flow rate | |
| mole flow rate | |
| number of stacks | |
| heat flow rate | |
| entropy per unit mass | |
| entropy flow rate | |
| entropy generation rate | |
| temperature | |
| ambient temperature | |
| workflow rate | |
| capital cost flow rate | |
| Greek letters | |
| annual operating hours | |
| maintenance cost factor | |
| Superscripts | |
| chemical | |
| fuel | |
| exergy destruction | |
| mechanical | |
| thermal | |
| work or electricity | |
| Subscripts | |
| chemical | |
| control volume | |
| reference point | |
| mechanical | |
| thermal reservoir | |
| entropy | |
| thermal | |
| work or electricity | |
Abbreviations
| CCHP | combined cooling, heating, and power |
| CHP | cooling, heating, and power |
| CRF | capital recovery factor |
| DI | deionized |
| F | Faraday constant |
| FCS | fuel cell stack |
| HHV | higher heating value |
| LHV | lower heating value |
| PEMFC | proton-exchange membrane fuel cell |
| HTX | heat exchanger |
| PWF | present worth factor |
| SV | salvage value |
Appendix A
References
- Gigliucci, G.; Petruzzi, L.; Cerelli, E.; Garzisi, A.; La Mendola, A. Demonstration of a residential CHP system based on PEM fuel cells. J. Power Sources 2004, 131, 62–68. [Google Scholar] [CrossRef]
- Chen, J.C.; Chen, X.H.; Chen, L.W.; Guo, J.C. An available method exploiting the waste heat in a proton exchange membrane fuel cell system. Int. J. Hydrogen Energy 2011, 36, 6099–6104. [Google Scholar] [CrossRef]
- Hwang, J.J.; Zou, M.L.; Chang, W.R.; Su, A.; Weng, F.B.; Wu, W. Implementation of a heat recovery unit in a proton exchange membrane fuel cell system. Int. J. Hydrogen Energy 2010, 35, 8644–8653. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. An exergetic analysis of a residential CHP system based on PEM fuel cell. Appl. Energy 2011, 88, 4334–4342. [Google Scholar] [CrossRef]
- Chen, X.; Gong, G.; Wan, Z.; Luo, L.; Wan, J. Performance analysis of 5 kW PEMFC based residential micro-CCHP with absorption chiller. Int. J. Hydrogen Energy 2015, 40, 10647–10657. [Google Scholar] [CrossRef]
- Seo, S.-H.; Oh, S.-D.; Kwak, H. Thermodynamic, exergetic and thermoeconomic analyses of double-effect LiBr-water absorption refrigeration systems with a 5 kW high temperature PEMFC as heat source for data center applicaions. Energies 2022, 15, 3101. [Google Scholar] [CrossRef]
- Oh, S.D.; Kim, K.Y.; Oh, S.B.; Kwak, H. Optimal operation of a 1-kW PEMFC-based CHP system for residential applications. Appl. Energy 2012, 95, 93–101. [Google Scholar] [CrossRef]
- Uysal, C.; Kurt, H.; Kwak, H. Exergetic and thermoeconomic analyses of a coal-fired power plant. Int. J. Thermal Sci. 2017, 117, 106–120. [Google Scholar] [CrossRef]
- Valero, A.; Lerch, F.; Serra, L.; Royo, J. Structural theory and thermoeconomic diagnosis Part II: Application to an actual power plant. Energy Convers. Manag. 2002, 43, 1519–1535. [Google Scholar] [CrossRef]
- Wang, L.; Fu, P.; Wang, N.; Morosuk, T.; Yang, Y.; Tsatsaronis, G. Malfunction diagnosis of thermal power plants based on advanced exergy analysis: The case with multiple malfunctions occurring simultaneously. Energy Convers. Manag. 2017, 144, 1453–1467. [Google Scholar] [CrossRef]
- Oh, H.S.; Lee, Y.; Kwak, H. Diagnosis of combined cycle power plant based on thermoeconomic analysis: A computer simulation study. Entropy 2017, 19, 643. [Google Scholar] [CrossRef]
- Seo, S.H.; Oh, S.-D.; Oh, H.; Kim, M.; Lee, W.Y.; Kwak, H. Thermal management for a hydrogen-fueled 1-kW PEMFC based on thermoeconomic analysis. Int. J. Hydrogen Energy 2019, 44, 24934–24946. [Google Scholar] [CrossRef]
- Piacentino, A.; Talamo, M. Critical analysis of conventional thermoeconomic approaches to the diagnosis of multiple faults in air conditioning units: Capabilities, drawbacks and improvement directions. A case studu for an air-cooled system with 120 kW capacity. Int. J. Refrig. 2013, 36, 24–44. [Google Scholar] [CrossRef]
- Yoo, Y.; Oh, H.-S.; Uysal, C.; Kwak, H. Thermoeconomic diagnosis of an air-cooled air conditioning systems. Int. J. Exergy 2018, 26, 393–417. [Google Scholar] [CrossRef]
- Morosuk, T.; Tsatsaronis, G. A new approach to the exergy analysis of absorption refrigeration machines. Energy 2008, 33, 890–907. [Google Scholar] [CrossRef]
- Kwak, H.; Kim, D.J.; Jeon, J.S. Exergetic and thermoeconomic analyses of power plant. Energy 2003, 28, 343–360. [Google Scholar] [CrossRef]
- Kwak, H.; You, Y.; Oh, S.D.; Jang, H.N. Thermoeconomic analysis of ground-source heat pump systems. It. J. Energy Res. 2014, 38, 259–269. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Oh, S.; Pang, H.; Kim, S.; Kwak, H. Exergy analysis for a gas turbine cogeneration system. J. Eng. Gas. Turbine Power 1996, 118, 782–791. [Google Scholar] [CrossRef]
- Kotas, J. The Exergy Method of Thermal Plant Analysis; Krieger: Malabar, FL, USA, 1995. [Google Scholar]
- Moran, J. Availability Analysis: A Guide to Efficient Energy Use; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Pei, P.; Meng, Y.; Chen, D.; Ren, P.; Wang, M.; Wang, X. Life time prediction method of proton exchange method fuel cells based on current degradation law. Energy 2023, 265, 126341. [Google Scholar] [CrossRef]
- Ye, L.; Du, Q.; Yin, Y. Exergy analysis of high-temperature proton exchange membrane fuel cell systems. Int. J. Green Energy 2015, 12, 917–929. [Google Scholar] [CrossRef]
- O’hayre, R.; Cha, S.W.; Colella, W.G.; Prinz, F.B. Fuel Cell Fundamentals, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Wei, M.; Lipman, T.; Mayyas, A.; Chan, S.H.; Gosselin, D.; Breunig, H.; McKone, T. A Total Cost of Ownership Model for High-Temperature PEM Fuel Cells in Combined Heat and Power Applications; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2014.
- Kim, D.J.; Kim, J.H.; Barry, K.F.; Kwak, H. Thermoeconomic analysis of high-temperature gas-cooled reactors with steam methane reforming for hydrogen production. Nucl. Technol. 2011, 176, 337–351. [Google Scholar] [CrossRef]
- Olateju, B.; Kumer, A.; Secanell, M. A techno-economic assessment of large-scale wind-hydrogen production with energy storage in Western Canada. Int. J. Hydrogen Energy 2016, 41, 8755–8766. [Google Scholar] [CrossRef]
- Shaner, M.R.; Atwater, H.A.; Lewis, N.S.; McFarland, E.W. A comparative technoeconomic analysis of renewable hydrogen production using solar energy. Energy Environ. Sci. 2016, 9, 2354–2371. [Google Scholar] [CrossRef]

| States | (kmol/h) | (kPa) | (K) | (kJ/h) | (kJ/h/K) | (kJ/h) |
|---|---|---|---|---|---|---|
| 101 | 0.0846 | 100.90 | 299.40 | 3.0821 | 0.471 | −1.186 |
| 102 | 0.0846 | 113.36 | 305.99 | 19.340 | 0.443 | 23.461 |
| 103 | 0.0846 | 105.40 | 322.14 | 59.280 | 0.621 | 10.214 |
| 104 | 0.0748 | 102.28 | 332.99 | 76.067 | 0.540 | 35.345 |
| 105 | 0.0748 | 102.42 | 312.52 | 31.335 | 0.407 | 30.376 |
| 206 | 0.0275 | 103.98 | 299.97 | 1.443 | 0.005 | 0.0 |
| 207 | 0.0079 | 102.05 | 326.10 | 6.368 | 0.020 | 0.002 |
| 508 | 4.8295 | 99.80 | 325.69 | 19,136.736 | 64.053 | 435.754 |
| 509 | 4.8295 | 143.63 | 325.59 | 19,103.614 | 63.940 | 436.496 |
| 510 | 4.8295 | 122.48 | 333.13 | 21,846.193 | 72.273 | 694.585 |
| 511 | 4.8295 | 110.48 | 326.14 | 19,301.256 | 64.555 | 450.631 |
| 512 | 2.2926 | 102.35 | 303.10 | 5185.052 | 17.998 | 7.057 |
| 513 | 2.2926 | 114.85 | 303.03 | 5173.442 | 17.958 | 7.378 |
| 514 | 2.2926 | 105.72 | 331.47 | 10,082.861 | 33.445 | 299.545 |
| 515 | 2.2926 | 103.72 | 331.47 | 10,082.791 | 33.445 | 299.463 |
| 516 | 2.2926 | 101.75 | 303.05 | 5176.401 | 17.970 | 6.891 |
| 518 | 2.2926 | 100.75 | 302.05 | 5003.788 | 17.400 | 4.340 |
| Enthalpy Inflow | Enthalpy Outflow | Workflow | Heat Flow | Irreversibility Rate | ||
|---|---|---|---|---|---|---|
| Air blower | −3.082 | 19.340 | −16.258 | 0.0 | −8.389 | −8.389 |
| Anode | −1.443 | 6.368 | 0.0 | −4.925 | 4.648 | −0.277 |
| Cathode | −59.280 | 76.067 | 0.0 | −16.787 | −24.097 | −40.884 |
| Humidifier | −95.408 | 90.615 | 0.0 | 4.793 | 13.484 | 18.277 |
| HTX for the FCS | −19,103.614 | 21,486.193 | −2742.579 | 2484.490 | −258.089 | |
| HTXDI | −27,019.635 | 29,384.117 | 0.0 | −2364.482 | 2316.269 | −48.213 |
| DIWT | −19,301.256 | 19,136.736 | 164.521 | −149.644 | 14.877 | |
| Pump 1 | −19,136.736 | 19,103.614 | −5.503 | 38.625 | −33.864 | 4.762 |
| HTXWC | −10,082.791 | 5176.401 | −18.000 | 4924.390 | −4613.819 | 310.572 |
| Hot WT | −5003.788 | 5185.052 | 0.0 | −181.264 | 178.548 | −2.716 |
| Pump 2 | −5185.052 | 5173.442 | −0.645 | 12.255 | −11.931 | 0.324 |
| Component | Net Exergy Flow Rates (kJ/h) | Irreversibility | |||
|---|---|---|---|---|---|
| Rate (kJ/h) | |||||
| Air blower | −16.258 | 0.0 | 0.244 | 24.403 | −8.389 |
| Anode | 0.0 | 0.0 | 1.622 | −1.620 | −0.002 |
| Cathode | 0.0 | 0.0 | 31.651 | −6.521 | −25.131 |
| Humidifier | 0.0 | 0.0 | −1.381 | −16.834 | 18.215 |
| HTX in the FCS | 0.0 | 0.0 | 259.935 | −1.845 | −258.090 |
| FCS | 2923.596 | −5666.175 | (2642.475) | 0.0 | 100.104 |
| HTX DI | 49.638 | −1.425 | −48.213 | ||
| DIWT | 0.0 | 0.0 | −13.945 | −0.932 | 14.877 |
| Pump 1 | −5.503 | 0.0 | −3.083 | 3.824 | 4.762 |
| HTXWC | −18.0 | 0.0 | −292.490 | −0.082 | 310.572 |
| Hot WT | 2.650 | 0.066 | −2.716 | ||
| Pump 2 | −0.645 | −0.196 | 0.518 | 0.324 | |
| Total | 2883.19 | −5666.175 | (2677.12) | −0.448 | 106.313 |
| C1P | C2T | C3T | C4C | C5T | C6W | C7T |
| −0.8955 | −230.52 | 102.99 | −86,238.0 | −4.173 | 0.2703 | −3.9587 |
| C8T | C9P | C10T | C11T | C12P | CT | CP |
| 5.80 | 94.494 | −4.790 | 2.065 | 52.719 | 114.76 | 12.759 |
| CC | CW | CS | ||||
| −86,238.0 | 0.2703 | −4.483 |
| Component | Electricity Cost Flow | Thermal Exergy Cost Flow | Mechanical Exergy Cost Flow | Lost Cost Flow | Invest Cost Flow | Investment (USD) |
|---|---|---|---|---|---|---|
| Air blower | −0.004 | 0.028 | −0.022 | 0.038 | −0.039 | 1431.5 |
| Anode | 0.167 | −0.021 | −0.146 | 5332.4 | ||
| Cathode | −3.515 * | 3.632 | −0.083 | 0.113 | −0.146 | 5332.4 |
| Humidifier | 0.318 | −0.215 | −0.082 | −0.022 | 800.0 | |
| HTX in the FCS | −1.085 | −0.024 | 1.157 | −0.049 | 1775.3 | |
| FCS | 0.790 | −0.449 | −0.342 | 7856.6 | ||
| HTX DI | −0.197 | −0.018 | 0.216 | −0.001 | 52.2 | |
| DIWT | 0.081 | −0.012 | −0.067 | −0.002 | 84.2 | |
| Pump 1 | −0.001 | −0.354 | 0.361 | −0.001 | −0.005 | 168.4 |
| HTXWC | −0.005 | 1.401 | −0.001 | −1.392 | −0.003 | 111.1 |
| Pump 2 | −0.022 | 0.027 | −0.0 | −0.005 | 168.4 | |
| Hot WT | 0.005 | 0.001 | 0.012 | −0.018 | 673.7 | |
| Total | −2.735 (0.78+) | 3.974 | −0.007 | −0.455 | −0.778 | 23,786.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, Y.; Lee, S.-Y.; Seo, S.-H.; Oh, S.-D.; Kwak, H.-Y. Energy, Exergetic, and Thermoeconomic Analyses of Hydrogen-Fueled 1-kW Proton-Exchange Membrane Fuel Cell. Entropy 2024, 26, 566. https://doi.org/10.3390/e26070566
Yoo Y, Lee S-Y, Seo S-H, Oh S-D, Kwak H-Y. Energy, Exergetic, and Thermoeconomic Analyses of Hydrogen-Fueled 1-kW Proton-Exchange Membrane Fuel Cell. Entropy. 2024; 26(7):566. https://doi.org/10.3390/e26070566
Chicago/Turabian StyleYoo, Yungpil, Sang-Yup Lee, Seok-Ho Seo, Si-Doek Oh, and Ho-Young Kwak. 2024. "Energy, Exergetic, and Thermoeconomic Analyses of Hydrogen-Fueled 1-kW Proton-Exchange Membrane Fuel Cell" Entropy 26, no. 7: 566. https://doi.org/10.3390/e26070566
APA StyleYoo, Y., Lee, S. -Y., Seo, S. -H., Oh, S. -D., & Kwak, H. -Y. (2024). Energy, Exergetic, and Thermoeconomic Analyses of Hydrogen-Fueled 1-kW Proton-Exchange Membrane Fuel Cell. Entropy, 26(7), 566. https://doi.org/10.3390/e26070566







