Tunneling Currents in the Hyperbolic Phase Space
Abstract
:1. Introduction
2. Q-Function on the Hyperboloid
3. Tunneling Currents on the Hyperboloid
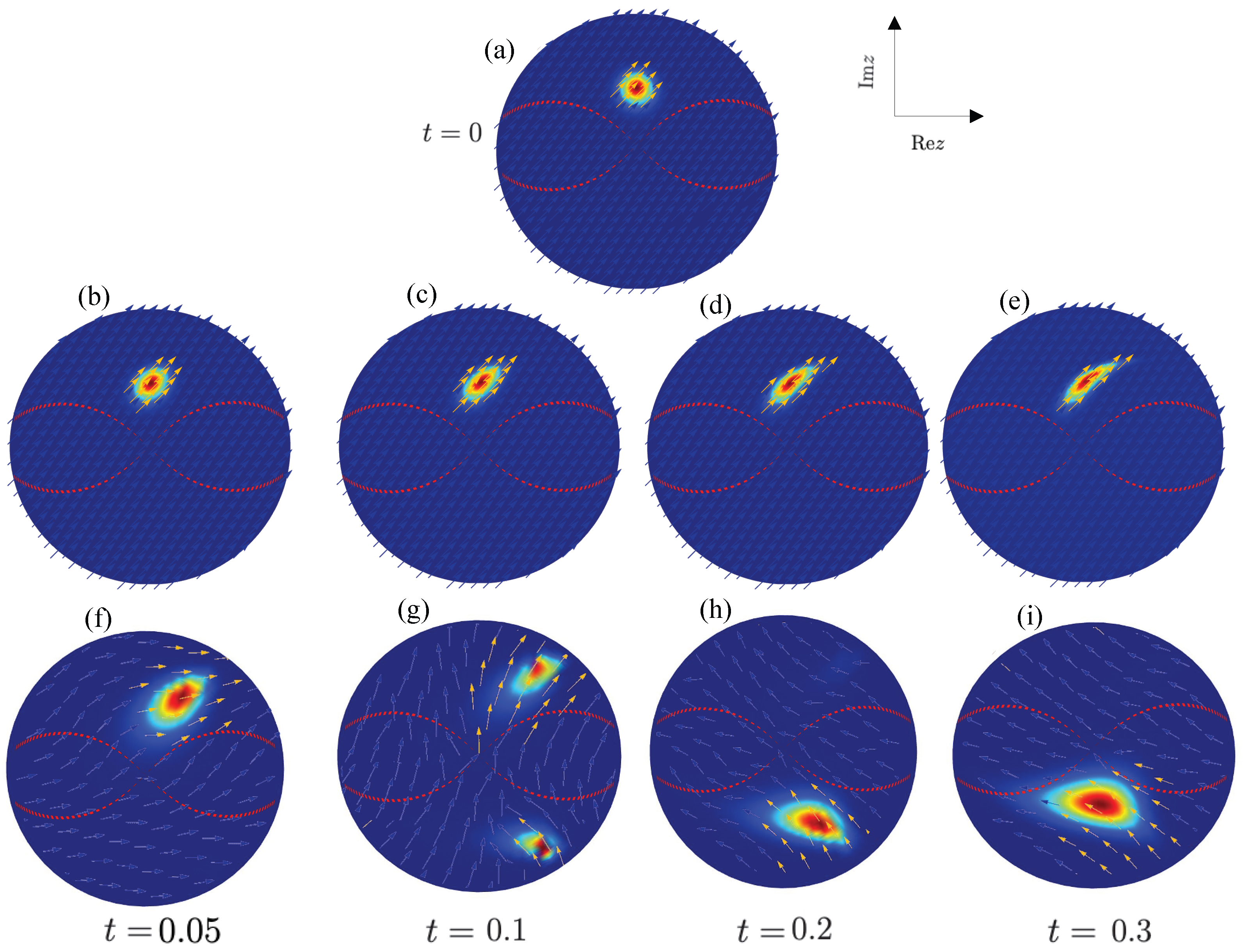
3.1. Semiclassical Evolution
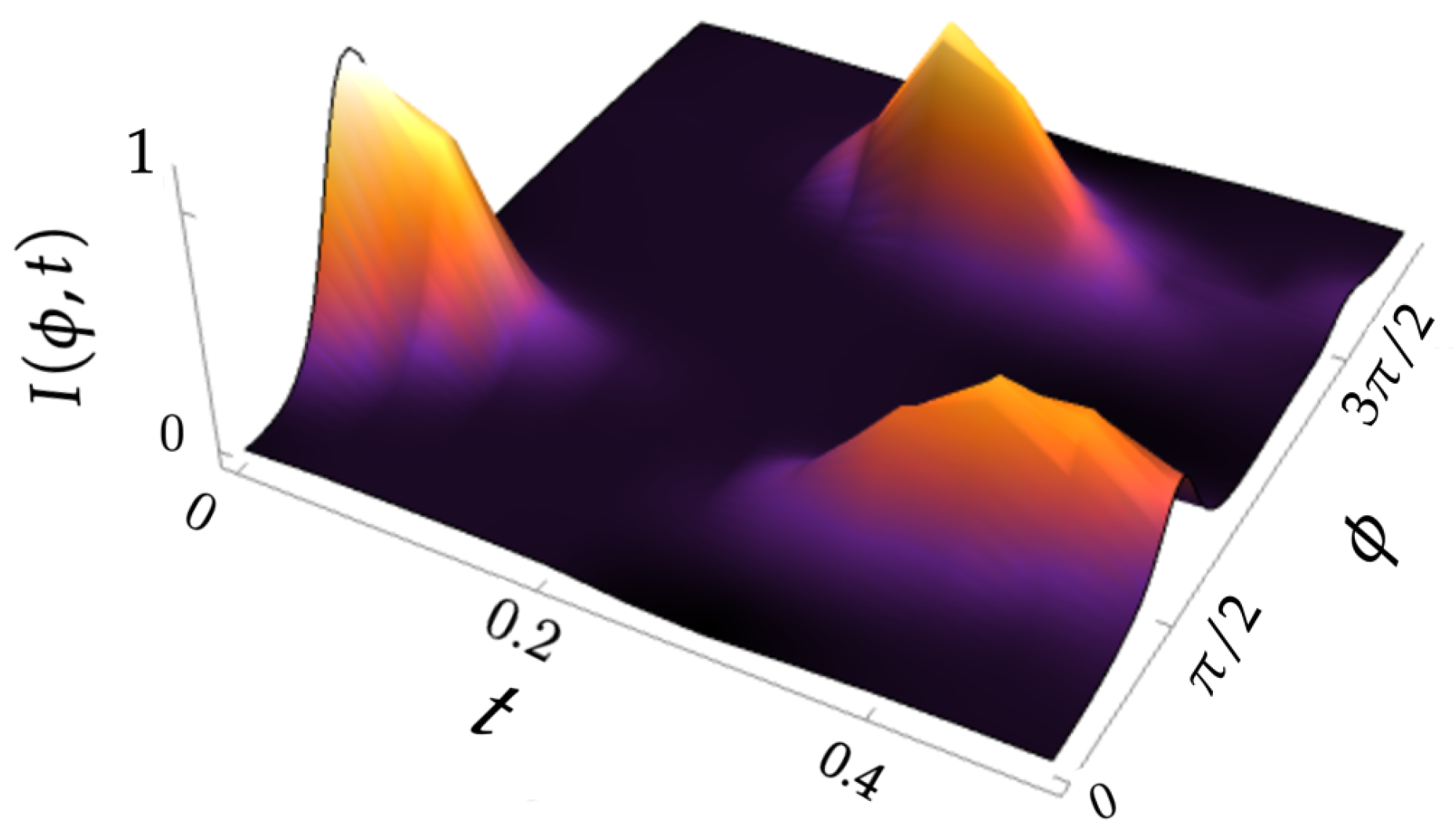
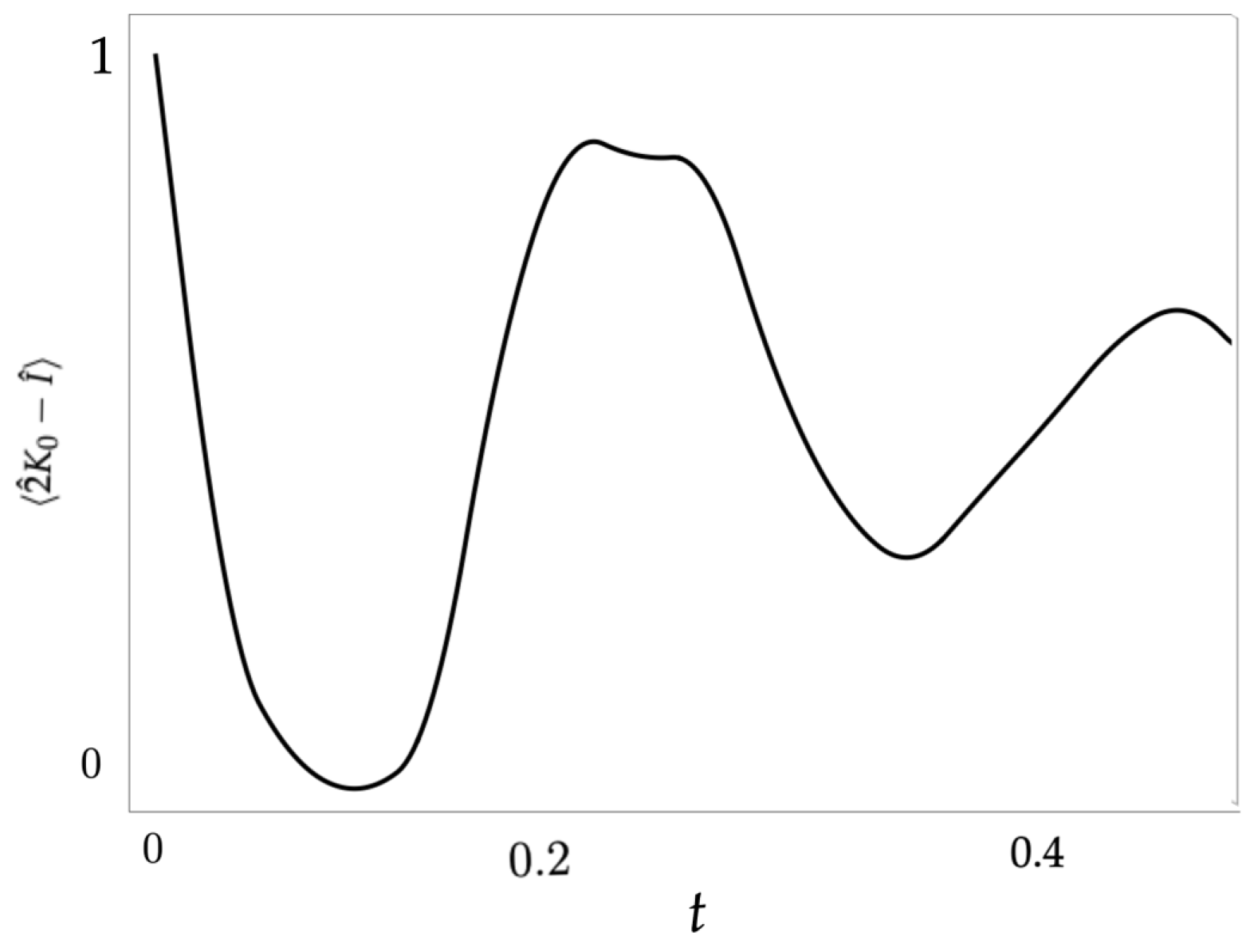
3.2. Quantum Evolution
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Davis, M.J.; Heller, E.J. Quantum dynamical tunneling in bound states. J. Chem. Phys. 1981, 75, 246. [Google Scholar] [CrossRef]
- Dmitriev, A.; D’yakonov, M.; Loffe, A.F. Activated and tunneling transitions between the two forced-oscillation regimes of an 222 anharmonic oscillator. Sov. J. Exp. Theor. Phys. 1986, 63, 838. [Google Scholar]
- Dumont, R.S.; Marchioro, T., II. Tunneling-time probability distribution. Phys. Rev. A 1993, 47, 85. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.Y.; Lee, H.W. Quantum tunneling, dynamical symmetry, and quantum revival. Phys. Rev. E 1996, 53, 3096. [Google Scholar] [CrossRef] [PubMed]
- Takagi, S. Macroscopic Quantum Tunneling; Cambrige University Press: Cambrige, UK, 2002. [Google Scholar]
- Zachos, C.; Fairlie, D.; Curtright, T. Quantum Mechanics in Phase Space: An Overview with Selected Papers; World Scientific: Singapore, 2005. [Google Scholar]
- De Almeida, A.M.O. The Weyl representation in classical and quantum mechanics. Phys. Rep. 1998, 295, 265–342. [Google Scholar] [CrossRef]
- Rajaraman, R. Solitons and Instantons. An Introduction to Solitons and Instantons in Quantum Field Theory; North Holland: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Hagino, K.; Takigawa, N. Subbarrier fusion reactions and many-particle quantum tunneling. Prog. Theor. Phys. 2012, 128, 1061–1106. [Google Scholar] [CrossRef]
- Skodje, R.T.; Rohrs, H.W.; VanBuskirk, J. Flux analysis, the correspondence principle, and the structure of quantum phase space. Phys. Rev. A 1989, 40, 2894. [Google Scholar] [CrossRef] [PubMed]
- Heim, D.; Schleich, W.; Alsing, P.; Dahl, J.; Varro, S. Tunneling through a parabolic barrier viewed from Wigner phase space. arXiv 2013, arXiv:1302.1030. [Google Scholar]
- Lin, Y.L.; Dahlsten, O.C. Necessity of negative Wigner function for tunneling. Phys. Rev. A 2020, 102, 062210. [Google Scholar] [CrossRef]
- Reynoso, M.A.P.; Nader, D.; Chávez-Carlos, J.; Ordaz-Mendoza, B.; Cortiñas, R.G.; Batista, V.S.; Lerma-Hernández, S.; Pérez-Bernal, F.; Santos, L.F. Quantum tunneling and level crossings in the squeeze-driven Kerr oscillator. Phys. Rev. A 2023, 108, 033709. [Google Scholar] [CrossRef]
- Donoso, A.; Martens, C.C. Quantum tunneling using entangled classical trajectories. Phys. Rev. Lett. 2001, 87, 223202. [Google Scholar] [CrossRef] [PubMed]
- Klimov, A.B.; Romero, J.L.; de Guise, H. Generalized SU(2) covariant Wigner functions and some of their applications. J. Phys. A Math. Theor. 2017, 50, 323001. [Google Scholar] [CrossRef]
- Wodkiewicz, K.; Eberly, J.H. Coherent states, squeezed fluctuations, and the SU(2) and SU(1,1) groups in quantum-optics applications. J. Opt. Soc. Am. B 1985, 2, 458. [Google Scholar] [CrossRef]
- Gerry, C.C. Dynamics of SU(1,1) coherent states. Phys. Rev. A 1985, 31, 2721. [Google Scholar] [CrossRef]
- Orłowski, A.; Wódkiewicz, K. On the SU(1, 1) phase-space description of reduced and squeezed quantum fluctuations. J. Mod. Opt. 1990, 37, 295. [Google Scholar] [CrossRef]
- Jezek, D.M.; Hernandez, E.S. Nonlinear pseudospiin dynamics on a noncompact manifold. Phys. Rev. A 1990, 42, 96. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Liu, C.; Zhou, Z.; Ou, Z.Y.; Zhang, W. Realization of a nonlinear interferometer with parametric amplifiers. Appl. Phys. Lett. 2011, 99, 011110. [Google Scholar] [CrossRef]
- Tilma, T.; Everitt, M.J.; Samson, J.H.; Munro, W.J.; Nemoto, K. Wigner Functions for Arbitrary Quantum Systems. Phys. Rev. Lett. 2016, 117, 180401. [Google Scholar] [CrossRef] [PubMed]
- Klimov, A.B.; de Guise, H. General approach to SU(n) quasi-distribution functions. J. Phys. A Math. Theor. 2010, 43, 402001. [Google Scholar] [CrossRef]
- Perelomov, A.M. Generalized Coherent States and Some of Their Applications. Sov. Phys. Uspekhi 1977, 20, 703. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, D.; Gilmore, R. Coherent states. Rev. Mod. Phys. 1990, 62, 240. [Google Scholar] [CrossRef]
- Gazeau, J.P. Coherent states in quantum physics: An overview. J. Physics Conf. Ser. 2023, 2667, 012052. [Google Scholar] [CrossRef]
- Husimi, K. Some formal properties of the density matrix. In Proceedings of the Physico-Mathematical Society of Japan 3rd Series; The Physical Society of Japan: Tokyo, Japan, 1940; Volume 22, pp. 264–314. [Google Scholar]
- Steuernagel, O.; Kakofengitis, D.; Ritter, G. Wigner flow reveals topological order in quantum phase space dynamics. Phys. Rev. Lett. 2013, 110, 030401. [Google Scholar] [CrossRef] [PubMed]
- Kakofengitis, D.; Steuernagel, O. Wigner’s quantum phase-space current in weakly-anharmonic weakly-excited two-state systems. Eur. Phys. J. Plus 2017, 132, 1–13. [Google Scholar] [CrossRef]
- Kakofengitis, D.; Oliva, M.; Steuernagel, O. Wigner’s representation of quantum mechanics in integral form and its applications. Phys. Rev. A 2017, 95, 022127. [Google Scholar] [CrossRef]
- Veronez, M.; de Aguiar, M.A. Phase space flow in the Husimi representation. J. Phys. A Math. Theor. 2013, 46, 485304. [Google Scholar] [CrossRef]
- Veronez, M.; de Aguiar, M.A. Topological structures in the Husimi flow. J. Phys. A Math. Theor. 2016, 49, 065301. [Google Scholar] [CrossRef]
- Yang, P.; Valtierra, I.F.; Klimov, A.B.; Wu, S.T.; Lee, R.K.; Sánchez-Soto, L.L.; Leuchs, G. The Wigner flow on the sphere. Phys. Scr. 2019, 94, 044001. [Google Scholar] [CrossRef]
- Valtierra, I.F.; Klimov, A.B.; Leuchs, G.; Sánchez-Soto, L.L. Quasiprobability currents on the sphere. Phys. Rev. A 2020, 101, 033803. [Google Scholar] [CrossRef]
- Klimov, A.B.; Seyfarth, U.; de Guise, H.; Sánchez-Soto, L.L. SU (1, 1) covariant s-parametrized maps. J. Phys. A Math. Theor. 2021, 54, 065301. [Google Scholar] [CrossRef]
- Gerry, C.C. Application of SU (1, 1) coherent states to the interaction of squeezed light in an anharmonic oscillator. Phys. Rev. A 1987, 35, 2146. [Google Scholar] [CrossRef] [PubMed]
- Gerry, C.C. Correlated two-mode SU (1, 1) coherent states: Nonclassical properties. JOSA B 1991, 8, 685–690. [Google Scholar] [CrossRef]
- Gerry, C.C.; Grobe, R. Two-mode intelligent SU (1, 1) states. Phys. Rev. A 1995, 51, 4123. [Google Scholar] [CrossRef]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU (2) and SU (1, 1) interferometers. Phys. Rev. A 1986, 33, 4033. [Google Scholar] [CrossRef]
- Gerry, C.C.; Birrittella, R.; Raymond, A.; Carranza, R. Photon statistics, parity measurements, and Heisenberg-limited interferometry: Example of the two-mode SU (1, 1) SU (1, 1) coherent states. J. Mod. Opt. 2011, 58, 1509–1517. [Google Scholar] [CrossRef]
- Li, D.; Gard, B.T.; Gao, Y.; Yuan, C.H.; Zhang, W.; Lee, H.; Dowling, J.P. Phase sensitivity at the Heisenberg limit in an SU(1,1) interferometer via parity detection. Phys. Rev. A 2016, 94, 063840. [Google Scholar] [CrossRef]
- Baltazar, M.; Valtierra, I.F.; Klimov, A.B. Correspondence Rules for SU (1, 1) Quasidistribution Functions and Quantum Dynamics in the Hyperbolic Phase Space. Entropy 2022, 24, 1580. [Google Scholar] [CrossRef]
- Hauge, E.; Støvneng, J. Tunneling times: A critical review. Rev. Mod. Phys. 1989, 61, 917. [Google Scholar] [CrossRef]
- Olkhovsky, V.S.; Recami, E. Recent developments in the time analysis of tunneling processes. Phys. Rep. 1992, 214, 339–356. [Google Scholar] [CrossRef]
- Kuriyan, J.G.; Mukunda, N.; Sudarshan, E. Master analytic representation: Reduction of O (2, 1) in an O (1, 1) basis. J. Math. Phys. 1968, 9, 2100–2108. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valtierra, I.F.; Klimov, A.B. Tunneling Currents in the Hyperbolic Phase Space. Entropy 2024, 26, 639. https://doi.org/10.3390/e26080639
Valtierra IF, Klimov AB. Tunneling Currents in the Hyperbolic Phase Space. Entropy. 2024; 26(8):639. https://doi.org/10.3390/e26080639
Chicago/Turabian StyleValtierra, Ivan F., and Andrei B. Klimov. 2024. "Tunneling Currents in the Hyperbolic Phase Space" Entropy 26, no. 8: 639. https://doi.org/10.3390/e26080639





