Survival Probability, Particle Imbalance, and Their Relationship in Quadratic Models
Abstract
:1. Introduction
2. Models
3. Survival Probability and Particle Imbalance
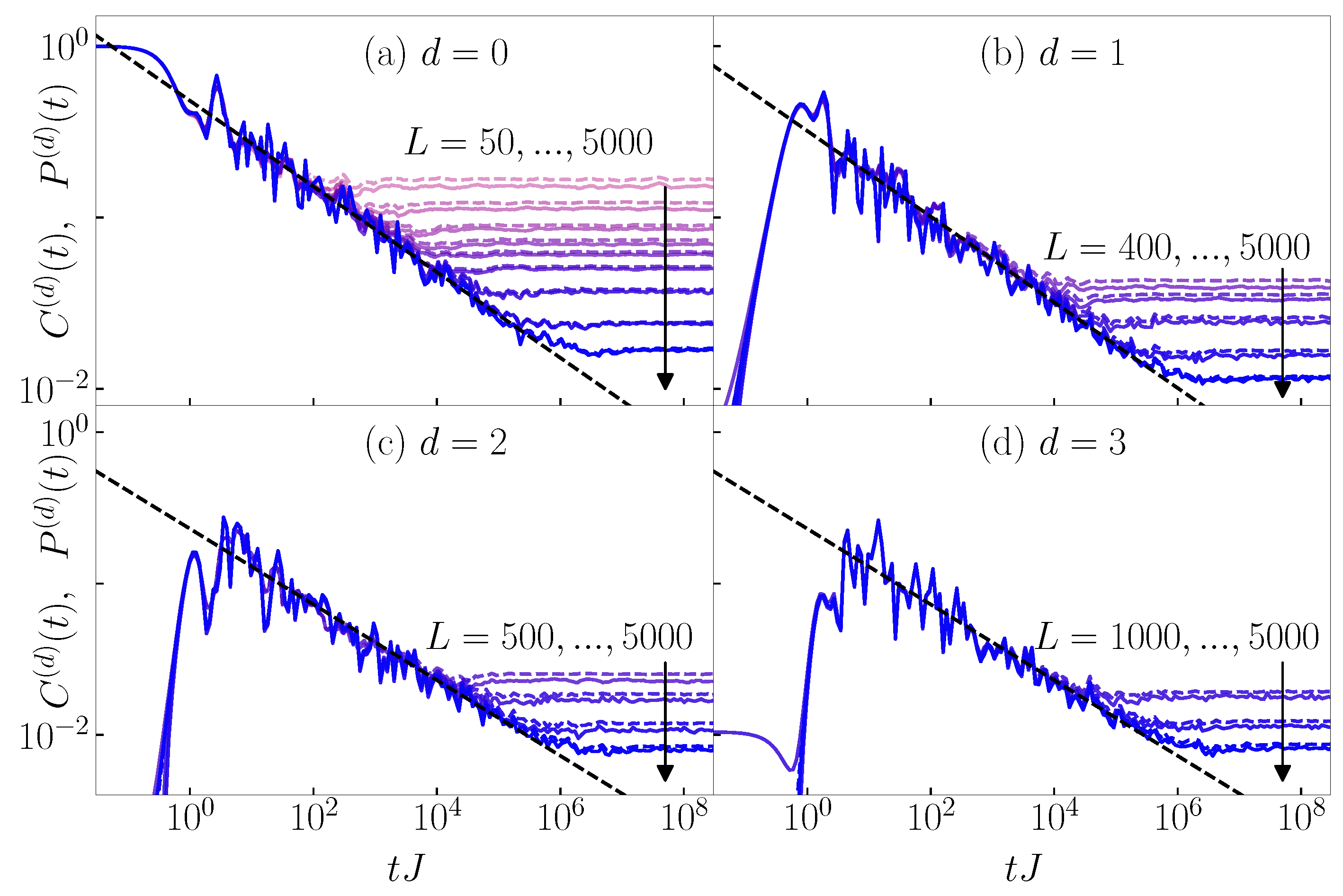
4. Transition Probabilities and Density Correlation Functions (Generalized Imbalance)
5. Equal Time Connected Density–Density Correlation Functions
6. Discussion
- (i)
- We relate the dynamics of particle imbalance to the dynamics of single-particle survival probability, and we show that the two become nearly indistinguishable.
- (ii)
- We extend the result (i) by showing that the generalized imbalance, i.e., the non-equal time and space density correlation function, also becomes nearly indistinguishable from the single-particle transition probabilities. Results (i) and (ii) give a recipe for experiments on how to measure the properties of survival and transition probabilities using one-body observables.
- (iii)
- We discuss the other experimentally relevant observables, i.e., the equal-time connected density–density correlation functions, which can be related to the one-particle density matrix observables. We showed that these observables have qualitative, but not quantitative, similarities with the survival and transition probabilities. Importantly, they also appear to exhibit the scale-invariant dynamics at localization transitions; thus, they constitute an alternative route for the experimental observation of critical dynamics.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
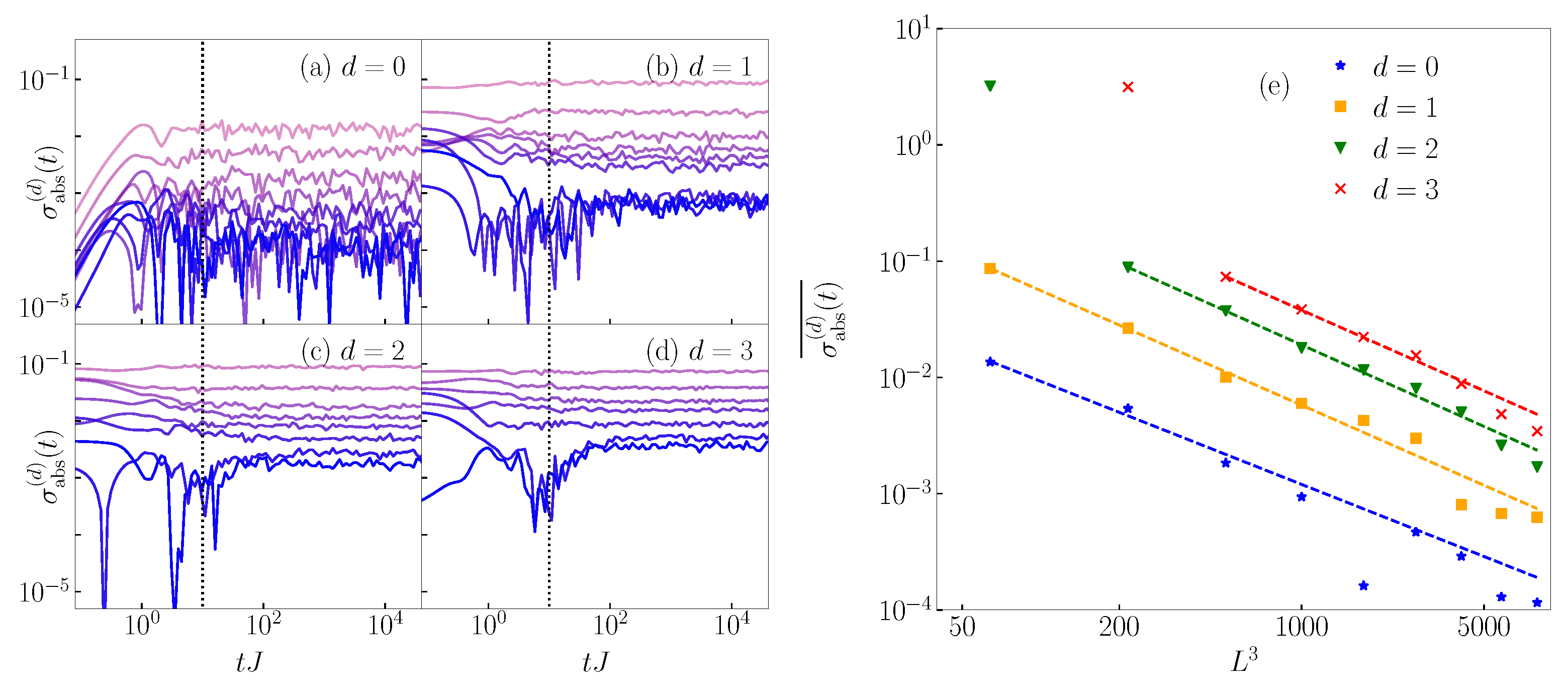
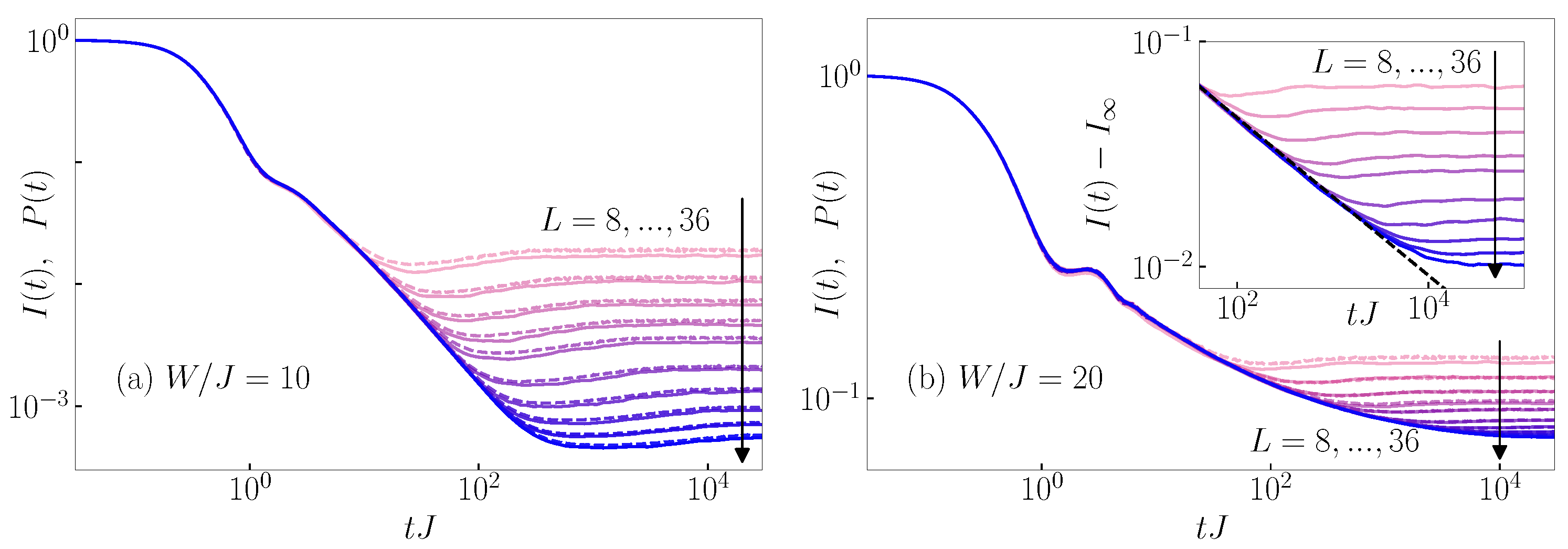
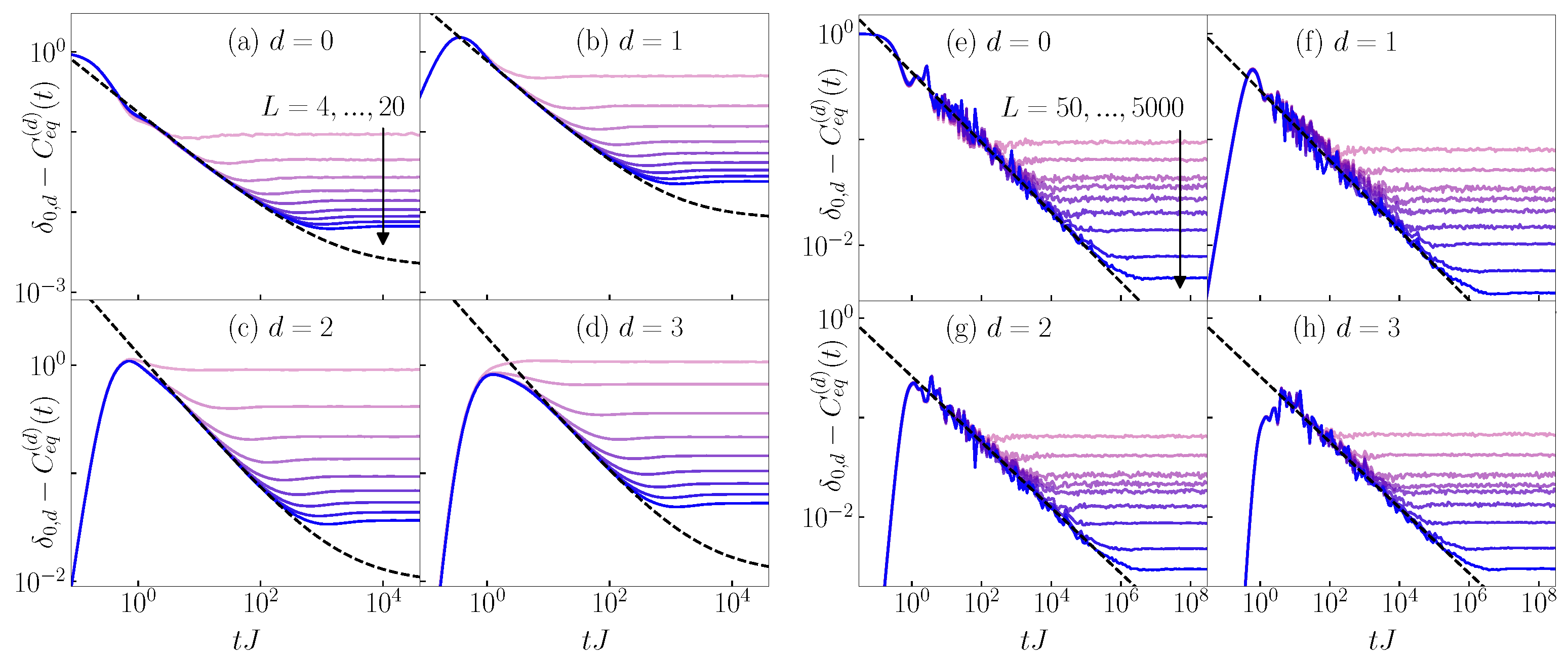
Appendix A. System Size Dependence of Differences between P(d) and C(d)

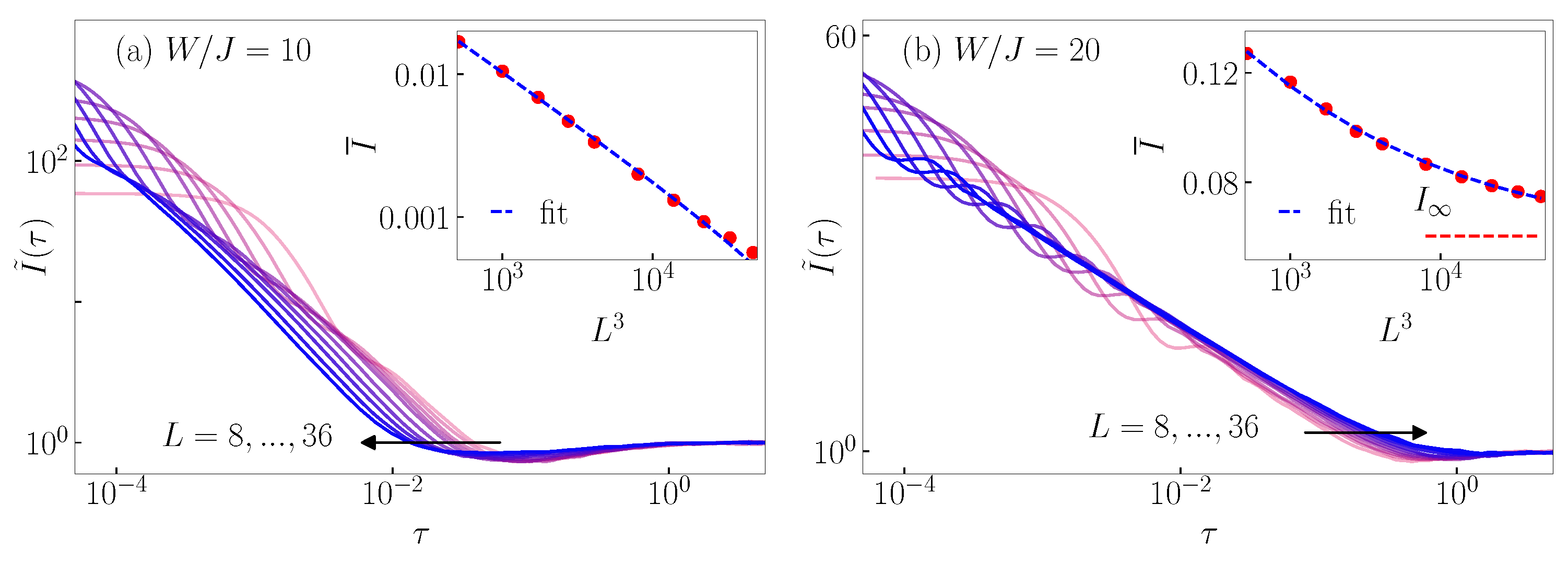
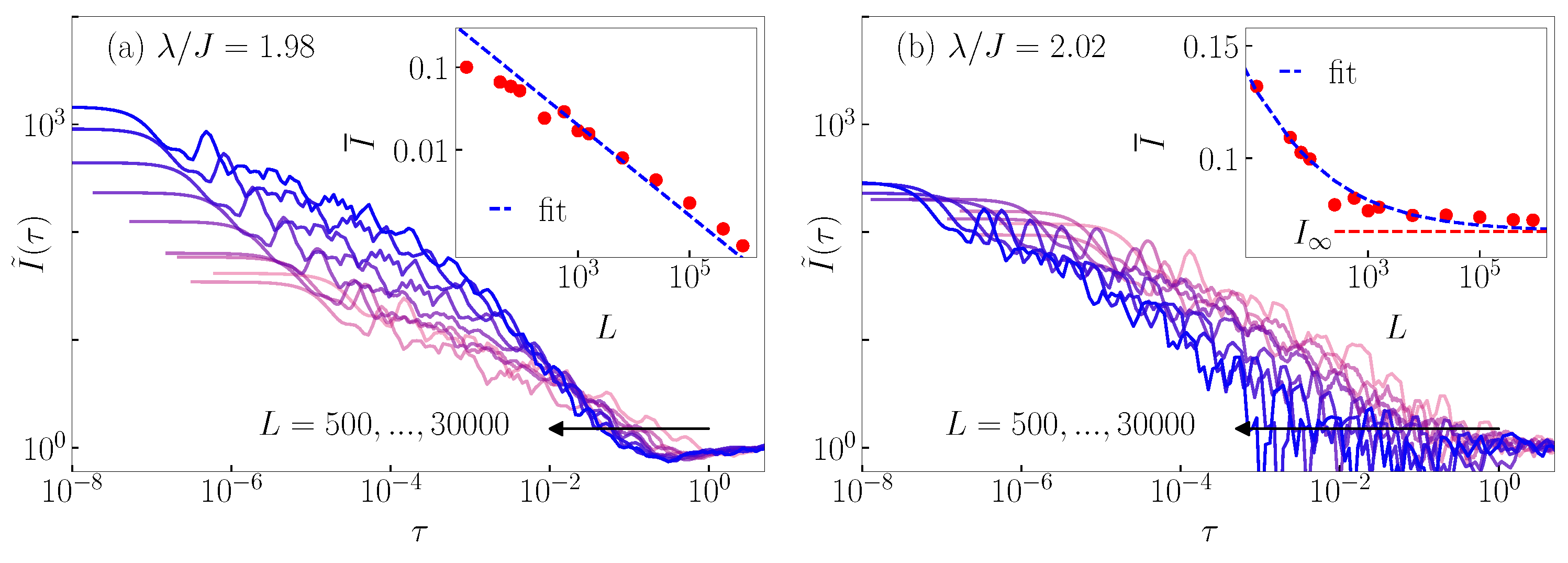
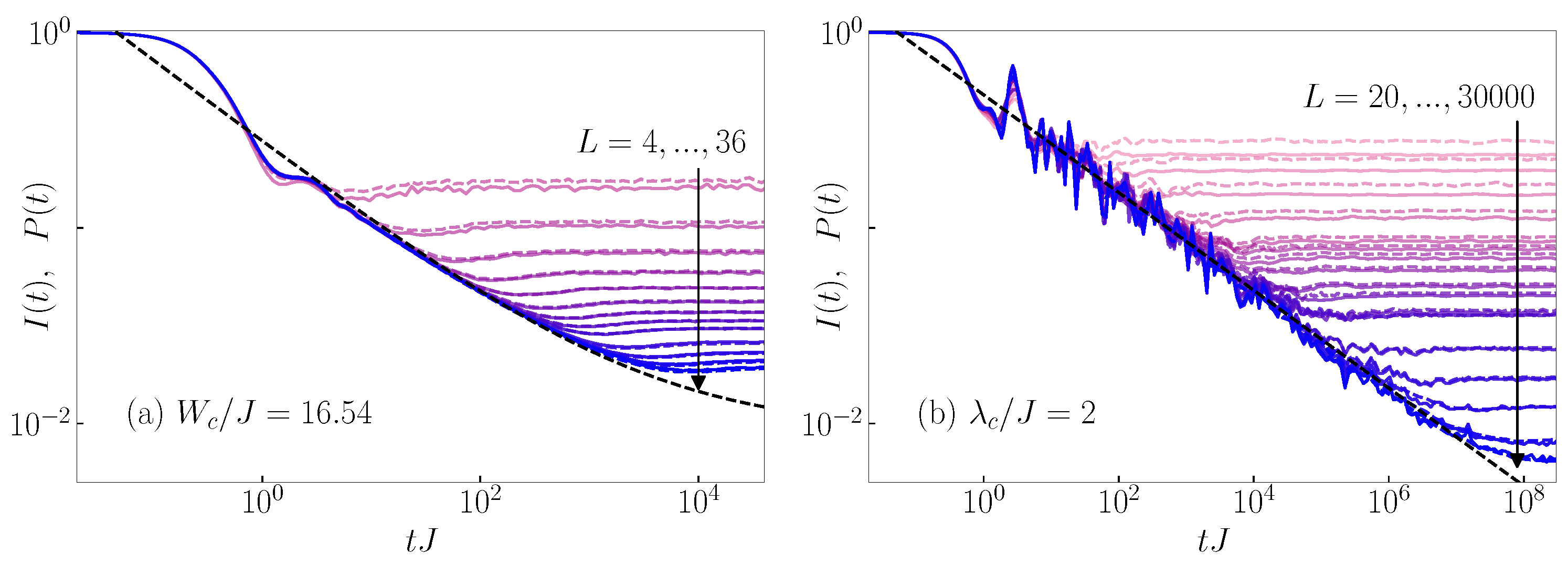
Appendix B. Rescaled Imbalance and Transition Probabilities: Scale-Invariant Dynamics at Eigenstate Transitions

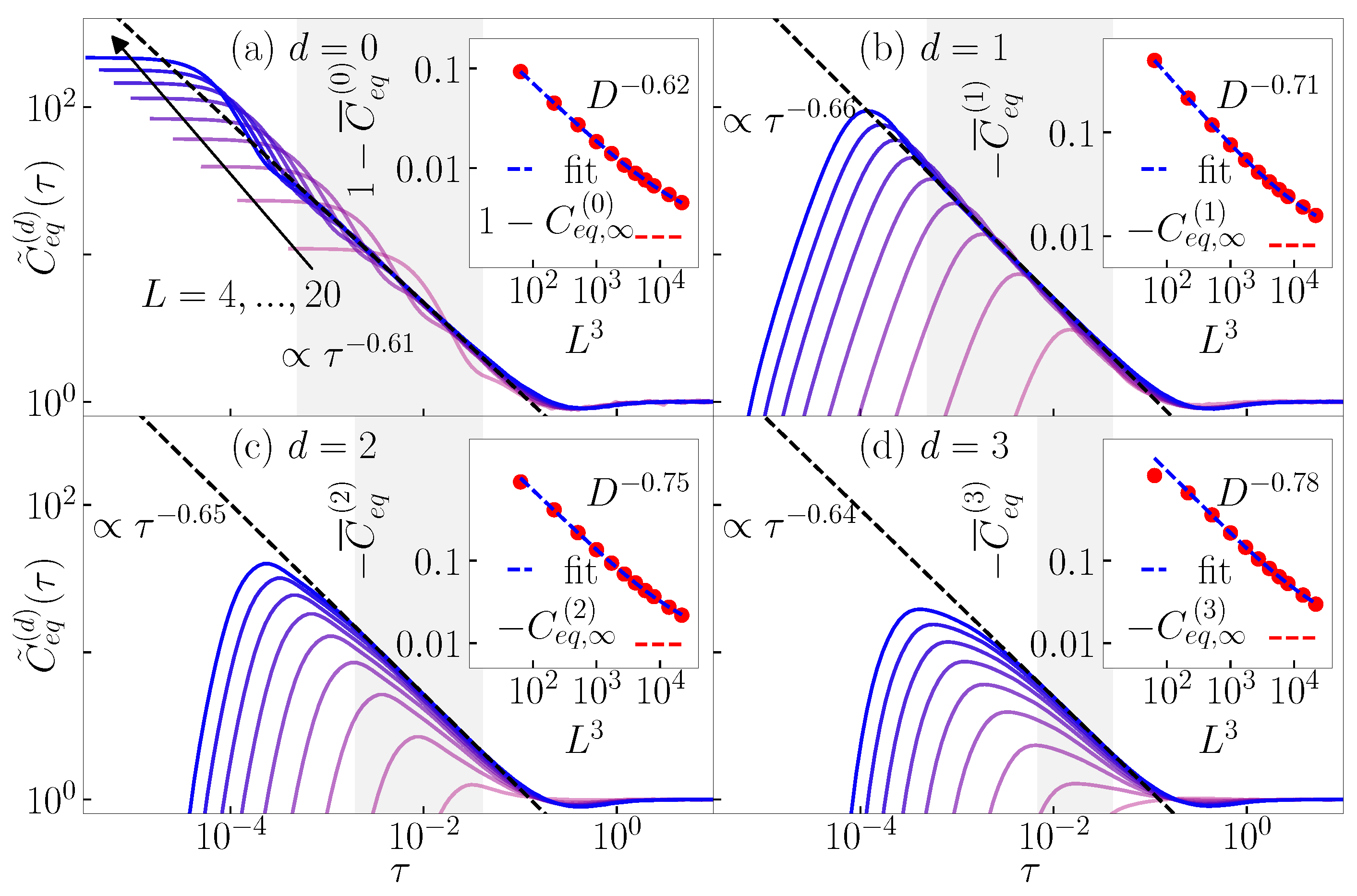
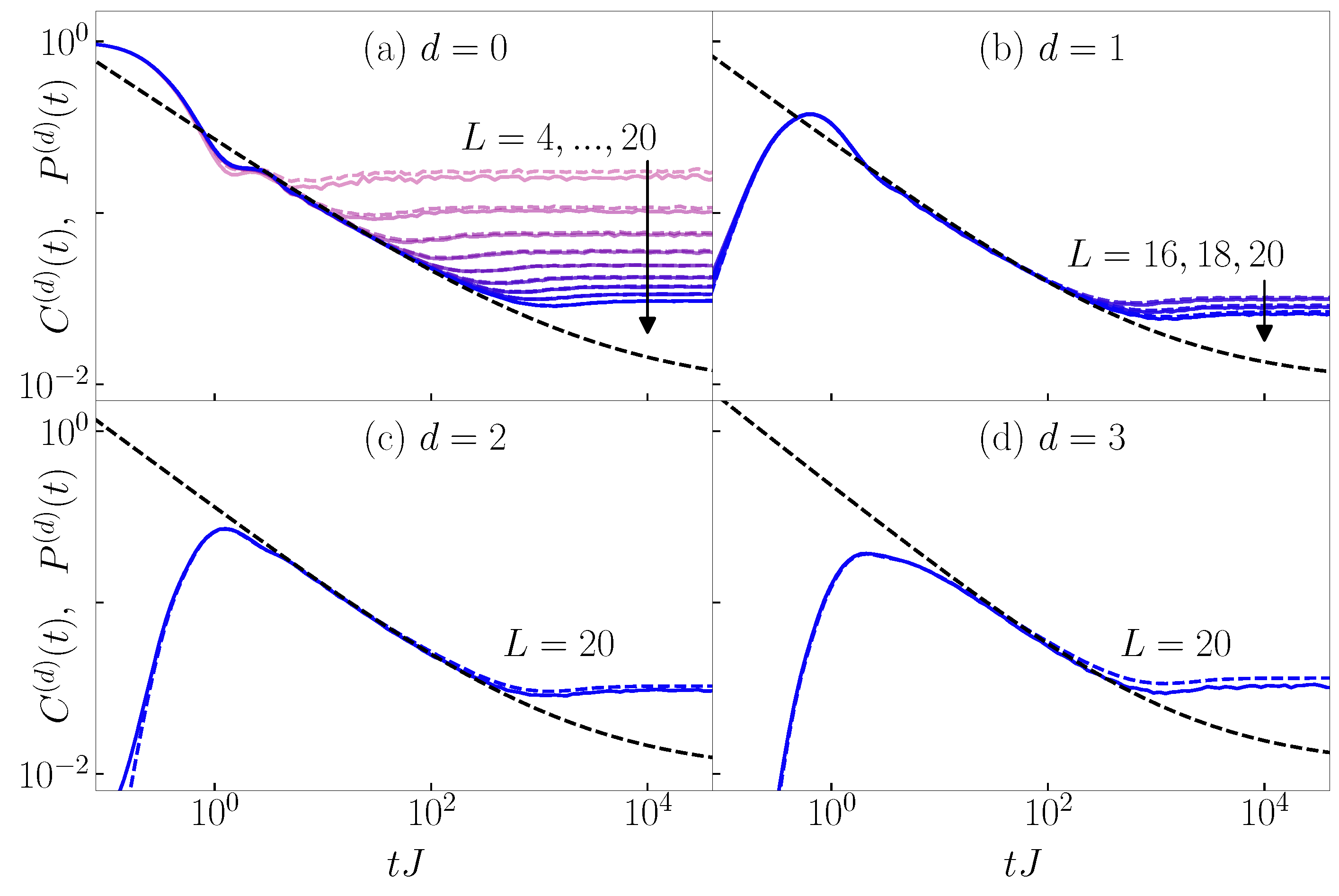
Appendix C. Equal-Time Connected Density–Density Correlation Functions: Scale-Invariant Dynamics at Eigenstate Transitions
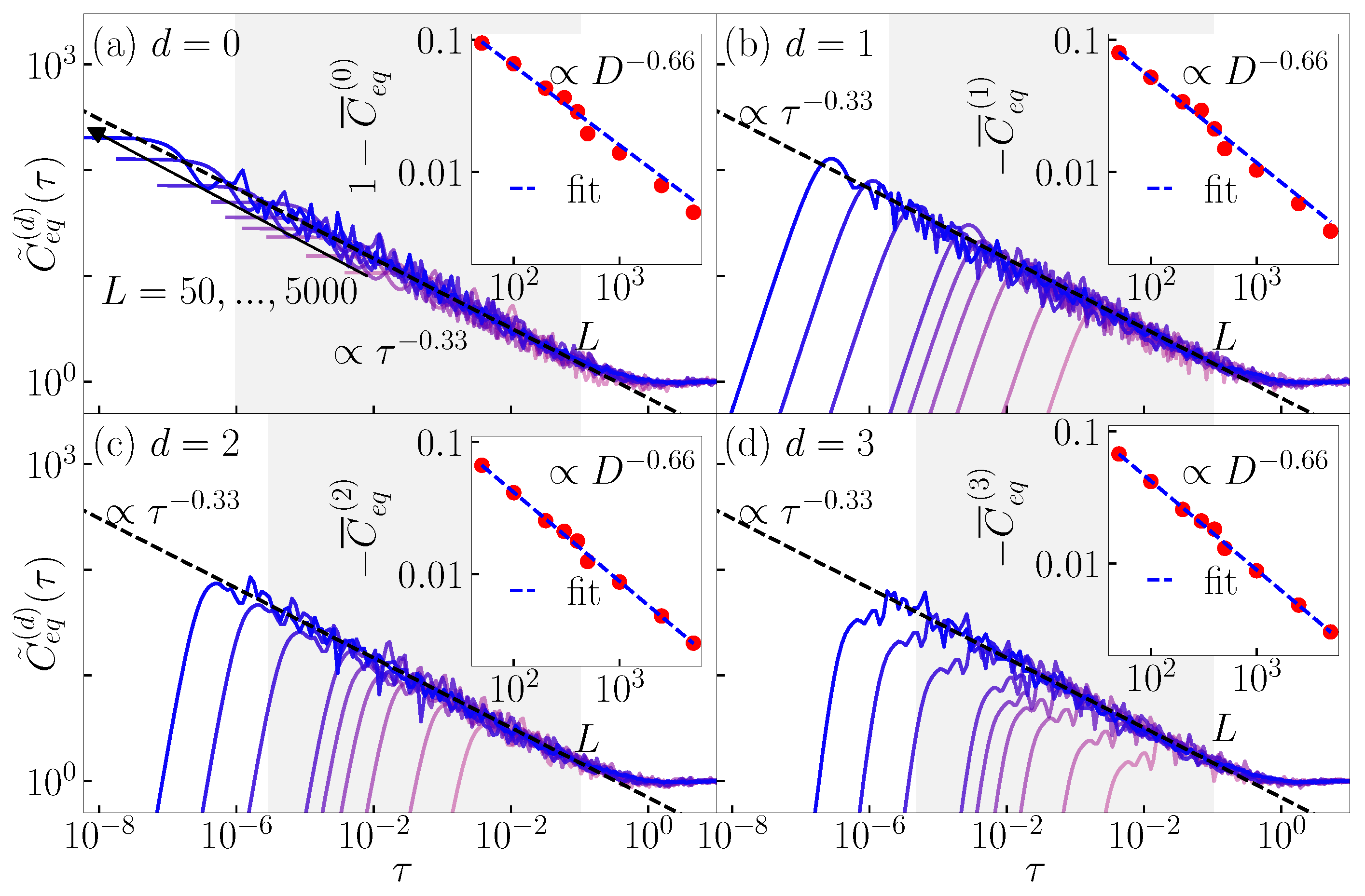
Appendix D. Connection to Fractal Dimension
References
- Ketzmerick, R.; Petschel, G.; Geisel, T. Slow decay of temporal correlations in quantum systems with Cantor spectra. Phys. Rev. Lett. 1992, 69, 695–698. [Google Scholar] [CrossRef] [PubMed]
- Huckestein, B.; Schweitzer, L. Relation between the correlation dimensions of multifractal wave functions and spectral measures in integer quantum Hall systems. Phys. Rev. Lett. 1994, 72, 713–716. [Google Scholar] [CrossRef] [PubMed]
- Schofield, S.A.; Wolynes, P.G.; Wyatt, R.E. Computational Study of Many-Dimensional Quantum Energy Flow: From Action Diffusion to Localization. Phys. Rev. Lett. 1995, 74, 3720–3723. [Google Scholar] [CrossRef] [PubMed]
- Schofield, S.A.; Wyatt, R.E.; Wolynes, P.G. Computational study of many-dimensional quantum vibrational energy redistribution. I. Statistics of the survival probability. J. Chem. Phys. 1996, 105, 940–952. [Google Scholar] [CrossRef]
- Brandes, T.; Huckestein, B.; Schweitzer, L. Critical dynamics and multifractal exponents at the Anderson transition in 3d disordered systems. Ann. Phys. 1996, 508, 633–651. [Google Scholar] [CrossRef]
- Ketzmerick, R.; Kruse, K.; Kraut, S.; Geisel, T. What Determines the Spreading of a Wave Packet? Phys. Rev. Lett. 1997, 79, 1959–1963. [Google Scholar] [CrossRef]
- Ohtsuki, T.; Kawarabayashi, T. Anomalous Diffusion at the Anderson Transitions. J. Phys. Soc. Jpn. 1997, 66, 314–317. [Google Scholar] [CrossRef]
- Gruebele, M. Intramolecular vibrational dephasing obeys a power law at intermediate times. Proc. Natl. Acad. Sci. USA 1998, 95, 5965–5970. [Google Scholar] [CrossRef]
- Ng, G.S.; Bodyfelt, J.; Kottos, T. Critical Fidelity at the Metal-Insulator Transition. Phys. Rev. Lett. 2006, 97, 256404. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Local quenches with global effects in interacting quantum systems. Phys. Rev. E 2014, 89, 062110. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Dynamics at the many-body localization transition. Phys. Rev. B 2015, 92, 014208. [Google Scholar] [CrossRef]
- Leitner, D.M. Quantum ergodicity and energy flow in molecules. Adv. Phys. 2015, 64, 445–517. [Google Scholar] [CrossRef]
- Santos, L.F.; Torres-Herrera, E.J. Analytical expressions for the evolution of many-body quantum systems quenched far from equilibrium. AIP Conf. Proc. 2017, 1912, 020015. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; García-García, A.M.; Santos, L.F. Generic dynamical features of quenched interacting quantum systems: Survival probability, density imbalance, and out-of-time-ordered correlator. Phys. Rev. B 2018, 97, 060303. [Google Scholar] [CrossRef]
- Bera, S.; De Tomasi, G.; Khaymovich, I.M.; Scardicchio, A. Return probability for the Anderson model on the random regular graph. Phys. Rev. B 2018, 98, 134205. [Google Scholar] [CrossRef]
- Prelovšek, P.; Barišić, O.S.; Mierzejewski, M. Reduced-basis approach to many-body localization. Phys. Rev. B 2018, 97, 035104. [Google Scholar] [CrossRef]
- Schiulaz, M.; Torres-Herrera, E.J.; Santos, L.F. Thouless and relaxation time scales in many-body quantum systems. Phys. Rev. B 2019, 99, 174313. [Google Scholar] [CrossRef]
- Karmakar, S.; Keshavamurthy, S. Intramolecular vibrational energy redistribution and the quantum ergodicity transition: A phase space perspective. Phys. Chem. Chem. Phys. 2020, 22, 11139–11173. [Google Scholar] [CrossRef] [PubMed]
- Lezama, T.L.M.; Torres-Herrera, E.J.; Pérez-Bernal, F.; Bar Lev, Y.; Santos, L.F. Equilibration time in many-body quantum systems. Phys. Rev. B 2021, 104, 085117. [Google Scholar] [CrossRef]
- Hopjan, M.; Vidmar, L. Scale-Invariant Survival Probability at Eigenstate Transitions. Phys. Rev. Lett. 2023, 131, 060404. [Google Scholar] [CrossRef]
- Hopjan, M.; Vidmar, L. Scale-invariant critical dynamics at eigenstate transitions. Phys. Rev. Res. 2023, 5, 043301. [Google Scholar] [CrossRef]
- Das, A.K.; Pinney, P.; Zarate-Herrada, D.A.; Pilatowsky-Cameo, S.; Matsoukas-Roubeas, A.S.; Cabral, D.G.A.; Cianci, C.; Batista, V.S.; del Campo, A.; Torres-Herrera, E.J.; et al. Proposal for many-body quantum chaos detection. arXiv 2024, arXiv:2401.01401. [Google Scholar]
- Jiricek, S.; Hopjan, M.; Łydżba, P.; Heidrich-Meisner, F.; Vidmar, L. Critical quantum dynamics of observables at eigenstate transitions. Phys. Rev. B 2024, 109, 205157. [Google Scholar] [CrossRef]
- Schreiber, M.; Hodgman, S.S.; Bordia, P.; Lüschen, H.P.; Fischer, M.H.; Vosk, R.; Altman, E.; Schneider, U.; Bloch, I. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 2015, 349, 842–845. [Google Scholar] [CrossRef]
- Choi, J.Y.; Hild, S.; Zeiher, J.; Schauß, P.; Rubio-Abadal, A.; Yefsah, T.; Khemani, V.; Huse, D.A.; Bloch, I.; Gross, C. Exploring the many-body localization transition in two dimensions. Science 2016, 352, 1547–1552. [Google Scholar] [CrossRef]
- Lüschen, H.P.; Bordia, P.; Scherg, S.; Alet, F.; Altman, E.; Schneider, U.; Bloch, I. Observation of Slow Dynamics near the Many-Body Localization Transition in One-Dimensional Quasiperiodic Systems. Phys. Rev. Lett. 2017, 119, 260401. [Google Scholar] [CrossRef]
- Bordia, P.; Lüschen, H.; Scherg, S.; Gopalakrishnan, S.; Knap, M.; Schneider, U.; Bloch, I. Probing Slow Relaxation and Many-Body Localization in Two-Dimensional Quasiperiodic Systems. Phys. Rev. X 2017, 7, 041047. [Google Scholar] [CrossRef]
- Kohlert, T.; Scherg, S.; Li, X.; Lüschen, H.P.; Das Sarma, S.; Bloch, I.; Aidelsburger, M. Observation of Many-Body Localization in a One-Dimensional System with a Single-Particle Mobility Edge. Phys. Rev. Lett. 2019, 122, 170403. [Google Scholar] [CrossRef]
- Rubio-Abadal, A.; Choi, J.Y.; Zeiher, J.; Hollerith, S.; Rui, J.; Bloch, I.; Gross, C. Many-Body Delocalization in the Presence of a Quantum Bath. Phys. Rev. X 2019, 9, 041014. [Google Scholar] [CrossRef]
- Guo, Q.; Cheng, C.; Sun, Z.H.; Song, Z.; Li, H.; Wang, Z.; Ren, W.; Dong, H.; Zheng, D.; Zhang, Y.R.; et al. Observation of energy-resolved many-body localization. Nat. Phys. 2021, 17, 234–239. [Google Scholar] [CrossRef]
- Pöpperl, P.; Gornyi, I.V.; Mirlin, A.D. Memory effects in the density-wave imbalance in delocalized disordered systems. Phys. Rev. B 2022, 106, 094201. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Abrahams, E.; Anderson, P.W.; Licciardello, D.C.; Ramakrishnan, T.V. Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions. Phys. Rev. Lett. 1979, 42, 673–676. [Google Scholar] [CrossRef]
- Evers, F.; Mirlin, A.D. Anderson transitions. Rev. Mod. Phys. 2008, 80, 1355–1417. [Google Scholar] [CrossRef]
- Aubry, S.; André, G. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Isr. Phys. Soc. 1980, 3, 18. [Google Scholar]
- Suslov, I. Anderson Localization in Incommensurate Systems. J. Exp. Theor. Phys. 1982, 56, 612. [Google Scholar]
- Kramer, B.; MacKinnon, A. Localization: Theory and experiment. Rep. Prog. Phys. 1993, 56, 1469–1564. [Google Scholar] [CrossRef]
- Brandes, T.; Kettemann, S. Anderson Localization and Its Ramifications: Disorder, Phase Coherence, and Electron Correlations; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Lagendijk, A.; Tiggelen, B.V.; Wiersma, D.S. Fifty years of Anderson localization. Phys. Today 2009, 62, 24–29. [Google Scholar] [CrossRef]
- Šuntajs, J.; Prosen, T.; Vidmar, L. Spectral properties of three-dimensional Anderson model. Ann. Phys. 2021, 435, 168469. [Google Scholar] [CrossRef]
- MacKinnon, A.; Kramer, B. One-Parameter Scaling of Localization Length and Conductance in Disordered Systems. Phys. Rev. Lett. 1981, 47, 1546–1549. [Google Scholar] [CrossRef]
- MacKinnon, A.; Kramer, B. The scaling theory of electrons in disordered solids: Additional numerical results. Z. Phys. B 1983, 53, 1–13. [Google Scholar] [CrossRef]
- Tarquini, E.; Biroli, G.; Tarzia, M. Critical properties of the Anderson localization transition and the high-dimensional limit. Phys. Rev. B 2017, 95, 094204. [Google Scholar] [CrossRef]
- Slevin, K.; Ohtsuki, T. Critical Exponent of the Anderson Transition Using Massively Parallel Supercomputing. J. Phys. Soc. Jpn. 2018, 87, 094703. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, D.; Hu, Y.; Guo, S.; Sirker, J. Entanglement dynamics in the three-dimensional Anderson model. Phys. Rev. B 2020, 102, 195132. [Google Scholar] [CrossRef]
- Prelovšek, P.; Herbrych, J. Diffusion in the Anderson model in higher dimensions. Phys. Rev. B 2021, 103, L241107. [Google Scholar] [CrossRef]
- Rodriguez, A.; Vasquez, L.J.; Römer, R.A. Multifractal Analysis with the Probability Density Function at the Three-Dimensional Anderson Transition. Phys. Rev. Lett. 2009, 102, 106406. [Google Scholar] [CrossRef]
- Rodriguez, A.; Vasquez, L.J.; Slevin, K.; Römer, R.A. Critical Parameters from a Generalized Multifractal Analysis at the Anderson Transition. Phys. Rev. Lett. 2010, 105, 046403. [Google Scholar] [CrossRef]
- Schubert, G.; Weiße, A.; Wellein, G.; Fehske, H. HQS@HPC: Comparative numerical study of Anderson localisation in disordered electron systems. In Proceedings of the High Performance Computing in Science and Engineering, Garching, Germany, 14–15 October 2004; Bode, A., Durst, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 237–249. [Google Scholar]
- Li, X.; Pixley, J.H.; Deng, D.L.; Ganeshan, S.; Das Sarma, S. Quantum nonergodicity and fermion localization in a system with a single-particle mobility edge. Phys. Rev. B 2016, 93, 184204. [Google Scholar] [CrossRef]
- Hopjan, M.; Orso, G.; Heidrich-Meisner, F. Detecting delocalization-localization transitions from full density distributions. Phys. Rev. B 2021, 104, 235112. [Google Scholar] [CrossRef]
- Bhakuni, D.S.; Lev, Y.B. Dynamic scaling relation in quantum many-body systems. Phys. Rev. B 2024, 110, 014203. [Google Scholar] [CrossRef]
- Domínguez-Castro, G.A.; Paredes, R. The Aubry–André model as a hobbyhorse for understanding the localization phenomenon. Eur. J. Phys. 2019, 40, 045403. [Google Scholar] [CrossRef]
- Kohmoto, M. Metal-Insulator Transition and Scaling for Incommensurate Systems. Phys. Rev. Lett. 1983, 51, 1198–1201. [Google Scholar] [CrossRef]
- Tang, C.; Kohmoto, M. Global scaling properties of the spectrum for a quasiperiodic schrödinger equation. Phys. Rev. B 1986, 34, 2041–2044. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B.; Tang, C. Critical wave functions and a Cantor-set spectrum of a one-dimensional quasicrystal model. Phys. Rev. B 1987, 35, 1020–1033. [Google Scholar] [CrossRef]
- Siebesma, A.P.; Pietronero, L. Multifractal Properties of Wave Functions for One-Dimensional Systems with an Incommensurate Potential. Europhys. Lett. 1987, 4, 597. [Google Scholar] [CrossRef]
- Hiramoto, H.; Kohmoto, M. Scaling analysis of quasiperiodic systems: Generalized Harper model. Phys. Rev. B 1989, 40, 8225–8234. [Google Scholar] [CrossRef]
- Hiramoto, H.; Kohmoto, M. Electronic spectral and wavefunction properties of one-dimensional quasiperiodic systems: A scaling approach. Int. J. Mod. Phys. B 1992, 6, 281–320. [Google Scholar] [CrossRef]
- Maciá, E. On the Nature of Electronic Wave Functions in One-Dimensional Self-Similar and Quasiperiodic Systems. ISRN Condens. Matter Phys. 2014, 2014, 165943. [Google Scholar] [CrossRef]
- Wu, A.K. Fractal Spectrum of the Aubry-André Model. arXiv 2021, arXiv:2109.07062. [Google Scholar]
- Geisel, T.; Ketzmerick, R.; Petschel, G. New class of level statistics in quantum systems with unbounded diffusion. Phys. Rev. Lett. 1991, 66, 1651–1654. [Google Scholar] [CrossRef]
- Harper, P.G. Single Band Motion of Conduction Electrons in a Uniform Magnetic Field. Proc. Phys. Soc. A 1955, 68, 874. [Google Scholar] [CrossRef]
- Lahini, Y.; Pugatch, R.; Pozzi, F.; Sorel, M.; Morandotti, R.; Davidson, N.; Silberberg, Y. Observation of a Localization Transition in Quasiperiodic Photonic Lattices. Phys. Rev. Lett. 2009, 103, 013901. [Google Scholar] [CrossRef] [PubMed]
- Roati, G.; D’Errico, C.; Fallani, L.; Fattori, M.; Fort, C.; Zaccanti, M.; Modugno, G.; Modugno, M.; Inguscio, M. Anderson localization of a non-interacting Bose–Einstein condensate. Nature 2008, 453, 895–898. [Google Scholar] [CrossRef] [PubMed]
- Lüschen, H.P.; Scherg, S.; Kohlert, T.; Schreiber, M.; Bordia, P.; Li, X.; Das Sarma, S.; Bloch, I. Single-Particle Mobility Edge in a One-Dimensional Quasiperiodic Optical Lattice. Phys. Rev. Lett. 2018, 120, 160404. [Google Scholar] [CrossRef] [PubMed]
- De Tomasi, G.; Khaymovich, I.M.; Pollmann, F.; Warzel, S. Rare thermal bubbles at the many-body localization transition from the Fock space point of view. Phys. Rev. B 2021, 104, 024202. [Google Scholar] [CrossRef]
- Roy, N.; Sharma, A. Entanglement entropy and out-of-time-order correlator in the long-range Aubry–André–Harper model. J. Phys. Condens. Matter 2021, 33, 334001. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Roy, N.; Sharma, A. Dynamics of spectral correlations in the entanglement Hamiltonian of the Aubry-André-Harper model. Phys. Rev. B 2021, 104, 155137. [Google Scholar] [CrossRef]
- Aditya, S.; Roy, N. Family-Vicsek dynamical scaling and Kardar-Parisi-Zhang-like superdiffusive growth of surface roughness in a driven one-dimensional quasiperiodic model. Phys. Rev. B 2024, 109, 035164. [Google Scholar] [CrossRef]
- Richerme, P.; Gong, Z.X.; Lee, A.; Senko, C.; Smith, J.; Foss-Feig, M.; Michalakis, S.; Gorshkov, A.V.; Monroe, C. Non-local propagation of correlations in quantum systems with long-range interactions. Nature 2014, 511, 198–201. [Google Scholar] [CrossRef]
- Colmenarez, L.; McClarty, P.A.; Haque, M.; Luitz, D.J. Statistics of correlation functions in the random Heisenberg chain. SciPost Phys. 2019, 7, 064. [Google Scholar] [CrossRef]
- Lezama, T.L.M.; Lev, Y.B.; Santos, L.F. Temporal fluctuations of correlators in integrable and chaotic quantum systems. SciPost Phys. 2023, 15, 244. [Google Scholar] [CrossRef]
- Colbois, J.; Alet, F.; Laflorencie, N. Interaction-Driven Instabilities in the Random-Field XXZ Chain. arXiv 2024, arXiv:2403.09608. [Google Scholar]
- Available online: www.hpc-rivr.si (accessed on 31 May 2024).
- Available online: https://eurohpc-ju.europa.eu/ (accessed on 31 May 2024).
- Available online: www.izum.si (accessed on 31 May 2024).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hopjan, M.; Vidmar, L. Survival Probability, Particle Imbalance, and Their Relationship in Quadratic Models. Entropy 2024, 26, 656. https://doi.org/10.3390/e26080656
Hopjan M, Vidmar L. Survival Probability, Particle Imbalance, and Their Relationship in Quadratic Models. Entropy. 2024; 26(8):656. https://doi.org/10.3390/e26080656
Chicago/Turabian StyleHopjan, Miroslav, and Lev Vidmar. 2024. "Survival Probability, Particle Imbalance, and Their Relationship in Quadratic Models" Entropy 26, no. 8: 656. https://doi.org/10.3390/e26080656




