Fractional Telegrapher’s Equation under Resetting: Non-Equilibrium Stationary States and First-Passage Times
Abstract
1. Introduction
2. FTE-I under Resetting
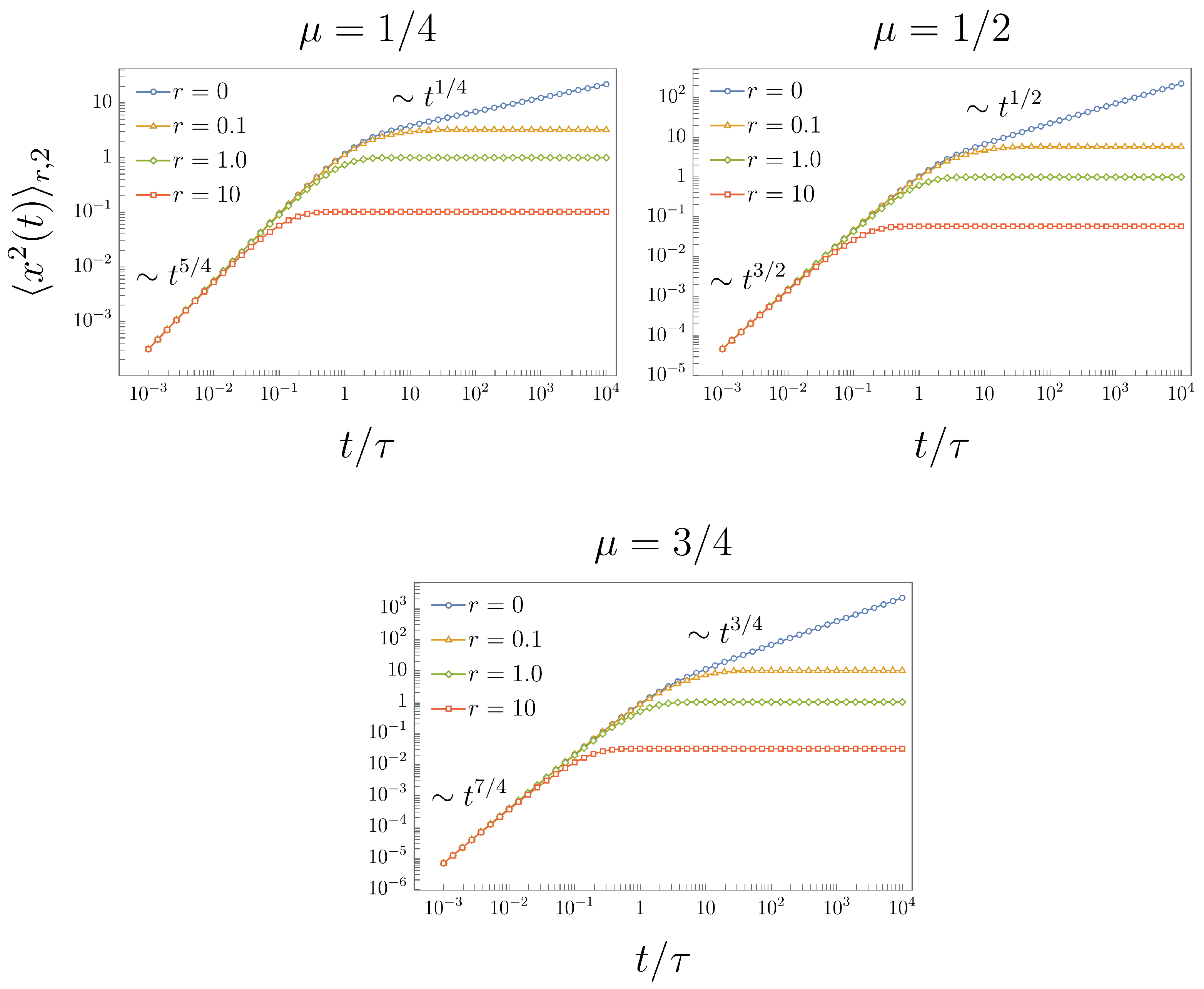
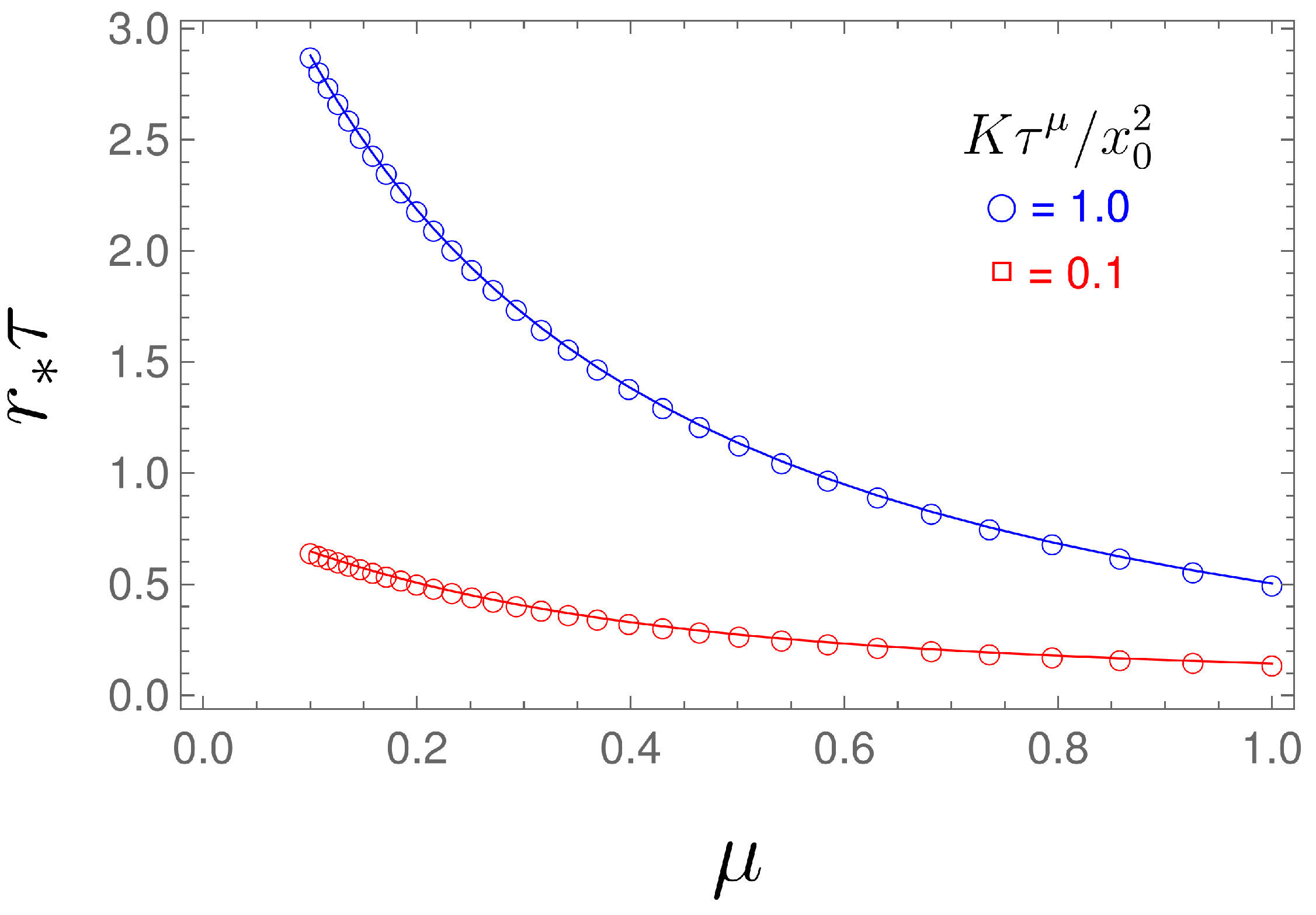
2.1. Resetting of FTE-I—The First Possibility
2.2. Resetting of FTE-I—The Second Possibility
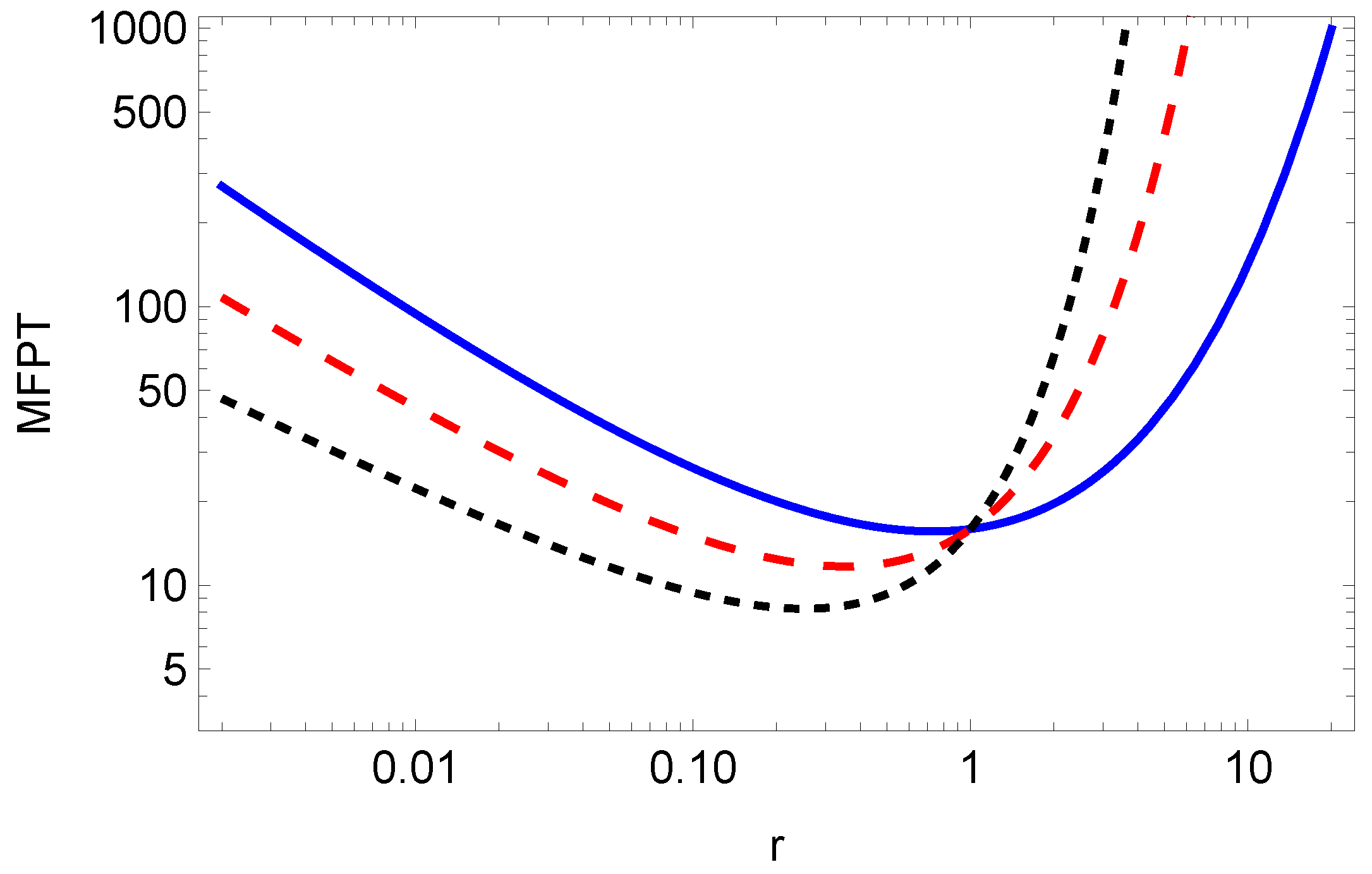
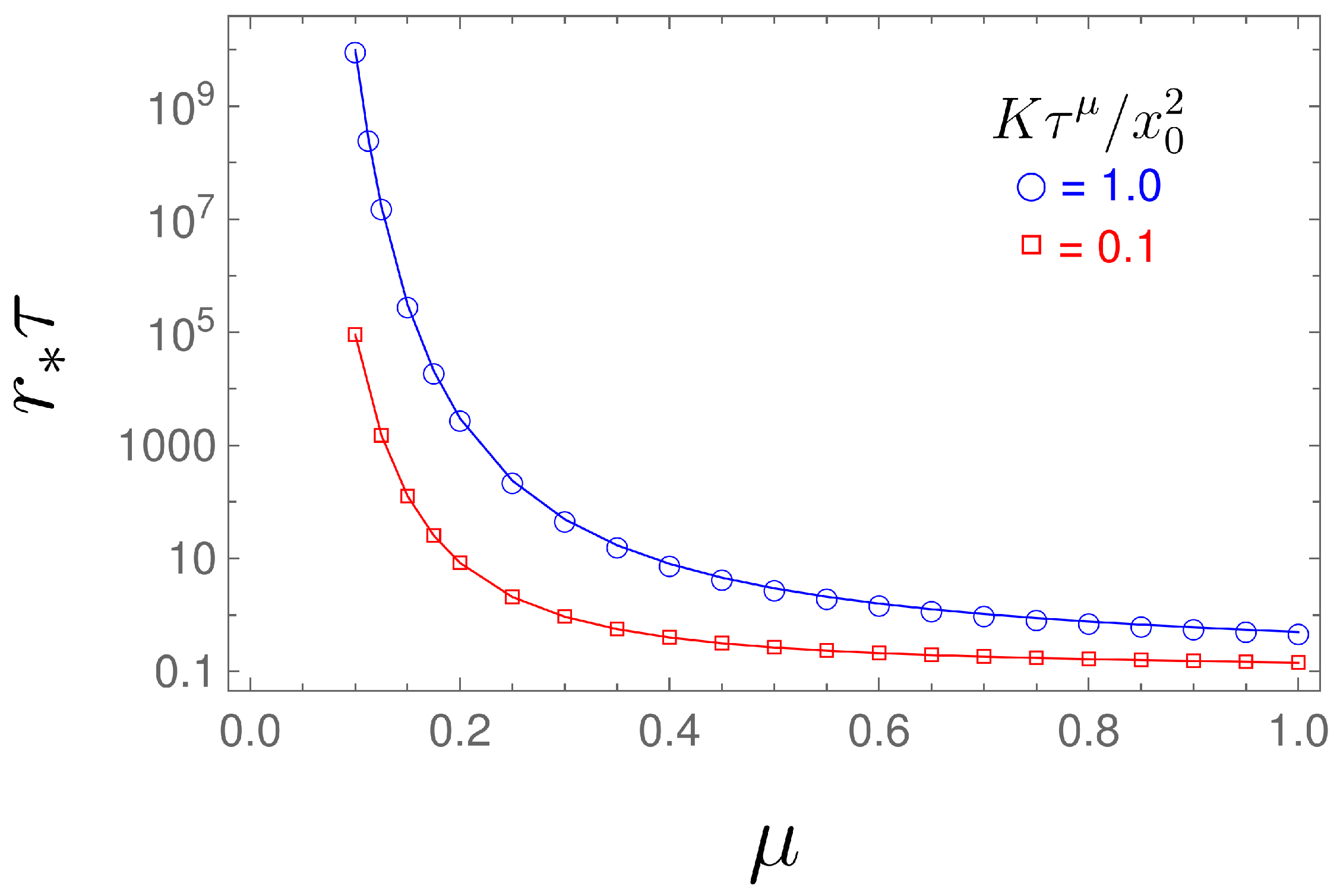
2.3. First-Passage Time Problem
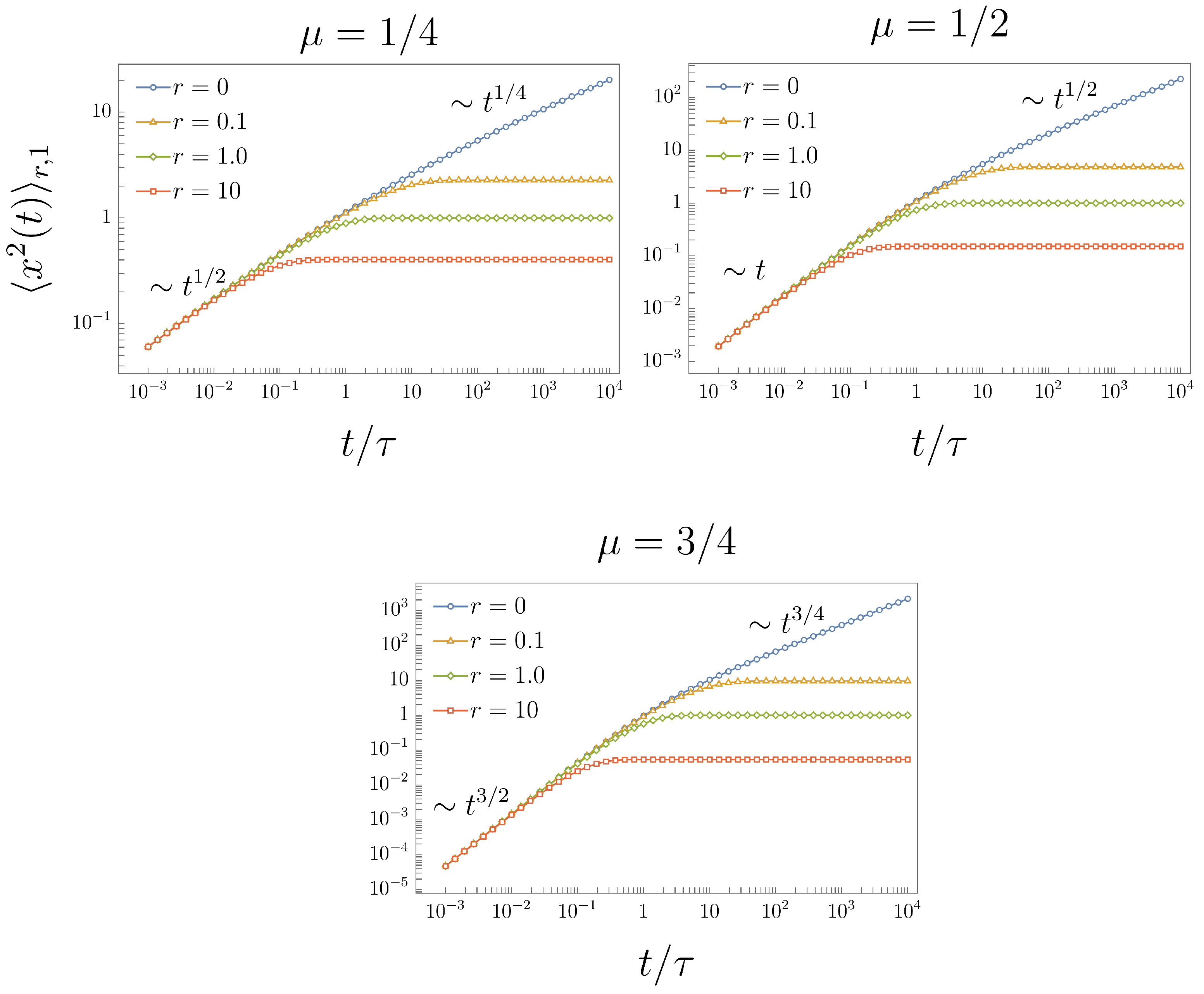
3. FTE-II under Resetting
First-Passage Time Problem
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TE | Telegrapher’s Equation |
| FTE | Fractional Telegrapher’s Equation |
| MSD | Mean Squared Displacement |
| MFPT | Mean First-Passage Time |
Appendix A. Fractional Calculus and Mittag–Leffler Functions
Appendix B. Completely Monotone and Bernstein Functions
Appendix C. Efros Theorem
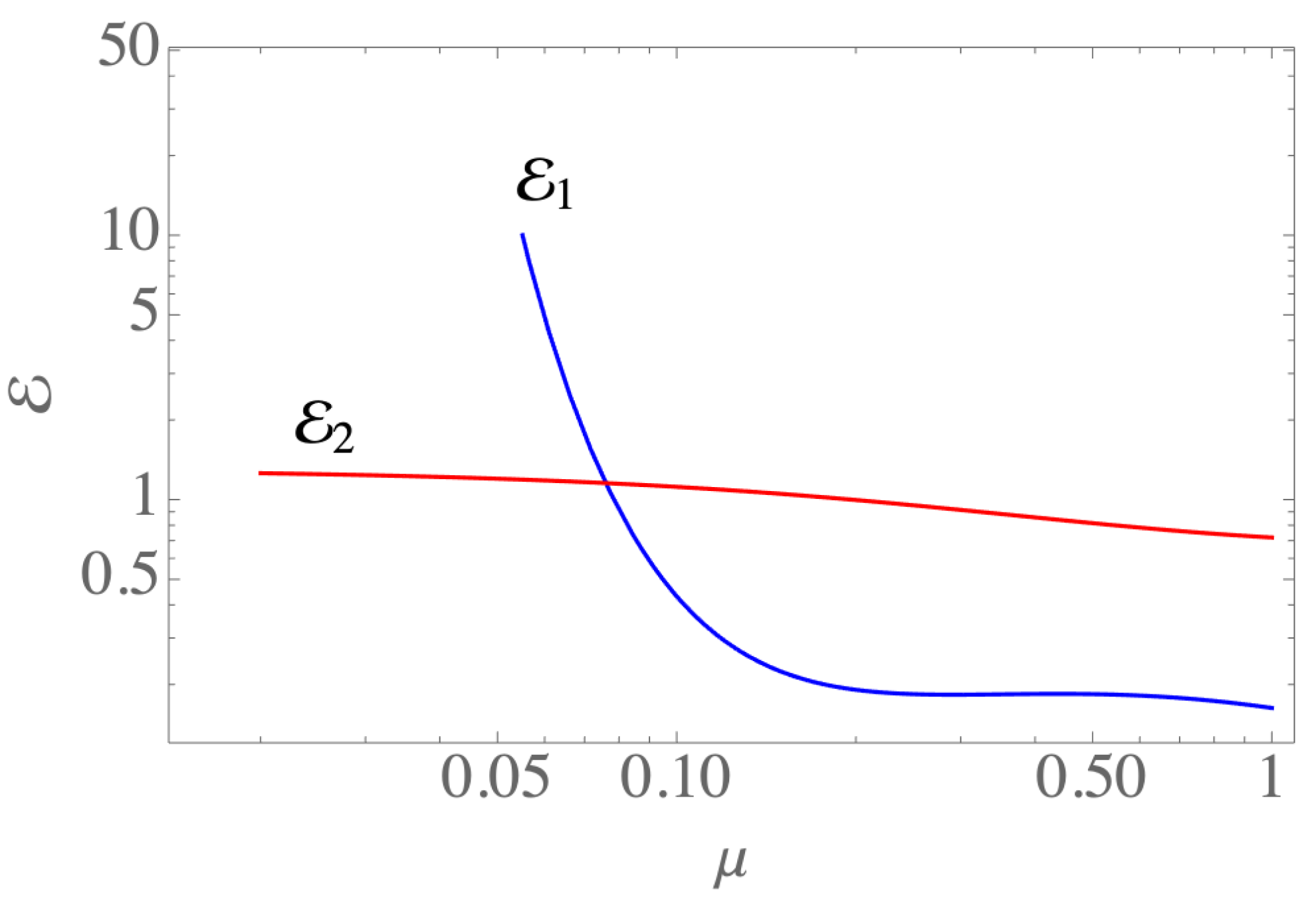
Appendix D. Derivation of the Efficiencies and
References
- Heaviside, O. On induction between parallel wires. J. Soc. Telegr. Eng. 1880, 9, 427–458. [Google Scholar] [CrossRef]
- Cattaneo, C.R. Sulla conduzione del calore. Atti. Sem. Mat. Fis. Univ. Modena 1948, 3, 83. [Google Scholar]
- Cattaneo, C.R. Sur une forme de l’equation de la chaleur eliminant le paradoxe d’une propagation instantanee’. C. R. Acad. Sci. Paris 1958, 247, 431. [Google Scholar]
- Vernotte, P. Les paradoxes de la théories continue de l’equation de la chaleur. C. R. Acad. Sci. Paris 1958, 246, 3154–3155. [Google Scholar]
- Górska, K.; Horzela, A.; Lenzi, E.K.; Pagnini, G.; Sandev, T. Generalized Cattaneo (telegrapher’s) equations in modeling anomalous diffusion phenomena. Phys. Rev. E 2020, 102, 022128. [Google Scholar] [CrossRef] [PubMed]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill Book Co.: New York, NY, USA, 1941. [Google Scholar]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill Book Co.: New York, NY, USA, 1953. [Google Scholar]
- Masoliver, J. Telegraphic processes with stochastic resetting. Phys. Rev. E 2019, 99, 012121. [Google Scholar] [CrossRef] [PubMed]
- Masoliver, J.; Weiss, G.H. Finite-velocity diffusion. Eur. J. Phys. 1996, 17, 190. [Google Scholar] [CrossRef]
- Masoliver, J.; Lindenberg, K. Continuous time persistent random walk: A review and some generalizations. Eur. J. Phys. B 2017, 90, 107. [Google Scholar] [CrossRef]
- Kac, M. A stochastic model related to the telegrapher’s equation. Rocky Mt. J. Math. 1974, 4, 497. [Google Scholar] [CrossRef]
- Weiss, G.H. Some applications of persistent random walks and the telegrapher’s equation. Phys. A 2002, 311, 381. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A. Subordination and memory dependent kinetics in diffusion and relaxation phenomena. Fract. Calc. Appl. Anal. 2023, 26, 480. [Google Scholar] [CrossRef]
- Górska, K. Integral decomposition for the solutions of the generalized Cattaneo equation. Phys. Rev. E 2021, 104, 024113. [Google Scholar] [CrossRef] [PubMed]
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A Math. Gen. 1997, 30, 7277–7289. [Google Scholar] [CrossRef]
- Kosztołowicz, T. Cattaneo-type subdiffusion-reaction equation. Phys. Rev. E 2014, 90, 042151. [Google Scholar] [CrossRef] [PubMed]
- D’Ovidio, M.; Polito, F. Fractional Diffusion—Telegraph Equations and Their Associated Stochastic Solutions. Theory Probab. Appl. 2018, 62, 552–574. [Google Scholar] [CrossRef]
- Awad, E.; Metzler, R. Crossover dynamics from superdiffusion to subdiffusion: Models and solutions. Fract. Calc. Appl. Anal. 2020, 23, 55–102. [Google Scholar] [CrossRef]
- Michelitsch, T.M.; Polito, F.; Riascos, A.P. Squirrels can remember little: A random walk with jump reversals induced by a discrete-time renewal process. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107031. [Google Scholar] [CrossRef]
- Cáceres, M.O. Finite-velocity diffusion in random media. J. Stat. Phys. 2020, 179, 729–747. [Google Scholar] [CrossRef]
- Cáceres, M.O. Localization of plane waves in the stochastic telegrapher’s equation. Phys. Rev. E 2022, 105, 014110. [Google Scholar] [CrossRef]
- Cáceres, M.O.; Nizama, M. Stochastic telegrapher’s approach for solving the random Boltzmann-Lorentz gas. Phys. Rev. E 2022, 105, 044131. [Google Scholar] [CrossRef]
- Stadje, W.; Zacks, S. Telegraph processes with random velocities. J. Appl. Probab. 2004, 41, 665–678. [Google Scholar] [CrossRef]
- Masó-Puigdellosas, A.; Campos, D.; Méndez, V. Transport properties and first-arrival statistics of random motion with stochastic reset times. Phys. Rev. E 2019, 99, 012141. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.R.; Majumdar, S.N. Diffusion with resetting in arbitrary spatial dimension. J. Phys. A Math. Theor. 2014, 47, 285001. [Google Scholar] [CrossRef]
- Bodrova, A.S.; Chechkin, A.V.; Sokolov, I.M. Scaled Brownian motion with renewal resetting. Phys. Rev. E 2019, 100, 012120. [Google Scholar] [CrossRef] [PubMed]
- Tal-Friedman, O.; Pal, A.; Sekhon, A.; Reuveni, S.; Roichman, Y. Experimental realization of diffusion with stochastic resetting. J. Phys. Chem. Lett. 2020, 11, 7350–7355. [Google Scholar] [CrossRef] [PubMed]
- Besga, B.; Bovon, A.; Petrosyan, A.; Majumdar, S.N.; Ciliberto, S. Optimal mean first-passage time for a Brownian searcher subjected to resetting: Experimental and theoretical results. Phys. Rev. Res. 2020, 2, 032029. [Google Scholar] [CrossRef]
- Schilling, R.L.; Song, R.; Vondraček, Z. Bernstein Functions: Theory and Applications; Walter de Gruyter: Berlin, Germany, 2009. [Google Scholar]
- Masoliver, J.; Montero, M. Anomalous diffusion under stochastic resettings: A general approach. Phys. Rev. E 2019, 100, 042103. [Google Scholar] [CrossRef] [PubMed]
- Kuśmierz, Ł.; Gudowska-Nowak, E. Subdiffusive continuous-time random walks with stochastic resetting. Phys. Rev. E 2019, 99, 052116. [Google Scholar] [CrossRef] [PubMed]
- Stanislavsky, A.; Weron, A. Optimal non-Gaussian search with stochastic resetting. Phys. Rev. E 2021, 104, 014125. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.K.; Gorska, K.; Sandev, T. General approach to stochastic resetting. Phys. Rev. E 2022, 105, 064133. [Google Scholar] [CrossRef] [PubMed]
- Pollard, H. The representation of e−xλ as a Laplace integral. Bull. Am. Math. Soc. 1946, 52, 908. [Google Scholar] [CrossRef]
- Hilfer, R. H-function representations for stretched exponential relaxation and non-Debye susceptibilities in glassy systems. Phys. Rev. E 2002, 65, 061510. [Google Scholar] [CrossRef] [PubMed]
- Penson, K.A.; Górska, K. Exact and Explicit Probability Densities for One-Sided Lévy Stable Distributions. Phys. Rev. Lett. 2010, 105, 210604. [Google Scholar] [CrossRef] [PubMed]
- Fogedby, H.C. Langevin equations for continuous time Lévy flights. Phys. Rev. E 1994, 50, 1657. [Google Scholar] [CrossRef] [PubMed]
- Baule, A.; Friedrich, R. Joint probability distributions for a class of non-Markovian processes. Phys. Rev. E 2005, 71, 026101. [Google Scholar] [CrossRef] [PubMed]
- Chechkin, A.V.; Hofmann, M.; Sokolov, I.M. Continuous-time random walk with correlated waiting times. Phys. Rev. E 2009, 80, 031112. [Google Scholar] [CrossRef] [PubMed]
- Redner, S. A Guide to First-Passage Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Bray, A.J.; Majumdar, S.N.; Schehr, G. Persistence and first-passage properties in nonequilibrium systems. Adv. Phys. 2013, 62, 225–361. [Google Scholar] [CrossRef]
- Pal, A.; Kundu, A.; Evans, M.R. Diffusion under time-dependent resetting. J. Phys. A Math. Theor. 2016, 49, 225001. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Chechkin, A.V.; Metzler, R. Space-fractional Fokker–Planck equation and optimization of random search processes in the presence of an external bias. J. Stat. Mech. 2014, 2014, P11031. [Google Scholar] [CrossRef]
- Pal, A.; Stojkoski, V.; Sandev, T. Random resetting in search problems. arXiv 2023, arXiv:2310.12057. [Google Scholar]
- Sandev, T.; Kocarev, L.; Metzler, R.; Chechkin, A. Stochastic dynamics with multiplicative dichotomic noise: Heterogeneous telegrapher’s equation, anomalous crossovers and resetting. Chaos Solitons Fractals 2022, 165, 112878. [Google Scholar] [CrossRef]
- Shkilev, V. Continuous-time random walk under time-dependent resetting. Phys. Rev. E 2017, 96, 012126. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.E.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [PubMed]
- Kochubei, A.N. General Fractional Calculus, Evolution Equations, and Renewal Processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Bodrova, A.S.; Sokolov, I.M. Resetting processes with noninstantaneous return. Phys. Rev. E 2020, 101, 052130. [Google Scholar] [CrossRef]
- Tucci, G.; Gambassi, A.; Majumdar, S.N.; Schehr, G. First-passage time of run-and-tumble particles with noninstantaneous resetting. Phys. Rev. E 2022, 106, 044127. [Google Scholar] [CrossRef] [PubMed]
- Radice, M. One-dimensional telegraphic process with noninstantaneous stochastic resetting. Phys. Rev. E 2021, 104, 044126. [Google Scholar] [CrossRef] [PubMed]
- Tal-Friedman, O.; Roichman, Y.; Reuveni, S. Diffusion with partial resetting. Phys. Rev. E 2022, 106, 054116. [Google Scholar] [CrossRef]
- Di Bello, C.; Chechkin, A.V.; Hartmann, A.K.; Palmowski, Z.; Metzler, R. Time-dependent probability density function for partial resetting dynamics. New J. Phys. 2023, 25, 082002. [Google Scholar] [CrossRef]
- Christou, C.; Schadschneider, A. Diffusion with resetting in bounded domains. J. Phys. A Math. Theor. 2015, 48, 285003. [Google Scholar] [CrossRef]
- Pal, A.; Prasad, V. First passage under stochastic resetting in an interval. Phys. Rev. E 2019, 99, 032123. [Google Scholar] [CrossRef] [PubMed]
- Tucci, G.; Gambassi, A.; Gupta, S.; Roldán, É. Controlling particle currents with evaporation and resetting from an interval. Phys. Rev. Res. 2020, 2, 043138. [Google Scholar] [CrossRef]
- Julián-Salgado, P.; Dagdug, L.; Boyer, D. Diffusion with two resetting points. Phys. Rev. E 2024, 109, 024134. [Google Scholar] [CrossRef] [PubMed]
- Mendez, V.; Flaquer-Galmés, R.; Campos, D. First-passage time of a Brownian searcher with stochastic resetting to random positions. Phys. Rev. E 2024, 109, 044134. [Google Scholar] [CrossRef] [PubMed]
- Cáceres, M.O.; Nizama, M.; Pennini, F. Fisher and Shannon Functionals for Hyperbolic Diffusion. Entropy 2023, 25, 1627. [Google Scholar] [CrossRef] [PubMed]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7. [Google Scholar]
- Efros, A.M. The application of the operational calculus to the analysis. in Russian. Mat. Sborni 1935, 42, 699. [Google Scholar]
- Włodarski, L. Sur une formule de Efros. Stud. Math. 1952, 13, 183. [Google Scholar] [CrossRef]
- Graf, U. Applied Laplace Transforms and z-Transforms for Sciences and Engineers; Birkhäuser: Basel, Switzerland, 2004. [Google Scholar]
- Górska, K.; Penson, K.A. Lévy stable distributions via associated integral transform. J. Math. Phys. 2012, 53, 053302. [Google Scholar] [CrossRef]
- Apelblat, A.; Mainardi, F. Application of the Efros theorem to the function represented by the inverse Laplace transform of s−μexp(-sν). Symmetry 2021, 13, 354. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series. Direct Laplace Transforms; Gordon and Breach: London, UK, 1992; Volume 4. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series. Special Functions; Taylor & Francis: Abingdon, UK, 1998; Volume 2. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series. More Special Functions; Gordon and Breach: London, UK, 1990; Volume 3. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Górska, K.; Sevilla, F.J.; Chacón-Acosta, G.; Sandev, T. Fractional Telegrapher’s Equation under Resetting: Non-Equilibrium Stationary States and First-Passage Times. Entropy 2024, 26, 665. https://doi.org/10.3390/e26080665
Górska K, Sevilla FJ, Chacón-Acosta G, Sandev T. Fractional Telegrapher’s Equation under Resetting: Non-Equilibrium Stationary States and First-Passage Times. Entropy. 2024; 26(8):665. https://doi.org/10.3390/e26080665
Chicago/Turabian StyleGórska, Katarzyna, Francisco J. Sevilla, Guillermo Chacón-Acosta, and Trifce Sandev. 2024. "Fractional Telegrapher’s Equation under Resetting: Non-Equilibrium Stationary States and First-Passage Times" Entropy 26, no. 8: 665. https://doi.org/10.3390/e26080665
APA StyleGórska, K., Sevilla, F. J., Chacón-Acosta, G., & Sandev, T. (2024). Fractional Telegrapher’s Equation under Resetting: Non-Equilibrium Stationary States and First-Passage Times. Entropy, 26(8), 665. https://doi.org/10.3390/e26080665