Free Energy Evaluation of Cavity Formation in Metastable Liquid Based on Stochastic Thermodynamics
Abstract
1. Introduction
2. Stochastic Thermodynamics: Theoretical Background
3. System and Method
3.1. Simulation System and Procedure
- Liquid in equilibrium at given temperature and pressure is prepared using a standard procedure of MD simulation.
- A spherical force field at the center of the system box is applied for all LJ particles, and the system is equilibrated again at . We assume an LJ-type field aswhere is the distance of each particle from the box center. The field is also truncated at .
- For the main simulation, the radius of the force field is increased and the resulting “bubble” growth is monitored.where is a time-dependent variable corresponding to the bubble radius, where the bubble is the region of excluding LJ particles. In this paper, we simply adopted with a size linearly increasing with time,where is a positive constant. dependence is briefly discussed in Section 5.4.
3.2. Free Energy Evaluation
- Step 1:
- The work during a short period from time t and is evaluated asIn this simulation, we chose [].
- Step 2:
- The accumulated work, which is the sum of the stepwise work up to time , is determined.
- Step 3:
- We perform simulations multiple times, calculating for each case. The free energy change from the initial state is evaluated by taking the ensemble average as the Jarzynski equality, Equation (6), as a function of t.
- Step 4:
- Since the bubble “radius” is directly related to time t with Equation (10), we finally obtain the free energy as a function of bubble radius.
4. Results
4.1. Thermodynamic Properties
4.2. Bubble Growth
4.3. Work and Free Energy
5. Discussion
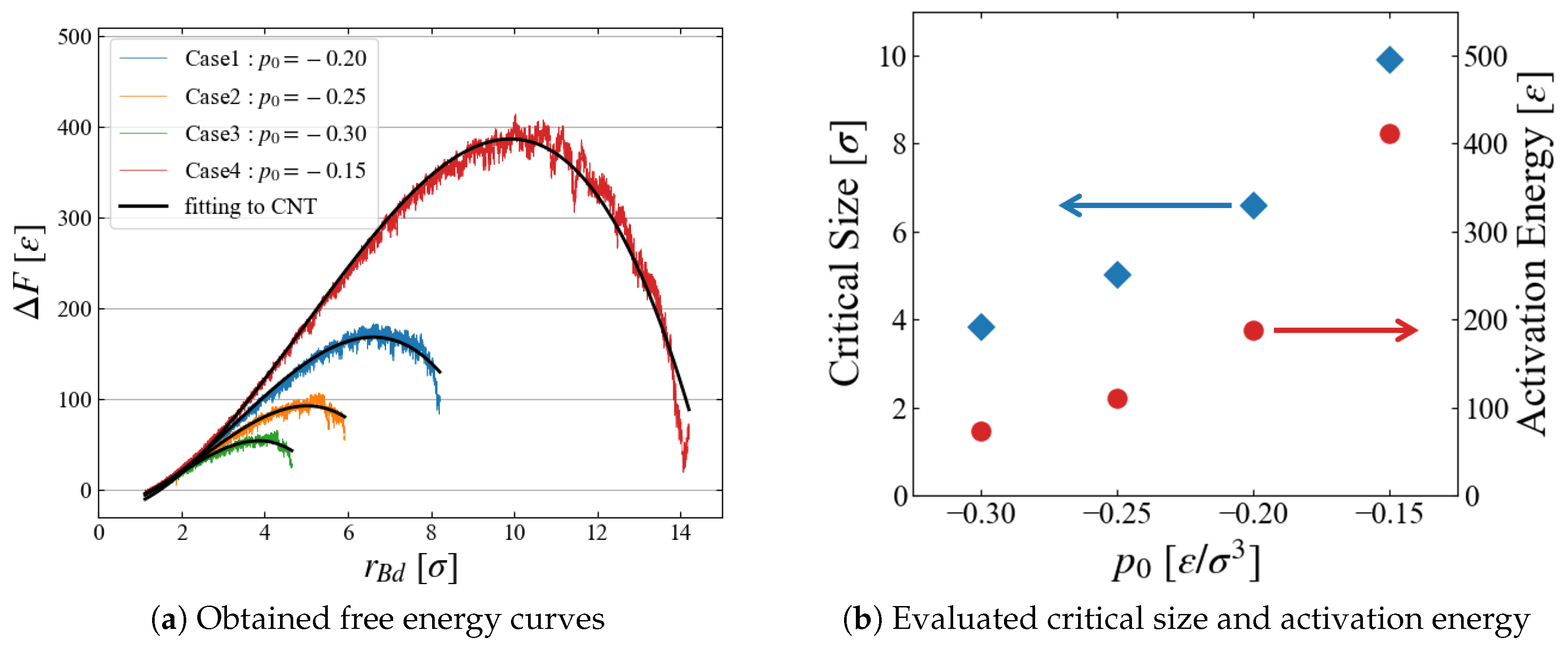
5.1. Critical Size
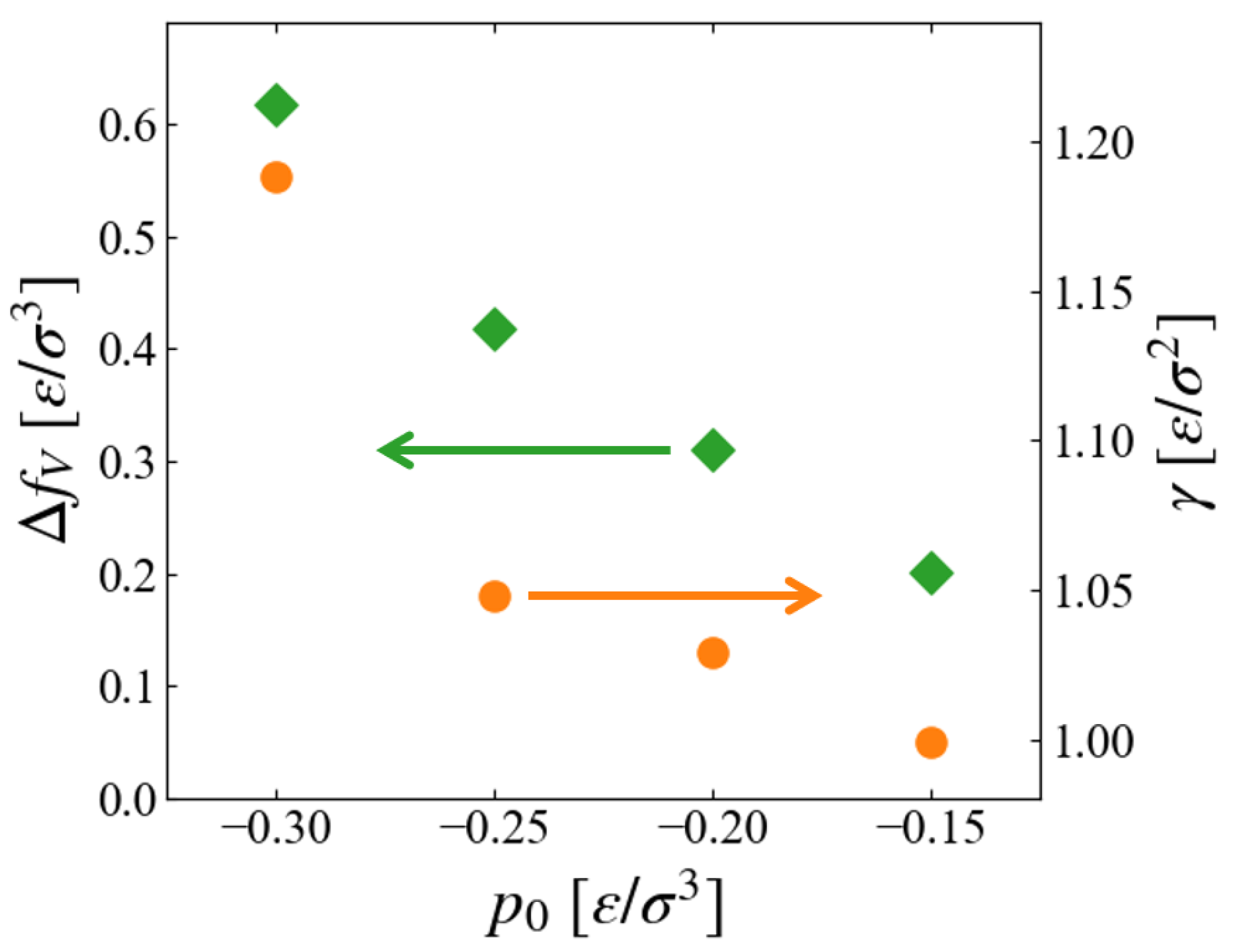
5.2. Comparison with CNT
5.3. Sampling
5.4. Growth Speed
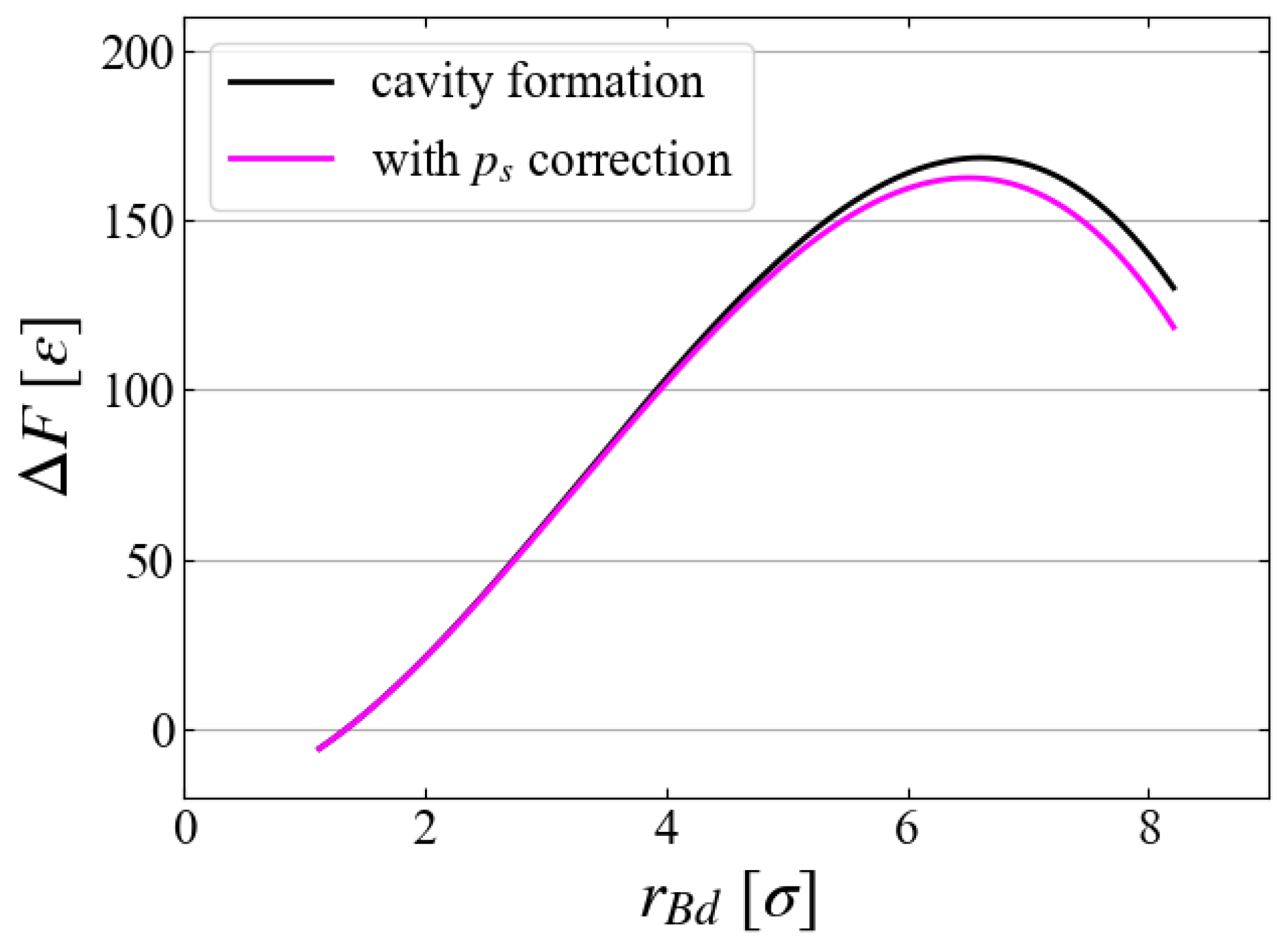
5.5. Relation to Bubble Formation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brennen, C.E. Cavitation and Bubble Dyamics; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Duana, C.; Karnik, R.; Lu, M.C.; Majumdar, A. Evaporation-induced cavitation in nanofluidic channels. Porc. Natl. Acad. Sci. USA 2012, 109, 3688–3693. [Google Scholar] [CrossRef]
- Thome, J.R. Enhanced Boiling Heat Transfer, 1st ed.; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Karayiannis, T.; Mahmoud, M. Flow boiling in microchannels: Fundamentals and applications. Appl. Therm. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Skripov, V.P. Metastable Liquids; Wiley: Hoboken, NJ, USA, 1974. [Google Scholar]
- Debenedetti, P.G. Metastable Liquids: Concepts and Principles, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Wheeler, T.D.; Stroock, A.D. Stability Limit of Liquid Water in Metastable Equilibrium with Subsaturated Vapors. Langmuir 2009, 25, 7602–7622. [Google Scholar] [CrossRef]
- Caupin, F.; Stroock, A.D. The Stability Limit and Other Open Questions on Water. Adv. Chem. Phys. 2013, 152, 51–80. [Google Scholar]
- Hirth, J.P.; Pound, G.M.; Pierre, G.R.S. Bubble Nucleation. Metall. Trans. 1970, 1, 939–945. [Google Scholar] [CrossRef]
- Oxtoby, D.W. Homogeneous nucleation: Theory and experiment. J. Phys. Condens. Matter 1992, 4, 7627–7650. [Google Scholar] [CrossRef]
- Baidakov, V.G. Attainable superheating of liquefied gases and their solutions. Low Temp. Phys. 2013, 39, 643–664. [Google Scholar] [CrossRef]
- Zeng, X.C.; Oxtoby, D.W. Gas-liquid nucleation in Lennard-Jones fluids. J. Chem. Phys. 1991, 94, 4472–4478. [Google Scholar] [CrossRef]
- Delale, C.F.; Hruby, J.; Marsik, F. Homogeneous bubble nucleation in liquids: The classical theory revisited. J. Chem. Phys. 2003, 118, 792–806. [Google Scholar] [CrossRef]
- Lutsko, J.F. Density functional theory of inhomogeneous liquids. III. Liquid-vapor nucleation. J. Chem. Phys. 2008, 129, 244501. [Google Scholar] [CrossRef]
- Němec, T. Scaled nucleation theory for bubble nucleation of lower alkanes. Eur. Phys. J. E 2014, 37, 111. [Google Scholar] [CrossRef]
- Kinjo, T.; Matsumoto, M. Cavitation Processes and Negative Pressure. Fluid Phase Equilibria 1998, 144, 343–350. [Google Scholar] [CrossRef]
- Park, S.; Weng, J.G.; Tien, C.L. Cavitation and Bubble Nucleation using Molecular Dynamics Simulation. Microscale Thermophys. Eng. 2000, 4, 161–175. [Google Scholar] [CrossRef]
- Tsuda, S.; Takagi, S.; Matsumoto, Y. A study on the growth of cavitation bubble nuclei using large-scale molecular dynamics simulations. Fluid Dyn. Res. 2008, 40, 606–615. [Google Scholar] [CrossRef]
- Baidakov, V.; Protsenko, K. Molecular dynamics simulation of cavitation in a Lennard-Jones liquid at negative pressures. Chem. Phys. Lett. 2020, 760, 138030. [Google Scholar] [CrossRef]
- Xie, H.; Xu, Y.; Zhong, C. A study of cavitation nucleation in pure water using molecular dynamics simulation. Chin. Phys. B 2022, 31, 114701. [Google Scholar] [CrossRef]
- Peliti, L.; Pigolotti, S. Stochastic Thermodynamics: An Introduction; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Torabi, K.; Corti, D.S. Molecular simulation study of cavity-generated instabilities in the superheated Lennard-Jones liquid. J. Chem. Phys. 2010, 133, 134505. [Google Scholar] [CrossRef]
- LAMMPS. Molecular Dynamics Simulator. Available online: https://www.lammps.org (accessed on 1 May 2024).
- Thompsona, A.P.; Aktulgab, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.; Crozier, P.S.; Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- OVITO. Open Visualization Tool. Available online: https://www.ovito.org/ (accessed on 1 May 2024).
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Punnathanam, S.; Corti, D.S. Work of cavity formation inside a fluid using free-energy perturbation theory. Phys. Rev. E 2004, 69, 036105. [Google Scholar] [CrossRef] [PubMed]
- Stephan, S.; Thol, M.; Vrabec, J.; Hasse, H. Thermophysical Properties of the Lennard-Jones Fluid: Database and Data Assessment. J. Chem. Inf. Model. 2019, 59, 4248–4265. [Google Scholar] [CrossRef]
- Stephan, S.; Staubach, J.; Hasse, H. Review and comparison of equations of state for the Lennard-Jones fluid. Fluid Phase Equilibria 2020, 523, 112772. [Google Scholar] [CrossRef]
- Zou, Y.; Huai, X.; Lin, L. A Molecular Dynamics Simulation of Bubble Nucleation in Homogeneous Liquid under Heating with Constant Mean Negative Presure. Appl. Therm. Eng. 2010, 30, 859–863. [Google Scholar] [CrossRef]
- Kwak, H.Y.; Panton, R.L. Tensile strength of simple liquids predicted by a model of molecular interactions. J. Phys. D Appl. Phys. 1985, 18, 647. [Google Scholar] [CrossRef]
- Matsumoto, M.; Tanaka, K. Nano bubble–Size dependence of surface tension and inside pressure. Fluid Dyn. Res. 2008, 40, 546–553. [Google Scholar] [CrossRef]
- Block, B.J.; Das, S.K.; Oettel, M.; Virnau, P.; Binder, K. Curvature dependence of surface free energy of liquid drops and bubbles: A simulation study. J. Chem. Phys. 2010, 133, 154702. [Google Scholar] [CrossRef]
- Hewage, S.A.; Meegoda, J.N. Molecular dynamics simulation of bulk nanobubbles. Colloids Surf. A Physicochem. Eng. Asp. 2020, 650, 129565. [Google Scholar] [CrossRef]
- Bosserta, M.; Trimaille, I.; Cagnon, L.; Chabau, B.; Gueneau, C.; Spathis, P.; Wolf, P.E.; Rolley, E. Surface tension of cavitation bubbles. Porc. Natl. Acad. Sci. USA 2023, 120, e2300499120. [Google Scholar] [CrossRef]
- Thomson, W. On the equilibrium of vapour at a curved surface of liquid. Proc. R. Soc. Edinb. 1872, 7, 63–68. [Google Scholar] [CrossRef]
- Jarzynski, C. Equalities and Inequalities: Irreversibility and the Second Law of Thermodynamics at the Nanoscale. Annu. Rev. Condens. Matter Phys. 2011, 2, 329–351. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]

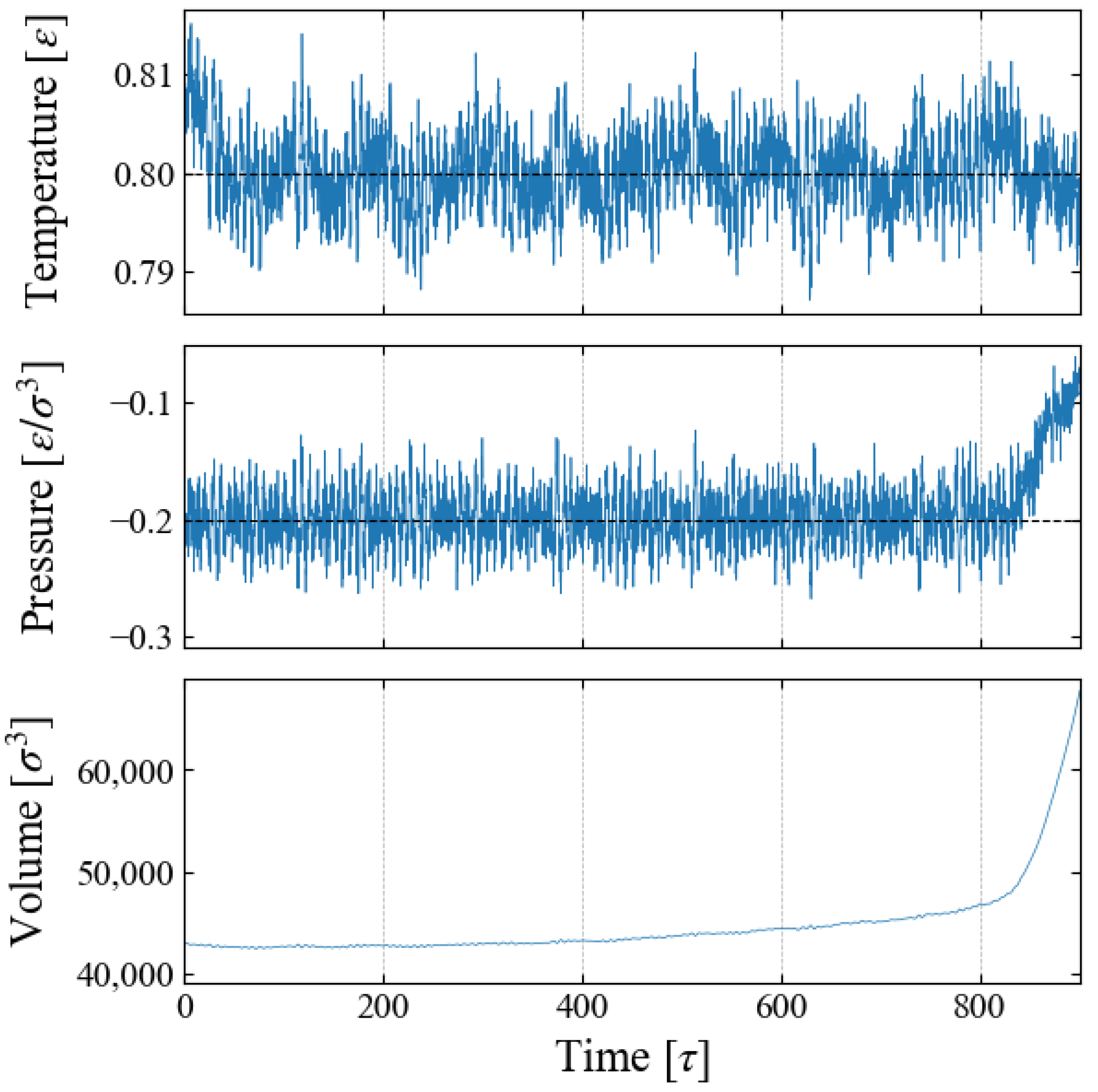

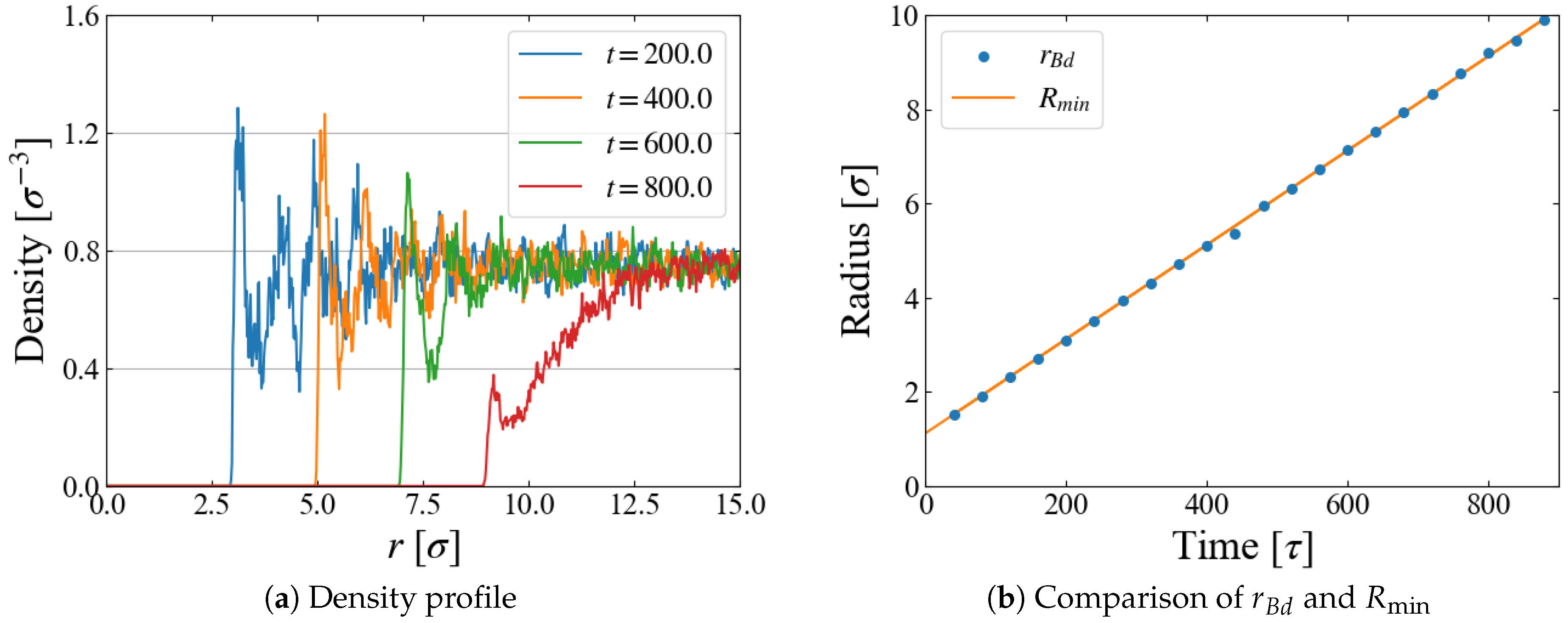

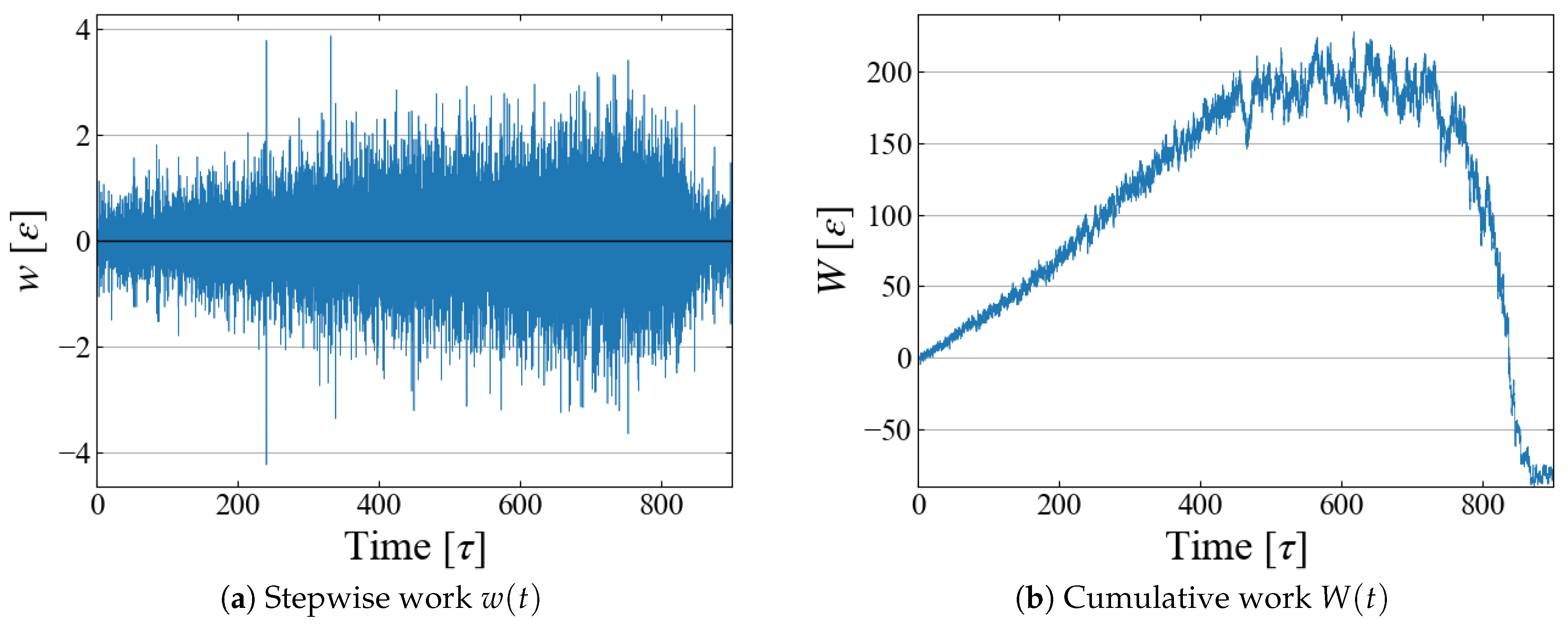

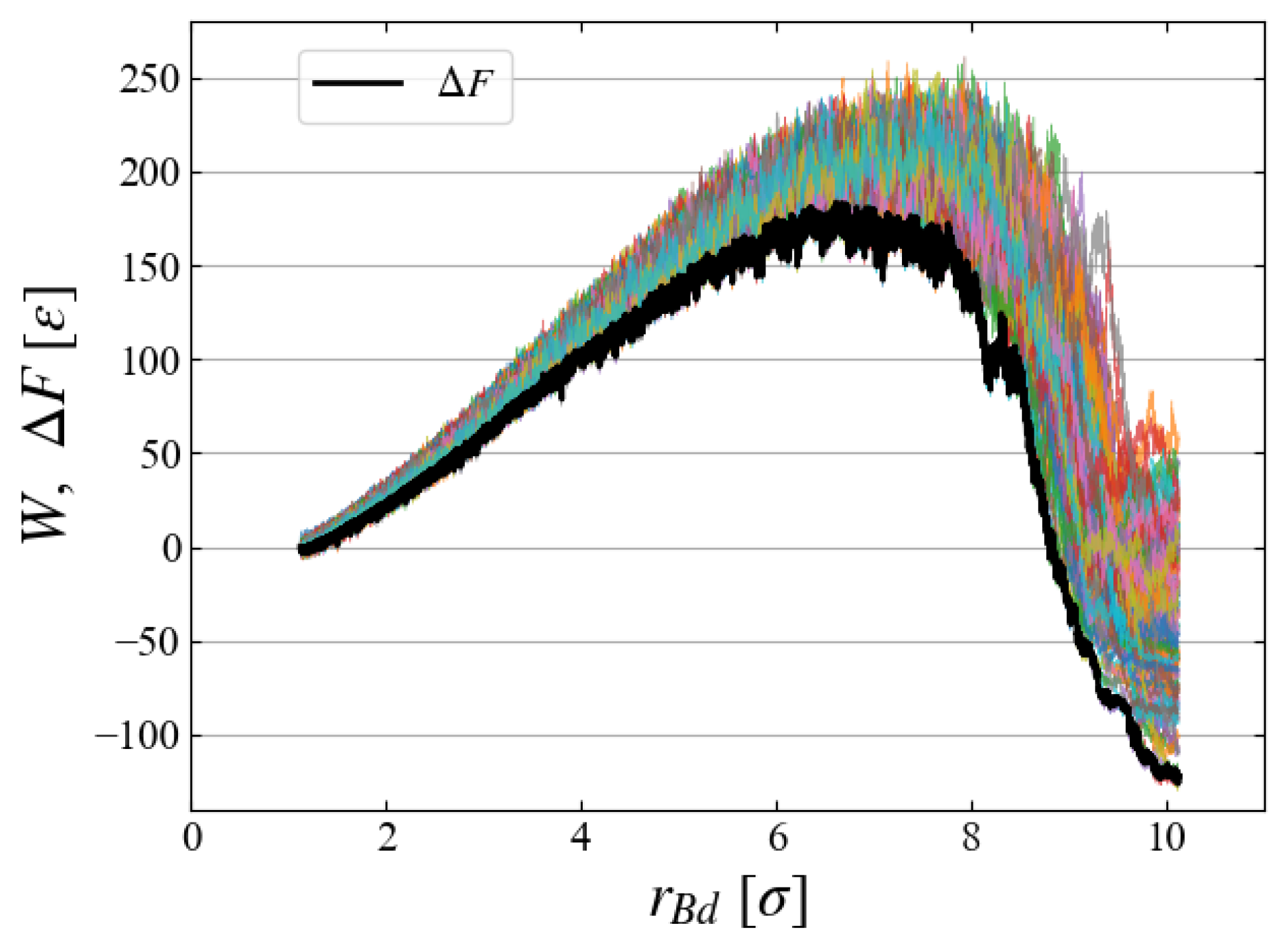



| Number of Particles [–] | Temperature [] | Pressure [] | Equilibrium Density [] | Growth Speed [] | Number of Samplings [–] | |
|---|---|---|---|---|---|---|
| Case 1 | 32,000 | 0.752 | 100 | |||
| Case 2 | 32,000 | 0.745 | 100 | |||
| Case 3 | 32,000 | 0.737 | 100 | |||
| Case 4 | 108,000 | 0.759 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, I.; Matsumoto, M. Free Energy Evaluation of Cavity Formation in Metastable Liquid Based on Stochastic Thermodynamics. Entropy 2024, 26, 700. https://doi.org/10.3390/e26080700
Shimizu I, Matsumoto M. Free Energy Evaluation of Cavity Formation in Metastable Liquid Based on Stochastic Thermodynamics. Entropy. 2024; 26(8):700. https://doi.org/10.3390/e26080700
Chicago/Turabian StyleShimizu, Issei, and Mitsuhiro Matsumoto. 2024. "Free Energy Evaluation of Cavity Formation in Metastable Liquid Based on Stochastic Thermodynamics" Entropy 26, no. 8: 700. https://doi.org/10.3390/e26080700
APA StyleShimizu, I., & Matsumoto, M. (2024). Free Energy Evaluation of Cavity Formation in Metastable Liquid Based on Stochastic Thermodynamics. Entropy, 26(8), 700. https://doi.org/10.3390/e26080700







