Multifractal Hopscotch in Hopscotch by Julio Cortázar
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
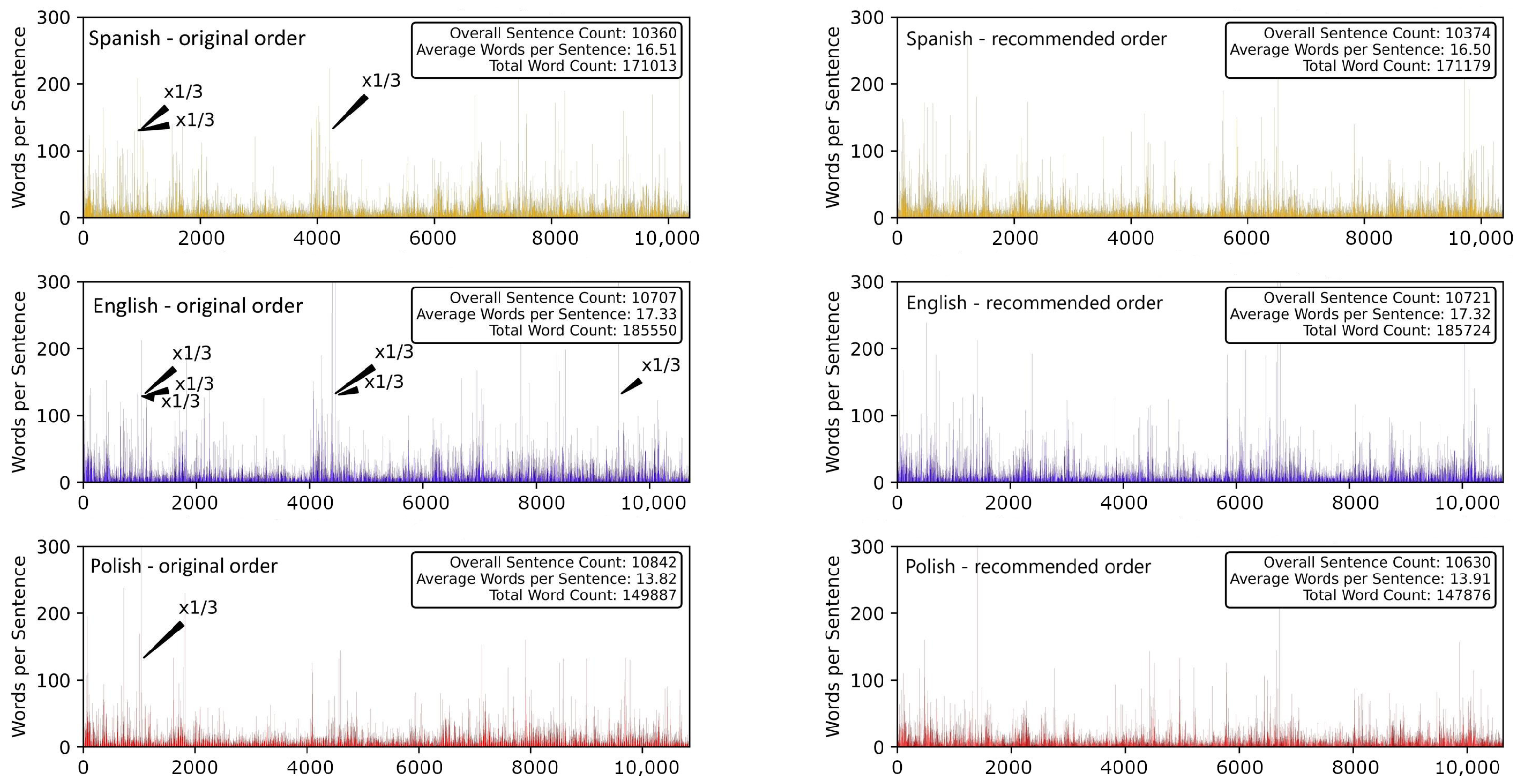
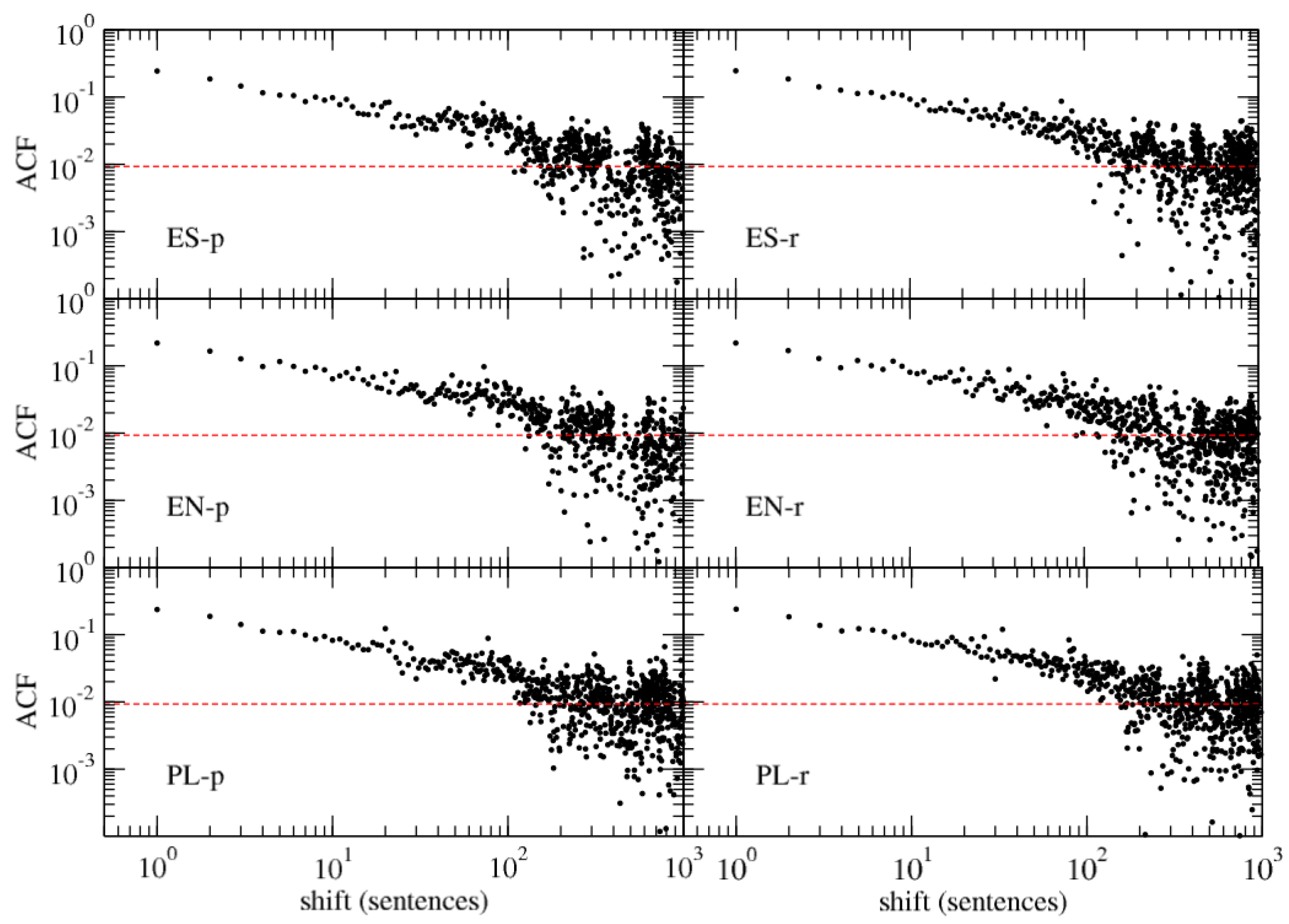
3.1. Linear Correlations
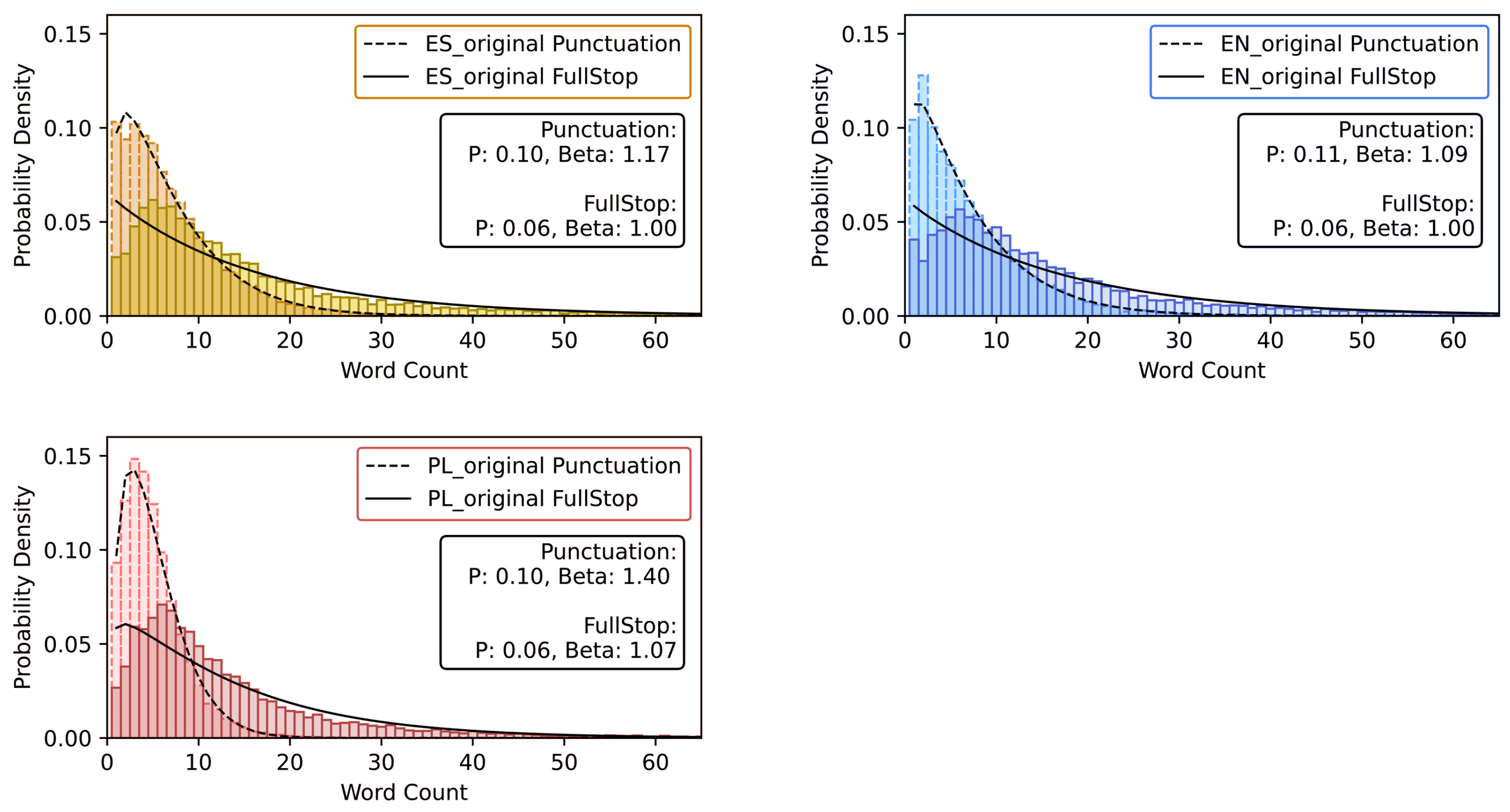
3.2. The Weibull Analysis
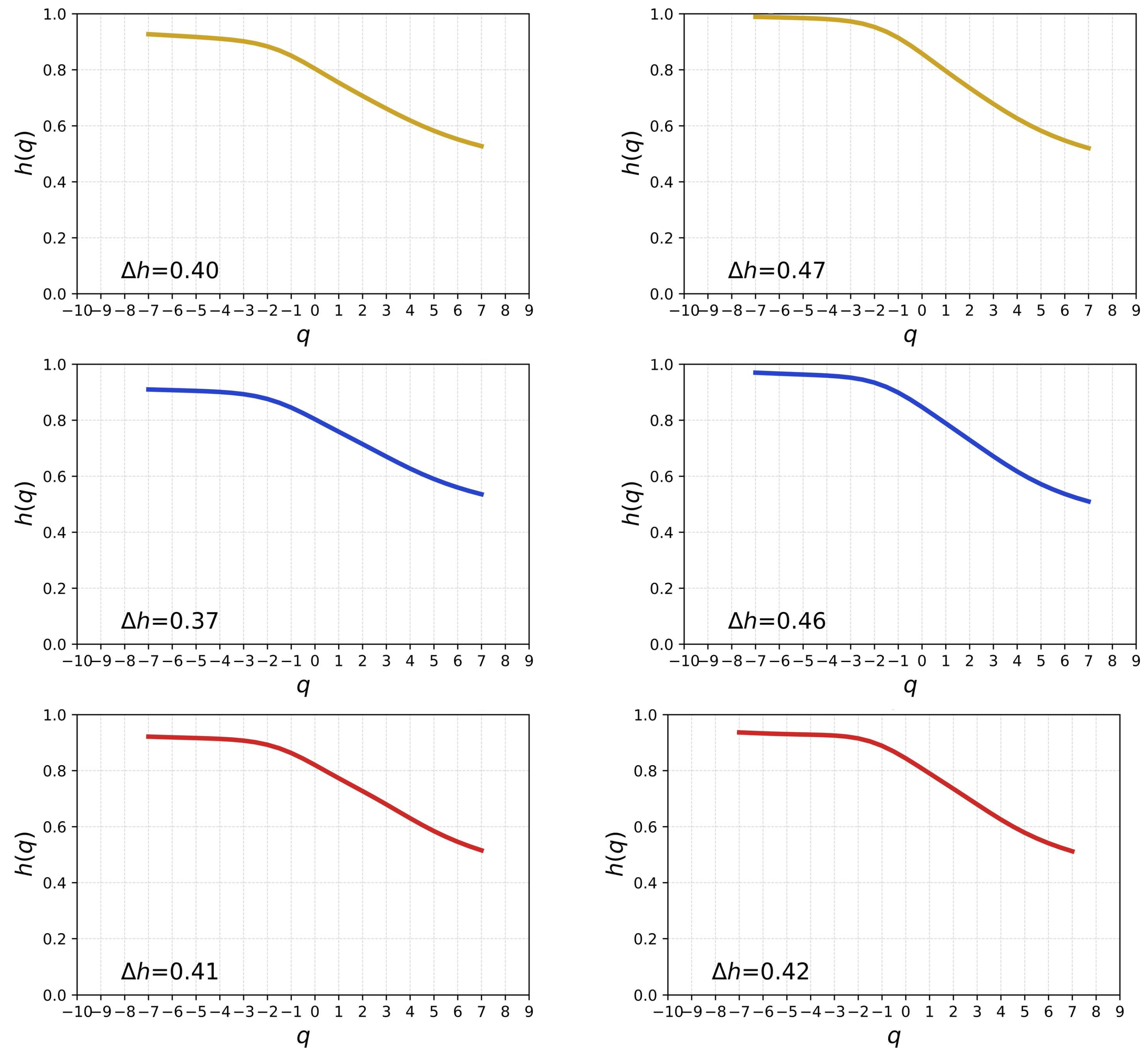
3.3. Generalised Hurst Exponents
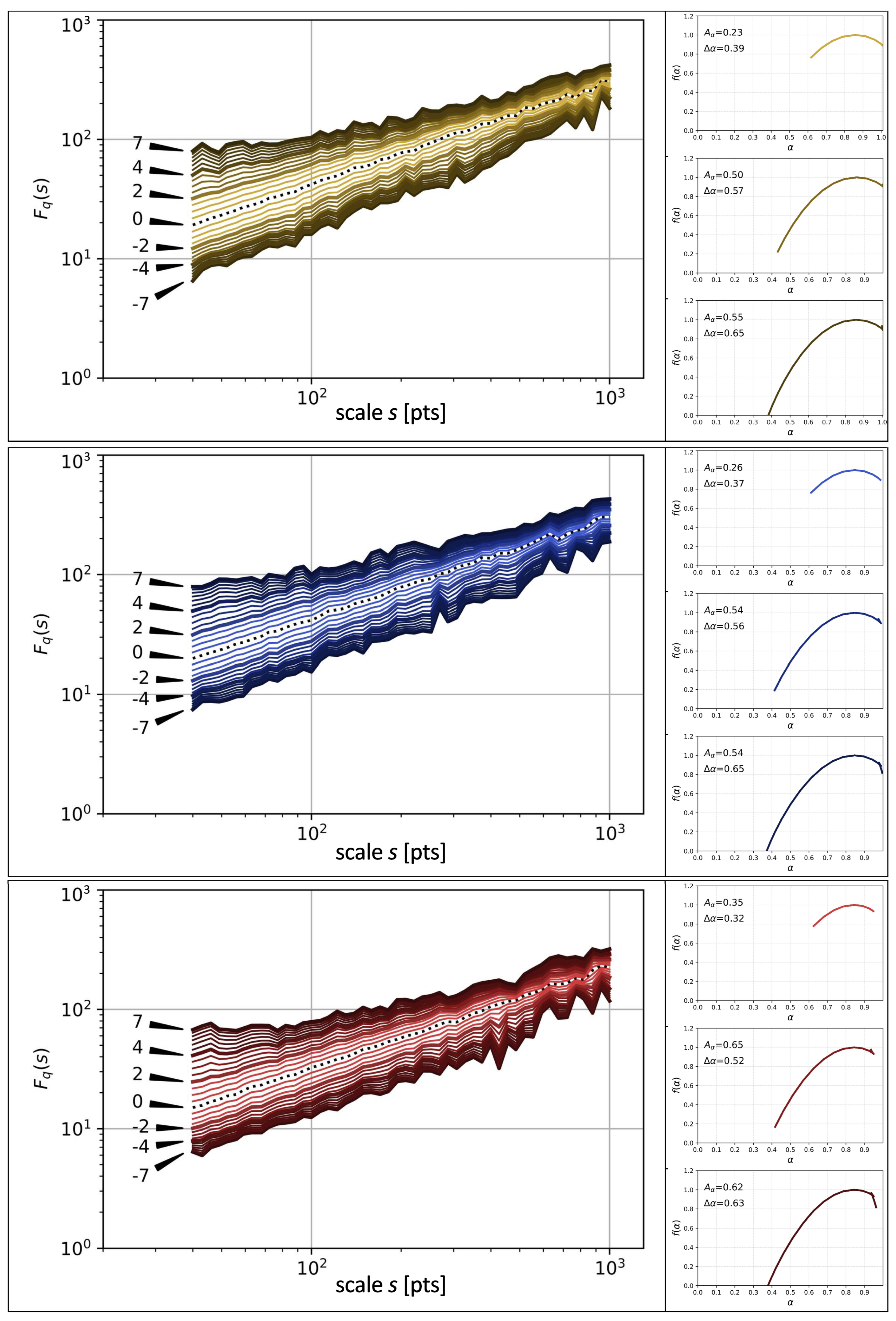
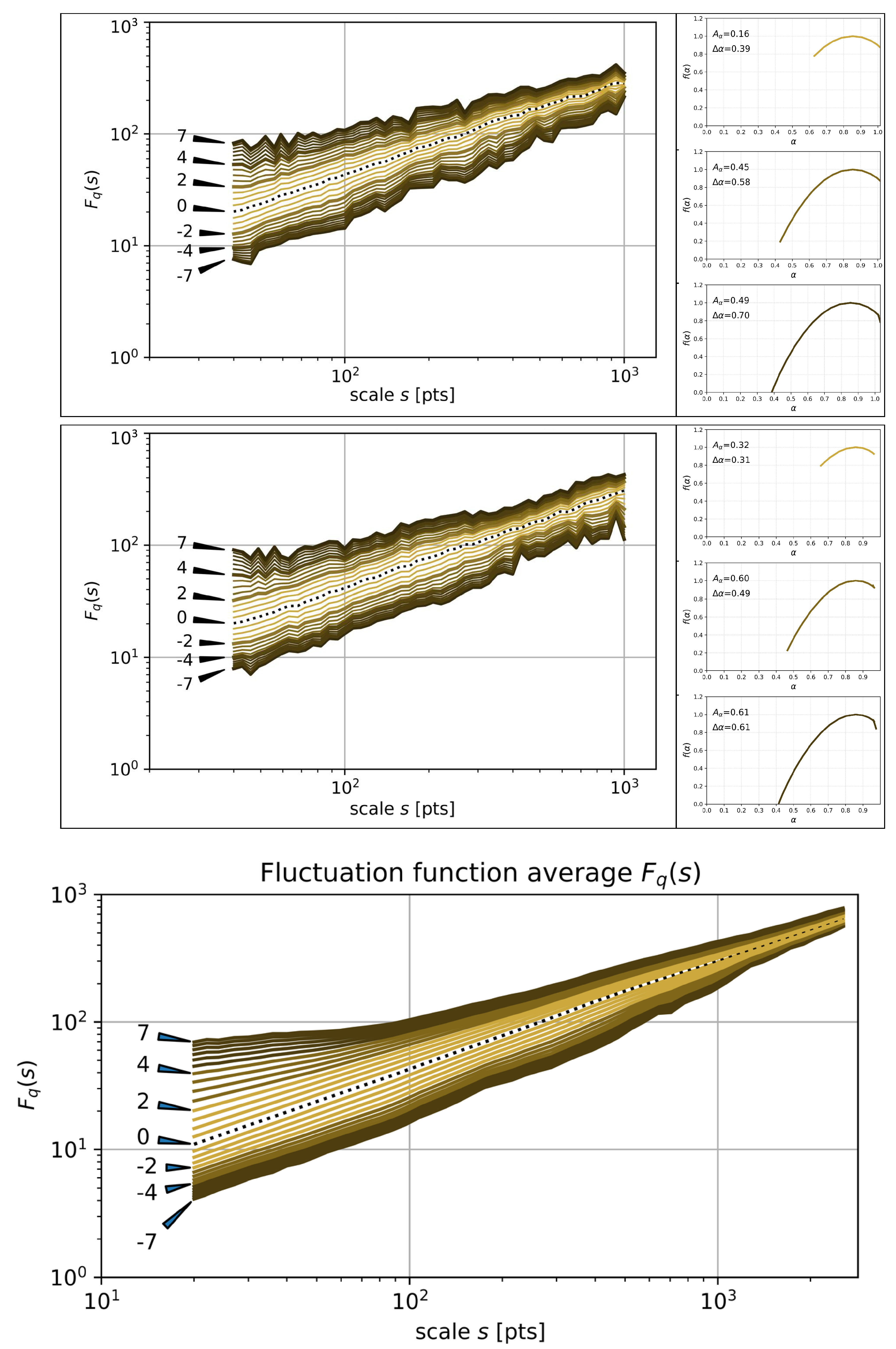
3.4. Multifractal Analysis
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hébert-Dufresne, L.; Allard, A.; Garland, J.; Hobson, E.A.; Zaman, L. The path of complexity. NPJ Complex. 2024, 1, 4. [Google Scholar] [CrossRef]
- Kwapień, J.; Drożdż, S. Physical approach to complex systems. Phys. Rep. 2012, 515, 115–226. [Google Scholar] [CrossRef]
- Stanisz, T.; Drożdż, S.; Kwapień, J. Complex systems approach to natural language. Phys. Rep. 2024, 1053, 1–84. [Google Scholar] [CrossRef]
- Dębowski, L. Information Theory Meets Power Laws: Stochastic Processes and Language Models; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Takahira, R.; Tanaka-Ishii, K.; Dębowski, L. Entropy Rate Estimates for Natural Language—A New Extrapolation of Compressed Large-Scale Corpora. Entropy 2016, 18, 364. [Google Scholar] [CrossRef]
- Montemurro, M.A.; Zanette, D.H. Universal Entropy of Word Ordering Across Linguistic Families. PLoS ONE 2011, 6, e19875. [Google Scholar] [CrossRef]
- Alvarez-Lacalle, E.; Dorow, B.; Eckmann, J.P.; Moses, E. Hierarchical structures induce long-range dynamical correlations in written texts. Proc. Natl. Acad. Sci. USA 2006, 103, 7956–7961. [Google Scholar] [CrossRef]
- Liu, J.; Gunn, E.; Youssef, F.; Tharayil, J.; Lansford, W.; Zeng, Y. Fractality in Chinese prose. Digit. Scholarsh. Humanit. 2023, 38, 604–620. [Google Scholar] [CrossRef]
- Sánchez, D.; Zunino, L.; Gregorio, J.D.; Toral, R.; Mirasso, C. Ordinal analysis of lexical patterns. Chaos 2023, 33, 033121. [Google Scholar] [CrossRef]
- Pawłowski, A. Time-Series analysis in linguistics: Application of the ARIMA method to cases of spoken Polish. J. Quant. Linguist. 1997, 4, 203–221. [Google Scholar] [CrossRef]
- Kosmidis, K.; Kalampokis, A.; Argyrakis, P. Language time series analysis. Physica A 2006, 370, 808–816. [Google Scholar] [CrossRef]
- Cancho, R.F.I.; Solé, R.V. The small world of human language. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2001, 268, 2261–2265. [Google Scholar] [CrossRef]
- Liu, H.; Xu, C. Can syntactic networks indicate morphological complexity of a language? Europhys. Lett. 2011, 93, 28005. [Google Scholar] [CrossRef]
- Cong, J.; Liu, H. Approaching human language with complex networks. Phys. Life Rev. 2014, 11, 598–618. [Google Scholar] [CrossRef] [PubMed]
- Wachs-Lopes, G.A.; Rodrigues, P.S. Analyzing natural human language from the point of view of dynamic of a complex network. Expert Syst. Appl. 2016, 45, 8–22. [Google Scholar] [CrossRef]
- Kulig, A.; Kwapień, J.; Stanisz, T.; Drożdż, S. In narrative texts punctuation marks obey the same statistics as words. Inf. Sci. 2017, 375, 98–113. [Google Scholar] [CrossRef]
- Stanisz, T.; Kwapień, J.; Drożdż, S. Linguistic data mining with complex networks: A stylometric-oriented approach. Inf. Sci. 2019, 482, 301–320. [Google Scholar] [CrossRef]
- Raducha, T.; Gubiec, T. Predicting language diversity with complex networks. PLoS ONE 2018, 13, e0196593. [Google Scholar] [CrossRef] [PubMed]
- Naranan, S.; Balasubrahmanyan, V. Models for power law relations in linguistics and information science. J. Quant. Linguist. 1998, 5, 35–61. [Google Scholar] [CrossRef]
- Newman, M. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Ausloos, M. Punctuation effects in english and esperanto texts. Physica A 2010, 389, 2835–2840. [Google Scholar] [CrossRef]
- Piantadosi, S.T. Zipf’s word frequency law in natural language: A critical review and future directions. Psychon. Bull. Rev. 2014, 21, 1112–1130. [Google Scholar] [CrossRef] [PubMed]
- Shanahan, M.; McDonell, K.; Reynolds, L. Role play with large language models. Nature 2023, 623, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.X.; Zhou, K.; Li, J.; Tang, T.; Wang, X.; Hou, Y.; Min, Y.; Zhang, B.; Zhang, J.; Dong, Z.; et al. A Survey of Large Language Models. arXiv 2023, arXiv:2303.18223v13. [Google Scholar]
- Stanisz, T.; Drożdż, S.; Kwapień, J. Universal versus system-specific features of punctuation usage patterns in major Western languages. Chaos Solitons Fractals 2023, 168, 113183. [Google Scholar] [CrossRef]
- Dec, J.; Dolina, M.; Drożdż, S.; Kwapień, J.; Liu, J.; Stanisz, T. Quantifying patterns of punctuation in modern Chinese prose. 2024. submitted. [Google Scholar]
- Bernstein, J. Rayuela, Chapter 34: A structural reading. Hispanófila 1974, 52, 61–70. [Google Scholar]
- Simpkins, S. “The Infinite Game”: Cortázar’s “Hopscotch”. J. Midwest Mod. Lang. Assoc. 1990, 23, 61–74. [Google Scholar] [CrossRef]
- Cortázar, J. Rayuela; Sudamericana: Buenos Aires, Argentina, 1963. [Google Scholar]
- Cortázar, J. Hopscotch; Rabassa, G., Translator; Pantheon Books: New York, NY, USA, 1966. [Google Scholar]
- Cortázar, J. Gra w Klasy; Chądzyńska, Z., Translator; Wydawnictwo Literackie: Kraków. Poland, 1985. [Google Scholar]
- Drożdż, S.; Oświęcimka, P.; Kulig, A.; Kwapień, J.; Bazarnik, K.; Grabska-Gradzińska, I.; Rybicki, J.; Stanuszek, M. Quantifying origin and character of long-range correlations in narrative texts. Inf. Sci. 2016, 331, 32–44. [Google Scholar] [CrossRef]
- Miller, R. Survival Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Nakagawa, T.; Osaki, S. The discrete Weibull distribution. IEEE Trans. Reliab. 1975, R-24, 300–301. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley-Interscience: Hoboken, NJ, USA, 1994. [Google Scholar]
- Altmann, E.G.; Pierrehumbert, J.B.; Motter, A.E. Beyond Word Frequency: Bursts, Lulls, and Scaling in the Temporal Distributions of Words. PLoS ONE 2009, 4, e7678. [Google Scholar] [CrossRef]
- Jimenez, J. Intermittency and cascades. J. Fluid Mech. 2000, 409, 99–120. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Oświęcimka, P.; Kwapień, J.; Drożdż, S. Wavelet versus detrended fluctuation analysis of multifractal structures. Phys. Rev. E 2006, 74, 016103. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Hurst, H.E. The long-term storage capacity of reservoir. Trans. Am. Soc. Civ. Eng. 1951, 116, 2447. [Google Scholar] [CrossRef]
- Heneghan, C.; McDarby, G. Establishing the relation between detrended fluctuation analysis and power spectral density analysis for stochastic processes. Phys. Rev. E 2000, 62, 6103–6110. [Google Scholar] [CrossRef] [PubMed]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraimant, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Ohashi, K.; Amaral, L.A.; Natelson, B.H.; Yamamoto, Y. Asymmetrical singularities in real-world signals. Phys. Rev. E 2003, 68, 065204. [Google Scholar] [CrossRef]
- Cao, G.; Cao, J.; Xu, L. Asymmetric multifractal scaling behavior in the Chinese stock market: Based on asymmetric MF-DFA. Physica A 2013, 392, 797–807. [Google Scholar] [CrossRef]
- Drożdż, S.; Oświęcimka, P. Detecting and interpreting distortions in hierarchical organization of complex time series. Phys. Rev. E 2015, 91, 030902. [Google Scholar] [CrossRef]
- Gómez-Gómez, J.; Carmona-Cabezas, R.; Ariza-Villaverde, A.B.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Multifractal detrended fluctuation analysis of temperature in Spain (1960–2019). Physica A 2021, 578, 126118. [Google Scholar] [CrossRef]
- Stanisz, T.; Drożdż, S.; Kwapień, J. Statistics of punctuation in experimental literature—The remarkable case of Finnegans Wake by James Joyce. Chaos 2024, 34, 083124. [Google Scholar] [CrossRef] [PubMed]
- Monjo, R.; Meseguer-Ruiz, O. Review: Fractal Geometry in Precipitation. Atmosphere 2024, 15, 135. [Google Scholar] [CrossRef]
- Theiler, J.; Prichard, D. Constrained-realization Monte-Carlo method for hypothesis testing. Physica D 1996, 94, 221–235. [Google Scholar] [CrossRef]
- Drożdż, S.; Kwapień, J.; Oświęcimka, P.; Rak, R. Quantitative features of multifractal subtleties in time series. Europhys. Lett. 2009, 88, 60003. [Google Scholar] [CrossRef]
- Kwapień, J.; Blasiak, P.; Drożdż, S.; Oświęcimka, P. Genuine multifractality in time series is due to temporal correlations. Phys. Rev. E 2023, 107, 034139. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Ausloos, M. Measuring complexity with multifractals in texts. Translation effects. Chaos Solitons Fractals 2012, 45, 1349–1357. [Google Scholar] [CrossRef]

| Spanish | English | Polish | |
|---|---|---|---|
| Minimum sentence length (words) | 1 | 1 | 1 |
| Maximum sentence length (words) | 850 | 860 | 681 |
| Average sentence length (words) | 16.6 | 17.4 | 13.9 |
| Minimum sentence length (characters) | 1 | 1 | 1 |
| Maximum sentence length (characters) | 4037 | 4058 | 3730 |
| Average sentence length (characters) | 77.3 | 77.7 | 74.9 |
| Minimum chapter length (sentences) | 4 | 3 | 3 |
| Maximum chapter length (sentences) | 1710 | 1720 | 1873 |
| Average chapter length (sentences) | 108.0 | 109.3 | 125.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dec, J.; Dolina, M.; Drożdż, S.; Kwapień, J.; Stanisz, T. Multifractal Hopscotch in Hopscotch by Julio Cortázar. Entropy 2024, 26, 716. https://doi.org/10.3390/e26080716
Dec J, Dolina M, Drożdż S, Kwapień J, Stanisz T. Multifractal Hopscotch in Hopscotch by Julio Cortázar. Entropy. 2024; 26(8):716. https://doi.org/10.3390/e26080716
Chicago/Turabian StyleDec, Jakub, Michał Dolina, Stanisław Drożdż, Jarosław Kwapień, and Tomasz Stanisz. 2024. "Multifractal Hopscotch in Hopscotch by Julio Cortázar" Entropy 26, no. 8: 716. https://doi.org/10.3390/e26080716
APA StyleDec, J., Dolina, M., Drożdż, S., Kwapień, J., & Stanisz, T. (2024). Multifractal Hopscotch in Hopscotch by Julio Cortázar. Entropy, 26(8), 716. https://doi.org/10.3390/e26080716









