The Second Law of Infodynamics: A Thermocontextual Reformulation
Abstract
:1. Introduction
2. The Two Entropies
3. The Thermocontextual State
3.1. TCI Postulates of State
3.2. Thermocontextual Properties of State
3.3. Energy States
- The system is isolated from exchanges with the surroundings. Isolation means that it is fixed in energy and composition.
- The system is non-dissipative. This means that there is no irreversible dissipation of exergy to ambient heat.
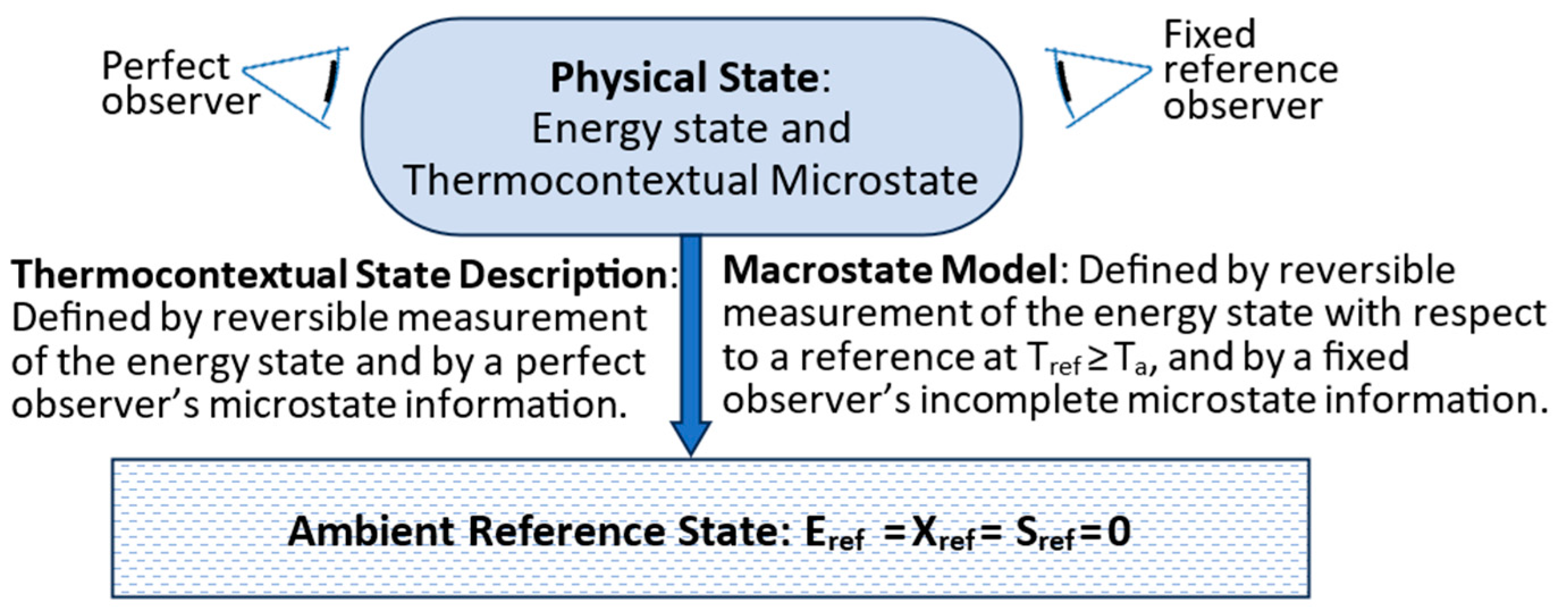
3.4. Microstates, Macrostates, and Information
4. Transitions
4.1. Updated Postulates of Transitions
4.2. Transitions, Dissipation, and Dispersion
4.3. Efficiency and Refinement
5. Applications
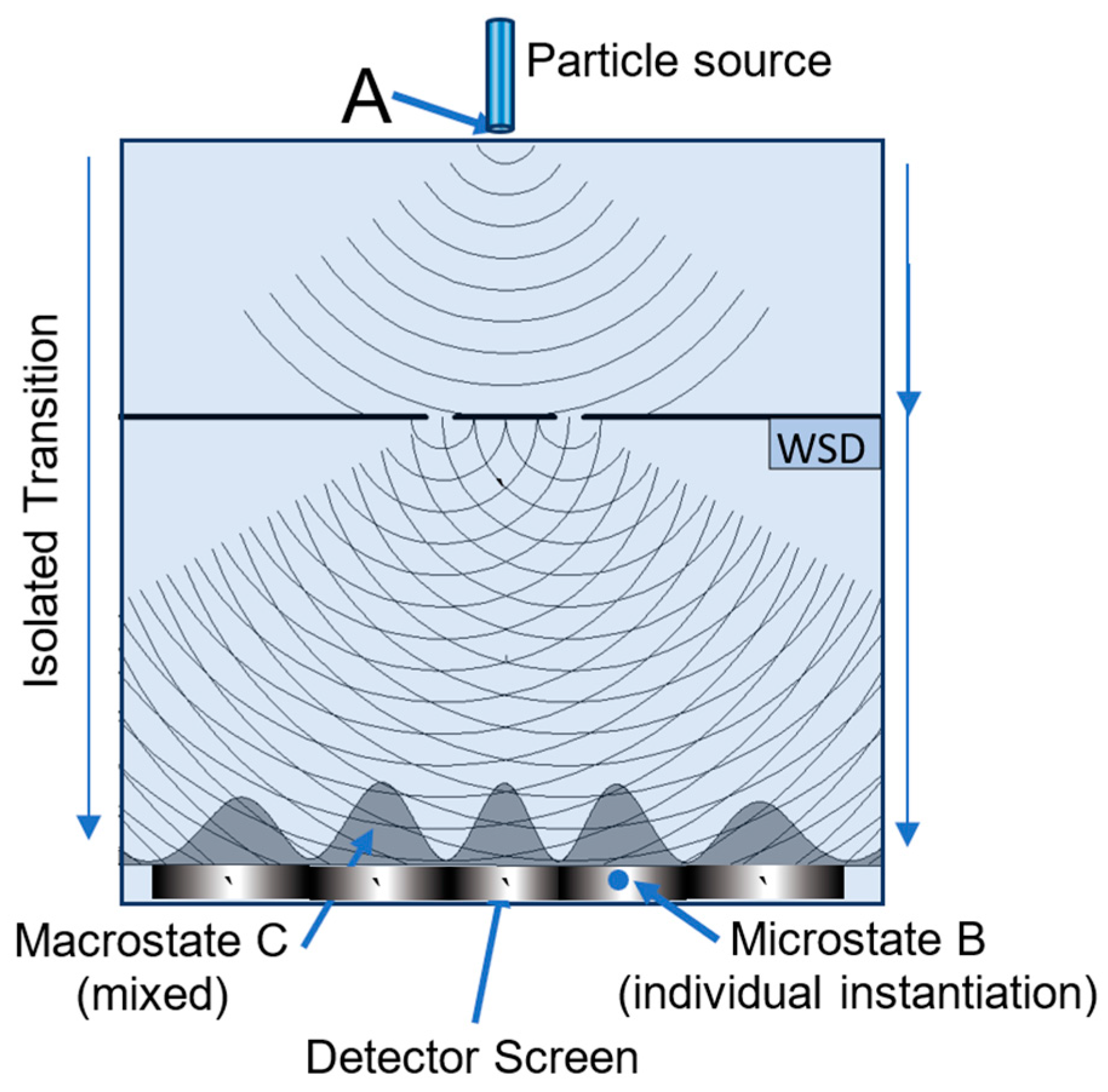
5.1. MaxEnt and the Double-Slit Experiment
5.2. Configurational Refinement and Replication
6. Summary and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. State, Macrotate Model, and Transactional Properties
| Physical State and State Properties: Based on Perfect Ambient Measurement and Observation | ||
| Ambient Temperature and pressure | Ta and Pa | The minimum temperature and pressure of the system’s physical surroundings with which it could interact. |
| Ambient Surroundings | Idealized equilibrium surroundings at Ta and Pa | |
| Ambient Reference State | ARS | State in thermodynamic equilibrium with ambient surroundings. It defines zero values for thermocontextual state properties. |
| Perfect ambient observer | An ambient observer’s resolution is based on ambient temperature. A perfect ambient observer maintains complete information on the thermocontextual microstate. | |
| Total Energy | Etot | Total energy relative to reference state at absolute zero (0 K) |
| Volumetric heat capacity | Change in a system’s thermal energy with a change in temperature at a fixed volume. | |
| Ambient-state energy | Ambient reference state’s energy with respect to zero kelvin. | |
| System Energy | E = Etot − Eas = X + Q | System Energy with respect to ambient reference state at Ta |
| Thermal energy (heat) | System’s thermal energy with respect to ARS. Equals a system’s energy loss as it irreversibly cools to the ambient temperature | |
| Exergy | X ≡ Xm + Xq | System’s reversible work potential on the ambient surroundings. Sum of mechanical and thermal exergy. |
| Thermal exergy | Reversible work potential by thermal energy on the ARS | |
| Mechanical exergy | Xm ≡ X − Xq | System’s work potential on the ARS after cooling to Ta |
| Entropic energy | Q ≡ E − X = qa | Thermal energy at Ta with zero ambient work potential. |
| Thermocontextual Entropy | dS = dq/T = thermodynamic entropy | |
| Thermal Entropy | σq = S/kB | Dimensionless thermocontextual entropy |
| Ambient heat | qa | Output of heat at ambient temperature |
| Ambient work | wa = wout + Xout | Output of work plus exergy to the ambient surroundings |
| Energy state | Defined by ambient temperature and by reversible measurements of thermally equilibrated system’s temperature, energy, and exergy with respect to the ARS. | |
| Thermocontextual microstate | Mechanical configuration of a system’s irreducibly resolvable parts. Completely described by the perfect ambient observer. | |
| Physical State | Defined by the energy state plus the thermocontextual microstate | |
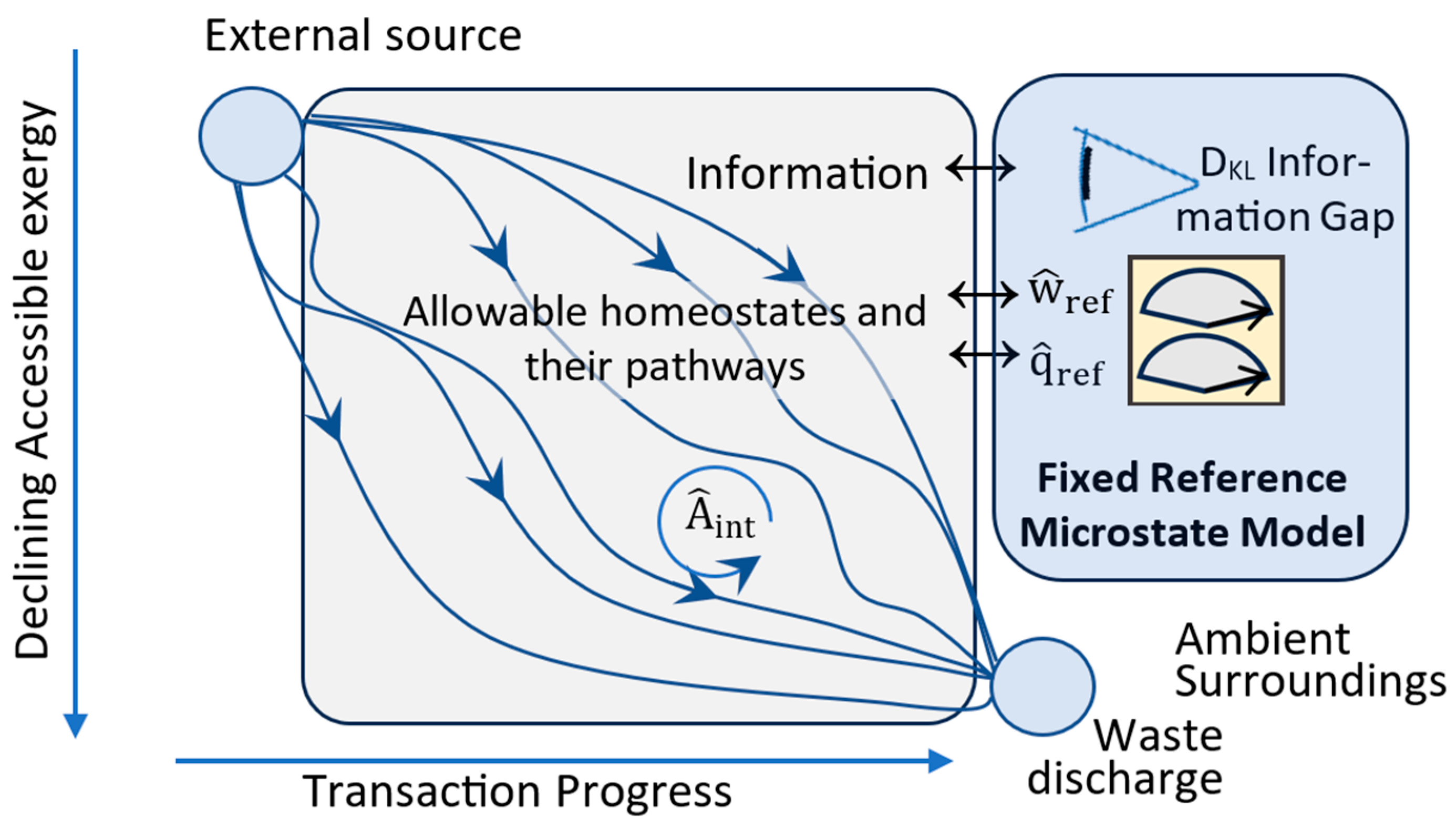
| Macrostate Model and Transactional (1) Properties: Based on Fixed Reference Observer and Temperature | ||
| Fixed-Reference Observer | An observer’s resolution is fixed by reference temperature. It creates a macrostate model based on resolvable observations at time zero. | |
| Fixed Reference Temperature | Tref | Fixed reference temperature for the measurements of accessible energy and configurational energy. By convention, it is set to ambient temperature at time zero. |
| Fixed-information reference model | A fixed information model allows tracking random changes in a system. By convention, it is based on perfect ambient observation of a system at time zero. | |
| Macrostate Model | [P1, P2, … PNobs] | Statistical description of a system’s microstate configuration based on the reference observer’s Bayesian expectation probabilities for the system’s resolvable microstates. |
| Configurational Entropy | Describes the macrostate model’s imprecision. The sum is over the microstates resolvable by the reference observer. Pi is the reference observer’s Bayesian expectation probability that the system exists in microstate i. Low entropy means high macrostate model precision. | |
| DKL Divergence (information gap) | Expresses the statistical separation between a reference observer’s macrostate model, with Bayesian probability distribution P2, and the system’s actual microstate. The physical state is statistically described by frequentist probability distribution P1. The physical state’s actual microstate configuration is ‘a’, with probability P1,a=1, and the macrostate model’s Bayesian expectation of microstate ‘a’ is P2,a. A high P2,a and low DKL means high accuracy. | |
| Configurational energy | C=Cm+Cq=kBTrefDKL + | Exergy that is not accessible for work by the reference observer. Mechanical Cm is due to incomplete information (DKL > 0) for the microstate. Thermal Cq is due to Tref >T a. |
| Accessibility | A ≡ X – C | Energy accessible for work measured at Tref. It is based on the reference temperature and the observer’s information. |
| Reference heat | Output of heat at Tref (per transition) | |
| Reference work | ) = w + Aout | Output of work plus accessibility to Tref (per transition) |
| Internal work | Work within a network of dissipators of increasing internal accessibility. | |
| Utilization | Reversible per-transition output of external work at the reference temperature (work plus accessible energy) plus the internal work. | |
| Other transactional properties | Per-transition increases in entropic energy, configurational entropy, and DKL information gap; and decreases in exergy and accessibility. | |
| (1) transactional properties are designated by ^ or ˇ to indicate increases or decreases per unit transition. | ||
References
- Vopson, M.; Lepadatu, S. Second law of information dynamics. AIP Adv. 2022, 12, 075310. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wikipedia Entropy (Information Theory). Available online: https://en.wikipedia.org/wiki/Entropy_(information_theory) (accessed on 10 August 2024).
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Wikipedia Boltzmann Distribution. Available online: https://en.wikipedia.org/wiki/Boltzmann_distribution (accessed on 10 August 2024).
- Crecraft, H. Time and Causality: A Thermocontextual Perspective. Entropy 2021, 23, 1705. [Google Scholar] [CrossRef]
- Lieb, E.; Yngvason, J. The physics and mathematics of the second law of thermodynamics. Phys. Rep. 1999, 310, 1–96. [Google Scholar] [CrossRef]
- Gyftopoulos, E.; Beretta, G. Thermodynamics: Foundations and Applications; Dover Publications: Mineola, NY, USA, 2012; 800p, ISBN 978048613. [Google Scholar]
- Dias, T.C.M.; Diniz, M.A.; Pereira, C.A.d.B.; Polpo, A. Overview of the 37th MaxEnt. Entropy 2018, 20, 694. [Google Scholar] [CrossRef] [PubMed]
- D’Ariano, G.M.; Paris, G.A.; Sacchi, M.F. Quantum Tomography. arXiv 2008, arXiv:quant-ph/0302028v1. [Google Scholar]
- Wikipedia Interpretations of Quantum Mechanics. Available online: https://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics (accessed on 10 July 2024).
- Takahiro, S. Thermodynamic and logical reversibilities revisited. J. Stat. Mech. Theory Exp. 2014, 2014, 03025. [Google Scholar] [CrossRef]
- Wikipedia Bell Test. Available online: https://en.wikipedia.org/wiki/Bell_test (accessed on 10 August 2024).
- Crecraft, H. Dissipation + Utilization = Self-Organization. Entropy 2023, 25, 229. [Google Scholar] [CrossRef] [PubMed]
- Wikipedia Bayesian Statistics. Available online: https://en.wikipedia.org/wiki/Bayesian_statistics (accessed on 10 August 2024).
- Wikipedia Frequentist Probability. Available online: https://en.wikipedia.org/wiki/Frequentist_probability (accessed on 10 August 2024).
- Wikipedia Kullback–Leibler Divergence. Available online: https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence (accessed on 10 August 2024).
- Ribó, J.; Hochberg, D. Stoichiometric network analysis of entropy production in chemical reactions. Phys. Chem. Chem. Phys. 2018, 20, 23726–23739. [Google Scholar] [CrossRef]
- Ribó, J.; Hochberg, D. Physical Chemistry Models for Chemical Research in the XXth and XXIst Centuries. ACS Phys. Chem. Au 2024, 4, 122–134. [Google Scholar] [CrossRef]
- Niven, R.K.; Abel, M.; Schlegel, M.; Waldrip, S.H. Maximum Entropy Analysis of Flow Networks: Theoretical Foundation and Applications. Entropy 2019, 21, 776. [Google Scholar] [CrossRef] [PubMed]
- Niven, R.K.; Schlegel, M.; Abel, M.; Waldrip, S.H.; Guimera, R. Entropy Analysis of Flow Networks with Structural Uncertainty (Graph Ensembles). In Bayesian Inference and Maximum Entropy Methods in Science and Engineering: MaxEnt 37; Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2018; Volume 239. [Google Scholar] [CrossRef]
- Martyushev, L. Maximum entropy production principle: History and current status. Phys. Uspekhi 2021, 64, 558. [Google Scholar] [CrossRef]
- Paltridge, G.W. Stumbling into the MEP Racket: An Historical Perspective. In Non-Equilibrium Thermodynamics and the Production of Entropy—Life, Earth, and Beyond; Kleidon, A., Lorenz, R.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; 260p, ISBN 3-540-22495-5. [Google Scholar]
- Paltridge, G.W. A Story and a Recommendation about the Principle of Maximum Entropy Production. Entropy 2009, 11, 945–948. [Google Scholar] [CrossRef]
- Wikipedia Baryogenesis. Available online: https://en.wikipedia.org/wiki/Baryogenesis (accessed on 10 August 2024).
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J.; et al. Bayesian statistics and modelling. Nat. Rev. Methods Primers 2021, 1, 1. [Google Scholar] [CrossRef]
- Modeling Galaxy formation: Verdoolaege, G. Regression of Fluctuating System Properties: Baryonic Tully–Fisher Scaling in Disk Galaxies. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering: MaxEnt 2017; Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2018; Volume 239. [Google Scholar] [CrossRef]
- Rapid medical diagnostics: Ranftl, S.; Melito, G.M.; Badeli, V.; Reinbacher-Köstinger, A.; Ellermann, K.; von der Linden, W. Bayesian Uncertainty Quantification with Multi-Fidelity Data and Gaussian Processes for Impedance Cardiography of Aortic Dissection. Entropy 2020, 22, 58. [Google Scholar] [CrossRef]
- Rapid medical diagnostics: Makaremi, M.; Lacaule, C.; Mohammad-Djafari, A. Deep Learning and Artificial Intelligence for the Determination of the Cervical Vertebra Maturation Degree from Lateral Radiography. Entropy 2019, 21, 1222. [Google Scholar] [CrossRef]
- Thermodynamic computing: Fry, R.L. Physical Intelligence and Thermodynamic Computing. Entropy 2017, 19, 107. [Google Scholar] [CrossRef]
- Thermodynamic computing: Hylton, T. Thermodynamic Computing: An Intellectual and Technological Frontier. Proceedings 2020, 47, 23. [Google Scholar] [CrossRef]
- AI and ML: Enßlin, T. Information Field Theory and Artificial Intelligence. Entropy 2022, 24, 374. [Google Scholar] [CrossRef] [PubMed]
- Machine learning: Mohammad-Djafari, A. Regularization, Bayesian Inference, and Machine Learning Methods for Inverse Problems. Entropy 2021, 23, 1673. [Google Scholar] [CrossRef]
- Ecology: Albert, C.G.; Callies, U.; von Toussaint, U. A Bayesian Approach to the Estimation of Parameters and Their Interdependencies in Environmental Modeling. Entropy 2022, 24, 231. [Google Scholar] [CrossRef] [PubMed]
- MaxEnt applications to macroeconomics: Hubert, P.; Stern, J.M. Probabilistic Equilibrium: A Review on the Application of MAXENT to Macroeconomic Models. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering: MaxEnt 2017; Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2018; Volume 239. [Google Scholar] [CrossRef]
- Optimizing imaging: Spector-Zabusky, A.; Spector, D. Schrödinger’s Zebra: Applying Mutual Information Maximization to Graphical Halftoning. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering: MaxEnt 2017; Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2018; Volume 239. [Google Scholar] [CrossRef]
- Enhancing MRI: Earle, K.A.; Broderick, T.; Kazakov, O. Effect of Hindered Diffusion on the Parameter Sensitivity of Magnetic Resonance Spectra. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering: MaxEnt 2017; Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2018; Volume 239. [Google Scholar] [CrossRef]
- Image reconstruction: Denisova, N. Bayesian Maximum-A-Posteriori Approach with Global and Local Regularization to Image Reconstruction Problem in Medical Emission Tomography. Entropy 2019, 21, 1108. [Google Scholar] [CrossRef]
- Caticha, N. Entropic Dynamics in Neural Networks, the Renormalization Group and the Hamilton-Jacobi-Bellman Equation. Entropy 2020, 22, 587. [Google Scholar] [CrossRef] [PubMed]
- Optimizing fusion realtors: Nille, D.; von Toussaint, U.; Sieglin, B.; Faitsch, M. Probabilistic Inference of Surface Heat Flux Densities from Infrared Thermography. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering: MaxEnt 2017; Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2018; Volume 239. [Google Scholar] [CrossRef]
- Wikipedia Double-Slit Experiment. Available online: https://en.wikipedia.org/wiki/Double-slit_experiment (accessed on 10 August 2024).
- Feynman, R.; Leighton, R.; Sands, M. The Feynman Lectures on Physics Vol. I: Mainly Mechanics, Radiation, and Heat, Millennium Edition Chapter 37 (Quantum Behavior); California Institute of Technology: Pasadena, CA, USA, 2013; Available online: https://www.feynmanlectures.caltech.edu/I_37.html (accessed on 30 March 2022).
- Crecraft, H. MaxEnt: Selection at the Heart of Quantum Mechanics. Preprints 2022. [Google Scholar] [CrossRef]
- University Physics III—Optics and Modern Physics (OpenStax) Chapter 3: Interference. Available online: https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/03%3A_Interference (accessed on 4 June 2022).
- Miller, S.L. Production of Amino Acids Under Possible Primitive Earth Conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef]
- Michaelian, K. The Dissipative Photochemical Origin of Life: UVC Abiogenesis of Adenine. Entropy 2021, 23, 217. [Google Scholar] [CrossRef]
- Cornish-Bowden, A.; Cárdenas, M.L. Contrasting theories of life: Historical context, current theories. In search of an ideal theory. Biosystems 2020, 188, 104063. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C. Relational quantum mechanics. Int. J. Theor. Phys. 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
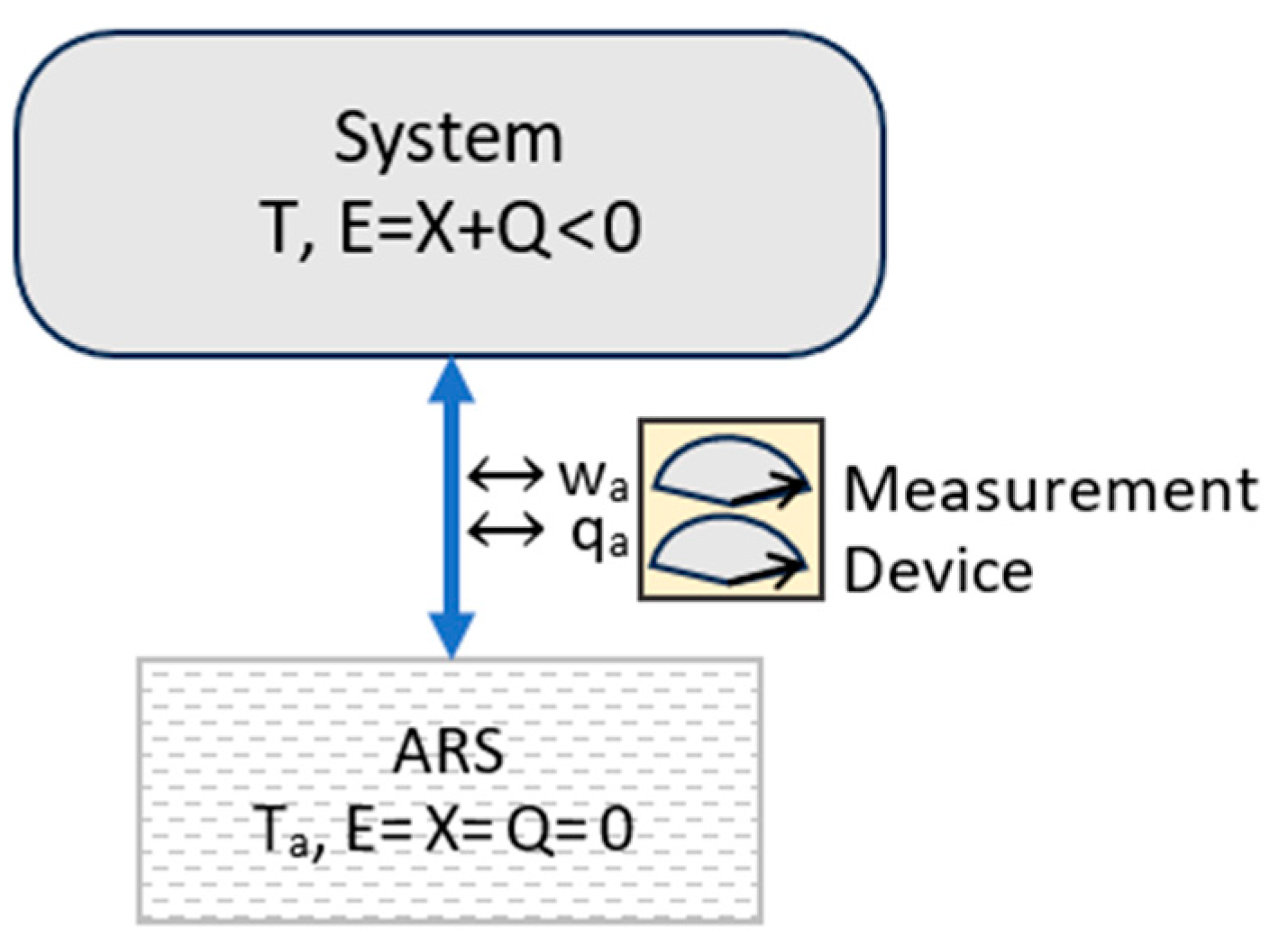
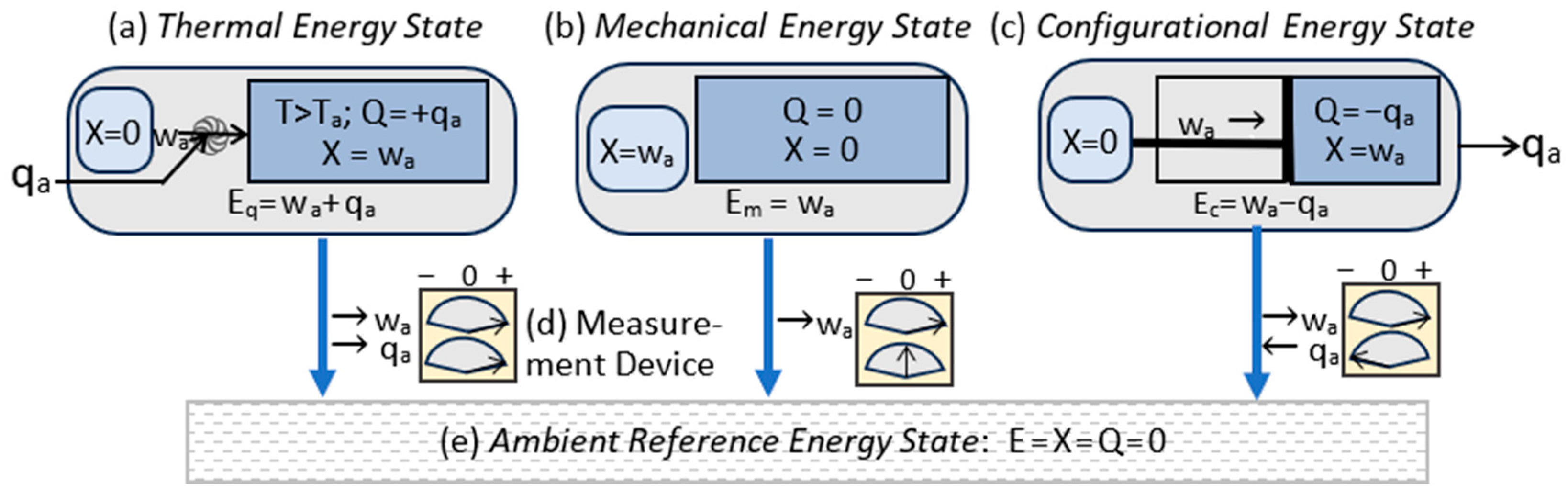
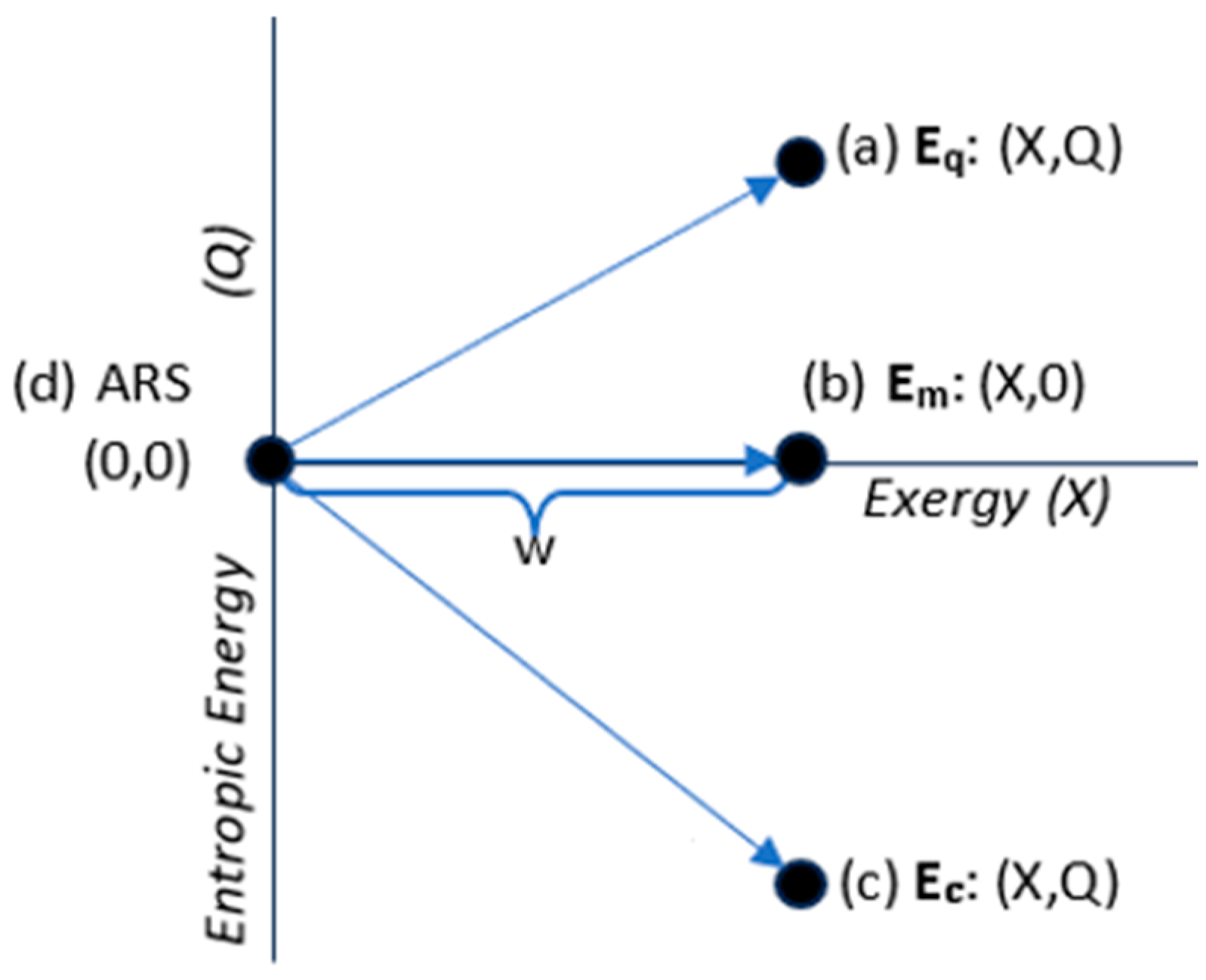





| Energy State Classification | Energy Components |
|---|---|
| Thermal state energy (Q > 0): | Eq = (X, Q); Eq = X + Q > X |
| Mechanical state energy (Q = 0): | Em = (X, 0); Em = X |
| Configurational state energy (Q < 0): | Ec = (X, Q); Ec = X + Q < X. |
| Detector Width | Slit Width | Slit Positions | Slit-Detector Separation | Observer’s Resolution |
|---|---|---|---|---|
| 200 λ | 7 λ | ±15 λ | 300 λ | 0.5 λ |
| Entropy | Transition (Normalized Probability Distribution) | |
|---|---|---|
| 1 | 4.69 | No WSD—source to detector (red profile) |
| 2 | 0.69 | WSD on—source to one of the slits (50–50%) |
| 3 | 5.02 | WSD on—slit to detector (green or blue profile) |
| 4 | 5.71 | WSD on—overall: source to detector (purple profile) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crecraft, H. The Second Law of Infodynamics: A Thermocontextual Reformulation. Entropy 2025, 27, 22. https://doi.org/10.3390/e27010022
Crecraft H. The Second Law of Infodynamics: A Thermocontextual Reformulation. Entropy. 2025; 27(1):22. https://doi.org/10.3390/e27010022
Chicago/Turabian StyleCrecraft, Harrison. 2025. "The Second Law of Infodynamics: A Thermocontextual Reformulation" Entropy 27, no. 1: 22. https://doi.org/10.3390/e27010022
APA StyleCrecraft, H. (2025). The Second Law of Infodynamics: A Thermocontextual Reformulation. Entropy, 27(1), 22. https://doi.org/10.3390/e27010022







