Coexistence Demonstration and Wavelength Dependency Analysis of S-Band CV-QKD Signal with Fully Loaded C+L-Band DWDM Signals
Abstract
:1. Introduction
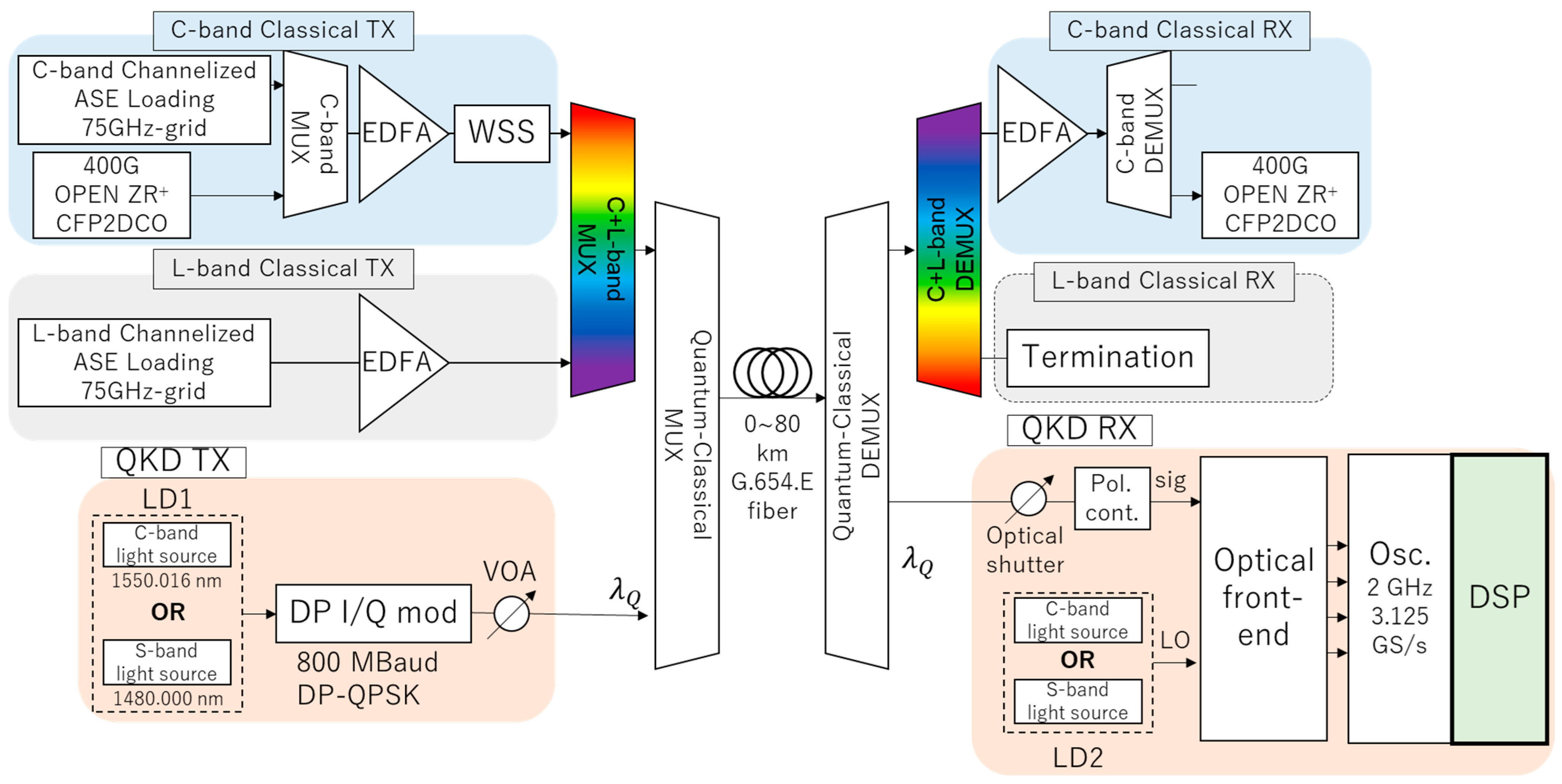
2. Experimental Setup
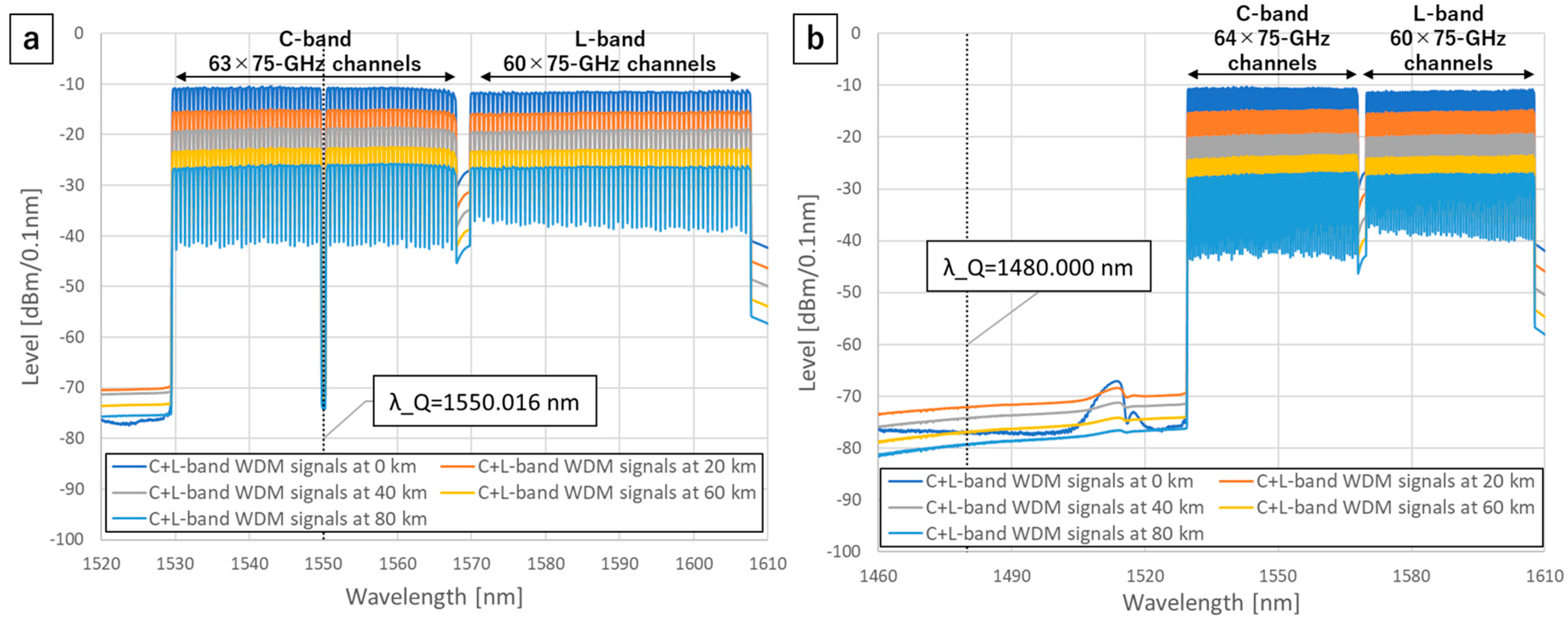
3. Results
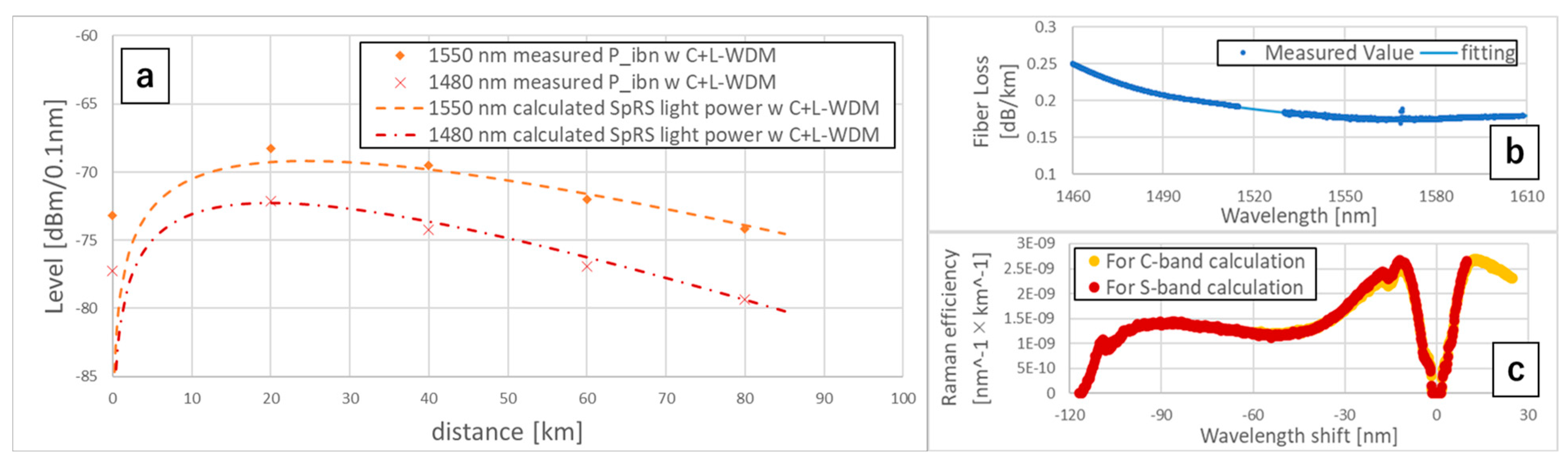
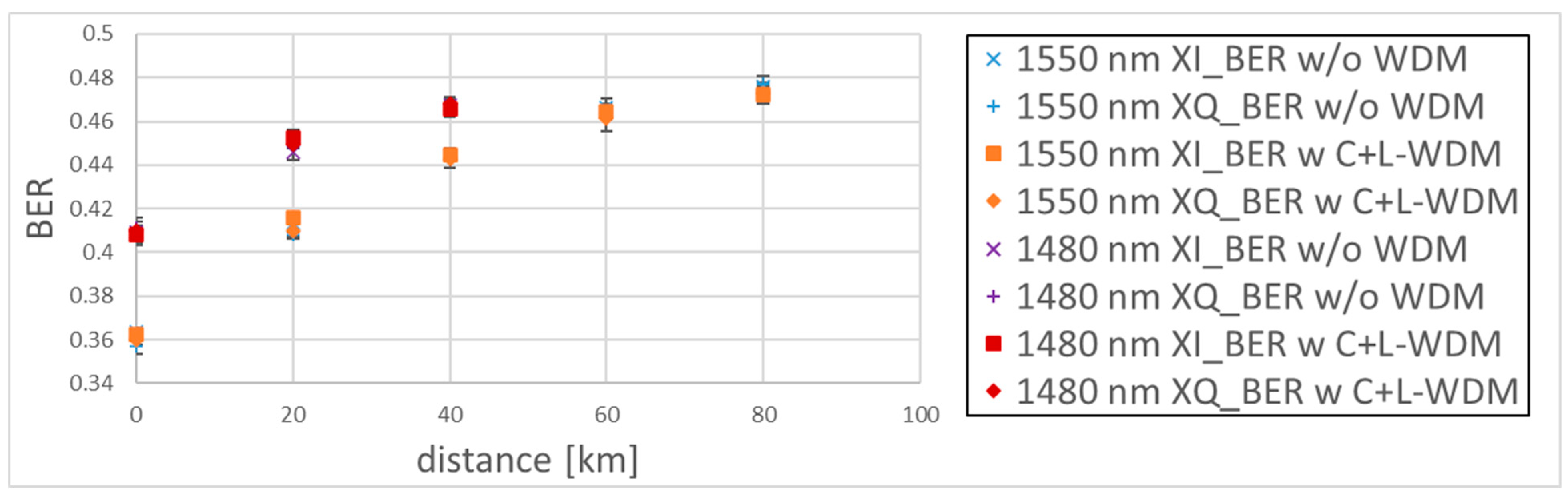
3.1. Analyzation of the QKD In-Band Noise Power
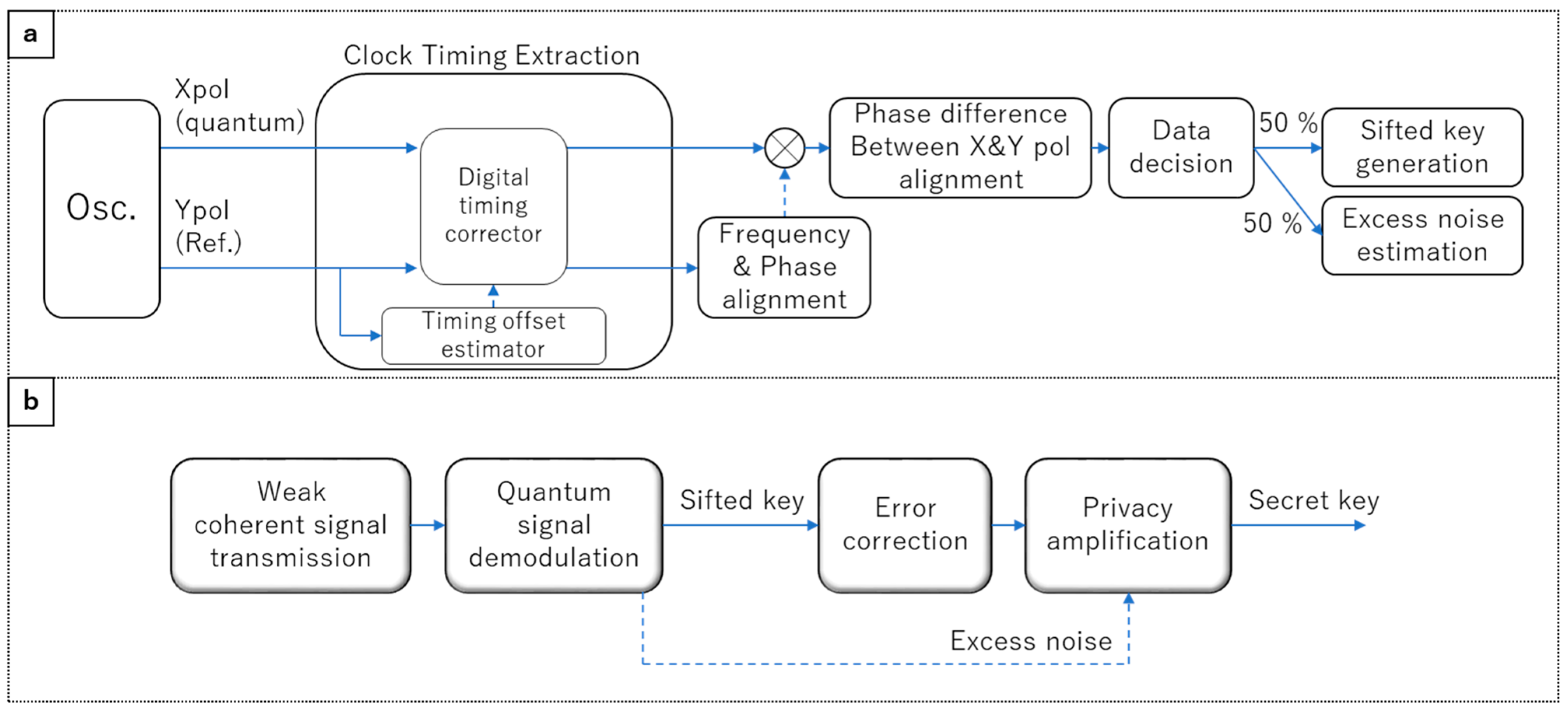
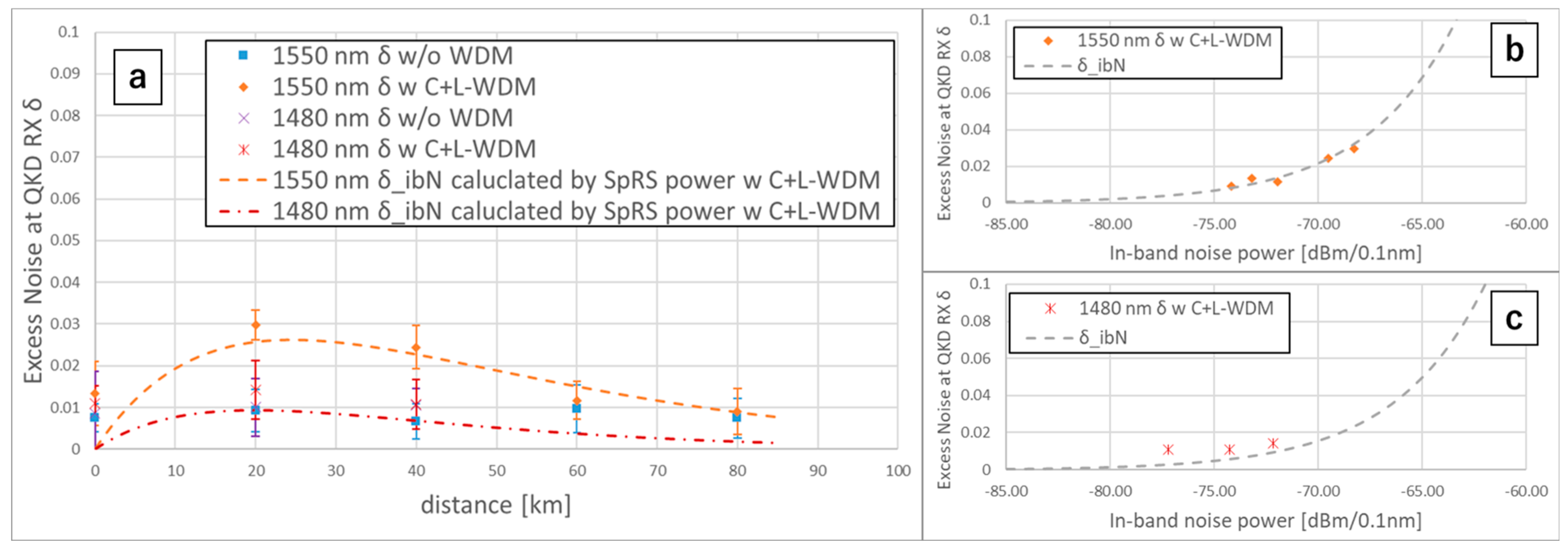
3.2. Analysis of the Excess Noise at the QKD RX
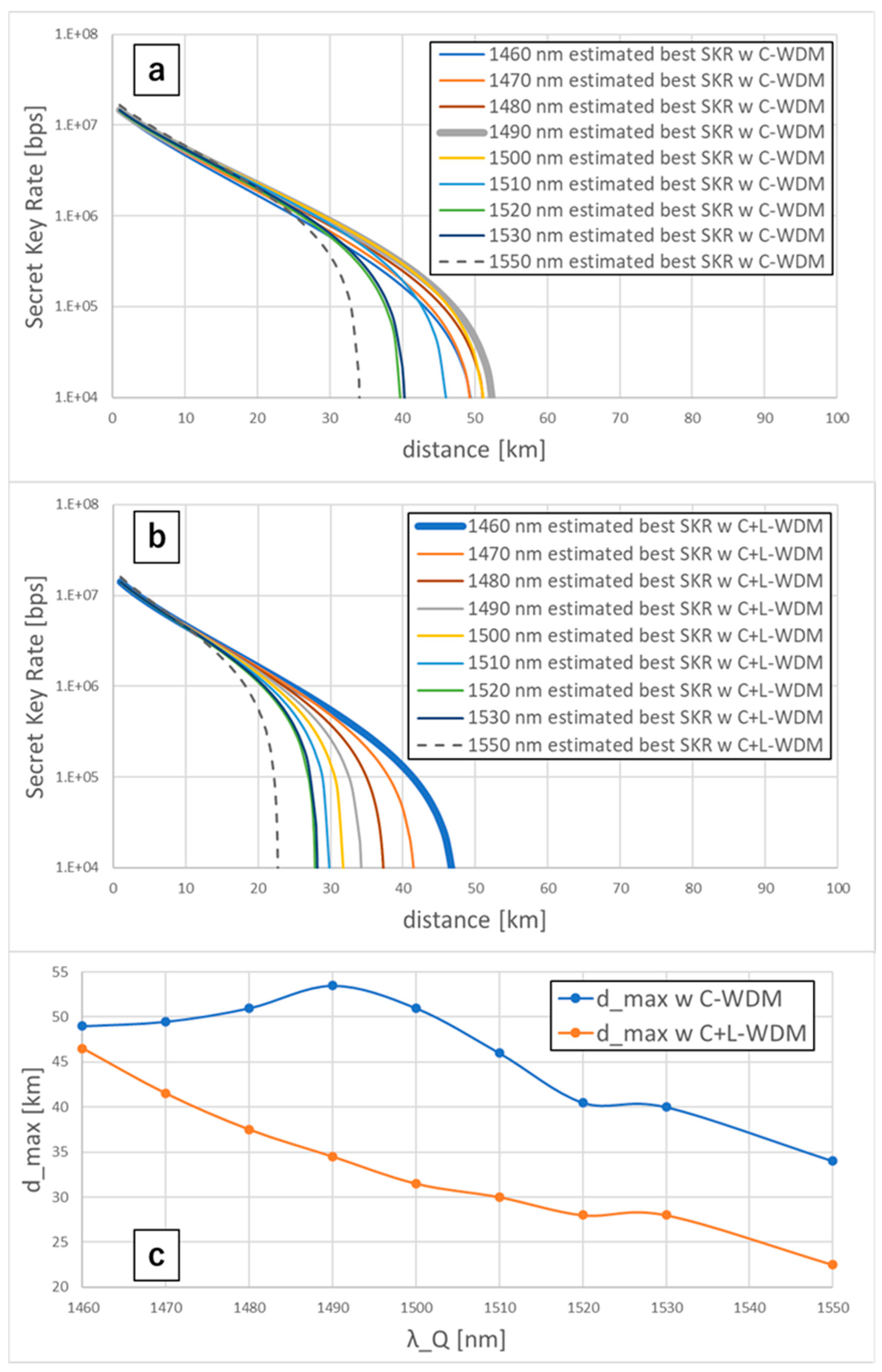
3.3. Secret Key Rate of Our CV-QKD System
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar]
- Hirano, T.; Ichikawa, T.; Matsubara, T.; Ono, M.; Oguri, Y.; Namiki, R.; Kasai, K.; Matsumoto, R.; Tsurumaru, T. Implementation of continuous-variable quantum key distribution with discrete modulation. Quantum Sci. Technol. 2017, 2, 2. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Hirano, T.; Puttnam, B.J.; Rademacher, G.; Luís, R.S.; Fujiwara, M.; Namiki, R.; Awaji, Y.; Takeoka, M.; Wada, N.; et al. Wavelength division multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun. Phys. 2019, 2, 9. [Google Scholar] [CrossRef]
- Gavignet, P.; Mondain, F.; Pincemin, E.; Grant, A.J.; Johnson, L.; Woodward, R.I.; Dynes, J.F.; Shields, A. Co-propagation of 6 Tb/s (60*100Gb/s) DWDM & QKD channels with ~17 dBm aggregated WDM power over 50 km Standard Single Mode Fiber. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 5–9 March 2023. [Google Scholar] [CrossRef]
- Pistoia, M.; Amer, O.; Behera, M.R.; Joseph, A.D.; Dynes, J.F.; John, B.; Haigh, P.A.; Kawakura, Y.; Kramer, D.H.; Lyon, J. Paving the way toward 800 Gbps quantum-secured optical channel deployment in mission-critical environments. Quantum Sci. Technol. 2023, 8, 035015. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Hirano, T.; Rademacher, G.; Puttnam, B.J.; Luís, R.S.; Fujiwara, M. Joint Propagation of Continuous Variable Quantum Key Distribution and 1824. In Proceeding of the 5 Gbaud PM-16QAM Channels. In Proceedings of the European Conference on Optical Communication, Roma, Italy, 23–27 September 2018. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, B.; Zhao, C.; Wang, G.; Wang, R.; Wang, H.; Zhou, F.; Nie, J.; Chen, Q.; Zhao, Y.; et al. Integrating quantum key distribution with classical communications in backbone fiber network. Opt. Express 2018, 26, 6010–6020. [Google Scholar] [CrossRef] [PubMed]
- Dynes, J.F.; Tam, W.W.; Plews, A.; Fröhlich, B.; Sharpe, A.W.; Lucamarini, M.; Yuan, Z.; Radig, C.; Straw, A.; Edwards, T.; et al. Ultra-high bandwidth quantum secured data transmission. Sci. Rep. 2016, 6, 35149. [Google Scholar] [CrossRef] [PubMed]
- Sebastian, K.; Joachim, S.; Rainer, H.D.; Christian, G.S. Experimental investigation of heterodyne quantum key distribution in the S-band or L-band embedded in a commercial C-band DWDM system. Opt. Express 2019, 27, 16540–16549. [Google Scholar] [CrossRef]
- Kawakami, T.; Kawahara, H.; Okamura, T.; Maeda, W. Integration of a C-band Digital Coherent CV-QKD Signal into Fully Loaded 9. In Proceeding of the 23-THz C+L-band DWDM Signals with a Total WDM Power of +19 dBm. In Proceedings of the European Conference on Optical Communication, Frankfurt, Germany, 22–26 September 2024. [Google Scholar]
- Xiang, Z. Efficient Clock and Carrier Recovery Algorithms for Single-Carrier Coherent Optical Systems: A systematic review on challenges and recent progress. IEEE Signal Process. Mag. 2014, 31, 35–45. [Google Scholar] [CrossRef]
- Kawahara, H.; Medhipour, A.; Inoue, K. Effect of spontaneous Raman scattering on quantum channel wavelength-multiplexed with classical channel. Opt. Commun. 2011, 284, 691–696. [Google Scholar] [CrossRef]
- Inoue, K.; Terazawa, D. Robustness of Intensity-Modulation/Direct-Detection Secret Key Distribution against Spontaneous Raman Scattering in Wavelength-Multiplexed Systems with Existing Optical Transmission Signals. IEICE Trans. Commun. 2023, 106, 1418–1423. [Google Scholar] [CrossRef]
- Peters, N.A.; Peters, P.; Toliver, T.E.; Chapuran, R.J.; Runser, S.R.; McNown, C.G.; Peterson, D.; Rosenberg, N.; Dallmann, R.J.; Hughes, K.P.; et al. Dense wavelength multiplexing of 1550 nm QKD with strong classical channels in reconfigurable networking environments. New J. Phys. 2009, 11, 045012. [Google Scholar] [CrossRef]
- Kumar, R.; Qin, H.; Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 2015, 17, 043027. [Google Scholar] [CrossRef]
- Nelson, L.E.; Woodward, S.L.; Foo, S.; Moyer, M.; Beckett DJ, S.; O’Sullivan, M.; Magill, P.D. Detection of a Single 40 Gb/s Polarization-Multiplexed QPSK Channel with a Real-Time Intradyne Receiver in the Presence of Multiple Coincident WDM Channels. J. Light. Technol. 2010, 28, 2933–2943. [Google Scholar] [CrossRef]
- Lin, J.; Upadhyaya, T.; Lütkenhaus, N. Asymptotic Security Analysis of Discrete-Modulated Continuous-Variable Quantum Key Distribution. Phys. Rev. X 2019, 9, 041064. [Google Scholar] [CrossRef]
- Kawakami, T.; Kawahara, H.; Okamura, T.; Yoshino, K.; Maeda, W. No-guard-band integration of a digital coherent CV-QKD system into 400 Gbits 75 GHz grid DWDM systems. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 March 2024. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawakami, T.; Kawahara, H.; Okamura, T.; Maeda, W. Coexistence Demonstration and Wavelength Dependency Analysis of S-Band CV-QKD Signal with Fully Loaded C+L-Band DWDM Signals. Entropy 2025, 27, 45. https://doi.org/10.3390/e27010045
Kawakami T, Kawahara H, Okamura T, Maeda W. Coexistence Demonstration and Wavelength Dependency Analysis of S-Band CV-QKD Signal with Fully Loaded C+L-Band DWDM Signals. Entropy. 2025; 27(1):45. https://doi.org/10.3390/e27010045
Chicago/Turabian StyleKawakami, Tetsuo, Hiroki Kawahara, Toshihiko Okamura, and Wakako Maeda. 2025. "Coexistence Demonstration and Wavelength Dependency Analysis of S-Band CV-QKD Signal with Fully Loaded C+L-Band DWDM Signals" Entropy 27, no. 1: 45. https://doi.org/10.3390/e27010045
APA StyleKawakami, T., Kawahara, H., Okamura, T., & Maeda, W. (2025). Coexistence Demonstration and Wavelength Dependency Analysis of S-Band CV-QKD Signal with Fully Loaded C+L-Band DWDM Signals. Entropy, 27(1), 45. https://doi.org/10.3390/e27010045





