Discontinuous Structural Transitions in Fluids with Competing Interactions
Abstract
:1. Introduction
2. The 1D System: Exact Results
2.1. Theoretical Background
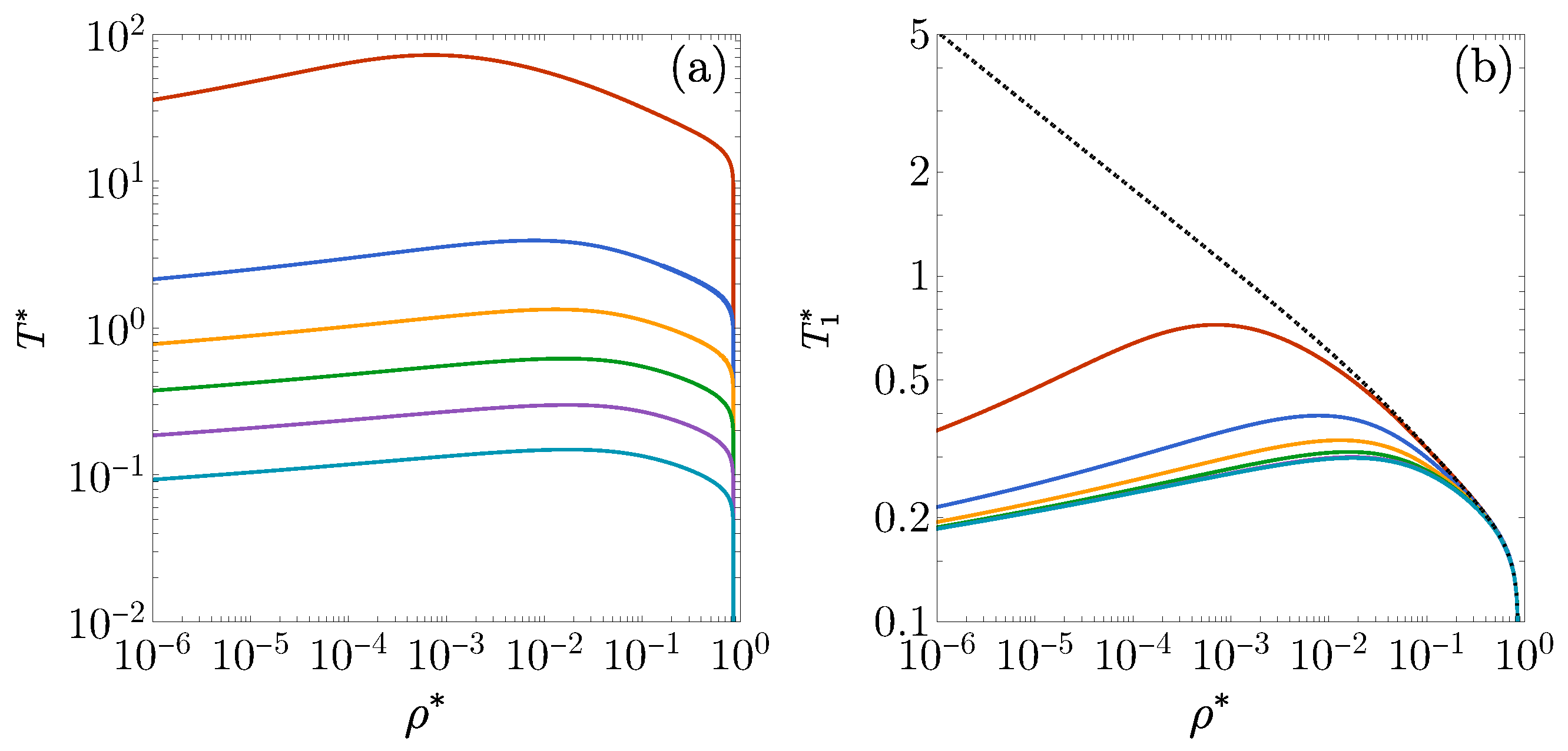
2.2. : Influence of on DOC Line
2.3. and : Influence of on DOC Line
2.4. , , and : Influence of on FW Line
3. The 3D System: RFA Results
3.1. Theoretical Background
3.2. : Influence of on DOC Line
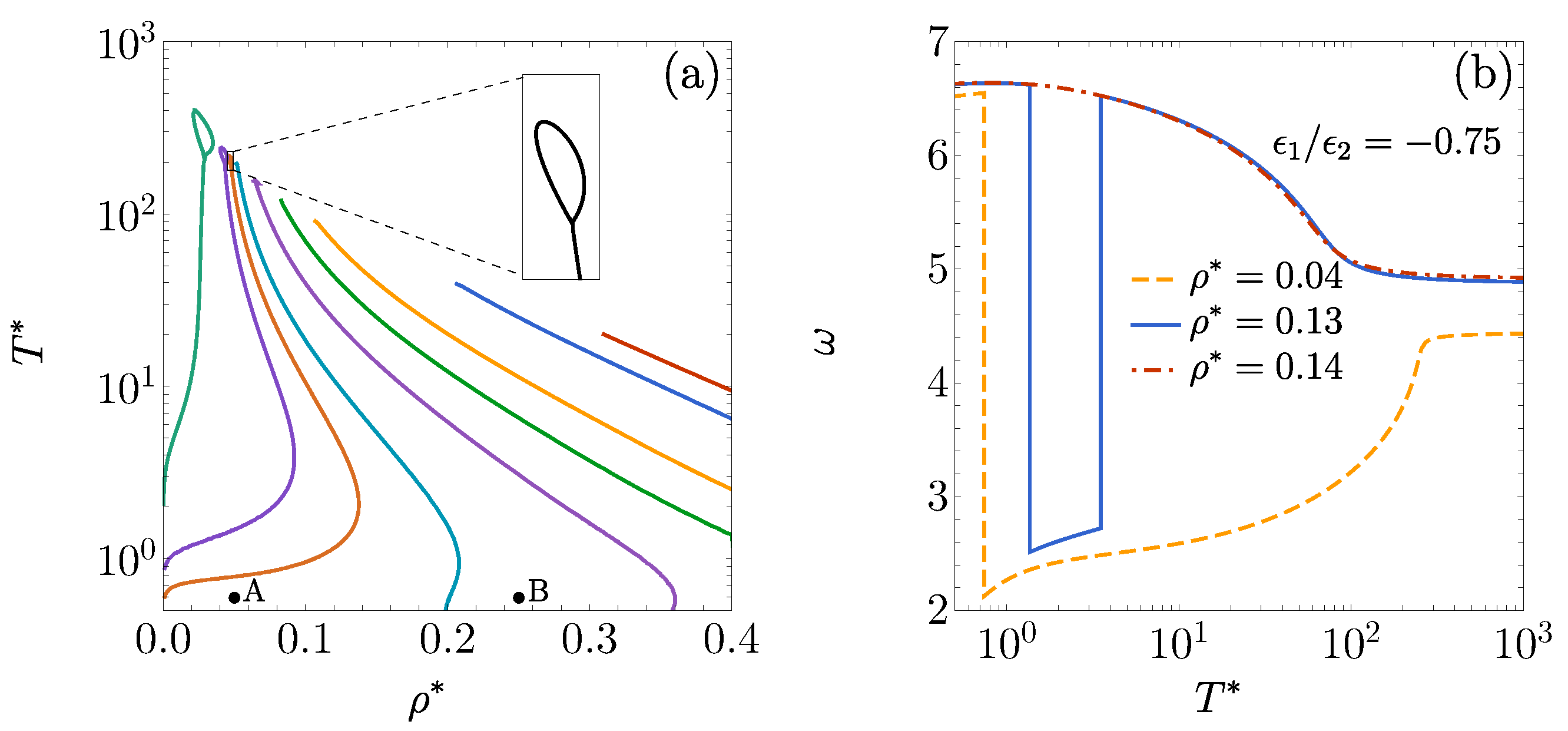
3.3. and : Influence of on DOC Line
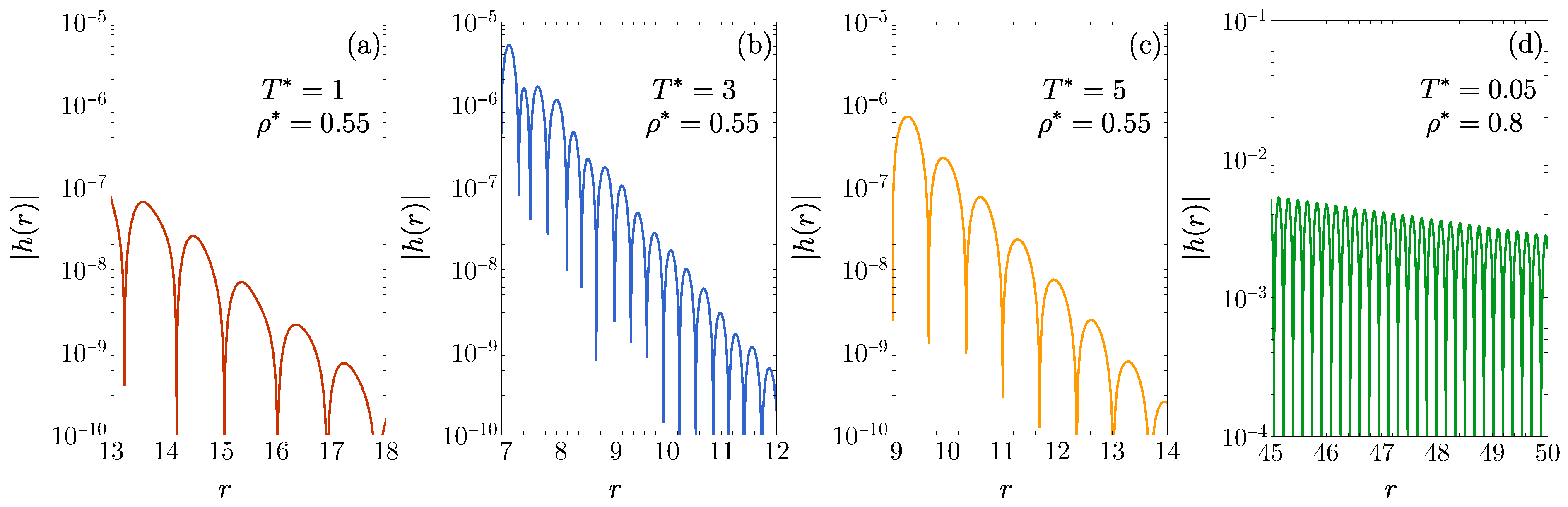
3.4. , , and : Influence of on FW Line
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 1D | One-dimensional |
| 3D | Three-dimensional |
| DOC | Discontinuous oscillation crossover |
| FW | Fisher–Widom |
| HR | Hard rod |
| RFA | Rational function approximation |
| SALR | Short-range attraction and long-range repulsion |
Appendix A. Some Mathematical Details in the Case of the 1D Fluid
Appendix A.1. Absence of Real Poles If φ(r)≥0
Appendix A.2. Poles for the High-Temperature Limit
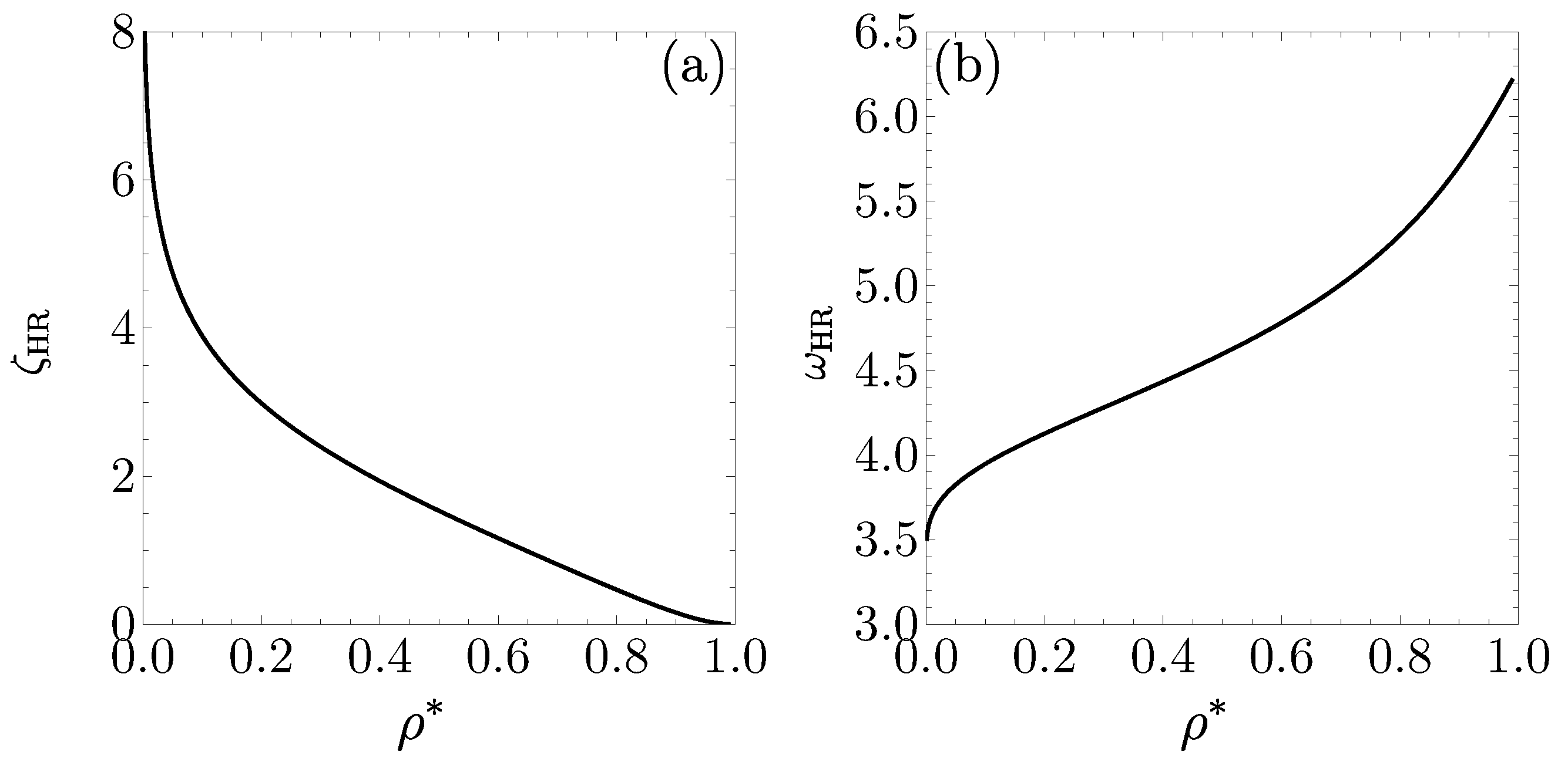
Appendix A.3. Poles for the Low-Temperature Limit with ϵ 1 >0
Appendix A.3.1. Case
Appendix A.3.2. Case
| p | ||||
|---|---|---|---|---|
Appendix B. Parameters in Equation (15)
References
- McQuarrie, D.A. Statistical Mechanics; Harper & Row: New York, NY, USA, 1976. [Google Scholar]
- Chapela, G.A.; Martínez-Casas, S.E.; Alejandre, J. Molecular dynamics for discontinuous potentials. I. General method and simulation of hard polyatomic molecules. Mol. Phys. 1984, 53, 139–159. [Google Scholar] [CrossRef]
- Chapela, G.A.; Scriven, L.E.; Davis, H.T. Molecular dynamics for discontinuous potential. IV. Lennard-Jonesium. J. Chem. Phys. 1989, 91, 4307–4313. [Google Scholar] [CrossRef]
- Benavides, A.L.; Gil-Villegas, A. The thermodynamics of molecules with discrete potentials. Mol. Phys. 1999, 97, 1225–1232. [Google Scholar] [CrossRef]
- Franzese, G.; Malescio, G.; Skibinsky, A.; Buldyrev, S.V.; Stanley, H.E. Generic mechanism for generating a liquid-liquid phase transition. Nature 2001, 409, 692–695. [Google Scholar] [CrossRef] [PubMed]
- Malescio, G.; Franzese, G.; Pellicane, G.; Skibinsky, A.; Buldyrev, S.V.; Stanley, H.E. Liquid-liquid phase transition in one-component fluids. J. Phys. Condens. Matter 2002, 14, 2193–2200. [Google Scholar] [CrossRef]
- Skibinsky, A.; Buldyrev, S.V.; Franzese, G.; Malescio, G.; Stanley, H.E. Liquid-liquid phase transitions for soft-core attractive potentials. Phys. Rev. E 2004, 69, 061206. [Google Scholar] [CrossRef]
- Malescio, G.; Franzese, G.; Skibinsky, A.; Buldyrev, S.V.; Stanley, H.E. Liquid-liquid phase transition for an attractive isotropic potential with wide repulsive range. Phys. Rev. E 2005, 71, 061504. [Google Scholar] [CrossRef]
- Benavides, A.L.; del Pino, L.A.; Gil-Villegas, A.; Sastre, F. Thermodynamic and structural properties of confined discrete-potential fluids. J. Chem. Phys. 2006, 125, 204715. [Google Scholar] [CrossRef] [PubMed]
- Cervantes, L.A.; Benavides, A.L.; del Río, F. Theoretical prediction of multiple fluid-fluid transitions in monocomponent fluids. J. Chem. Phys. 2007, 126, 084507. [Google Scholar] [CrossRef] [PubMed]
- Guillén-Escamilla, I.; Chávez-Páez, M.; Castañeda-Priego, R. Structure and thermodynamics of discrete potential fluids in the OZ-HMSA formalism. J. Phys. Condens. Matter 2007, 19, 086224. [Google Scholar] [CrossRef]
- Rżysko, W.; Pizio, O.; Patrykiejew, A.; Sokolowski, S. Phase diagram of a square-shoulder, square-well fluid revisited. J. Chem. Phys. 2008, 129, 124502. [Google Scholar] [CrossRef]
- de Oliveira, A.B.; Franzese, G.; Netz, P.A.; Barbosa, M.C. Waterlike hierarchy of anomalies in a continuous spherical shouldered potential. J. Chem. Phys. 2008, 128, 064901. [Google Scholar] [CrossRef]
- de Oliveira, A.B.; Netz, P.A.; Barbosa, M.C. An ubiquitous mechanism for water-like anomalies. Europhys. Lett. 2009, 85, 36001. [Google Scholar] [CrossRef]
- Rżysko, W.; Patrykiejew, A.; Sokołowski, S.; Pizio, O. Phase behavior of a two-dimensional and confined in slitlike pores square-shoulder, square-well fluid. J. Chem. Phys. 2010, 132, 164702. [Google Scholar] [CrossRef]
- Hlushak, S.P.; Trokhymchuk, A.D.; Sokołowski, S. Direct correlation function for complex square barrier-square well potentials in the first-order mean spherical approximation. J. Chem. Phys. 2011, 134, 114101. [Google Scholar] [CrossRef]
- Yuste, S.B.; Santos, A.; López de Haro, M. Structure of the square-shoulder fluid. Mol. Phys. 2011, 109, 987–995. [Google Scholar] [CrossRef]
- Bárcenas, M.; Odriozola, G.; Orea, P. Propiedades termodinámicas de fluidos de hombro/pozo cuadrado. Rev. Mex. Fís. 2011, 57, 485–490. [Google Scholar]
- Loredo-Osti, A.; Castañeda-Priego, R. Analytic Structure Factor of Discrete Potential Fluids: Cluster-Like Correlations and Micro-Phases. J. Nanofluids 2012, 1, 36–43. [Google Scholar] [CrossRef]
- Santos, A.; Yuste, S.B.; López de Haro, M. Rational-function approximation for fluids interacting via piece-wise constant potentials. Condens. Matter Phys. 2012, 15, 23602. [Google Scholar] [CrossRef]
- Bárcenas, M.; Odriozola, G.; Orea, P. Structure and coexistence properties of shoulder-square well fluids. J. Mol. Liq. 2013, 185, 70–75. [Google Scholar] [CrossRef]
- Santos, A.; Yuste, S.B.; López de Haro, M.; Bárcenas, M.; Orea, P. Structural properties of fluids interacting via piece-wise constant potentials with a hard core. J. Chem. Phys. 2013, 139, 074505. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.Y.; Kim, S.C. Structure of discrete-potential fluids interacting via two piece-wise constant potentials with a hard-core. J. Mol. Liq. 2013, 187, 326–331. [Google Scholar] [CrossRef]
- Yuste, S.B.; Santos, A.; López de Haro, M. Structural and thermodynamic properties of fluids whose molecules interact via one-, two-, and three-step potentials. J. Mol. Liq. 2022, 364, 119890. [Google Scholar] [CrossRef]
- Perdomo-Pérez, R.; Martínez-Rivera, J.; Palmero-Cruz, N.C.; Sandoval-Puentes, M.A.; Gallegos, J.A.S.; Lázaro-Lázaro, E.; Valadez-Pérez, N.E.; Torres-Carbajal, A.; Castañeda-Priego, R. Thermodynamics, static properties and transport behaviour of fluids with competing interactions. J. Phys. Condens. Matter 2022, 34, 144005. [Google Scholar] [CrossRef] [PubMed]
- Largo, J.; Solana, J.R. Liquid-liquid transition in a simple model fluid with competitive interactions. Mol. Phys. 2014, 122, e2356756. [Google Scholar] [CrossRef]
- Ruiz-Franco, J.; Zaccarelli, E. On the Role of Competing Interactions in Charged Colloids with Short-Range Attraction. Annu. Rev. Condens. Matter Phys. 2021, 12, 51–70. [Google Scholar] [CrossRef]
- Kravtsiv, I.; Patsahan, T.; Holovko, M.; di Caprio, D. Soft core fluid with competing interactions at a hard wall. J. Mol. Liq. 2022, 362, 119652. [Google Scholar] [CrossRef]
- Carretas-Talamante, A.G.; Zepeda-López, J.B.; Lázaro-Lázaro, E.; Elizondo-Aguilera, L.F.; Medina-Noyola, M. Non-equilibrium view of the amorphous solidification of liquids with competing interactions. J. Chem. Phys. 2023, 158, 064506. [Google Scholar] [CrossRef]
- Tan, Z.; Calandrini, V.; Dhont, J.K.G.; Nägele, G. Quasi-two-dimensional dispersions of Brownian particles with competitive interactions: Phase behavior and structural properties. Soft Matter 2024, 20, 9528–9546. [Google Scholar] [CrossRef] [PubMed]
- Imperio, A.; Reatto, L. Microphase separation in two-dimensional systems with competing interactions. J. Chem. Phys. 2006, 124, 164712. [Google Scholar] [CrossRef]
- Archer, A.J.; Wilding, N.B. Phase behavior of a fluid with competing attractive and repulsive interactions. Phys. Rev. E 2007, 76, 031501. [Google Scholar] [CrossRef] [PubMed]
- Bomont, J.M.; Bretonnet, J.L.; Costa, D.; Hansen, J.P. Communication: Thermodynamic signatures of cluster formation in fluids with competing interactions. J. Chem. Phys. 2012, 137, 011101. [Google Scholar] [CrossRef]
- Bollinger, J.A.; Truskett, T.M. Fluids with competing interactions. I. Decoding the structure factor to detect and characterize self-limited clustering. J. Chem. Phys. 2016, 145, 064902. [Google Scholar] [CrossRef]
- Bollinger, J.A.; Truskett, T.M. Fluids with competing interactions. II. Validating a free energy model for equilibrium cluster size. J. Chem. Phys. 2016, 145, 064903. [Google Scholar] [CrossRef]
- Hu, Y.; Charbonneau, P. Clustering and assembly dynamics of a one-dimensional microphase former. Soft Matter 2018, 14, 4101–4109. [Google Scholar] [CrossRef] [PubMed]
- Malescio, G.; Sciortino, F. Aggregate formation in fluids with bounded repulsive core and competing interactions. J. Mol. Liq. 2020, 303, 12601. [Google Scholar] [CrossRef]
- Bomont, J.M.; Costa, D.; Bretonnet, J.L. Local order and cluster formation in model fluids with competing interactions: A simulation and theoretical study. Phys. Chem. Chem. Phys. 2020, 22, 5355–5365. [Google Scholar] [CrossRef] [PubMed]
- Guillén-Escamilla, I.; Méndez-Bermúdez, J.G.; Mixteco-Sánchez, J.C.; Méndez-Maldonado, G.A. Microphase and macrophase separations in discrete potential fluids. Rev. Mex. Fís. 2022, 68, 050502. [Google Scholar] [CrossRef]
- Munaò, G.; Costa, D.; Malescio, G.; Bomont, J.M.; Prestipino, S. Competition between clustering and phase separation in binary mixtures containing SALR particles. Soft Matter 2022, 18, 6453–6464. [Google Scholar] [CrossRef]
- Munaò, G.; Prestipino, S.; Bomont, J.M.; Costa, D. Clustering in Mixtures of SALR Particles and Hard Spheres with Cross Attraction. J. Phys. Chem. B 2022, 126, 2027–2039. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.; Munaò, G.; Bomont, J.M.; Malescio, G.; Palatella, A.; Prestipino, S. Microphase versus macrophase separation in the square-well-linear fluid: A theoretical and computational study. Phys. Rev. E 2023, 108, 034602. [Google Scholar] [CrossRef]
- Bomont, J.M.; Pastore, G.; Costa, D.; Munaò, G.; Malescio, G.; Prestipino, S. Arrested states in colloidal fluids with competing interactions: A static replica study. J. Chem. Phys. 2024, 160, 214504. [Google Scholar] [CrossRef]
- Denton, A.R.; Löwen, H. The influence of short-range attractive and repulsive interactions on the phase behaviour of model colloidal suspensions. J. Phys. Condens. Matter 1997, 9, 8907–8919. [Google Scholar] [CrossRef]
- Sear, R.P.; Gelbart, W.M. Microphase separation versus the vapor-liquid transition in systems of spherical particles. J. Chem. Phys. 1999, 110, 4582–4588. [Google Scholar] [CrossRef]
- Pini, D.; Jialin, G.; Parola, A.; Reatto, L. Enhanced density fluctuations in fluid systems with competing interactions. Chem. Phys. Lett. 2000, 327, 209–215. [Google Scholar] [CrossRef]
- Mossa, S.; Sciortino, F.; Tartaglia, P.; Zaccarelli, E. Ground-State Clusters for Short-Range Attractive and Long-Range Repulsive Potentials. Langmuir 2004, 20, 10756–10763. [Google Scholar] [CrossRef] [PubMed]
- Sciortino, F.; Mossa, S.; Zaccarelli, E.; Tartaglia, P. Equilibrium Cluster Phases and Low-Density Arrested Disordered States: The Role of Short-Range Attraction and Long-Range Repulsion. Phys. Rev. Lett. 2004, 93, 055701. [Google Scholar] [CrossRef]
- Archer, A.J.; Pini, D.; Evans, R.; Reatto, L. Model colloidal fluid with competing interactions: Bulk and interfacial properties. J. Chem. Phys. 2007, 126, 014104. [Google Scholar] [CrossRef] [PubMed]
- Archer, A.J.; Ionescu, C.; Pini, D.; Reatto, L. Theory for the phase behaviour of a colloidal fluid with competing interactions. J. Phys. Condens. Matter 2008, 20, 415106. [Google Scholar] [CrossRef]
- Bomont, J.M.; Costa, D. A theoretical study of structure and thermodynamics of fluids with long-range competing interactions exhibiting pattern formation. J. Chem. Phys. 2012, 137, 164901. [Google Scholar] [CrossRef] [PubMed]
- Pȩkalski, J.; Ciach, A.; Almarza, N.G. Periodic ordering of clusters in a one-dimensional lattice model. J. Chem. Phys. 2013, 138, 144903. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.Y.; Kim, S.C. Structural properties of fluids with short-range attractive and repulsive tails: Inverse temperature expansion. J. Kor. Phys. Soc. 2014, 64, 844–851. [Google Scholar] [CrossRef]
- Godfrin, P.D.; Valadez-Pérez, N.E.; Castañeda Priego, R.; Wagner, N.J.; Liu, Y. Generalized phase behavior of cluster formation in colloidal dispersions with competing interactions. Soft Matter 2014, 10, 5061–5071. [Google Scholar] [CrossRef] [PubMed]
- Sweatman, M.B.; Fartaria, R.; Lue, L. Cluster formation in fluids with competing short-range and long-range interactions. J. Chem. Phys. 2014, 140, 124508. [Google Scholar] [CrossRef] [PubMed]
- Cigala, G.; Costa, D.; Bomont, J.M.; Caccamo, C. Aggregate formation in a model fluid with microscopic piecewise-continuous competing interactions. Mol. Phys. 2015, 113, 2583–2592. [Google Scholar] [CrossRef]
- Zhuang, Y.; Charbonneau, P. Recent Advances in the Theory and Simulation of Model Colloidal Microphase Formers. J. Phys. Chem. B 2016, 120, 7775–7782. [Google Scholar] [CrossRef]
- Liu, Y.; Xi, Y. Colloidal systems with a short-range attraction and long-range repulsion: Phase diagrams, structures, and dynamics. Curr. Opin. Colloid Interface Sci. 2019, 39, 123–136. [Google Scholar] [CrossRef]
- Bretonnet, J.L. Competing interactions in colloidal suspensions. AIMS Mater. Sci. 2019, 6, 509–548. [Google Scholar] [CrossRef]
- Charbonneau, P.; Kundu, J. Postponing the dynamical transition density using competing interactions. Granul. Matter 2020, 22, 55. [Google Scholar] [CrossRef]
- Valadez-Pérez, N.E.; Liu, Y.; Castañeda-Priego, R. Cluster Morphology of Colloidal Systems With Competing Interactions. Front. Phys. 2021, 9, 637138. [Google Scholar] [CrossRef]
- López de Haro, M.; Yuste, S.B.; Santos, A. Alternative Approaches to the Equilibrium Properties of Hard-Sphere Liquids. In Theory and Simulation of Hard-Sphere Fluids and Related Systems; Mulero, A., Ed.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 753, pp. 183–245. [Google Scholar] [CrossRef]
- Santos, A. A Concise Course on the Theory of Classical Liquids. Basics and Selected Topics; Lecture Notes in Physics; Springer: New York, NY, USA, 2016; Volume 923. [Google Scholar] [CrossRef]
- Pieprzyk, S.; Brańka, A.C.; Yuste, S.B.; Santos, A.; López de Haro, M. Structural properties of additive binary hard-sphere mixtures. Phys. Rev. E 2020, 101, 012117. [Google Scholar] [CrossRef]
- Pieprzyk, S.; Yuste, S.B.; Santos, A.; López de Haro, M.; Brańka, A.C. Structural properties of additive binary hard-sphere mixtures. II. Asymptotic behavior and structural crossovers. Phys. Rev. E 2021, 104, 024128. [Google Scholar] [CrossRef]
- Grodon, C.; Dijkstra, M.; Evans, R.; Roth, R. Decay of correlation functions in hard-sphere mixtures: Structural crossover. J. Chem. Phys. 2004, 121, 7869–7882. [Google Scholar] [CrossRef]
- Grodon, C.; Dijkstra, M.; Evans, R.; Roth, R. Homogeneous and inhomogeneous hard-sphere mixtures: Manifestations of structural crossover. Mol. Phys. 2005, 103, 3009–3023. [Google Scholar] [CrossRef]
- Statt, A.; Pinchaipat, R.; Turci, F.; Evans, R.; Royall, C.P. Direct observation in 3d of structural crossover in binary hard sphere mixtures. J. Chem. Phys. 2016, 144, 144506. [Google Scholar] [CrossRef]
- Royall, C.P.; Charbonneau, P.; Dijkstra, M.; Russo, J.; Smallenburg, F.; Speck, T.; Valeriani, C. Colloidal hard spheres: Triumphs, challenges, and mysteries. Rev. Mod. Phys. 2024, 96, 045003. [Google Scholar] [CrossRef]
- Salsburg, Z.W.; Zwanzig, R.W.; Kirkwood, J.G. Molecular distribution functions in a one-dimensional fluid. J. Chem. Phys. 1953, 21, 1098–1107. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Zomick, D. Mixtures of hard spheres with nonadditive diameters: Some exact results and solution of PY equation. J. Chem. Phys. 1971, 54, 3335–3346. [Google Scholar] [CrossRef]
- Percus, J.K. Equilibrium state of a classical fluid of hard rods in an external field. J. Stat. Phys. 1976, 15, 505–511. [Google Scholar] [CrossRef]
- Percus, J.K. One-dimensional classical fluid with nearest-neighbor interaction in arbitrary external field. J. Stat. Phys. 1982, 28, 67–81. [Google Scholar] [CrossRef]
- Heying, M.; Corti, D.S. The one-dimensional fully non-additive binary hard rod mixture: Exact thermophysical properties. Fluid Phase Equilib. 2004, 220, 85–103. [Google Scholar] [CrossRef]
- Montero, A.M.; Santos, A. Triangle-Well and Ramp Interactions in One-Dimensional Fluids: A Fully Analytic Exact Solution. J. Stat. Phys. 2019, 175, 269–288. [Google Scholar] [CrossRef]
- Montero, A.M.; Rodríguez-Rivas, A.; Yuste, S.B.; Santos, A.; López de Haro, M. On a conjecture concerning the Fisher–Widom line and the line of vanishing excess isothermal compressibility in simple fluids. Mol. Phys. 2024, 122, e2357270. [Google Scholar] [CrossRef]
- Yuste, S.B. Numerical Inversion of Laplace Transforms Using the Euler Method of Abate and Whitt. 2023. Available online: https://github.com/SantosBravo/Numerical-Inverse-Laplace-Transform-Abate-Whitt (accessed on 2 December 2024).
- Alder, B.J.; Wainwright, T.E. Phase Transition for a Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
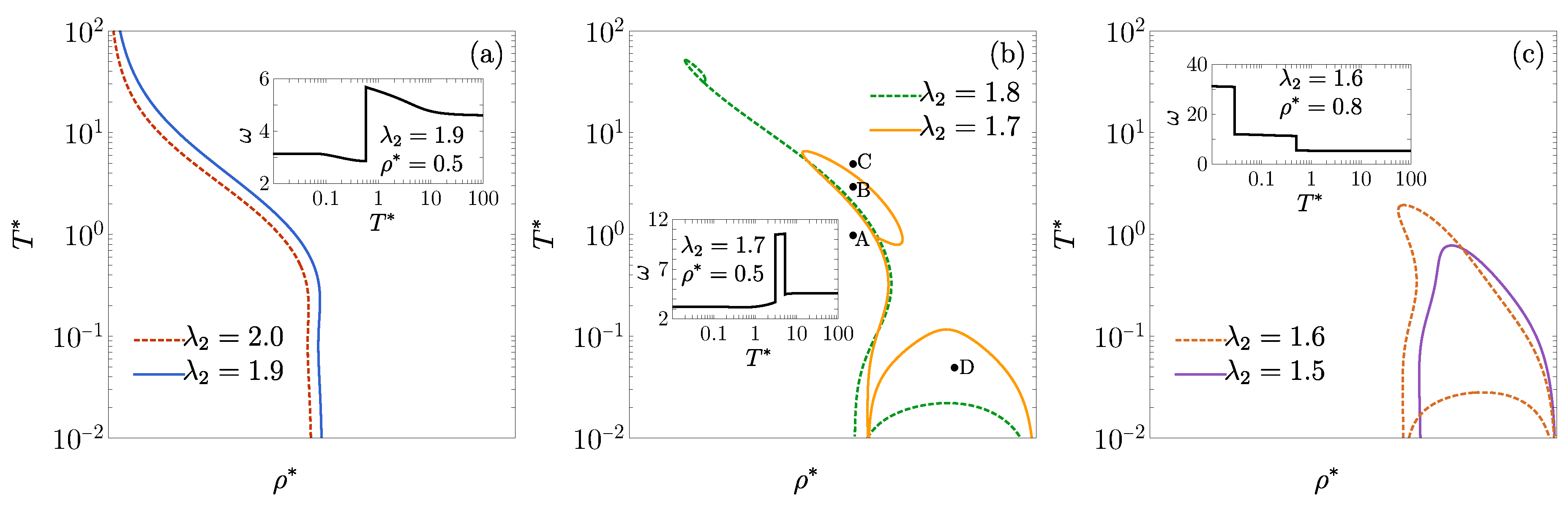
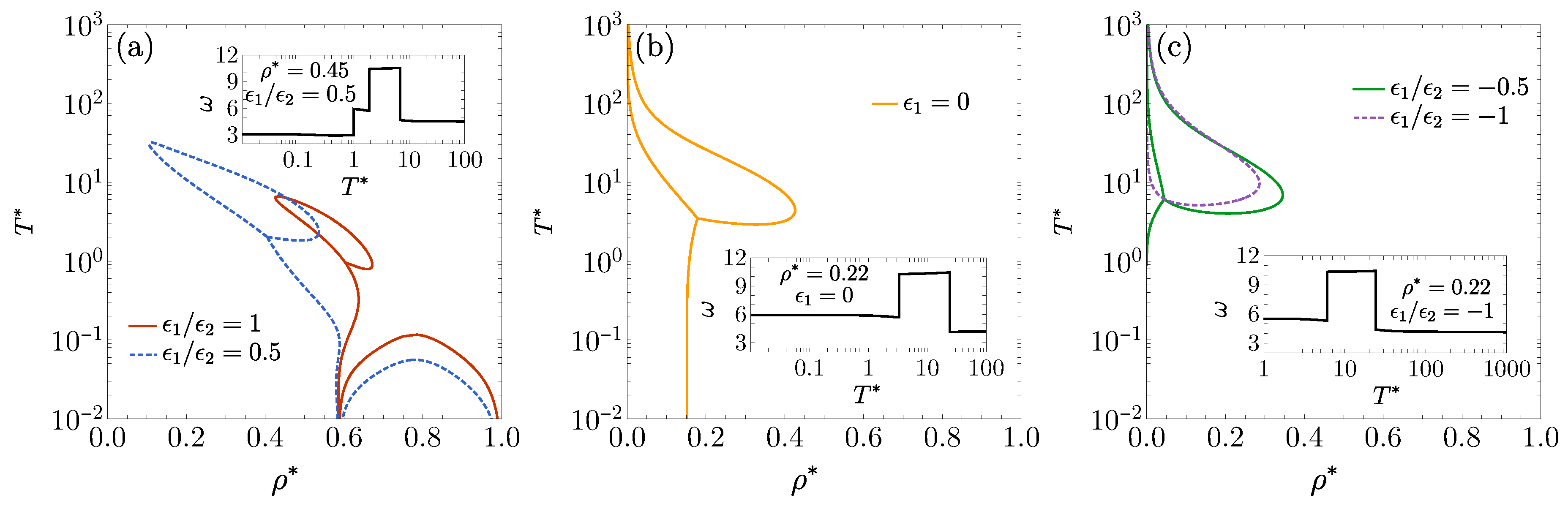
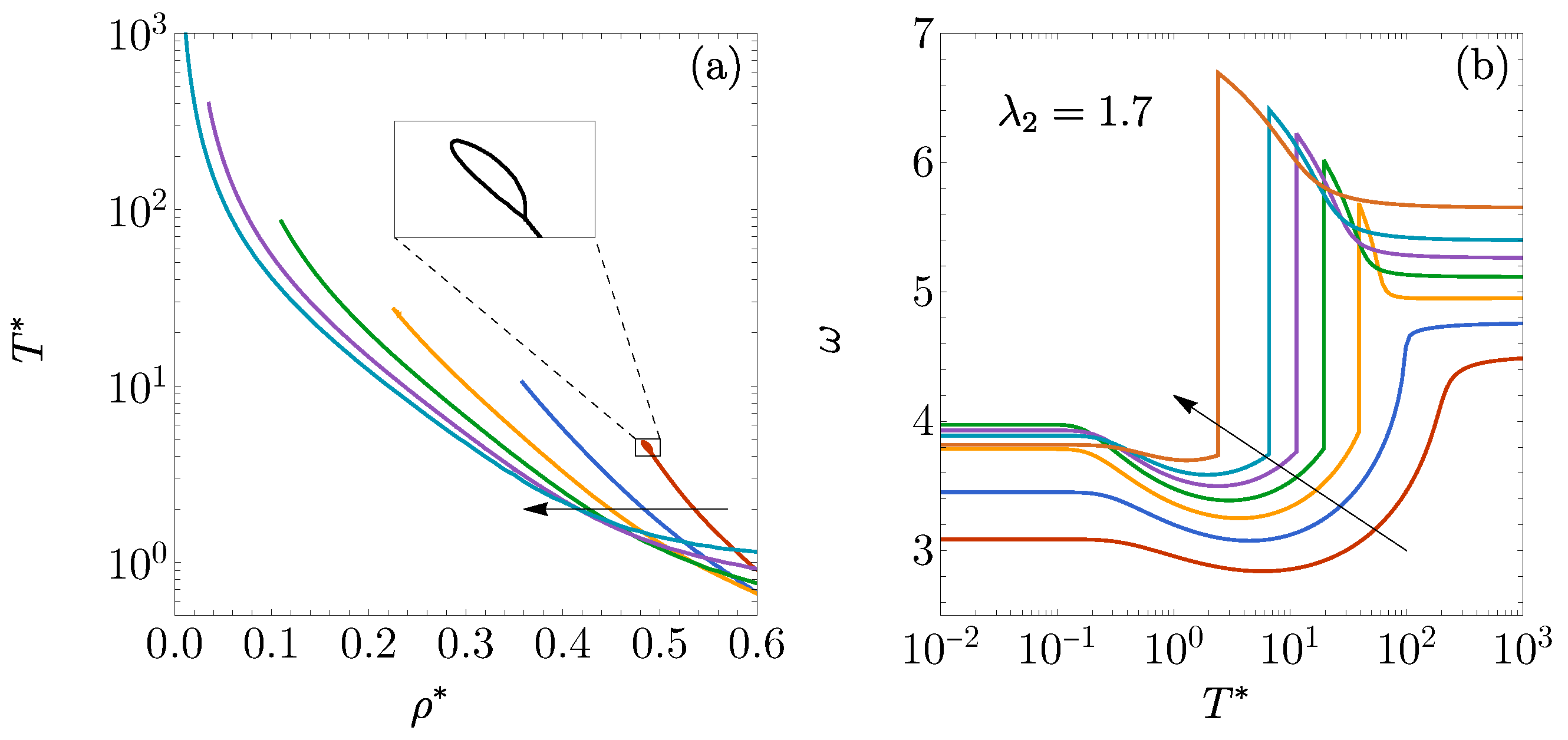

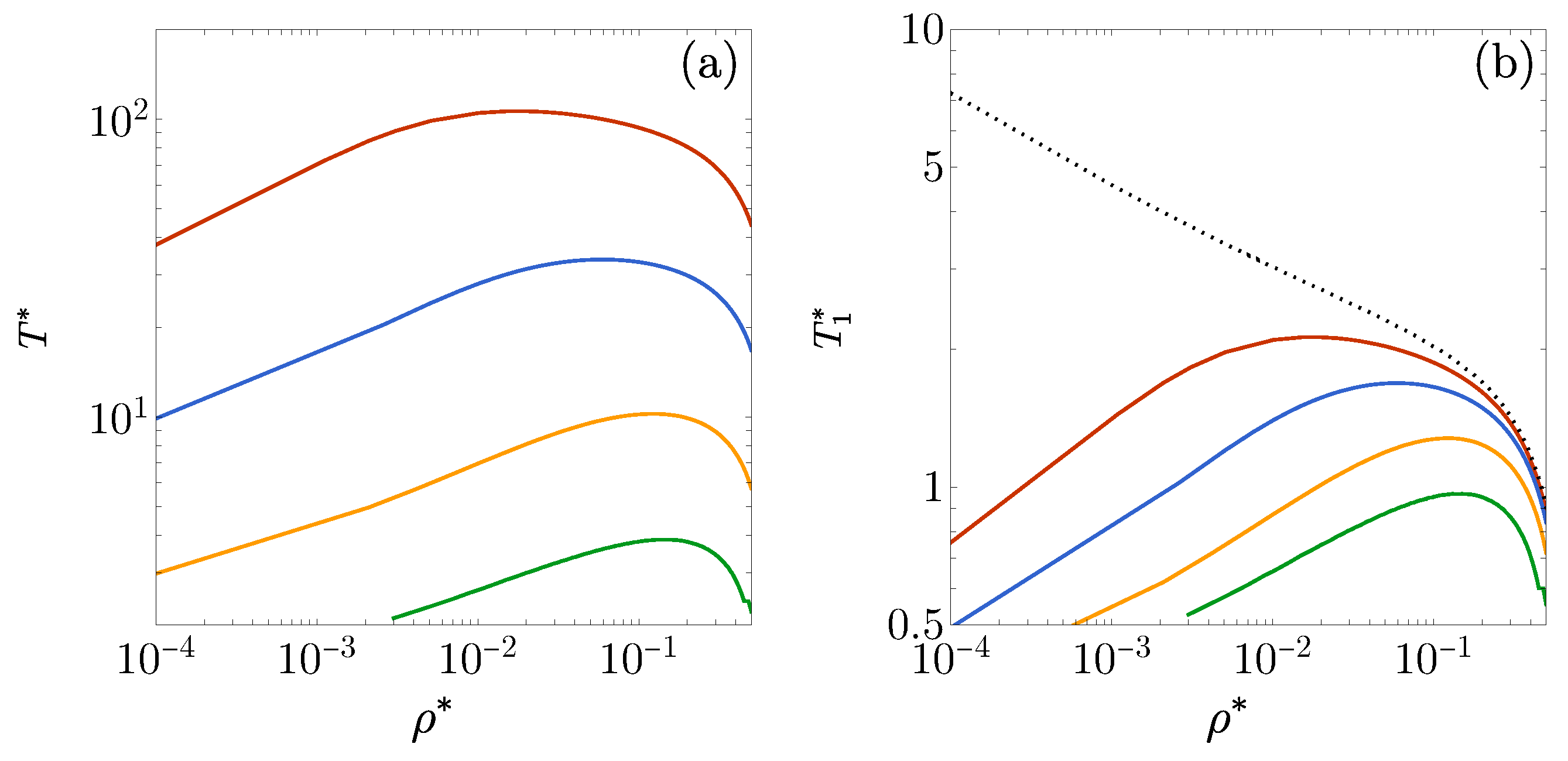
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montero, A.M.; Yuste, S.B.; Santos, A.; de Haro, M.L. Discontinuous Structural Transitions in Fluids with Competing Interactions. Entropy 2025, 27, 95. https://doi.org/10.3390/e27010095
Montero AM, Yuste SB, Santos A, de Haro ML. Discontinuous Structural Transitions in Fluids with Competing Interactions. Entropy. 2025; 27(1):95. https://doi.org/10.3390/e27010095
Chicago/Turabian StyleMontero, Ana M., Santos B. Yuste, Andrés Santos, and Mariano López de Haro. 2025. "Discontinuous Structural Transitions in Fluids with Competing Interactions" Entropy 27, no. 1: 95. https://doi.org/10.3390/e27010095
APA StyleMontero, A. M., Yuste, S. B., Santos, A., & de Haro, M. L. (2025). Discontinuous Structural Transitions in Fluids with Competing Interactions. Entropy, 27(1), 95. https://doi.org/10.3390/e27010095








