An Approximate Bayesian Approach to Optimal Input Signal Design for System Identification
Abstract
1. Introduction
2. Formulation of the Problem
3. Approximate Solutions
3.1. Finite Parameter Space
3.2. Infinite Parameter Space
4. Bayesian Input Signal Design in Quasi-Linear Control Systems
5. Comparison with Classical Methods of Input Signal Design
6. Examples of Input Signal Design
6.1. Elementary Example
6.2. Example with a Non-Gaussian Prior Distribution
6.3. Optimal Input Design for the Atomic Sensor Model
6.4. Bayesian Input Signal Design for the Pump Laser in an Optically Pumped Magnetometer
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
Appendix A. Proofs
- (1)
- Set the initial conditions:
- (2)
- For , calculate
Appendix B. An Example of the Gap Between the ITB and BCRB
Appendix C. Discretization of Linear SDE
References
- Goodwin, G.C.; Payne, R.L. Dynamic System Identification: Experiment Design and Data Analysis; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall PTR: Saddle River, NJ, USA, 1999. [Google Scholar]
- Söderström, T.; Stoica, P. System Identification; Prentice-Hall International Series in Systems and Control Engineering; Prentice-Hall: Saddle River, NJ, USA, 1989. [Google Scholar]
- Pronzato, L. Optimal experimental design and some related control problems. Automatica 2008, 44, 303–325. [Google Scholar] [CrossRef]
- Huan, X.; Jagalur, J.; Marzouk, Y. Optimal experimental design: Formulations and computations. Acta Numer. 2024, 33, 715–840. [Google Scholar] [CrossRef]
- Rainforth, T.; Foster, A.; Ivanova, D.R.; Bickford Smith, F. Modern Bayesian Experimental Design. Stat. Sci. 2024, 39, 100–114. [Google Scholar] [CrossRef]
- Fedorov, V.V.; Hackl, P. Model-Oriented Design of Experiments; Springer: Berlin/Heidelberg, Germany, 1997; Volume 125. [Google Scholar]
- Lindley, D.V. On a Measure of the Information Provided by an Experiment. Ann. Math. Stat. 1956, 27, 986–1005. [Google Scholar] [CrossRef]
- Arimoto, S.; Kimura, H. Optimum input test signals for system identification—An information-theoretical approach. Int. J. Syst. Sci. 1971, 1, 279–290. [Google Scholar] [CrossRef]
- Chaloner, K.; Verdinelli, I. Bayesian Experimental Design: A Review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Ryan, E.; Drovandi, C.; McGree, J.; Pettitt, A. A Review of Modern Computational Algorithms for Bayesian Optimal Design. Int. Stat. Rev. 2015, 84, 128–154. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.D. Estimating Mixture Entropy with Pairwise Distances. Entropy 2017, 19, 361. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.D. Estimating Mixture Entropy with Pairwise Distances. arXiv 2017, arXiv:1706.02419. [Google Scholar]
- Altafini, C.; Ticozzi, F. Modeling and Control of Quantum Systems: An Introduction. IEEE Trans. Autom. Control 2012, 57, 1898–1917. [Google Scholar] [CrossRef]
- Dong, D.; Petersen, I.R. Quantum control theory and applications: A survey. IET Control Theory Appl. 2010, 4, 2651–2671. [Google Scholar] [CrossRef]
- Friedly, J.C. Dynamic Behavior of Processes; Prentice-Hall International Series in the Physical and Chemical Engineering Sciences; Prentice-Hall: Englewood Cliffs, NJ, USA, 1972; p. 590. [Google Scholar]
- Lorenz, S.; Diederichs, E.; Telgmann, R.; Schütte, C. Discrimination of Dynamical System Models for Biological and Chemical Processes. J. Comput. Chem. 2007, 28, 1384–1399. [Google Scholar] [CrossRef]
- Bania, P. Bayesian Input Design for Linear Dynamical Model Discrimination. Entropy 2019, 21, 351. [Google Scholar] [CrossRef] [PubMed]
- Bania, P.; Baranowski, J. Field Kalman Filter and its approximation. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 2875–2880. [Google Scholar] [CrossRef]
- Bania, P. Example for equivalence of dual and information based optimal control. Int. J. Control 2018, 92, 2339–2348. [Google Scholar] [CrossRef]
- Baranowski, J.; Bania, P.; Prasad, I.; Cong, T. Bayesian fault detection and isolation using Field Kalman Filter. EURASIP J. Adv. Signal Process. 2017, 2017, 79. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Lee, K.Y. New Information Inequalities with Applications to Statistics. Ph.D. Thesis, EECS Department, University of California, Berkeley, CA, USA, 2022. UC Berkeley Technical Report. [Google Scholar]
- Van Trees, H.L. Detection, Estimation and Modulation Theory; Wiley: Hoboken, NJ, USA, 1968; Volume I. [Google Scholar]
- Efroimovich, S.Y. Information Contained in a Sequence of Observations. Probl. Peredachi Informatsii 1979, 15, 24–39. [Google Scholar]
- Van Trees, H.L.; Bell, K.L. (Eds.) Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking; Wiley-IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Jakowluk, W. Optimal Input Signal Design in Control Systems Identification; Oficyna Wydawnicza Politechniki Białostockiej: Białystok, Poland, 2024; Available online: https://pb.edu.pl/oficyna-wydawnicza/wp-content/uploads/sites/4/2024/06/Optimal-input-signal-design-in-control-systems-identification.pdf (accessed on 29 September 2025).
- Jiménez-Martínez, R.; Kołodyński, J.; Troullinou, C.; Lucivero, V.G.; Kong, J.; Mitchell, M.W. Signal Tracking Beyond the Time Resolution of an Atomic Sensor by Kalman Filtering. Phys. Rev. Lett. 2018, 120, 040503. [Google Scholar] [CrossRef]
- Troullinou, C.; Shah, V.; Lucivero, V.G.; Mitchell, M.W. Squeezed-Light Enhancement and Backaction Evasion in a High-Sensitivity Optically Pumped Magnetometer. Phys. Rev. Lett. 2021, 127, 193601. [Google Scholar] [CrossRef]
- Bobrovsky, B.Z.; Mayer-Wolf, E.; Zakai, M. Some Classes of Global Cramér–Rao Bounds. Ann. Stat. 1987, 15, 1421–1438. [Google Scholar] [CrossRef]
- Jeong, M.; Dytso, A.; Cardone, M. A Comprehensive Study on Ziv-Zakai Lower Bounds on the MMSE. IEEE Trans. Inf. Theory 2025, 71, 3214–3236. [Google Scholar] [CrossRef]
- Huber, M.F.; Bailey, T.; Durrant-Whyte, H.; Hanebeck, U.D. On entropy approximation for Gaussian mixture random vectors. In Proceedings of the 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Republic of Korea, 20–22 August 2008; pp. 181–188. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration, 2nd ed.; Academic Press: Orlando, FL, USA, 1984. [Google Scholar]
- Stroud, A.H. Approximate Calculation of Multiple Integrals; Prentice Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Smolyak, S.A. Quadrature and interpolation formulas for tensor products of certain classes of functions. Sov. Math. Dokl. 1963, 4, 240–243. [Google Scholar]
- Jansson, H. Experiment Design with Applications in Identification for Control; Royal Institute of Technology (KTH): Stockholm, Sweden, 2004. [Google Scholar]
- Annergren, M.; Larsson, C.A. MOOSE2—A toolbox for least-costly application-oriented input design. SoftwareX 2016, 5, 96–100. [Google Scholar] [CrossRef]
- Fabricant, A.; Novikova, I.; Bison, G. How to build a magnetometer with thermal atomic vapor: A tutorial. New J. Phys. 2023, 25, 025001. [Google Scholar] [CrossRef]
- Budker, D.; Jackson Kimball, D.F. (Eds.) Optical Magnetometry; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Shen, H.Z.; Shang, C.; Zhou, Y.H.; Yi, X.X. Unconventional single-photon blockade in non-Markovian systems. Phys. Rev. A 2018, 98, 023856. [Google Scholar] [CrossRef]
- Magrini, L.; Rosenzweig, P.; Bach, C.; Deutschmann-Olek, A.; Hofer, S.G.; Hong, S.; Kiesel, N.; Kugi, A.; Aspelmeyer, M. Real-time optimal quantum control of mechanical motion at room temperature. Nature 2021, 595, 373–377. [Google Scholar] [CrossRef]
- Amorós-Binefa, J.; Kołodyński, J. Noisy Atomic Magnetometry with Kalman Filtering and Measurement-Based Feedback. PRX Quantum 2025, 6, 030331. [Google Scholar] [CrossRef]
- Särkkä, S. Bayesian Filtering and Smoothing; Institute of Mathematical Statistics Textbooks; Cambridge University Press: Cambridge, UK, 2013; Volume 3. [Google Scholar] [CrossRef]
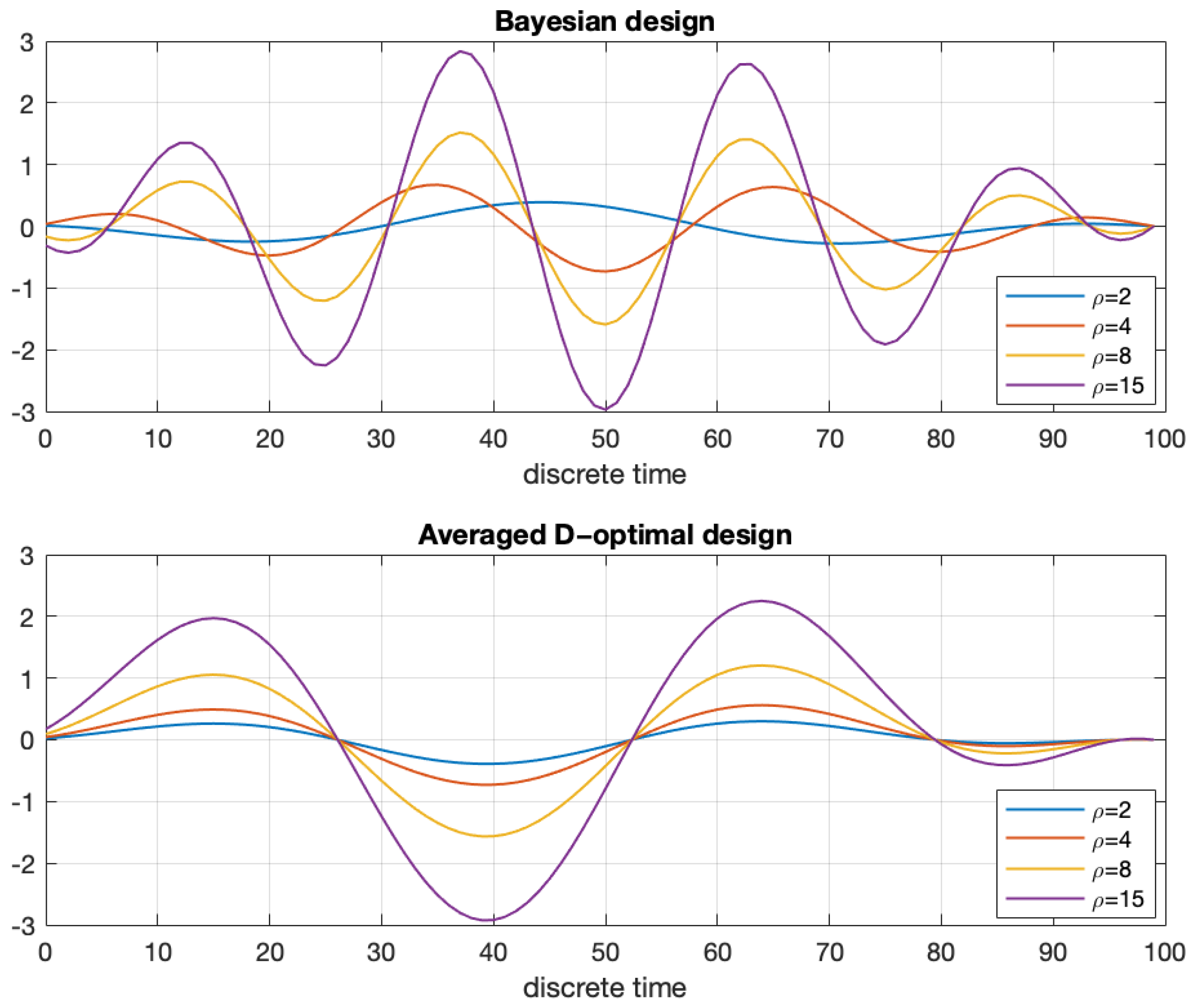
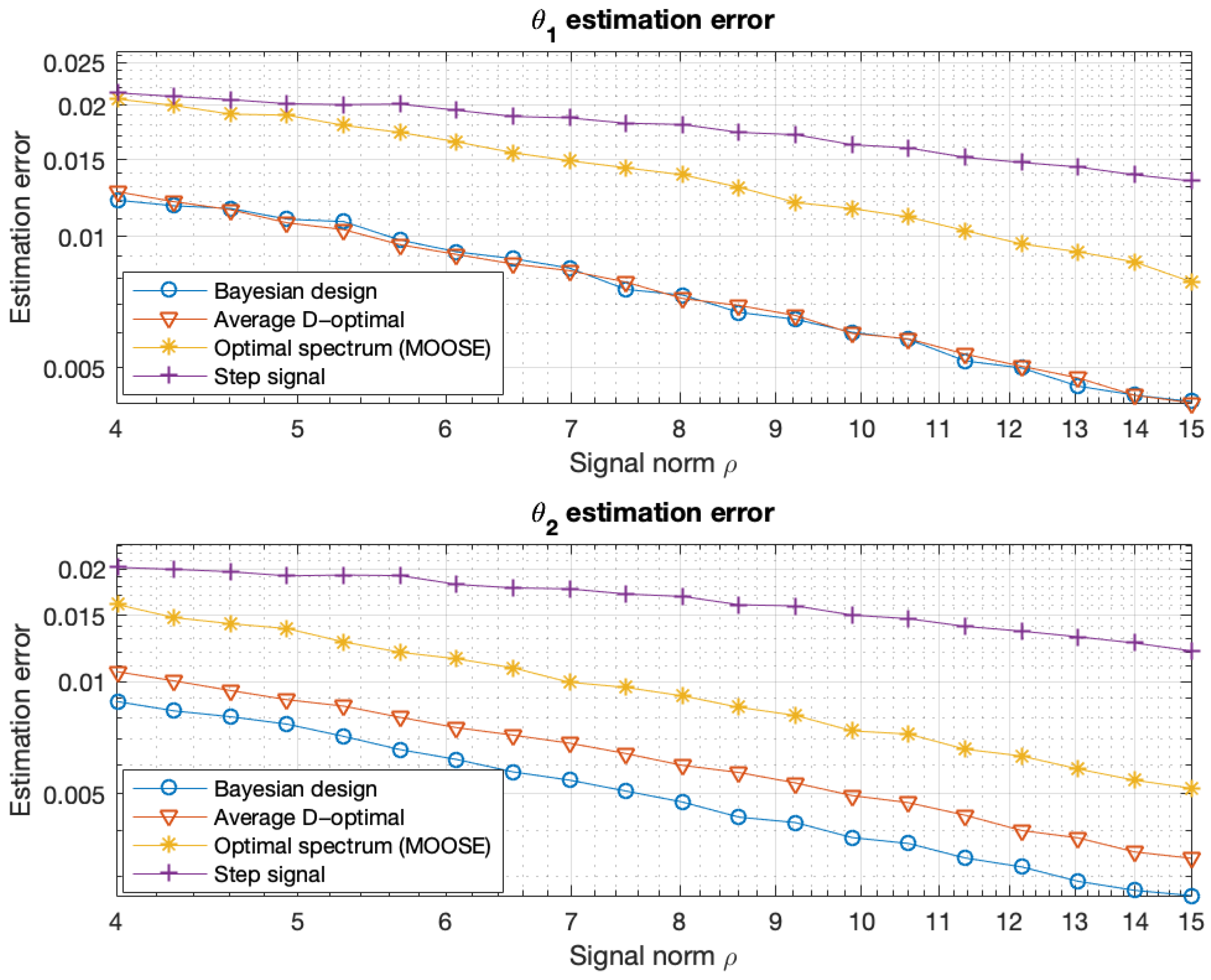

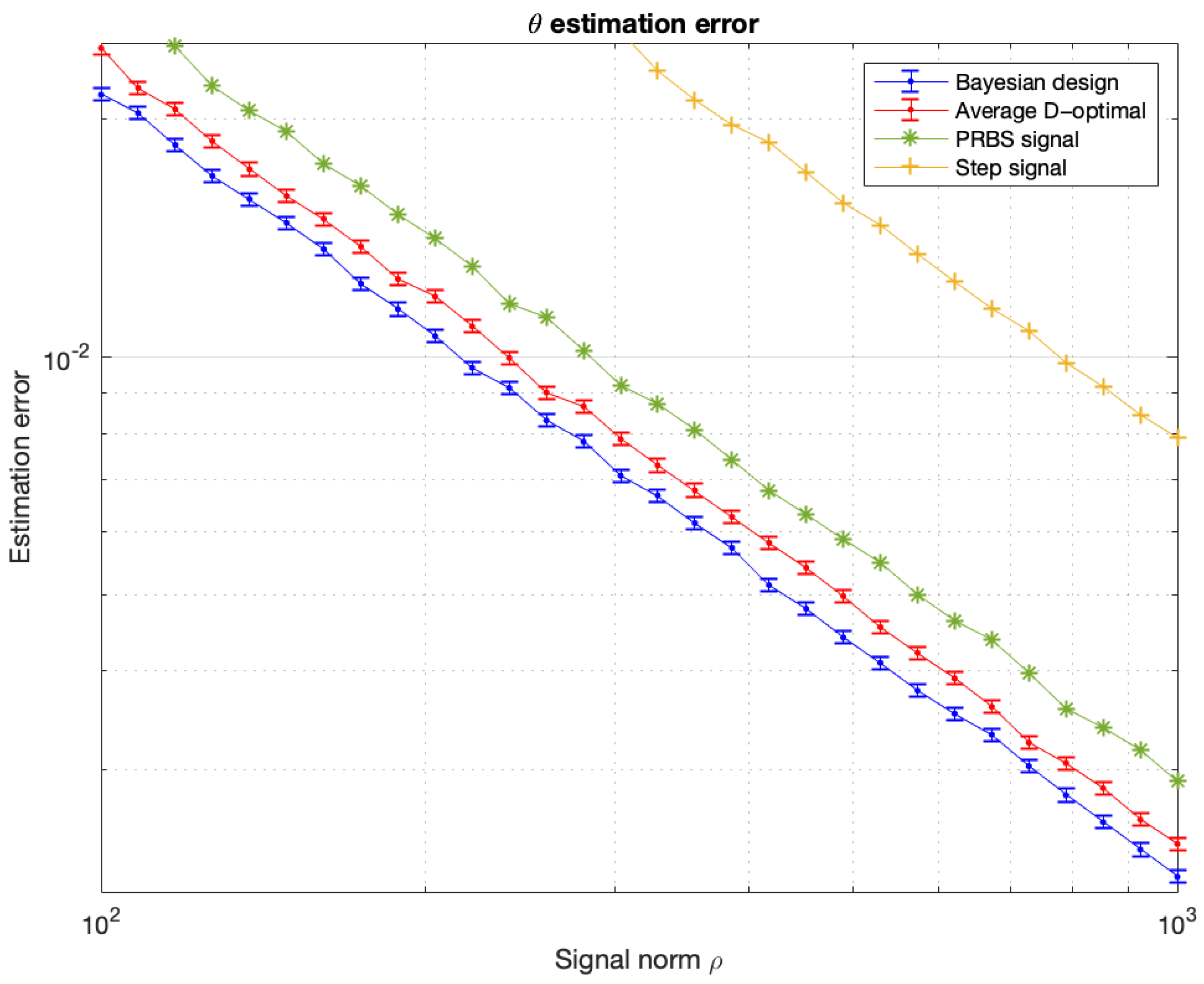
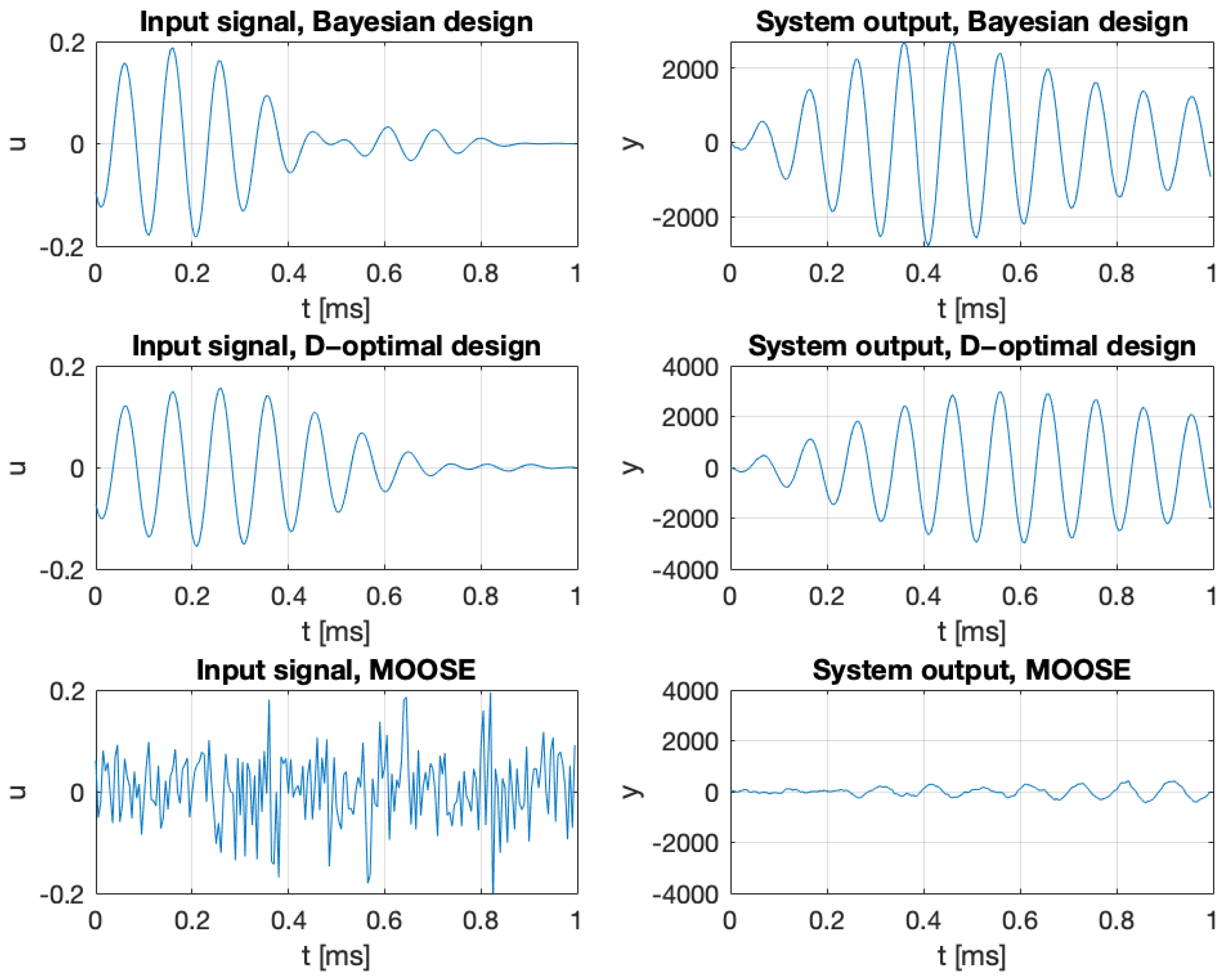
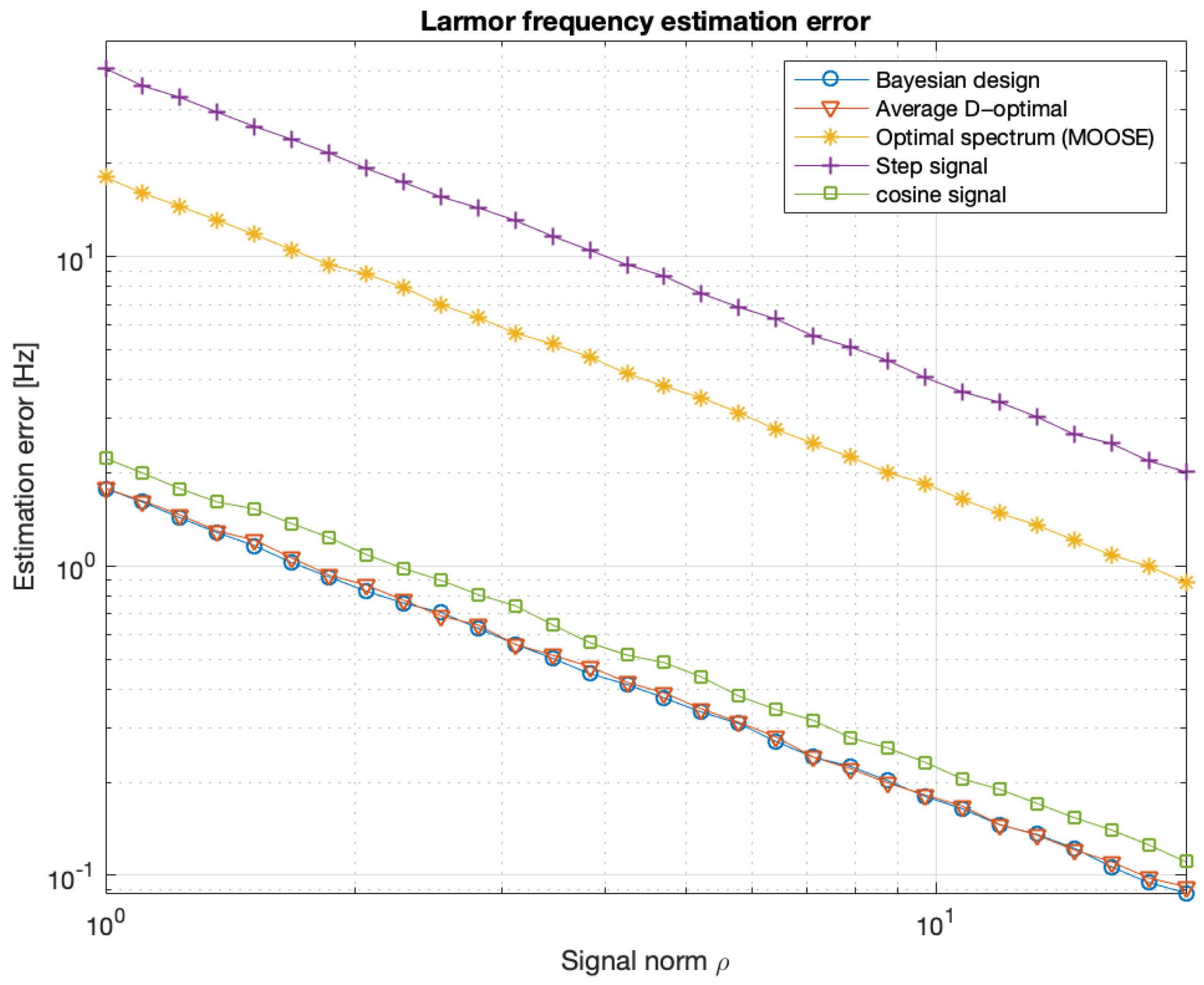
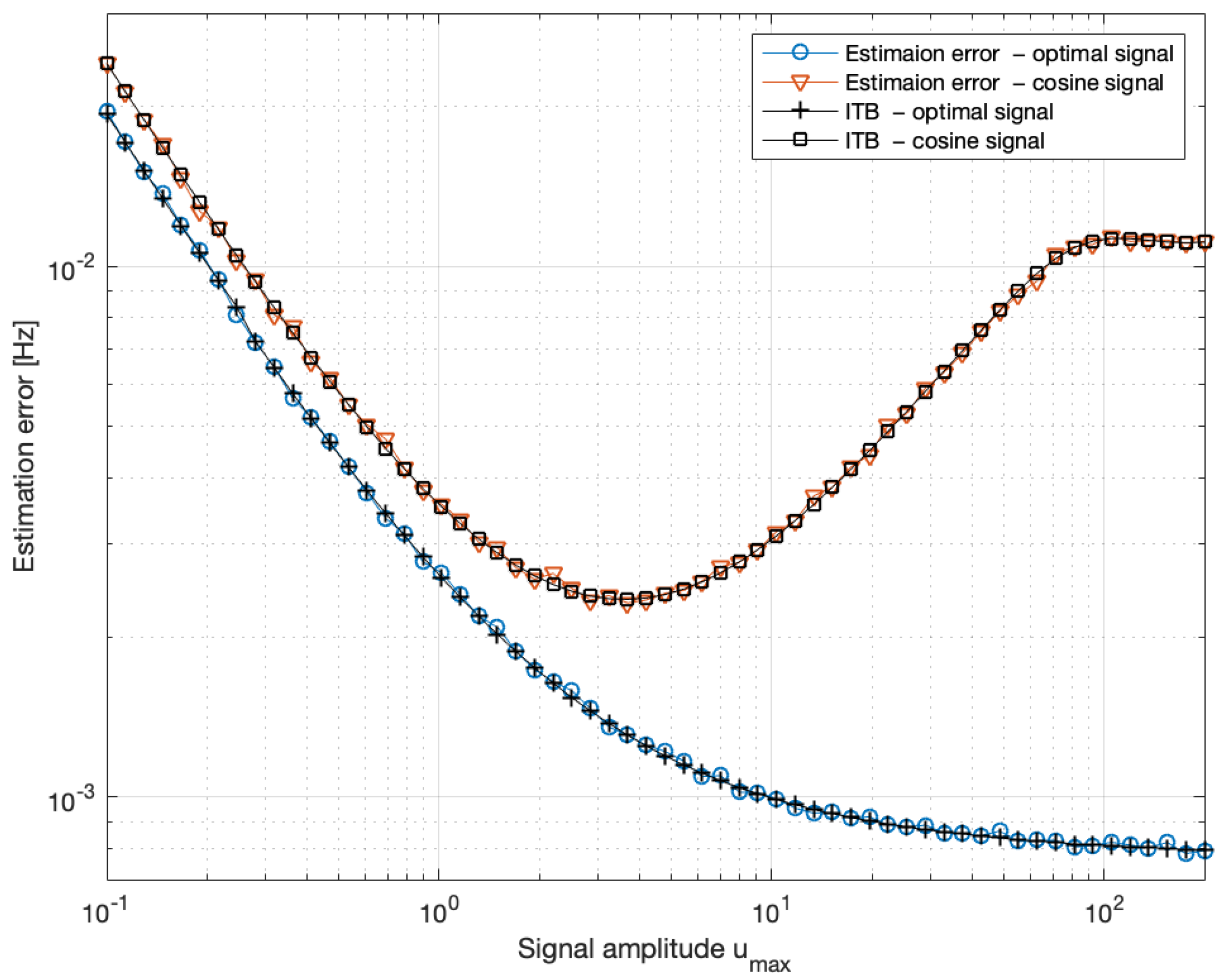

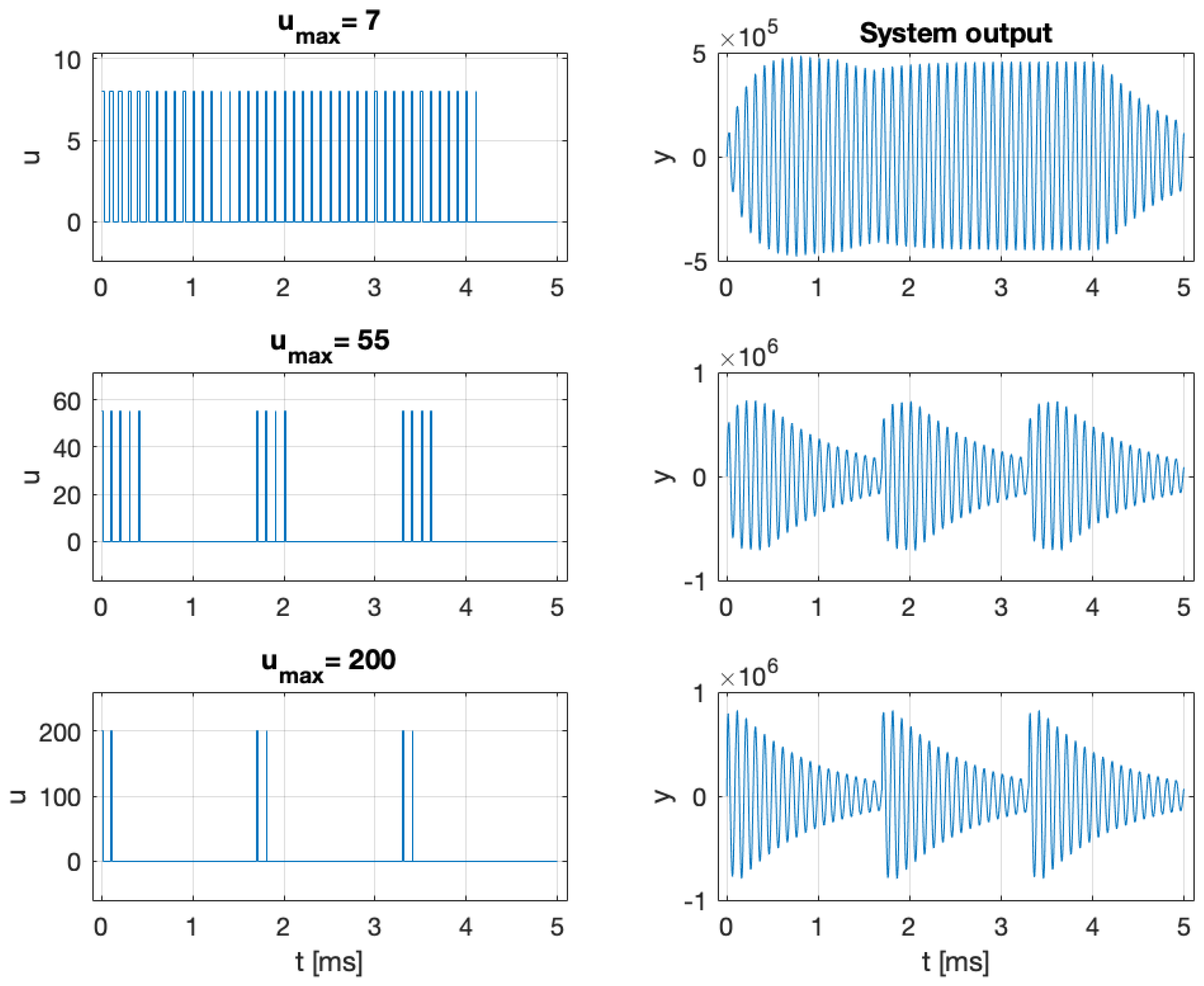
| Parameter | Abbreviation | Typical Value |
|---|---|---|
| Number of atoms | ||
| Spin number | F | 1 |
| Larmor frequencies | kHz | |
| Parameter | 600 Hz | |
| Parameter | 550 Hz | |
| Typical relaxation time | 0.87 ms | |
| Typical relaxation rate | 1149 Hz | |
| Pumping rate | P | 0–200 kHz |
| Measurement noise level | ||
| Sampling time | 5 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bania, P.; Wójcik, A. An Approximate Bayesian Approach to Optimal Input Signal Design for System Identification. Entropy 2025, 27, 1041. https://doi.org/10.3390/e27101041
Bania P, Wójcik A. An Approximate Bayesian Approach to Optimal Input Signal Design for System Identification. Entropy. 2025; 27(10):1041. https://doi.org/10.3390/e27101041
Chicago/Turabian StyleBania, Piotr, and Anna Wójcik. 2025. "An Approximate Bayesian Approach to Optimal Input Signal Design for System Identification" Entropy 27, no. 10: 1041. https://doi.org/10.3390/e27101041
APA StyleBania, P., & Wójcik, A. (2025). An Approximate Bayesian Approach to Optimal Input Signal Design for System Identification. Entropy, 27(10), 1041. https://doi.org/10.3390/e27101041






