Quantum Entanglement Asymmetry and the Cosmic Matter–Antimatter Imbalance: A Theoretical and Observational Analysis
Abstract
:1. Introduction
- To develop a theoretical framework incorporating QEA into cosmology, providing clear justification for how the asymmetry in the initial entangled states—under CP-violating dynamics—translates into a real matter–antimatter imbalance.
- To demonstrate through numerical simulations that QEA can produce a net baryon asymmetry consistent with observational data, thereby addressing the insufficiency of currently observed CP violation.
- To identify potential observational signatures of QEA in the Cosmic Microwave Background (CMB) anisotropies and large-scale structure, offering avenues for empirical verification and placing constraints on early-universe CP-violating physics.
2. Theoretical Framework
2.1. Quantum Entanglement Asymmetry in the Early Universe
- Extension to Fermionic Fields and Gauge Interactions
- Impact on the Time Evolution of Entangled States
- Amplification During Cosmic Inflation
- Origin of CP-Violating Terms
- Comparison with Standard Model CP Violation
- Quantifying the Generated Asymmetry
- Boltzmann Equation Framework
2.2. Integration into the Cosmological Model
- Energy-Momentum Tensor for Scalar and Fermionic Fields
- Calculating and
- Net Contribution Due to Asymmetry
- Parameterizing the Asymmetry
- Impact on Cosmological Observables
- Including Fermionic Fields and Gauge Interactions
2.3. Justification of the Asymmetric Terms
- From the Standard Model to BeyondIn the Standard Model, CP violation arises from complex phases in the Cabibbo–Kobayashi–Maskawa (CKM) matrix for quarks and the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix for neutrinos [9]. However, the amount of CP violation within the Standard Model is insufficient to account for the observed baryon asymmetry of the universe [14].Extensions of the Standard Model, such as the Minimal Supersymmetric Standard Model (MSSM) [13] and grand unified theories (GUTs) [12], introduce additional sources of CP violation. In the MSSM, complex phases in the soft supersymmetry-breaking terms can lead to significant CP-violating effects [15].
- Embedding CP-Violating Terms in GUTsIn GUTs like SO(10) and SU(5), quarks and leptons are unified into larger multiplets, and new interactions can naturally introduce CP violation [12]. The decay of heavy GUT gauge bosons or scalar fields can produce CP asymmetries through interference between tree-level and one-loop diagrams involving complex Yukawa couplings [11].These CP-violating decays can generate a net baryon number in the early universe. The CP asymmetry parameter in such decays is given bywhere X is the heavy particle and denotes the decay rates.
- Leptogenesis and Neutrino MassesLeptogenesis is a prominent mechanism where CP-violating decays of heavy right-handed Majorana neutrinos generate a lepton asymmetry, which is partially converted to a baryon asymmetry through sphaleron processes [16]. The CP violation arises from complex Yukawa couplings in the neutrino sector.
- CP Violation in String TheoryIn string theory, CP violation can emerge from the compactification of extra dimensions and the presence of complex moduli fields [15]. These moduli fields can acquire complex expectation values, leading to CP-violating couplings in the low-energy effective action. Non-perturbative effects like string instantons can also generate CP-violating interactions [17].
- Impact on Entangled StatesThe CP-violating interactions derived from these fundamental theories modify the equations of motion for the fields, leading to differences in the energies and evolution of particle and antiparticle states.Starting from the Lagrangian density for a complex scalar field , which represents a particle species in the early universe, we havewhere the first two terms constitute the standard kinetic and mass terms of the scalar field and represents the CP-violating interaction responsible for the asymmetry in particle–antiparticle creation rates.We introduce the CP-violating term aswhere is a real coupling constant characterizing the strength of CP violation. This term is odd under CP transformation and introduces a difference in the behavior of particles and antiparticles.For fermionic fields, similar CP-violating terms can be included. Consider a Dirac fermion with the standard Lagrangian from Equation (5):A CP-violating term for fermions is given by Equation (6):where is the fifth gamma matrix, and characterizes the strength of CP violation [9].Including these CP-violating terms in the Lagrangian leads to modifications in the equations of motion derived from the Euler–Lagrange equation. For the scalar field, substituting the Lagrangian density, we obtain the modified Klein–Gordon equation:Similarly, the equation for becomesFor fermions, the modified Dirac equation isThese CP-violating terms introduce differences in the dispersion relations for particles and antiparticles. Solving the modified equations perturbatively for small , we find energy differences that lead to asymmetries in their production rates and occupation numbers.
- Baryon Number ViolationIn addition to CP violation, baryon number violation is necessary for baryogenesis, as per the Sakharov conditions [3]. In the electroweak theory, non-perturbative processes known as sphalerons can violate baryon and lepton numbers while conserving [18].CP-violating interactions can bias the sphaleron transitions in favor of baryon over antibaryon production, contributing to the baryon asymmetry.
3. Methodology
3.1. Numerical Simulations
- Incorporating Fermions and Gauge Fields
- Discretization of CP-Violating Terms
- Simulation Details
- Calculation of Observables
- Analyzing the Results
3.2. Analysis of CMB Anisotropies
- Modifying the Boltzmann Equations
- Numerical Implementation
- Parameter Space Exploration
- Statistical Analysis
3.3. Analysis of Large-Scale Structure
- Matter Power Spectrum
- Numerical Implementation
- Comparisons with Observations
3.4. Big Bang Nucleosynthesis Constraints
3.5. Overall Methodology
4. Results
4.1. Simulation Outcomes
- Effects on the Expansion Rate
4.2. Predictions for Observations
4.3. Discussion of Numerical Results
4.4. Limitations and Future Work
- Finite Lattice Effects: The simulations are performed at a finite lattice spacing and volume, which could introduce systematic errors. Future work should include extrapolations to the continuum () and infinite-volume limits to ensure that the results are not artifacts of the lattice parameters.
- Uncertainties in CP-Violating Parameters: The value of is not precisely known. A deeper theoretical understanding of its origin from fundamental theories (e.g., detailed model building in GUT or string-theoretic contexts) could provide more accurate predictions.
- Inclusion of Additional Processes: Incorporating other baryon number-violating processes, such as sphaleron transitions, and considering the interplay with electroweak baryogenesis or leptogenesis could offer a more comprehensive picture, further strengthening the link between QEA and known baryogenesis frameworks.
- Statistical Analysis: Increasing the number of Monte Carlo samples and employing improved statistical methods can reduce uncertainties in the simulation results, leading to tighter constraints on the model parameters.
4.5. Consistency and Figure Referencing
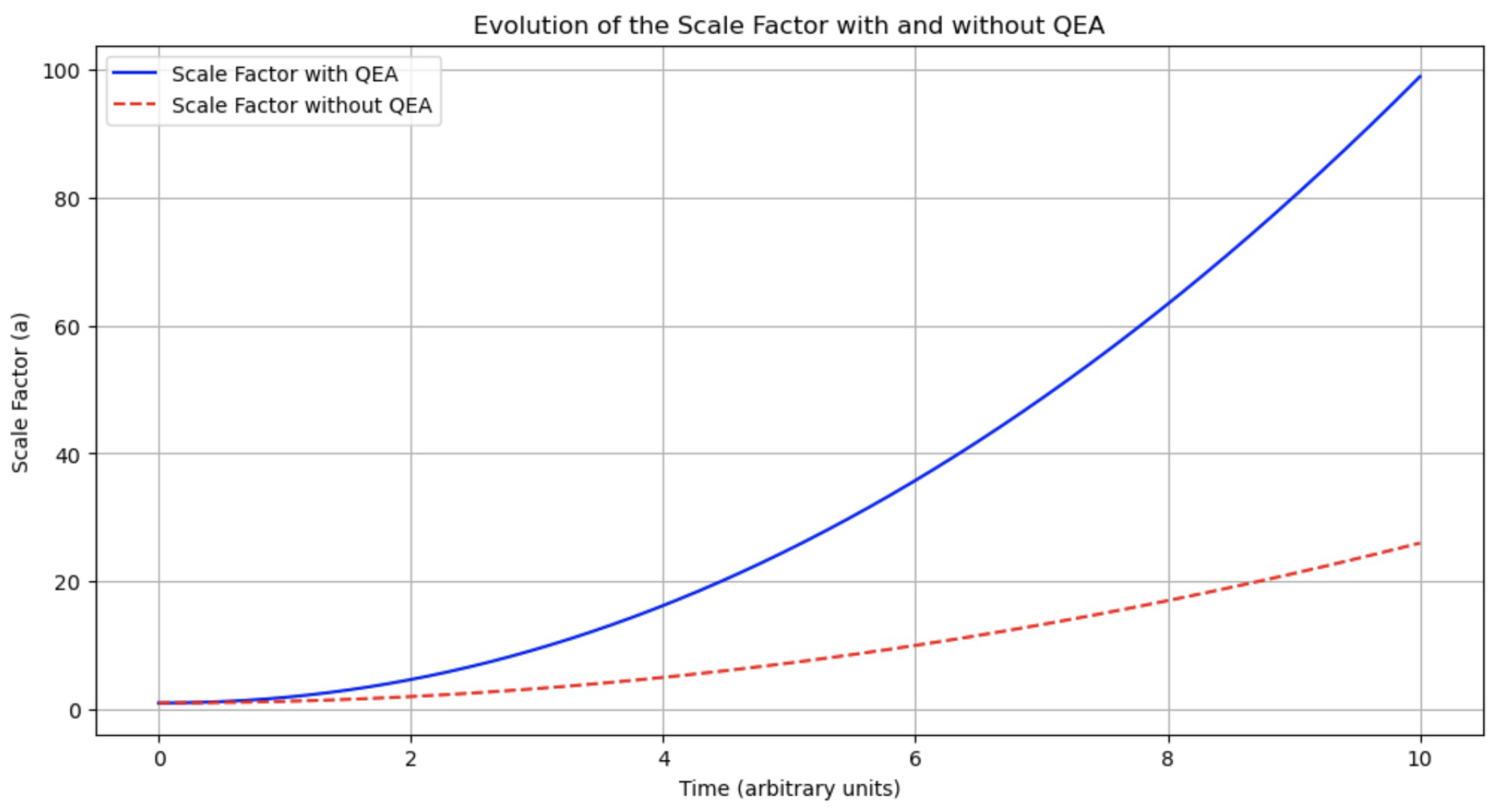
- Figure 1 illustrates the impact of QEA on cosmic expansion, providing visual evidence of the acceleration effect due to the additional energy density and pressure contributions.
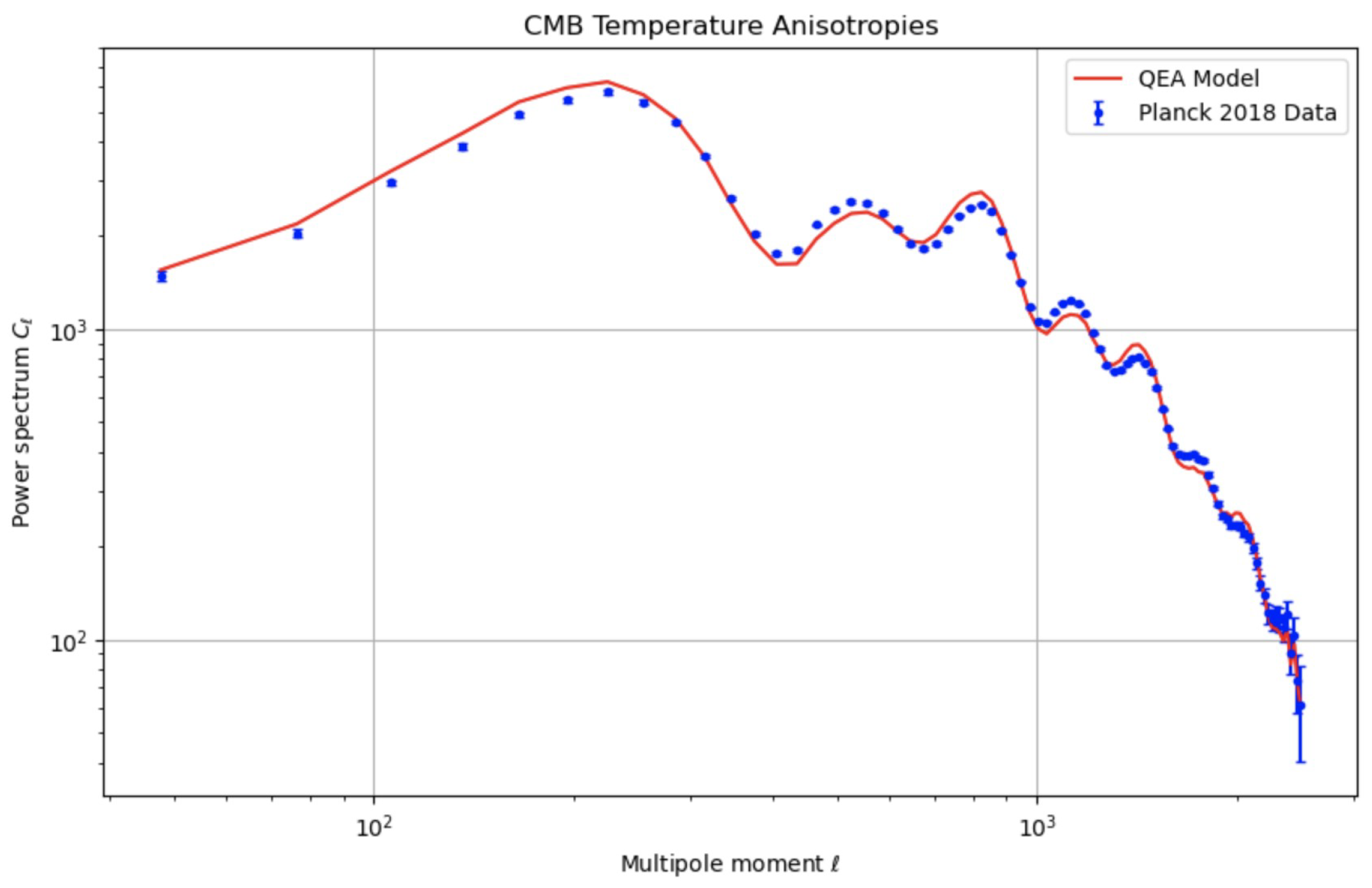
- Figure 2 compares the theoretical CMB power spectra to observational data, showcasing the potential observational signatures of the QEA mechanism.
5. Discussion
5.1. Consistency with Sakharov Conditions
- Baryon Number Violation: Processes must exist that violate baryon number conservation.
- C and CP Violation: Charge conjugation (C) and charge-parity (CP) symmetries must be violated to differentiate between matter and antimatter.
- Departure from Thermal Equilibrium: The universe must have undergone periods out of thermal equilibrium to prevent the annihilation of generated asymmetries.
- Baryon Number Violation
- C and CP Violation
- Departure from Thermal Equilibrium
5.2. Implications for Particle Physics and Cosmology
- Constraints on CP Violation
- Modifications to Cosmological Models
5.3. Limitations and Future Work
- Model Assumptions and Simplifications
- Numerical Precision and Computational Resources
6. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Canetti, L.; Drewes, M.; Shaposhnikov, M. Matter and antimatter in the universe. New J. Phys. 2012, 14, 095012. [Google Scholar] [CrossRef]
- Dine, M.; Kusenko, A. The origin of the matter–antimatter asymmetry. Rev. Mod. Phys. 2003, 76, 1. [Google Scholar] [CrossRef]
- Sakharov, A.D. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. Sov. Phys. Uspekhi 1991, 34, 392–393. [Google Scholar] [CrossRef]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π decay of the meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Riotto, A.; Trodden, M. Recent progress in baryogenesis. Annu. Rev. Nucl. Part. Sci. 1999, 49, 35–75. [Google Scholar] [CrossRef]
- Friis, N.; Huber, M.; Perarnau-Llobet, M. Entanglement asymmetry as a probe of superselection rules. Phys. Rev. A 2012, 86, 042111. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison–Wesley: Boston, MA, USA, 1995. [Google Scholar]
- Cheng, T.-P.; Li, L.-F. Gauge Theory of Elementary Particle Physics; Oxford University Press: Oxford, UK, 1984. [Google Scholar]
- Branco, G.C.; Lavoura, L.; Silva, J.P. CP Violation; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields, Vol. II: Modern Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison–Wesley: Boston, MA, USA, 1990. [Google Scholar]
- Langacker, P. Grand unified theories and proton decay. Phys. Rep. 1981, 72, 185–385. [Google Scholar] [CrossRef]
- Nilles, H.P. Supersymmetry, supergravity and particle physics. Phys. Rep. 1984, 110, 1–162. [Google Scholar] [CrossRef]
- Gavela, M.B.; Hernández, P.; Orloff, J.; Pène, O. Standard Model CP violation and baryon asymmetry. Mod. Phys. Lett. A 1994, 9, 795–810. [Google Scholar] [CrossRef]
- Dine, M. Supersymmetry and String Theory: Beyond the Standard Model; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fukugita, M.; Yanagida, T. Baryogenesis without Grand Unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Cvetič, M.; Weigand, T. Spacetime instanton corrections in 4D string vacua—The seesaw mechanism for D-brane models. Nucl. Phys. B 2009, 771, 113–142. [Google Scholar] [CrossRef]
- Kuzmin, V.A.; Rubakov, V.A.; Shaposhnikov, M.E. Anomalous electroweak baryon-number non-conservation and GUT mechanisms for baryogenesis. Phys. Lett. B 1985, 155, 36–42. [Google Scholar] [CrossRef]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient computation of cosmic microwave background anisotropies in closed Friedmann–Robertson–Walker models. Astrophys. J. 2000, 538, 473–476. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D 2002, 66, 103511. [Google Scholar] [CrossRef]
- Blas, D.; Lesgourgues, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS). Part II: Approximation schemes. J. Cosmol. Astropart. Phys. 2011, 2011, 034. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Consiglio, R.; Mangano, G.; Miele, G.; Pisanti, O. PArthENoPE reloaded. Comput. Phys. Commun. 2018, 233, 237–242. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.-H. Big Bang Nucleosynthesis: 2015. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neukart, F. Quantum Entanglement Asymmetry and the Cosmic Matter–Antimatter Imbalance: A Theoretical and Observational Analysis. Entropy 2025, 27, 103. https://doi.org/10.3390/e27020103
Neukart F. Quantum Entanglement Asymmetry and the Cosmic Matter–Antimatter Imbalance: A Theoretical and Observational Analysis. Entropy. 2025; 27(2):103. https://doi.org/10.3390/e27020103
Chicago/Turabian StyleNeukart, Florian. 2025. "Quantum Entanglement Asymmetry and the Cosmic Matter–Antimatter Imbalance: A Theoretical and Observational Analysis" Entropy 27, no. 2: 103. https://doi.org/10.3390/e27020103
APA StyleNeukart, F. (2025). Quantum Entanglement Asymmetry and the Cosmic Matter–Antimatter Imbalance: A Theoretical and Observational Analysis. Entropy, 27(2), 103. https://doi.org/10.3390/e27020103





