Physical Realizations of Interdependent Networks: Analogy to Percolation
Abstract
:1. Introduction
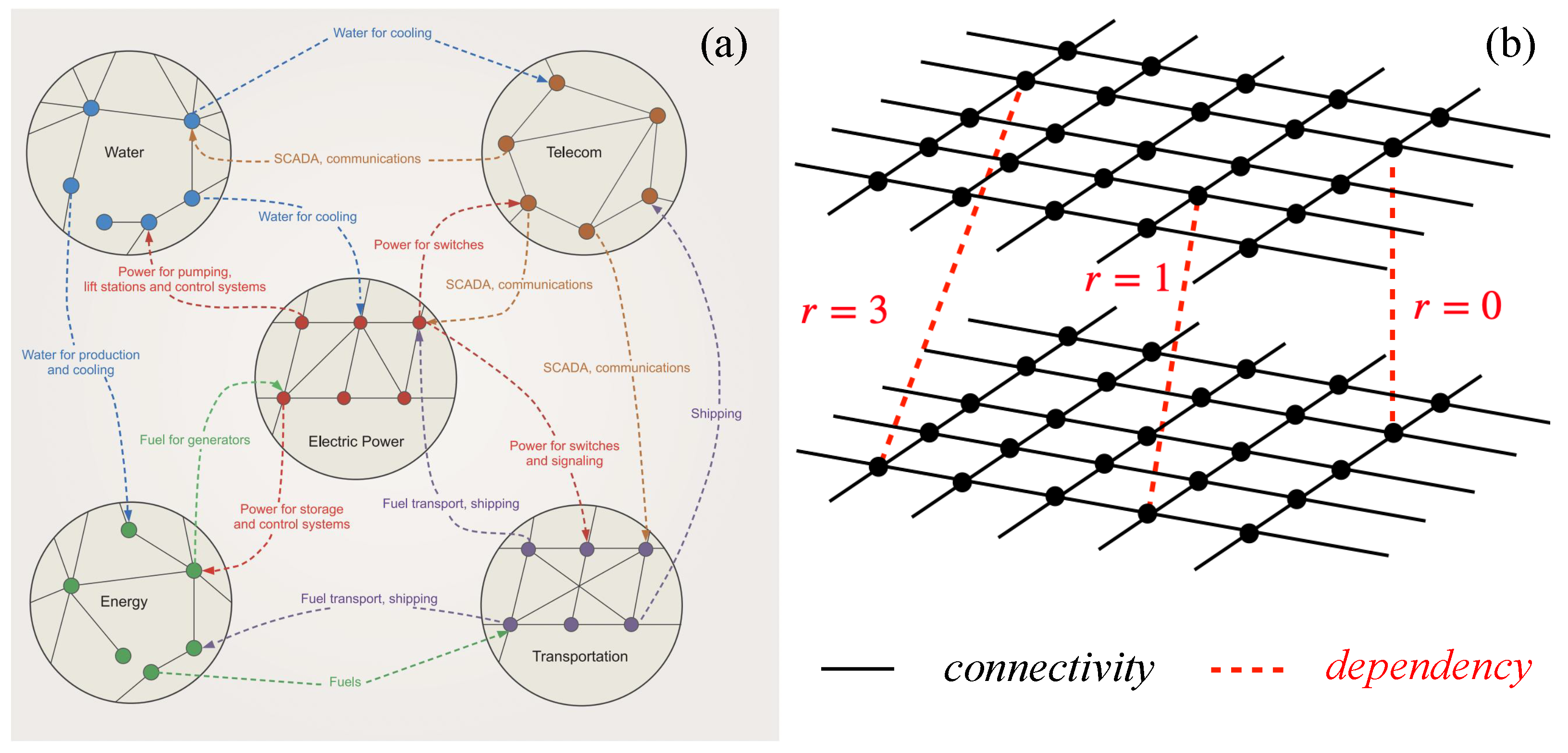
2. Percolation on Interdependent Networks
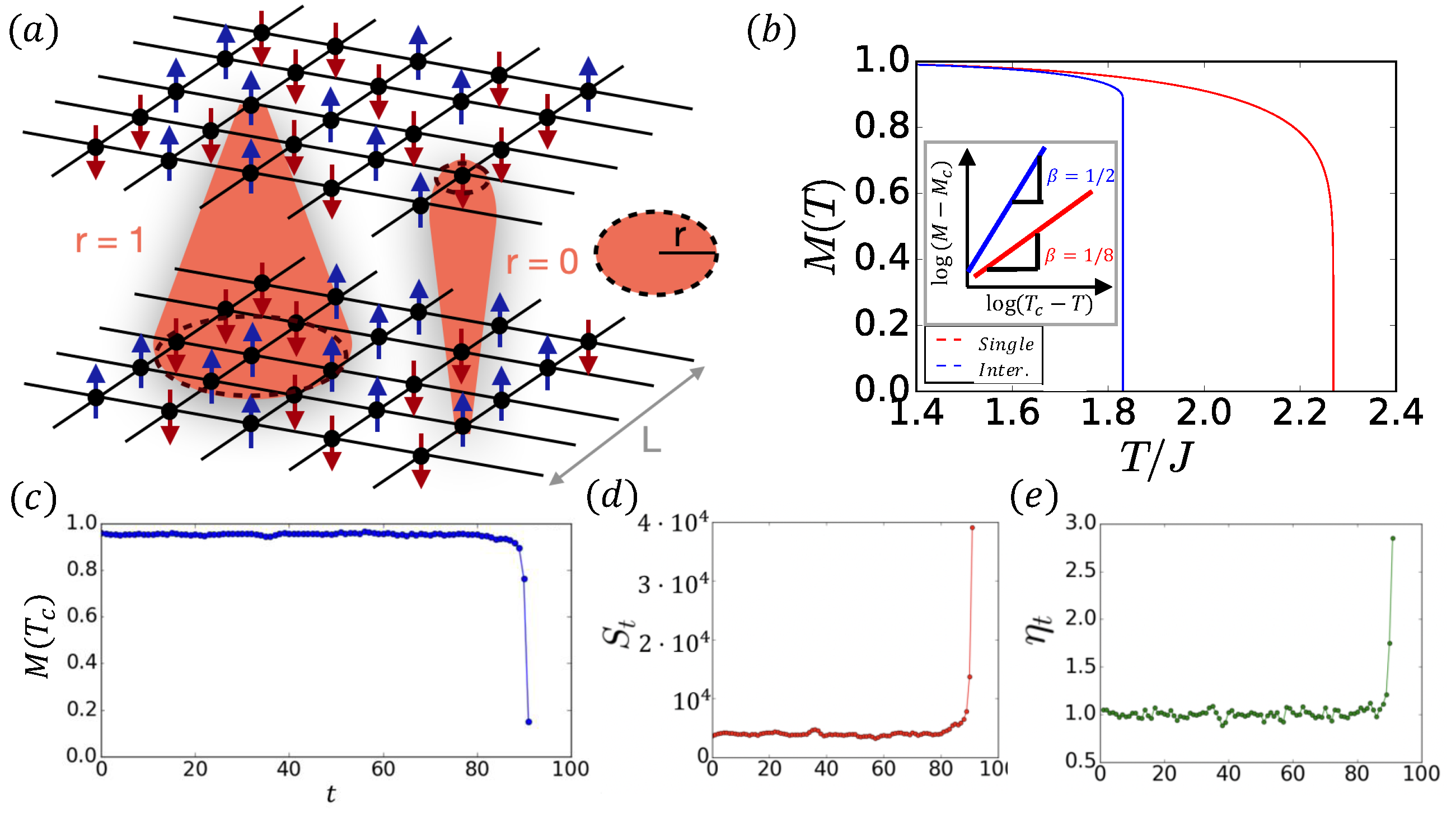
3. Interdependent Ferromagnetic Networks
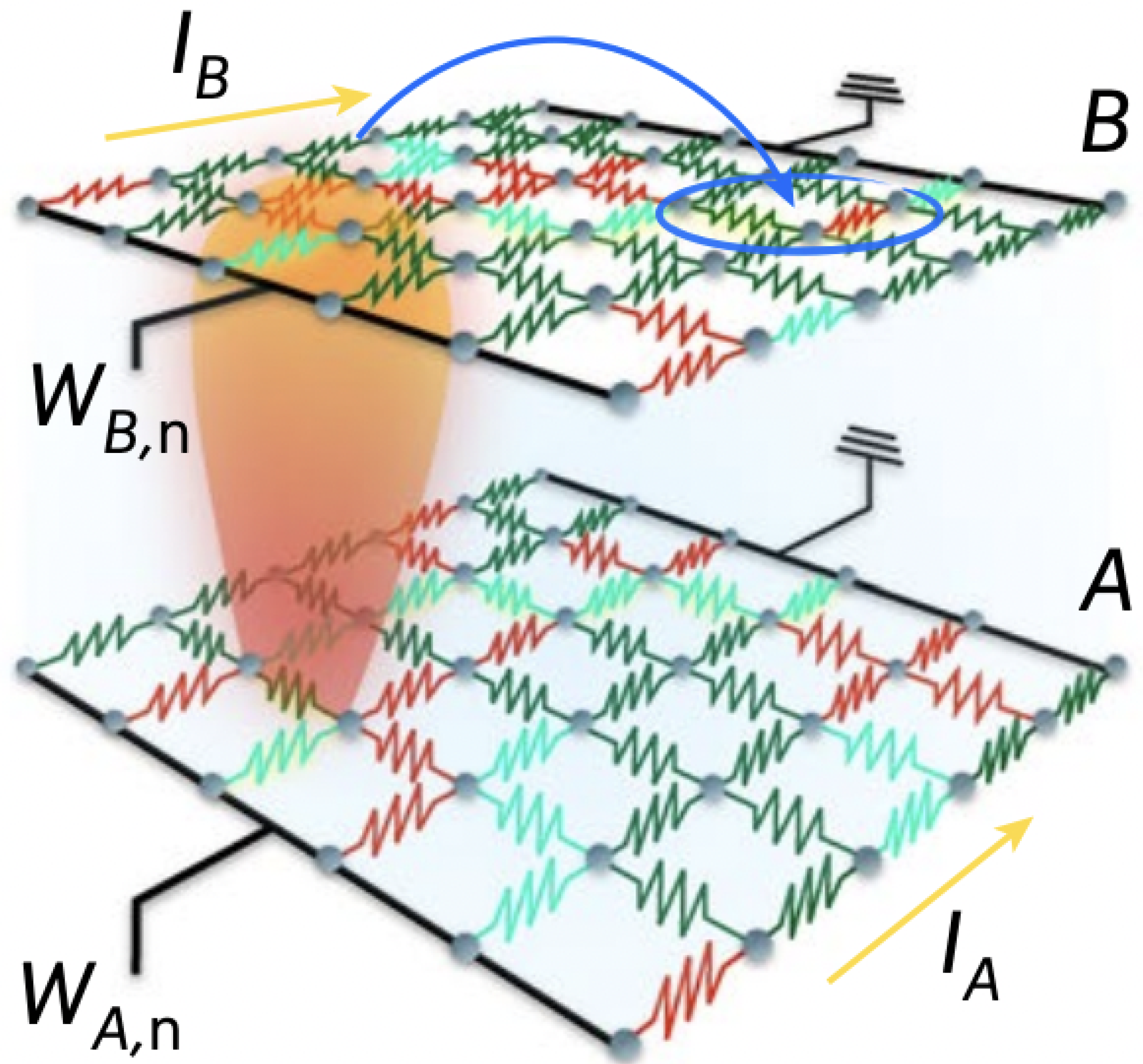
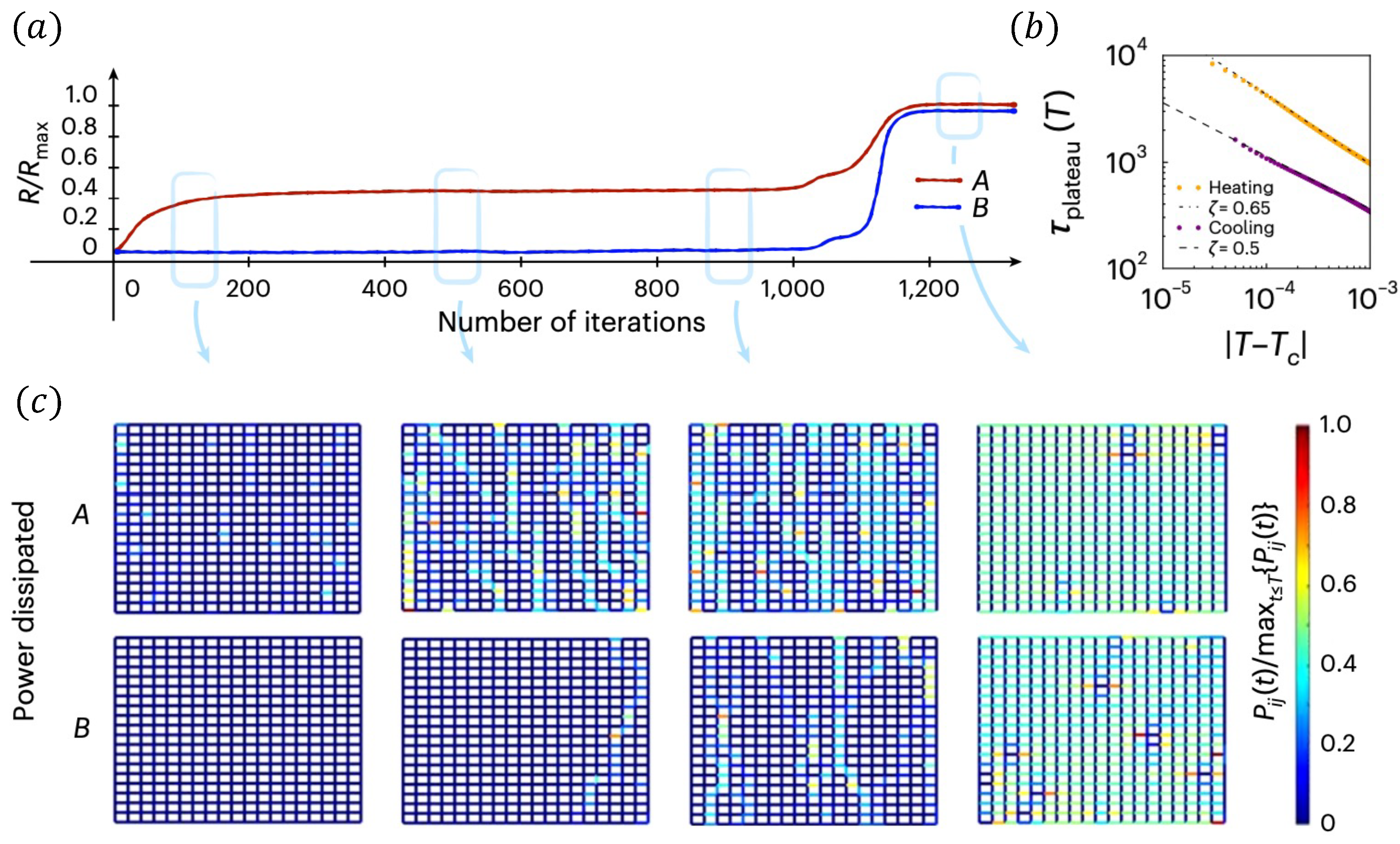
4. Interdependent Superconducting Networks
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GCC | giant connected component |
| MGCC | mutual giant connected component |
| IFN | interdependent ferromagnetic networks |
| ISN | interdependent superconducting networks |
| SC-state | superconducting state |
| N-state | normal state |
References
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function; Cambridge University Press: Oxford, UK, 2010. [Google Scholar]
- Erdős, P.; Rényi, A. On Random Graphs I. Publ. Math. Debr. 1959, 6, 290. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci 1960, 5, 17–60. [Google Scholar]
- Bollobás, B.; Bollobás, B. Random Graphs; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Newman, M.; Ziff, R.M. Efficient Monte Carlo algorithm and high-precision results for percolation. Phys. Rev. Lett. 2000, 85, 4104. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef]
- Alert, R.; Tierno, P.; Casademunt, J. Mixed-order phase transition in a colloidal crystal. Proc. Natl. Acad. Sci. USA 2017, 114, 12906–12909. [Google Scholar] [CrossRef] [PubMed]
- Gross, B.; Bonamassa, I.; Havlin, S. Fractal fluctuations at mixed-order transitions in interdependent networks. Phys. Rev. Lett. 2022, 129, 268301. [Google Scholar] [CrossRef]
- Gao, J.; Li, D.; Havlin, S. From a single network to a network of networks. Natl. Sci. Rev. 2014, 1, 346–356. [Google Scholar] [CrossRef]
- Berezin, Y.; Bashan, A.; Danziger, M.M.; Li, D.; Havlin, S. Localized attacks on spatially embedded networks with dependencies. Sci. Rep. 2015, 5, 8934. [Google Scholar] [CrossRef]
- Parshani, R.; Buldyrev, S.V.; Havlin, S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition. Phys. Rev. Lett. 2010, 105, 048701. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Bashan, A.; Cohen, R.; Berezin, Y.; Shnerb, N.; Havlin, S. Simultaneous first-and second-order percolation transitions in interdependent networks. Phys. Rev. E 2014, 90, 012803. [Google Scholar] [CrossRef]
- Dorogovtsev, S.N.; Goltsev, A.V.; Mendes, J.F.F. K-core organization of complex networks. Phys. Rev. Lett. 2006, 96, 040601. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Jo, M.; Kahng, B. Critical behavior of k-core percolation: Numerical studies. Phys. Rev. E 2016, 94, 062307. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Xue, L.; Gross, B.; She, Z.; Li, D.; Havlin, S. Possible origin for the similar phase transitions in k-core and interdependent networks. New J. Phys. 2024, 26, 013006. [Google Scholar] [CrossRef]
- Xue, L.; Gao, S.; Gallos, L.K.; Levy, O.; Gross, B.; Di, Z.; Havlin, S. Nucleation phenomena and extreme vulnerability of spatial k-core systems. Nat. Commun. 2024, 15, 5850. [Google Scholar] [CrossRef] [PubMed]
- Motter, A.E.; Lai, Y.C. Cascade-based attacks on complex networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef] [PubMed]
- Motter, A.E. Cascade control and defense in complex networks. Phys. Rev. Lett. 2004, 93, 098701. [Google Scholar] [CrossRef] [PubMed]
- Perez, I.A.; Ben Porath, D.; La Rocca, C.E.; Braunstein, L.A.; Havlin, S. Critical behavior of cascading failures in overloaded networks. Phys. Rev. E 2024, 109, 034302. [Google Scholar] [CrossRef] [PubMed]
- Bonamassa, I.; Gross, B.; Laav, M.; Volotsenko, I.; Frydman, A.; Havlin, S. Interdependent superconducting networks. Nat. Phys. 2023, 19, 1163–1170. [Google Scholar] [CrossRef]
- Gross, B.; Volotsenko, I.; Bonamassa, I.; Havlin, S.; Frydman, A. Microscopic origin of abrupt transition in interdependent superconducting networks. arXiv 2024, arXiv:2403.03050. [Google Scholar]
- Danziger, M.M.; Bashan, A.; Havlin, S. Interdependent resistor networks with process-based dependency. New J. Phys. 2015, 17, 043046. [Google Scholar] [CrossRef]
- Bonamassa, I.; Gross, B.; Havlin, S. Interdependent couplings map to thermal, higher-order interactions. arXiv 2021, arXiv:2110.08907. [Google Scholar]
- Gross, B.; Bonamassa, I.; Havlin, S. Microscopic Intervention Yields Abrupt Transition in Interdependent Ferromagnetic Networks. Phys. Rev. Lett. 2024, 132, 227401. [Google Scholar] [CrossRef] [PubMed]
- Ising, E. Beitrag zur Theorie des Ferro-und Paramagnetismus. Ph.D. Thesis, Grefe & Tiedemann, Hamburg, Germany, 1924. [Google Scholar]
- McCoy, B.M.; Wu, T.T. The Two-Dimensional Ising Model; Harvard University Press: Cambridge, MA, USA, 1973. [Google Scholar]
- Pippard, A.B. Magnetoresistance in Metals; Cambridge University Press: Cambridge, UK, 1989; Volume 2. [Google Scholar]
- Xiao, J.Q.; Jiang, J.S.; Chien, C.L. Giant magnetoresistance in nonmultilayer magnetic systems. Phys. Rev. Lett. 1992, 68, 3749. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Buldyrev, S.V.; Stanley, H.E.; Havlin, S. Networks formed from interdependent networks. Nat. Phys. 2012, 8, 40–48. [Google Scholar] [CrossRef]
- Zapperi, S.; Vespignani, A.; Stanley, H.E. Plasticity and avalanche behaviour in microfracturing phenomena. Nature 1997, 388, 658–660. [Google Scholar] [CrossRef]
- Zapperi, S.; Lauritsen, K.B.; Stanley, H.E. Self-organized branching processes: Mean-field theory for avalanches. Phys. Rev. Lett. 1995, 75, 4071. [Google Scholar] [CrossRef] [PubMed]
- Alava, M.J.; Nukala, P.K.; Zapperi, S. Statistical models of fracture. Adv. Phys. 2006, 55, 349–476. [Google Scholar] [CrossRef]
- Pradhan, S.; Hansen, A.; Chakrabarti, B.K. Failure processes in elastic fiber bundles. Rev. Mod. Phys. 2010, 82, 499–555. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Peng, H.; Zhao, Y.; Zhao, D.; Zhong, M.; Hu, Z.; Han, J.; Li, R.; Wang, W. Robustness of higher-order interdependent networks. Chaos Solitons Fractals 2023, 171, 113485. [Google Scholar] [CrossRef]
- Lai, Y.; Liu, Y.; Zheng, K.; Wang, W. Robustness of interdependent higher-order networks. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 073121. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Zhao, D.; Zhong, M.; Peng, H.; Wang, W. Cascading failures on interdependent hypergraph. Commun. Nonlinear Sci. Numer. Simul. 2024, 138, 108237. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, Y.; Meng, F.; Liu, R.R. Catastrophic cascade of failures in interdependent hypergraphs. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34. [Google Scholar] [CrossRef]
- Liu, R.R.; Chu, C.; Meng, F. Higher-order interdependent percolation on hypergraphs. Chaos Solitons Fractals 2023, 177, 114246. [Google Scholar] [CrossRef]
- Gerber, A.; Milner, A.; Groisman, B.; Karpovsky, M.; Gladkikh, A.; Sulpice, A. Magnetoresistance of granular ferromagnets. Phys. Rev. B 1997, 55, 6446. [Google Scholar] [CrossRef]
- Milner, A.; Gerber, A.; Groisman, B.; Karpovsky, M.; Gladkikh, A. Spin-dependent electronic transport in granular ferromagnets. Phys. Rev. Lett. 1996, 76, 475. [Google Scholar] [CrossRef]
- Nika, G.; Constantinescu, A. Design of multi-layer materials using inverse homogenization and a level set method. Comput. Methods Appl. Mech. Eng. 2019, 346, 388–409. [Google Scholar] [CrossRef]
- Roudgé, M.; Cherif, M.; Cahuc, O.; Darnis, P.; Danis, M. Multi-layer materials. Qualitative approach of the process. Int. J. Mater. Form. 2008, 1, 949–952. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gross, B.; Havlin, S. Physical Realizations of Interdependent Networks: Analogy to Percolation. Entropy 2025, 27, 109. https://doi.org/10.3390/e27020109
Gross B, Havlin S. Physical Realizations of Interdependent Networks: Analogy to Percolation. Entropy. 2025; 27(2):109. https://doi.org/10.3390/e27020109
Chicago/Turabian StyleGross, Bnaya, and Shlomo Havlin. 2025. "Physical Realizations of Interdependent Networks: Analogy to Percolation" Entropy 27, no. 2: 109. https://doi.org/10.3390/e27020109
APA StyleGross, B., & Havlin, S. (2025). Physical Realizations of Interdependent Networks: Analogy to Percolation. Entropy, 27(2), 109. https://doi.org/10.3390/e27020109






