Next Article in Journal
Fault Diagnosis of Semi-Supervised Electromechanical Transmission Systems Under Imbalanced Unlabeled Sample Class Information Screening
Next Article in Special Issue
Analysis of Aftershocks from California and Synthetic Series by Using Visibility Graph Algorithm
Previous Article in Journal
Multi-Space Feature Fusion and Entropy-Based Metrics for Underwater Image Quality Assessment
Previous Article in Special Issue
Mathematical Theory of Seismic Activity and Its Specific Cases: Gutenberg–Richter Law, Omori Law, Roll-Off Effect, and Negative Binomial Distribution
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Entropy
Volume 27
Issue 2
10.3390/e27020174
entropy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Statistical Characteristics of Strong Earthquake Sequence in Northeastern Tibetan Plateau

by
Ying Wang
1,
Rui Wang
2,3,*,
Peng Han
2,3,4,
Tao Zhao
1,
Miao Miao
2,5,
Lina Su
1,
Zhaodi Jin
1 and
Jiancang Zhuang
6
1
Shaanxi Earthquake Agency, Xi’an 710068, China
2
Department of Earth and Space Science, Southern University of Science and Technology, Shenzhen 518055, China
3
Key Laboratory of Earthquake Forecasting and Risk Assessment, Ministry of Emergency Management, Southern University of Science and Technology, Shenzhen 518055, China
4
Guangdong Provincial Key Laboratory of Geophysical High-Resolution Imaging Technology, Southern University of Science and Technology, Shenzhen 518055, China
5
China Nuclear Power Engineering Co., Ltd., Shenzhen 518172, China
6
Institute of Statistical Mathematics, Tokyo 190-8562, Japan
*
Author to whom correspondence should be addressed.
Entropy 2025, 27(2), 174; https://doi.org/10.3390/e27020174
Submission received: 15 December 2024 / Revised: 28 January 2025 / Accepted: 4 February 2025 / Published: 6 February 2025
(This article belongs to the Special Issue Time Series Analysis in Earthquake Complex Networks)
Browse Figures
Versions Notes

Abstract

:
As the forefront of inland extension on the Indian plate, the northeastern Tibetan Plateau, marked by low strain rates and high stress levels, is one of the regions with the highest seismic risk. Analyzing seismicity through statistical methods holds significant scientific value for understanding tectonic conditions and assessing earthquake risk. However, seismic monitoring capacity in this region remains limited, and earthquake frequency is low, complicating efforts to improve earthquake catalogs through enhanced identification and localization techniques. Bi-scale empirical probability integral transformation (BEPIT), a statistical method, can address these data gaps by supplementing missing events shortly after moderate to large earthquakes, resulting in a more reliable statistical data set. In this study, we analyzed six earthquake sequences with magnitudes of MS ≥ 6.0 that occurred in northeastern Tibet since 2009, following the upgrade of the regional seismic network. Using BEPIT, we supplemented short-term missing aftershocks in these sequences, creating a more complete earthquake catalog. ETAS model parameters and b values for these sequences were then estimated using maximum likelihood methods to analyze parameter variability across sequences. The findings indicate that the b value is low, reflecting relatively high regional stress. The background seismicity rate is very low, with most mainshocks in these sequences being background events rather than foreshock-driven events. The p-parameter of the ETAS model is high, indicating that aftershocks decay relatively quickly, while the α-parameter is also elevated, suggesting that aftershocks are predominantly induced by the mainshock. These conditions suggest that earthquake prediction in this region is challenging through seismicity analysis alone, and alternative approaches integrating non-seismic data, such as electromagnetic and fluid monitoring, may offer more viable solutions. This study provides valuable insights into earthquake forecasting in the northeastern Tibetan Plateau.

1. Introduction

Earthquakes are among the most devastating natural disasters worldwide. The largest and most destructive seismic events typically occur at plate boundaries. Notable examples include the 1960 MW9.5 Valdivia earthquake in Chile, the 2010 MW8.8 Maule earthquake in Chile, the 2011 MW9.0 Tohoku earthquake in Japan, and the 2007 MW8.5 Sumatra earthquake, among others [1,2,3,4,5]. However, accurate earthquake prediction remains an unsolved challenge. To advance this field, many researchers have concentrated on seismically active regions, including Sichuan-Yunnan in China, Japan, California in the United States, and New Zealand, and conducted extensive observations. Utilizing a wealth of data from these regions, researchers have developed various statistical and physical methods to identify patterns of seismic activity, which has led to improvements in prediction efficiency. Examples of such methods include the b value, the Epidemic-Type Aftershock Sequence (ETAS) model, as well as methods for earthquake identification and localization [6,7,8,9,10,11,12]. However, these methods are not applicable in certain regions, making earthquake prediction in these areas particularly challenging.
The Tibetan Plateau is a region of particular geological significance, characterized by its highly complex geological structure. The northeastern section of the plateau represents the frontal region, extending into the mainland [13,14]. Due to the extension of the plateau, stress continuously accumulates; however, the strain rate is approximately 2 mm/year [15], significantly lower than that observed in subduction zones, and the earthquake frequency is relatively low [16]. This discrepancy results in a high level of stress within the region. The high stress levels combined with the complex geological conditions make this region one of the areas with the highest earthquake hazard, contributing to its complex seismicity. Historically, the region has experienced numerous large earthquakes, one of the most notable being the 1920 M81/2 Haiyuan earthquake, renowned as one of the most destructive events in seismic history. In recent years, significant seismic events have occurred, including the MS7.4 earthquake in Maduo in 2021; the MS6.9 earthquake in Menyuan, Qinghai Province, in 2022; and the Maerkang MS6.0 earthquake swarm in Sichuan Province in 2022. These events suggest increased seismic activity in the northwestern part of the Qinghai–Tibet Plateau, highlighting the region’s substantial earthquake hazard and drawing considerable attention from seismologists. A clear understanding of seismicity characteristics in this area is essential for effective earthquake prevention and disaster response efforts. With the comprehensive upgrade of the seismic network since 2009, earthquake monitoring capabilities have significantly improved, providing an invaluable opportunity to investigate seismicity characteristics through statistical approaches.
The ETAS model is a widely used tool for simulating the temporal evolution of seismicity rates. As one of the most realistic time series models, the ETAS model has been employed by researchers to analyze earthquake sequences across different regions, yielding insights into the characteristics of seismic activity. In China, some scholars [17,18] have utilized the ETAS model to investigate the distribution characteristics of earthquake sequence parameters. As a method based on statistics, the ETAS model relies heavily on earthquake catalogs as its data source. However, the effectiveness of earthquake monitoring can decline significantly following a major earthquake, both within the affected area and potentially in surrounding regions, due to the difficulty of detecting smaller earthquakes amidst the occurrence of numerous moderate to large earthquakes [19,20]. Consequently, a significant amount of post-earthquake data remain unrecorded, resulting in an increase in the number of incomplete magnitude readings. This scarcity can severely undermine the accuracy and stability of parameters fitting within the ETAS model. One relatively straightforward approach to mitigate this issue is to select a higher threshold magnitude; however, a low number of recorded earthquakes can also lead to unstable results [21,22]. Alternative methods aim to address catalog completeness. The template matching technique and other earthquake recognition methods are frequently employed to identify smaller earthquakes, but they require an extensive earthquake observation system [23,24,25,26,27]. The complex terrain of the northeastern Tibetan Plateau complicates the establishment of a dense seismic network, making the application of template matching in this region challenging. The bi-scale empirical probability integral transformation (BEPIT) method proposed by Zhuang et al. [28,29] can be applied to seismic sequences with sparse seismic stations and weak early monitoring ability based on the statistical law of aftershock attenuation. This method has been proven to help estimate stable attenuation parameters and obtain parameter information of early post-earthquake aftershock sequences [30,31]. Consequently, this method is employed in the present investigation to replenish the catalog of earthquake events immediately following the main shock.
In this study, we investigate the statistical characteristics of strong earthquake sequences (MS ≥ 6.0) in the northeastern Tibetan Plateau since 2009. Prior to analysis, we apply a seismic event replenishment technique based on statistical seismology to address the low seismicity rate and the incompleteness of the earthquake catalog following major earthquakes. Our analysis focuses on the seismic sequence parameters of these events, utilizing the ETAS model and the b value to elucidate the characteristics of seismicity in the region. Subsequently, we discuss the implications and potential applications of these findings in earthquake forecasting. This study seeks to contribute meaningful insights toward improving earthquake forecasting in the northeastern Tibetan Plateau.

2. Materials and Methods

2.1. Study Area and Data Selection

Six earthquake sequences with MS ≥ 6.0 have occurred on the northeastern Tibetan Plateau since 2009 and were selected for investigation. In the study region, seismic station coverage is sparse; as shown in Figure 1, there are four or fewer seismic stations within 100 km of each mainshock epicenter. Figure 1 displays the locations of these seismic events, which include the following: the 2013 MS6.6 earthquake sequence in Minxian, Gansu Province; the 2016 MS6.4 earthquake sequence in Menyuan, Qinghai Province; the 2017 MS7.0 earthquake sequence in Jiuzhaigou, Sichuan Province; the 2021 MS7.4 earthquake sequence in Maduo, Qinghai Province; the 2022 MS6.9 earthquake sequence in Menyuan, Qinghai Province; and the 2022 MS6.0 earthquake cluster in Maerkang, Sichuan Province. The earthquake data utilized in this study were obtained from the China Earthquake Networks Center (CENC). Only events with ML ≥ 0.0 are included in the data set. In selecting earthquake sequences, priority is given to intensive aftershock areas that develop within one month following each main event. The data retained for analysis also include the period preceding the main earthquake, enabling an examination of background seismic activity based on the level of seismicity and magnitude of the main event within the selected region.
Complete seismic samples are the basis of reliable results. The complete magnitude of completeness (MC) is the smallest magnitude at which an earthquake can be completely monitored. It is an index to evaluate the quality of an earthquake catalog. In this study, the maximum curvature (MAXC) method is applied to estimate the temporal MC of the sequence catalog [32]. This approach aids in estimating a new empirical distribution function based on fully recorded seismic data. However, previous studies indicate that the complete magnitude calculated by the MAXC method tends to be relatively low [33]. Therefore, in this study, we adjusted the MAXC result by adding 0.2 to define the complete magnitude. Using a moving time window, we conducted a temporal MC. The higher MC before and after the main shock are set to be the thresholds of magnitude for replenishing to ensure the completeness of the earthquake catalog for most of the time except for immediately after the mainshock. The MC after supplementing is shown in Table 1.

2.2. Seismic Event Supplement Technique Based on Statistical Seismology

Randomly occurring seismic events are commonly regarded as marking point processes [34,35,36,37]. Based on this framework, Zhuang et al. [28,29] proposed a novel algorithm, the BEPIT, employing a two-scale transformation technique. This algorithm was designed to supplement missing seismic events in incomplete records.
Suppose N = t i ,   m i : i = 1 ,   2 ,   … ,   n is a temporal marked point process in a time–magnitude domain [ 0 , T ] × M , where M is the space of marks. Using the following BEPIT, the empirical distribution function of time and magnitude is defined:
Γ N : 0 , T × M   →   0 , 1 × [ 0 , 1 ]
t , m   →   t ′ , m ′ = 1 n ∑ j = 1 n I t j < t ,   1 n ∑ j = 1 m I m j < m
where I is a logical function. It is defined as I(x) = 1 if x is true or as I(x) = 0 if x is false.
BEPIT is used to convert the non-uniform mode generated by the actual point process into a uniform mode, and then the missing aftershock events are filled in. The method comprises the following five main steps (for a detailed description of the method, see Zhuang et al. [28,29]):
Step 1. Seismic events are transformed to a [0, 1] × [0, 1] range using the BEPIT point processing technique, and the approximate time–magnitude range is established for missing events, S.
Step 2. Based on the seismic events within the time–magnitude range that should be fully observed, a new empirical distribution function is obtained by searching for the uniform distribution of events through an iterative process and adjusting the missing event region, S.
Step 3. Based on the empirical distribution function of the previous step, independent and uniformly distributed events are generated in the missing event region.
Step 4. Since the missing region will also contain some real seismic events, the supplementary data set needs to be adjusted. Duplicate events in the synthetic data set can be avoided by deleting the most recent supplementary data point for each real event.
Step 5. By means of linear interpolation, the magnitude of each supplementary event is assigned based on the observed relationship between magnitude and time.

2.3. ETAS Model

Ogata [38] extended the Omori–Utsu law by applying the Hawkes point process, positing that aftershocks exhibit self-similarity and that each earthquake has the potential to generate aftershocks. This leads to a cascading series of direct and indirect aftershocks following a main event. He introduced the ETAS model, characterized by a branching point process structure.
The intensity function of the seismic series t i ,     M i ; i = 1 , 2 , … , N in the subsequent observation period [0, T] with parameters [μ, A, c, α, p] can be expressed as follows [34,38]:
λ t = μ + ∑ t i < t A e α ( M i − M 0 ) p − 1 c ( t − t i c + 1 ) − p     M i > M 0
where t represents the elapsed time after the initial zero time. Mi and ti refer to the magnitude and onset time of the ith event, respectively. M0 is the reference magnitude, which is usually taken as the cutoff magnitude that is equal to or greater than the complete magnitude MC. The background seismicity rate is denoted by μ and is caused by the loading of regional stress, but it is usually negligible when compared to the aftershock sequence. The p value indicates how quickly the sequence decays; the larger this value is, the faster the decay, and vice versa. The length of time during which the frequency of aftershocks reaches its peak after the main earthquake is represented by c. A represents the average number of earthquakes triggered by an earthquake of magnitude MC. α indicates the ability to trigger aftershocks. When it comes to swarm-type sequences, α is generally less than 1; if there is no obvious stimulated aftershock in the earthquake sequence, α is generally greater than 1 [39].
The ETAS model parameters are estimated using the maximum likelihood method, with the likelihood function L taking the form in [S, T] in the fitting time range.
l n L = ∑ i : S ≤ t i < T l n λ t i − ∫ S T λ t d t
We perform the maximum likelihood estimation of parameters [μ, A, c, α, p] by bringing Equation (3) into Equation (4) and maximizing Equation (4).

2.4. b Value

The Gutenberg–Richter (G-R) law indicates the frequency–magnitude distribution of earthquakes [40,41] as follows:
l g N = a − b M   ( M ≥ M C )
where N is the number of earthquakes with a magnitude greater than or equal to M, a is the earthquake productivity, and b is the slope indicating the relative proportion of large and small earthquakes. Research has demonstrated that the b value is inversely related to the underground stress level [42,43,44,45,46,47]. As such, the b value serves as an indicator of geological structure and stress conditions and is widely used in earthquake forecasting and related research [10,48,49].

3. Results

Supplemental Data on Missing Earthquakes

To address the shortage of short-term aftershock data following an earthquake, we employed the BEPIT method. Using a moving time window, we conducted a temporal Mc analysis for each of the six sequences, and the maximum Mc values are summarized; the resulting MC values are shown in Table 1. In the immediate aftermath of the main earthquake, some aftershock signals were obscured by large-amplitude tail waves [50,51], leading to a temporary increase in MC. As monitoring capabilities in the aftershock region gradually improved, MC began to decrease. However, with the reduction in mobile observation stations, MC gradually increased again, eventually stabilizing at levels similar to those observed prior to the main event.
The BEPIT method was applied to supplement missing earthquake data immediately following the main shock. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 illustrate the results of this supplementation for the early aftershock data of six sequences. The findings show a significant increase in the number of recorded seismic events shortly after the main earthquake, highlighting the effectiveness of this supplementation technique. The enhanced seismic catalog provides a more comprehensive primary data set for subsequent research, enabling the derivation of more stable parameters.
The ETAS model parameters for the six seismic sequences are estimated using maximum likelihood estimation based on a relatively complete catalog. To facilitate comparison and analysis across the six sequences, a unified MC = ML1.7 is selected for calculation. Table 2 presents the estimated model parameters. Additionally, the maximum likelihood method is employed to estimate the b values of each seismic sequence (Figure 8).
An analysis of six earthquake sequences in the northeastern Tibetan Plateau revealed that although these sequences occur within the same tectonic region and share some general characteristics, they also display distinct parameter differences. As shown in Table 2, the μ values for all six sequences are low, indicating generally low seismic activity in these areas, with few earthquakes occurring before the main shock, particularly in sequences 2, 4, 5, and 6. Observational records confirm that no significant earthquakes occurred near the epicenters in the months preceding the 2013 Minxian MS6.6, 2017 Jiuzhaigou MS7.0, 2022 Menyuan MS6.9, and 2022 Maerkang MS6.0 earthquakes, making it challenging to assess earthquake hazards through foreshock activity. Sequence 3, however, has a relatively higher μ value, suggesting that background seismic activity in this region was higher than in the other sequences.
Parameters A and α collectively reflect aftershock productivity [52,53]. Specifically, parameter A represents the number of aftershocks triggered by an earthquake of magnitude MC, while parameter α indicates the relationship between an earthquake’s magnitude and its potential to generate aftershocks [7,54]. A high α suggests that a significant portion of aftershocks are triggered by larger earthquakes, primarily the mainshock. In sequences 2, 3, and 5, the high α value indicates a lower proportion of high-order aftershocks, with most aftershocks primarily being triggered by the mainshock.
The statistical decay of aftershocks is governed by parameters c and p. Sequence 5 exhibits the smallest c value, indicating a shorter time for the aftershock frequency to peak. A larger p value suggests a faster decay rate. Utzu et al. [55], in their analysis of over 200 global seismic sequences, reported an average p of 1.1. In the six sequences presented in Table 2, sequences 1–4 display a p value exceeding this average, suggesting that aftershocks decay rapidly following large earthquakes, potentially reducing the relative damage from aftershock sequences. The b value reveals that aside from sequence 6, overall, the b values are lower, reflecting regional seismic statistical characteristics and indicating high stress levels in the northeastern Tibetan Plateau [56,57,58].

4. Discussion

4.1. ETAS Parameter

The effect of different cutoff magnitudes on seismic sequence parameters is analyzed using the 2017 Jiuzhaigou MS7.0 earthquake sequence as a case study, and the results are presented in Table 3. By varying the cutoff magnitudes to ML 1.7, 1.8, and 1.9, parameters μ, A, and c gradually decrease while α increases, and p remains largely unchanged. These results align with the typical parameter variation characteristics of the ETAS model, indicating that the supplementary catalog is relatively stable. Furthermore, the b value decreases slightly as the cutoff value increases, remaining within the margin of error, which suggests the stability of b and the suitability of the chosen cutoff magnitudes. Therefore, when examining seismic sequence parameters, the selection of the cutoff magnitude should be carefully considered.
Among the six seismic sequences analyzed in this study, five are mainshock–aftershock types, with sequence 6 exhibiting a swarm-type clustering pattern. As shown in Table 2, the ETAS model parameters vary significantly across these sequence types. The swarm-type sequence (sequence 6) demonstrates a higher b value, lower α value, and reduced c value and p value compared to the five mainshock–aftershock sequences. These parameter differences suggest that swarm sequences may feature relatively frequent aftershocks, slower attenuation rates post-event, and a heightened capacity to trigger second-order aftershocks. After a major earthquake, determining the sequence type is essential for assessing post-earthquake trends. The parameter characteristics observed here provide valuable insights for post-earthquake sequence classification and trend assessment.
The six seismic sequences examined in this study are situated on the Tibetan Plateau and represent continental intraplate earthquakes. Compared with subduction zone earthquakes, such as those in Japan, these intraplate sequences exhibit higher p and lower c values [7,59,60]. Consequently, the p and c values can also serve as indicators of tectonic environments.

4.2. Implication on Earthquake Forecasting

To investigate this further, we analyzed the probability of each mainshock being a background event [36], and the findings are presented in Table 2. With the exception of the 2022 Ms6.0 Maerkang earthquake, most of the primary earthquakes exhibit a high probability of being background events, indicating limited foreshock activity and suggesting that these main events were not foreshock-triggered. Indeed, none of these significant earthquakes were preceded by foreshocks. Furthermore, due to the sparse earthquake activity before the main events, it is challenging to observe the long-term decline in the b value that has been observed before some major earthquakes, such as the Wenchuan earthquake, the Tohoku earthquake in Japan, and the Sumatra earthquake [48,49,61,62]. This scarcity of pre-event seismicity complicates earthquake risk assessment based solely on precursor activity.
Due to the low incidence of background earthquakes in the northeastern Tibetan Plateau, seismicity-based prediction methods are challenging to apply in this area. In addition to statistical seismicity modeling, other effective earthquake prediction approaches rely on non-seismic precursors. Currently, geomagnetic field variations and underground fluid anomalies serve as relatively mature earthquake precursors in this region. Approximately six months prior to the 2022 Menyuan MS6.9 earthquake, eight underground fluid anomalies were observed, primarily within a 200 km radius of the epicenter [63]. Approximately two months before the Menyuan MS 6.9 earthquake, anomalously high geomagnetic polarization values exceeding the threshold were detected [64]. These geomagnetic observations, combined with recorded underground fluid anomalies, facilitated a successful prediction of the event [65]. Thus, earthquake forecasting in the northeastern Tibetan Plateau might be enhanced by integrating precursor-based approaches [66,67,68]. In addition to advancing seismic network capabilities, establishing dedicated precursor observation stations should be prioritized to improve predictive accuracy in this region.
The probability of the mainshock in the 2022 Ms6.0 Maerkang earthquake sequence being a background event is nearly zero, indicating that it was triggered by preceding foreshock activity. Consistent with previous findings, this sequence exhibited a concentration of foreshocks across multiple faults prior to the mainshock, likely attributable to the region’s complex seismogenic environment. The Ms6.0 Maerkang earthquake, the largest event in this swarm, was preceded by an Ms5.8 foreshock and was followed by an Ms5.2 event, resulting in three earthquakes being above Ms5.0. This earthquake swarm occurred at the intersection of the Songgang and Longriba faults within the Bayan Har block, an area characterized by a complex epicentral structure. Studies on the precise location of the sequences suggest that the Maerkang swarm is influenced by multiple parallel and small-scale conjugate faults in proximity to the epicenter [69,70,71]. These three Ms5.0+ earthquakes took place on distinct fault sections, forming a swarm driven by multi-fault planes [72]. Compared to single-fault systems, such complex, multi-fault structures can yield more intricate earthquake sequences. Thus, in regions with similarly complex fault systems, the possibility of subsequent moderate to large earthquakes following an initial significant event should be anticipated.

4.3. Constraints and Challenges

As this research progressed, constraints in the application of certain methods also became apparent. One notable limitation pertains to the Gutenberg–Richter (G-R) law. Beyond the requirement that earthquakes used for a b value analysis must have magnitudes equal to or greater than the completeness magnitude, the G-R law may not hold for large-magnitude earthquakes, as illustrated in Figure 8. To address this issue, some studies have introduced derivative forms of the G-R law based on statistical methods, but their practical application remains limited [73]. From the perspective of physical properties, the statistical analysis of seismic energy has been shown to yield more accurate fits and robust results [74,75].
Another limitation involves the determination of the missing event range in the BEPTI algorithm. In Step 2 of BEPTI, the time–magnitude range for missing events, SS, must be manually estimated. This range should encompass the entire region where earthquakes are missing and extend beyond it. However, the manual estimation of this range introduces subjectivity, which may affect the results, as discussed by Zhuang et al. [29]. While it has been suggested that the selection of this range is not highly sensitive to the final outcomes, the development of an algorithm for the objective determination of missing earthquakes is necessary to improve the method’s reliability and objectivity.

5. Conclusions

This study examined six MS ≥ 6.0 earthquake sequences that have occurred in the northeastern Tibetan Plateau since 2009. Using the BEPIT method, missing earthquakes from the short-term period following major events were supplemented, resulting in a more comprehensive seismic sequence catalog. The findings confirm that BEPIT is a highly efficient method suitable for supplementing any earthquake sequence initially affected by limited early monitoring, facilitating the assessment of missing data impacts and the correction of related biases. A subsequent analysis of the ETAS model parameters for these six sequences yielded the following conclusions.
The μ values for the six seismic sequences in the northeastern Tibetan Plateau are uniformly low, suggesting a generally low background seismicity rate with few foreshocks preceding major earthquakes. This underscores the challenges in forecasting earthquakes in this region solely through seismic activity analysis and foreshock observations, providing critical insights for the strategic planning of earthquake prediction efforts. The findings of this research provide valuable reference points for designing seismic monitoring strategies prior to large earthquakes and for analyzing changes in regional seismic sequence parameters. Additionally, they can contribute to improving the scientific accuracy of early assessments of post-earthquake trends.
The parameters of the six earthquake sequences in the northeastern Qinghai–Tibet Plateau examined in this study differ from those observed in previous earthquake cases within mainland China and subduction zones [59,60,76]. These differences arise from variations in regional stress conditions, seismogenic structures, and crustal medium properties.
It is important to note that the study area experienced a limited number of strong earthquakes after the upgrade of the seismic network, resulting in the selection of only six earthquake sequences for analysis. Consequently, the findings of this study may capture only a subset of statistical characteristics. Further research incorporating a larger set of earthquake cases is needed for a more comprehensive and in-depth analysis.

Author Contributions

Conceptualization, Y.W., R.W. and P.H.; methodology, Y.W., R.W. and J.Z.; software, Y.W. and R.W.; validation, Y.W., R.W. and P.H.; formal analysis, Y.W. and R.W.; investigation, R.W. and P.H.; resources, L.S.; data curation, T.Z. and Z.J.; writing—original draft preparation, Y.W.; writing—review and editing, R.W., M.M. and P.H.; visualization, Y.W. and R.W.; supervision, P.H. and J.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key R&D Program of China, grant number 2023YFC3012005; the Special Fund of the Institute of Geophysics, China Earthquake Administration, grant number DQJB24Z014; the National Natural Science Foundation of China, grant number 42304004, 42404063; and the Earthquake Science and Technology Spark Program, grant number XH23038A.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The catalog in this study was provided by the China Earthquake Networks Center from 2009 to June 2023.

Acknowledgments

We would like to thank the anonymous reviewers who helped to improve the manuscript. We thank Wessel et al. for providing the Generic Mapping Tools (GMT6.5.0) used to plot some of the figures [77].

Conflicts of Interest

Author Miao Miao was employed by the China Nuclear Power Engineering Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Chapron, E.; Ariztegui, D.; Mulsow, S.; Villarosa, G.; Pino, M.; Outes, V.; Juvignié, E.; Crivelli, E. Impact of the 1960 major subduction earthquake in northern patagonia (Chile, Argentina). Quat. Int. 2006, 158, 58–71. [Google Scholar] [CrossRef]
  2. Elnashai, A.S.; Gencturk, B.; Kwon, O.S.; Hashash, Y.M.A.; Kim, S.J.; Jeong, S.H.; Dukes, J. The maule (Chile) earthquake of february 27, 2010: Development of hazard, site specific ground motions and back-analysis of structures. Soil Dyn. Earthq. Eng. 2012, 42, 229–245. [Google Scholar] [CrossRef]
  3. Marsan, D.; Enescu, B. Modeling the foreshock sequence prior to the 2011, MW9.0 Tohoku, Japan, earthquake. J. Geophys. Res. Solid Earth 2012, 117, B06316. [Google Scholar] [CrossRef]
  4. Muda, L.A.; Akinori, H.; Toshinori, S. Analysis of afterslip distribution following the 2007 september 12 southern sumatra earthquake using poroelastic and viscoelastic media. Geophys. J. Int. 2013, 192, 18–37. [Google Scholar] [CrossRef]
  5. Tsang, L.L.H.; Hill, E.M.; Barbot, S.; Qiu, Q.; Feng, L.; Hermawan, I.; Banerjee, P.; Natawidjaja, D.H. Afterslip following the 2007 MW8.4 Bengkulu earthquake in Sumatra loaded the 2010 MW7.8 Mentawai tsunami earthquake rupture zone. J. Geophys. Res. Solid Earth 2016, 121, 9034–9049. [Google Scholar] [CrossRef]
  6. Lengliné, O.; Enescu, B.; Peng, Z.; Shiomi, K. Decay and expansion of the early aftershock activity following the 2011, MW9.0 Tohoku earthquake. Geophys. Res. Lett. 2012, 39, L18309. [Google Scholar] [CrossRef]
  7. Harte, D.S. Bias in fitting the ETAS model: A case study based on New Zealand seismicity. Geophys. J. Int. 2013, 192, 390–412. [Google Scholar] [CrossRef]
  8. Ross, Z.E.; Trugman, D.T.; Hauksson, E.; Shearer, P.M. Searching for hidden earthquakes in southern California. Science 2019, 364, 767–771. [Google Scholar] [CrossRef]
  9. Long, F.; Zhang, Z.; Qi, Y.; Liang, M.; Ruan, X.; Wu, W.; Jiang, G.; Zhou, L. Three dimensional velocity structure and accurate earthquake location in Changning–Gongxian area of southeast Sichuan. Earth Planet. Phys. 2020, 4, 163–177. [Google Scholar] [CrossRef]
  10. Wang, R.; Chang, Y.; Miao, M.; Zeng, Z.; Chen, H.; Shi, H.; Li, D.; Liu, L.; Su, Y.; Han, P. Assessing earthquake forecast performance based on b value in Yunnan Province. China. Entropy 2021, 23, 730. [Google Scholar] [CrossRef]
  11. Manganiello, E.; Herrmann, M.; Marzocchi, W. New physical implications from revisiting foreshock activity in southern California. Geophys. Res. Lett. 2022, 50, e2022GL098737. [Google Scholar] [CrossRef]
  12. Kumazawa, T.; Ogata, Y.; Tsuruoka, H. Characteristics of seismic activity before and after the 2018 M6.7 Hokkaido Eastern Iburi earthquake. Earth Planets Space 2019, 71, 130. [Google Scholar] [CrossRef]
  13. Zhang, P.; Deng, Q.; Zhang, G.; Ma, J.; Gan, W.; Min, W.; Mao, F.; Wang, Q. Active tectonic blocks and strong earthquakes in the continent of China. Sci. China Ser. D-Earth Sci. 2003, 46, 13–24. [Google Scholar] [CrossRef]
  14. Zhang, P.; Deng, Q.; Zhang, Z.; Li, H. Active faults, earthquake hazards and associated geodynamic processes in continental China. Sci. Sin. Terrae 2013, 43, 1607–1620. [Google Scholar] [CrossRef]
  15. Song, X.; Jiang, Y.; Shan, X.; Gong, W.; Qu, C. A fine velocity and strain rate field of present-day crustal motion of the northeastern Tibetan Plateau inverted jointly by InSAR and GPS. Remote Sens. 2019, 11, 435. [Google Scholar] [CrossRef]
  16. Fukahata, Y. Estimate of the contraction rate of central Japan through the deformation of the Philippine Sea slab. Prog. Earth Planet. Sci. 2019, 6, 4. [Google Scholar] [CrossRef]
  17. Jiang, H.; Zheng, J.; Wu, Q.; Qu, Y.; Li, Y. Earlier statistical features of ETAS model parameters and their seismological meanings. Chin. J. Geophys. 2007, 50, 1778–1786. [Google Scholar] [CrossRef]
  18. Jiang, C.; Han, L.; Guo, L. Parameter characteristics in the early period of three earthquake sequences in Yutian, Xinjiang since 2008. Acta Seismol. Sin. 2014, 36, 165–174. [Google Scholar] [CrossRef]
  19. Enescu, B.; Mori, J.; Miyazawa, M.; Kano, Y. Omori-Utsu law c-values associated with recent moderate earthquakes in Japan. Bull. Seismol. Soc. Am. 2009, 99, 884–891. [Google Scholar] [CrossRef]
  20. Sawazaki, K.; Enescu, B. Imaging the high-frequency energy radiation process of a main shock and its early aftershock sequence: The case of the 2008 Iwate-Miyagi Nairiku earthquake, Japan. J. Geophys. Res. Solid Earth 2014, 119, 4729–4746. [Google Scholar] [CrossRef]
  21. Lippiello, E.; Cirillo, A.; Godano, C.; Papadimitriou, E.; Karakostas, V. Post seismic catalog incompleteness and aftershock forecasting. Geosciences 2019, 9, 355. [Google Scholar] [CrossRef]
  22. Omi, T.; Ogata, Y.; Shiomi, K.; Enescu, B.; Sawazaki, K.; Aihara, K. Implementation of a real-time system for automatic aftershock forecasting in Japan. Seismol. Res. Lett. 2018, 90, 242–250. [Google Scholar] [CrossRef]
  23. Peng, Z.; Zhao, P. Migration of early aftershocks following the 2004 Parkfield earthquake. Nat. Geosci. 2009, 2, 877–881. [Google Scholar] [CrossRef]
  24. Kato, A.; Nakagawa, S. Multiple slow-slip events during a foreshock sequence of the 2014 Iquique, Chile MW8.1 earthquake. Geophys. Res. Lett. 2014, 41, 5420–5427. [Google Scholar] [CrossRef]
  25. Zhang, M.; Wen, L. An effective method for small event detection: Match and Locate (M&L). Geophys. J. Int. 2015, 200, 1523–1537. [Google Scholar] [CrossRef]
  26. Liu, M.; Li, H.; Zhang, M.; Wang, T. Graphics processing unit-based Match and Locate (GPU-M&L): An improved Match and Locate method and its application. Seismol. Res. Lett. 2020, 91, 1019–1029. [Google Scholar] [CrossRef]
  27. Zhou, Y.; Yue, H.; Fang, L.; Zhou, S.; Li, Z.; Ghosh, A. An earthquake detection and location architecture for continuous seismograms: Phase picking, association, location, and matched filter (PALM). Seismol. Res. Lett. 2022, 93, 413–425. [Google Scholar] [CrossRef]
  28. Zhuang, J.; Ogata, Y.; Wang, T. Data completeness of the Kumamoto earthquake sequence in the JMA catalog and its influence on the estimation of the ETAS parameters. Earth Planets Space 2017, 69, 36. [Google Scholar] [CrossRef]
  29. Zhuang, J.; Wang, T.; Kiyosugi, K. Detection and replenishment of missing data in marked point processes. Stat. Sin. 2020, 30, 2105–2130. [Google Scholar] [CrossRef]
  30. Seif, S.; Mignan, A.; Zechar, J.D.; Werner, M.J.; Wiemer, S. Estimating ETAS: The effects of truncation, missing data, and model assumptions. J. Geophys. Res. Solid Earth 2017, 122, 449–469. [Google Scholar] [CrossRef]
  31. Zheng, Y.; Enescu, B.; Zhuang, J.; Yu, C. Data replenishment of five moderate earthquake sequences in Japan, with semiautomatic cluster selection. Earthq. Sci. 2021, 34, 310–322. [Google Scholar] [CrossRef]
  32. Wiemer, S.; Wyss, M. Minimum magnitude of complete reporting in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
  33. Woessner, J.; Wiemer, S. Assessing the quality of earthquake catalogues: Estimating the magnitude of completeness and its uncertainty. Bull. Seismol. Soc. Am. 2005, 95, 684–698. [Google Scholar] [CrossRef]
  34. Ogata, Y.; Zhuang, J. Space–time ETAS models and an improved extension. Tectonophysics 2006, 413, 13–23. [Google Scholar] [CrossRef]
  35. Werner, M.J.; Helmstetter, A.; Jackson, D.D.; Kagan, Y.Y. High-resolution long-term and short-term earthquake forecasts for California. Bull. Seismol. Soc. Am. 2011, 101, 1630–1648. [Google Scholar] [CrossRef]
  36. Zhuang, J.; Ogata, Y.; Vere-Jones, D. Stochastic declustering of space-time earthquake occurrences. J. Am. Stat. Assoc. 2002, 97, 369–380. [Google Scholar] [CrossRef]
  37. Zhuang, J.; Ogata, Y.; Vere-Jones, D. Analyzing earthquake clustering features by using stochastic reconstruction. J. Geophys. Res. 2004, 109, B05301. [Google Scholar] [CrossRef]
  38. Ogata, Y. Statistical models for earthquake occurrences and residual analysis for point processes. J. Am. Stat. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
  39. Ogata, Y. Increased probability of large earthquakes near aftershock regions with relative quiescence. J. Geophys. Res. 2001, 106, 8729–8744. [Google Scholar] [CrossRef]
  40. Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
  41. Utsu, T. A method for determing the value of b in a formula log N=a-bM showing the magnitude frequency relation for earthquakes. Geophys. Bull. Hokkaido Univ. 1965, 13, 99–103. (In Japanese) [Google Scholar]
  42. Convertito, V.; Tramelli, A.; Godano, C. b map evaluation and on-fault stress state for the Antakya 2023 earthquakes. Sci. Rep. 2024, 14, 1596. [Google Scholar] [CrossRef] [PubMed]
  43. Scholz, C.H. On the stress dependence of earthquake b value. Geophys. Res. Lett. 2015, 42, 1399–1402. [Google Scholar] [CrossRef]
  44. Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef]
  45. Spada, M.; Tormann, T.; Wiemer, S.; Enescu, B. Generic dependence of the frequency-size distribution of earthquakes on depth and its relation to the strength profile of the crust. Geophys. Res. Lett. 2013, 40, 709–714. [Google Scholar] [CrossRef]
  46. Tan, Y.J.; Waldhauser, F.; Tolstoy, M.; Wilcock, W.S.D. Axial Seamount: Periodic tidal loading reveals stress dependence of the earthquake size distribution (b value). Earth Planet. Sci. Lett. 2019, 512, 39–45. [Google Scholar] [CrossRef]
  47. Wu, Y.M.; Chen, S.K.; Huang, T.C.; Huang, H.H.; Chao, W.A.; Koulakov, I. Relationship between earthquake b-values and crustal stresses in a young orogenic belt. Geophys. Res. Lett. 2018, 45, 1832–1837. [Google Scholar] [CrossRef]
  48. Nanjo, K.Z.; Hirata, N.; Obara, K.; Kasahara, K. Decade-scale decrease in b value prior to the M9-class 2011 Tohoku and 2004 Sumatra quakes. Geophys. Res. Lett. 2012, 39, 20304. [Google Scholar] [CrossRef]
  49. Xie, W.; Hattori, K.; Han, P. Temporal variation and statistical assessment of the b value off the Pacific Coast of Tokachi, Hokkaido, Japan. Entropy 2019, 21, 249. [Google Scholar] [CrossRef]
  50. Iwata, T. Low detection capability of global earthquakes after the occurrence of large earthquakes: Investigation of the Harvard CMT catalogue. Geophys. J. Int. 2008, 174, 849–856. [Google Scholar] [CrossRef]
  51. Mignan, A.; Woessner, J. Estimating the Magnitude of Completeness for Earthquake Catalogs. Community Online Resource for Statistical Seismicity Analysis. 2012. Available online: https://episodesplatform.eu/eprints/1587/ (accessed on 10 October 2024).
  52. Nandan, S.; Ouillon, G.; Wiemer, S.; Sornette, D. Objective estimationof spatially variable parameters of epidemic type aftershock sequence model: Application to California. J. Geophys. Res. 2017, 122, 5118–5143. [Google Scholar] [CrossRef]
  53. Dascher-Cousineau, K.; Brodsky, E.E.; Lay, T.; Goebel, T. What controls variations in aftershock productivity? J. Geophys. Res. 2020, 125, e2019JB018111. [Google Scholar] [CrossRef]
  54. Shebalin, P.; Baranov, S.; Vorobieva, I. Earthquake productivity law in a wide magnitude range. Front. Earth Sci. 2022, 10, 881425. [Google Scholar] [CrossRef]
  55. Utsu, T.; Ogata, Y.; Matsu’ura, R.S. The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
  56. Jiang, J.; Feng, J. Stress state and b-value anomalies before the Jiuzhaigou MS7.0 earthquake in 2017. Chin. Earthq. Eng. J. 2021, 43, 575–582. [Google Scholar] [CrossRef]
  57. Guo, Y.; Zhu, Y.; Yu, T.; Li, Q.; Zhang, L.; Yu, N. Research on spatio-temporal characteristics of b-value before and after the 2022 Menyuan MS6.9 earthquake. J. Geod. Geodyn. 2023, 43, 1155–1161. [Google Scholar] [CrossRef]
  58. Hu, N.; Han, P.; Wang, R.; Shi, F.; Chen, L.; Li, H. Spatial heterogeneity of b values in northeastern Tibetan Plateau and its interpretation. Entropy 2024, 26, 182. [Google Scholar] [CrossRef]
  59. Chu, A.; Schoenberg, F.P.; Bird, P.; Jackson, D.D.; Kagan, Y.Y. Comparison of ETAS parameter estimates across different global tectonic zones. Bull. Seismol. Soc. Am. 2011, 101, 2323–2339. [Google Scholar] [CrossRef]
  60. Zhang, L.; Werner, M.J.; Goda, K. Variability of ETAS parameters in global subduction zones and applications to mainshock-aftershock hazard assessment. Bull. Seismol. Soc. Am. 2020, 110, 191–212. [Google Scholar] [CrossRef]
  61. Nuannin, P.; Kulhánek, O.; Persson, L. Spatial and temporal b value anomalies preceding the devastating off coast of NW Sumatra earthquake of December 26, 2004. Geophys. Res. Lett. 2005, 32, L11307. [Google Scholar] [CrossRef]
  62. Shi, H.; Meng, L.; Zhang, X.; Chang, Y.; Yang, Z.; Xie, W.; Hattori, K.; Han, P. Decrease in b value prior to the Wenchuan earthquake (Ms8.0). Chin. J. Geophys. 2018, 61, 1874–1882. [Google Scholar] [CrossRef]
  63. Zhong, J.; Feng, X.; Wang, B.; Zhou, Z.; Yan, R. Analysis on anomalous characteristics of underground fluid before the Menyuan, Qinghai MS6.9 earthquake in 2022. J. Seismol. Res. 2022, 45, 308–317. [Google Scholar] [CrossRef]
  64. Fan, W.; Feng, L.; Li, X.; He, C.; Liao, X.; Yao, X. Characteristic of geomagnetic vertical intensity polarization anomalies before the Menyuan, Qinghai MS6.9 earthquake on January 8, 2022. Chin. Earthq. Eng. J. 2022, 44, 744–750. [Google Scholar] [CrossRef]
  65. Feng, L.; Li, X.; Zhao, Y.; Zhang, P. A short-term prediction practice on the Menyuan M6.9 earthquake on January 8, 2022. Earthq. Res. China 2022, 38, 12–20. [Google Scholar] [CrossRef]
  66. Han, P.; Hattori, K.; Zhuang, J.; Chen, C.H.; Liu, J.Y.; Yoshida, S. Evaluation of ULF seismo-magnetic phenomena in Kakioka, Japan by using Molchan’s error diagram. Geophys. J. Int. 2017, 208, 482–490. [Google Scholar] [CrossRef]
  67. Qiu, L.; Zhu, Y.; Liu, Q.; Guo, M.; Song, D.; Wang, A. Response law and indicator selection of seismic wave velocity for coal seam outburst risk. Adv. Geo-Energy Res. 2023, 9, 198–210. [Google Scholar] [CrossRef]
  68. Song, D.; Liu, Q.; Qiu, L.; Zhang, J.; Khan, M.; Peng, Y.; Zhao, Y.; Wang, M.; Guo, M.; Hong, T. Experimental study on resistivity evolution law and precursory signals in the damage process of gas-bearing coal. Fuel 2024, 362, 130798. [Google Scholar] [CrossRef]
  69. Long, F.; He, C.; Yi, G.; He, X.; Li, L.; Shi, F.; Yue, C.; Peng, L. Seismogenic structures and spatiotemporal seismicity patterns of the 2022 MS6.0 Maerkang earthquake sequence, Sichuan, China. Front. Earth Sci. 2023, 10, 1049911. [Google Scholar] [CrossRef]
  70. Xu, Y.; Guo, X. Relocation of the 2022 MS6.0 Maerkang earthquake swarm in Sichuan Province and its seismic fault analysis. Seismol. Geol. 2023, 45, 1006–1024. [Google Scholar] [CrossRef]
  71. Xiao, Y.; Shan, B.; Xiong, X.; Xie, Z.; Zhou, W. Probing into the mechanism of earthquake swarms: A case study of the 2022 Barkam earthquake swarm. Chin. J. Geophys. 2024, 67, 2159–2174. [Google Scholar] [CrossRef]
  72. Du, F.; Long, F.; Liang, M.; Qi, Y.; Gong, Y.; Wu, J. Characteristics of the Ma’erkang MS6.0 earthquake-swarm triggered along multiple fault planes in 2022. Earthq. Res. Sichuan 2022, 185, 1–10. [Google Scholar] [CrossRef]
  73. Utsu, T. Representation and analysis of the earthquake size distribution: A historical review and some new approaches. Pure Appl. Geophys. 1999, 155, 509–535. [Google Scholar] [CrossRef]
  74. da Silva, S.L.E.F. κ-generalised Gutenberg–Richter law and the self-similarity of earthquakes. Chaos Solitons Fractals 2021, 143, 110622. [Google Scholar] [CrossRef]
  75. Sotolongo-Costa, O.; Posadas, A. Fragment-asperity interaction model for earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef] [PubMed]
  76. Jiang, H.; Qu, Y.; Li, Y.; Zheng, J.; Hua, A.; Dai, L.; Hou, H. Some statistic features of aftershock sequences in Chinese mainland. Chin. J. Geophys. 2006, 49, 1110–1117. [Google Scholar] [CrossRef]
  77. Wessel, P.; Luis, J.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.; Tian, D. The generic mapping tools version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]
Entropy 27 00174 g001
Figure 1. The spatial distribution of six earthquake sequences with a mainshock of MS ≥ 6.0 in the northeastern Tibetan Plateau since 2010. The seismic events are represented by red dots, scaled according to their magnitudes. The mainshocks of each sequence are distinguished by yellow five-pointed stars, and the individual focal mechanisms of the mainshocks are marked. Tectonic blocks are delineated by solid blue lines, while tectonic fractures are depicted by solid black lines. Additionally, observation stations are denoted by light blue triangles in the diagram. The focal mechanism results were obtained from the Global CMT Catalog (www.globalcmt.org).
Figure 1. The spatial distribution of six earthquake sequences with a mainshock of MS ≥ 6.0 in the northeastern Tibetan Plateau since 2010. The seismic events are represented by red dots, scaled according to their magnitudes. The mainshocks of each sequence are distinguished by yellow five-pointed stars, and the individual focal mechanisms of the mainshocks are marked. Tectonic blocks are delineated by solid blue lines, while tectonic fractures are depicted by solid black lines. Additionally, observation stations are denoted by light blue triangles in the diagram. The focal mechanism results were obtained from the Global CMT Catalog (www.globalcmt.org).
Entropy 27 00174 g001
Entropy 27 00174 g002
Figure 2. The supplementary results of the aftershock data of the 2021 MS7.4 Maduo earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon on (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots on (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Figure 2. The supplementary results of the aftershock data of the 2021 MS7.4 Maduo earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon on (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots on (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Entropy 27 00174 g002
Entropy 27 00174 g003
Figure 3. The supplementary results of the aftershock data of the 2013 MS6.6 Minxian earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and the timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Figure 3. The supplementary results of the aftershock data of the 2013 MS6.6 Minxian earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and the timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Entropy 27 00174 g003
Entropy 27 00174 g004
Figure 4. The supplementary results of aftershock data of the 2016 MS6.4 Menyuan earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and the timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Figure 4. The supplementary results of aftershock data of the 2016 MS6.4 Menyuan earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and the timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Entropy 27 00174 g004
Entropy 27 00174 g005
Figure 5. The supplementary results of aftershock data of the 2017 MS7.0 Jiuzhaigou earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Figure 5. The supplementary results of aftershock data of the 2017 MS7.0 Jiuzhaigou earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
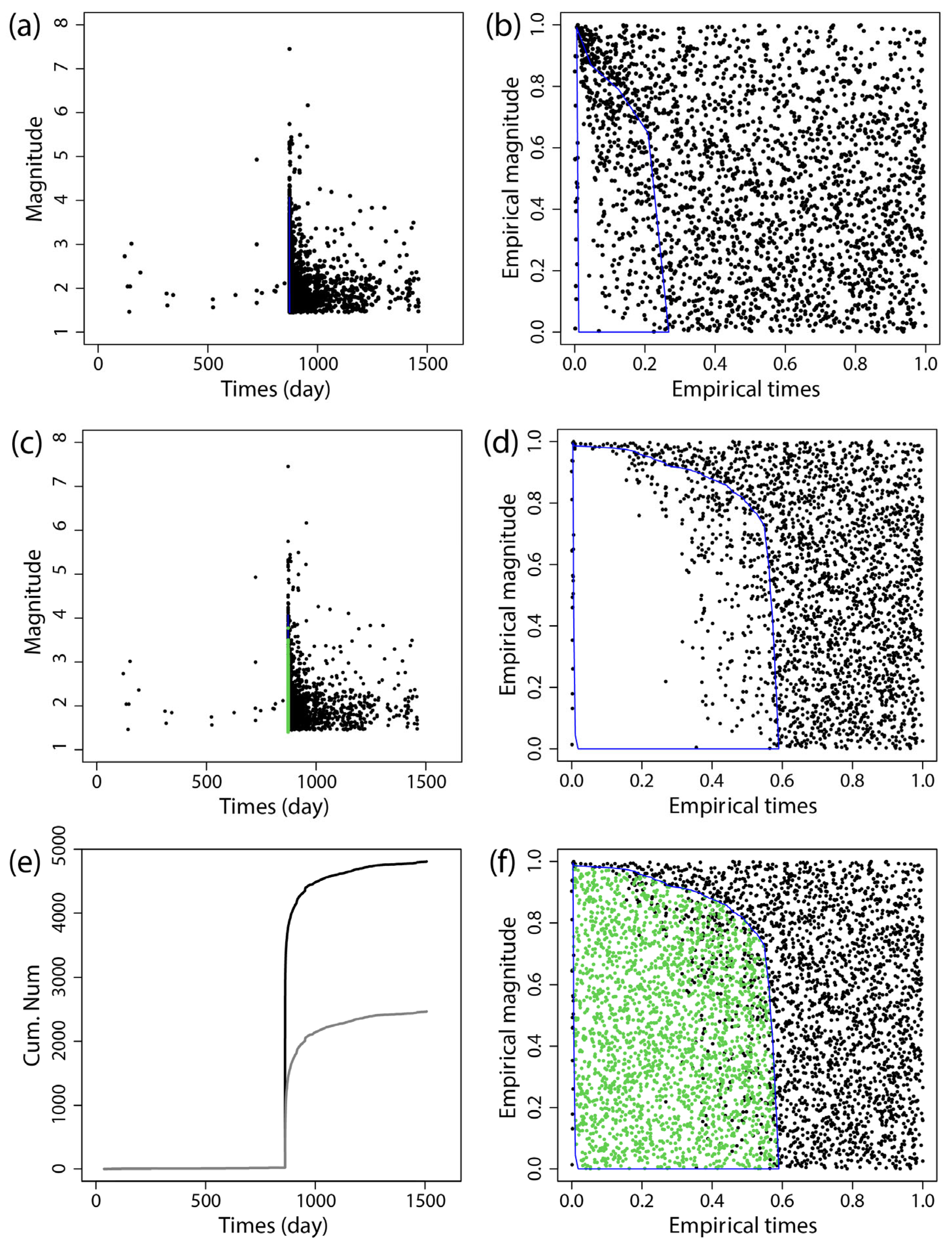
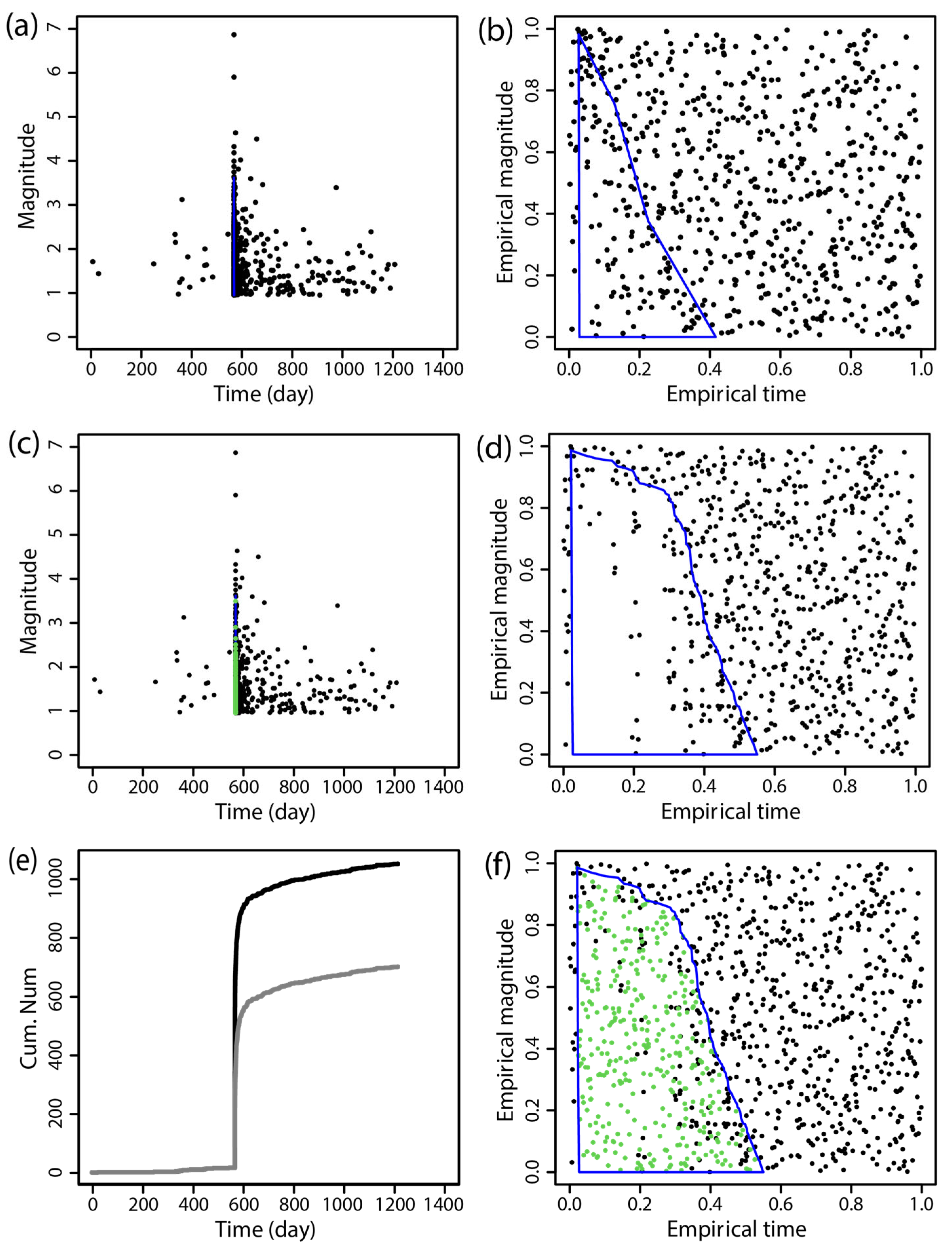
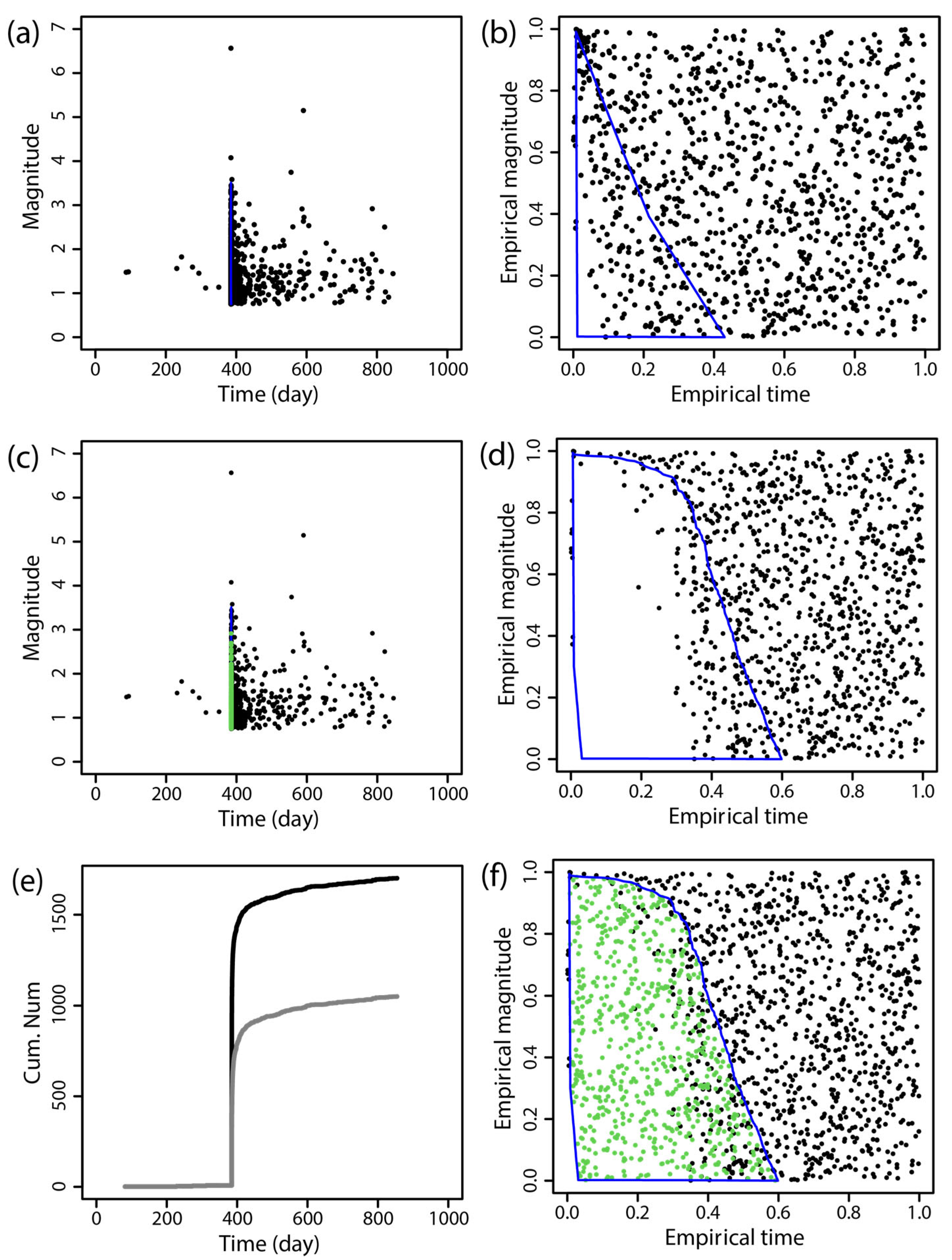
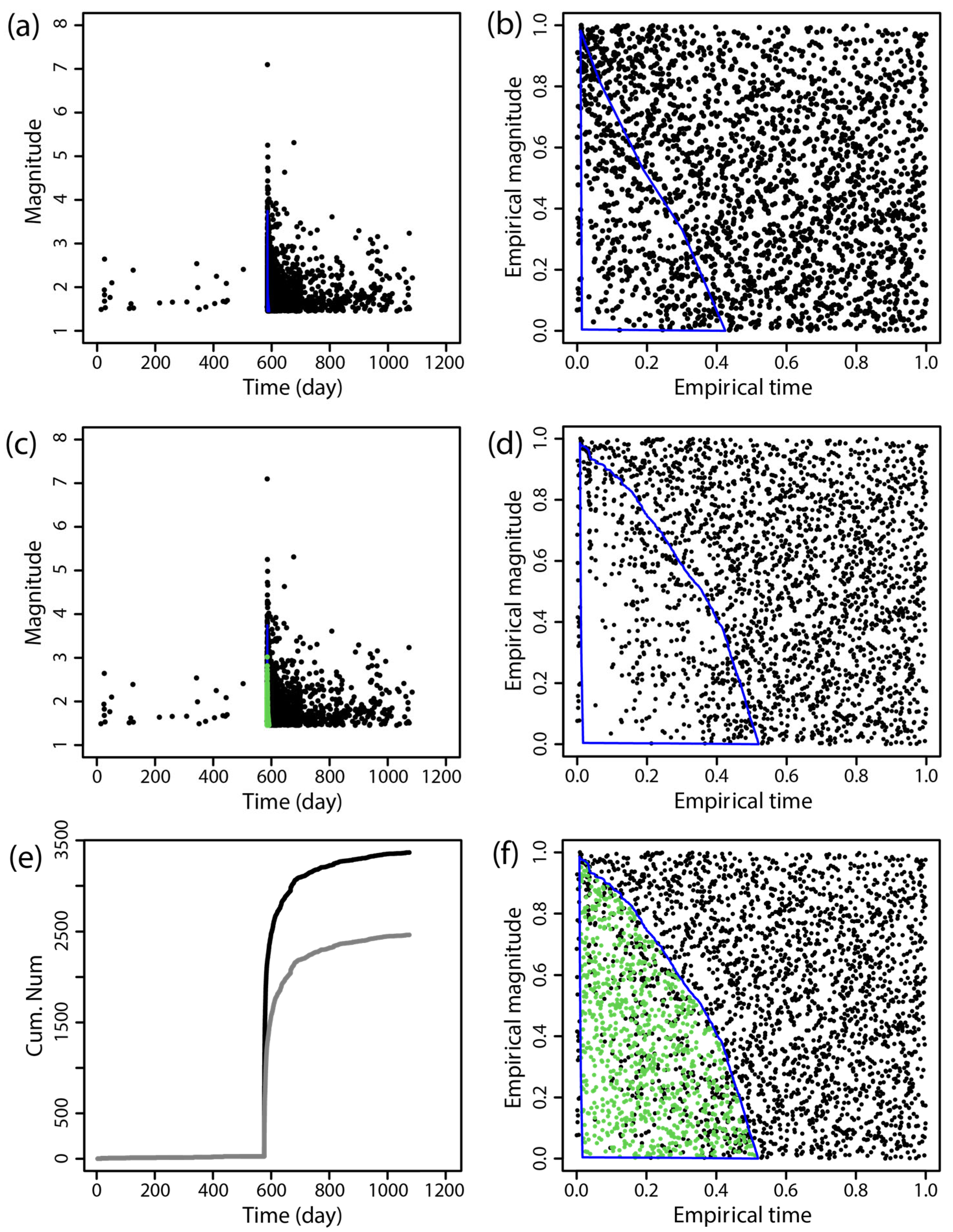
Entropy 27 00174 g005
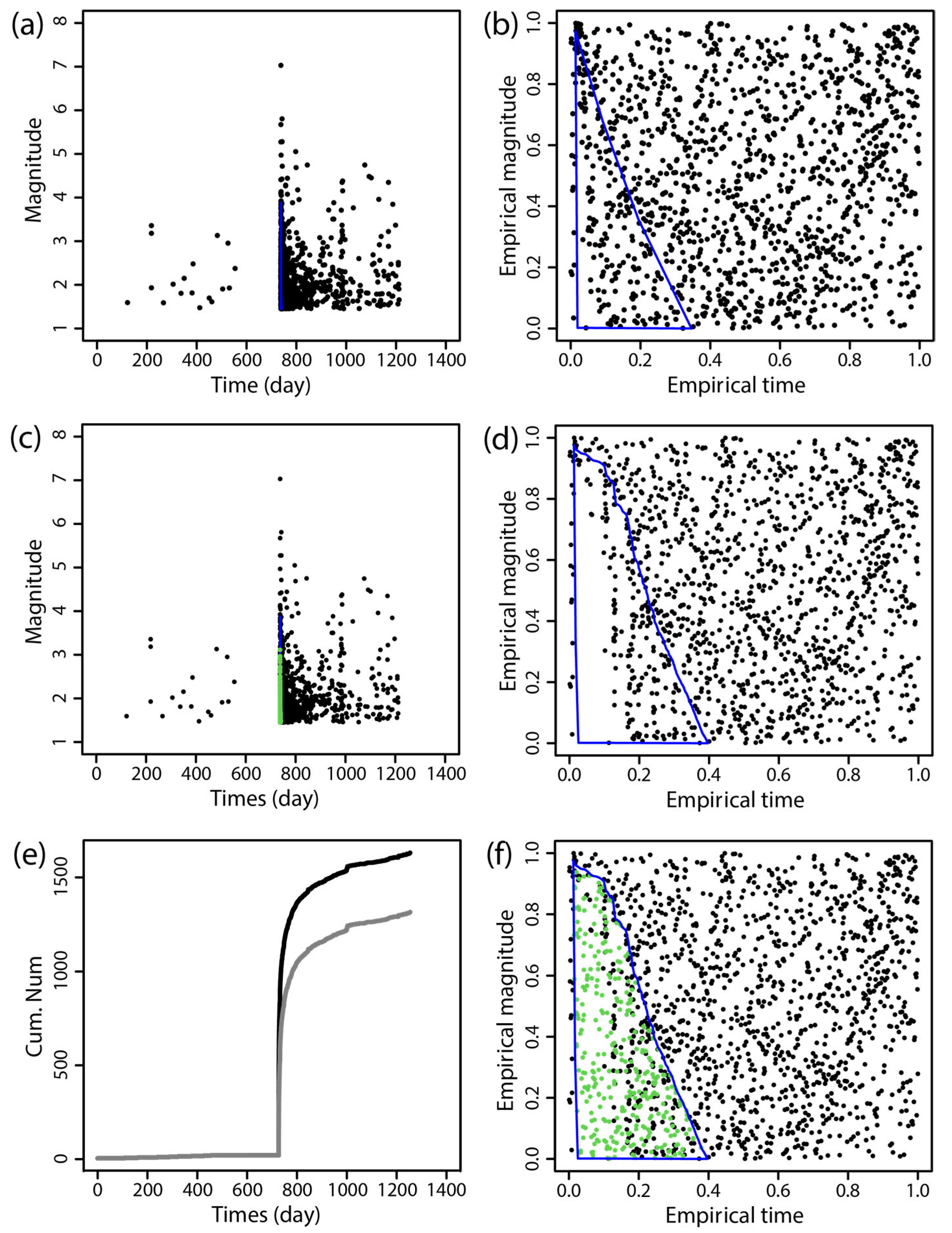
Entropy 27 00174 g006
Figure 6. The supplementary results of aftershock data of the 2022 MS6.9 Menyuan earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Figure 6. The supplementary results of aftershock data of the 2022 MS6.9 Menyuan earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside of the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Entropy 27 00174 g006
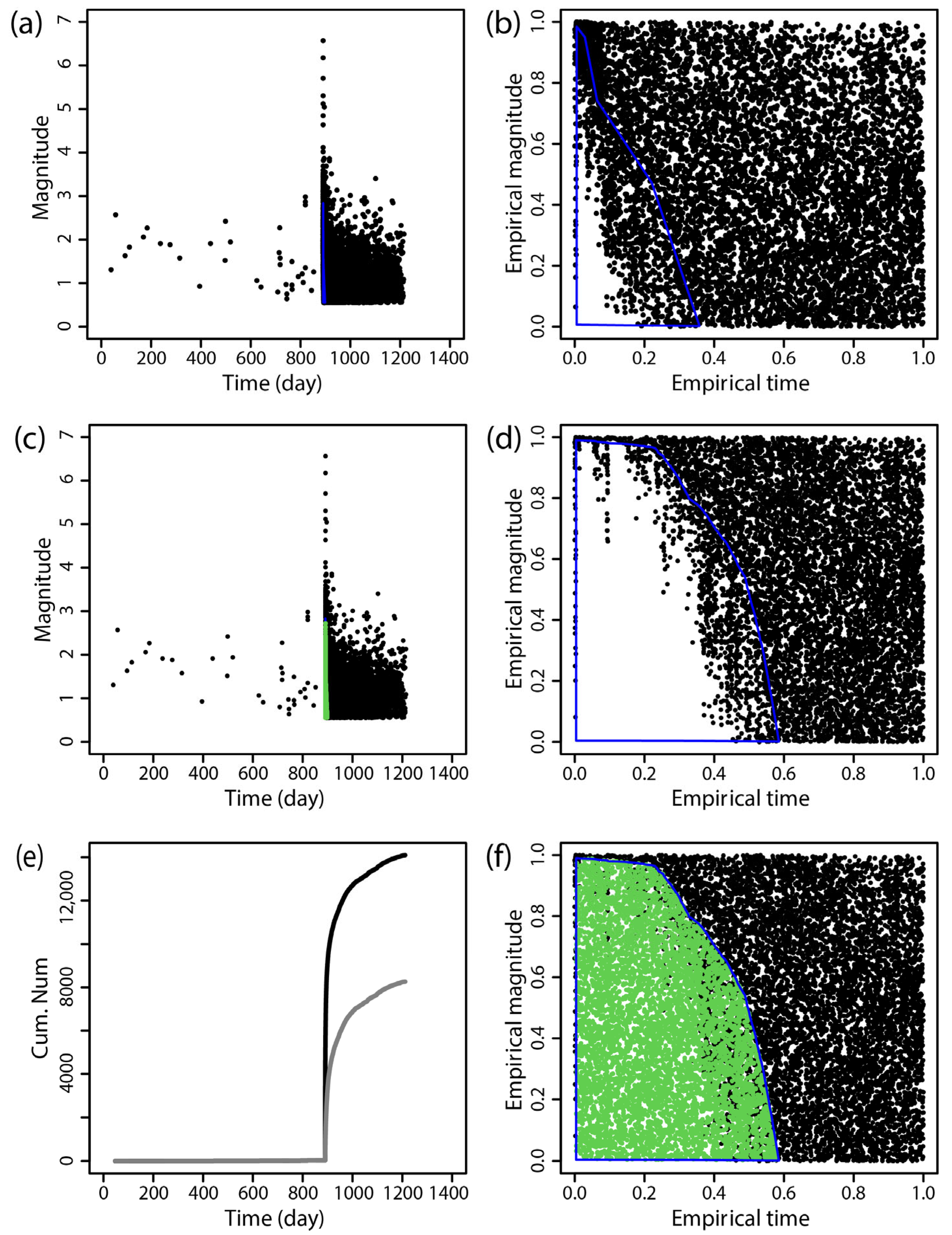
Entropy 27 00174 g007
Figure 7. The supplementary results of aftershock data of the 2022 MS6.0 Maerkang earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Figure 7. The supplementary results of aftershock data of the 2022 MS6.0 Maerkang earthquake obtained by using BEPIT. (a) shows the magnitude and occurrence time of actual seismic events and missing event ranges; (b) shows the empirical distribution of magnitude and the event occurrence time after the double-scale transformation technique (Step 1); (c) shows the magnitude and occurrence time of actual and supplementary seismic events (Step 5); (d) shows the empirical distribution of magnitude and the event occurrence time outside the missing event range after the double-scale transformation technique (Steps 2 and 3); (e) shows the cumulative number of earthquakes in the original data set (gray curve) and the supplementary data set (black curve); and (f) shows the empirical distribution of the magnitude and timing of actual and supplementary seismic events (Step 4). The blue polygon in (a,b,d,f) is the region where the missing event is located, and its corresponding mapping and the green dots in (c,f) are the supplementary events. The x-axis and y-axis in (b,d,f) are the empirical time and empirical magnitude transformed from time and magnitude by BEPIT.
Entropy 27 00174 g007
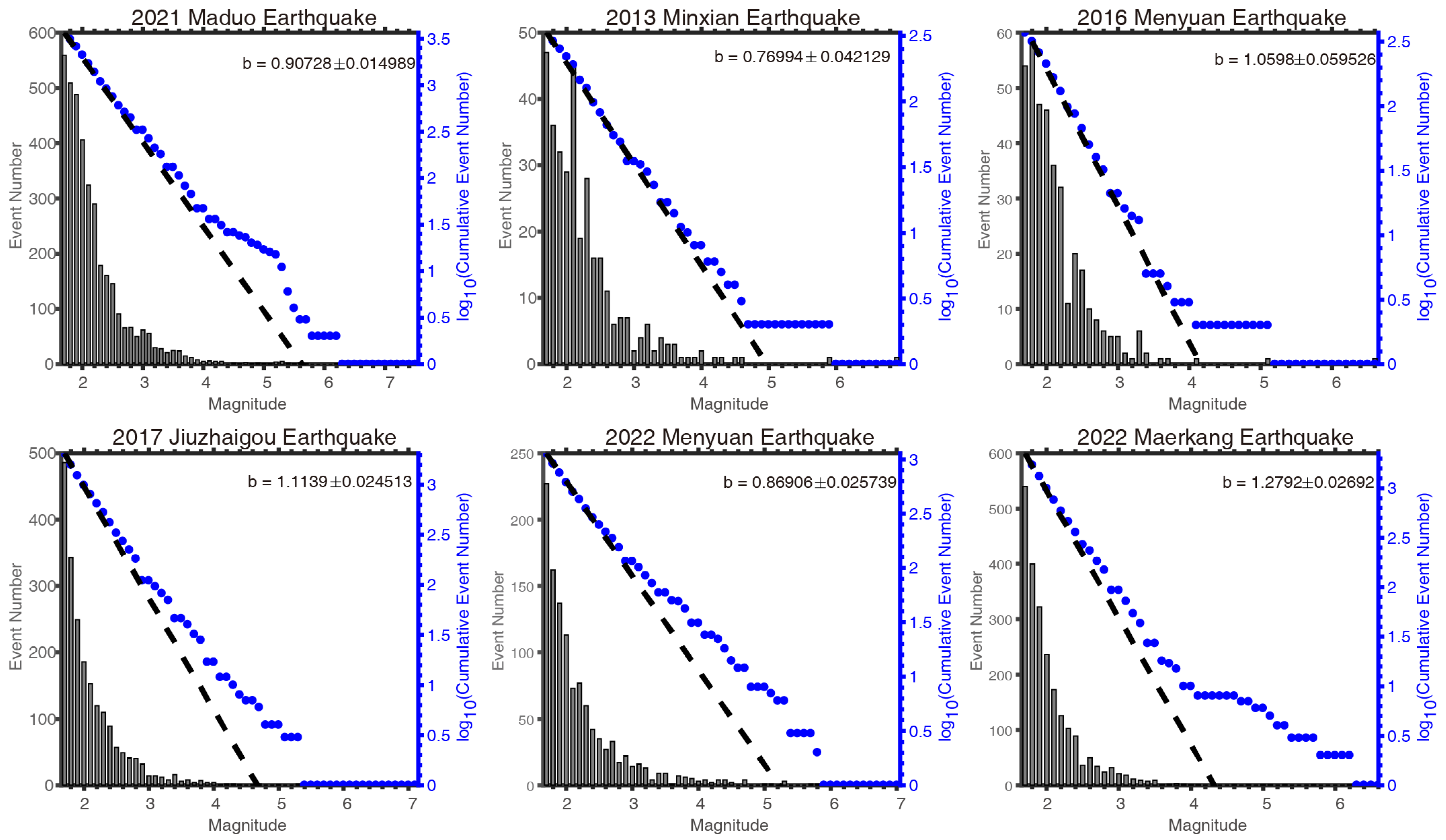
Entropy 27 00174 g008
Figure 8. The b values of the six seismic sequences. The histogram represents the magnitude–frequency distribution of the sequence, the blue dots represent the magnitude–frequency distribution under the logarithmic relationship, and the black dashed lines represent the results of fitting using the G-R.
Figure 8. The b values of the six seismic sequences. The histogram represents the magnitude–frequency distribution of the sequence, the blue dots represent the magnitude–frequency distribution under the logarithmic relationship, and the black dashed lines represent the results of fitting using the G-R.
Entropy 27 00174 g008
Table 1. The MC and the supplementary results of six seismic sequences.
Table 1. The MC and the supplementary results of six seismic sequences.
Time
(dd-mm-yyyy)		RegionMSMc Before
Supplementing		Mc After
Supplementing
22 May 2021Maduo7.42.91.5
22 July 2013Minxian6.62.41.0
22 January 2016Menyuan6.41.50.8
8 August 2017Jiuzhaigou7.02.11.5
8 January 2022Menyuan6.92.01.5
10 June 2022Maerkang6.02.00.6
Table 2. ETAS model parameter, b values and background earthquake probability of main earthquake of six seismic sequence.
Table 2. ETAS model parameter, b values and background earthquake probability of main earthquake of six seismic sequence.
IndexSeismic SequenceSequence TypeFault TypeμAαcpbBackground Earthquake Probability of Main Earthquake
Time
(dd-mm-yyyy)		RegionMS
122 May 2021Maduo7.4M-Astrike-slip0.01820.27111.07670.08231.18420.9073 ± 0.0150.7625
222 July 2013Minxian6.6M-Astrike-slip and thrust0.00010.00322.24390.01211.10320.7700 ± 0.0420.7522
322 January 2016Menyuan6.4M-Athrust0.03280.00052.68920.10871.27761.0598 ± 0.0601.0000
48 August 2017Jiuzhaigou7.0M-Astrike-slip0.00020.07381.92140.02911.15471.1139 ± 0.0250.2853
58 January 2022Menyuan6.9M-Astrike-slip0.00220.01732.26010.00511.03880.8691 ± 0.0260.9241
610 June 2022Maerkang6.0Sstrike-slip<0.00010.26891.77130.00711.05761.2792 ± 0.027<0.001
M-A: mainshock–aftershock type; S: earthquake swarm type.
Table 3. ETAS model parameter and b values of 2017 Jiuzhaigou MS7.0 earthquake sequence at different cutoff magnitudes.
Table 3. ETAS model parameter and b values of 2017 Jiuzhaigou MS7.0 earthquake sequence at different cutoff magnitudes.
Cutoff MagnitudeμAαcpb
ML1.70.0001920.0737821.9213650.0291171.1547181.1139 ± 0.025
ML1.80.0002930.0201832.2303460.0163991.1786451.0088 ± 0.032
ML1.90.0002550.0184942.2578870.0095181.1689211.0089 ± 0.035
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, Y.; Wang, R.; Han, P.; Zhao, T.; Miao, M.; Su, L.; Jin, Z.; Zhuang, J. Statistical Characteristics of Strong Earthquake Sequence in Northeastern Tibetan Plateau. Entropy 2025, 27, 174. https://doi.org/10.3390/e27020174

AMA Style

Wang Y, Wang R, Han P, Zhao T, Miao M, Su L, Jin Z, Zhuang J. Statistical Characteristics of Strong Earthquake Sequence in Northeastern Tibetan Plateau. Entropy. 2025; 27(2):174. https://doi.org/10.3390/e27020174

Chicago/Turabian Style

Wang, Ying, Rui Wang, Peng Han, Tao Zhao, Miao Miao, Lina Su, Zhaodi Jin, and Jiancang Zhuang. 2025. "Statistical Characteristics of Strong Earthquake Sequence in Northeastern Tibetan Plateau" Entropy 27, no. 2: 174. https://doi.org/10.3390/e27020174

APA Style

Wang, Y., Wang, R., Han, P., Zhao, T., Miao, M., Su, L., Jin, Z., & Zhuang, J. (2025). Statistical Characteristics of Strong Earthquake Sequence in Northeastern Tibetan Plateau. Entropy, 27(2), 174. https://doi.org/10.3390/e27020174

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop