Dual-Regularized Feature Selection for Class-Specific and Global Feature Associations
Abstract
1. Introduction
- We propose a novel dual-regularization approach for FS, balancing class-specific feature interactions and global redundancy elimination.
- We theoretically show that our dual regularization effectively preserves class-specific feature geometry while addressing global redundancies.
- Extensive experiments on eight real-world datasets show that DRFS consistently outperforms existing FS methods in classification accuracy.
2. Related Works
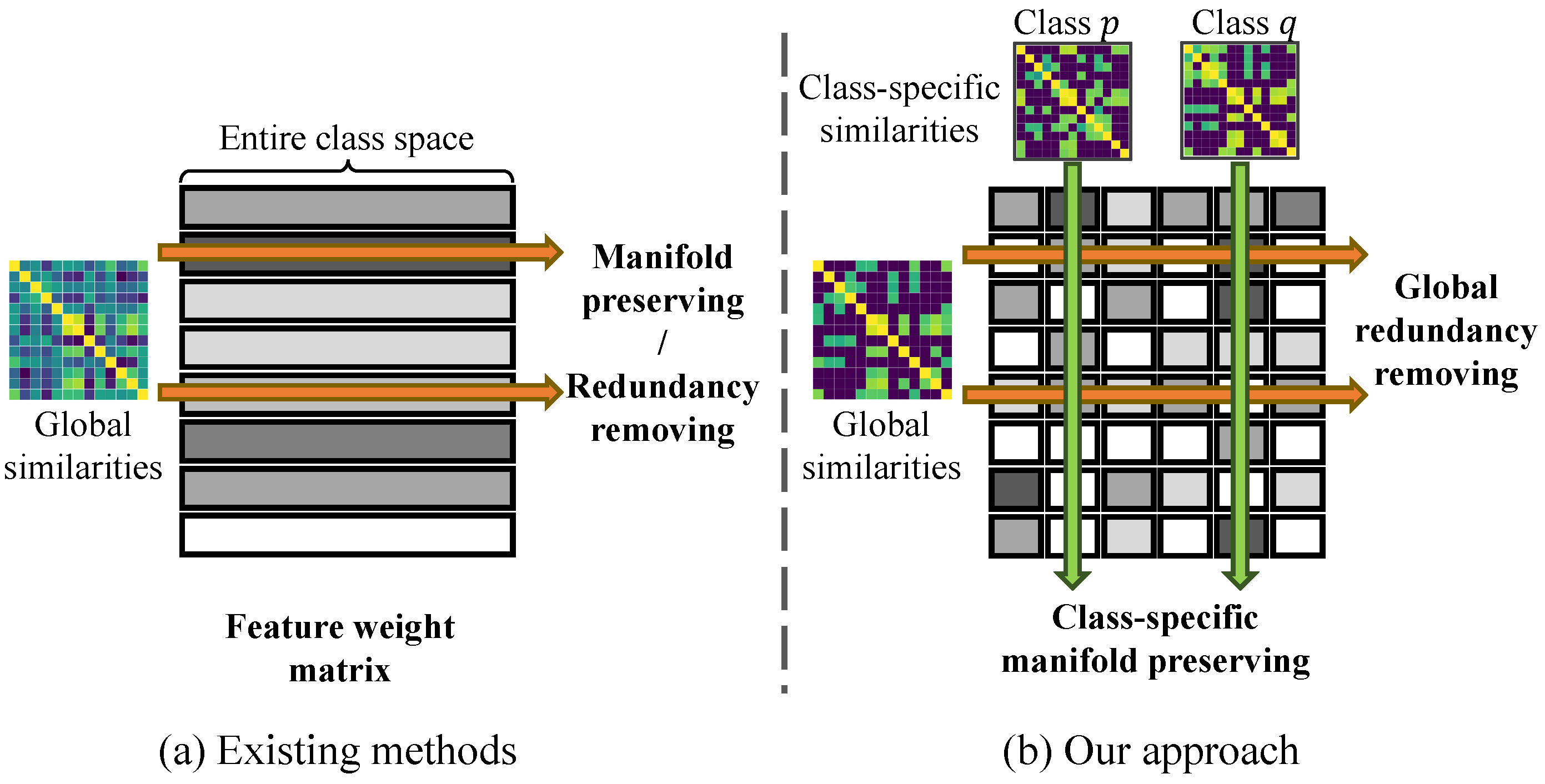
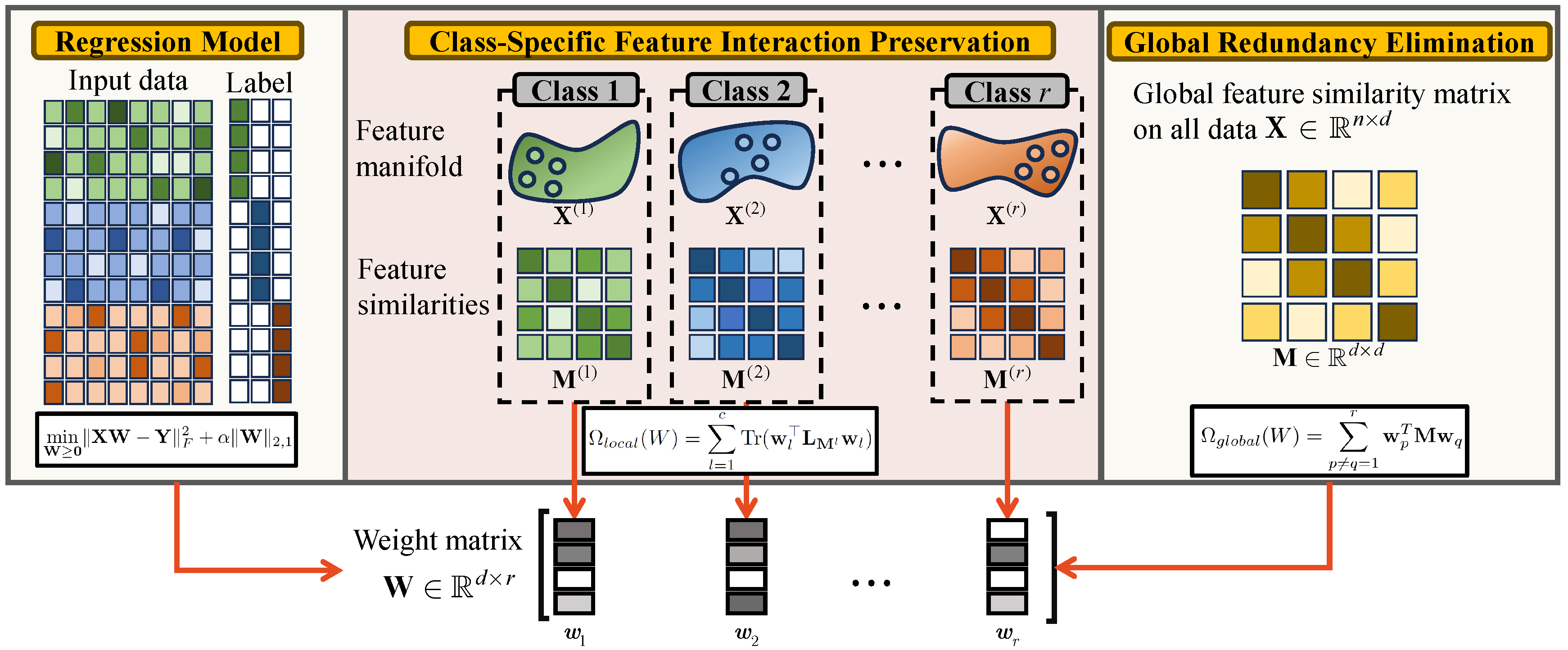
3. Methods
3.1. Class-Specific Feature Interaction Preservation
3.2. Global Feature Redundancy Elimination
3.3. Unified Objective Function
4. Optimization
4.1. Optimize
4.2. Optimize
| Algorithm 1 DRFS |
Input: Data matrix , label matrix , . Initialize . Output: Feature weight matrix .
|
4.3. Complexity and Convergence
5. Experiments
5.1. Datasets
5.2. Experiment Settings
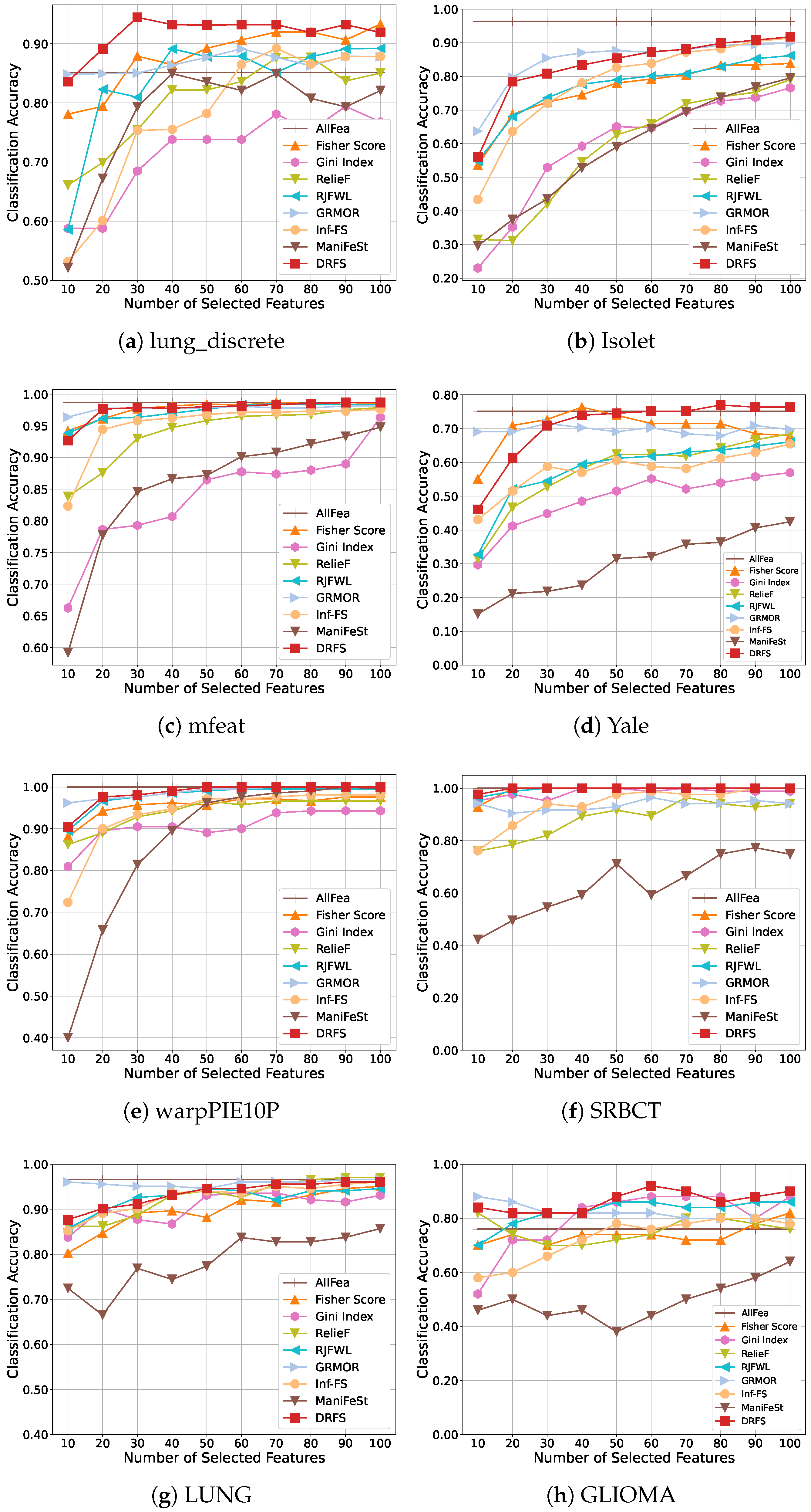
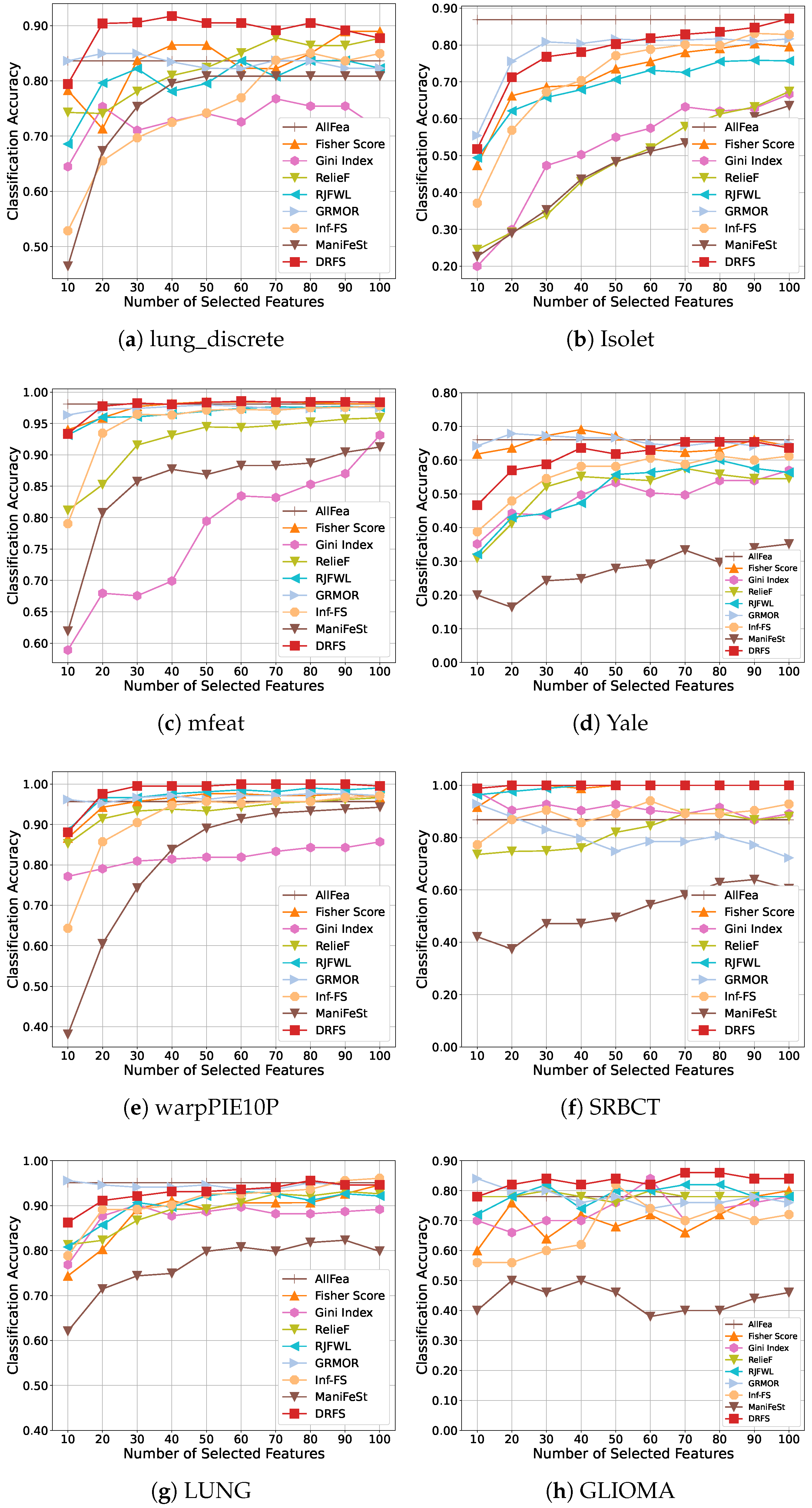
5.3. Results and Analysis
5.4. Ablation Study
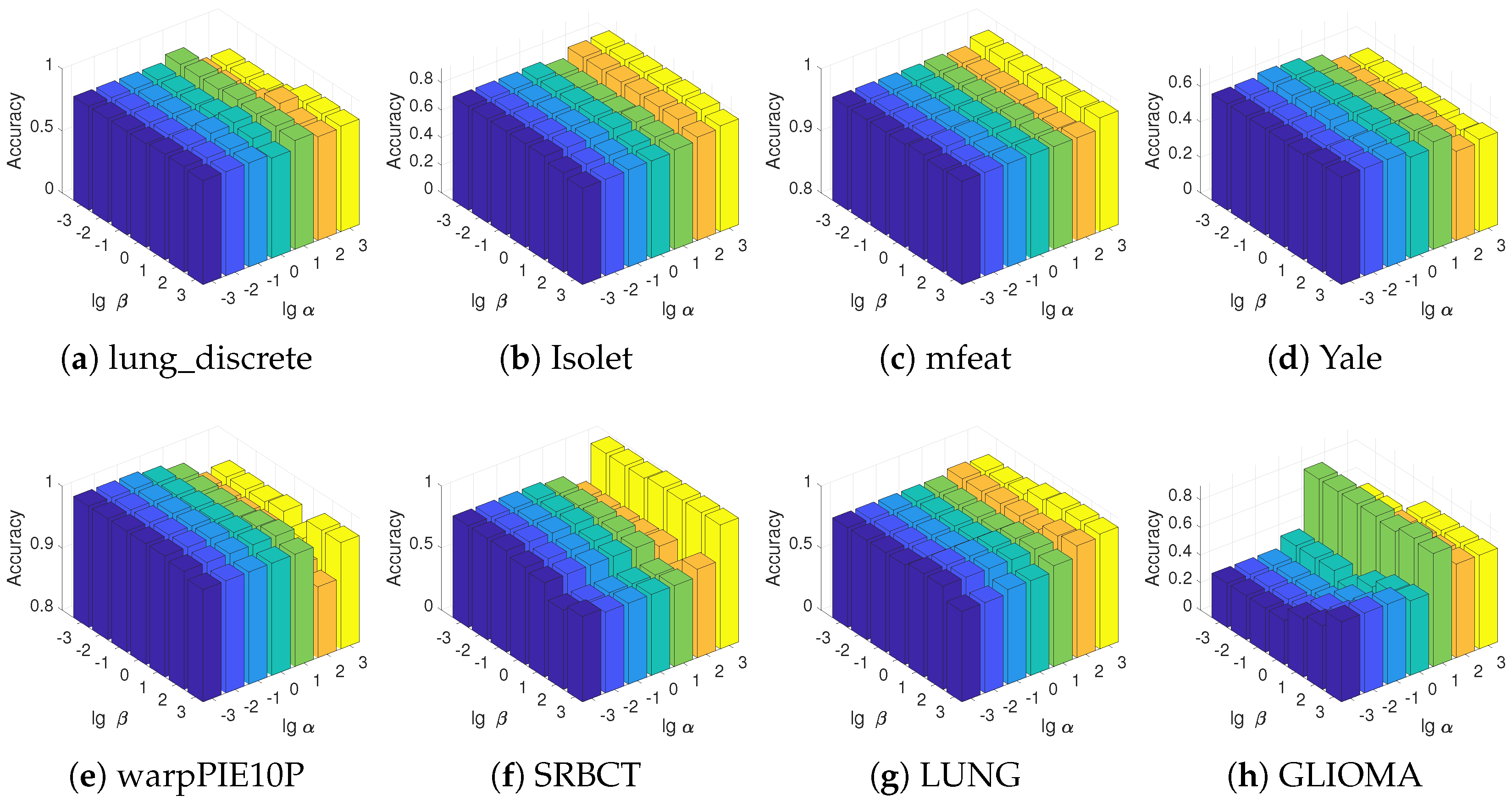
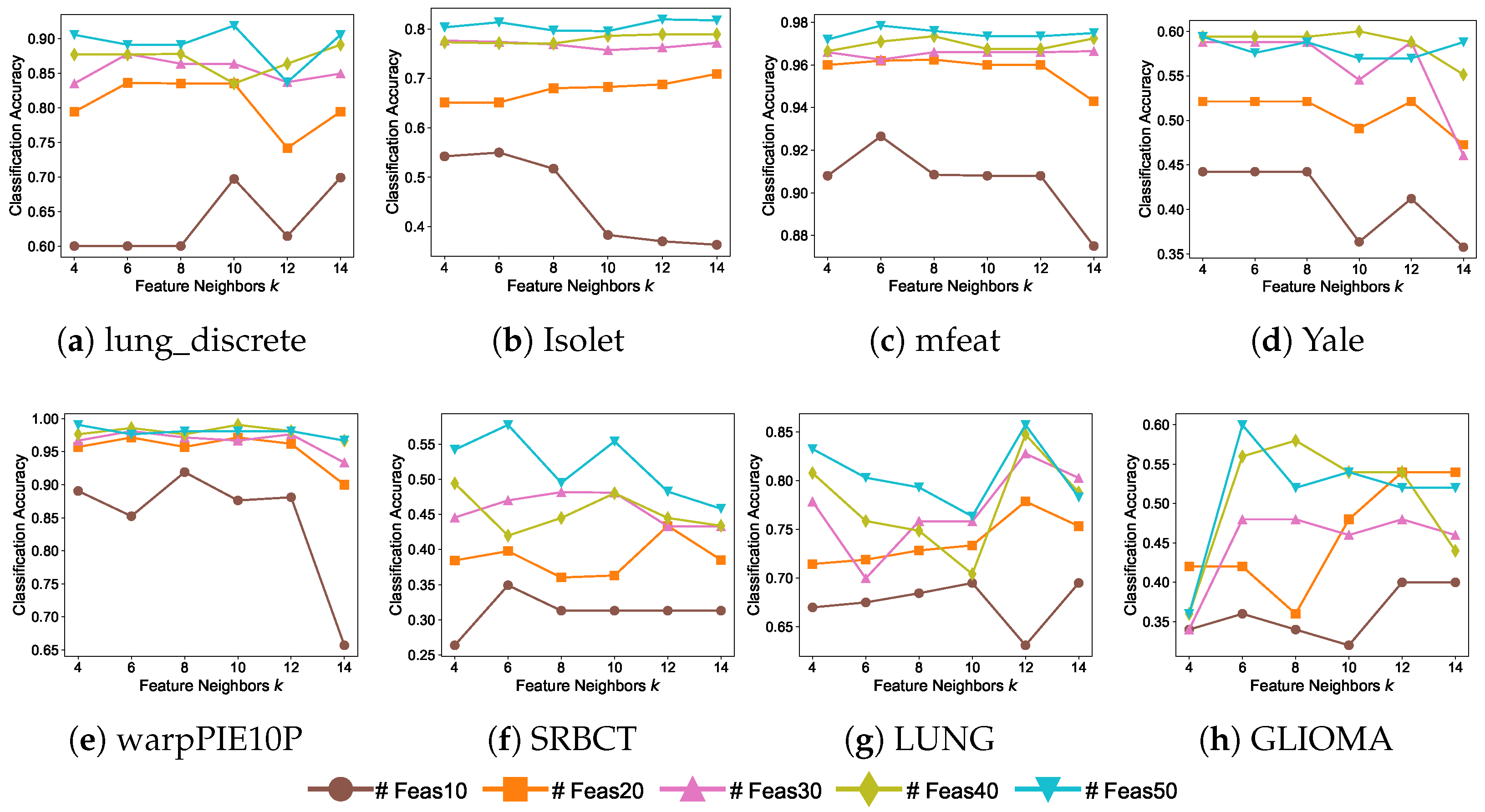
5.5. Parameter Sensitivity
5.6. Convergence Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2018, 50, 94. [Google Scholar] [CrossRef]
- Yue, H.; Li, J.; Liu, H. Second-Order Unsupervised Feature Selection via Knowledge Contrastive Distillation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 15577–15587. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Wei, J. To avoid the pitfall of missing labels in feature selection: A generative model gives the answer. In Proceedings of the Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 6534–6541. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Yamada, M.; Tang, J.; Lugo-Martinez, J.; Hodzic, E.; Shrestha, R.; Saha, A.; Ouyang, H.; Yin, D.; Mamitsuka, H.; Sahinalp, C.; et al. Ultra high-dimensional nonlinear feature selection for big biological data. IEEE Trans. Knowl. Data Eng. 2018, 30, 1352–1365. [Google Scholar] [CrossRef]
- Ang, J.C.; Mirzal, A.; Haron, H.; Hamed, H.N.A. Supervised, unsupervised, and semi-supervised feature selection: A review on gene selection. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 13, 971–989. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, M.; Zhou, X. RealNet: A feature selection network with realistic synthetic anomaly for anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 16699–16708. [Google Scholar]
- Zhang, C.; Fang, Y.; Liang, X.; Wu, X.; Jiang, B. Efficient multi-view unsupervised feature selection with adaptive structure learning and inference. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI-24), Jeju, Republic of Korea, 3–9 August 2024; pp. 5443–5452. [Google Scholar]
- Zhang, R.; Nie, F.; Li, X.; Wei, X. Feature selection with multi-view data: A survey. Inf. Fusion 2019, 50, 158–167. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, X.; Xu, T.; Wu, X. Autofield: Automating feature selection in deep recommender systems. In Proceedings of the ACM Web Conference, Lyon, France, 25–29 April 2022; pp. 1977–1986. [Google Scholar]
- Cohen, D.; Shnitzer, T.; Kluger, Y.; Talmon, R. Few-Sample Feature Selection via Feature Manifold Learning. In Proceedings of the International Conference on Machine Learning (ICML’23), Zhuhai, China, 17–20 February 2023. [Google Scholar]
- Wang, C.; Wang, J.; Gu, Z.; Wei, J.M.; Liu, J. Unsupervised feature selection by learning exponential weights. Pattern Recogn. 2024, 148, 110183. [Google Scholar] [CrossRef]
- Wang, J.; Wei, J.M.; Yang, Z.; Wang, S.Q. Feature selection by maximizing independent classification information. IEEE Trans. Knowl. Data Eng. 2017, 29, 828–841. [Google Scholar] [CrossRef]
- Chen, S.B.; Ding, C.; Luo, B.; Xie, Y. Uncorrelated lasso. In Proceedings of the AAAI Conference on Artificial Intelligence, Bellevue, WA, USA, 14–18 July 2013; Volume 27, pp. 166–172. [Google Scholar]
- Xu, X.; Wu, X.; Wei, F.; Zhong, W.; Nie, F. A general framework for feature selection under orthogonal regression with global redundancy minimization. IEEE Trans. Knowl. Data Eng. 2021, 34, 5056–5069. [Google Scholar] [CrossRef]
- Shang, R.; Wang, W.; Stolkin, R.; Jiao, L. Non-negative spectral learning and sparse regression-based dual-graph regularized feature selection. IEEE Trans. Cybern. 2017, 48, 793–806. [Google Scholar] [CrossRef]
- Shang, R.; Zhang, W.; Lu, M.; Jiao, L.; Li, Y. Feature selection based on non-negative spectral feature learning and adaptive rank constraint. Knowl.-Based Syst. 2022, 236, 107749. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; An, S.; Wei, J.; Ruan, J. Semi-supervised multi-label feature selection by preserving feature-label space consistency. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, Torino, Italy, 22–26 October 2018; pp. 783–792. [Google Scholar]
- Brezočnik, L.; Fister, I., Jr.; Podgorelec, V. Swarm intelligence algorithms for feature selection: A review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef]
- Shang, W.; Huang, H.; Zhu, H.; Lin, Y.; Qu, Y.; Wang, Z. A novel feature selection algorithm for text categorization. Expert Syst. Appl. 2007, 33, 1–5. [Google Scholar] [CrossRef]
- El Aboudi, N.; Benhlima, L. Review on wrapper feature selection approaches. In Proceedings of the 2016 International Conference on Engineering & MIS (ICEMIS), Agadir, Morocco, 22–24 September 2016; pp. 1–5. [Google Scholar]
- Maldonado, J.; Riff, M.C.; Neveu, B. A review of recent approaches on wrapper feature selection for intrusion detection. Expert Syst. Appl. 2022, 198, 116822. [Google Scholar] [CrossRef]
- Yan, H.; Yang, J.; Yang, J. Robust joint feature weights learning framework. IEEE Trans. Knowl. Data Eng. 2016, 28, 1327–1339. [Google Scholar] [CrossRef]
- Nie, F.; Huang, H.; Cai, X.; Ding, C. Efficient and robust feature selection via joint ℓ2,1-norms minimization. In Proceedings of the Advances in Neural Information Processing Systems 23 (NIPS 2010), Vancouver, BC, Canada, 6–9 December 2010. [Google Scholar]
- Xu, S.; Dai, J.; Shi, H. Semi-supervised feature selection based on least square regression with redundancy minimization. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Zhang, Z.; Tian, Y.; Bai, L.; Xiahou, J.; Hancock, E. High-order covariate interacted Lasso for feature selection. Pattern Recognit. Lett. 2017, 87, 139–146. [Google Scholar] [CrossRef]
- Cui, L.; Bai, L.; Zhang, Z.; Wang, Y.; Hancock, E.R. Identifying the most informative features using a structurally interacting elastic net. Neurocomputing 2019, 336, 13–26. [Google Scholar] [CrossRef]
- Cui, L.; Bai, L.; Wang, Y.; Philip, S.Y.; Hancock, E.R. Fused lasso for feature selection using structural information. Pattern Recogn. 2021, 119, 108058. [Google Scholar] [CrossRef]
- Lai, J.; Chen, H.; Li, T.; Yang, X. Adaptive graph learning for semi-supervised feature selection with redundancy minimization. Inf. Sci. 2022, 609, 465–488. [Google Scholar] [CrossRef]
- Roffo, G.; Melzi, S.; Castellani, U.; Vinciarelli, A.; Cristani, M. Infinite Feature Selection: A Graph-based Feature Filtering Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4396–4410. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Garber, M.E.; Troyanskaya, O.G.; Schluens, K.; Petersen, S.; Thaesler, Z.; Pacyna-Gengelbach, M.; Van De Rijn, M.; Rosen, G.D.; Perou, C.M.; Whyte, R.I.; et al. Diversity of gene expression in adenocarcinoma of the lung. Proc. Natl. Acad. Sci. USA 2001, 98, 13784–13789. [Google Scholar] [CrossRef]
- Khan, J.; Wei, J.S.; Ringner, M.; Saal, L.H.; Ladanyi, M.; Westermann, F.; Berthold, F.; Schwab, M.; Antonescu, C.R.; Peterson, C.; et al. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001, 7, 673–679. [Google Scholar] [CrossRef]
- Singh, D.; Febbo, P.G.; Ross, K.; Jackson, D.G.; Manola, J.; Ladd, C.; Tamayo, P.; Renshaw, A.A.; D’Amico, A.V.; Richie, J.P.; et al. Gene expression correlates of clinical prostate cancer behavior. Cancer Cell 2002, 1, 203–209. [Google Scholar] [CrossRef]
- Fanty, M.; Cole, R. Spoken letter recognition. Adv. Neural Inf. Process. Syst. 1990, 3, 220–226. [Google Scholar]
- Breukelen, M.V.; Duin, R.P.W.; Tax, D.M.J.; Hartog, J.E.D. Handwritten Digit Recognition by Combined Classifiers. Kybernetika 1998, 34, 381–386. [Google Scholar]
- Cai, D.; Zhang, C.; He, X. Unsupervised feature selection for multi-cluster data. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; pp. 333–342. [Google Scholar]
- Ming, D.; Ding, C. Robust flexible feature selection via exclusive L21 regularization. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3158–3164. [Google Scholar]



| Method | Global Association | Class-Specific Association | Similarity Measure | Task |
|---|---|---|---|---|
| UnLasso [15] | √ | × | Square cosine similarity | S |
| GRMOR [16] | √ | × | Square cosine similarity | S |
| InteractedLasso [27] | √ | × | Hypergraph | S |
| InElasticNet [28] | √ | × | Information theory | S |
| InFusedLasso [29] | √ | × | Information theory | S |
| SFSRM_MI [26] | √ | × | Information theory | SE |
| SFSRM_P [26] | √ | × | Pearson correlation coefficient | SE |
| AGLRM [30] | √ | × | Gaussian function | SE |
| NSSRD [17] | √ | × | Gaussian function | U |
| NSSRD_PF [17] | √ | × | Parameter-free methods | U |
| NNSAFS [18] | √ | × | Parameter-free methods | U |
| ManiFeSt [12] | × | √ | Gaussian function | S |
| Inf-FS [31] | √ | × | Weighted strategy | S/U |
| DRFS (ours) | √ | √ | Gaussian function | S |
| Dataset | # Features | # Samples | # Classes | Class Distribution | Type |
|---|---|---|---|---|---|
| lung_discrete | 325 | 73 | 7 | [6, 5, 5, 16, 7, 13, 21] | Bioinformatics |
| Isolet | 617 | 1560 | 26 | 60 samples per class | Spoken Letter |
| mfeat | 649 | 2000 | 10 | 200 samples per class | Image |
| Yale | 1024 | 165 | 15 | 11 samples per class | Image |
| warpPIE10P | 2420 | 210 | 10 | 21 samples per class | Image |
| SRBCT | 2308 | 83 | 4 | [29, 11, 18, 25] | Bioinformatics |
| LUNG | 3312 | 203 | 5 | [139, 17, 21, 20, 6] | Bioinformatics |
| GLIOMA | 4434 | 50 | 4 | [14, 7, 14, 15] | Bioinformatics |
| Dataset | AllFea | Fisher [5] | Gini Index [21] | RelieF [4] | RJFWL [24] | GRMOR [16] | Inf-FS [31] | ManiFeSt [12] | DRFS (ours) |
|---|---|---|---|---|---|---|---|---|---|
| lung_discrete | 0.8514 | 0.9333 | 0.7943 | 0.8771 | 0.8924 | 0.8914 | 0.8924 | 0.8495 | 0.9448 |
| Isolet | 0.9635 | 0.8385 | 0.7660 | 0.7910 | 0.8622 | 0.8994 | 0.9141 | 0.7955 | 0.9179 |
| mfeat | 0.9870 | 0.9875 | 0.9635 | 0.9790 | 0.9850 | 0.9820 | 0.9760 | 0.9480 | 0.9870 |
| Yale | 0.7515 | 0.7636 | 0.5697 | 0.6848 | 0.6606 | 0.7152 | 0.6545 | 0.4242 | 0.7697 |
| warpPIE10P | 1.0000 | 0.9762 | 0.9429 | 0.9667 | 0.9952 | 1.0000 | 0.9810 | 1.0000 | 1.0000 |
| SRBCT | 1.0000 | 1.0000 | 1.0000 | 0.9647 | 1.0000 | 0.9647 | 1.0000 | 0.7728 | 1.0000 |
| LUNG | 0.9659 | 0.9510 | 0.9360 | 0.9705 | 0.9461 | 0.9657 | 0.9607 | 0.8572 | 0.9607 |
| GLIOMA | 0.7600 | 0.8200 | 0.8800 | 0.8200 | 0.8600 | 0.8800 | 0.8000 | 0.6400 | 0.9200 |
| Dataset | AllFea | Fisher [5] | Gini Index [21] | RelieF [4] | RJFWL [24] | GRMOR [16] | Inf-FS [31] | ManiFeSt [12] | DRFS (ours) |
|---|---|---|---|---|---|---|---|---|---|
| lung_discrete | 0.8362 | 0.8895 | 0.7676 | 0.8781 | 0.8371 | 0.8495 | 0.8505 | 0.8086 | 0.9171 |
| Isolet | 0.8686 | 0.8038 | 0.6667 | 0.6737 | 0.7583 | 0.8167 | 0.8314 | 0.6353 | 0.8718 |
| mfeat | 0.9810 | 0.9845 | 0.9315 | 0.9590 | 0.9775 | 0.9795 | 0.9785 | 0.9125 | 0.9855 |
| Yale | 0.6606 | 0.6909 | 0.5697 | 0.5758 | 0.6000 | 0.6788 | 0.6121 | 0.3515 | 0.6545 |
| warpPIE10P | 0.9571 | 0.9762 | 0.8571 | 0.9667 | 0.9905 | 0.9762 | 0.9714 | 0.9429 | 1.0000 |
| SRBCT | 0.8684 | 1.0000 | 0.9765 | 0.8926 | 1.0000 | 0.9294 | 0.9404 | 0.6397 | 1.0000 |
| LUNG | 0.9510 | 0.9460 | 0.9016 | 0.9312 | 0.9313 | 0.9557 | 0.9609 | 0.8230 | 0.9559 |
| GLIOMA | 0.7800 | 0.8000 | 0.8400 | 0.8000 | 0.8200 | 0.8400 | 0.8200 | 0.5000 | 0.8600 |
| Metric | p-Value | |
|---|---|---|
| SVM | 25.57 | |
| 1-NN | 37.49 |
| Classifier | Regularization | Modules | |||
|---|---|---|---|---|---|
| Class-Specific Global | × | × | √ | √ | |
| × | √ | × | √ | ||
| SVM | lung_discrete | 0.8380 | 0.9115 | 0.9171 | 0.9226 |
| Isolet | 0.7683 | 0.8310 | 0.8318 | 0.8320 | |
| mfeat | 0.9729 | 0.9752 | 0.9766 | 0.9766 | |
| Yale | 0.5794 | 0.6982 | 0.7079 | 0.7091 | |
| warpPIE10P | 0.9790 | 0.9814 | 0.9871 | 0.9881 | |
| SRBCT | 0.9953 | 0.9965 | 0.9976 | 1.0000 | |
| LUNG | 0.9248 | 0.9257 | 0.9331 | 0.9346 | |
| GLIOMA | 0.8240 | 0.8460 | 0.8620 | 0.8740 | |
| Classifier | Regularization | Modules | |||
|---|---|---|---|---|---|
| Class-Specific Global | × | × | √ | √ | |
| × | √ | × | √ | ||
| 1-NN | lung_discrete | 0.8020 | 0.8770 | 0.8895 | 0.8937 |
| Isolet | 0.6886 | 0.7744 | 0.7785 | 0.7790 | |
| mfeat | 0.9666 | 0.9758 | 0.9780 | 0.9780 | |
| Yale | 0.5103 | 0.6091 | 0.6109 | 0.6164 | |
| warpPIE10P | 0.9710 | 0.9824 | 0.9829 | 0.9838 | |
| SRBCT | 0.9929 | 0.9988 | 0.9988 | 1.0000 | |
| LUNG | 0.9007 | 0.8913 | 0.9292 | 0.9307 | |
| GLIOMA | 0.7860 | 0.7800 | 0.8320 | 0.8500 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, J.; Li, Y.; Piao, C.; Wei, J. Dual-Regularized Feature Selection for Class-Specific and Global Feature Associations. Entropy 2025, 27, 190. https://doi.org/10.3390/e27020190
Wang C, Wang J, Li Y, Piao C, Wei J. Dual-Regularized Feature Selection for Class-Specific and Global Feature Associations. Entropy. 2025; 27(2):190. https://doi.org/10.3390/e27020190
Chicago/Turabian StyleWang, Chenchen, Jun Wang, Yanfei Li, Chengkai Piao, and Jinmao Wei. 2025. "Dual-Regularized Feature Selection for Class-Specific and Global Feature Associations" Entropy 27, no. 2: 190. https://doi.org/10.3390/e27020190
APA StyleWang, C., Wang, J., Li, Y., Piao, C., & Wei, J. (2025). Dual-Regularized Feature Selection for Class-Specific and Global Feature Associations. Entropy, 27(2), 190. https://doi.org/10.3390/e27020190





