Exploring the Evolution-Coupling Hypothesis: Do Enzymes’ Performance Gains Correlate with Increased Dissipation?
Abstract
1. Introduction
1.1. What Is the Relationship Between Universal (Thermodynamic) and Biological Evolution?
1.2. On the Joint Evolution of Enzymes, Dissipative Fluxes, and Catalytic Performance Parameters
2. Materials and Methods
2.1. Statistical Analysis and Software Tools
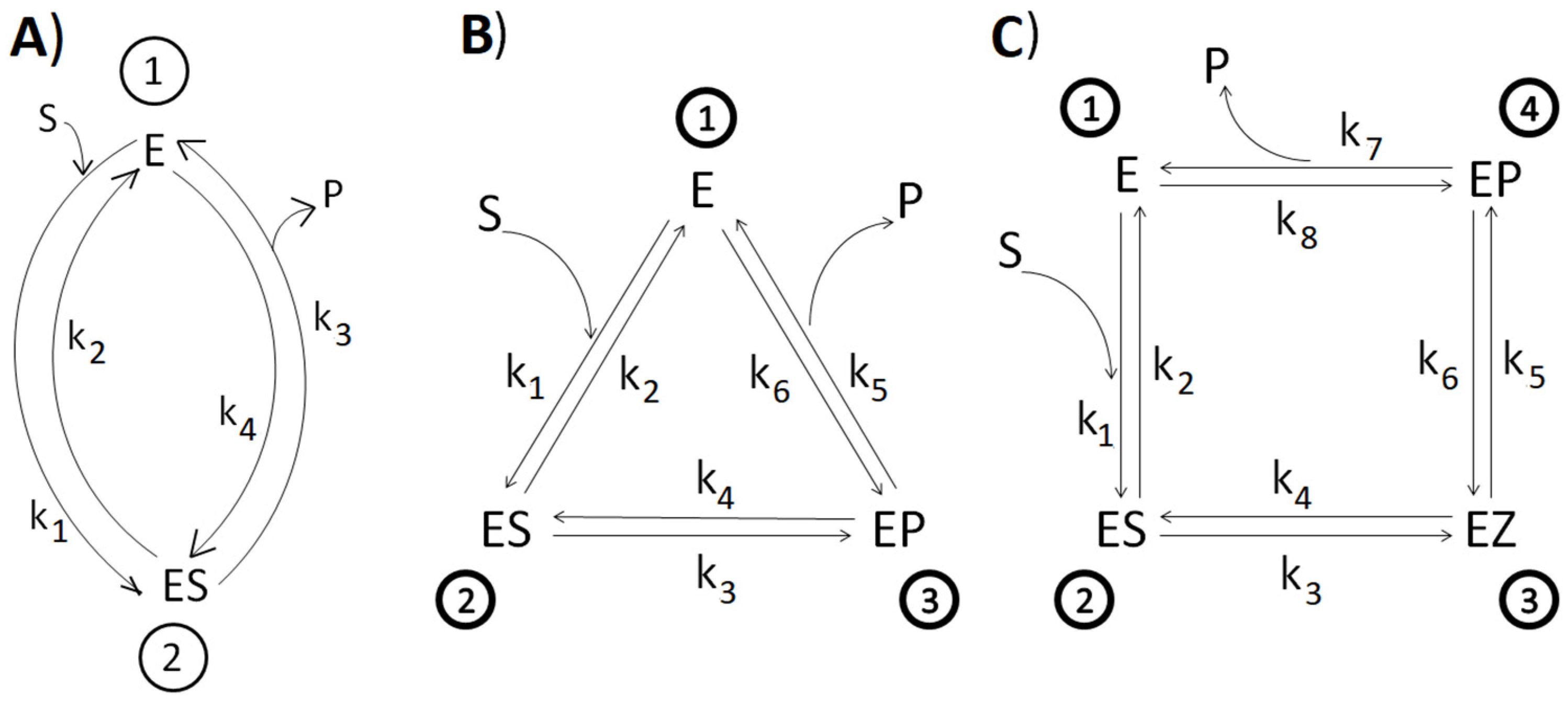
2.2. Equations for kcat, kcat/Km, and the Dissipation Function
2.3. Introducing Normal Noise in Microscopic Rate Constants
2.4. The Dataset Collection
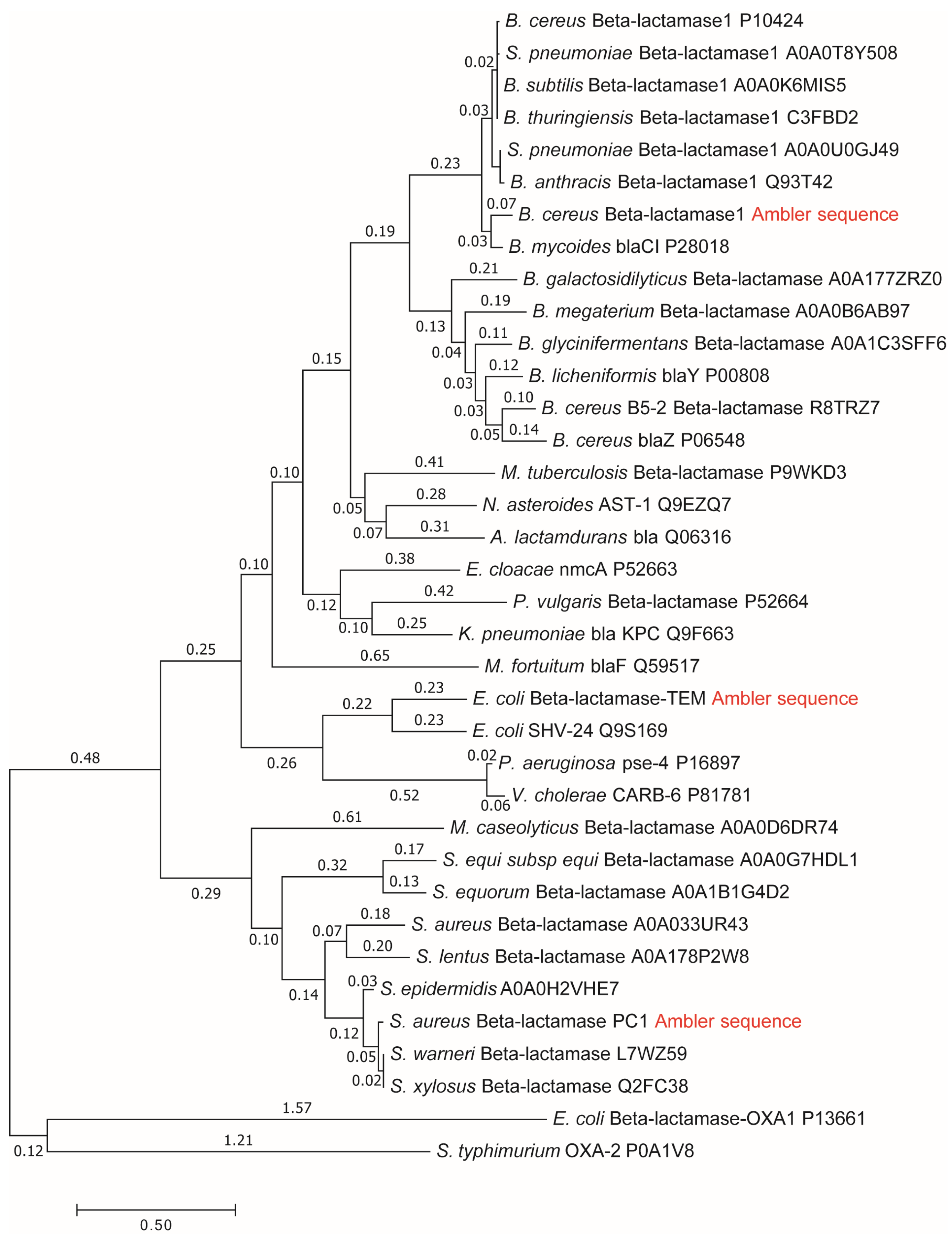
2.5. The Phylogenetic Tree Construction
3. Results
3.1. The Database
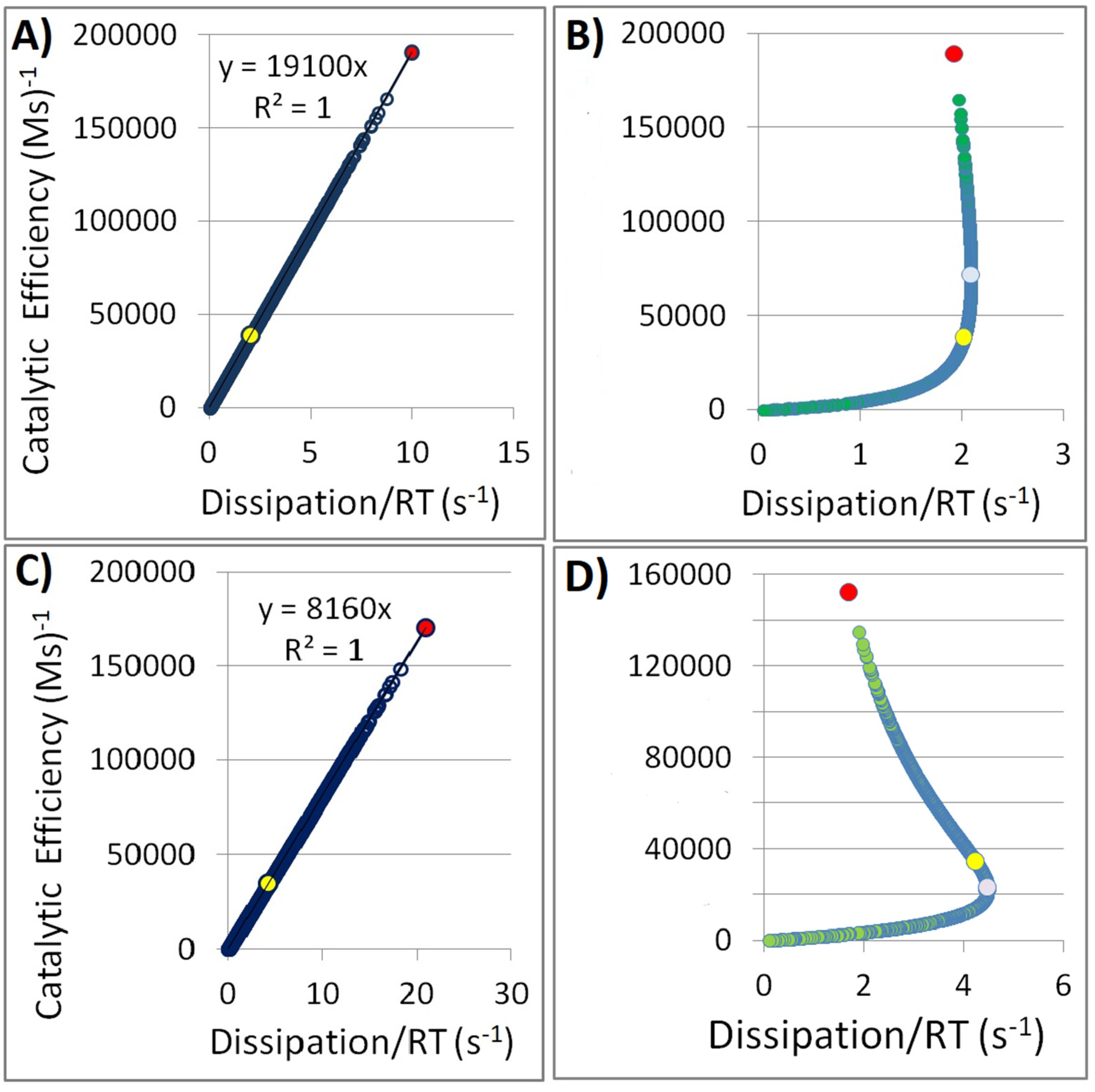
3.2. The Regular Relationships Between Dissipation and the Performance Parameters of Enzymes
3.3. Can Regular Dissipation–Performance Relationships Be Obtained for Individual Reactions After Introducing the Stochastic Noise to Obtain Synthetic Data?
4. Discussion
4.1. Is the Proportionality Between Dissipation and Kinetic Parameters of Enzymes Expected (Trivial) or a Scientifically Valuable Result?
4.2. Why Must Performance Gain Be Paid with Higher Dissipation?
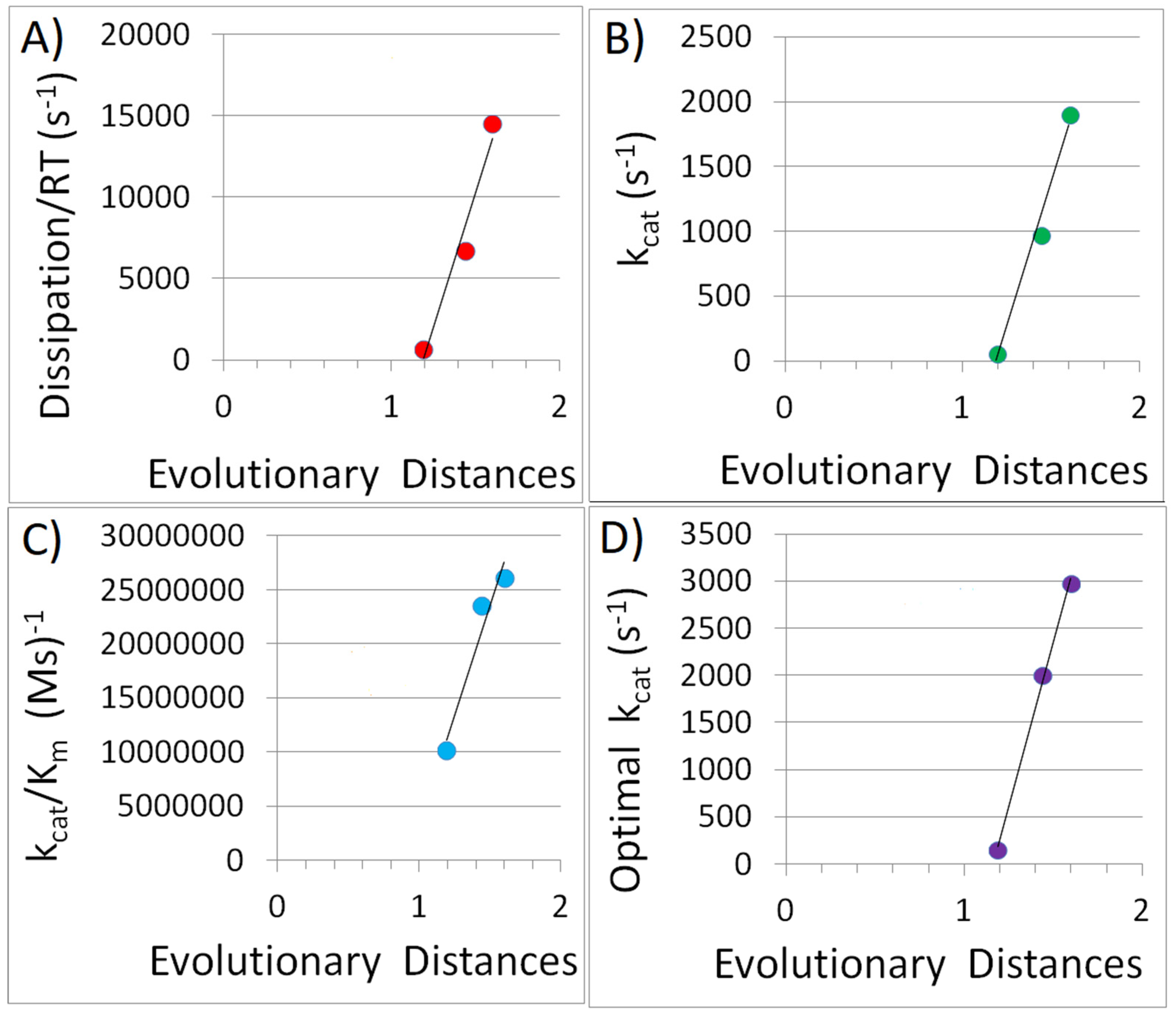
4.3. Does the Sublinear Scaling Law for Enzymes Point Toward the Origin of Kleiber’s Law?
4.4. Did We Gain Additional Insight into the Proposal That Specialized Enzymes Evolved from Primitive Generalist Enzymes?
4.5. Simulating the Effect of Stochastic Noise
4.6. Comparison with Earlier Simulations
4.7. The Support for the “Evolution-Coupling Hypothesis”
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Chaisson, E.J. A unifying concept for astrobiology. Int. J. Astrobiol. 2003, 2, 91–101. [Google Scholar] [CrossRef]
- Boltzmann, L. The second law of thermodynamics (reprinted and translated). In Theoretical Physics and Philosophical Problems: Selected Writings by Ludwig Boltzmann (Vienna Circle Collection); McGuinness, B., Ed.; D. Reidel Publishing Co.: Dordrecht, Holland, 1974; Chapter 2; pp. 1886–1974, pp. 13–32. [Google Scholar] [CrossRef]
- Lotka, A.J. Natural Selection as a Physical Principle. Proc. Natl. Acad. Sci. USA 1922, 8, 151–154. [Google Scholar] [CrossRef] [PubMed]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Cannon, W.R.; Zucker, J.D.; Baxter, D.J.; Kumar, N.; Baker, S.E.; Hurley, J.M.; Dunlap, J.C. Prediction of Metabolite Concentrations, Rate Constants and Post-Translational Regulation Using Maximum Entropy-Based Simulations with Application to Central Metabolism of Neurospora crassa. Processes 2018, 6, 63. [Google Scholar] [CrossRef]
- Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell; CABI Record Number: 19450100320; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Hill, T.L. Free Energy Transduction in Biology: The Steady State Kinetic and Thermodynamic Formalism; Academic Press: New York, NY, USA, 1977. [Google Scholar] [CrossRef]
- Qian, H. Phosphorylation energy hypothesis: Open chemical systems and their biological functions. Annu. Rev. Phys. Chem. 2007, 58, 113–142. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability, and Fluctuations; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Hochberg, D.; Ribó, J.M. Thermodynamic evolution theorem for chemical reactions. Phys. Rev. Res. 2020, 2, 043367. [Google Scholar] [CrossRef]
- Annila, A.; Salthe, S. Physical foundations of evolutionary theory. J. Non-Equilib. Thermodyn. 2010, 35, 301–321. [Google Scholar] [CrossRef]
- England, J.L. Dissipative adaptation in driven self-assembly. Nat. Nanotechnol. 2015, 10, 919–923. [Google Scholar] [CrossRef]
- Black, S. On the Thermodynamics of Evolution. Perspect. Biol. Med. 1978, 21, 348–356. [Google Scholar] [CrossRef]
- Juretić, D.; Županović, P. The free-energy transduction and entropy production in initial photosynthetic reactions. In Non-Equilibrium Thermodynamics and the Production of Entropy; Kleidon, A., Lorenz, R.D., Eds.; Springer: Berlin, Germany, 2005; pp. 161–171. [Google Scholar] [CrossRef]
- Dobovišek, A.; Županović, P.; Brumen, M.; Juretić, D. Maximum entropy production and maximum Shannon entropy as germane principles for the evolution of enzyme kinetics. In Beyond the Second Law. Understanding Complex Systems; Dewar, R.C., Lineweaver, C.H., Niven, R.K., Regenauer-Lieb, K., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2014; pp. 361–382. [Google Scholar] [CrossRef]
- Juretić, D.; Bonačić Lošić, Ž.; Domagoj Kuić, D.; Juraj Simunić, J.; Dobovišek, A. The maximum entropy production requirement for proton transfers enhances catalytic efficiency for β-lactamases. Biophys. Chem. 2019, 244, 11–21. [Google Scholar] [CrossRef]
- Juretić, D.; Simunić, J.; Bonačić Lošić, Ž. Maximum entropy production theorem for transitions between enzyme functional states and its application. Entropy 2019, 21, 743. [Google Scholar] [CrossRef] [PubMed]
- Juretić, D. Bioenergetics: A Bridge Across Life and Universe; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Juretić, D.; Bonačić Lošić, Ž. Theoretical Improvements in Enzyme Efficiency Associated with Noisy Rate Constants and Increased Dissipation. Entropy 2024, 26, 151. [Google Scholar] [CrossRef] [PubMed]
- Hill, A. Entropy production as the selection rule between different growth morphologies. Nature 1990, 348, 426–428. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Santillán, M.; Santos, M.J.; Calvo Hernández, A.; Mateos Roco, J.M. Optimization and Stability of Heat Engines: The Role of Entropy Evolution. Entropy 2018, 20, 865. [Google Scholar] [CrossRef]
- Zanetti-Polzi, L.; Daidone, I.; Iacobucci, C.; Amadei, A. Thermodynamic Evolution of a Metamorphic Protein: A Theoretical-Computational Study of Human Lymphotactin. Protein J. 2023, 42, 219–228. [Google Scholar] [CrossRef]
- Schreiber, A.; Gimbel, S. Evolution and the Second Law of Thermodynamics: Effectively Communicating to Non-technicians. Evo. Edu. Outreach 2010, 3, 99–106. [Google Scholar] [CrossRef]
- Endres, R.G. Entropy production selects nonequilibrium states in multistable systems. Sci. Rep. 2017, 7, 14437. [Google Scholar] [CrossRef]
- Kaila, V.R.I.; Annila, A. Natural selection for least action. Proc. R. Soc. A 2008, 464, 3055–3070. [Google Scholar] [CrossRef]
- Schneider, E.D.; Kay, J.J. Life as a manifestation of the second law of thermodynamics. Mathl. Comput. Modelling 1994, 19, 25–48. [Google Scholar] [CrossRef]
- Prigogine, I.; Nicolis, G. Biological order, structure and instabilities. Q. Rev. Biophys. 1971, 4, 107–148. [Google Scholar] [CrossRef]
- Wicken, J.S. The cosmic breath: Reflections on the thermodynamics of creation. Zygon 1984, 19, 487–505. [Google Scholar] [CrossRef]
- Tomé, T.; de Oliveira, M.J. Stochastic thermodynamics and entropy production of chemical reaction systems. J. Chem. Phys. 2018, 148, 224104. [Google Scholar] [CrossRef] [PubMed]
- Ulanowicz, R.E.; Hannon, B.M. Life and the production of entropy. Proc. R. Soc. Lond. B. 1987, 232, 181–192. [Google Scholar] [CrossRef]
- Metzner, H. Bioelectrochemistry of photosynthesis: A theoretical approach. Bioelectrochem. Bioenerg. 1984, 13, 183–190. [Google Scholar] [CrossRef]
- Harold, F.H. The Vital Force: Study of Bioenergetics; WH Freeman: New York, NY, USA, 1986; p. 45. ISBN 0-7167-1734-4. [Google Scholar]
- Chaisson, E.J. Energy Rate Density as a Complexity Metric and Evolutionary Driver. Complexity 2010, 16, 27–40. [Google Scholar] [CrossRef]
- Chaisson, E.J. Energy Rate Density. II. Probing Further a New Complexity Metric. Complexity 2011, 17, 44–63. [Google Scholar] [CrossRef]
- Blow, D. So do we understand how enzymes work? Structure 2000, 8, R77–R81. [Google Scholar] [CrossRef]
- Agarwal, P.K. A Biophysical Perspective on Enzyme Catalysis. Biochemistry 2019, 58, 438–449. [Google Scholar] [CrossRef]
- Yabukarski, F.; Biel, J.T.; Pinney, M.M.; Doukov, T.; Powers, A.S.; Fraser, J.S.; Herschlag, D. Assessment of enzyme active site positioning and tests of catalytic mechanisms through X-ray-derived conformational ensembles. Proc. Natl. Acad. Sci. USA 2020, 117, 33204–33215. [Google Scholar] [CrossRef]
- Hay, S.; Scrutton, N.S. Good vibrations in enzyme-catalysed reactions. Nat. Chem. 2012, 4, 161–168. [Google Scholar] [CrossRef]
- Richard, J.P. Protein Flexibility and Stiffness Enable Efficient Enzymatic Catalysis. J. Am. Chem. Soc. 2019, 141, 3320–3331. [Google Scholar] [CrossRef] [PubMed]
- English, B.P.; Min, W.; van Oijen, A.M.; Lee, K.T.; Luo, G.; Sun, H.; Cherayil, B.J.; Kou, S.C.; Xie, X.S. Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited. Nat. Chem. Biol. 2006, 2, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Stochastic thermodynamics of single enzymes and molecular motors. Eur. Phys. J. E. Soft Matter 2011, 34, 26. [Google Scholar] [CrossRef] [PubMed]
- Astumian, R.D. Trajectory and Cycle-Based Thermodynamics and Kinetics of Molecular Machines: The Importance of Microscopic Reversibility. Acc. Chem. Res. 2018, 51, 2653–2661. [Google Scholar] [CrossRef]
- Cannon, W.R.; Britton, S.; Banwarth-Kuhn, M.; Alber, M. Probabilistic and maximum entropy modeling of chemical reaction systems: Characteristics and comparisons to mass action kinetic models. J. Chem. Phys. 2024, 160, 214123. [Google Scholar] [CrossRef]
- Qian, H.; Beard, D.A. Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium. Biophys. Chem. 2005, 114, 213–220. [Google Scholar] [CrossRef]
- von Stockar, U. Biothermodynamics of live cells: A tool for biotechnology and biochemical engineering. J. Non-Equilib. Thermodyn. 2010, 35, 415–475. [Google Scholar] [CrossRef]
- Jensen, R.A. Enzyme recruitment in evolution of new function. Annu. Rev. Microbiol. 1976, 30, 409–425. [Google Scholar] [CrossRef]
- Karamitros, C.S.; Murray, K.; Kumada, Y.; Johnson, K.A.; D’Arcy, S.; Georgiou, G. Mechanistic conformational and substrate selectivity profiles emerging in the evolution of enzymes via parallel trajectories. Nat. Commun. 2024, 15, 7068. [Google Scholar] [CrossRef]
- Juretić, D.; Županović, P. Photosynthetic models with maximum entropy production in irreversible charge transfer steps. J. Comp. Biol. Chem. 2003, 27, 541–553. [Google Scholar] [CrossRef]
- Bonačić Lošić, Ž.; Donđivić, T.; Juretić, D. Is the catalytic activity of triosephosphate isomerase fully optimized? An investigation based on maximization of entropy production. J. Biol. Phys. 2017, 43, 69–86. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.A. New standards for collecting and fitting steady state kinetic data. Beilstein J. Org. Chem. 2019, 15, 16–29. [Google Scholar] [CrossRef] [PubMed]
- Sica, L.; Gilli, R.; Briand, C.; Sari, J.C. A flow microcalorimetric method for enzyme activity measurements: Application to dihydrofolate reductase. Anal. Biochem. 1987, 165, 341–348. [Google Scholar] [CrossRef] [PubMed]
- Todd, M.J.; Gomez, J. Enzyme kinetics determined using calorimetry: A general assay for enzyme activity? Anal. Biochem. 2001, 296, 179–187. [Google Scholar] [CrossRef]
- Riedel, C.; Gabizon, R.; Wilson, C.A.M.; Hamadani, K.; Tsekouras, K.; Marqusee, S.; Pressé, S.; Bustamante, C. The heat released during catalytic turnover enhances the diffusion of an enzyme. Nature 2015, 517, 227–230. [Google Scholar] [CrossRef]
- Das, B.; Banerjee, K.; Gangopadhyay, G. Propensity approach to nonequilibrium thermodynamics of a chemical reaction network: Controlling single E. coli β-galactosidase enzyme catalysis through the elementary reaction steps. J. Chem. Phys. 2013, 139, 244104. [Google Scholar] [CrossRef]
- Brown, A.I.; Sivak, D.A. Allocating dissipation across a molecular machine cycle to maximize flux. Proc. Natl. Acad. Sci. USA 2017, 114, 11057–11062. [Google Scholar] [CrossRef]
- Wagoner, J.A.; Dill, K.A. Opposing Pressures of Speed and Efficiency Guide the Evolution of Molecular Machines. Mol. Biol. Evol. 2019, 36, 2813–2822. [Google Scholar] [CrossRef]
- Niebel, B.; Leupold, S.; Heinemann, M. An upper limit on Gibbs energy dissipation governs cellular metabolism. Nat. Metab. 2019, 1, 125–132. [Google Scholar] [CrossRef]
- Bar-Even, A.; Noor, E.; Savir, Y.; Liebermeister, W.; Davidi, D.; Tawfik, D.S.; Milo, R. The moderately efficient enzyme: Evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 2011, 50, 4402–4410. [Google Scholar] [CrossRef]
- Kleiber, M. Body size and metabolism. Hilgardia 1932, 6, 315–353. [Google Scholar] [CrossRef]
- Albery, W.J.; Knowles, J.R. Evolution of enzyme function and the development of catalytic efficiency. Biochemistry 1976, 15, 5631–5640. [Google Scholar] [CrossRef] [PubMed]
- Newton, M.S.; Arcus, V.L.; Patrick, W.M. Rapid bursts and slow declines: On the possible evolutionary trajectories of enzymes. J. R. Soc. Interface 2015, 12, 20150036. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, T.; Hoffmann-Klipp, E.; Heinrich, R. An evolutionary approach to enzyme kinetics: Optimization of ordered mechanisms. Bull. Math. Biol. 1994, 56, 65–106. [Google Scholar]
- Heinrich, R.; Schuster, S.; Holzhutter, H.-G. Mathematical analysis of enzymic reaction systems using optimmization principles. Eur. J. Biochem. 1991, 201, 1–21. [Google Scholar] [CrossRef]
- Toney, M.D. Common Enzymological Experiments Allow Free Energy Profile Determination. Biochemistry 2013, 52, 5952–5965. [Google Scholar] [CrossRef]
- Box, G.E.P.; Muller, M.E. A note on the generation of random normal deviates. Ann. Math. Stat. 1958, 29, 610–611. [Google Scholar] [CrossRef]
- Behravan, G.; Jonsson, B.H.; Lindskog, S. Fine tuning of the catalytic properties of carbonic anhydrase. Studies of a Thr200→His variant of human isoenzyme II. Eur. J. Biochem. 1990, 190, 351–357. [Google Scholar] [CrossRef]
- Toney, M.D. Carbon Acidity in Enzyme Active Sites. Front. Bioeng. Biotechnol. 2019, 7, 25. [Google Scholar] [CrossRef]
- Zyryanov, A.B.; Vener, A.V.; Salminen, A.; Goldman, A.; Lahti, R.; Baykov, A.A. Rates of elementary catalytic steps for different metal forms of the family II pyrophosphatase from Streptococcus gordonii. Biochemistry 2004, 43, 1065–1074. [Google Scholar] [CrossRef]
- McIntyre, L.M.; Thorburn, D.R.; Bubb, W.A.; Kuchel, P.W. Comparison of computer simulations of the F-type and L-type non-oxidative hexose monophosphate shunts with 31P-NMR experimental data from human erythrocytes. Eur. J. Biochem. 1989, 180, 399–420. [Google Scholar] [CrossRef] [PubMed]
- Käpylä, J.; Hyytiä, T.; Lahti, R.; Goldman, A.; Baykov, A.A.; Cooperman, B.S. Effect of D97E substitution on the kinetic and thermodynamic properties of Escherichia coli inorganic pyrophosphatase. Biochemistry 1995, 34, 792–800. [Google Scholar] [CrossRef] [PubMed]
- Cooperman, B.S.; Baykov, A.A.; Lahti, R. Evolutionary conservation of the active site of soluble inorganic pyrophosphatase. Trends Biochem. Sci. 1992, 17, 262–266. [Google Scholar] [CrossRef] [PubMed]
- St Maurice, M.; Bearne, S.L. Kinetics and thermodynamics of mandelate racemase catalysis. Biochemistry 2002, 41, 4048–4058. [Google Scholar] [CrossRef]
- Darvey, I.G.; Shrager, R.; Kohn, L.D. Integrated steady state rate equations and the determination of individual rate constants. J. Biol. Chem. 1975, 250, 4696–4701. [Google Scholar] [CrossRef]
- Zawrotny, M.E.; Pollack, R.M. Reaction energetics of a mutant 3-oxo-delta 5-steroid isomerase with an altered active site base (D38E). Biochemistry 1994, 33, 13896–13902. [Google Scholar] [CrossRef]
- Hwang, W.; Hyeon, C. Quantifying the Heat Dissipation from a Molecular Motor’s Transport Properties in Nonequilibrium Steady States. J. Phys. Chem. Lett. 2017, 8, 250–256. [Google Scholar] [CrossRef]
- Fraser, H.I.; Kvaratskhelia, M.; White, M.F. The two analogous phosphoglycerate mutases of Escherichia coli. FEBS Lett. 1999, 455, 344–348. [Google Scholar] [CrossRef]
- Mattei, P.; Kast, P.; Hilvert, D. Bacillus subtilis chorismate mutase is partially diffusion-controlled. Eur. J. Biochem. 1999, 261, 25–32. [Google Scholar] [CrossRef]
- Holliday, M.J.; Armstrong, G.S.; Eisenmesser, E.Z. Determination of the Full Catalytic Cycle among Multiple Cyclophilin Family Members and Limitations on the Application of CPMG-RD in Reversible Catalytic Systems. Biochemistry 2015, 54, 5815–5827. [Google Scholar] [CrossRef]
- Mutaguchi, Y.; Ohmori, T.; Wakamatsu, T.; Doi, K.; Ohshima, T. Identification, purification, and characterization of a novel amino acid racemase, isoleucine 2-epimerase, from Lactobacillus species. J. Bacteriol. 2013, 195, 5207–5215. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Yeom, S.J.; Kim, K.; Rhee, S.; Kim, D.; Oh, D.K. Mutational analysis of the active site residues of a D-psicose 3-epimerase from Agrobacterium tumefaciens. Biotechnol. Lett. 2010, 32, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Pozo-Dengra, J.; Martínez-Gómez, A.I.; Martínez-Rodríguez, S.; Clemente-Jiménez, J.M.; Rodríguez-Vico, F.; Las Heras-Vázquez, F.J. Racemization study on different N-acetylamino acids by a recombinant N-succinylamino acid racemase from Geobacillus kaustophilus CECT4264. Process Biochem. 2009, 44, 835–841. [Google Scholar] [CrossRef]
- Mehboob, S.; Guo, L.; Fu, W.; Mittal, A.; Yau, T.; Truong, K.; Johlfs, M.; Long, F.; Fung, L.W.-M.; Johnson, M.E. Glutamate racemase dimerization inhibits dynamic conformational flexibility and reduces catalytic rates. Biochemistry 2009, 48, 7045–7055. [Google Scholar] [CrossRef]
- Watanabe, S.; Tanimoto, Y.; Nishiwaki, H.; Watanabe, Y. Identification and characterization of bifunctional proline racemase/hydroxyproline epimerase from archaea: Discrimination of substrates and molecular evolution. PLoS ONE 2015, 10, e0120349. [Google Scholar] [CrossRef]
- Kato, S.; Hemmi, H.; Yoshimura, T. Lysine racemase from a lactic acid bacterium, Oenococcus oeni: Structural basis of substrate specificity. J. Biochem. 2012, 152, 505–508. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Severin, L.C.; Lyu, C.-J.; Zhu, W.-L.; Wang, H.-P.; Jiang, C.-J.; Mei, L.-H.; Liu, H.-G.; Huang, J. Improving thermostability of (R)-selective amine transaminase from Aspergillus terreus by evolutionary coupling saturation mutagenesis. Biochem. Eng. J. 2021, 167, 107926. [Google Scholar] [CrossRef]
- Miyamoto, T.; Moriya, T.; Katane, M.; Saitoh, Y.; Sekine, M.; Sakai-Kato, K.; Oshima, T.; Homma, H. Identification of a novel D-amino acid aminotransferase involved in D-glutamate biosynthetic pathways in the hyperthermophile Thermotoga maritime. FEBS J. 2022, 289, 5933–5946. [Google Scholar] [CrossRef]
- Yaneva, N.; Schuster, J.; Schäfer, F.; Lede, V.; Przybylski, D.; Paproth, T.; Harms, H.; Müller, R.H.; Rohwerder, T. Bacterial acyl-CoA mutase specifically catalyzes coenzyme B12-dependent isomerization of 2-hydroxyisobutyryl-CoA and (S)-3-hydroxybutyryl-CoA. J. Biol. Chem. 2012, 287, 15502–15511. [Google Scholar] [CrossRef]
- Gogami, Y.; Kobayashi, A.; Ikeuchi, T.; Oikawa, T. Site-directed mutagenesis of rice serine racemase: Evidence that Glu219 and Asp225 mediate the effects of Mg2+ on the activity. Chem. Biodivers. 2010, 7, 1579–1590. [Google Scholar] [CrossRef]
- Christenson, S.D.; Wu, W.; Spies, M.A.; Shen, B.; Toney, M.D. Kinetic analysis of the 4-methylideneimidazole-5-one-containing tyrosine aminomutase in enediyne antitumor antibiotic C-1027 biosynthesis. Biochemistry 2003, 42, 12708–12718. [Google Scholar] [CrossRef] [PubMed]
- Converti, A.; Borghi, M.D. Kinetics of glucose isomerization to fructose by immobilized glucose isomerase in the presence of substrate protection. Bioprocess Eng. 1998, 18, 27–33. [Google Scholar] [CrossRef]
- Gaily, M.H.; Sulieman, A.K.; Abasaeed, A.E. Kinetics of a three-step isomerization of glucose to fructose using immobilized enzyme. Int. J. Chem. Eng. Appl. 2013, 4, 31–34. [Google Scholar] [CrossRef]
- Schomburg, I.; Jeske, L.; Ulbrich, M.; Placzek, S.; Chang, A.; Schomburg, D. The BRENDA enzyme information system-From a database to an expert system. J. Biotechnol. 2017, 261, 194–206. [Google Scholar] [CrossRef]
- Kumar, S.; Stecher, G.; Tamura, K. MEGA7: Molecular evolutionary genetics analysis version 7.0 for bigger datasets. Mol. Biol. Evol. 2016, 33, 1870–1874. [Google Scholar] [CrossRef]
- Ambler, R.P. The structure of β-lactamases. Philos. Trans. R Soc. Lond. B Biol. Sci. 1980, 289, 321–331. [Google Scholar] [CrossRef]
- Hussain, M.; Pastor, F.I.; Lampen, J.O. Cloning and sequencing of the blaZ gene encoding beta-lactamase III, a lipoprotein of Bacillus cereus 569/H. J. Bacteriol. 1987, 169, 579–586. [Google Scholar] [CrossRef]
- Jones, D.T.; Taylor, W.R.; Thornton, J.M. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 1992, 8, 275–282. [Google Scholar] [CrossRef]
- Christensen, H.; Martin, M.T.; Waley, G. β-lactamases as fully efficient enzymes. Determination of all the rate constants in the acyl-enzyme mechanism. Biochem. J. 1990, 266, 853–861. [Google Scholar] [CrossRef]
- Williams, D.L.; Sikora, V.M.; Hammer, M.A.; Amin, S.; Brinjikji, T.; Brumley, E.K.; Burrows, C.J.; Carrillo, P.M.; Cromer, K.; Edwards, S.J.; et al. May the Odds Be Ever in Your Favor: Non-deterministic Mechanisms Diversifying Cell Surface Molecule Expression. Front. Cell Dev. Biol. 2022, 9, 720798. [Google Scholar] [CrossRef]
- Banerjee, K.; Bhattacharyya, K. States with identical steady dissipation rate in reaction networks: A nonequilibrium thermodynamic insight in enzyme efficiency. Chem. Phys. 2014, 438, 1–6. [Google Scholar] [CrossRef]
- Agarwal, P.K. Role of protein dynamics in reaction rate enhancement by enzymes. J. Am. Chem. Soc. 2005, 127, 15248–15256. [Google Scholar] [CrossRef] [PubMed]
- Northrop, D.B. On the Meaning of Km and V/K in Enzyme Kinetics. J. Chem. Educ. 1998, 75, 1153–1157. [Google Scholar] [CrossRef]
- Park, C. Visual Interpretation of the Meaning of kcat/KM in Enzyme Kinetics. J. Chem. Educ. 2022, 99, 2556–2562. [Google Scholar] [CrossRef]
- Kleiber, M. Body size and metabolic rate. Physiol. Rev. 1947, 27, 511–541. [Google Scholar] [CrossRef]
- White, C.R.; Blackburn, T.M.; Seymour, R.S. Phylogenetically informed analysis of the allometry of mammalian basal metabolic rate supports neither geometric nor quarter-power scaling. Evolution 2009, 63, 2658–2667. [Google Scholar] [CrossRef]
- Hulbert, A.J. A Sceptics View: “Kleiber’s Law” or the “3/4 Rule” is neither a Law nor a Rule but Rather an Empirical Approximation. Systems 2014, 2, 186–202. [Google Scholar] [CrossRef]
- Niklas, K.J.; Kutschera, U. Kleiber’s Law: How the Fire of Life ignited debate, fueled theory, and neglected plants as model organisms. Plant Signal. Behav. 2015, 10, e1036216. [Google Scholar] [CrossRef]
- DeLong, J.P.; Okie, J.G.; Moses, M.E.; Sibly, R.M.; Brown, J.H. Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. USA 2010, 107, 12941–12945. [Google Scholar] [CrossRef]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.-L.; Chown, S.L.; Reich, P.B.; Gavrilov, V.M. Mean mass-specific metabolic rates are strikingly similar across life’s major domains: Evidence for life’s metabolic optimum. Proc. Natl. Acad. Sci. USA 2008, 105, 16994–16999. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.R.; Cooke, T.J.; Rinaldo, A.; Maritan, A. Form, function, and evolution of living organisms. Proc. Natl. Acad. Sci. USA 2014, 111, 3332–3337. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Size matters in metabolic scaling: Critical role of the thermodynamic efficiency of ATP synthesis and its dependence on mitochondrial H+ leak across mammalian species. Biosystems 2024, 242, 105255. [Google Scholar] [CrossRef] [PubMed]
- Arnold, F.H. Directed Evolution: Bringing New Chemistry to Life. Angew. Chem. Int. Ed. Engl. 2018, 57, 4143–4148. [Google Scholar] [CrossRef]
- Šterk, M.; Markovič, R.; Marhl, M.; Fajmut, A.; Dobovišek, A. Flexibility of enzymatic transitions as a hallmark of optimized enzyme steady-state kinetics and thermodynamics. Comput. Biol. Chem. 2021, 91, 107449. [Google Scholar] [CrossRef]
- Juretić, D.; Bonačić Lošić, Ž. Comments on ’Flexibility of enzymatic transitions as a hallmark of optimized enzyme steady-state kinetics and thermodynamics’. Comput. Biol. Chem. 2021, 95, 107571. [Google Scholar] [CrossRef]
- Lan, G.; Pablo Sartori, P.; Neumann, S.; Sourjik, V.; Tu, Y. The energy-speed-accuracy tradeoff in sensory adaptation. Nat. Phys. 2012, 8, 422–428. [Google Scholar] [CrossRef]
- Pross, A.; Pascal, R. How and why kinetics, thermodynamics, and chemistry induce the logic of biological evolution. Beilstein. J. Org. Chem. 2017, 13, 665–674. [Google Scholar] [CrossRef]
- Nader, S.; Sebastianelli, L.; Mansy, S.S. Protometabolism as out-of-equilibrium chemistry. Phil. Trans. R. Soc. A 2022, 380, 20200423. [Google Scholar] [CrossRef]
- Lane, N.; Martin, W.F. The origin of membrane bioenergetics. Cell 2012, 151, 1406–1416. [Google Scholar] [CrossRef]
- England, J.L. Statistical physics of self-replication. J. Chem. Phys. 2013, 139, 121923. [Google Scholar] [CrossRef] [PubMed]

| # | Enzyme & | kcat/Km (Ms)−1 | kcat (s−1) | J (s−1) | X/(RT) | ϕ/(RT) (s−1) | # | Enzyme | kcat/Km (Ms)−1 | kcat (s−1) | J (s−1) | X/(RT) | ϕ/(RT) (s−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | CAII | 83,600,000 | 805,433 | 421,874 | 1.81 | 125,000 | 30 | GeoCyp | 847,000 | 36.85 | 33.75 | 2.73 | 92.19 |
| 2 | KSI | 302,000,000 | 35,031 | 13,756 | 8.43 | 115,900 | 31 | ALaO | 295,908 | 6.8 | 6.58 | 9.83 | 64.72 |
| 3 | CAII-T200H | 67,700,000 | 209,682 | 33,593 | 1.87 | 62,920 | 32 | EpiT | 10,333 | 341 | 28 | 1.03 | 28.9 |
| 4 | CAI | 24,810,000 | 77,746 | 15,691 | 1.81 | 28,370 | 33 | NSAAR | 2857 | 20 | 10.1 | 2.34 | 23.67 |
| 5 | Lac1 | 26,030,200 | 1905 | 1757 | 8.27 | 14,526 | 34 | iPGM | 104,762 | 22 | 8.75 | 2.32 | 20.29 |
| 6 | RTEM | 23,513,000 | 975 | 873 | 7.74 | 6757 | 35 | ALiO | 8890 | 1.602 | 1.276 | 10.01 | 12.77 |
| 7 | sgPPase | 70,427,239 | 812 | 625 | 9.95 | 6214 | 36 | API | 50,333 | 100 | 10.7 | 1.08 | 11.58 |
| 8 | GPI * | 21,721,831 | 1550 | 855 | 3.42 | 2928 | 37 | RPI | 15,143 | 33.3 | 5.16 | 2.12 | 10.93 |
| 9 | GAL | 1,918,000 | 730 | 152 | 7.6 | 1154 | 38 | RacE2mut | 14,081 | 81.67 | 4.36 | 2.24 | 9.76 |
| 10 | coliMgPPase | 44,481,928 | 147 | 128 | 8.71 | 1116 | 39 | TIProRC * | 1996 | 12.13 | 1.64 | 3.54 | 5.82 |
| 11 | yeastPPase | 29,765,749 | 189 | 122 | 7.74 | 946 | 40 | LYSROEN | 318 | 3.5 | 2.39 | 2.4 | 5.73 |
| 12 | MR | 1,080,105 | 632 | 317 | 2.52 | 798 | 41 | TIProR * | 2300 | 2.783 | 1.989 | 2.26 | 4.485 |
| 13 | PC1 | 10,100,000 | 60.8 | 60.6 | 11.37 | 689 | 42 | KYNase_66 | 34,526 | 0.74 | 0.602 | 7.03 | 4.233 |
| 14 | FH | 6,355,555 | 1833 | 508 | 1.35 | 687 | 43 | RacE2 | 5311 | 32.4 | 1.39 | 2.84 | 3.958 |
| 15 | KSI-D38E | 2,769,512 | 129 | 73 | 8.97 | 655 | 44 | ATAmut2 | 1427 | 1.87 | 0.986 | 2.07 | 2.037 |
| 16 | KIN | 2,225,553 | 106 | 41.4 | 13.73 | 569 | 45 | KYNase_93D9 * | 38,565 | 0.67 | 0.424 | 4.77 | 2.022 |
| 17 | RPE | 1,605,047 | 305 | 191 | 2.91 | 554 | 46 | ATAmut1 | 4875 | 1.95 | 1.123 | 1.59 | 1.785 |
| 18 | dPGM | 1,650,000 | 330 | 179 | 2.37 | 423 | 47 | TM0831 * | 17.9 | 2.156 | 0.244 | 2.53 | 0.618 |
| 19 | PMI | 595,000 | 800 | 161 | 2.27 | 365 | 48 | ATA | 217 | 0.5 | 0.216 | 2.06 | 0.444 |
| 20 | AROH | 589,474 | 50.4 | 12.8 | 22.59 | 289 | 49 | FAProR * | 18.9 | 0.597 | 0.164 | 1.32 | 0.216 |
| 21 | CypC | 471,129 | 115 | 99.6 | 2.71 | 270 | 50 | HcmABwt | 481 | 0.05 | 0.048 | 3.43 | 0.163 |
| 22 | ALF | 5,086,315 | 52.6 | 51.8 | 5.14 | 266 | 51 | SerR | 31 | 0.31 | 0.056 | 2.62 | 0.148 |
| 23 | CypB | 379,186 | 103 | 90.1 | 2.73 | 246 | 52 | TAM | 37.8 | 0.0209 | 0.0135 | 8.47 | 0.114 |
| 24 | EpiI | 100,400 | 502 | 92.6 | 2.65 | 245 | 53 | HcmAmut | 10.9 | 0.02 | 0.0165 | 4.05 | 0.0666 |
| 25 | TPI | 542,518 | 714 | 209 | 1.16 | 242 | 54 | NSAARN | 3.89 | 0.07 | 0.023 | 2.86 | 0.0659 |
| 26 | ALS | 3,255,879 | 40.2 | 39.4 | 6.05 | 239 | 55 | EpiTmut | 15.9 | 4.9 | 0.0474 | 0.94 | 0.044 |
| 27 | CypA | 936,569 | 97.3 | 87.0 | 2.73 | 238 | 56 | GI * | 0.0365 | 0.029 | 0.0097 | 2.36 | 0.023 |
| 28 | AR | 172,197 | 1692 | 827 | 1.80 | 229 | 57 | HcmIcm | 1.8182 | 0.001 | 0.00094 | 5.21 | 0.0049 |
| 29 | yPGM | 747,211 | 380 | 93.4 | 1.03 | 96.2 | 58 | GI3 * | 0.00018 | 0.00012 | 0.000015 | 2.96 | 0.000044 |
| # | Enzyme & | kcat/Km Fold | kcat Fold | J (s−1) | X/(RT) | ϕ/(RT) max (s−1) | # | Enzyme | kcat/Km Fold | kcat Fold | J (s−1) | X/(RT) | ϕ/(RT) max (s−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | CAII | 2.85 | 0.85 | 516,052 | 4.12 | 2.1 × 106 | 30 | GeoCyp | 0.13 | 21.9 | 362 | 2.73 | 989 |
| 2 | KSI | 2.23 | 0.78 | 15,963 | 8.43 | 134,498 | 31 | ALaO | 0.34 | 1.07 | 6.86 | 9.83 | 67.5 |
| 3 | CAII-T200H | 3.77 | 0.67 | 45,786 | 1.87 | 85,759 | 32 | EpiT | 1.20 | 0.60 | 29.6 | 1.03 | 30.6 |
| 4 | CAI | 1.98 | 0.63 | 18,986 | 1.81 | 34,328 | 33 | NSAAR | 0.74 | 1.75 | 11.2 | 2.34 | 26.3 |
| 5 | Lac1 | 0.33 | 1.56 | 2364 | 8.27 | 18,719 | 34 | iPGM | 0.89 | 1.17 | 8.84 | 2.32 | 20.5 |
| 6 | RTEM | 0.21 | 2.05 | 1365 | 7.74 | 10,570 | 35 | ALiO | 1.98 | 0.98 | 1.30 | 10.01 | 13.0 |
| 7 | sgPPase | 0.95 | 1.02 | 625 | 9.95 | 6218 | 36 | API | 1.08 | 0.78 | 10.9 | 1.08 | 11.7 |
| 8 | GPI * | 0.75 | 1.60 | 931 | 3.42 | 3185 | 37 | RPI | 1.44 | 0.58 | 5.73 | 2.12 | 12.1 |
| 9 | GAL | 0.94 | 2.62 | 165 | 7.60 | 1253 | 38 | RacE2mut | 3.18 | 0.29 | 6.54 | 2.24 | 14.6 |
| 10 | coliMgPPase | 0.44 | 1.31 | 145 | 8.71 | 1263 | 39 | TIProRC * | 1.68 | 0.47 | 2.01 | 3.54 | 7.14 |
| 11 | yeastPPase | 0.56 | 1.30 | 131 | 7.74 | 1013 | 40 | LYSROEN | 0.49 | 2.86 | 3.50 | 2.40 | 8.41 |
| 12 | MR | 1.40 | 0.88 | 329 | 2.52 | 829 | 41 | TIProR * | 0.39 | 3.64 | 3.54 | 2.26 | 7.98 |
| 13 | PC1 | 0.06 | 2.55 | 60.6 | 11.37 | 1519 | 42 | KYNase_66 | 0.64 | 1.23 | 0.637 | 7.03 | 4.48 |
| 14 | FH | 0.88 | 1.29 | 513 | 1.35 | 694 | 43 | RacE2 | 3.45 | 0.28 | 1.94 | 2.84 | 5.50 |
| 15 | KSI-D38E | 3.41 | 1.00 | 126 | 11.97 | 1507 | 44 | ATAmut2 | 0.67 | 1.93 | 1.15 | 2.07 | 2.37 |
| 16 | KIN | 1.30 | 0.85 | 42.3 | 13.73 | 580 | 45 | KYNase_93D9 * | 1.86 | 0.95 | 0.438 | 4.77 | 2.09 |
| 17 | RPE | 0.66 | 2.27 | 240 | 2.91 | 697 | 46 | ATAmut1 | 0.43 | 3.55 | 1.77 | 1.59 | 2.82 |
| 18 | dPGM | 0.68 | 1.77 | 201 | 2.37 | 477 | 47 | TM0831 * | 2.17 | 0.42 | 0.317 | 2.53 | 0.804 |
| 19 | PMI | 1.13 | 0.77 | 164 | 2.27 | 372 | 48 | ATA | 0.77 | 1.66 | 0.231 | 2.06 | 0.475 |
| 20 | AROH | 2.47 | 0.71 | 15.1 | 22.59 | 341 | 49 | FAProR * | 0.56 | 1.93 | 0.180 | 1.32 | 0.237 |
| 21 | CypC | 0.22 | 2.43 | 188 | 2.71 | 509 | 50 | HcmABwt | 0.19 | 22.0 | 0.449 | 3.43 | 1.54 |
| 22 | ALF | 0.06 | 16.4 | 520 | 5.14 | 2671 | 51 | SerR | 1.28 | 0.65 | 0.060 | 2.62 | 0.157 |
| 23 | CypB | 0.26 | 3.43 | 214 | 2.73 | 584 | 52 | TAM | 3.75 | 1.00 | 0.0208 | 10.08 | 0.210 |
| 24 | EpiI | 1.06 | 0.85 | 93.2 | 2.65 | 247 | 53 | HcmAmut | 0.49 | 4.00 | 0.0302 | 4.05 | 0.122 |
| 25 | TPI | 0.88 | 1.39 | 218 | 1.16 | 253 | 54 | NSAARN | 0.99 | 1.01 | 0.023 | 2.86 | 0.066 |
| 26 | ALS | 0.10 | 2.50 | 84.5 | 6.05 | 512 | 55 | EpiTmut | 1.13 | 0.35 | 0.0516 | 0.94 | 0.048 |
| 27 | CypA | 0.15 | 8.35 | 407 | 2.73 | 1110 | 56 | GI * | 0.98 | 1.03 | 0.0097 | 2.36 | 0.023 |
| 28 | AR | 3.68 | 0.91 | 977 | 1.79 | 1751 | 57 | HcmIcm | 0.35 | 9.00 | 0.0037 | 5.21 | 0.0192 |
| 29 | yPGM | 0.88 | 1.32 | 95.5 | 1.03 | 98.4 | 58 | GI3 * | 2.49 | 0.48 | 0.000024 | 2.96 | 0.00007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juretić, D. Exploring the Evolution-Coupling Hypothesis: Do Enzymes’ Performance Gains Correlate with Increased Dissipation? Entropy 2025, 27, 365. https://doi.org/10.3390/e27040365
Juretić D. Exploring the Evolution-Coupling Hypothesis: Do Enzymes’ Performance Gains Correlate with Increased Dissipation? Entropy. 2025; 27(4):365. https://doi.org/10.3390/e27040365
Chicago/Turabian StyleJuretić, Davor. 2025. "Exploring the Evolution-Coupling Hypothesis: Do Enzymes’ Performance Gains Correlate with Increased Dissipation?" Entropy 27, no. 4: 365. https://doi.org/10.3390/e27040365
APA StyleJuretić, D. (2025). Exploring the Evolution-Coupling Hypothesis: Do Enzymes’ Performance Gains Correlate with Increased Dissipation? Entropy, 27(4), 365. https://doi.org/10.3390/e27040365






