Correlations and Kappa Distributions: Numerical Experiment and Physical Understanding
Abstract
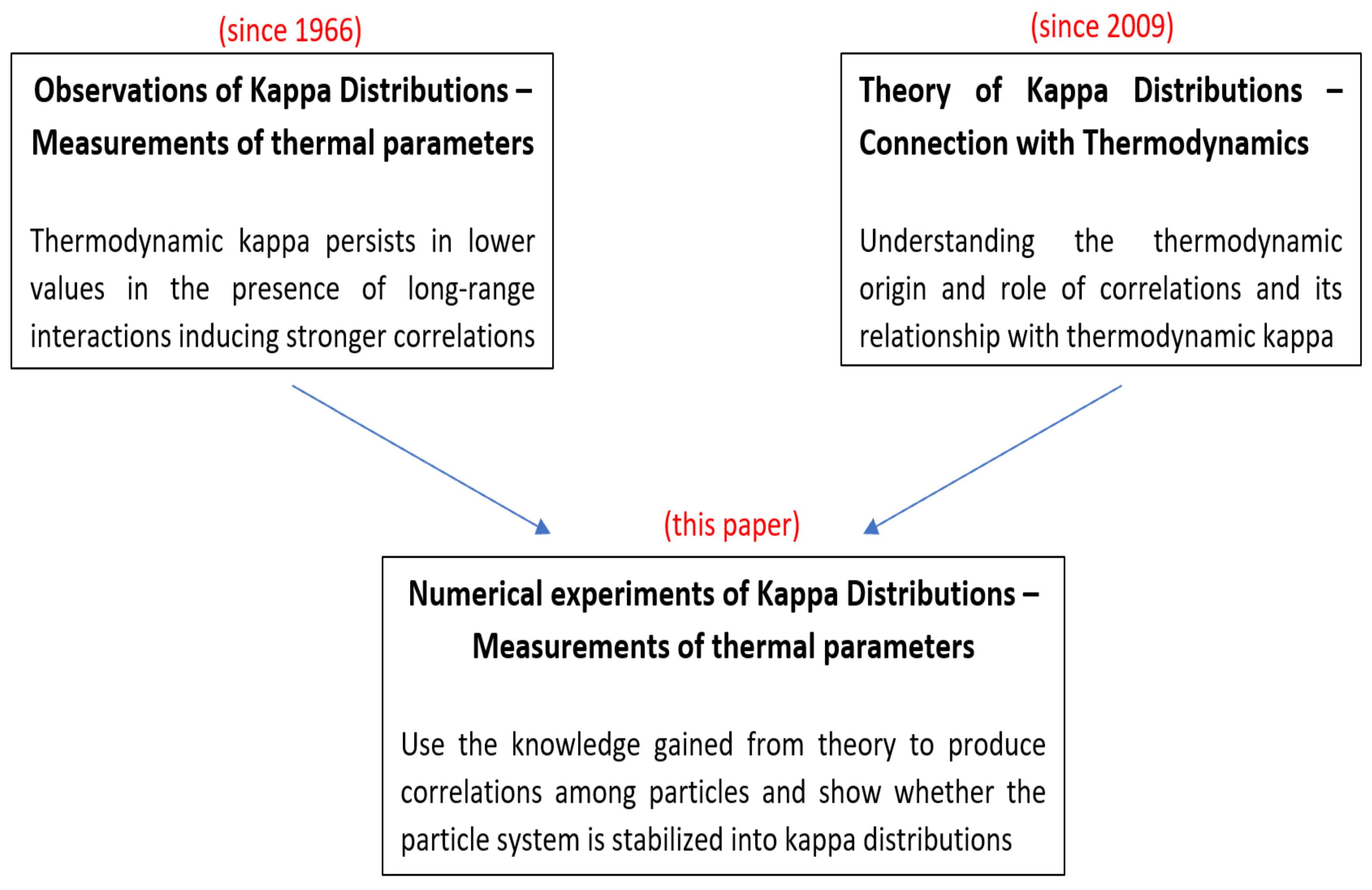
:1. Introduction
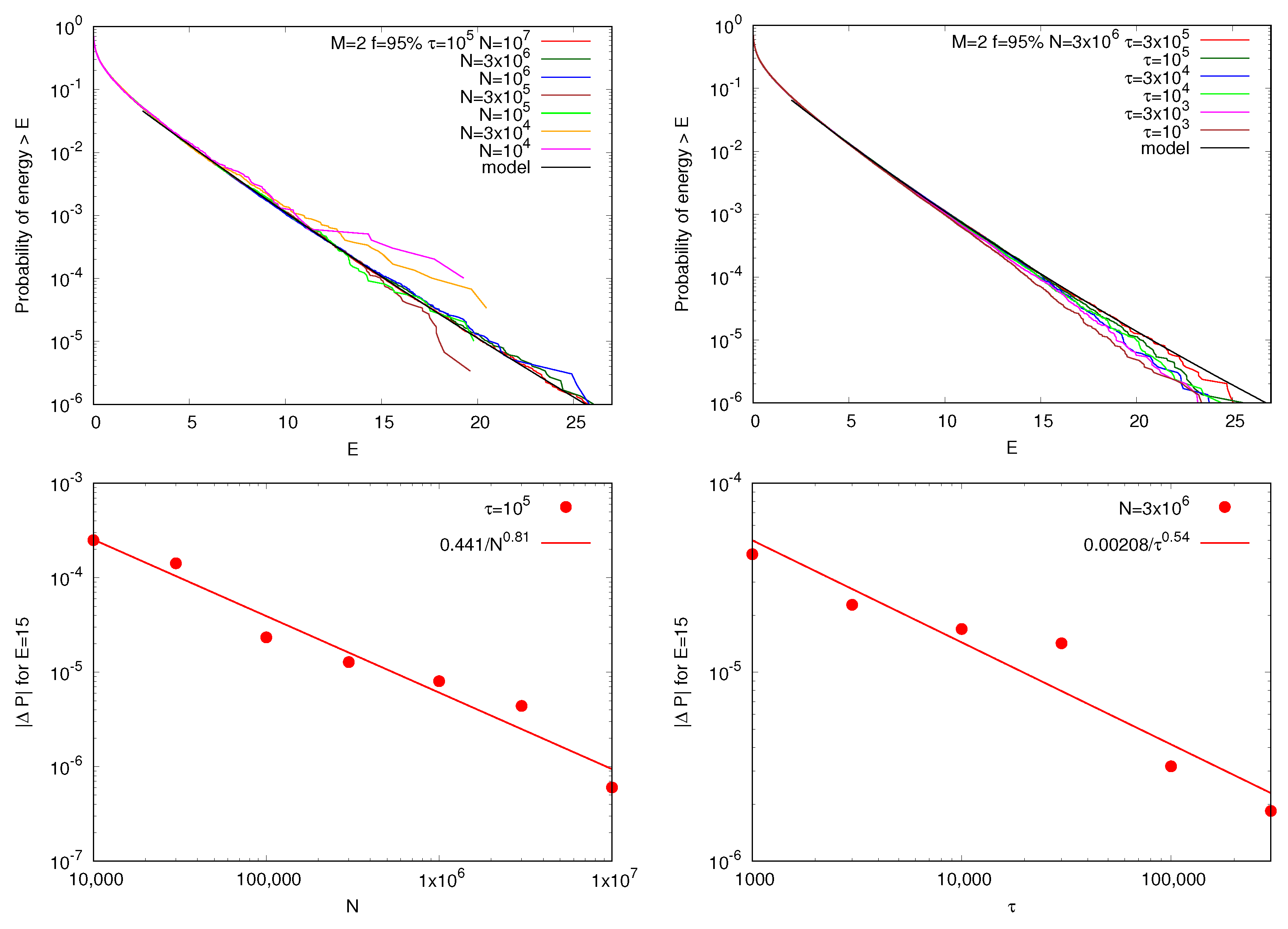
2. Method of the Numerical Experiment
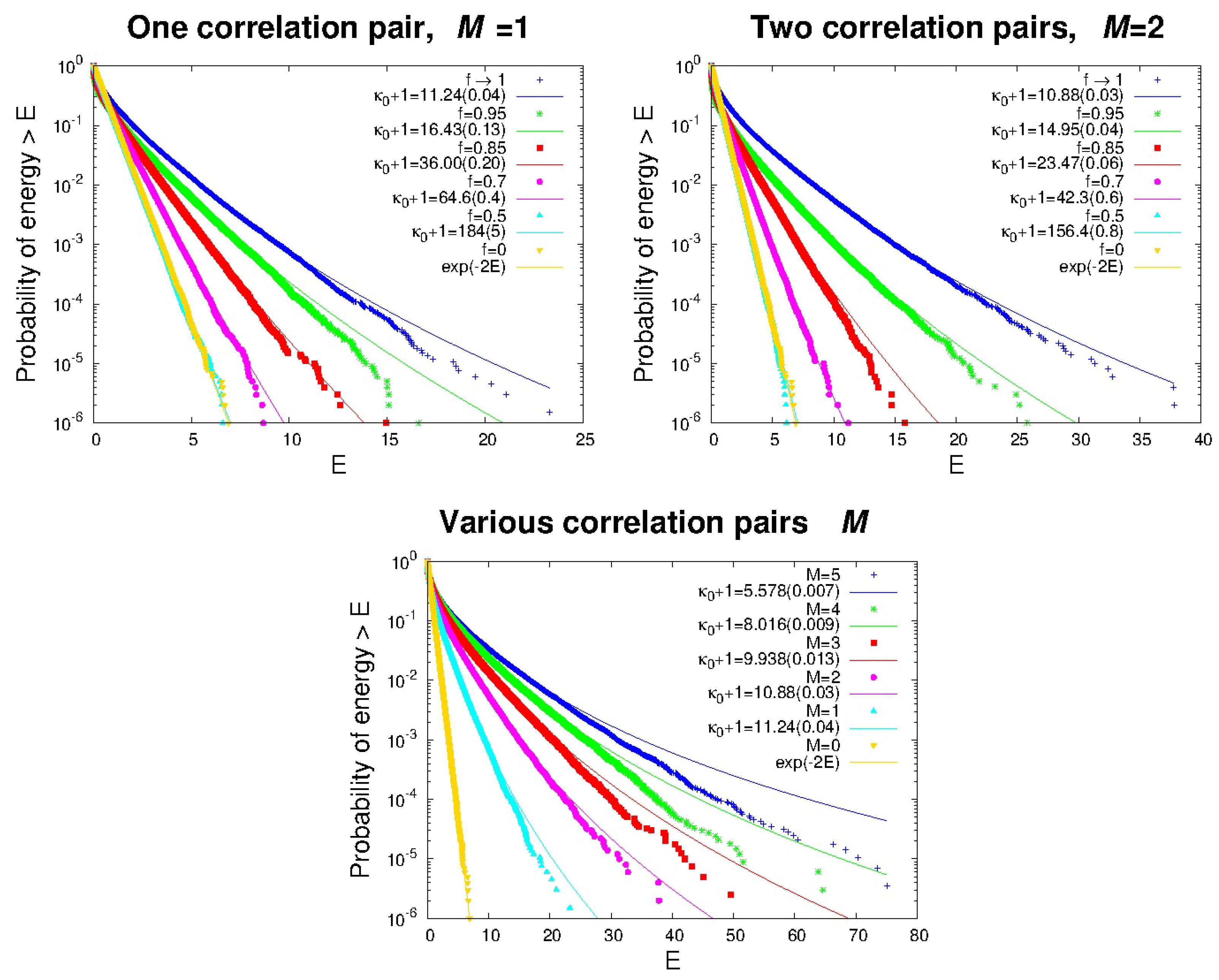
3. Results
4. Conclusions and Discussion
- Stationary states are described by kappa distributions (see also the work of Milovanov et al. [155]).
- Correlations compete with collisions driving the stationary state to lower thermodynamic kappa.
- Inverse thermodynamic kappa describes a measure of correlations.
- Thermodynamic kappa tends to infinity (MB distribution), when no correlations exist.
- Thermodynamic kappa tends to its lowest limit (), when the number of correlated particles approaches the whole number of particles.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Formulation of Kappa Distributions
Appendix B. Description of the Code
- (1)
- The collision step according to which we randomly select a “particle”, say with , and collide it with the particle by randomly redistributing their total energy, , among themselves. This means that we select a random number uniformly distributed in the region [0, 1] and attribute the new particle energies as, (after collision) and (after collision) , (see lines 9–16 in Figure A1).
- (2)
- The pseudo-collision or correlation step where we randomly select a “particle”, say with index , and give its whole energy or a fraction , see lines 18 to 29 in Figure A1) of it to the particle with index . For symmetry reasons, with probability is for the particle with index that gives its whole energy or a fraction f of it to the particle. (We note that, for technical reasons, we do not plot the exact case of ; this special case corresponds to a standing particle population whose size is governed by nonlinear effects discussed further below).

References
- Maxwell, J.C. Illustrations of the Dynamical Theory of Gases. Philos. Mag. 1860, 19, 19. [Google Scholar]
- Boltzmann, L. Über die Mechanische Bedeutung des Zweiten Hauptsatzes der Wärmetheorie. Wien. Berichte 1866, 53, 195. [Google Scholar]
- Binsack, J.H. Plasma Studies with the IMP-2 Satellite. Ph.D. Thesis, MIT, Cambridge, MA, USA, 1966. [Google Scholar]
- Olbert, S. Summary of Experimental Results from M.I.T. Detector on IMP-1. In Physics of the Magnetosphere; Carovillano, R.D.L., McClay, J.F., Eds.; Astrophysics and Space Science Library; Springer: Dordrecht, The Netherlands; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1968; Volume 10, p. 641. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- Treumann, R.A. Theory of super-diffusion for the magnetopause. Geophys. Res. Lett. 1997, 24, 1727–1730. [Google Scholar] [CrossRef]
- Milovanov, A.V.; Zelenyi, L.M. Functional background of the Tsallis entropy: “coarse-grained” systems and “kappa” distribution functions. Nonlinear Process. Geophys. 2000, 7, 211–221. [Google Scholar] [CrossRef]
- Leubner, M.P. A Nonextensive Entropy Approach to Kappa-Distributions. Astrophys. Space Sci. 2002, 282, 573–579. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis statistical mechanics in space plasmas. J. Geophys. Res. (Space Phys.) 2009, 114, A11105. [Google Scholar] [CrossRef]
- Livadiotis, G. “Lagrangian Temperature”: Derivation and Physical Meaning for Systems Described by Kappa Distributions. Entropy 2014, 16, 4290–4308. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa Distributions: Theory and Applications in Plasmas; Elsevier: Amsterdam, The Netherlands, 2017; 738p. [Google Scholar]
- Yoon, P.H. Classical Kinetic Theory of Weakly Turbulent Nonlinear Plasma Processes; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M. Kappa Distributions: Theory and Applications in Space Plasmas. Sol. Phys. 2010, 267, 153–174. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Understanding Kappa Distributions: A Toolbox for Space Science and Astrophysics. Space Sci. Rev. 2013, 175, 183–214. [Google Scholar] [CrossRef]
- Livadiotis, G. Introduction to special section on Origins and Properties of Kappa Distributions: Statistical Background and Properties of Kappa Distributions in Space Plasmas. J. Geophys. Res. (Space Phys.) 2015, 120, 1607–1619. [Google Scholar] [CrossRef]
- Tsallis, C. Beyond Boltzmann-Gibbs-Shannon in Physics and Elsewhere. Entropy 2019, 21, 696. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Thermodynamic Definitions of Temperature and Kappa and Introduction of the Entropy Defect. Entropy 2021, 23, 1683. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Physical Correlations Lead to Kappa Distributions. Astrophys. J. 2022, 940, 83. [Google Scholar] [CrossRef]
- Vocks, C.; Mann, G.; Rausche, G. Formation of suprathermal electron distributions in the quiet solar corona. Astron. Astrophys. 2008, 480, 527–536. [Google Scholar] [CrossRef]
- Lee, E.; Williams, D.R.; Lapenta, G. Spectroscopic indication of suprathermal ions in the solar corona. arXiv 2013, arXiv:1305.2939. [Google Scholar]
- Cranmer, S.R. Suprathermal Electrons in the Solar Corona: Can Nonlocal Transport Explain Heliospheric Charge States? Astrophys. J. 2014, 791, L31. [Google Scholar] [CrossRef]
- Xiao, F.; Shen, C.; Wang, Y.; Zheng, H.; Wang, S. Energetic electron distributions fitted with a relativistic kappa-type function at geosynchronous orbit. J. Geophys. Res. (Space Phys.) 2008, 113, A05203. [Google Scholar] [CrossRef]
- Laming, J.M.; Moses, J.D.; Ko, Y.K.; Ng, C.K.; Rakowski, C.E.; Tylka, A.J. On the Remote Detection of Suprathermal Ions in the Solar Corona and their Role as Seeds for Solar Energetic Particle Production. Astrophys. J. 2013, 770, 73. [Google Scholar] [CrossRef]
- Schwadron, N.A.; Bale, S.; Bonnell, J.; Case, A.; Christian, E.R.; Cohen, C.M.S.; Cummings, A.C.; Davis, A.J.; Dudok de Wit, T.; de Wet, W.; et al. Seed Population Preconditioning and Acceleration Observed by the Parker Solar Probe. Astrophys. J. 2020, 246, 33. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Livadiotis, G.; McComas, D.J.; Cuesta, M.E.; Khoo, L.Y.; Cohen, C.M.S.; Mitchell, D.G.; Schwadron, N.A. Persistent Behavior in Solar Energetic Particle Time Series. Astrophys. J. 2024, 969, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; Cummings, A.T.; Cuesta, M.E.; Bandyopadhyay, R.; Farooki, H.A.; Khoo, L.Y.; McComas, D.J.; Rankin, J.S.; Sharma, T.; Shen, M.M.; et al. Kappa-tail Technique: Modeling and Application to Solar Energetic Particles Observed by Parker Solar Probe. Astrophys. J. 2024, 973, 6. [Google Scholar] [CrossRef]
- Cohen, C.M.S.; Leske, R.A.; Christian, E.R.; Cummings, A.C.; de Nolfo, G.A.; Desai, M.I.; Giacalone, J.; Hill, M.E.; Labrador, A.W.; McComas, D.J.; et al. Observations of the 2022 September 5 Solar Energetic Particle Event at 15 Solar Radii. Astrophys. J. 2024, 966, 148. [Google Scholar] [CrossRef]
- Cuesta, M.E.; Cummings, A.T.; Livadiotis, G.; McComas, D.J.; Cohen, C.M.S.; Khoo, L.Y.; Sharma, T.; Shen, M.M.; Bandyopadhyay, R.; Rankin, J.S.; et al. Observations of Kappa Distributions in Solar Energetic Protons and Derived Thermodynamic Properties. Astrophys. J. 2024, 973, 76. [Google Scholar] [CrossRef]
- Mann, G.; Warmuth, A.; Aurass, H. Generation of highly energetic electrons at reconnection outflow shocks during solar flares. Astron. Astrophys. 2009, 494, 669–675. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Evidence of Large-Scale Quantization in Space Plasmas. Entropy 2013, 15, 1118–1134. [Google Scholar] [CrossRef]
- Bian, N.H.; Emslie, A.G.; Stackhouse, D.J.; Kontar, E.P. The Formation of Kappa-distribution Accelerated Electron Populations in Solar Flares. Astrophys. J. 2014, 796, 142. [Google Scholar] [CrossRef]
- Jeffrey, N.L.S.; Fletcher, L.; Labrosse, N. Non-Gaussian Velocity Distributions in Solar Flares from Extreme Ultraviolet Lines: A Possible Diagnostic of Ion Acceleration. Astrophys. J. 2017, 836, 35. [Google Scholar] [CrossRef]
- Cairns, I.H.; Mitchell, J.J.; Knock, S.A.; Robinson, P.A. Towards a quantitative theory for 2-3 kHz radio emission from beyond the heliopause. Adv. Space Res. 2004, 34, 88–93. [Google Scholar] [CrossRef]
- Li, B.; Cairns, I.H. Type III Radio Bursts in Coronal Plasmas with Kappa Particle Distributions. Astrophys. J. 2013, 763, L34. [Google Scholar] [CrossRef]
- Schmidt, J.M.; Cairns, I.H. Quantitative prediction of type II solar radio emission from the Sun to 1 AU. Geophys. Res. Lett. 2016, 43, 50–57. [Google Scholar] [CrossRef]
- Dzifčáková, E.; Dudík, J. H to Zn Ionization Equilibrium for the Non-Maxwellian Electron κ-distributions: Updated Calculations. Astrophys. J. 2013, 206, 6. [Google Scholar] [CrossRef]
- Dzifčáková, E.; Dudík, J.; Kotrč, P.; Fárník, F.; Zemanová, A. KAPPA: A Package for Synthesis of Optically Thin Spectra for the Non-Maxwellian κ-distributions Based on the Chianti Database. Astrophys. J. 2015, 217, 14. [Google Scholar] [CrossRef]
- Lörinčík, J.; Dudík, J.; del Zanna, G.; Dzifčáková, E.; Mason, H.E. Plasma Diagnostics from Active Region and Quiet-Sun Spectra Observed by Hinode/EIS: Quantifying the Departures from a Maxwellian Distribution. Astrophys. J. 2020, 893, 34. [Google Scholar] [CrossRef]
- Maksimovic, M.; Pierrard, V.; Lemaire, J.F. A kinetic model of the solar wind with Kappa distribution functions in the corona. Astron. Astrophys. 1997, 324, 725–734. [Google Scholar]
- Pierrard, V.; Maksimovic, M.; Lemaire, J. Electron velocity distribution functions from the solar wind to the corona. J. Geophys. Res. 1999, 104, 17021–17032. [Google Scholar] [CrossRef]
- Mann, G.; Classen, H.T.; Keppler, E.; Roelof, E.C. On electron acceleration at CIR related shock waves. Astron. Astrophys. 2002, 391, 749–756. [Google Scholar] [CrossRef]
- Marsch, E. Kinetic Physics of the Solar Corona and Solar Wind. Living Rev. Sol. Phys. 2006, 3, 1. [Google Scholar] [CrossRef]
- Štverák, Š.; Maksimovic, M.; Trávníček, P.M.; Marsch, E.; Fazakerley, A.N.; Scime, E.E. Radial evolution of nonthermal electron populations in the low-latitude solar wind: Helios, Cluster, and Ulysses Observations. J. Geophys. Res. (Space Phys.) 2009, 114, A05104. [Google Scholar] [CrossRef]
- Yoon, P.H.; Ziebell, L.F.; Gaelzer, R.; Lin, R.P.; Wang, L. Langmuir Turbulence and Suprathermal Electrons. Space Sci. Rev. 2012, 173, 459–489. [Google Scholar] [CrossRef]
- Yoon, P.H.; López, R.A.; Salem, C.S.; Bonnell, J.W.; Kim, S. Non-Thermal Solar Wind Electron Velocity Distribution Function. Entropy 2024, 26, 310. [Google Scholar] [CrossRef]
- Yoon, P.H. Electron kappa distribution and quasi-thermal noise. J. Geophys. Res. (Space Phys.) 2014, 119, 7074–7087. [Google Scholar] [CrossRef]
- Pierrard, V.; Pieters, M. Coronal heating and solar wind acceleration for electrons, protons, and minor ions obtained from kinetic models based on kappa distributions. J. Geophys. Res. (Space Phys.) 2014, 119, 9441–9455. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Malandraki, O.E.; Pavlos, E.G.; Iliopoulos, A.C.; Karakatsanis, L.P. Non-extensive statistical analysis of magnetic field during the March 2012 ICME event using a multi-spacecraft approach. Phys. A Stat. Mech. Its Appl. 2016, 464, 149–181. [Google Scholar] [CrossRef]
- Zouganelis, I. Measuring suprathermal electron parameters in space plasmas: Implementation of the quasi-thermal noise spectroscopy with kappa distributions using in situ Ulysses/URAP radio measurements in the solar wind. J. Geophys. Res. (Space Phys.) 2008, 113, A08111. [Google Scholar] [CrossRef]
- Livadiotis, G. Using Kappa Distributions to Identify the Potential Energy. J. Geophys. Res. (Space Phys.) 2018, 123, 1050–1060. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G.; Wicks, R.T. On the Calculation of the Effective Polytropic Index in Space Plasmas. Entropy 2019, 21, 997. [Google Scholar] [CrossRef]
- Osuna Alcalaya, P.; Zouganelis, I.; Rodríguez Pacheco, J. Analytic solution for the electrostatic potential of the solar wind. Astron. Astrophys. 2021, 653, A75. [Google Scholar] [CrossRef]
- Li, Y.L.; Chen, L.; Wu, D.J. Radial Distribution of Electron Quasi-thermal Noise in the Inner Heliosphere. Astrophys. J. 2024, 976, 192. [Google Scholar] [CrossRef]
- Chotoo, K.; Schwadron, N.A.; Mason, G.M.; Zurbuchen, T.H.; Gloeckler, G.; Posner, A.; Fisk, L.A.; Galvin, A.B.; Hamilton, D.C.; Collier, M.R. The suprathermal seed population for corotating interaction region ions at 1 AU deduced from composition and spectra of H+, He++, and He+ observed on Wind. J. Geophys. Res. 2000, 105, 23107–23122. [Google Scholar] [CrossRef]
- Formisano, V.; Moreno, G.; Palmiotto, F.; Hedgecock, P.C. Solar wind interaction with the Earth’s magnetic field: 1. Magnetosheath. J. Geophys. Res. 1973, 78, 3714. [Google Scholar] [CrossRef]
- Ogasawara, K.; Angelopoulos, V.; Dayeh, M.A.; Fuselier, S.A.; Livadiotis, G.; McComas, D.J.; McFadden, J.P. Characterizing the dayside magnetosheath using energetic neutral atoms: IBEX and THEMIS observations. J. Geophys. Res. (Space Phys.) 2013, 118, 3126–3137. [Google Scholar] [CrossRef]
- Ogasawara, K.; Dayeh, M.A.; Funsten, H.O.; Fuselier, S.A.; Livadiotis, G.; McComas, D.J. Interplanetary magnetic field dependence of the suprathermal energetic neutral atoms originated in subsolar magnetopause. J. Geophys. Res. (Space Phys.) 2015, 120, 964–972. [Google Scholar] [CrossRef]
- Grabbe, C. Generation of Broadband Electrostatic Waves in Earth’s Magnetotail. Phys. Rev. Lett. 2000, 84, 3614–3617. [Google Scholar] [CrossRef] [PubMed]
- Pisarenko, N.F.; Budnik, E.Y.; Yermolaev, Y.I.; Kirpichev, I.P.; Lutsenko, V.N.; Morozova, E.I.; Antonova, E.E. The ion differential spectra in outer boundary of the ring current: November 17, 1995 case study. J. Atmos.-Sol.-Terr. Phys. 2002, 64, 573–583. [Google Scholar] [CrossRef]
- Christon, S.P. A comparison of the Mercury and Earth magnetospheres: Electron measurements and substorm time scales. Icarus 1987, 71, 448–471. [Google Scholar] [CrossRef]
- Kletzing, C.A.; Scudder, J.D.; Dors, E.E.; Curto, C. Auroral source region: Plasma properties of the high-latitude plasma sheet. J. Geophys. Res. (Space Phys.) 2003, 108, 1360. [Google Scholar] [CrossRef]
- Wang, C.P.; Lyons, L.R.; Chen, M.W.; Wolf, R.A.; Toffoletto, F.R. Modeling the inner plasma sheet protons and magnetic field under enhanced convection. J. Geophys. Res. (Space Phys.) 2003, 108, 1074. [Google Scholar] [CrossRef]
- Hapgood, M.; Perry, C.; Davies, J.; Denton, M. The role of suprathermal particle measurements in CrossScale studies of collisionless plasma processes. Planet. Space Sci. 2011, 59, 618–629. [Google Scholar] [CrossRef]
- Ogasawara, K.; Livadiotis, G.; Grubbs, G.A.; Jahn, J.M.; Michell, R.; Samara, M.; Sharber, J.R.; Winningham, J.D. Properties of suprathermal electrons associated with discrete auroral arcs. Geophys. Res. Lett. 2017, 44, 3475–3484. [Google Scholar] [CrossRef]
- Collier, M.R.; Hamilton, D.C. The relationship between kappa and temperature in energetic ion spectra at Jupiter. Geophys. Res. Lett. 1995, 22, 303–306. [Google Scholar] [CrossRef]
- Mauk, B.H.; Mitchell, D.G.; McEntire, R.W.; Paranicas, C.P.; Roelof, E.C.; Williams, D.J.; Krimigis, S.M.; Lagg, A. Energetic ion characteristics and neutral gas interactions in Jupiter’s magnetosphere. J. Geophys. Res. (Space Phys.) 2004, 109, A09S12. [Google Scholar] [CrossRef]
- Nicolaou, G.; McComas, D.J.; Bagenal, F.; Elliott, H.A. Properties of plasma ions in the distant Jovian magnetosheath using Solar Wind Around Pluto data on New Horizons. J. Geophys. Res. (Space Phys.) 2014, 119, 3463–3479. [Google Scholar] [CrossRef]
- Carbary, J.F.; Kane, M.; Mauk, B.H.; Krimigis, S.M. Using the kappa function to investigate hot plasma in the magnetospheres of the giant planets. J. Geophys. Res. (Space Phys.) 2014, 119, 8426–8447. [Google Scholar] [CrossRef]
- Livi, R.; Goldstein, J.; Burch, J.L.; Crary, F.; Rymer, A.M.; Mitchell, D.G.; Persoon, A.M. Multi-instrument analysis of plasma parameters in Saturn’s equatorial, inner magnetosphere using corrections for corrections for spacecraft potential and penetrating background radiation. J. Geophys. Res. (Space Phys.) 2014, 119, 3683–3707. [Google Scholar] [CrossRef]
- Dialynas, K.; Roussos, E.; Regoli, L.; Paranicas, C.P.; Krimigis, S.M.; Kane, M.; Mitchell, D.G.; Hamilton, D.C.; Krupp, N.; Carbary, J.F. Energetic Ion Moments and Polytropic Index in Saturn’s Magnetosphere using Cassini/MIMI Measurements: A Simple Model Based on κ-Distribution Functions. J. Geophys. Res. (Space Phys.) 2018, 123, 8066–8086. [Google Scholar] [CrossRef]
- Mauk, B.H.; Krimigis, S.M.; Keath, E.P.; Cheng, A.F.; Armstrong, T.P.; Lanzerotti, L.J.; Gloeckler, G.; Hamilton, D.C. The hot plasma and radiation environment of the Uranian magnetosphere. J. Geophys. Res. 1987, 92, 15283–15308. [Google Scholar] [CrossRef]
- Moncuquet, M.; Bagenal, F.; Meyer-Vernet, N. Latitudinal structure of outer Io plasma torus. J. Geophys. Res. (Space Phys.) 2002, 107, 1260. [Google Scholar] [CrossRef]
- Jurac, S.; McGrath, M.A.; Johnson, R.E.; Richardson, J.D.; Vasyliunas, V.M.; Eviatar, A. Saturn: Search for a missing water source. Geophys. Res. Lett. 2002, 29, 2172. [Google Scholar] [CrossRef]
- Broiles, T.W.; Livadiotis, G.; Burch, J.L.; Chae, K.; Clark, G.; Cravens, T.E.; Davidson, R.; Eriksson, A.; Frahm, R.A.; Fuselier, S.A.; et al. Characterizing cometary electrons with kappa distributions. J. Geophys. Res. (Space Phys.) 2016, 121, 7407–7422. [Google Scholar] [CrossRef]
- Myllys, M.; Henri, P.; Galand, M.; Heritier, K.L.; Gilet, N.; Goldstein, R.; Eriksson, A.I.; Johansson, F.; Deca, J. Plasma properties of suprathermal electrons near comet 67P/Churyumov-Gerasimenko with Rosetta. Astron. Astrophys. 2019, 630, A42. [Google Scholar] [CrossRef]
- Decker, R.B.; Krimigis, S.M.; Roelof, E.C.; Hill, M.E.; Armstrong, T.P.; Gloeckler, G.; Hamilton, D.C.; Lanzerotti, L.J. Voyager 1 in the Foreshock, Termination Shock, and Heliosheath. Science 2005, 309, 2020–2024. [Google Scholar] [CrossRef]
- Heerikhuisen, J.; Pogorelov, N.V.; Florinski, V.; Zank, G.P.; le Roux, J.A. The Effects of a κ-Distribution in the Heliosheath on the Global Heliosphere and ENA Flux at 1 AU. Astrophys. J. 2008, 682, 679–689. [Google Scholar] [CrossRef]
- Heerikhuisen, J.; Zirnstein, E.; Pogorelov, N. κ-distributed protons in the solar wind and their charge-exchange coupling to energetic hydrogen. J. Geophys. Res. (Space Phys.) 2015, 120, 1516–1525. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Exploring Transitions of Space Plasmas Out of Equilibrium. Astrophys. J. 2010, 714, 971–987. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Measure of the departure of the q-metastable stationary states from equilibrium. Phys. Scr. 2010, 82, 035003. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Invariant Kappa Distribution in Space Plasmas Out of Equilibrium. Astrophys. J. 2011, 741, 88. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. The Influence of Pick-up Ions on Space Plasma Distributions. Astrophys. J. 2011, 738, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Non-equilibrium Thermodynamic Processes: Space Plasmas and the Inner Heliosheath. Astrophys. J. 2012, 749, 11. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Transport Equation of Kappa Distributions in the Heliosphere. Astrophys. J. 2023, 954, 72. [Google Scholar] [CrossRef]
- McComas, D.J.; Allegrini, F.; Bochsler, P.; Bzowski, M.; Christian, E.R.; Crew, G.B.; DeMajistre, R.; Fahr, H.; Fichtner, H.; Frisch, P.C.; et al. Global Observations of the Interstellar Interaction from the Interstellar Boundary Explorer (IBEX). Science 2009, 326, 959. [Google Scholar] [CrossRef] [PubMed]
- Zank, G.P.; Heerikhuisen, J.; Pogorelov, N.V.; Burrows, R.; McComas, D. Microstructure of the Heliospheric Termination Shock: Implications for Energetic Neutral Atom Observations. Astrophys. J. 2010, 708, 1092–1106. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Dayeh, M.A.; Funsten, H.O.; Schwadron, N.A. First Sky Map of the Inner Heliosheath Temperature Using IBEX Spectra. Astrophys. J. 2011, 734, 1. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Randol, B.M.; Funsten, H.O.; Möbius, E.S.; Schwadron, N.A.; Dayeh, M.A.; Zank, G.P.; Frisch, P.C. Pick-up Ion Distributions and Their Influence on Energetic Neutral Atom Spectral Curvature. Astrophys. J. 2012, 751, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Schwadron, N.A.; Funsten, H.O.; Fuselier, S.A. Pressure of the Proton Plasma in the Inner Heliosheath. Astrophys. J. 2013, 762, 134. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Funsten, H.O.; Schwadron, N.A.; Szalay, J.R.; Zirnstein, E. Thermodynamics of the Inner Heliosheath. Astrophys. J. 2022, 262, 53. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Zirnstein, E.J. Temperature of the Polar Inner Heliosheath: Connection to Solar Activity. Astrophys. J. 2023, 951, 21. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Shrestha, B.L. Thermodynamics of Pickup Ions in the Heliosphere. Astrophys. J. 2024, 968, 66. [Google Scholar] [CrossRef]
- Fuselier, S.A.; Allegrini, F.; Bzowski, M.; Dayeh, M.A.; Desai, M.; Funsten, H.O.; Galli, A.; Heirtzler, D.; Janzen, P.; Kubiak, M.A.; et al. Low Energy Neutral Atoms from the Heliosheath. Astrophys. J. 2014, 784, 89. [Google Scholar] [CrossRef]
- Zank, G.P. Faltering Steps Into the Galaxy: The Boundary Regions of the Heliosphere. Annu. Rev. Astron. Astrophys. 2015, 53, 449–500. [Google Scholar] [CrossRef]
- Zirnstein, E.J.; McComas, D.J. Using Kappa Functions to Characterize Outer Heliosphere Proton Distributions in the Presence of Charge-exchange. Astrophys. J. 2015, 815, 31. [Google Scholar] [CrossRef]
- Livadiotis, G. Curie law for systems described by kappa distributions. EPL (Europhys. Lett.) 2016, 113, 10003. [Google Scholar] [CrossRef]
- Swaczyna, P.; McComas, D.J.; Schwadron, N.A. Non-equilibrium Distributions of Interstellar Neutrals and the Temperature of the Local Interstellar Medium. Astrophys. J. 2019, 871, 254. [Google Scholar] [CrossRef]
- Nicholls, D.C.; Dopita, M.A.; Sutherland, R.S. Resolving the Electron Temperature Discrepancies in H II Regions and Planetary Nebulae: κ-distributed Electrons. Astrophys. J. 2012, 752, 148. [Google Scholar] [CrossRef]
- Nicholls, D.C.; Dopita, M.A.; Sutherland, R.S.; Kewley, L.J.; Palay, E. Measuring Nebular Temperatures: The Effect of New Collision Strengths with Equilibrium and κ-distributed Electron Energies. Astrophys. J. 2013, 207, 21. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.W.; Zhang, B. H I Free-Bound Emission of Planetary Nebulae with Large Abundance Discrepancies: Two-component Models versus κ-distributed Electrons. Astrophys. J. 2014, 780, 93. [Google Scholar] [CrossRef]
- Lin, B.Z.; Zhang, Y. Can the Kappa-distributed Electron Energies Account for the Intensity Ratios of O II Lines in Photoionized Gaseous Nebulae? Astrophys. J. 2020, 899, 33. [Google Scholar] [CrossRef]
- Yao, Z.W.; Zhang, Y. The Ultraviolet C II Lines as a Diagnostic of κ-distributed Electrons in Planetary Nebulae. Astrophys. J. 2022, 936, 143. [Google Scholar] [CrossRef]
- Humphrey, A.; Villar-Martín, M.; Binette, L.; Raj, R. Photoionization models for extreme Lyα λ1216 and Hell λ1640 line ratios in quasar halos, and PopIII vs. AGN diagnostics. Astron. Astrophys. 2019, 621, A10. [Google Scholar] [CrossRef]
- Morais, S.G.; Humphrey, A.; Villar Martín, M.; Binette, L.; Silva, M. Electron energy distributions in the extended gas nebulae associated with high-z AGN: Maxwell-Boltzmann versus κ distributions. Mon. Not. R. Astron. Soc. 2021, 506, 1389–1405. [Google Scholar] [CrossRef]
- Davelaar, J.; Olivares, H.; Porth, O.; Bronzwaer, T.; Janssen, M.; Roelofs, F.; Mizuno, Y.; Fromm, C.M.; Falcke, H.; Rezzolla, L. Modeling non-thermal emission from the jet-launching region of M 87 with adaptive mesh refinement. Astron. Astrophys. 2019, 632, A2. [Google Scholar] [CrossRef]
- Raymond, J.C.; Winkler, P.F.; Blair, W.P.; Lee, J.J.; Park, S. Non-Maxwellian Hα Profiles in Tycho’s Supernova Remnant. Astrophys. J. 2010, 712, 901–907. [Google Scholar] [CrossRef]
- Hou, S.Q.; He, J.J.; Parikh, A.; Kahl, D.; Bertulani, C.A.; Kajino, T.; Mathews, G.J.; Zhao, G. Non-extensive Statistics to the Cosmological Lithium Problem. Astrophys. J. 2017, 834, 165. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Black-body radiation in space plasmas. EPL (Europhys. Lett.) 2021, 135, 49001. [Google Scholar] [CrossRef]
- McComas, D.; Allegrini, F.; Bagenal, F.; Casey, P.; Delamere, P.; Demkee, D.; Dunn, G.; Elliott, H.; Hanley, J.; Johnson, K.; et al. The Solar Wind Around Pluto (SWAP) Instrument Aboard New Horizons. Space Sci. Rev. 2008, 140, 261–313. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Livadiotis, G.; McComas, D.J.; Alimaganbetov, M.; Schwadron, N.A.; Fairchild, K. Persistent Behavior in Energetic Neutral Atom Time Series from IBEX. Astrophys. J. 2024, 976, 45. [Google Scholar] [CrossRef]
- McComas, D.J.; Christian, E.R.; Schwadron, N.A.; Fox, N.; Westlake, J.; Allegrini, F.; Baker, D.N.; Biesecker, D.; Bzowski, M.; Clark, G.; et al. Interstellar Mapping and Acceleration Probe (IMAP): A New NASA Mission. Space Sci. Rev. 2018, 214, 116. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Entropy defect in thermodynamics. Sci. Rep. 2023, 13, 9033. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa and q Indices: Dependence on the Degrees of Freedom. Entropy 2015, 17, 2062–2081. [Google Scholar] [CrossRef]
- Livadiotis, G.; Nicolaou, G.; Allegrini, F. Anisotropic Kappa Distributions. I. Formulation Based on Particle Correlations. Astrophys. J. 2021, 253, 16. [Google Scholar] [CrossRef]
- Livadiotis, G. Thermodynamic origin of kappa distributions. EPL (Europhys. Lett.) 2018, 122, 50001. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Entropy defect: Algebra and thermodynamics. EPL (Europhys. Lett.) 2023, 144, 21001. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Enciso, A.; Tempesta, P. Uniqueness and characterization theorems for generalized entropies. J. Stat. Mech. Theory Exp. 2017, 12, 123101. [Google Scholar] [CrossRef]
- Deppman, A.; Khalili Golmankhaneh, A.; Megías, E.; Pasechnik, R. From the Boltzmann equation with non-local correlations to a standard non-linear Fokker-Planck equation. Phys. Lett. B 2023, 839, 137752. [Google Scholar] [CrossRef]
- Abe, S. Correlation induced by Tsallis’ nonextensivity. Phys. A Stat. Mech. Its Appl. 1999, 269, 403–409. [Google Scholar] [CrossRef]
- Asgarani, S.; Mirza, B. Quasi-additivity of Tsallis entropies and correlated subsystems. Phys. A Stat. Mech. Its Appl. 2007, 379, 513–522. [Google Scholar] [CrossRef]
- Livadiotis, G. On the Origin of Polytropic Behavior in Space and Astrophysical Plasmas. Astrophys. J. 2019, 874, 10. [Google Scholar] [CrossRef]
- Nelson, K.P.; Umarov, S.R.; Kon, M.A. On the average uncertainty for systems with nonlinear coupling. Phys. A Stat. Mech. Its Appl. 2017, 468, 30–43. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Connection between Polytropic Index and Heating. Astrophys. J. 2023, 956, 88. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Extensive entropy: The case of zero entropy defect. Phys. Scr. 2023, 98, 105605. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Universality of kappa distributions. EPL (Europhys. Lett.) 2024, 146, 41003. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. The theory of thermodynamic relativity. Sci. Rep. 2024, 14, 22641. [Google Scholar] [CrossRef]
- Abe, S. General pseudoadditivity of composable entropy prescribed by the existence of equilibrium. Phys. Rev. E 2001, 63, 061105. [Google Scholar] [CrossRef] [PubMed]
- Ourabah, K. Superstatistics from a dynamical perspective: Entropy and relaxation. Phys. Rev. E 2024, 109, 014127. [Google Scholar] [CrossRef]
- Borges, E.P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Phys. A Stat. Mech. Its Appl. 2004, 340, 95–101. [Google Scholar] [CrossRef]
- Adhikari, L.; Zank, G.P.; Zhao, L.L.; Webb, G.M. Evolution of Entropy and Mediation of the Solar Wind by Turbulence. Astrophys. J. 2020, 891, 34. [Google Scholar] [CrossRef]
- Sackur, O. Die Anwendung der kinetischen Theorie der Gase auf chemische Probleme. Ann. Der Phys. 1911, 341, 958–980. [Google Scholar] [CrossRef]
- Tetrode, H. Die chemische Konstante der Gase und das elementare Wirkungsquantum. Ann. Der Phys. 1912, 343, 434–442. [Google Scholar] [CrossRef]
- Baierlein, R. Thermal Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Büyükkiliç, F.; Demirhan, D.; Tirnakli, U. Generalization of the mean-field Ising model within Tsallis thermostatistics. Phys. A Stat. Mech. Its Appl. 1997, 238, 285–294. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A Stat. Mech. Its Appl. 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Schwadron, N.A.; Dayeh, M.A.; Desai, M.; Fahr, H.; Jokipii, J.R.; Lee, M.A. Superposition of Stochastic Processes and the Resulting Particle Distributions. Astrophys. J. 2010, 713, 1386–1392. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S.; Gell-Mann, M. Generalized entropies and the transformation group of superstatistics. Proc. Natl. Acad. Sci. USA 2011, 108, 6390–6394. [Google Scholar] [CrossRef]
- Livadiotis, G.; Assas, L.; Dennis, B.; Elaydi, S.; Kwessi, E. Kappa Function as a Unifying Framework for Discrete Population Modeling. Nat. Resour. Model. 2016, 29, 130–144. [Google Scholar] [CrossRef]
- Livadiotis, G. Rankine-Hugoniot Shock Conditions for Space and Astrophysical Plasmas Described by Kappa Distributions. Astrophys. J. 2019, 886, 3. [Google Scholar] [CrossRef]
- Gravanis, E.; Akylas, E.; Livadiotis, G. Physical meaning of temperature in superstatistics. EPL (Europhys. Lett.) 2020, 130, 30005. [Google Scholar] [CrossRef]
- Sánchez, E.; González-Navarrete, M.; Caamaño-Carrillo, C. Bivariate superstatistics: An application to statistical plasma physics. Eur. Phys. J. B 2021, 94, 55. [Google Scholar] [CrossRef]
- Zank, G.P.; Li, G.; Florinski, V.; Hu, Q.; Lario, D.; Smith, C.W. Particle acceleration at perpendicular shock waves: Model and observations. J. Geophys. Res. (Space Phys.) 2006, 111, A06108. [Google Scholar] [CrossRef]
- Fisk, L.A.; Gloeckler, G. The case for a common spectrum of particles accelerated in the heliosphere: Observations and theory. J. Geophys. Res. (Space Phys.) 2014, 119, 8733–8749. [Google Scholar] [CrossRef]
- Randol, B.M.; Christian, E.R. Simulations of plasma obeying Coulomb’s law and the formation of suprathermal ion tails in the solar wind. J. Geophys. Res. (Space Phys.) 2014, 119, 7025–7037. [Google Scholar] [CrossRef]
- Sadeghzadeh, S.; Yang, J.; Toffoletto, F.; Wolf, R.; Mousavi, A.; Espinoza, C.M. RCM Modeling of Bubble Injections Into the Inner Magnetosphere: Spectral Properties of Plasma Sheet Particles. J. Geophys. Res. (Space Phys.) 2023, 128, e2022JA030673. [Google Scholar] [CrossRef]
- Zenitani, S.; Nakano, S. Loading Loss-Cone Distributions in Particle Simulations. J. Geophys. Res. (Space Phys.) 2023, 128, e2023JA031983. [Google Scholar] [CrossRef]
- Peterson, J.; Dixit, P.D.; Dill, K.A. A maximum entropy framework for nonexponential distributions. Proc. Natl. Acad. Sci. USA 2013, 110, 20380–20385. [Google Scholar] [CrossRef]
- Meyer-Vernet, N.; Moncuquet, M.; Hoang, S. Temperature inversion in the Io plasma torus. Icarus 1995, 116, 202–213. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G. Long-term Correlations of Polytropic Indices with Kappa Distributions in Solar Wind Plasma near 1 au. Astrophys. J. 2019, 884, 52. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G.; Wicks, R.T.; Verscharen, D.; Maruca, B.A. Polytropic Behavior of Solar Wind Protons Observed by Parker Solar Probe. Astrophys. J. 2020, 901, 26. [Google Scholar] [CrossRef]
- Katsavrias, C.; Nicolaou, G.; Di Matteo, S.; Kepko, L.; Viall, N.M.; Aminalragia-Giamini, S.; Livadiotis, G. Proton polytropic behavior of periodic density structures in the solar wind. Astron. Astrophys. 2024, 686, L10. [Google Scholar] [CrossRef]
- Livadiotis, G.; Desai, M.I.; Wilson, L.B., III. Generation of Kappa Distributions in Solar Wind at 1 au. Astrophys. J. 2018, 853, 142. [Google Scholar] [CrossRef]
- Milovanov, A.V.; Rasmussen, J.J.; Dif-Pradalier, G. Self-consistent model of the plasma staircase and nonlinear Schrödinger equation with subquadratic power nonlinearity. Phys. Rev. E 2021, 103, 052218. [Google Scholar] [CrossRef]

| 1. Inner Heliosphere | |
|---|---|
| solar corona | e.g., [20,21,22] |
| solar energetic particles | e.g., [23,24,25,26,27,28,29] |
| solar flares | e.g., [30,31,32,33] |
| solar radio emission | e.g., [34,35,36] |
| solar spectra | e.g., [37,38,39] |
| solar wind | e.g., [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54] |
| corotating interaction regions | e.g., [55] |
| 2. Planetary Magnetospheres | |
| magnetosheath | e.g., [56,57] |
| magnetopause | e.g., [58] |
| magnetotail | e.g., [59] |
| ring current | e.g., [60] |
| plasma sheet | e.g., [61,62,63] |
| magnetospheric substorms | e.g., [64] |
| aurorae | e.g., [65] |
| magnetospheres of giant planets, such as: | |
| - Jovian | e.g., [66,67,68] |
| - Saturnian | e.g., [69,70,71] |
| - Uranian | e.g., [72] |
| magnetospheres of planetary moons, such as: | |
| - Io | e.g., [73] |
| - Enceladus | e.g., [74] |
| cometary magnetospheres | e.g., [75,76] |
| 3. Outer Heliosphere and Astrophysical Plasmas | |
| inner heliosheath | e.g., [77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98] |
| H-II regions | e.g., [99] |
| planetary nebulae | e.g., [100,101,102,103] |
| active galactic nuclei | e.g., [104,105] |
| galactic jets | e.g., [106] |
| supernovae | e.g., [107] |
| cosmological scale phenomena | e.g., [108,109] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McComas, D.J.; Livadiotis, G.; Sarlis, N.V. Correlations and Kappa Distributions: Numerical Experiment and Physical Understanding. Entropy 2025, 27, 375. https://doi.org/10.3390/e27040375
McComas DJ, Livadiotis G, Sarlis NV. Correlations and Kappa Distributions: Numerical Experiment and Physical Understanding. Entropy. 2025; 27(4):375. https://doi.org/10.3390/e27040375
Chicago/Turabian StyleMcComas, David J., George Livadiotis, and Nicholas V. Sarlis. 2025. "Correlations and Kappa Distributions: Numerical Experiment and Physical Understanding" Entropy 27, no. 4: 375. https://doi.org/10.3390/e27040375
APA StyleMcComas, D. J., Livadiotis, G., & Sarlis, N. V. (2025). Correlations and Kappa Distributions: Numerical Experiment and Physical Understanding. Entropy, 27(4), 375. https://doi.org/10.3390/e27040375







