Stochastic Entropy Production for Classical and Quantum Dynamical Systems with Restricted Diffusion
Abstract
1. Introduction
2. Stochastic Entropy Production for Itô Processes
3. Defining Dynamical and Spectator Variables
3.1. Preliminaries
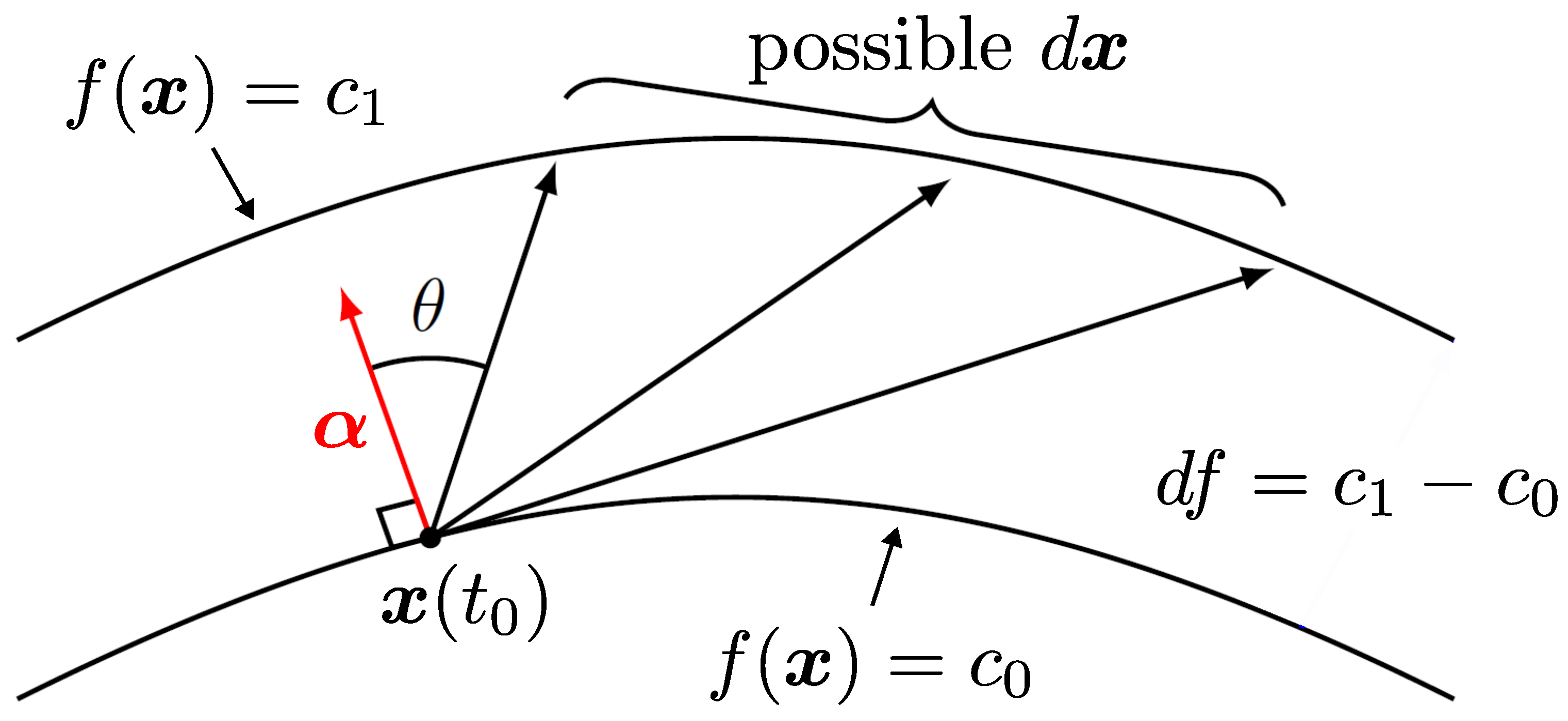
3.2. Identifying Constants of Motion
3.3. Identifying Deterministically Evolving Functions
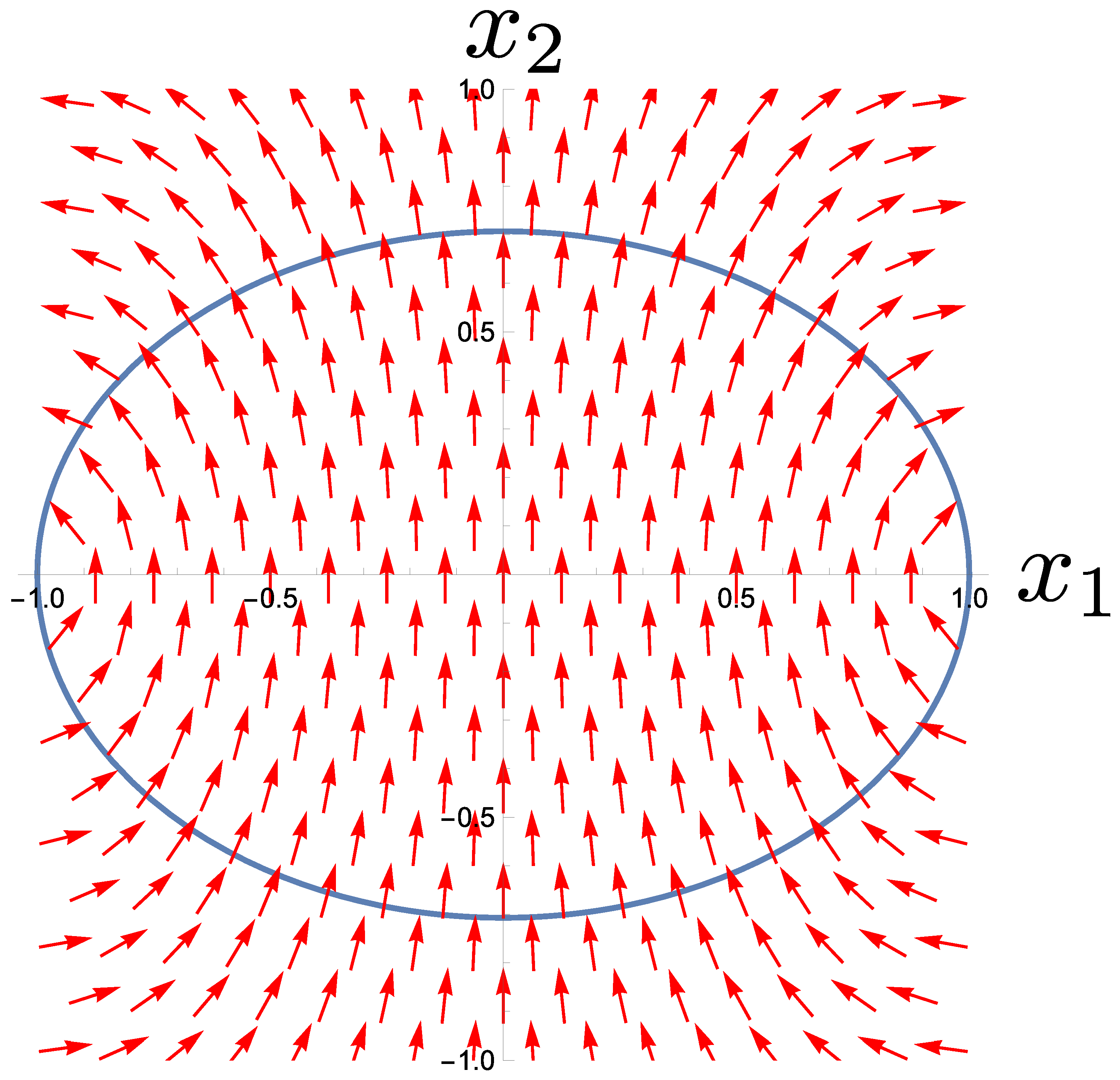
4. Example of Restricted Diffusive Evolution
5. An Open Three-Level Quantum System with Restricted Diffusion
5.1. SDEs and Selection of Spectator Variables
5.2. Equilibrium and Nonequilibrium Stationary States
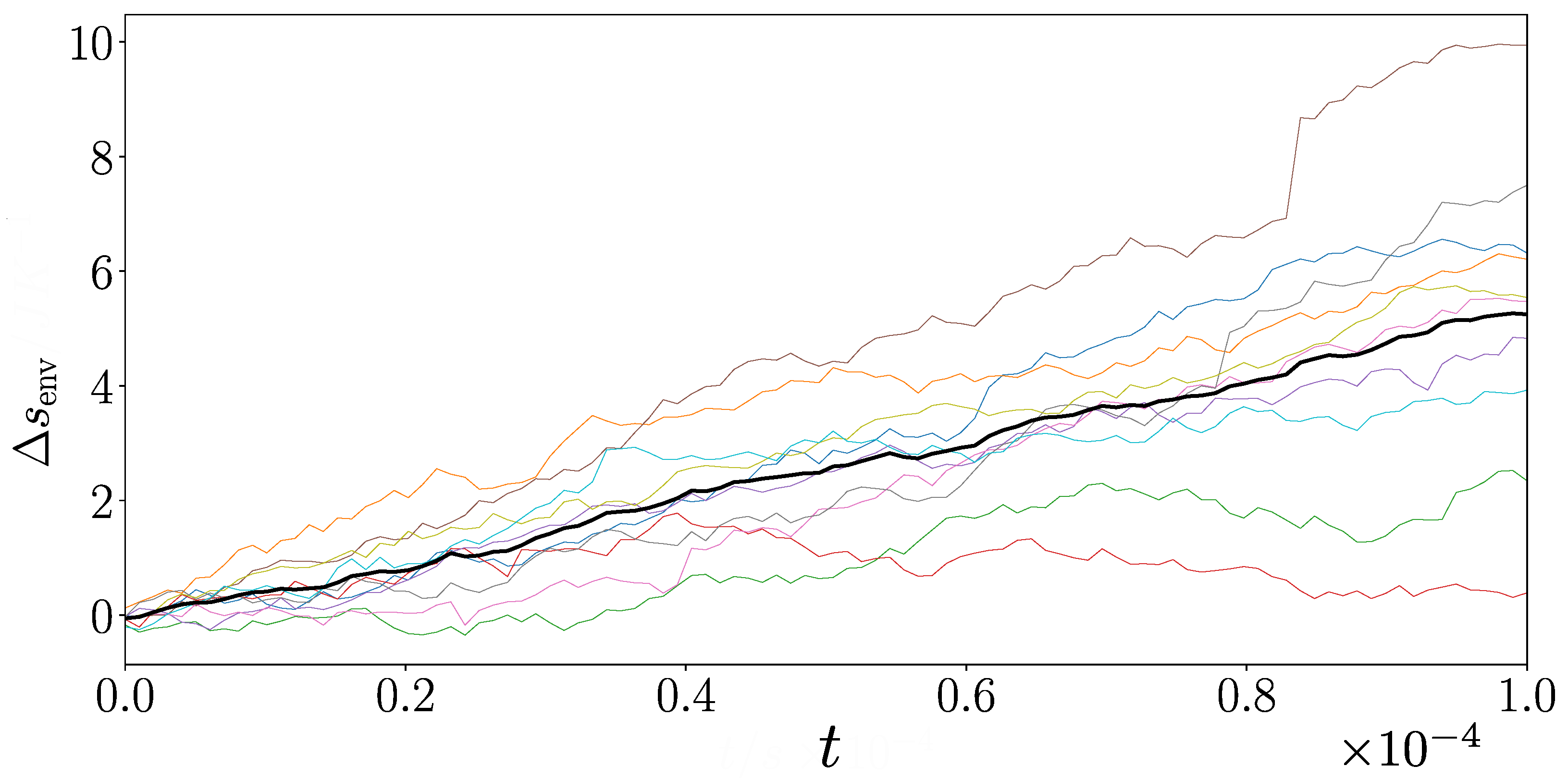
5.3. Stochastic Entropy Production in Quantum Mechanics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. General Expression for Environmental Stochastic Entropy Production
Appendix B. SDEs for Quantum State Diffusion
Appendix C. SDEs for the Three-Level System
References
- Ford, I.J. Statistical Physics: An Entropic Approach; Wiley: Chichester, UK, 2013. [Google Scholar]
- Seifert, U. Entropy Production along a Stochastic Trajectory and an Integral Fluctuation Theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Stochastic thermodynamics: Principles and perspectives. Eur. Phys. J. B 2008, 64, 423–431. [Google Scholar]
- Peliti, L.; Pigolotti, S. Stochastic Thermodynamics: An Introduction; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Spinney, R.E.; Ford, I.J. Entropy production in full phase space for continuous stochastic dynamics. Phys. Rev. E 2012, 85, 051113. [Google Scholar]
- Clarke, C.L.; Ford, I.J. Stochastic entropy production associated with quantum measurement in a framework of Markovian quantum state diffusion. Entropy 2024, 26, 1024. [Google Scholar] [CrossRef] [PubMed]
- Matos, D.; Kantorovich, L.; Ford, I.J. Stochastic Entropy Production for Continuous Measurements of an Open Quantum System. J. Phys. Commun. 2022, 6, 125003. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Spohn, H. A Gallavotti–Cohen-type symmetry in the large deviation functional for stochastic dynamics. J. Stat. Phys. 1999, 95, 333–365. [Google Scholar] [CrossRef]
- Gardiner, C. Handbook of Stochastic Methods; Springer: Berlin/Heidelberg, Germany, 2009; Volume 4. [Google Scholar]
- Gisin, N.; Percival, I.C. The quantum-state diffusion model applied to open systems. J. Phys. Math. Gen. 1992, 25, 5677. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Weiss, U. Quantum Dissipative Systems, 4th ed.; World Scientific: Singapore, 1999; Volume 10. [Google Scholar]
- Jacobs, K. Quantum Measurement Theory and its Applications; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Walls, S.M.; Schachter, J.M.; Qian, H.; Ford, I.J. Stochastic quantum trajectories demonstrate the Quantum Zeno Effect in open spin 1/2, spin 1 and spin 3/2 systems. J. Phys. A Math. Theor. 2024, 57, 175301. [Google Scholar] [CrossRef]
- Walls, S.M.; Ford, I.J. Memory effects in a sequence of measurements of non-commuting observables. Phys. Rev. A. 2024, 110, 032432. [Google Scholar]
- Percival, I. Quantum State Diffusion; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Esposito, M.; Mukamel, S. Fluctuation theorems for quantum master equations. Phys. Rev. E 2006, 73, 046129. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E. Quantum operation time reversal. Phys. Rev. A 2008, 77, 034101. [Google Scholar] [CrossRef]
- Elouard, C.; Herrera-Martí, D.A.; Clusel, M.; Auffèves, A. The role of quantum measurement in stochastic thermodynamics. NPJ Quantum Inf. 2017, 3, 9. [Google Scholar] [CrossRef]
- Monsel, J.; Elouard, C.; Auffèves, A. An autonomous quantum machine to measure the thermodynamic arrow of time. NPJ Quantum Inf. 2018, 4, 59. [Google Scholar]
- Manikandan, S.K.; Elouard, C.; Jordan, A.N. Fluctuation theorems for continuous quantum measurements and absolute irreversibility. Phys. Rev. A 2019, 99, 022117. [Google Scholar] [CrossRef]
- Cercignani, C. Ludwig Boltzmann: The Man Who Trusted Atoms; Oxford University Press: Oxford, UK, 1998. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dexter, J.; Ford, I.J. Stochastic Entropy Production for Classical and Quantum Dynamical Systems with Restricted Diffusion. Entropy 2025, 27, 383. https://doi.org/10.3390/e27040383
Dexter J, Ford IJ. Stochastic Entropy Production for Classical and Quantum Dynamical Systems with Restricted Diffusion. Entropy. 2025; 27(4):383. https://doi.org/10.3390/e27040383
Chicago/Turabian StyleDexter, Jonathan, and Ian J. Ford. 2025. "Stochastic Entropy Production for Classical and Quantum Dynamical Systems with Restricted Diffusion" Entropy 27, no. 4: 383. https://doi.org/10.3390/e27040383
APA StyleDexter, J., & Ford, I. J. (2025). Stochastic Entropy Production for Classical and Quantum Dynamical Systems with Restricted Diffusion. Entropy, 27(4), 383. https://doi.org/10.3390/e27040383




