An Informational–Entropic Approach to Exoplanet Characterization
Abstract
:1. Introduction
2. Information Measure
3. Data
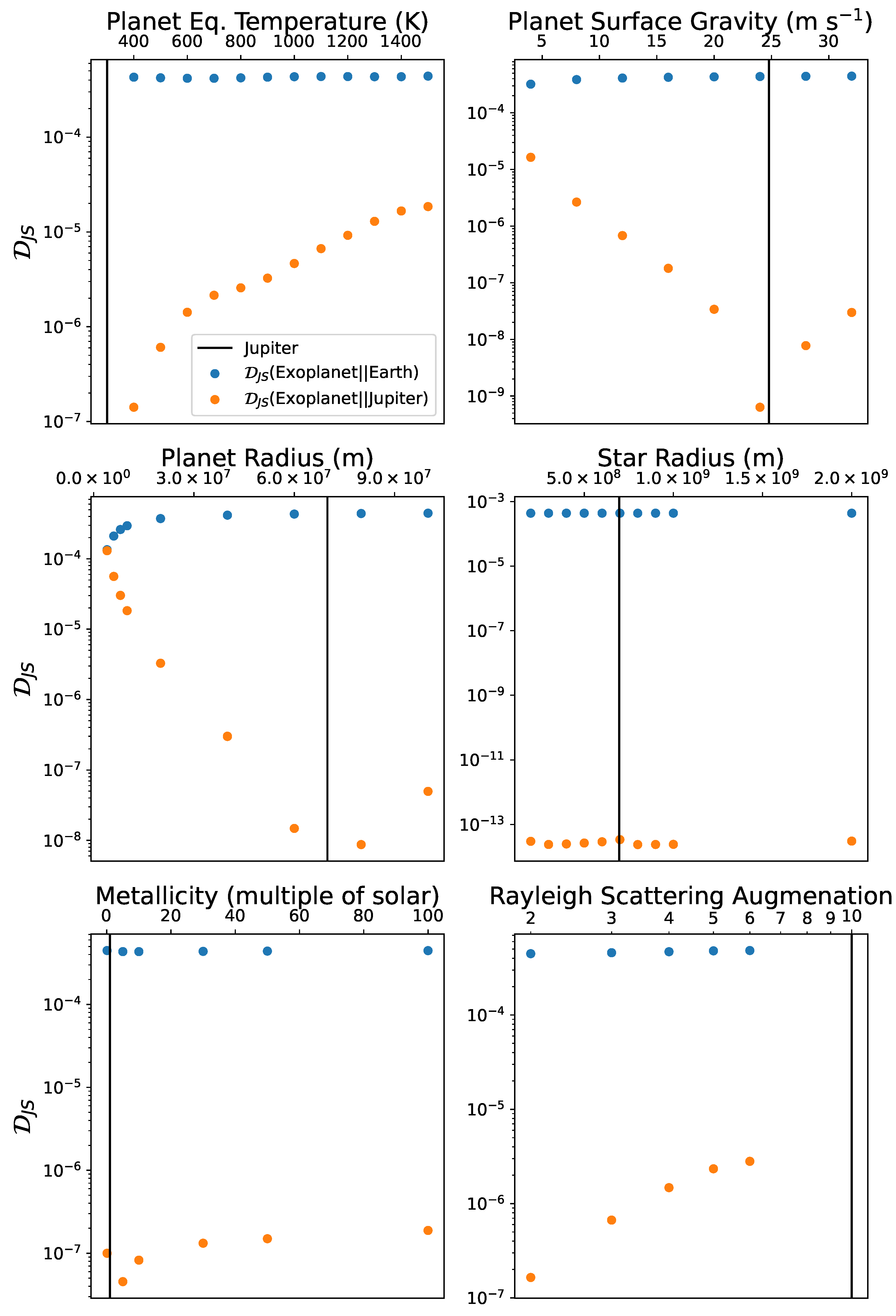
4. Results 1: Comparing Spectra by Changing Physical Parameters
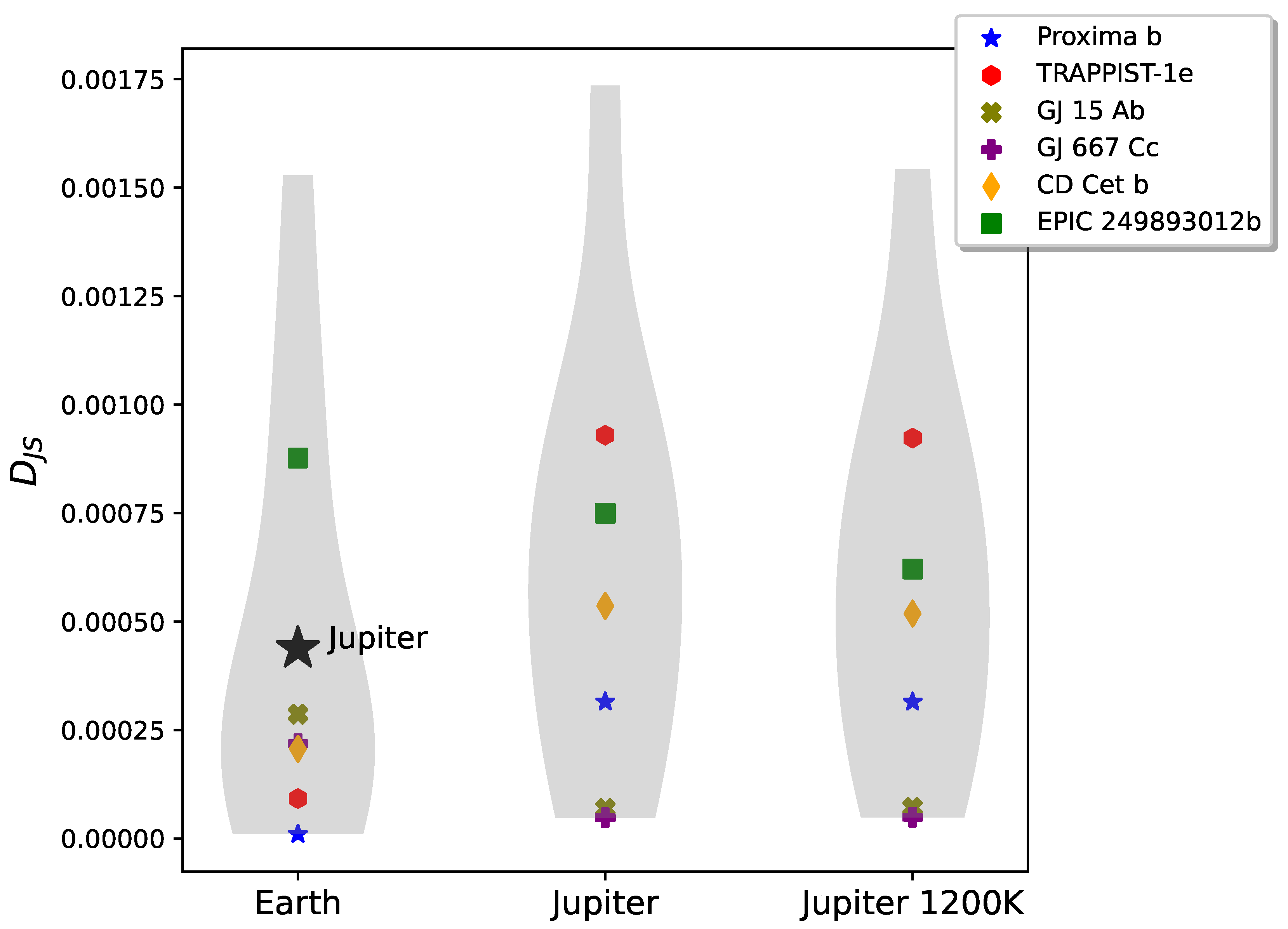
5. Results 2: Differentiating Between Exoplanet Types with the Information Metric
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Jensen–Shannon Divergence | |
| Kullback–Liebler Divergence | |
| HWO | Habitable Worlds Observatory |
| ESI | Earth Similarity Index |
Appendix A. Noise Dependence of Jensen–Shannon Divergence
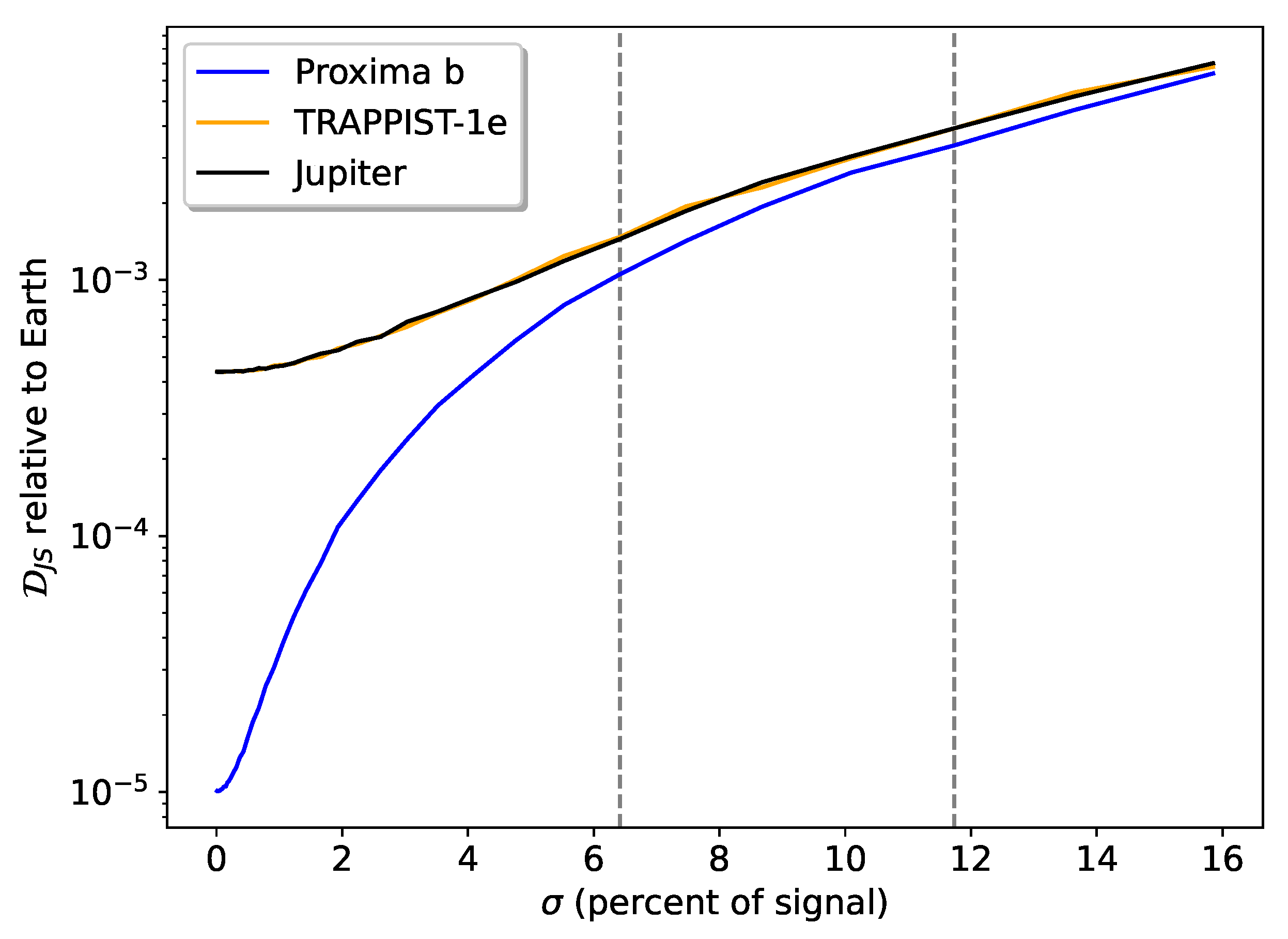
Appendix B. Simulated Spectra

References
- Tinetti, G.; Drossart, P.; Eccleston, P.; Hartogh, P.; Heske, A.; Leconte, J.; Micela, G.; Ollivier, M.; Pilbratt, G.; Puig, L.; et al. A chemical survey of exoplanets with ARIEL. Exp. Astron. 2018, 46, 135–209. [Google Scholar] [CrossRef]
- Quanz, S.P.; Ottiger, M.; Fontanet, E.; Kammerer, J.; Menti, F.; Dannert, F.; Gheorghe, A.; Absil, O.; Airapetian, V.S.; Alei, E.; et al. Large Interferometer For Exoplanets (LIFE)—I. Improved exoplanet detection yield estimates for a large mid-infrared space-interferometer mission. Astron. Astrophys. 2022, 664, A21. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Pathways to Discovery in Astronomy and Astrophysics for the 2020s; The National Academies Press: Washington, DC, USA, 2023. [Google Scholar] [CrossRef]
- Harada, C.K.; Dressing, C.D.; Kane, S.R.; Ardestani, B.A. Setting the Stage for the Search for Life with the Habitable Worlds Observatory: Properties of 164 Promising Planet-survey Targets. Astrophys. J. Suppl. Ser. 2024, 272, 30. [Google Scholar] [CrossRef]
- Ge, J.; Zhang, H.; Zang, W.; Deng, H.; Mao, S.; Xie, J.W.; Liu, H.G.; Zhou, J.L.; Willis, K.; Huang, C.; et al. ET White Paper: To Find the First Earth 2.0. arXiv 2022, arXiv:2206.06693. [Google Scholar] [CrossRef]
- Ramsay, S.; Amico, P.; Bezawada, N.; Cirasuolo, M.; Derie, F.; Egner, S.; George, E.; Gonté, F.; Herrera, J.C.G.; Hammersley, P.; et al. The ESO extremely large telescope instrumentation programme. In Proceedings of the Advances in Optical Astronomical Instrumentation 2019, Melbourne, Australia, 8–12 December 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11203, p. 1120303. [Google Scholar] [CrossRef]
- Rustamkulov, Z.; Sing, D.K.; Mukherjee, S.; May, E.M.; Kirk, J.; Schlawin, E.; Line, M.R.; Piaulet, C.; Carter, A.L.; Batalha, N.E.; et al. Early Release Science of the exoplanet WASP-39b with JWST NIRSpec PRISM. Nature 2023, 614, 659–663. [Google Scholar] [CrossRef]
- Ahrer, E.M.; Stevenson, K.B.; Mansfield, M.; Moran, S.E.; Brande, J.; Morello, G.; Murray, C.A.; Nikolov, N.K.; Petit Dit de la Roche, D.J.; Schlawin, E.; et al. Early Release Science of the exoplanet WASP-39b with JWST NIRCam. Nature 2023, 614, 653–658. [Google Scholar] [CrossRef]
- Alderson, L.; Wakeford, H.R.; Alam, M.K.; Batalha, N.E.; Lothringer, J.D.; Adams Redai, J.; Barat, S.; Brande, J.; Damiano, M.; Daylan, T.; et al. Early Release Science of the exoplanet WASP-39b with JWST NIRSpec G395H. Nature 2023, 614, 664–669. [Google Scholar] [CrossRef]
- Feinstein, A.D.; Radica, M.; Welbanks, L.; Murray, C.A.; Ohno, K.; Coulombe, L.P.; Espinoza, N.; Bean, J.L.; Teske, J.K.; Benneke, B.; et al. Early Release Science of the exoplanet WASP-39b with JWST NIRISS. Nature 2023, 614, 670–675. [Google Scholar] [CrossRef]
- Pontoppidan, K.M.; Barrientes, J.; Blome, C.; Braun, H.; Brown, M.; Carruthers, M.; Coe, D.; DePasquale, J.; Espinoza, N.; Marin, M.G.; et al. The JWST Early Release Observations. Astrophys. J. Lett. 2022, 936, L14. [Google Scholar] [CrossRef]
- Madhusudhan, N.; Nixon, M.C.; Welbanks, L.; Piette, A.A.A.; Booth, R.A. The Interior and Atmosphere of the Habitable-zone Exoplanet K2-18b. Astrophys. J. Lett. 2020, 891, L7. [Google Scholar] [CrossRef]
- Schulze-Makuch, D.; Méndez, A.; Fairén, A.G.; von Paris, P.; Turse, C.; Boyer, G.; Davila, A.F.; António, M.R.d.S.; Catling, D.; Irwin, L.N. A Two-Tiered Approach to Assessing the Habitability of Exoplanets. Astrobiology 2011, 11, 1041–1052. [Google Scholar] [CrossRef] [PubMed]
- Kashyap Jagadeesh, M.; Gudennavar, S.B.; Doshi, U.; Safonova, M. Indexing of exoplanets in search for potential habitability: Application to Mars-like worlds. Astrophys. Space Sci. 2017, 362, 146. [Google Scholar] [CrossRef]
- Jagadeesh, M.K. Earth Similarity Index and Habitability Studies of Exoplanets. arXiv 2018, arXiv:1801.07101. [Google Scholar] [CrossRef]
- Basak, S.; Saha, S.; Mathur, A.; Bora, K.; Makhija, S.; Safonova, M.; Agrawal, S. CEESA meets machine learning: A Constant Elasticity Earth Similarity Approach to habitability and classification of exoplanets. Astron. Comput. 2020, 30, 100335. [Google Scholar] [CrossRef]
- Bora, K.; Saha, S.; Agrawal, S.; Safonova, M.; Routh, S.; Narasimhamurthy, A. CD-HPF: New habitability score via data analytic modeling. Astron. Comput. 2016, 17, 129–143. [Google Scholar] [CrossRef]
- Irwin, L.N.; Méndez, A.; Fairén, A.G.; Schulze-Makuch, D. Assessing the Possibility of Biological Complexity on Other Worlds, with an Estimate of the Occurrence of Complex Life in the Milky Way Galaxy. Challenges 2014, 5, 159–174. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhatia, K.; Saha, S.; Safonova, M.; Sarkar, S. Postulating exoplanetary habitability via a novel anomaly detection method. Mon. Not. R. Astron. Soc. 2021, 510, 6022–6032. [Google Scholar] [CrossRef]
- Saha, S.; Basak, S.; Safonova, M.; Bora, K.; Agrawal, S.; Sarkar, P.; Murthy, J. Theoretical validation of potential habitability via analytical and boosted tree methods: An optimistic study on recently discovered exoplanets. Astron. Comput. 2018, 23, 141. [Google Scholar] [CrossRef]
- Seager, S. The future of spectroscopic life detection on exoplanets. Proc. Natl. Acad. Sci. USA 2014, 111, 12634–12640. [Google Scholar] [CrossRef]
- Seager, S. Exoplanet habitability. Science 2013, 340, 577–581. [Google Scholar] [CrossRef]
- Schwieterman, E.W.; Kiang, N.Y.; Parenteau, M.N.; Harman, C.E.; DasSarma, S.; Fisher, T.M.; Arney, G.N.; Hartnett, H.E.; Reinhard, C.T.; Olson, S.L.; et al. Exoplanet biosignatures: A review of remotely detectable signs of life. Astrobiology 2018, 18, 663–708. [Google Scholar] [CrossRef] [PubMed]
- Seager, S.; Turner, E.; Schafer, J.; Ford, E. Vegetation’s Red Edge: A Possible Spectroscopic Biosignature of Extraterrestrial Plants. Astrobiology 2005, 5, 372–390. [Google Scholar] [CrossRef] [PubMed]
- O’Malley-James, J.T.; Kaltenegger, L. The Vegetation Red Edge Biosignature Through Time on Earth and Exoplanets. Astrobiology 2018, 18, 1123–1136. [Google Scholar] [CrossRef] [PubMed]
- Sagan, C.; Thompson, W.R.; Carlson, R.; Gurnett, D.; Hord, C. A search for life on Earth from the Galileo spacecraft. Nature 1993, 365, 715–721. [Google Scholar] [CrossRef]
- Thompson, M.A.; Krissansen-Totton, J.; Wogan, N.; Telus, M.; Fortney, J.J. The case and context for atmospheric methane as an exoplanet biosignature. Proc. Natl. Acad. Sci. USA 2022, 119, e2117933119. [Google Scholar] [CrossRef]
- Tinetti, G.; Eccleston, P.; Haswell, C.; Lagage, P.O.; Leconte, J.; Lüftinger, T.; Micela, G.; Min, M.; Pilbratt, G.; Puig, L.; et al. Ariel: Enabling planetary science across light-years. arXiv 2021, arXiv:2104.04824. [Google Scholar] [CrossRef]
- Udry, S.; Lovis, C.; Bouchy, F.; Cameron, A.C.; Henning, T.; Mayor, M.; Pepe, F.; Piskunov, N.; Pollacco, D.; Queloz, D.; et al. Exoplanet science with the European Extremely Large Telescope. The case for visible and near-IR spectroscopy at high resolution. arXiv 2014, arXiv:1412.1048. [Google Scholar] [CrossRef]
- Wang, J.; Mawet, D.; Hu, R.; Ruane, G.; Delorme, J.R.; Klimovich, N. Baseline requirements for detecting biosignatures with the HabEx and LUVOIR mission concepts. J. Astron. Telesc. Instrum. Syst. 2018, 4, 035001. [Google Scholar] [CrossRef]
- Vannah, S.; Gleiser, M.; Kaltenegger, L. An information theory approach to identifying signs of life on transiting planets. Mon. Not. R. Astron. Soc. Lett. 2023, 528, L4–L9. [Google Scholar] [CrossRef]
- Gleiser, M.; Stamatopoulos, N. Entropic Measure for Localized Energy Configurations: Kinks, Bounces, and Bubbles. Phys. Lett. B 2012, 713, 304–307. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Gleiser, M.; Stamatopoulos, N. Information content of spontaneous symmetry breaking. Phys. Rev. D 2012, 86, 045004. [Google Scholar] [CrossRef]
- Kempton, E.M.R.; Lupu, R.; Owusu-Asare, A.; Slough, P.; Cale, B. Exo-Transmit: An Open-Source Code for Calculating Transmission Spectra for Exoplanet Atmospheres of Varied Composition. Publ. Astron. Soc. Pac. 2017, 129, 044402. [Google Scholar] [CrossRef]
- Lustig-Yaeger, J.; Meadows, V.S.; Crisp, D.; Line, M.R.; Robinson, T.D. Earth as a Transiting Exoplanet: A Validation of Transmission Spectroscopy and Atmospheric Retrieval Methodologies for Terrestrial Exoplanets. Planet. Sci. J. 2023, 4, 170. [Google Scholar] [CrossRef]
- Macdonald, E.J.R.; Cowan, N.B. An empirical infrared transit spectrum of Earth: Opacity windows and biosignatures. Mon. Not. R. Astron. Soc. 2019, 489, 196–204. [Google Scholar] [CrossRef]
- Kaltenegger, L.; Traub, W.A. Transits of Earth-Like Planets. Astrophys. J. 2009, 698, 519. [Google Scholar] [CrossRef]
- Robinson, T.D.; Meadows, V.S.; Crisp, D.; Deming, D.; A’Hearn, M.F.; Charbonneau, D.; Livengood, T.A.; Seager, S.; Barry, R.K.; Hearty, T.; et al. Earth as an Extrasolar Planet: Earth Model Validation Using EPOXI Earth Observations. Astrobiology 2011, 11, 393–408. [Google Scholar] [CrossRef] [PubMed]
- Kaltenegger, L.; Traub, W.A.; Jucks, K.W. Spectral Evolution of an Earth-like Planet. Astrophys. J. 2007, 658, 598. [Google Scholar] [CrossRef]
- Montañes-Rodriguez, P.; Gonzalez-Merino, B.; Palle, E.; Lopez-Puertas, M.; Garcia-Melendo, E. Jupiter as an exoplanet: UV to NIR transmission spectrum reveals hazes, a Na layer and possibly stratospheric H2O-ice clouds. Astrophys. J. 2015, 801, L8. [Google Scholar] [CrossRef]
- Sato, M.; Hansen, J.E. Jupiter’s Atmospheric Composition and Cloud Structure Deduced from Absorption Bands in Reflected Sunlight. J. Atmos. Sci. 1979, 36, 1133–1167. [Google Scholar] [CrossRef]
- Liu, F.; Asplund, M.; Ramirez, I.; Yong, D.; Melendez, J. A high precision chemical abundance analysis of the HAT-P-1 stellar binary: Constraints on planet formation. Mon. Not. R. Astron. Soc. Lett. 2014, 442, L51–L55. [Google Scholar] [CrossRef]
- Hartman, J.D.; Bakos, G.A.; Torres, G.; Kovács, G.; Noyes, R.W.; Pál, A.; Latham, D.W.; Sip\Hocz, B.; Fischer, D.A.; Johnson, J.A.; et al. HAT-P-12b: A low-density sub-saturn mass planet transiting a metal-poor K dwarf. Astrophys. J. 2009, 706, 785–796. [Google Scholar] [CrossRef]
- Boyajian, T.; von Braun, K.; Feiden, G.A.; Huber, D.; Basu, S.; Demarque, P.; Fischer, D.A.; Schaefer, G.; Mann, A.W.; White, T.R.; et al. Stellar diameters and temperatures—VI. High angular resolution measurements of the transiting exoplanet host stars HD 189733 and HD 209458 and implications for models of cool dwarfs. Mon. Not. R. Astron. Soc. 2015, 447, 846–857. [Google Scholar] [CrossRef]
- Del Burgo, C.; Allende Prieto, C. Accurate parameters for HD 209458 and its planet from HST spectrophotometry. Mon. Not. R. Astron. Soc. 2016, 463, 1400–1408. [Google Scholar] [CrossRef]
- Gillon, M.; Anderson, D.R.; Triaud, A.H.M.J.; Hellier, C.; Maxted, P.F.L.; Pollaco, D.; Queloz, D.; Smalley, B.; West, R.G.; Wilson, D.M.; et al. Discovery and characterization of WASP-6b, an inflated sub-Jupiter mass planet transiting a solar-type star. Astron. Astrophys. 2009, 501, 785–792. [Google Scholar] [CrossRef]
- Faedi, F.; Barros, S.C.C.; Anderson, D.R.; Brown, D.J.A.; Cameron, A.C.; Pollacco, D.; Boisse, I.; Hébrard, G.; Lendl, M.; Lister, T.A.; et al. WASP-39b: A highly inflated Saturn-mass planet orbiting a late G-type star. Astron. Astrophys. 2011, 531, A40. [Google Scholar] [CrossRef]
- Lin, Z.; Kaltenegger, L. High-resolution reflection spectra for Proxima b and Trappist-1e models for ELT observations. Mon. Not. R. Astron. Soc. 2020, 491, 2845–2854. [Google Scholar] [CrossRef]
- Barnes, R.; Deitrick, R.; Luger, R.; Driscoll, P.E.; Quinn, T.R.; Fleming, D.P.; Guyer, B.; McDonald, D.V.; Meadows, V.S.; Arney, G.; et al. The Habitability of Proxima Centauri b I: Evolutionary Scenarios. arXiv 2018, arXiv:1608.06919v2. [Google Scholar] [CrossRef]
- Delrez, L.; Gillon, M.; Triaud, A.H.M.J.; Demory, B.O.; de Wit, J.; Ingalls, J.G.; Agol, E.; Bolmont, E.; Burdanov, A.; Burgasser, A.J.; et al. Early 2017 observations of TRAPPIST-1 with Spitzer. Mon. Not. R. Astron. Soc. 2018, 475, 3577–3597. [Google Scholar] [CrossRef]
- Pinamonti, M.; Damasso, M.; Marzari, F.; Sozzetti, A.; Desidera, S.; Maldonado, J.; Scandariato, G.; Affer, L.; Lanza, A.F.; Bignamini, A.; et al. The HADES RV Programme with HARPS-N at TNG. VIII. GJ15A: A multiple wide planetary system sculpted by binary interaction. Astron. Astrophys. 2018, 617, A104. [Google Scholar] [CrossRef]
- Anglada-Escudé, G.; Tuomi, M.; Gerlach, E.; Barnes, R.; Heller, R.; Jenkins, J.S.; Wende, S.; Vogt, S.S.; Butler, R.P.; Reiners, A.; et al. A dynamically-packed planetary system around GJ 667C with three super-Earths in its habitable zone. Astron. Astrophys. 2013, 556, A126. [Google Scholar] [CrossRef]
- Bauer, F.F.; Zechmeister, M.; Kaminski, A.; Rodríguez López, C.; Caballero, J.A.; Azzaro, M.; Stahl, O.; Kossakowski, D.; Quirrenbach, A.; Becerril Jarque, S.; et al. The CARMENES search for exoplanets around M dwarfs. Measuring precise radial velocities in the near infrared: The example of the super-Earth CD Cet b. Astron. Astrophys. 2020, 640, A50. [Google Scholar] [CrossRef]
- Hidalgo, D.; Pallé, E.; Alonso, R.; Gandolfi, D.; Fridlund, M.; Nowak, G.; Luque, R.; Hirano, T.; Justesen, A.B.; Cochran, W.D.; et al. Three planets transiting the evolved star EPIC 249893012: A hot 8.8-M⊕ super-Earth and two warm 14.7 and 10.2-M⊕ sub-Neptunes. Astron. Astrophys. 2020, 636, A89. [Google Scholar] [CrossRef]
- Des Etangs, A.L.; Pont, F.; Vidal-Madjar, A.; Sing, D. Rayleigh scattering in the transit spectrum of HD 189733b. Astron. Astrophys. 2008, 481, L83–L86. [Google Scholar] [CrossRef]
- Stephens, M.; Vannah, S.; Gleiser, M. Informational approach to cosmological parameter estimation. Phys. Rev. D 2020, 102, 123514. [Google Scholar] [CrossRef]
- Thakur, P.; Gleiser, M.; Kumar, A.; Gupta, R. Configurational entropy of optical bright similariton in tapered graded-index waveguide. Phys. Lett. A 2020, 384, 126461. [Google Scholar] [CrossRef]
- Bernardini, A.E.; da Rocha, R. Cosmological comoving behavior of the configurational entropy. Phys. Lett. B 2019, 796, 107–111. [Google Scholar] [CrossRef]
- Gleiser, M.; Sowinski, D. Information-entropic stability bound for compact objects: Application to Q-balls and the Chandrasekhar limit of polytropes. Phys. Lett. B 2013, 727, 272–275. [Google Scholar] [CrossRef]
- Gleiser, M.; Sowinski, D. Configurational information approach to instantons and false vacuum decay in D-dimensional spacetime. Phys. Rev. D 2018, 98, 056026. [Google Scholar] [CrossRef]
- Bernardini, A.E.; Braga, N.R.F.; da Rocha, R. Configurational entropy of glueball states. Phys. Lett. B 2017, 765, 81–85. [Google Scholar] [CrossRef]
- Braga, N.R.F.; da Rocha, R. Configurational entropy of anti-de Sitter black holes. Phys. Lett. B 2017, 767, 386–391. [Google Scholar] [CrossRef]
- Sandford, E.; Kipping, D.; Collins, M. On planetary systems as ordered sequences. Mon. Not. R. Astron. Soc. 2021, 505, 2224–2246. [Google Scholar] [CrossRef]
- Guttenberg, N.; Chen, H.; Mochizuki, T.; Cleaves, H. Classification of the Biogenicity of Complex Organic Mixtures for the Detection of Extraterrestrial Life. Life 2021, 11, 234. [Google Scholar] [CrossRef]
- Marshall, S.M.; Mathis, C.; Carrick, E.; Keenan, G.; Cooper, G.J.T.; Graham, H.; Craven, M.; Gromski, P.S.; Moore, D.G.; Walker, S.I.; et al. Identifying molecules as biosignatures with assembly theory and mass spectrometry. Nat. Commun. 2021, 12, 3033. [Google Scholar] [CrossRef]
- Chou, L.; Mahaffy, P.; Trainer, M.; Eigenbrode, J.; Arevalo, R.; Brinckerhoff, W.; Getty, S.; Grefenstette, N.; Poian, V.D.; Fricke, G.M.; et al. Planetary Mass Spectrometry for Agnostic Life Detection in the Solar System. Front. Astron. Space Sci. 2021, 8, 755100. [Google Scholar] [CrossRef]
- Bartlett, S.; Li, J.; Gu, L.; Sinapayen, L.; Fan, S.; Natraj, V.; Jiang, J.H.; Crisp, D.; Yung, Y.L. Assessing planetary complexity and potential agnostic biosignatures using epsilon machines. Nat. Astron. 2022, 6, 387–392. [Google Scholar] [CrossRef]
- Fields, B.; Gupta, S.; Sandora, M. Information gain as a tool for assessing biosignature missions. Int. J. Astrobiol. 2023, 22, 583–607. [Google Scholar] [CrossRef]
- Sowinski, D.R.; Ghoshal, G.; Frank, A. Exo-Daisy World: Revisiting Gaia Theory through an Informational Architecture Perspective. arXiv 2024, arXiv:2411.03421. [Google Scholar] [CrossRef]
- Wong, M.L.; Prabhu, A.; Williams, J.; Morrison, S.M.; Hazen, R.M. Toward Network-Based Planetary Biosignatures: Atmospheric Chemistry as Unipartite, Unweighted, Undirected Networks. J. Geophys. Res. Planets 2023, 128, e2022JE007658. [Google Scholar] [CrossRef]
- Fisher, T.; Janin, E.; Walker, S.I. A Complex Systems Approach to Exoplanet Atmospheric Chemistry: New Prospects for Ruling Out the Possibility of Alien Life-As-We-Know-It. arXiv 2023, arXiv:2310.05359. [Google Scholar]
- Guez, I.A.; Claire, M. Reading Between the Rainbows: Comparative Exoplanet Characterisation through Molecule Agnostic Spectral Clustering. arXiv 2024, arXiv:2410.16986. [Google Scholar]
- Lovelock, J.E. A physical basis for life detection experiments. Nature 1965, 207, 568–570. [Google Scholar] [CrossRef]
- Lederberg, J. Signs of life. Nature 1965, 207, 9–13. [Google Scholar] [CrossRef]
- Cockell, C.; Léger, A.; Fridlund, M.; Herbst, T.; Kaltenegger, L.; Absil, O.; Beichman, C.; Benz, W.; Blanc, M.; Brack, A.; et al. Darwin—A Mission to Detect and Search for Life on Extrasolar Planets. Astrobiology 2009, 9, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Krissansen-Totton, J.; Olson, S.; Catling, D.C. Disequilibrium biosignatures over Earth history and implications for detecting exoplanet life. Sci. Adv. 2018, 4, eaao5747. [Google Scholar] [CrossRef]
- Young, A.V.; Robinson, T.D.; Krissansen-Totton, J.; Schwieterman, E.W.; Wogan, N.F.; Way, M.J.; Sohl, L.E.; Arney, G.N.; Reinhard, C.T.; Line, M.R.; et al. Inferring chemical disequilibrium biosignatures for Proterozoic Earth-like exoplanets. Nat. Astron. 2024, 8, 101–110. [Google Scholar] [CrossRef]
- Herbst, K.; Bartenschlager, A.; Grenfell, J.L.; Iro, N.; Sinnhuber, M.; Taysum, B.; Wunderlich, F.; Engelbrecht, N.E.; Light, J.; Moloto, K.D.; et al. Impact of Cosmic Rays on Atmospheric Ion Chemistry and Spectral Transmission Features of TRAPPIST-1e. Astrophys. J. 2024, 961, 164. [Google Scholar] [CrossRef]
- Doyon, R. Do Temperate Rocky Planets Around M Dwarfs have an Atmosphere? arXiv 2024, arXiv:2403.12617v3. [Google Scholar] [CrossRef]
- Lin, Z.; Kaltenegger, L. High-resolution spectral models of TRAPPIST-1e seen as a Pale Blue Dot for ELT and JWST observations. Mon. Not. R. Astron. Soc. 2022, 516, 3167–3174. [Google Scholar] [CrossRef]
- Fauchez, T.J.; Turbet, M.; Villanueva, G.L.; Wolf, E.T.; Arney, G.; Kopparapu, R.K.; Lincowski, A.; Mandell, A.; Wit, J.d.; Pidhorodetska, D.; et al. Impact of Clouds and Hazes on the Simulated JWST Transmission Spectra of Habitable Zone Planets in the TRAPPIST-1 System. Astrophys. J. 2019, 887, 194. [Google Scholar] [CrossRef]
- Sarkar, S.; Madhusudhan, N. JexoSim 2.0: End-to-End JWST Simulator for Exoplanet Spectroscopy—Implementation and Case Studies. Mon. Not. R. Astron. Soc. 2021, 508, 433–452. [Google Scholar] [CrossRef]
- Batalha, N.E.; Mandell, A.; Pontoppidan, K.; Stevenson, K.B.; Lewis, N.K.; Kalirai, J.; Earl, N.; Greene, T.; Albert, L.; Nielsen, L.D. PandExo: A Community Tool for Transiting Exoplanet Science with JWST & HST. Publ. Astron. Soc. Pac. 2017, 129, 064501. [Google Scholar] [CrossRef]
- Ahrer, E.M.; Alderson, L.; Batalha, N.M.; Batalha, N.E.; Bean, J.L.; Beatty, T.G.; Bell, T.J.; Benneke, B.; Berta-Thompson, Z.K.; Carter, A.L.; et al. Identification of carbon dioxide in an exoplanet atmosphere. Nature 2023, 614, 649–652. [Google Scholar] [CrossRef]
- Bell, T.J.; Welbanks, L.; Schlawin, E.; Line, M.R.; Fortney, J.J.; Greene, T.P.; Ohno, K.; Parmentier, V.; Rauscher, E.; Beatty, T.G.; et al. Methane throughout the atmosphere of the warm exoplanet WASP-80b. Nature 2023, 623, 709–712. [Google Scholar] [CrossRef]
- Madhusudhan, N.; Sarkar, S.; Constantinou, S.; Holmberg, M.; Piette, A.A.A.; Moses, J.I. Carbon-bearing Molecules in a Possible Hycean Atmosphere. Astrophys. J. 2023, 956, L13. [Google Scholar] [CrossRef]
- Schmidt, S.P.; MacDonald, R.J.; Tsai, S.M.; Radica, M.; Wang, L.C.; Ahrer, E.M.; Bell, T.J.; Fisher, C.; Thorngren, D.P.; Wogan, N.; et al. A Comprehensive Reanalysis of K2-18 b’s JWST NIRISS+NIRSpec Transmission Spectrum. arXiv 2025, arXiv:2501.18477. [Google Scholar]
- Vannah, S. Information Entropic Content of Astrophysical Spectra: Applications to Cosmology and Astrobiology. Ph.D. Thesis, Dartmouth College, Hanover, NH, USA, 2022. [Google Scholar]
- Beichman, C.A.; Greene, T.P. A White Paper Submitted to The National Academy of Science’s Committee on Exoplanet Science Strategy: Observing Exoplanets with the James Webb Space Telescope. arXiv 2018, arXiv:1803.03730. [Google Scholar] [CrossRef]

| Name | Equilib. Temp. (K) | Equation of State | Surface Gravity (g) | Planet Radius (m) | Stellar Radius (m) | Rayleigh Scattering Factor |
|---|---|---|---|---|---|---|
| Jupiter a | 300 | 1X | 24.79 | 6.99 × 107 | 6.96 × 108 | 10 |
| HAT-P-1b b | 1300 | 5X, graphite rainout | 7.5 | 9.44 × 107 | 8.17 × 108 | 10 |
| HAT-P-12b c | 1000 | 1X | 5.6 | 6.86 × 107 | 4.87 × 108 | 200 |
| HD 189733b d | 1200 | 1X | 21.4 | 8.15 × 107 | 5.60 × 108 | 500 |
| HD 209458b e | 1500 | 0.1X | 9.4 | 9.72 × 107 | 8.35 × 108 | 10 |
| WASP-6b f | 1200 | 1X | 8.7 | 8.72 × 107 | 6.05 × 108 | 1000 |
| WASP-39b g | 1100 | 1X | 4.1 | 9.08 × 107 | 6.23 × 108 | 1 |
| Gas giant 1 | 1400 | 5X, graphite rainout | 12.8 | 8.45 × 107 | 5.02 × 108 | 1000 |
| Gas giant 2 | 700 | 1X | 20.1 | 6.27 × 107 | 8.95 × 108 | 100 |
| Gas giant 3 | 1000 | 1X, 0.2 C/O ratio | 8.8 | 9.23 × 107 | 6.48 × 108 | 10 |
| Gas giant 4 | 1300 | 1X, 0.8 C/O ratio | 17.2 | 6.90 × 107 | 9.23 × 108 | 1 |
| Earth h | 300 | 1X | 9.8 | 6.37 × 106 | 6.96 × 108 | 1 |
| Proxima b i | 300 | 1X | 10.9 | 6.82 × 106 | 9.82 × 107 | 1 |
| TRAPPIST-1e j | 300 | 1X | 7.2 | 5.85 × 106 | 8.15 × 107 | 1 |
| GJ 15 Ab k | 300 | 0.1X | 12.4 | 9.88 × 106 | 2.85 × 108 | 10 |
| GJ 667 Cc l | 300 | 0.1X | 15.7 | 9.81 × 106 | 2.92 × 108 | 1 |
| CD Cet b m | 500 | 1X | 11.7 | 1.16 × 107 | 1.18 × 108 | 0 |
| EPIC 24983012b n | 1500 | 1X | 22.6 | 1.24 × 107 | 1.19 × 109 | 1 |
| Rocky planet 1 | 700 | 1X | 14.8 | 9.87 × 106 | 8.80 × 108 | 10 |
| Rocky planet 2 | 400 | 5X | 10.4 | 6.02 × 106 | 4.53 × 108 | 1 |
| Rocky planet 3 | 300 | 1X | 8.4 | 7.12 × 106 | 9.25 × 108 | 1000 |
| Rocky planet 4 | 1000 | 10X | 12.8 | 8.54 × 106 | 1.02 × 109 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vannah, S.; Stiehl, I.D.; Gleiser, M. An Informational–Entropic Approach to Exoplanet Characterization. Entropy 2025, 27, 385. https://doi.org/10.3390/e27040385
Vannah S, Stiehl ID, Gleiser M. An Informational–Entropic Approach to Exoplanet Characterization. Entropy. 2025; 27(4):385. https://doi.org/10.3390/e27040385
Chicago/Turabian StyleVannah, Sara, Ian D. Stiehl, and Marcelo Gleiser. 2025. "An Informational–Entropic Approach to Exoplanet Characterization" Entropy 27, no. 4: 385. https://doi.org/10.3390/e27040385
APA StyleVannah, S., Stiehl, I. D., & Gleiser, M. (2025). An Informational–Entropic Approach to Exoplanet Characterization. Entropy, 27(4), 385. https://doi.org/10.3390/e27040385






