The Dirac Equation, Mass and Arithmetic by Permutations of Automaton States
Abstract
1. Introduction
2. Results: An Automaton Beneath the Dirac Equation
2.1. The Weyl Equation
2.2. Reverse Engineering an Automaton Based on Permutations from the Dirac Equation
2.2.1. Doing Arithmetic by Permutations
3. Discussion
4. Conclusions
- The generalization to more than dimensions should be feasible, notwithstanding some necessary bookkeeping efforts.
- The effective Hamiltonian governing the discrete model should be derived and the continuum limit be understood.
- Symmetries and conservation laws of cellular automata are of general interest beyond the present context.
- A field theory of fermions obeying the Pauli principle should be formulated (relating two-state Ising spins to occupation numbers?).
- An external scalar potential can be considered as a spatially varying mass, yet interactions with dynamical gauge fields will require additional considerations.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Permutations and the Cogwheel Model

Appendix A.2. A Chain of Ising Spins with Exchange Interactions
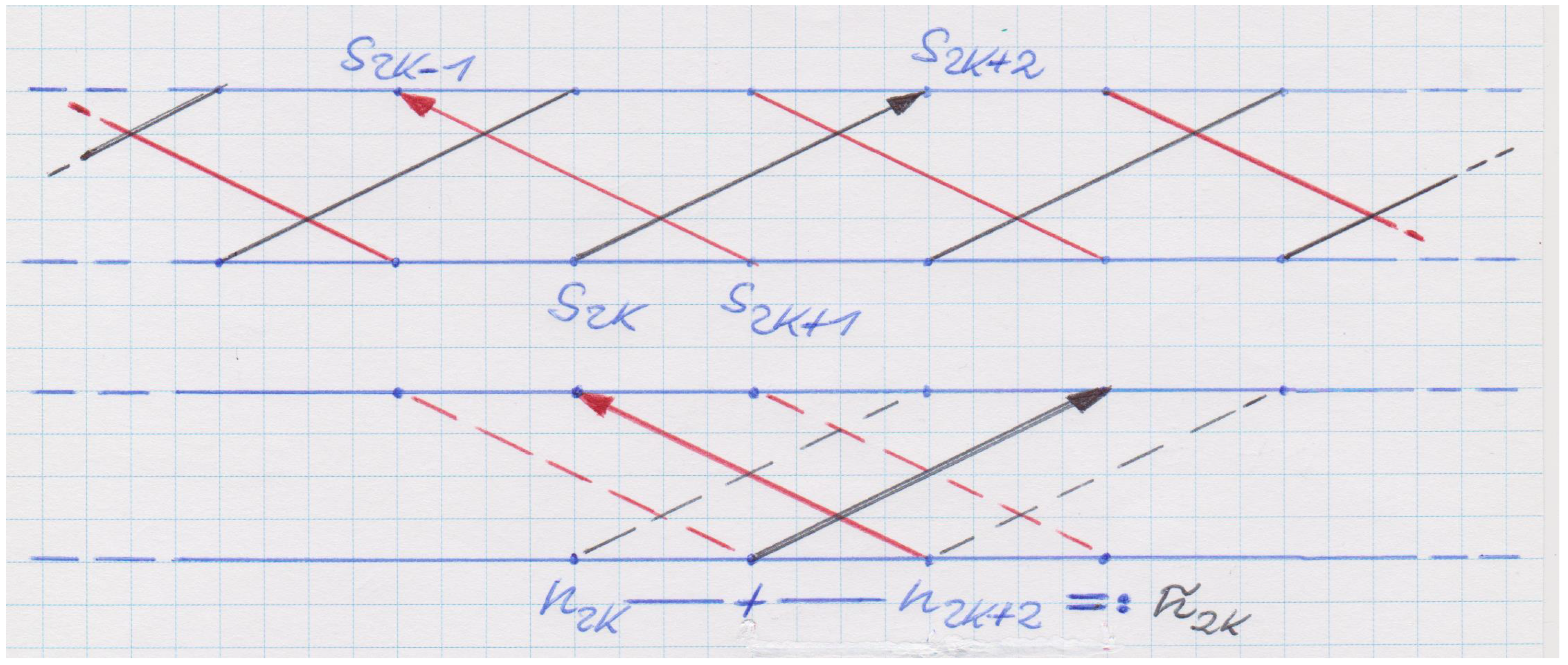
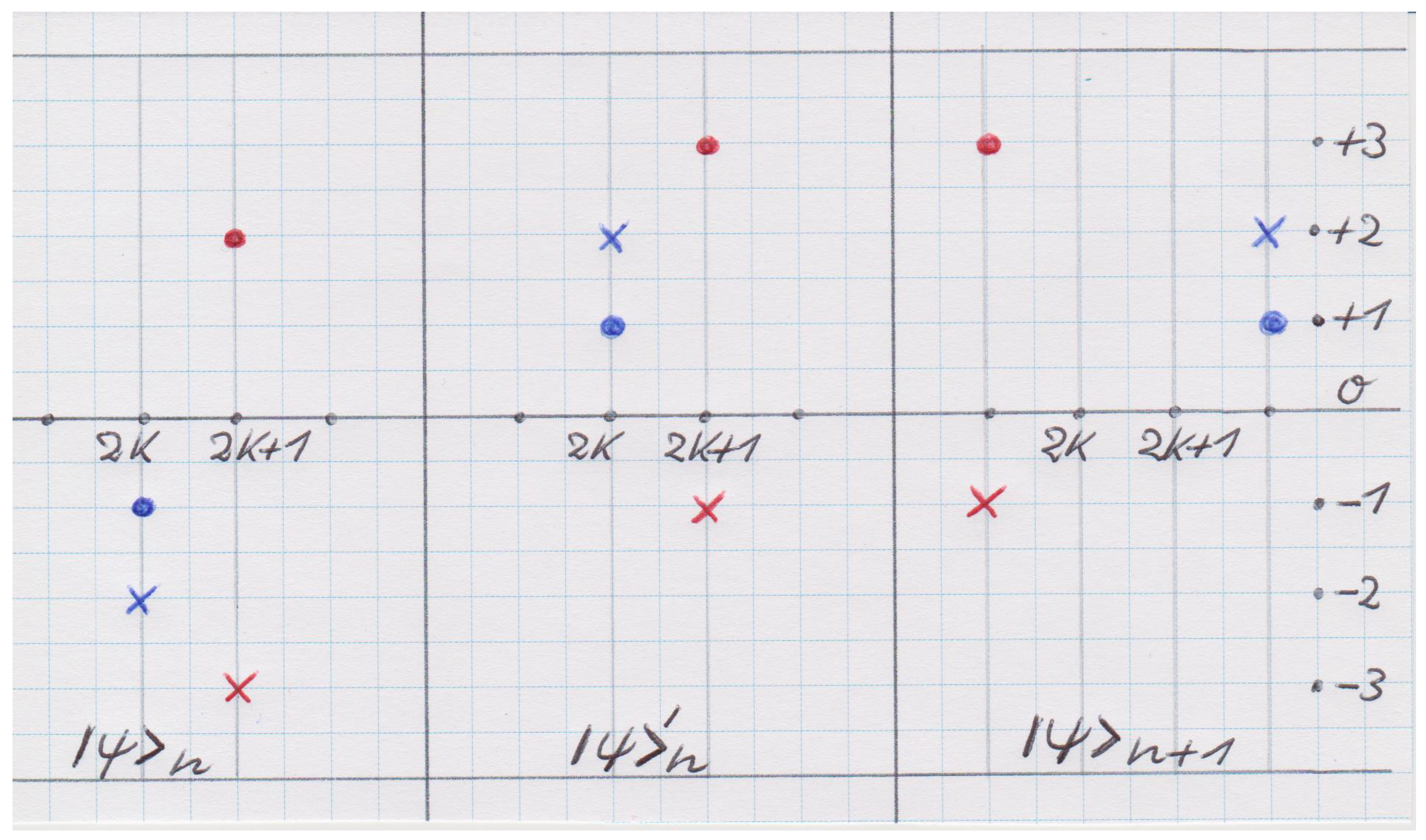
Appendix A.3. Illustration of Scattering Operator and Automaton Update
References
- Gisin, N. Quantum Chance: Nonlocality, Teleportation and Other Quantum Marvels; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Haag, R. On the Sharpness of Localization of Individual Events in Space and Time. Found. Phys. 2013, 43, 1295. [Google Scholar]
- Haag, R. On Quantum Theory. arXiv 2016, arXiv:1602.05426. [Google Scholar]
- ’t Hooft, G. The Cellular Automaton Interpretation of Quantum Mechanics; Fundamental Theories of Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 185. [Google Scholar]
- ’t Hooft, G. An ontological description for relativistic, massive bosons. arXiv 2023, arXiv:2306.09885. [Google Scholar]
- Wetterich, C. Cellular automaton for spinor gravity in four dimensions. J. Phys. Conf. Ser. 2023, 2533, 012016. [Google Scholar]
- Elze, H.-T. Action principle for cellular automata and the linearity of quantum mechanics. Phys. Rev. A 2014, 89, 012111. [Google Scholar]
- Vervoort, L. Bell’s Theorem: Two Neglected Solutions. Found. Phys. 2013, 43, 769. [Google Scholar]
- Vervoort, L. Probability theory as a physical theory points to superdeterminism. Entropy 2019, 21, 848. [Google Scholar] [CrossRef]
- Hossenfelder, S.; Palmer, T. Rethinking superdeterminism. Front. Phys. 2020, 8, 139. [Google Scholar]
- Nikolaev, V.; Vervoort, L. Aspects of superdeterminism made intuitive. Found. Phys. 2023, 53, 17. [Google Scholar]
- Wetterich, C. The probabilistic world. arXiv 2020, arXiv:2011.02867v3. [Google Scholar]
- Elze, H.-T. Linear dynamics of quantum-classical hybrids. Phys. Rev. A 2012, 85, 052109. [Google Scholar]
- Elze, H.-T. Are Quantum-Classical Hybrids compatible with Ontological Cellular Automata? Universe 2022, 8, 207. [Google Scholar] [CrossRef]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables, I and II. Phys. Rev. 1952, 85, 166. [Google Scholar]
- Tumulka, R. On Bohmian mechanics, particle creation, and relativistic space-time: Happy 100th Birthday, David Bohm! Entropy 2018, 20, 462. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N. Indeterminism in physics, classical chaos and Bohmian mechanics. Are real numbers really real? Erkenntnis 2021, 86, 1469. [Google Scholar]
- Santos, E. On the analogy between stochastic electrodynamics and nonrelativistic quantum electrodynamics. Eur. Phys. J. Plus 2022, 137, 1302. [Google Scholar]
- Boyer, T.H. Stochastic electrodynamics: The closest classical approximation to quantum theory. Atoms 2019, 7, 29. [Google Scholar] [CrossRef]
- de la Pena, L.; Cetto, A.M.; Valdes Hernandez, A. The Emerging Quantum: The Physics Beyond Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Khrennikov, A. Prequantum classical statistical field theory: Simulation of probabilities of photon detection with the aid of classical Brownian motion. J. Russ. Laser Res. 2015, 36, 237. [Google Scholar]
- Fuchs, C.A.; Schack, R. Quantum-Bayesian Coherence. Rev. Mod. Phys. 2013, 85, 1693. [Google Scholar]
- Elze, H.-T. Are quantum spins but small perturbations of ontological Ising spins? Found. Phys. 2020, 50, 1875. [Google Scholar]
- Elze, H.-T. Cellular automaton ontology, bits, qubits, and the Dirac equation. Int. J. Quantum Inf. 2024, 22, 2450013. [Google Scholar]
- Shannon, C.E. Communication in the presence of noise. Proc. IRE 1949, 37, 10. [Google Scholar]
- Jerri, A.J. The Shannon Sampling Theorem—Its Various Extensions and Applications: A Tutorial Review. Proc. IEEE 1977, 65, 1565. [Google Scholar]
- Kempf, A. Spacetime could be simultaneously continuous and discrete in the same way that information can. New J. Phys. 2010, 12, 115001. [Google Scholar]
- Kauffman, L.H.; Noyes, H.P. Discrete physics and the Dirac equation. Phys. Lett. A 1996, 218, 139. [Google Scholar]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Bialynicki-Birula, I. Dirac and Weyl equations on a lattice as quantum cellular automata. Phys. Rev. D 1994, 49, 6920. [Google Scholar]
- Bisio, A.; D’Ariano, G.M.; Tosini, A. Quantum field as a quantum cellular automaton: The Dirac free evolution in one dimension. Ann. Phys. 2015, 354, 244. [Google Scholar]
- Margolus, N. Mechanical systems that are both classical and quantum. Lect. Notes Comput. Sci. 2015, 9099, 169, see also preprint 2008, arXiv:0805.3357v2. [Google Scholar]
- Wetterich, C. Fermion picture for cellular automata. arXiv 2022, arXiv:2203.14081. [Google Scholar]
- Ord, G.N. The Feynman chessboard model in 3 + 1 dimensions. Front. Phys. 2023, 11, 1286030. [Google Scholar]
- Gupta, C.; Short, A.J. The Dirac Vacuum in Discrete Spacetime. arXiv 2024, arXiv:2412.03466. [Google Scholar]
- Khrennikov, A. Generalizations of quantum mechanics induced by classical statistical field theory. Found. Phys. Lett. 2005, 18, 637. [Google Scholar]
- Atmanspacher, H.; Primas, H. Epistemic and ontic quantum realities. In Foundations of Probability and Physics-3; Khrennikov, A., Ed.; Conf. Proc. Series; AIP: Melville, NY, USA, 2005; Volume 750, p. 49. [Google Scholar]
- Khrennikov, A.; Yurova, E. Automaton model of protein: Dynamics of conformational and functional states. Prog. Biophys. Mol. Biol. 2017, 130 Pt A, 2. [Google Scholar]
- Khrennikov, A.; Basieva, I.; Pothos, E.M.; Yamato, I. Quantum probability in decision making from quantum information representation of neuronal states. Sci. Rep. 2018, 8, 16225. [Google Scholar]
- Scholes, G.D. Quantum-like states on complex synchronized networks. arXiv 2024, arXiv:2405.07950. [Google Scholar]
- Wetterich, C. The probabilistic world II: Quantum mechanics from classical statistics. arXiv 2024, arXiv:2408.06379. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elze, H.-T. The Dirac Equation, Mass and Arithmetic by Permutations of Automaton States. Entropy 2025, 27, 395. https://doi.org/10.3390/e27040395
Elze H-T. The Dirac Equation, Mass and Arithmetic by Permutations of Automaton States. Entropy. 2025; 27(4):395. https://doi.org/10.3390/e27040395
Chicago/Turabian StyleElze, Hans-Thomas. 2025. "The Dirac Equation, Mass and Arithmetic by Permutations of Automaton States" Entropy 27, no. 4: 395. https://doi.org/10.3390/e27040395
APA StyleElze, H.-T. (2025). The Dirac Equation, Mass and Arithmetic by Permutations of Automaton States. Entropy, 27(4), 395. https://doi.org/10.3390/e27040395





