Instability of Financial Time Series Revealed by Irreversibility Analysis
Abstract
1. Introduction
2. Methods
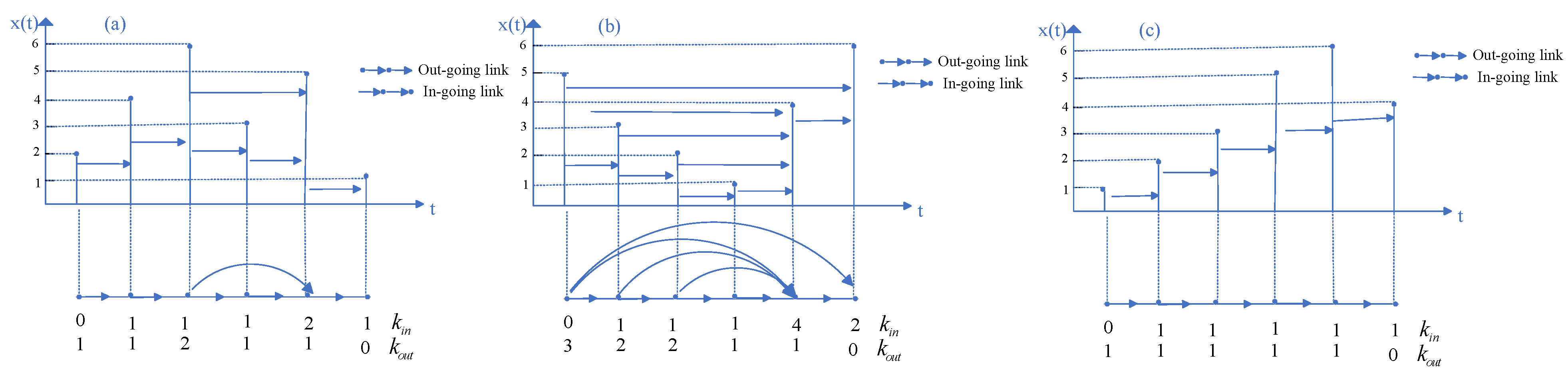
2.1. Visibility Graph, Horizontal Visibility Graph and Directed Horizontal Visibility Graph
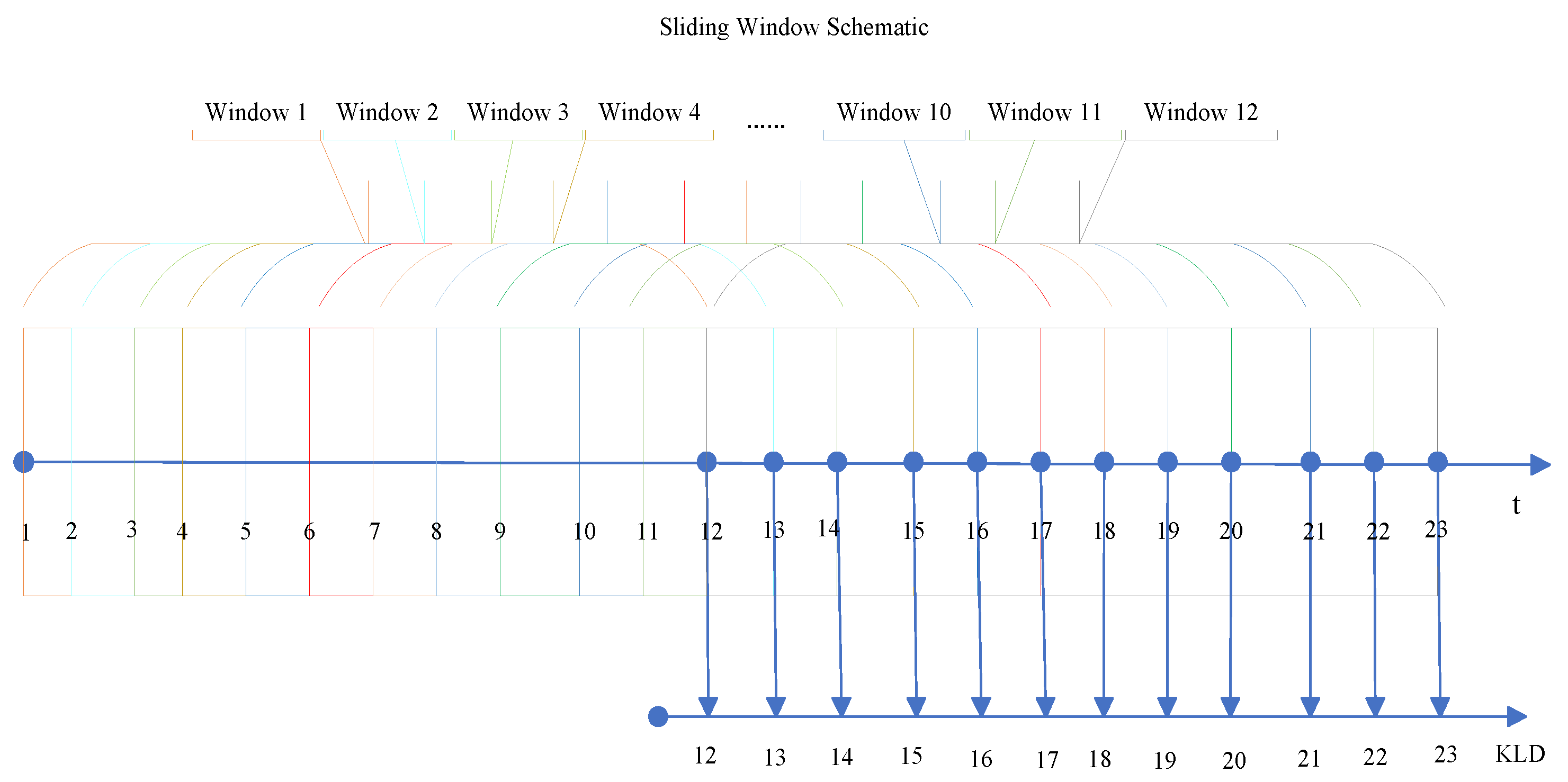
2.2. Kullback–Leibler Divergence (KLD) and Monte Carlo Test
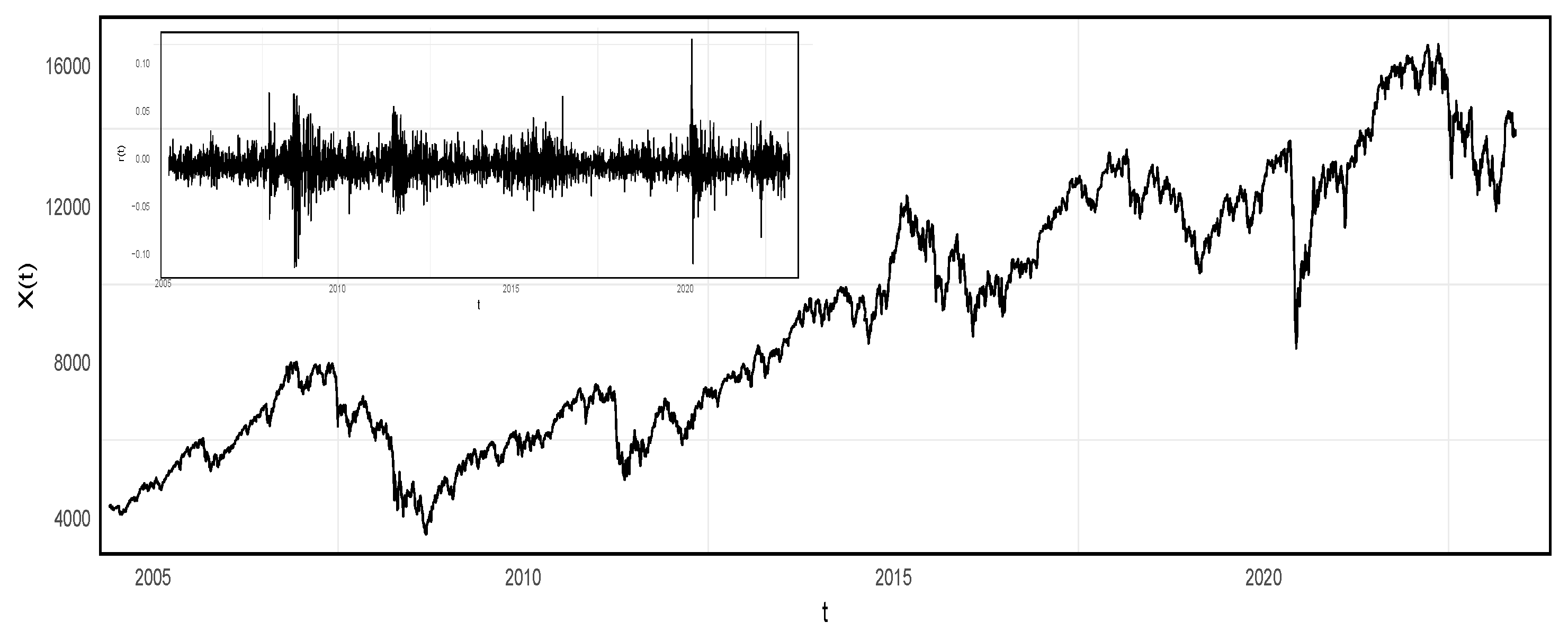
3. Data
4. Results
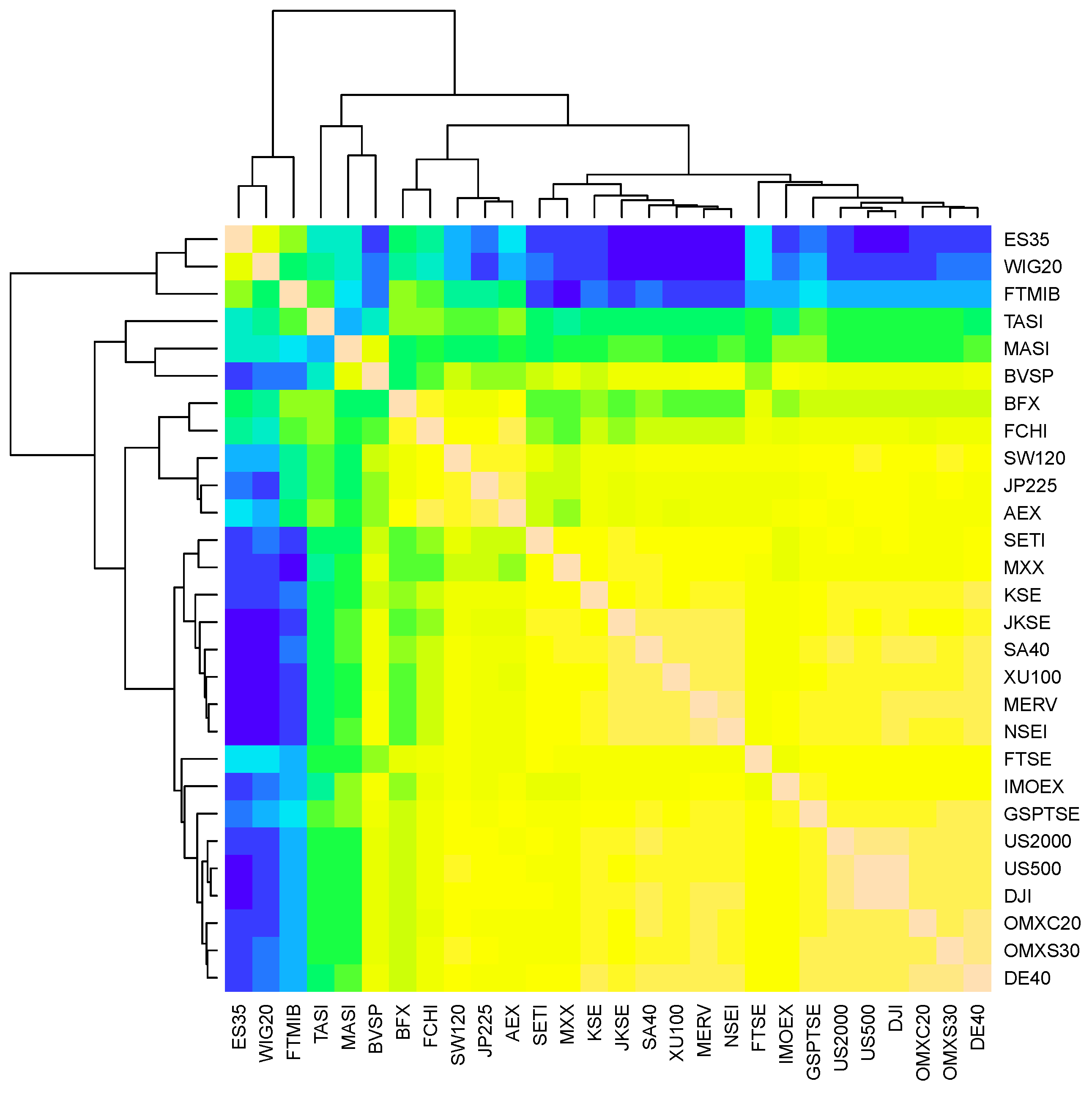
4.1. Clustering and Selection of Financial Time Series
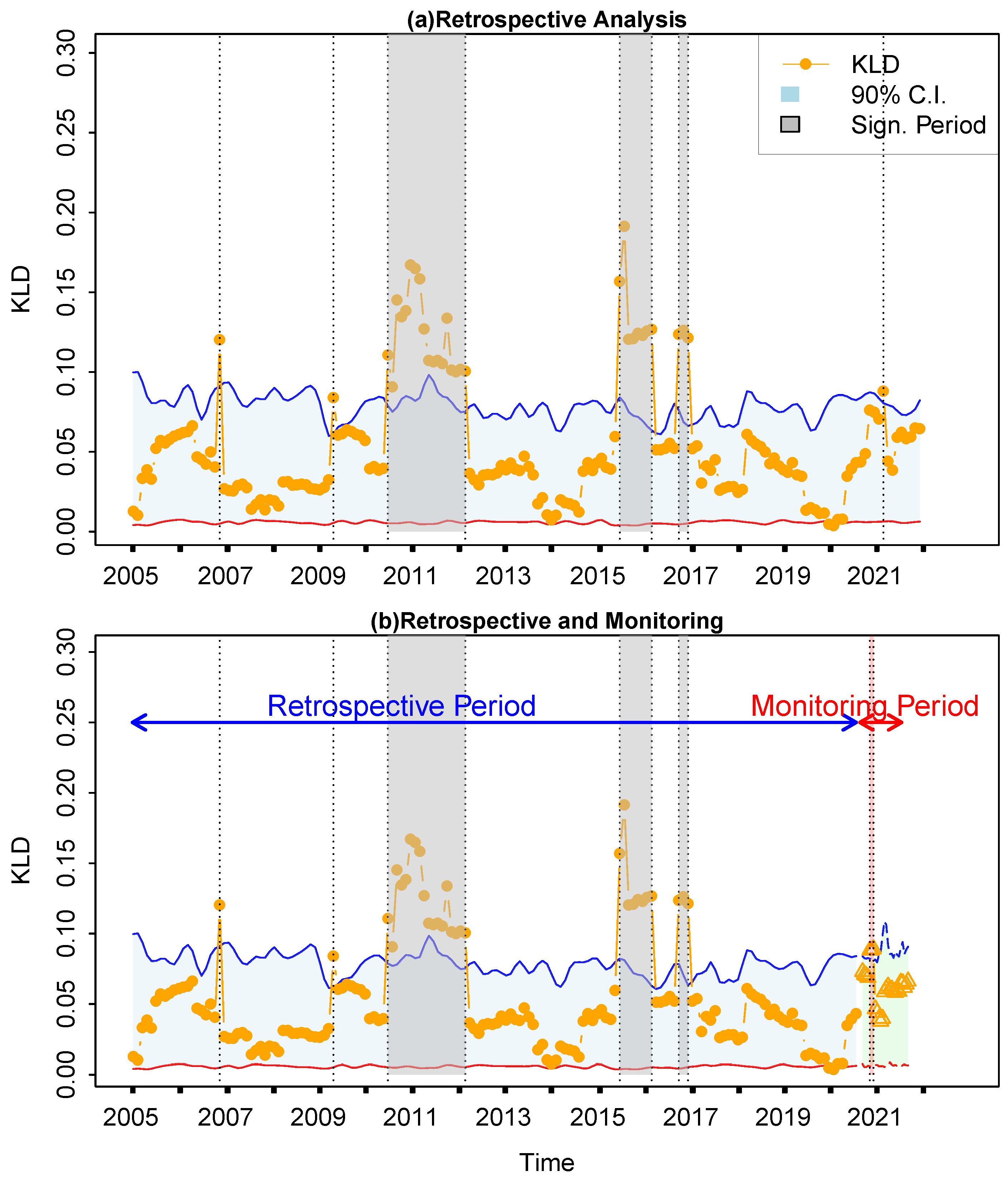
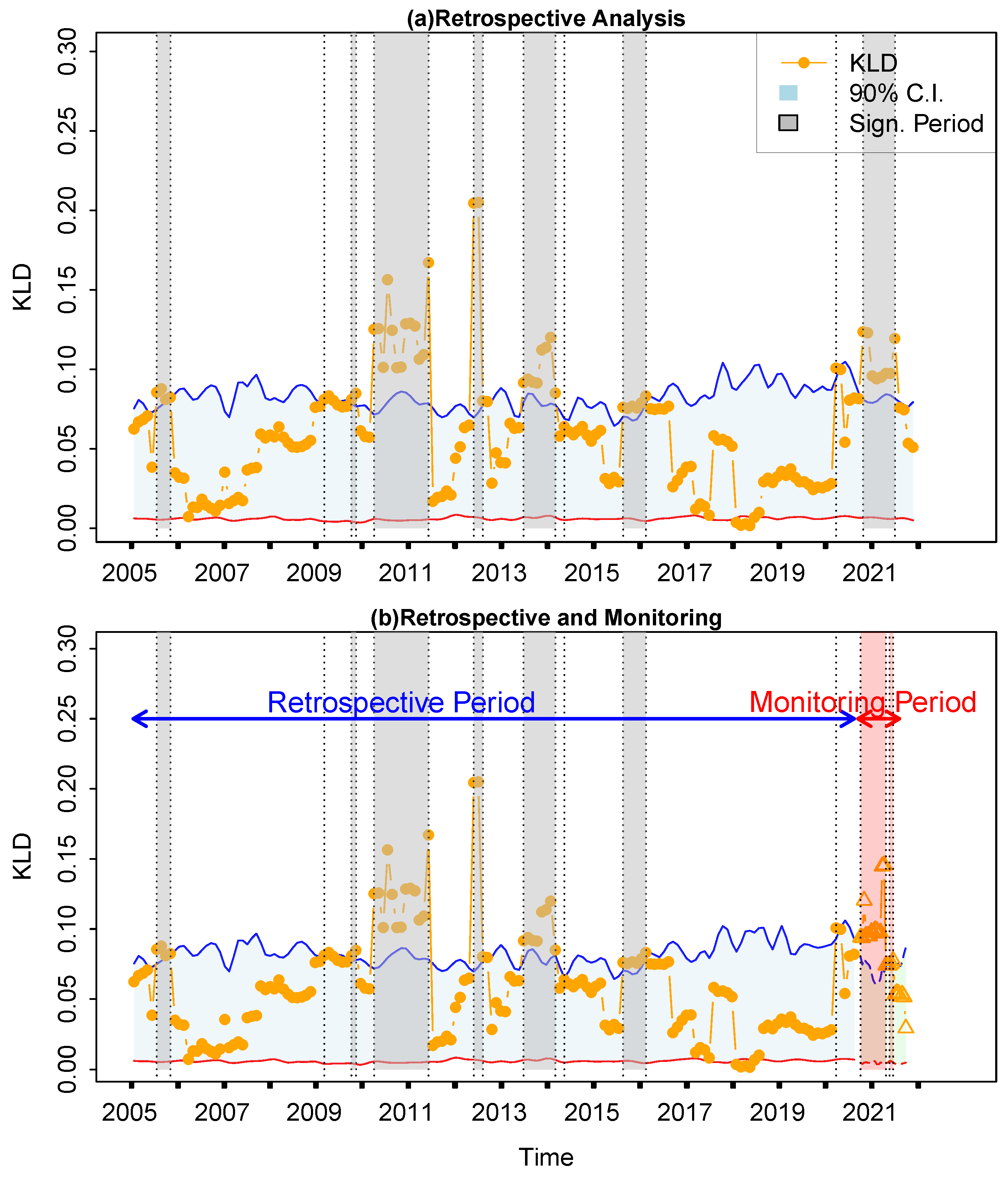
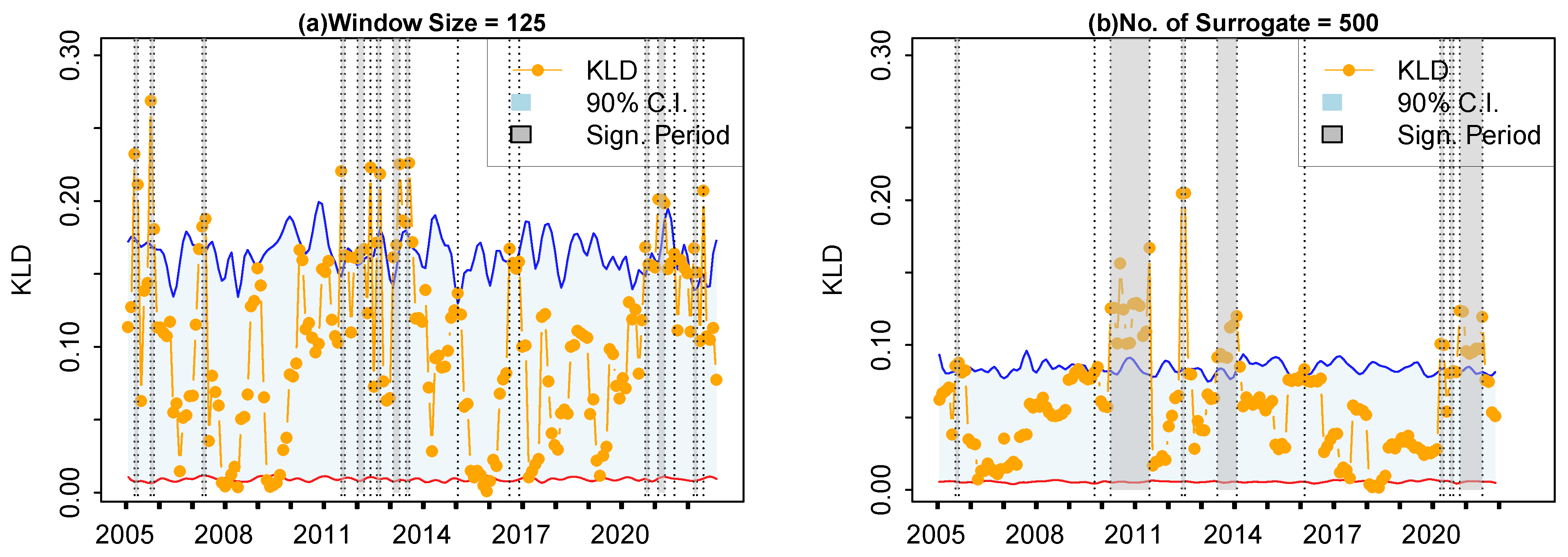
4.2. Evaluation of the KLD Method
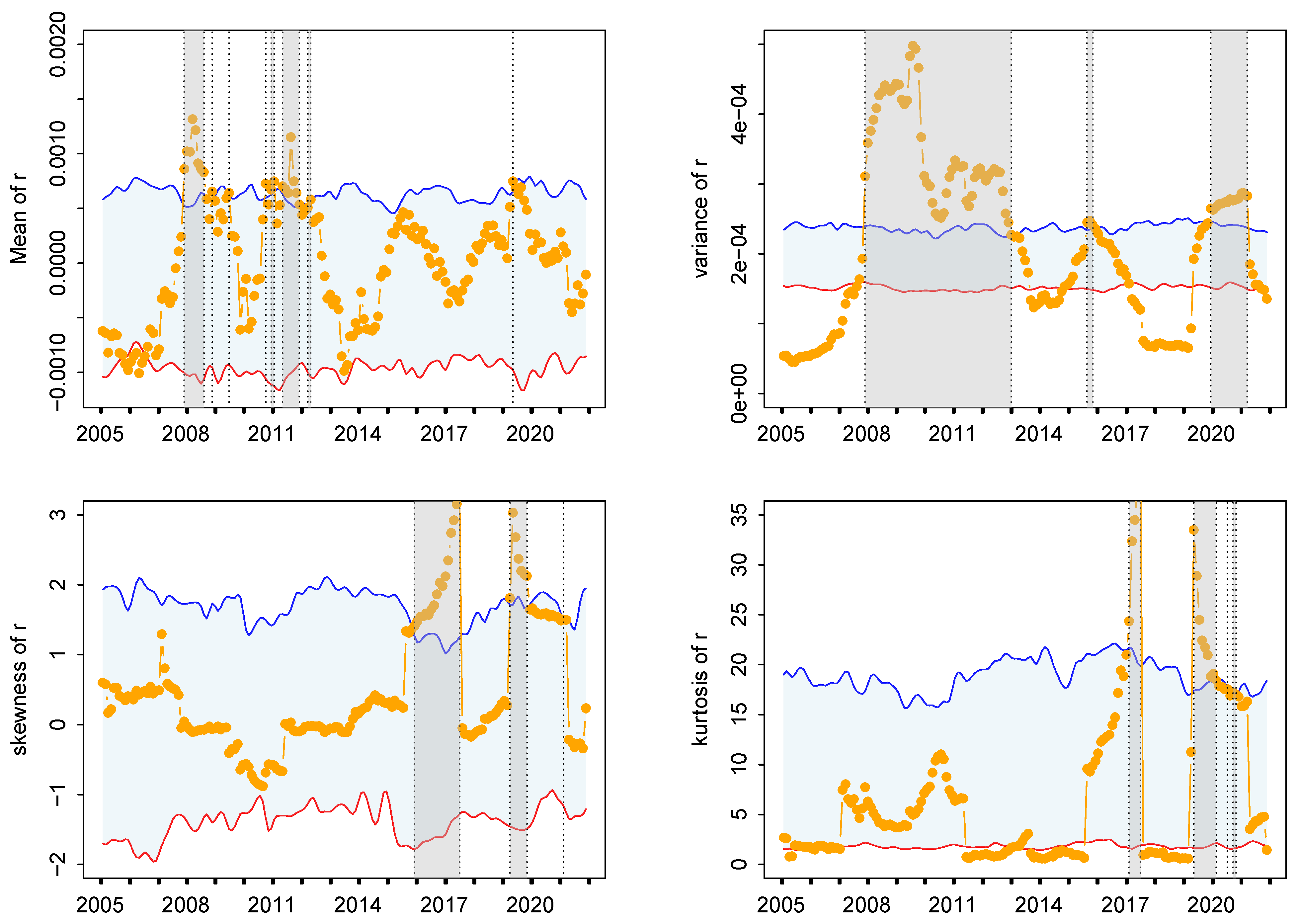
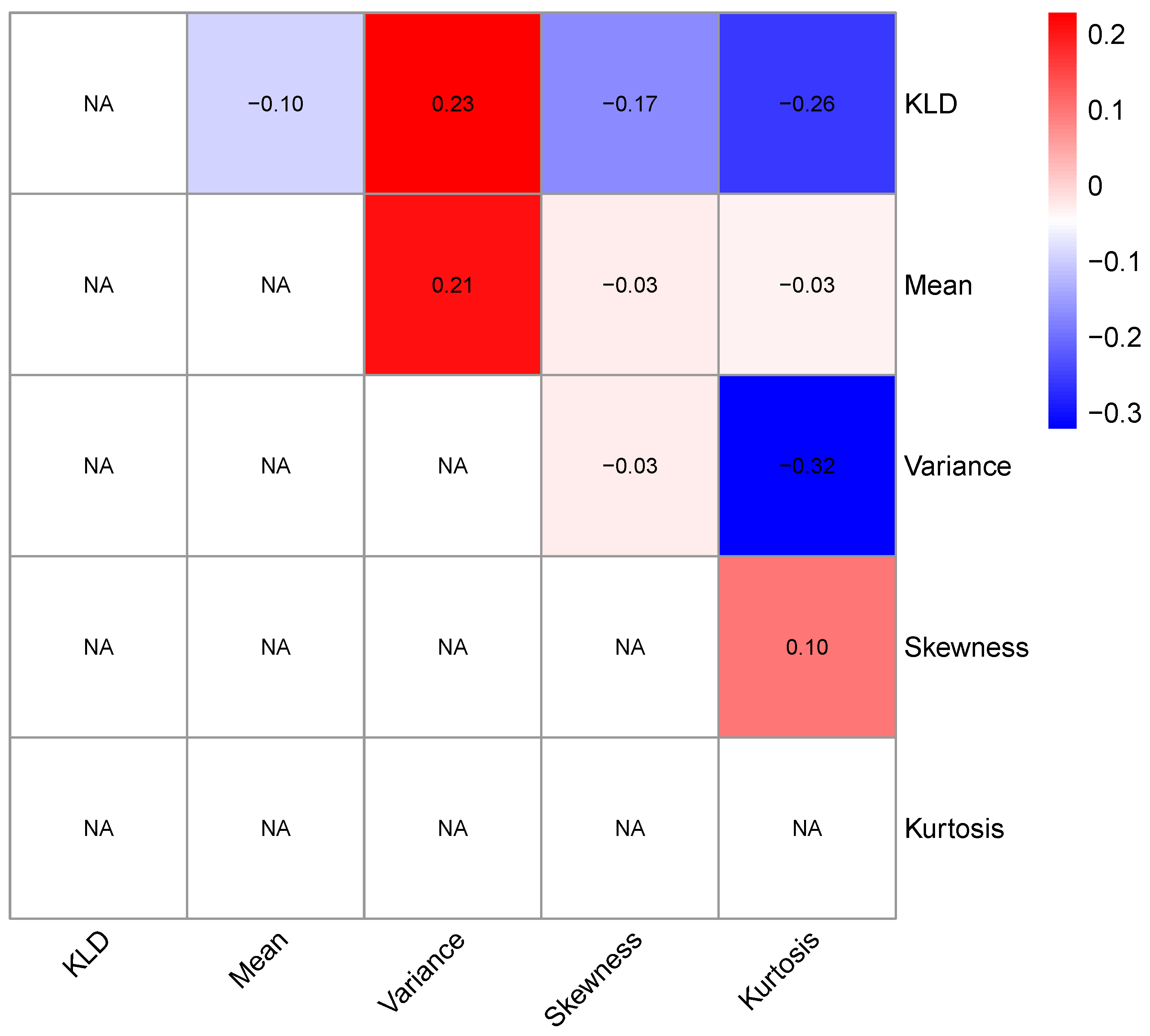
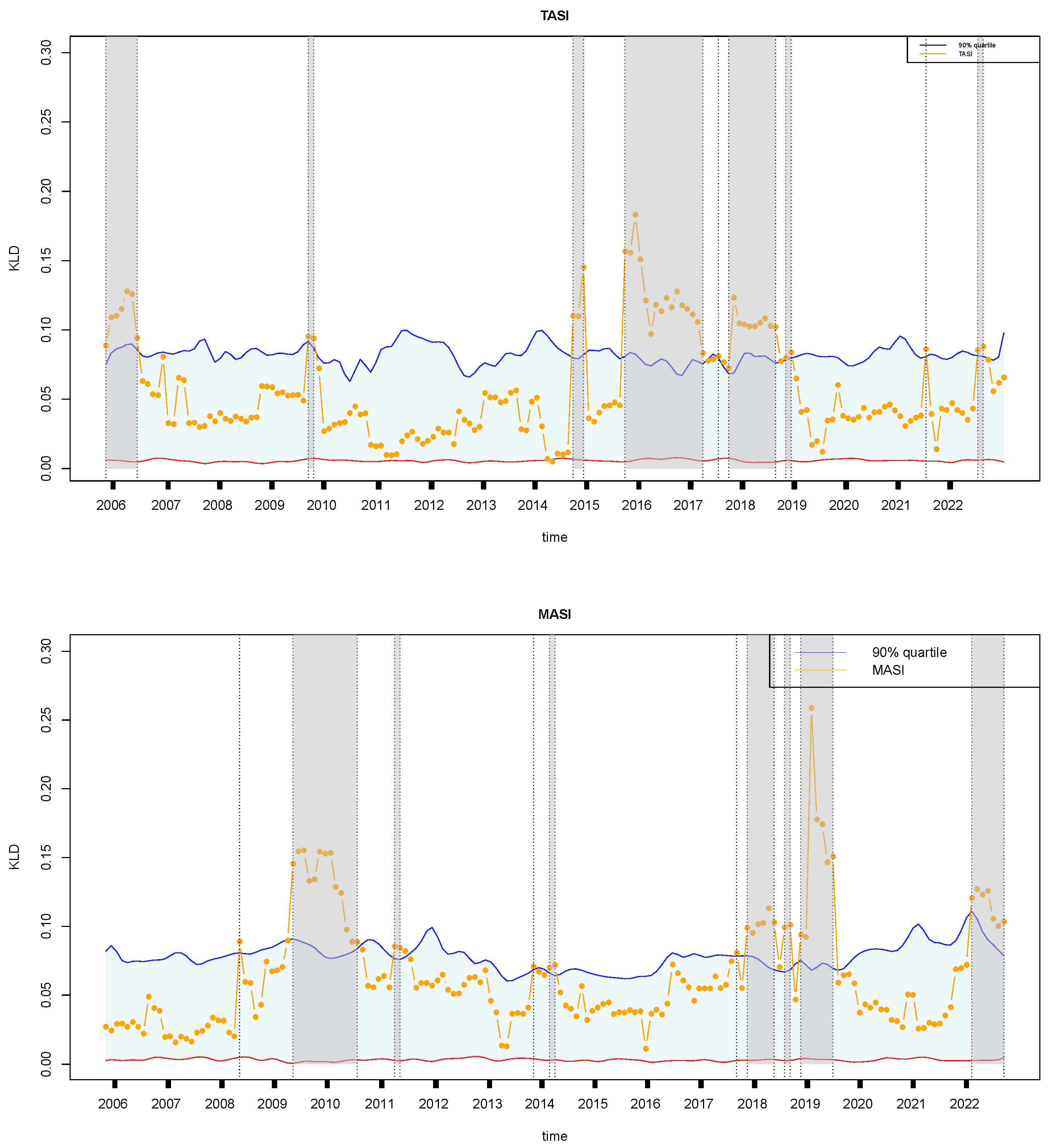
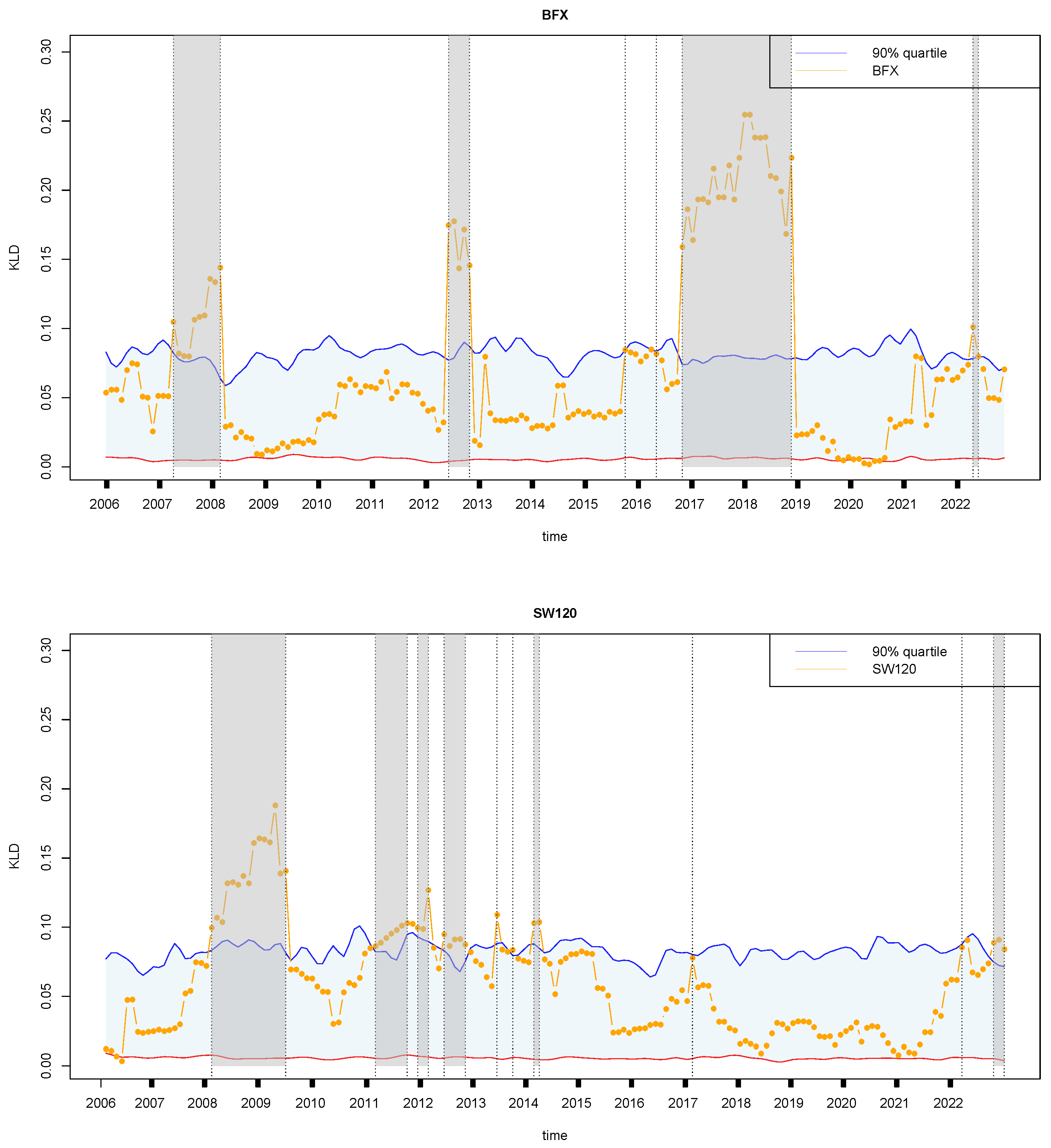
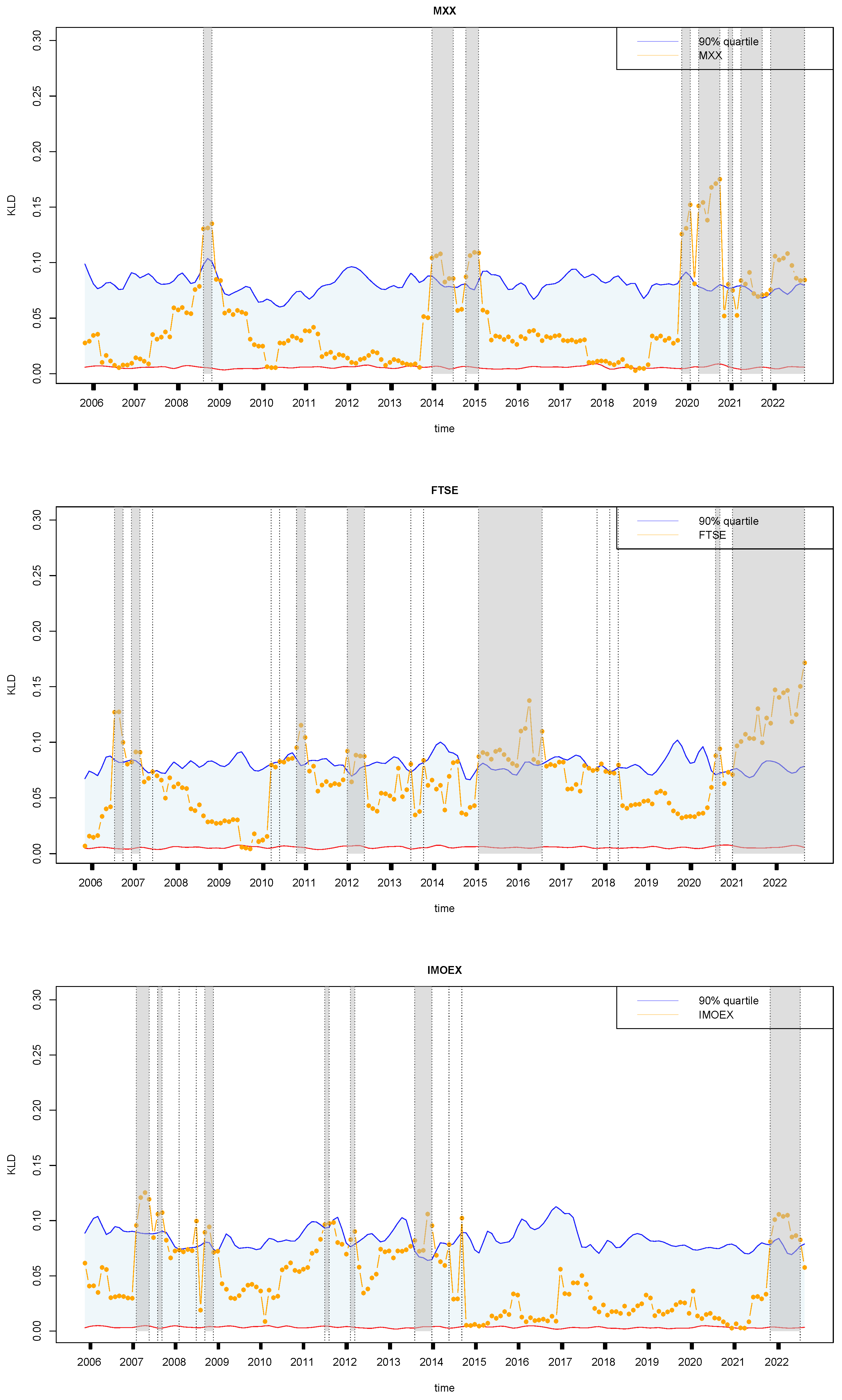
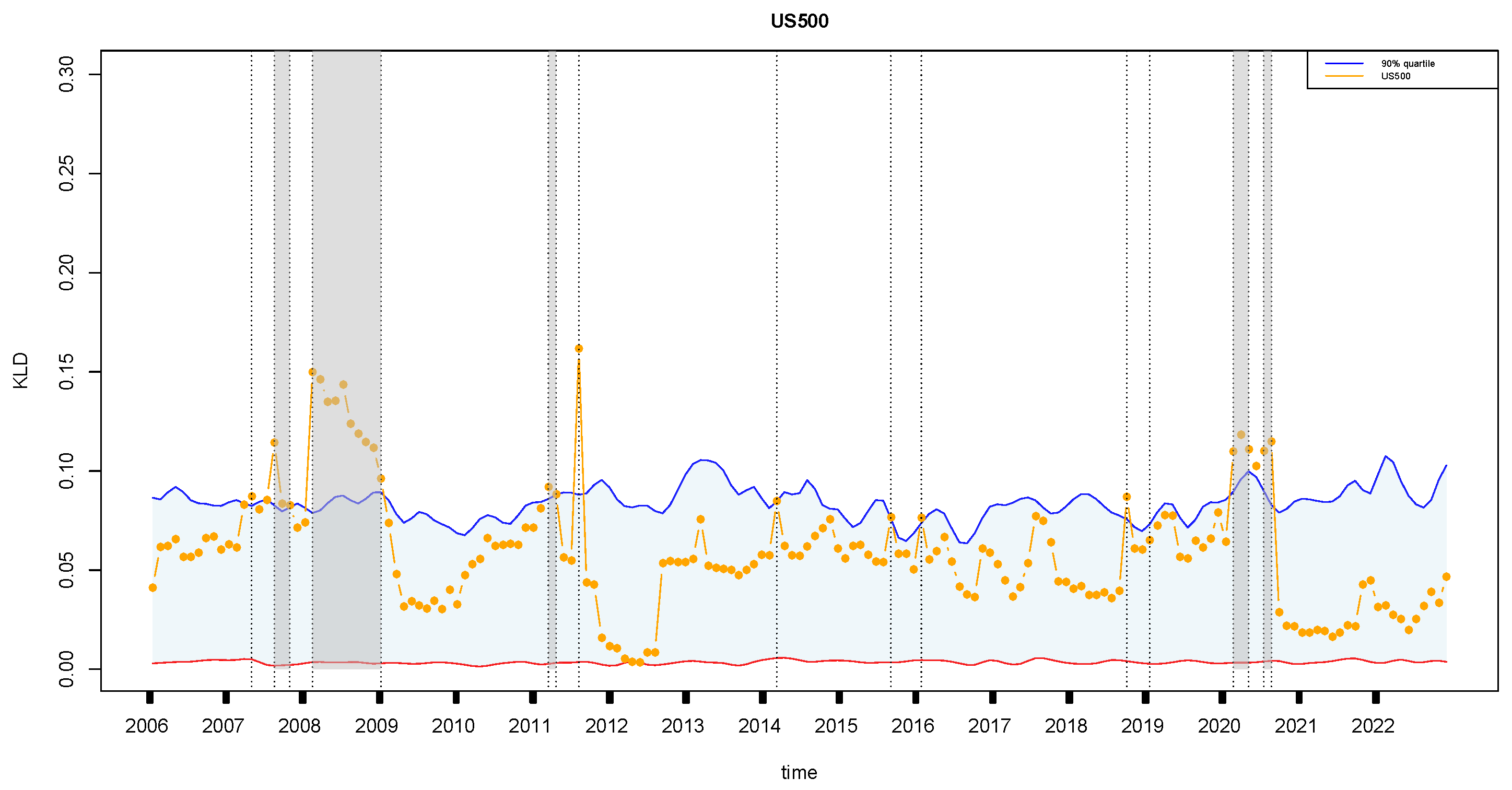
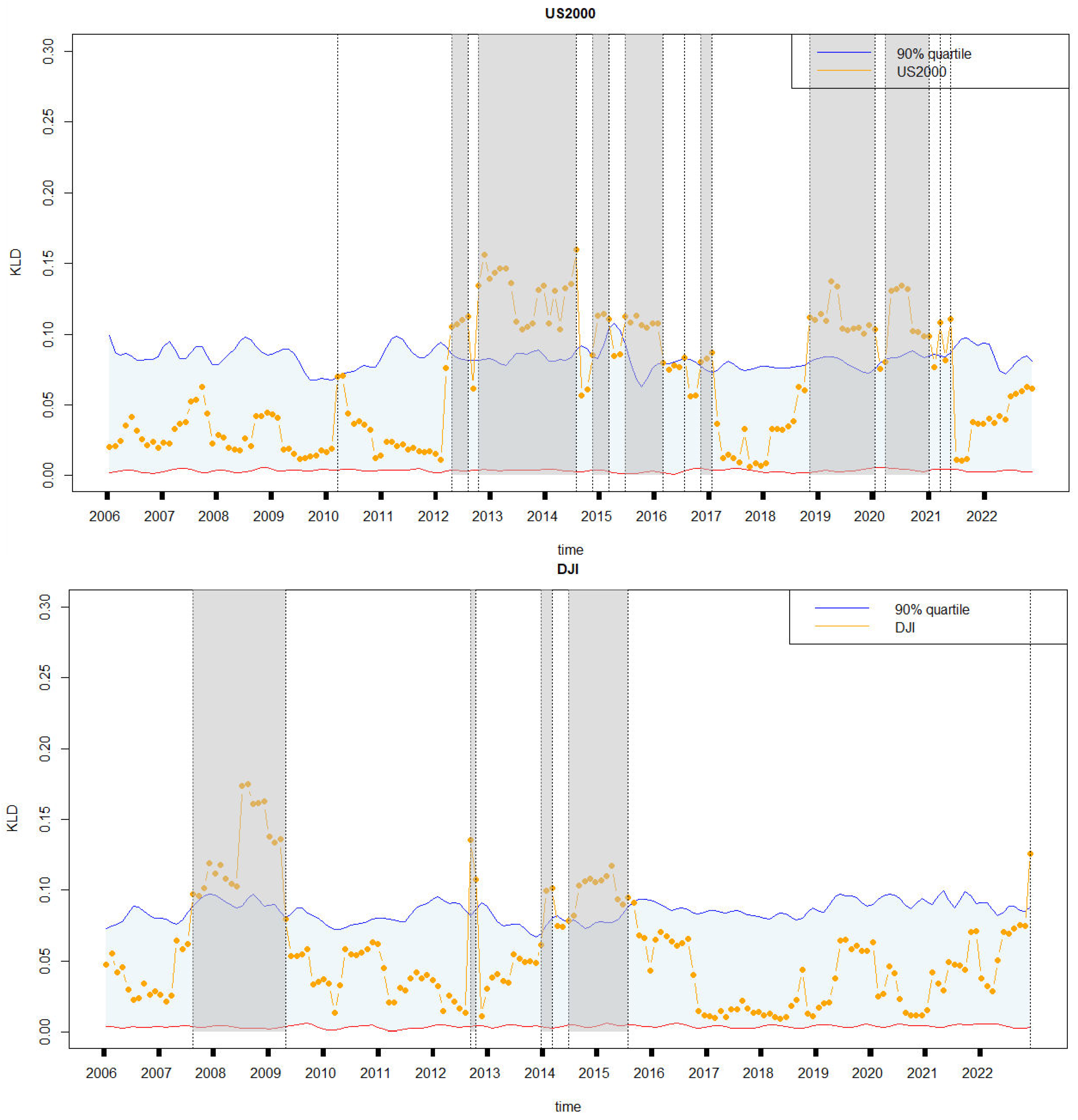
4.3. Retrospective Analysis for Other Financial Markets
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Donges, J.F.; Donner, R.V.; Kurths, J. Testing time series irreversibility using complex network methods. Europhys. Lett. 2013, 102, 10004. [Google Scholar] [CrossRef]
- Rong, L.; Shang, P. New irreversibility measure and complexity analysis based on singular value decomposition. Phys. A Stat. Mech. Its Appl. 2018, 512, 913–924. [Google Scholar] [CrossRef]
- Lacasa, L.; Flanagan, R. Time reversibility from visibility graphs of nonstationary processes. Phys. Rev. E 2015, 92, 022817. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, A. Weighted link entropy and multiscale weighted link entropy for complex time series. Nonlinear Dyn. 2021, 105, 541–554. [Google Scholar] [CrossRef]
- Yao, W.; Wang, J.; Perc, M.; Yao, W.; Dai, J.; Guo, D.; Yao, D. Time irreversibility and amplitude irreversibility measures for nonequilibrium processes. Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105688. [Google Scholar] [CrossRef]
- Li, J.; Shang, P.; Zhang, X. Time series irreversibility analysis using Jensen–Shannon divergence calculated by permutation pattern. Nonlinear Dyn. 2019, 96, 2637–2652. [Google Scholar] [CrossRef]
- Wang, Z.; Shang, P.; Shang, B. Time irreversibility analysis and abnormality detection based on Riemannian geometry for complex time series. Commun. Nonlinear Sci. Numer. Simul. 2023, 117, 106985. [Google Scholar] [CrossRef]
- Ding, D.; Gandy, A.; Hahn, G. A simple method for implementing Monte Carlo tests. Comput. Stat. 2020, 35, 1373–1392. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Chen, Y.; Mantegna, R.N.; Pantelous, A.A.; Zuev, K.M. A dynamic analysis of S&P 500, FTSE 100 and EURO STOXX 50 indices under different exchange rates. PLoS ONE 2018, 13, e0194067. [Google Scholar]
- Rasel, R.I.; Sultana, N.; Hasan, N. Financial Instability Analysis using ANN and Feature Selection Technique: Application to Stock Market Price Prediction. In Proceedings of the 2016 International Conference on Innovations in Science, Engineering and Technology (ICISET 2016), Dhaka, Bangladesh, 28–29 October 2016. [Google Scholar]
- Recchioni, M.C.; Tedeschi, G. From Bond Yield to Macroeconomic Instability: A Parsimonious Affine Model. Eur. J. Oper. Res. 2017, 262, 1116–1135. [Google Scholar] [CrossRef]
- Di Persio, L.; Frigo, M. Gibbs Sampling Approach to Regime Switching Analysis of Financial Time Series. J. Comput. Appl. Math. 2016, 300, 43–55. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Gonçalves, B.A.; Carpi, L.; Rosso, O.A.; Ravetti, M.G. Time series characterization via horizontal visibility graph and Information Theory. Phys. A Stat. Mech. Its Appl. 2016, 464, 93–102. [Google Scholar] [CrossRef]
- Schleussner, C.-F.; Divine, D.V.; Donges, J.F.; Miettinen, A.; Donner, R.V. Indications for a North Atlantic ocean circulation regime shift at the onset of the Little Ice Age. Clim. Dyn. 2015, 45, 3623–3633. [Google Scholar] [CrossRef]
- Vamvakaris, M.D.; Pantelous, A.A.; Zuev, K.M. Time series analysis of S&P 500 index: A horizontal visibility graph approach. Phys. A Stat. Mech. Its Appl. 2018, 497, 41–51. [Google Scholar]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef]
- Zou, Y.; Donner, R.V.; Marwan, N.; Donges, J.F.; Kurths, J. Complex network approaches to nonlinear time series analysis. Phys. Rep. 2019, 787, 1–97. [Google Scholar] [CrossRef]
- Lacasa, L.; Nunez, A.; Roldán, É.; Parrondo, J.M.; Luque, B. Time series irreversibility: A visibility graph approach. Eur. Phys. J. B 2012, 85, 217. [Google Scholar] [CrossRef]
- Flanagan, R.; Lacasa, L. Irreversibility of financial time series: A graph-theoretical approach. Phys. Lett. A 2016, 380, 1689–1697. [Google Scholar] [CrossRef]
- Sippel, S.; Lange, H.; Gans, F. Statcomp: Statistical Complexity and Information Measures for Time Series Analysis. 2019. Available online: https://CRAN.R-project.org/package=statcomp (accessed on 15 January 2025).
- Csárdi, G.; Nepusz, T. The igraph software package for complex network research. Inter J. Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Zeileis, A.; Leisch, F.; Hornik, K.; Kleiber, C. Strucchange: An R Package for Testing for Structural Change in Linear Regression Models. 2002. Available online: https://cran.r-project.org/web/packages/strucchange/index.html (accessed on 15 January 2025).
- Zeileis, A.; Leisch, F.; Hornik, K.; Kleiber, C. strucchange: An R Package for Testing for Structural Change in Linear Regression Models. J. Stat. Softw. 2002, 7, 1–38. [Google Scholar] [CrossRef]
- Nicolau, J. Modeling financial time series through second-order stochastic differential equations. Stat. Probab. Lett. 2008, 78, 2700–2704. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Heston, S.L. A Closed-Form Solution for Options with Stochastic Volatility. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Gatheral, J.; Jaisson, T.; Rosenbaum, M. Volatility is rough. Quant. Financ. 2018, 18, 933–949. [Google Scholar] [CrossRef]
- El Euch, O.; Rosenbaum, M. The characteristic function of rough Heston models. Math. Financ. 2019, 29, 3–38. [Google Scholar] [CrossRef]
- Merton, R.C. Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef]
- Cont, R.; Tankov, P. Financial Modelling with Jump Processes; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Hamilton, J.D. A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Sirignano, J.; Cont, R. Universal Features of Price Formation in Financial Markets: Perspectives from Deep Learning. Quant. Financ. 2019, 19, 1449–1459. [Google Scholar] [CrossRef]
- Beck, C.; Becker, S.; Grohs, P.; Jaafari, N.; Jentzen, A. Solving the Kolmogorov PDE by Means of Deep Learning. J. Sci. Comput. 2021, 88, 73. [Google Scholar] [CrossRef]
- Núñez, A.M.; Lacasa, L.; Valero, E.; Luque, B. Detecting series periodicity with horizontal visibility graphs. Int. J. Bifurc. Chaos 2012, 22, 1250160. [Google Scholar] [CrossRef]
- Gao, M.; Ge, R. Mapping time series into signed networks via horizontal visibility graph. Phys. A 2024, 633, 129404. [Google Scholar] [CrossRef]
| Country | Index |
|---|---|
| (1) Spain | IBEX 35 INDEX (ES35) |
| (2) Poland | WIG20 INDEX (WIG20) |
| (3) Belgium | Belgium BEL20 INDEX (BFX) |
| (4) France | France CAC40 INDEX (FCHI) |
| (5) Switzerland | Swiss SWI20 INDEX (SW120) |
| (6) The Netherlands | Netherlands AEX INDEX (AEX) |
| (7) England | UK FTSE 100(FTSE) |
| (8) Russia | MOEX Russia INDEX (IMOEX) |
| (9) Denmark | OMX20 INDEX (OMX20) |
| (10) Sweden | OMX Stockholm 30 INDEX (OMX30) |
| (11) Germany | Germany DAX 30 INDEX (DE40) |
| (12) Italy | Italy FTSE MIB INDEX (FTMIB) |
| (13) Saudi Arabia | TASI INDEX (TASI) |
| (14) Morocco | MASI INDEX (MASI) |
| (15) South Africa | South Africa 40 INDEX (SA40) |
| (16) Brazil | Brazil Stock INDEX (BVSP) |
| (17) Argentina | S&P Merval INDEX (MERV) |
| (18) Japan | Nikkei 225 INDEX (JP225) |
| (19) Thailand | Thailand SET INDEX (SETI) |
| (20) Pakistan | Karachi 100 INDEX (KSE) |
| (21) Indonesia | Jakarta Composite INDEX (JKSE) |
| (22) India | India S&P CNX NIFTY INDEX (NSEI) |
| (23) Turkey | Turkey Istanbul 100 INDEX (XU100) |
| (24) Mexico | Mexico S&P/BMV IPC INDEX (MXX) |
| (25) United States | S&P 500 INDEX (US 500) |
| (26) United States | US 2000 Cash INDEX (US2000) |
| (27) United States | Dow Jones industrial average INDEX (DJI) |
| (28) Canada | S&P/TSX Composite INDEX (GSPTSE) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Yang, Y.; Wang, Z.; Gao, M. Instability of Financial Time Series Revealed by Irreversibility Analysis. Entropy 2025, 27, 402. https://doi.org/10.3390/e27040402
Fan Y, Yang Y, Wang Z, Gao M. Instability of Financial Time Series Revealed by Irreversibility Analysis. Entropy. 2025; 27(4):402. https://doi.org/10.3390/e27040402
Chicago/Turabian StyleFan, Youping, Yutong Yang, Zhen Wang, and Meng Gao. 2025. "Instability of Financial Time Series Revealed by Irreversibility Analysis" Entropy 27, no. 4: 402. https://doi.org/10.3390/e27040402
APA StyleFan, Y., Yang, Y., Wang, Z., & Gao, M. (2025). Instability of Financial Time Series Revealed by Irreversibility Analysis. Entropy, 27(4), 402. https://doi.org/10.3390/e27040402