Quantum Synchronization via Active–Passive Decomposition Configuration: An Open Quantum-System Study
Abstract
1. Introduction
2. Criteria for Quantum Synchronization
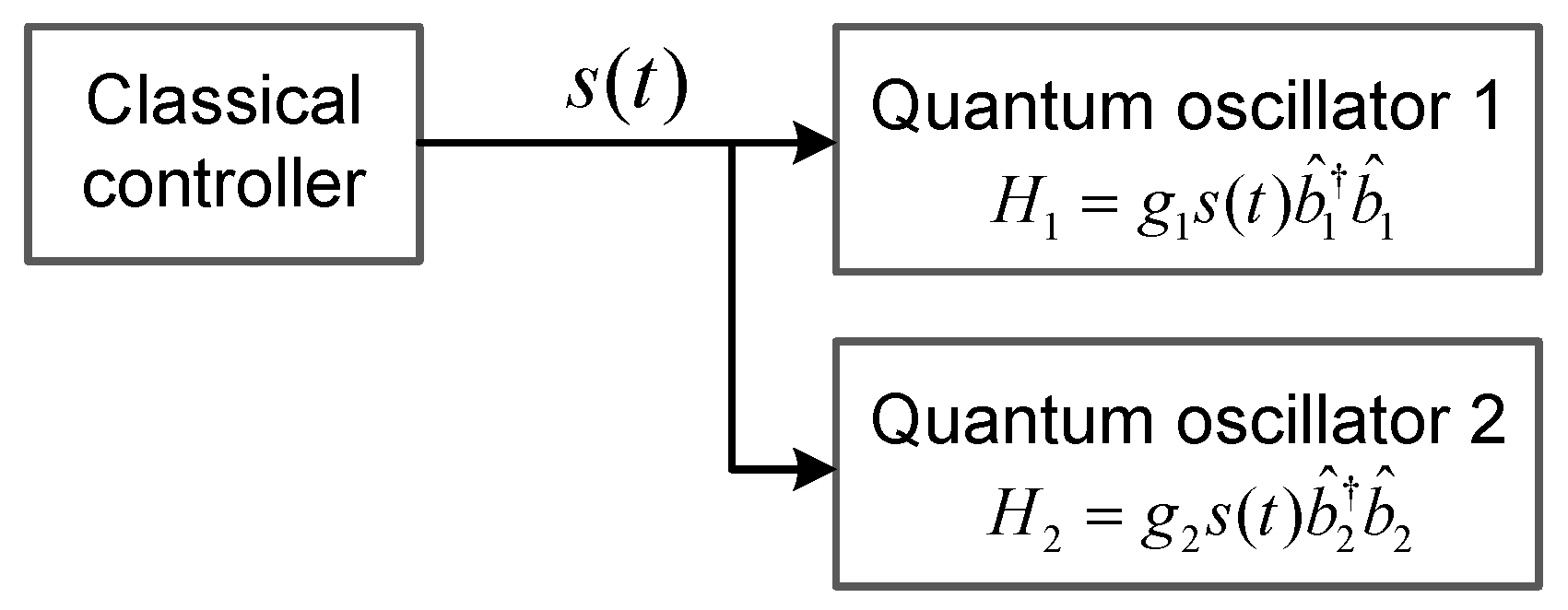
3. Synchronization of Two Quantum Harmonic Oscillators Based on Active–Passive Decomposition Configuration
3.1. The Equations of Motions for the Second-Order Terms of the Quantum Harmonic Oscillators and
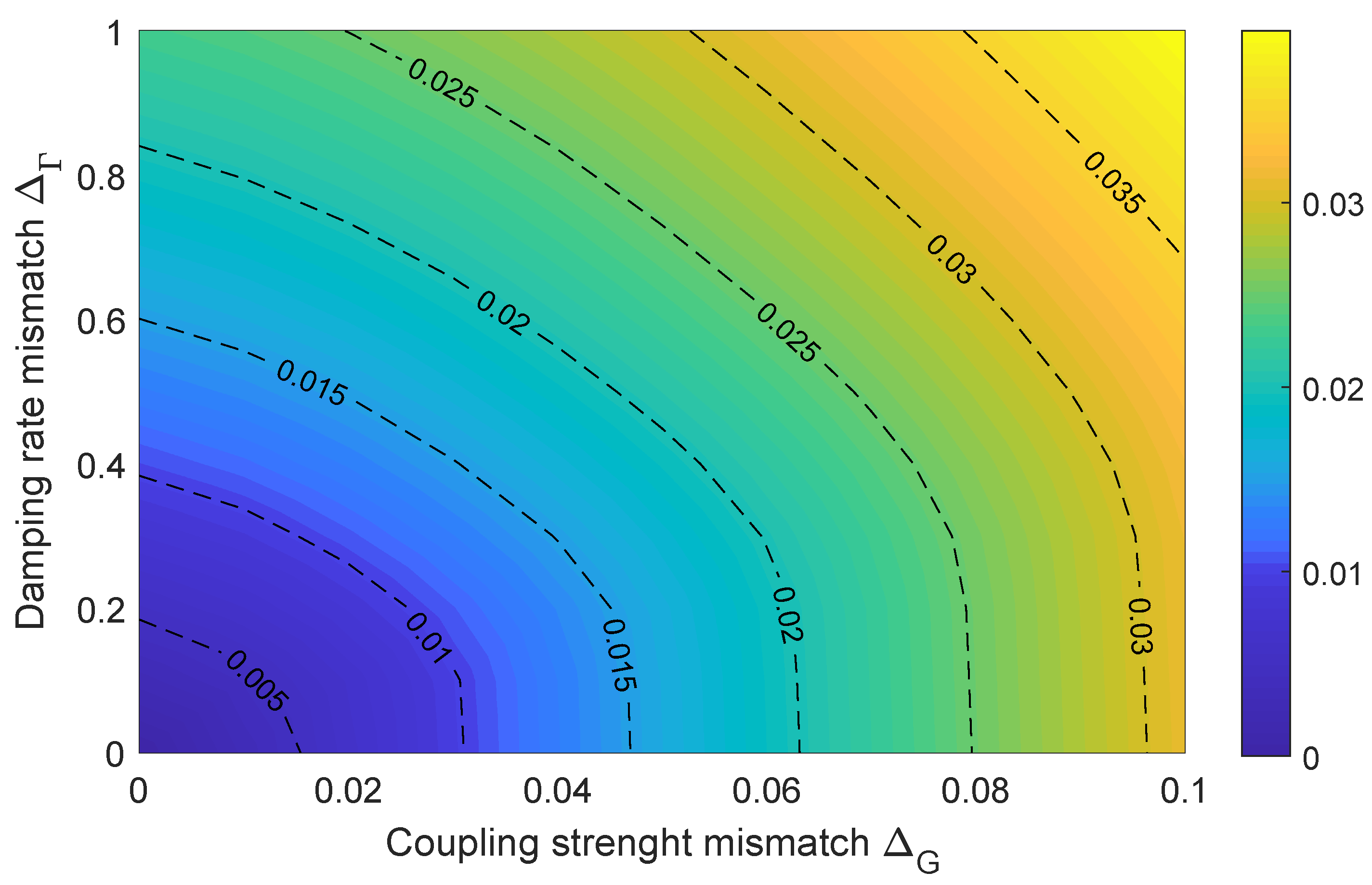
3.2. Quantum Synchronization of Dissipative Harmonic Oscillators
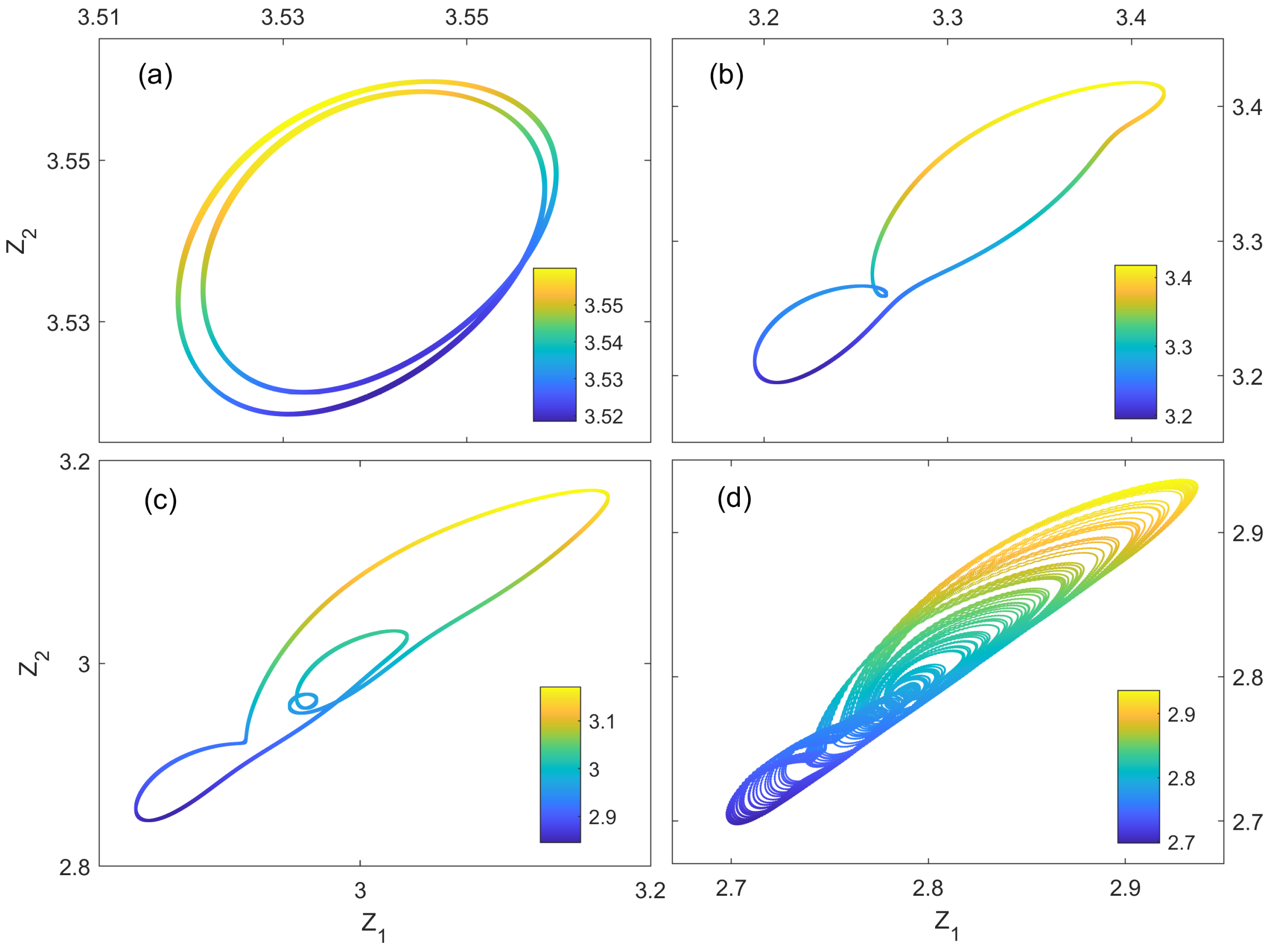
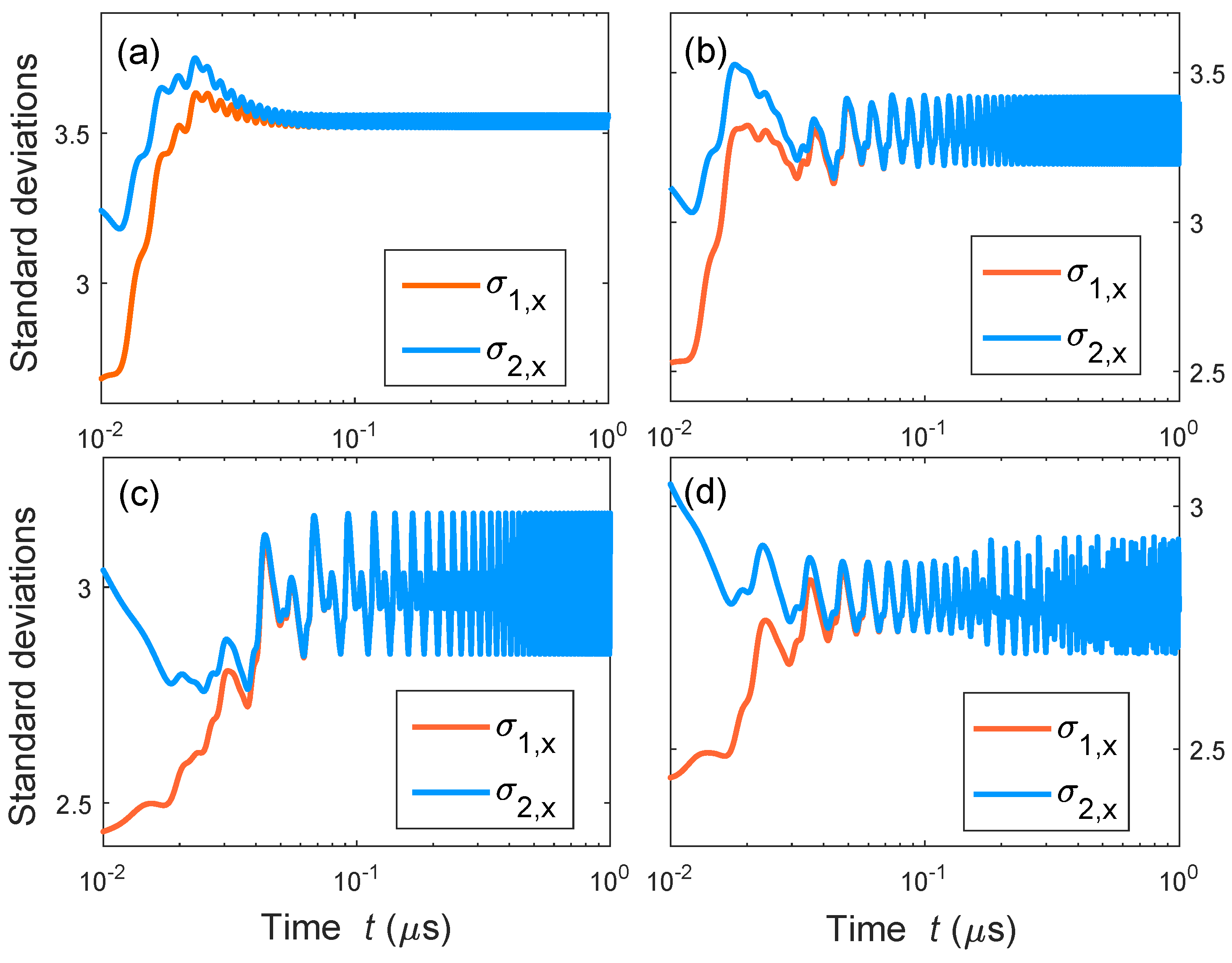
4. A Quantum Synchronization Model: Periodic and Chaotic Motions
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| APD | Active–Passive Decomposition |
References
- Hugenii, C. Horologium Oscillatorium; Apud F. Muguet: Paris, France, 1673. [Google Scholar]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Strogatz, S. Sync: The Emerging Science of Spontaneous Order; Penguin: London, UK, 2004. [Google Scholar]
- Adler, R. A Study of Locking Phenomena in Oscillators. Proc. IRE 1946, 34, 351–357. [Google Scholar] [CrossRef]
- Kuramoto, Y. Self-entrainment of a population of coupled non-linear oscillators. In International Symposium on Mathematical Problems in Theoretical Physics; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1975; Volume 39, pp. 420–422. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Kocarev, L.; Parlitz, U. General Approach for Chaotic Synchronization with Applications to Communication. Phys. Rev. Lett. 1995, 74, 5028. [Google Scholar] [CrossRef]
- Parlitz, U.; Kocarev, L.; Stojanovski, T.; Preckel, H. Encoding messages using chaotic synchronization. Phys. Rev. E 1996, 53, 4351. [Google Scholar] [CrossRef] [PubMed]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Phase Synchronization of Chaotic Oscillators. Phys. Rev. Lett. 1996, 76, 1804. [Google Scholar] [CrossRef]
- Rosa, E.; Ott, E.; Hess, M.H. Transition to Phase Synchronization of Chaos. Phys. Rev. Lett. 1998, 80, 1642. [Google Scholar] [CrossRef]
- Rulkov, N.F.; Sushchik, M.M.; Tsimring, L.S.; Abarbanel, H.D.I. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980. [Google Scholar] [CrossRef]
- Kocarev, L.; Parlitz, U. Generalized Synchronization, Predictability, and Equivalence of Unidirectionally Coupled Dynamical Systems. Phys. Rev. Lett. 1996, 76, 1816. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. From Phase to Lag Synchronization in Coupled Chaotic Oscillators. Phys. Rev. Lett. 1997, 78, 4193. [Google Scholar] [CrossRef]
- Xu, M.H.; Tieri, D.A.; Fine, E.C.; Thompson, J.K.; Holland, M.J. Synchronization of Two Ensembles of Atoms. Phys. Rev. Lett. 2014, 113, 154101. [Google Scholar] [CrossRef]
- Karpat, G.; Yalcinkaya, I.; Cakmak, B. Quantum synchronization of few-body systems under collective dissipation. Phys. Rev. A 2020, 101, 042121. [Google Scholar] [CrossRef]
- Siwiak-Jaszek, S.; Le, T.P.; Olaya-Castro, A. Synchronization phase as an indicator of persistent quantum correlations between subsystems. Phys. Rev. A 2020, 102, 032414. [Google Scholar] [CrossRef]
- Jaseem, N.; Hajdušek, M.; Vedral, V.; Fazio, R.; Kwek, L.C.; Vinjanampathy, S. Quantum synchronization in nanoscale heat engines. Phys. Rev. E 2020, 101, 020201. [Google Scholar] [CrossRef] [PubMed]
- Zhirov, O.V.; Shepelyansky, D.L. Synchronization and Bistability of a Qubit Coupled to a Driven Dissipative Oscillator. Phys. Rev. Lett. 2008, 100, 014101. [Google Scholar] [CrossRef]
- Zhirov, O.V.; Shepelyansky, D.L. Quantum synchronization and entanglement of two qubits coupled to a driven dissipative resonator. Phys. Rev. B 2009, 80, 014519. [Google Scholar] [CrossRef]
- Giorgi, G.L.; Galve, F.; Zambrini, R. Probing the spectral density of a dissipative qubit via quantum synchronization. Phys. Rev. A 2016, 94, 052121. [Google Scholar] [CrossRef]
- Cattaneo, M.; Giorgi, G.L.; Maniscalco, S.; Paraoanu, G.S.; Zambrini, R. Bath-Induced Collective Phenomena on Superconducting Qubits: Synchronization, Subradiance, and Entanglement Generation. Ann. Phys. 2021, 533, 2100038. [Google Scholar] [CrossRef]
- Hush, M.R.; Li, W.B.; Genway, S.; Lesanovsky, I.; Armour, A.D. Spin correlations as a probe of quantum synchronization in trapped-ion phonon lasers. Phys. Rev. A 2015, 91, 061401. [Google Scholar] [CrossRef]
- Orth, P.P.; Roosen, D.; Hofstetter, W.; Le Hur, K. Dynamics, synchronization, and quantum phase transitions of two dissipative spins. Phys. Rev. B 2010, 82, 144423. [Google Scholar] [CrossRef]
- Bellomo, B.; Giorgi, G.L.; Palma, G.M.; Zambrini, R. Quantum synchronization as a local signature of super- and subradiance. Phys. Rev. A 2017, 95, 043807. [Google Scholar] [CrossRef]
- Roulet, A.; Bruder, C. Synchronizing the Smallest Possible System. Phys. Rev. Lett. 2018, 121, 053601. [Google Scholar] [CrossRef] [PubMed]
- Giorgi, G.L.; Plastina, F.; Francica, G.; Zambrini, R. Spontaneous synchronization and quantum correlation dynamics of open spin systems. Phys. Rev. A 2013, 88, 042115. [Google Scholar] [CrossRef]
- Karpat, G.; Yalcinkaya, I.; Cakmak, B. Quantum synchronization in a collision model. Phys. Rev. A 2019, 100, 012133. [Google Scholar] [CrossRef]
- Tindall, J.; Muñoz, C.S.; Buča, B.; Jaksch, D. Quantum synchronisation enabled by dynamical symmetries and dissipation. New J. Phys. 2020, 22, 013026. [Google Scholar] [CrossRef]
- Goychuk, I.; Casado-Pascual, J.; Morillo, M.; Lehmann, J.; Hänggi, P. Quantum Stochastic Synchronization. Phys. Rev. Lett. 2006, 97, 210601. [Google Scholar] [CrossRef]
- Cabot, A.; Giorgi, G.L.; Galve, F.; Zambrini, R. Quantum Synchronization in Dimer Atomic Lattices. Phys. Rev. Lett. 2019, 123, 023604. [Google Scholar] [CrossRef] [PubMed]
- Michailidis, A.A.; Turner, C.J.; Papić, Z.; Abanin, D.A.; Serbyn, M. Stabilizing two-dimensional quantum scars by deformation and synchronization. Phys. Rev. Res. 2020, 2, 022065. [Google Scholar] [CrossRef]
- Siwiak-Jaszek, S.; Olaya-Castro, A. Transient synchronisation and quantum coherence in a bio-inspired vibronic dimer. Faraday Discuss. 2019, 216, 38–56. [Google Scholar] [CrossRef]
- Lee, T.E.; Sadeghpour, H.R. Quantum Synchronization of Quantum van der Pol Oscillators with Trapped Ions. Phys. Rev. Lett. 2013, 111, 234101. [Google Scholar] [CrossRef]
- Lee, T.E.; Chan, C.K.; Wang, S. Entanglement tongue and quantum synchronization of disordered oscillators. Phys. Rev. E 2014, 89, 022913. [Google Scholar] [CrossRef]
- Walter, S.; Nunnenkamp, A.; Bruder, C. Quantum synchronization of two Van der Pol oscillators. Ann. Phys. 2015, 527, 131. [Google Scholar] [CrossRef]
- Sonar, S.; Hajdušek, M.; Mukherjee, M.; Fazio, R.; Vedral, V.; Vinjanampathy, S.; Kwek, L.C. Squeezing Enhances Quantum Synchronization. Phys. Rev. Lett. 2018, 120, 163601. [Google Scholar] [CrossRef]
- Eneriz, H.; Rossatto, D.Z.; Cárdenas-López, F.A.; Solano, E.; Sanz, M. Degree of Quantumness in Quantum Synchronization. Sci. Rep. 2019, 9, 19933. [Google Scholar] [CrossRef]
- Mok, W.K.; Kwek, L.C.; Heimonen, H. Synchronization boost with single-photon dissipation in the deep quantum regime. Phys. Rev. Res. 2020, 2, 033422. [Google Scholar] [CrossRef]
- Yuzuru, K.; Nakao, H. Enhancement of quantum synchronization via continuous measurement and feedback control. New J. Phys. 2021, 23, 013007. [Google Scholar] [CrossRef]
- Giorgi, G.L.; Galve, F.; Manzano, G.; Colet, P.; Zambrini, R. Quantum correlations and mutual synchronization. Phys. Rev. A 2012, 85, 052101. [Google Scholar] [CrossRef]
- Manzano, G.; Galve, F.; Giorgi, G.; Hernandez-Garcia, E.; Zambrini, R. Quantum correlations and entanglement in oscillator networks. Sci. Rep. 2013, 3, 1439. [Google Scholar] [CrossRef]
- Benedetti, C.; Galve, F.; Mandarino, A.; Paris, M.G.A.; Zambrini, R. Minimal model for spontaneous quantum synchronization. Phys. Rev. A 2016, 94, 052118. [Google Scholar] [CrossRef]
- Davis-Tilley, C.; Armour, A.D. Synchronization of micromasers. Phys. Rev. A 2016, 94, 063819. [Google Scholar] [CrossRef]
- Walter, S.; Nunnenkamp, A.; Bruder, C. Quantum Synchronization of a Driven Self-Sustained Oscillator. Phys. Rev. Lett. 2014, 112, 094102. [Google Scholar] [CrossRef]
- Makino, K.; Hashimoto, Y.; Yoshikawa, J.I.; Ohdan, H.; Toyama, T.; Van Loock, P.; Furusawa, A. Synchronization of optical photons for quantum information processing. Sci. Adv. 2016, 2, e1501772. [Google Scholar] [CrossRef] [PubMed]
- Lörch, N.; Amitai, E.; Nunnenkamp, A.; Bruder, C. Genuine Quantum Signatures in Synchronization of Anharmonic Self-Oscillators. Phys. Rev. Lett. 2016, 117, 073601. [Google Scholar] [CrossRef] [PubMed]
- Lörch, N.; Nigg, S.E.; Nunnenkamp, A.; Tiwari, R.P.; Bruder, C. Quantum Synchronization Blockade: Energy Quantization Hinders Synchronization of Identical Oscillators. Phys. Rev. Lett. 2017, 118, 243602. [Google Scholar] [CrossRef]
- Nigg, S.E. Observing quantum synchronization blockade in circuit quantum electrodynamics. Phys. Rev. A 2018, 97, 013811. [Google Scholar] [CrossRef]
- Qiao, G.J.; Gao, H.X.; Liu, H.D.; Yi, X.X. Quantum synchronization of two mechanical oscillators in coupled optomechanical systems with Kerr nonlinearity. Sci. Rep. 2018, 8, 15614. [Google Scholar] [CrossRef] [PubMed]
- Wächtler, C.W.; Bastidas, V.M.; Schaller, G.; Munro, W.J. Dissipative nonequilibrium synchronization of topological edge states via self-oscillation. Phys. Rev. B 2020, 102, 014309. [Google Scholar] [CrossRef]
- Koppenhöfer, M.; Bruder, C.; Roulet, A. Quantum synchronization on the IBM Q system. Phys. Rev. Res. 2020, 2, 023026. [Google Scholar] [CrossRef]
- Amitai, E.; Lörch, N.; Nunnenkamp, A.; Walter, S.; Bruder, C. Synchronization of an optomechanical system to an external drive. Phys. Rev. A 2017, 95, 053858. [Google Scholar] [CrossRef]
- Liao, C.G.; Chen, R.X.; Xie, H.; He, M.Y.; Lin, X.M. Quantum synchronization and correlations of two mechanical resonators in a dissipative optomechanical system. Phys. Rev. A 2019, 99, 033818. [Google Scholar] [CrossRef]
- Heinrich, G.; Ludwig, M.; Qian, J.; Kubala, B.; Marquardt, F. Collective Dynamics in Optomechanical Arrays. Phys. Rev. Lett. 2011, 107, 043603. [Google Scholar] [CrossRef]
- Ludwig, M.; Marquardt, F. Quantum Many-Body Dynamics in Optomechanical Arrays. Phys. Rev. Lett. 2013, 111, 073603. [Google Scholar] [CrossRef]
- Weiss, T.; Kronwald, A.; Marquardt, F. Noise-induced transitions in optomechanical synchronization. New J. Phys. 2016, 18, 013043. [Google Scholar] [CrossRef]
- Li, T.; Bao, T.Y.; Zhang, Y.L.; Zou, C.L.; Zou, X.B.; Guo, G.C. Long-distance synchronization of unidirectionally cascaded optomechanical systems. Opt. Express 2016, 24, 12336. [Google Scholar] [CrossRef] [PubMed]
- Karpat, G.; Yalcinkaya, I.; Cakmak, B.; Giorgi, G.L.; Zambrini, R. Synchronization and non-Markovianity in open quantum systems. Phys. Rev. A 2021, 103, 062217. [Google Scholar] [CrossRef]
- Zhang, M.; Wiederhecker, G.S.; Manipatruni, S.; Barnard, A.; McEuen, P.; Lipson, M. Synchronization of Micromechanical Oscillators Using Light. Phys. Rev. Lett. 2012, 109, 233906. [Google Scholar] [CrossRef] [PubMed]
- Bagheri, M.; Poot, M.; Fan, L.; Marquardt, F.; Tang, H.X. Photonic Cavity Synchronization of Nanomechanical Oscillators. Phys. Rev. Lett. 2013, 111, 213902. [Google Scholar] [CrossRef]
- Matheny, M.H.; Grau, M.; Villanueva, L.G.; Karabalin, R.B.; Cross, M.C.; Roukes, M.L. Phase Synchronization of Two Anharmonic Nanomechanical Oscillators. Phys. Rev. Lett. 2014, 112, 014101. [Google Scholar] [CrossRef]
- Zhang, M.; Shah, S.; Cardenas, J.; Lipson, M. Synchronization and Phase Noise Reduction in Micromechanical Oscillator Arrays Coupled through Light. Phys. Rev. Lett. 2015, 115, 163902. [Google Scholar] [CrossRef]
- Shlomi, K.; Yuvaraj, D.; Baskin, I.; Suchoi, O.; Winik, R.; Buks, E. Synchronization in an optomechanical cavity. Phys. Rev. E 2015, 91, 032910. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Labousse, M.; Baker, C.; Goetschy, A.; Hease, W.; Gomez, C.; Lemaitre, A.; Leo, G.; Ciuti, C.; Favero, I. Light-Mediated Cascaded Locking of Multiple Nano-Optomechanical Oscillators. Phys. Rev. Lett. 2017, 118, 063605. [Google Scholar] [CrossRef]
- Kwasigroch, M.P.; Cooper, N.R. Synchronization transition in dipole-coupled two-level systems with positional disorder. Phys. Rev. A 2017, 96, 053610. [Google Scholar] [CrossRef]
- Pljonkin, A.; Rumyantsev, K.; Singh, P.K. Synchronization in Quantum Key Distribution Systems. Cryptography 2017, 1, 18. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Proceedings of the Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Sciamanna, M. Vibrations copying optical chaos. Nat. Photon. 2016, 10, 366. [Google Scholar] [CrossRef]
- Monifi, F.; Zhang, J.; Özdemir, S.K.; Peng, B.; Liu, Y.X.; Bo, F.; Nori, F.; Yang, L. Optomechanically induced stochastic resonance and chaos transfer between optical fields. Nat. Photon. 2016, 10, 399. [Google Scholar] [CrossRef]
- Bakemeier, L.; Alvermann, A.; Fehske, H. Route to Chaos in Optomechanics. Phys. Rev. Lett. 2015, 114, 013601. [Google Scholar] [CrossRef]
- Buters, F.M.; Eerkens, H.J.; Heeck, K.; Weaver, M.J.; Pepper, B.; de Man, S.; Bouwmeester, D. Experimental exploration of the optomechanical attractor diagram and its dynamics. Phys. Rev. A 2015, 92, 013811. [Google Scholar] [CrossRef]
- Carmon, T.; Cross, M.C.; Vahala, K.J. Chaotic Quivering of Micron-Scaled On-Chip Resonators Excited by Centrifugal Optical Pressure. Phys. Rev. Lett. 2007, 98, 167203. [Google Scholar] [CrossRef]
- Larson, J.; Horsdal, M. Photonic Josephson effect, phase transitions, and chaos in optomechanical systems. Phys. Rev. A 2011, 84, 021804. [Google Scholar] [CrossRef]
- Lee, S.B.; Yang, J.; Moon, S.; Lee, S.Y.; Shim, J.B.; Kim, S.W.; Lee, J.H.; An, K. Observation of an Exceptional Point in a Chaotic Optical Microcavity. Phys. Rev. Lett. 2009, 103, 134101. [Google Scholar] [CrossRef]
- Lü, X.Y.; Jing, H.; Ma, J.Y.; Wu, Y. PT-Symmetry-Breaking Chaos in Optomechanics. Phys. Rev. Lett. 2015, 114, 253601. [Google Scholar] [CrossRef]
- Wang, M.; Lü, X.Y.; Wang, Y.D.; You, J.Q.; Wu, Y. Macroscopic quantum entanglement in modulated optomechanics. Phys. Rev. A 2016, 94, 053807. [Google Scholar] [CrossRef]
- Ma, J.Y.; You, C.; Si, L.G.; Xiong, H.; Li, J.H.; Yang, X.X.; Wu, Y. Formation and manipulation of optomechanical chaos via a bichromatic driving. Phys. Rev. A 2014, 90, 043839. [Google Scholar] [CrossRef]
- Marino, F.; Marin, F. Coexisting attractors and chaotic canard explosions in a slow-fast optomechanical system. Phys. Rev. E 2013, 87, 052906. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Urrios, D.; Capuj, N.E.; Colombano, M.F.; Garcia, P.D.; Sledzinska, M.; Alzina, F.; Griol, A.; Martinez, A.; Sotomayor-Torres, C.M. Nonlinear dynamics and chaos in an optomechanical beam. Nat. Commun. 2017, 8, 14965. [Google Scholar] [CrossRef] [PubMed]
- Piazza, F.; Ritsch, H. Self-Ordered Limit Cycles, Chaos, and Phase Slippage with a Superfluid inside an Optical Resonator. Phys. Rev. Lett. 2015, 115, 163601. [Google Scholar] [CrossRef]
- Sun, Y.; Sukhorukov, A.A. Chaotic oscillations of coupled nanobeam cavities with tailored optomechanical potentials. Opt. Lett. 2014, 39, 3543–3546. [Google Scholar] [CrossRef]
- Suzuki, H.; Brown, E.; Sterling, R. Nonlinear dynamics of an optomechanical system with a coherent mechanical pump: Second-order sideband generation. Phys. Rev. A 2015, 92, 033823. [Google Scholar] [CrossRef]
- Walter, S.; Marquardt, F. Classical dynamical gauge fields in optomechanics. New J. Phys. 2016, 18, 113029. [Google Scholar] [CrossRef]
- Wang, G.L.; Huang, L.; Lai, Y.C.; Grebogi, C. Nonlinear Dynamics and Quantum Entanglement in Optomechanical Systems. Phys. Rev. Lett. 2014, 112, 110406. [Google Scholar] [CrossRef]
- Liao, J.Q.; Nori, F. Photon blockade in quadratically coupled optomechanical systems. Phys. Rev. A 2013, 88, 023853. [Google Scholar] [CrossRef]
- Wu, J.G.; Huang, S.W.; Huang, Y.J.; Zhou, H.; Yang, J.H.; Liu, J.M.; Yu, M.B.; Lo, G.Q.; Kwong, D.L.; Duan, S.K.; et al. Mesoscopic chaos mediated by Drude electron-hole plasma in silicon optomechanical oscillators. Nat. Commun. 2017, 8, 15570. [Google Scholar] [CrossRef] [PubMed]
- Yang, N.; Zhang, J.; Wang, H.; Liu, Y.X.; Wu, R.B.; Liu, L.Q.; Li, C.W.; Nori, F. Noise suppression of on-chip mechanical resonators by chaotic coherent feedback. Phys. Rev. A 2015, 92, 033812. [Google Scholar] [CrossRef]
- Yang, N.; Miranowicz, A.; Liu, Y.C.; Xia, K.; Nori, F. Chaotic synchronization of two optical cavity modes in optomechanical systems. Sci. Rep. 2019, 9, 15874. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, W.; Bhattacharya, M.; Meystre, P. Hamiltonian chaos in a coupled BEC–optomechanical-cavity system. Phys. Rev. A 2010, 81, 013802. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, B.; Kim, S.; Monifi, F.; Jiang, X.F.; Li, Y.H.; Yu, P.; Liu, L.Q.; Liu, Y.X.; Alù, A.; et al. Optomechanical dissipative solitons. Nature 2021, 600, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.L.; Wu, R.B.; Zhang, J.; Ozdemir, S.K.; Yang, L.; Nori, F.; Liu, Y.X. Controllable optical response by modifying the gain and loss of a mechanical resonator and cavity mode in an optomechanical system. Phys. Rev. A 2017, 95, 013843. [Google Scholar] [CrossRef]
- Wang, X.; Qin, W.; Miranowicz, A.; Savasta, S.; Nori, F. Unconventional cavity optomechanics: Nonlinear control of phonons in the acoustic quantum vacuum. Phys. Rev. A 2019, 100, 063827. [Google Scholar] [CrossRef]
- Qin, W.; Miranowicz, A.; Jing, H.; Nori, F. Generating Long-Lived Macroscopically Distinct Superposition States in Atomic Ensembles. Phys. Rev. Lett. 2021, 127, 093602. [Google Scholar] [CrossRef]
- Mari, A.; Farace, A.; Didier, N.; Giovannetti, V.; Fazio, R. Measures of Quantum Synchronization in Continuous Variable Systems. Phys. Rev. Lett. 2013, 111, 103605. [Google Scholar] [CrossRef]
- Buca, B.; Booker, C.; Jaksch, D. Algebraic theory of quantum synchronization and limit cycles under dissipation. SciPost Phys. 2022, 12, 097. [Google Scholar] [CrossRef]
- Gardiner, C.; Zoller, P. Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics; Springer Series in Synergetics; Springer: Berlin, Germany, 2004. [Google Scholar]
- Hu, B.L.; Paz, J.P.; Zhang, Y.H. Quantum Brownian motion in a general environment: Exact master equation with nonlocal dissipation and colored noise. Phys. Rev. D 1992, 45, 2843–2861. [Google Scholar] [CrossRef] [PubMed]
- Halliwell, J.J.; Yu, T. Alternative derivation of the Hu-Paz-Zhang master equation of quantum Brownian motion. Phys. Rev. D 1996, 53, 2012–2019. [Google Scholar] [CrossRef] [PubMed]
- Rivas, A.; Plato, A.D.K.; Huelga, S.F.; Plenio, M.B. Markovian master equations: A critical study. New J. Phys. 2010, 12, 113032. [Google Scholar] [CrossRef]
- Chou, C.H.; Yu, T.; Hu, B.L. Exact master equation and quantum decoherence of two coupled harmonic oscillators in a general environment. Phys. Rev. E 2008, 77, 011112. [Google Scholar] [CrossRef]
- Strunz, W.T.; Diósi, L.; Gisin, N.; Yu, T. Quantum Trajectories for Brownian Motion. Phys. Rev. Lett. 1999, 83, 4909. [Google Scholar] [CrossRef]
- Naghiloo, M.; Tan, D.; Harrington, P.M.; Lewalle, P.; Jordan, A.N.; Murch, K.W. Quantum caustics in resonance-fluorescence trajectories. Phys. Rev. A 2017, 96, 053807. [Google Scholar] [CrossRef]
- Mourik, V.; Asaad, S.; Firgau, H.; Pla, J.J.; Holmes, C.; Milburn, G.J.; McCallum, J.C.; Morello, A. Exploring quantum chaos with a single nuclear spin. Phys. Rev. E 2018, 98, 042206. [Google Scholar] [CrossRef]
- de Almeida, A.M.O. Hamiltonian Systems: Chaos and Quantization; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Ullmo, D. Many-body physics and quantum chaos. Rep. Prog. Phys. 2008, 71, 026001. [Google Scholar] [CrossRef]
- Wright, M.; Weaver, R. New Directions in Linear Acoustics and Vibration: Quantum Chaos, Random Matrix Theory and Complexity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Beenakker, C.W.J. Random-matrix theory of quantum transport. Rev. Mod. Phys. 1997, 69, 731. [Google Scholar] [CrossRef]
- Stockmann, H.J. Quantum Chaos: An Introduction; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Haake, F. Quantum signatures of chaos. In Quantum Coherence in Mesoscopic Systems; Springer: Berlin, Germany, 1991; pp. 583–595. [Google Scholar]
- Riser, R.; Osipov, V.A.; Kanzieper, E. Power Spectrum of Long Eigenlevel Sequences in Quantum Chaotic Systems. Phys. Rev. Lett. 2017, 118, 204101. [Google Scholar] [CrossRef] [PubMed]
- Neill, C.; Roushan, P.; Fang, M.; Chen, Y.; Kolodrubetz, M.; Chen, Z.; Megrant, A.; Barends, R.; Campbell, B.; Chiaro, B.; et al. Ergodic dynamics and thermalization in an isolated quantum system. Nat. Phys. 2016, 12, 1037–1041. [Google Scholar] [CrossRef]
- Słomczyński, W.; Życzkowski, K. Quantum chaos: An entropy approach. J. Math. Phys. 1994, 35, 5674. [Google Scholar] [CrossRef]
- Zurek, W.H.; Paz, J. Quantum chaos: A decoherent definition. Phys. D Nonlinear Phenom. 1995, 83, 300. [Google Scholar] [CrossRef]
- Chirikov, B.Y. Quantum Chaos and Ergodic Theory. In Bifurcation and Chaos: Theory and Applications; Awrejcewicz, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 9–16. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhang, J.M.; Chen, Y.S.; Jing, J.; Zhu, S.Y. Quantumness protection for open systems in a double-layer environment. Sci. China Phys. Mech. Astron. 2019, 63, 250312. [Google Scholar] [CrossRef]
- Kowalewska-Kudłaszyk, A.; Kalaga, J.K.; Leoński, W. Wigner-function nonclassicality as indicator of quantum chaos. Phys. Rev. E 2008, 78, 066219. [Google Scholar] [CrossRef]
- Geszti, T. Nonlinear deterministic-chaotic collapse model - preliminaries, philosophy, locality. J. Phys. Conf. Ser. 2019, 1275, 012014. [Google Scholar] [CrossRef]
- Geszti, T. Nonlinear unitary quantum collapse model with self-generated noise. J. Phys. A Math. Theor. 2018, 51, 175308. [Google Scholar] [CrossRef]
- Cornelius, J.; Xu, Z.Y.; Saxena, A.; Chenu, A.; del Campo, A. Spectral Filtering Induced by Non-Hermitian Evolution with Balanced Gain and Loss: Enhancing Quantum Chaos. Phys. Rev. Lett. 2022, 128, 190402. [Google Scholar] [CrossRef]
- Nakamura, K. Quantum Chaos: A New Paradigm of Nonlinear Dynamics; Cambridge Nonlinear Science Series; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Heller, E.J. The Semiclassical Way to Dynamics and Spectroscopy; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. Chaos in Classical and Quantum Mechanics; Springer: New York, NY, USA, 1990. [Google Scholar]
- Heller, E.J.; Tomsovic, S. Post-modern quantum mechanics. Phys. Today 1993, 46, 38. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, Chaos, Quantum-Classical Correspondence, and the Algorithmic Arrow of Time. Phys. Scr. 1998, T76, 186. [Google Scholar] [CrossRef]
- Habib, S.; Shizume, K.; Zurek, W.H. Decoherence, Chaos, and the Correspondence Principle. Phys. Rev. Lett. 1998, 80, 4361–4365. [Google Scholar] [CrossRef]
- Karkuszewski, Z.P.; Jarzynski, C.; Zurek, W.H. Quantum Chaotic Environments, the Butterfly Effect, and Decoherence. Phys. Rev. Lett. 2002, 89, 170405. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Bhattacharya, T.; Habib, S.; Jacobs, K. Continuous Quantum Measurement and the Emergence of Classical Chaos. Phys. Rev. Lett. 2000, 85, 4852–4855. [Google Scholar] [CrossRef]
- Xu, Z.Y.; García-Pintos, L.P.; Chenu, A.; del Campo, A. Extreme Decoherence and Quantum Chaos. Phys. Rev. Lett. 2019, 122, 014103. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, N.; Yu, T. Quantum Synchronization via Active–Passive Decomposition Configuration: An Open Quantum-System Study. Entropy 2025, 27, 432. https://doi.org/10.3390/e27040432
Yang N, Yu T. Quantum Synchronization via Active–Passive Decomposition Configuration: An Open Quantum-System Study. Entropy. 2025; 27(4):432. https://doi.org/10.3390/e27040432
Chicago/Turabian StyleYang, Nan, and Ting Yu. 2025. "Quantum Synchronization via Active–Passive Decomposition Configuration: An Open Quantum-System Study" Entropy 27, no. 4: 432. https://doi.org/10.3390/e27040432
APA StyleYang, N., & Yu, T. (2025). Quantum Synchronization via Active–Passive Decomposition Configuration: An Open Quantum-System Study. Entropy, 27(4), 432. https://doi.org/10.3390/e27040432





