Gaussian Versus Mean-Field Models: Contradictory Predictions for the Casimir Force Under Dirichlet–Neumann Boundary Conditions
Abstract
1. Introduction
2. The Casimir Force Within the Continuum Gaussian Model
3. The Casimir Force Within the Lattice Gaussian Model
- Periodic (p) boundary conditions:
- Neumann–Dirichlet (ND) boundary conditions:
- Under fully periodic (p) boundary conditions, i.e., , one has ; hence, .
- Under Neumann–Dirichlet boundary conditions along the z direction, i.e., , one has ; hence, .
3.1. The Gaussian Model on a Lattice for the Case
3.1.1. TheBehavior of the Interaction Term
3.1.2. The Behavior of the Interaction Term in the Bulk System
3.1.3. The Behavior of the Interaction Term in the Film System with Neumann–Dirichlet Boundary Conditions
3.1.4. The Behavior of the Field Term
- For boundary conditions,andObviously,
- For boundary conditions,
3.2. The Behavior of the Casimir Force
4. The Casimir Force Within the Mean-Field Model
4.1. The Ginzburg–Landau Functional
4.2. The Casimir Force for the Zero External Field
4.3. The Casimir Force for the Non-Zero External Field
5. Conclusions
- (I)
- We derived exact closed-form expression for the free energy of the Gaussian model in both the continuum version (CGM) and the lattice formulation of the model (LGM). The results for the Casimir force can be written as a sum of the following:
- (i)
- (ii)
We observe that these expressions are identical, as is to be expected on the ground of the universality hypothesis, provided proper definitions of the scaling variables are used. - (II)
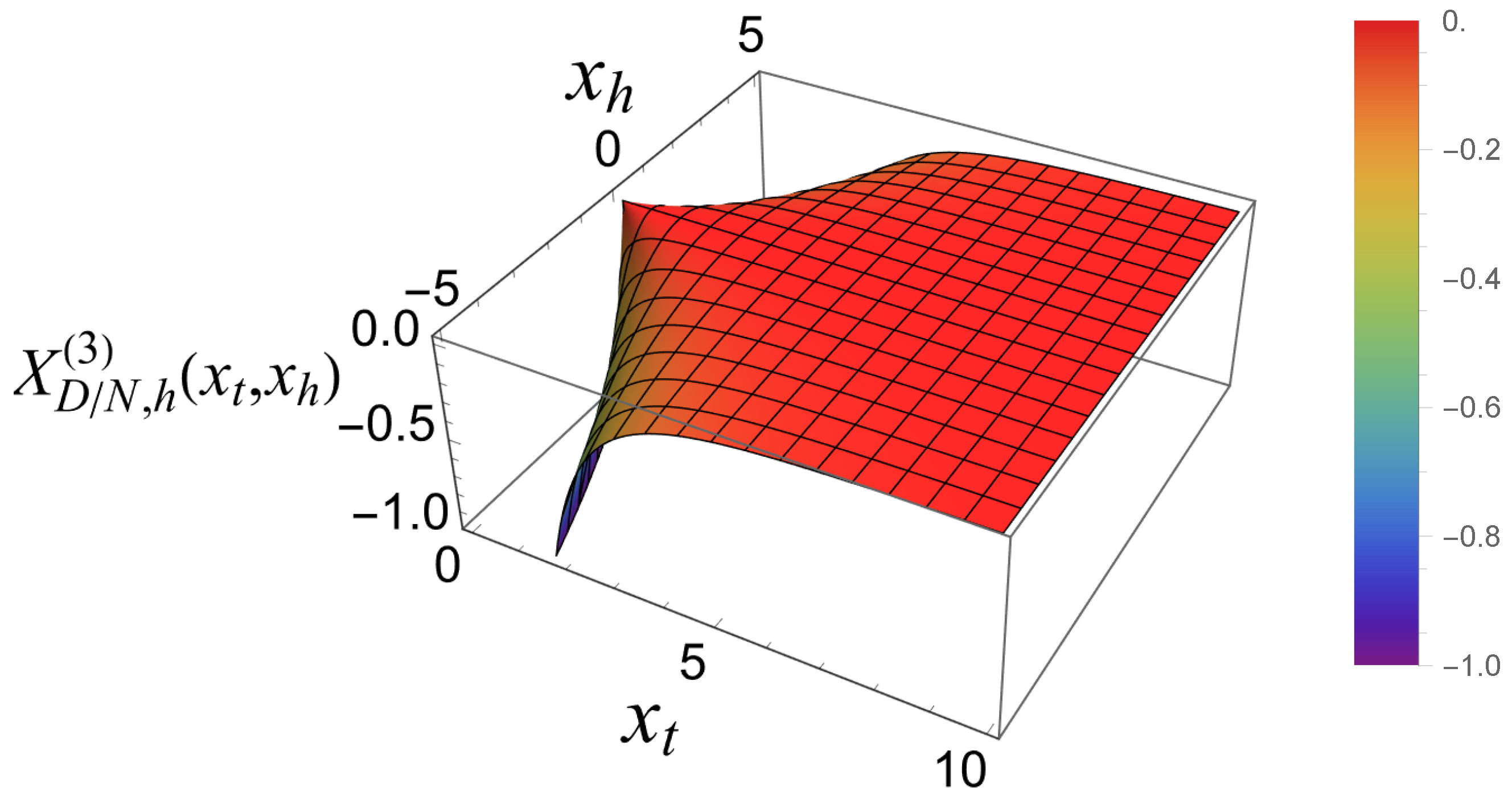
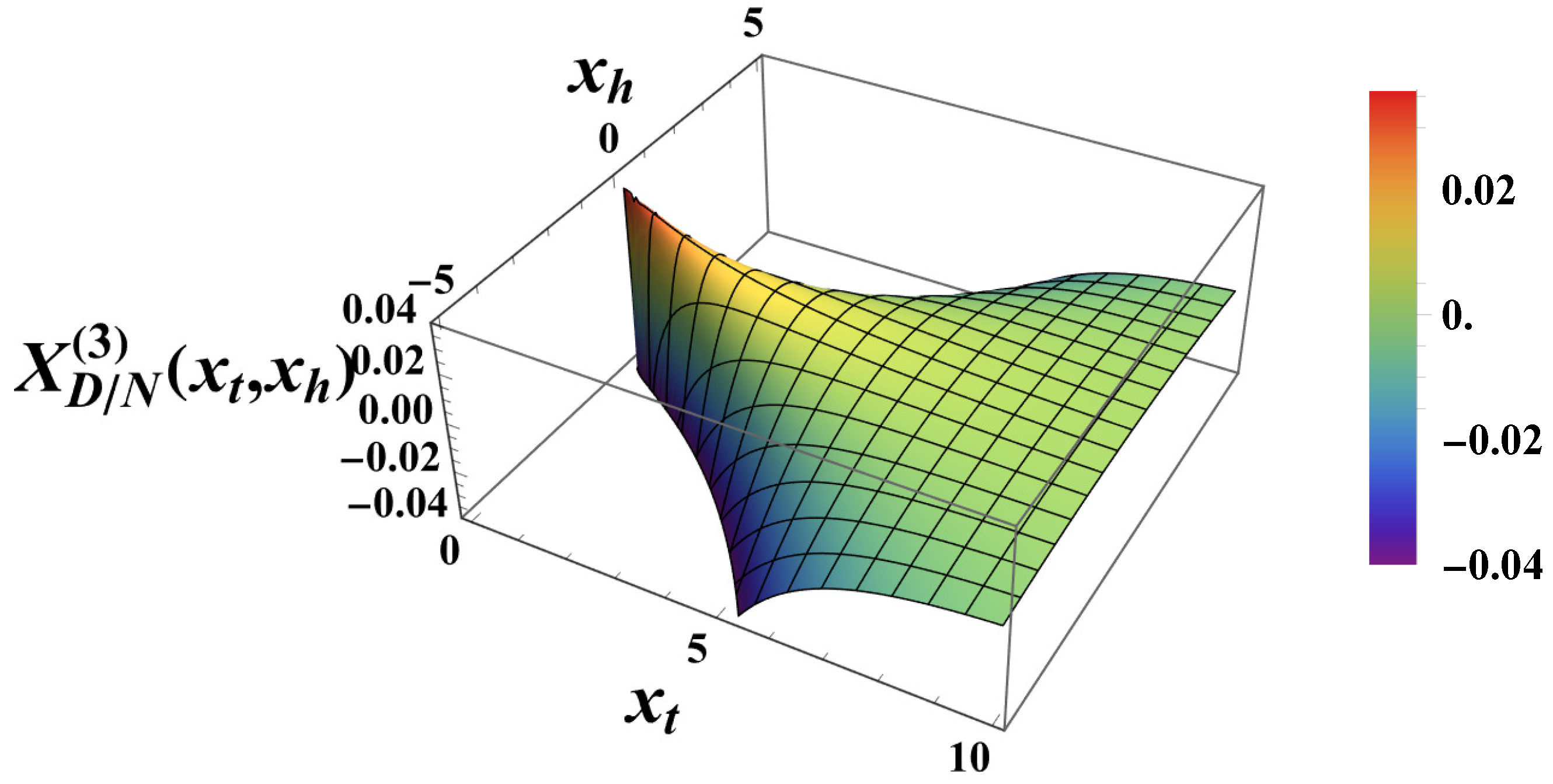
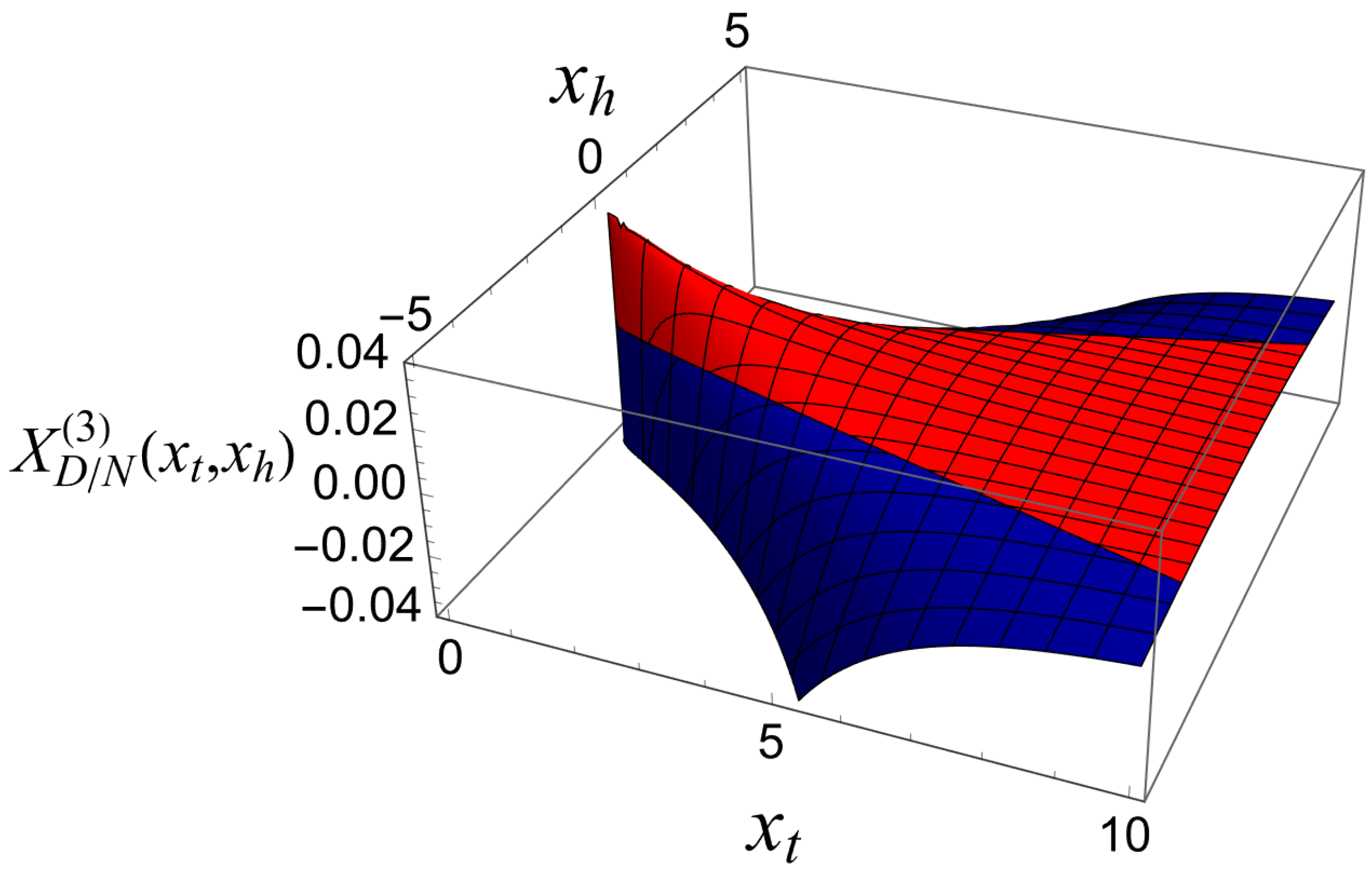
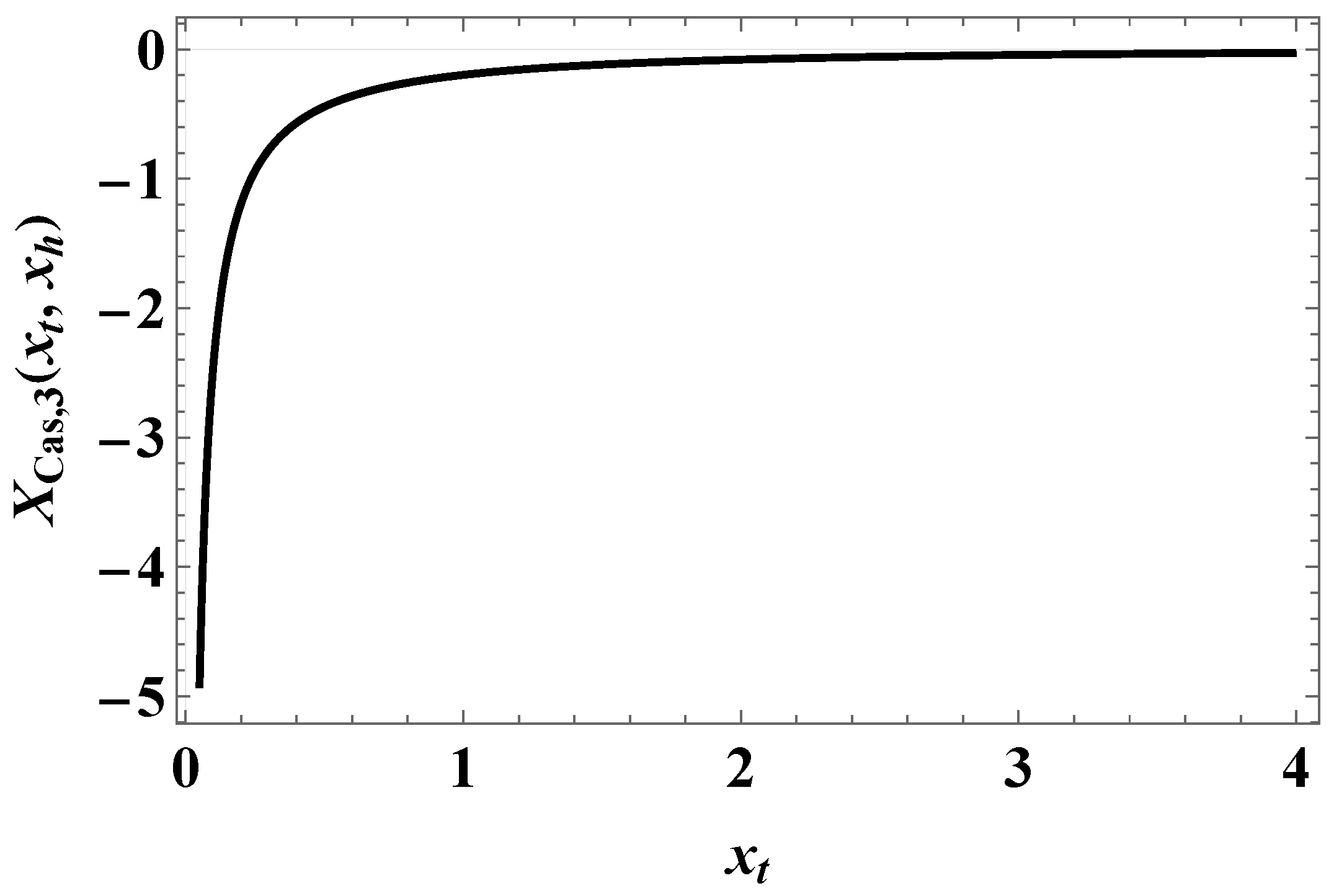
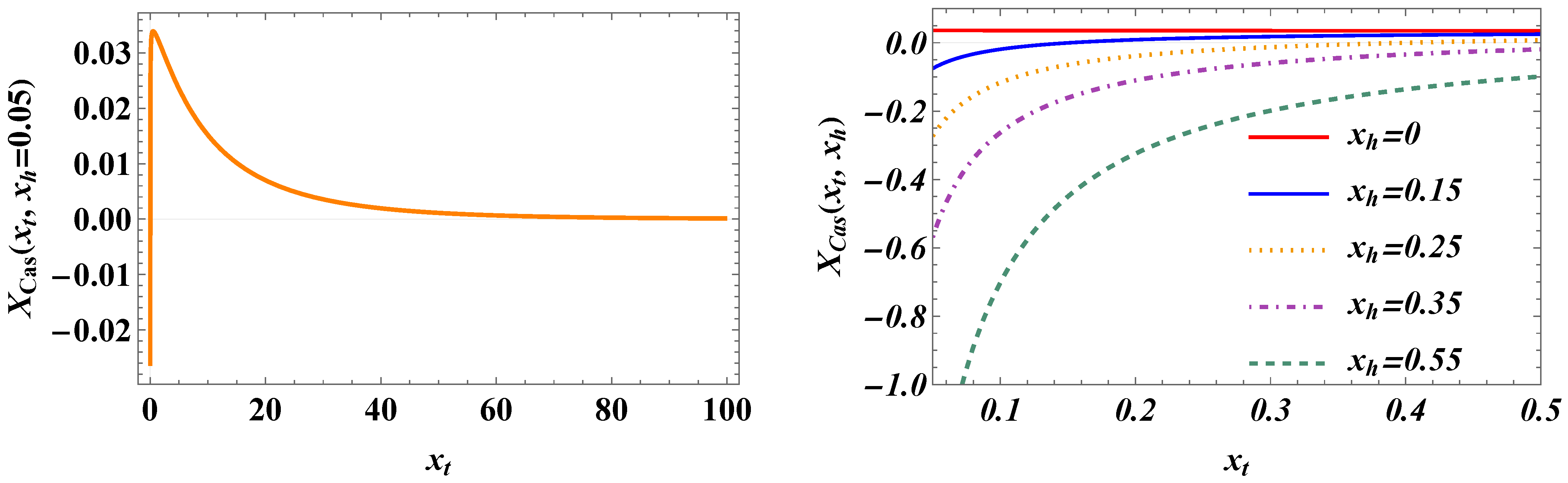
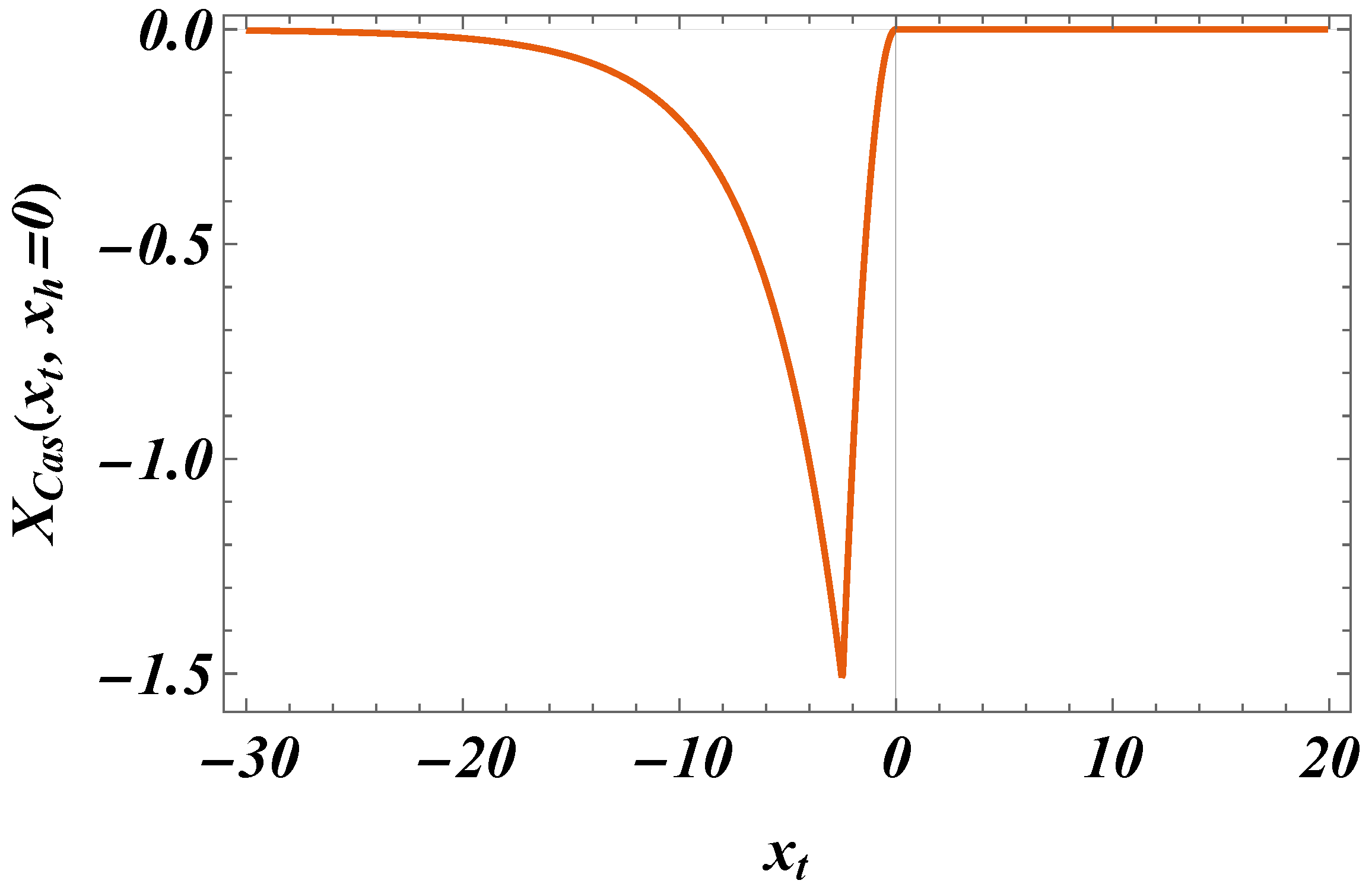
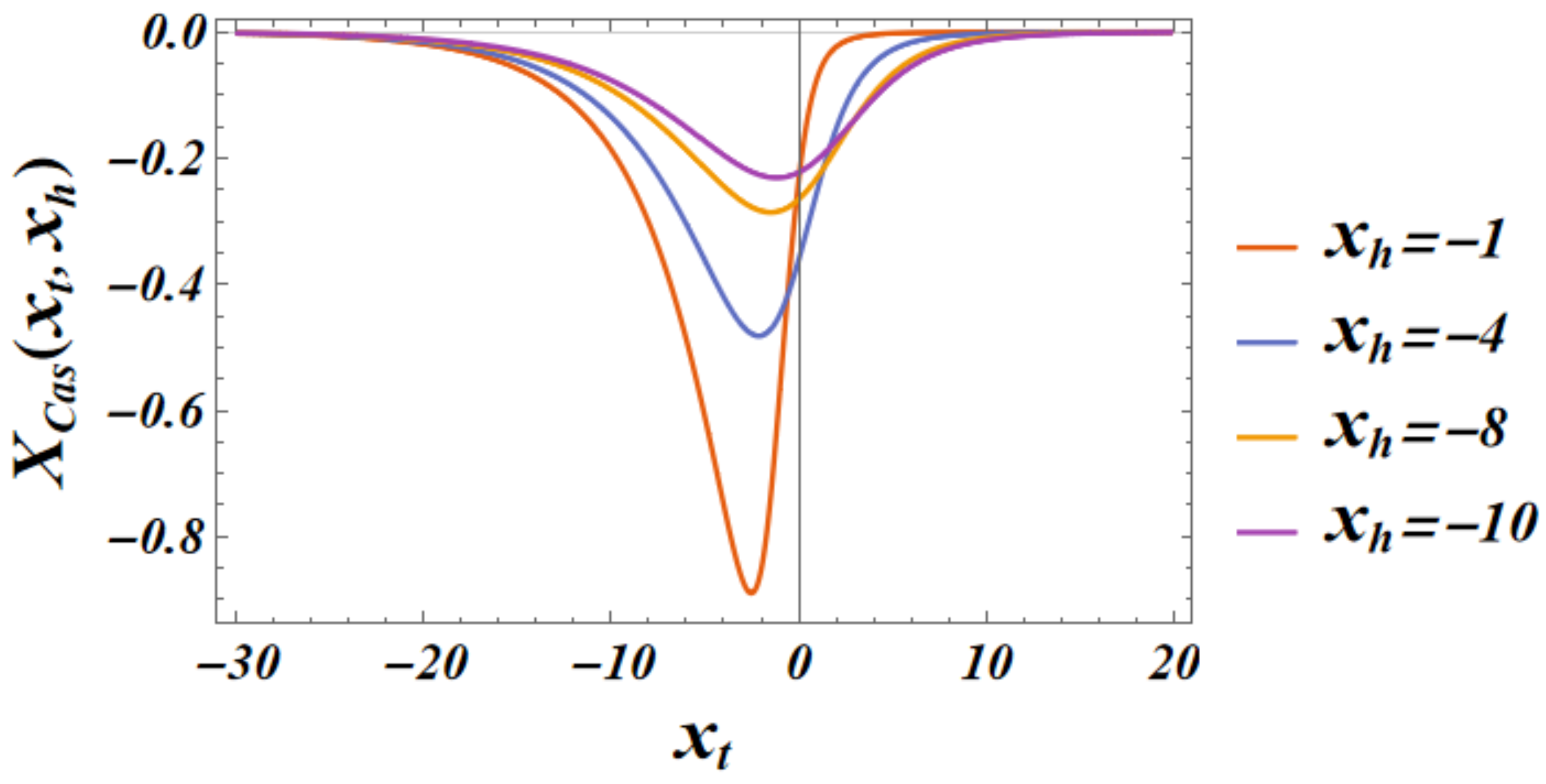
- The behavior of the Casimir force in the CGM is shown in Figure 3 and Figure 5, and the behavior of the LGM is shown in Figure 8, Figure 9, Figure 10 and Figure 11. We observe that for , the force is repulsive and, depending on the magnitude of h, it can be both repulsive or attractive for . Contrary to this behavior, we observe that the force in the MFM is always attractive, both for (see Figure 13) and (see Figure 14 and Figure 15).
- •
- •
- The predictions of the “workhorse” of statistical mechanics, i.e., the mean-field approach, particularly in studies of the Casimir force, can be wrong even with respect to the predicted sign of the force.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCF | critical Casimir force |
| BC’s | boundary conditions |
| DN | Dirichlet–Neumann |
| GCE | grand canonical ensemble |
| LGM | lattice Gaussian model |
| CGM | continuum Gaussian model |
References
- Casimir, H.B. On the Attraction Between Two Perfectly Conducting Plates. Proc. K. Ned. Akad. Wet. 1948, 51, 793–796. [Google Scholar]
- Mostepanenko, V.M.; Trunov, N.N. The Casimir Effect and Its Applications; Energoatomizdat: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Kardar, M.; Golestanian, R. The “friction” of vacuum, and other fluctuation-induced forces. Rev. Mod. Phys. 1999, 71, 1233–1245. [Google Scholar] [CrossRef]
- Milton, K.A. The Casimir Effect: Physical Manifestations of Zero-Point Energy; World Scientific: Singapore, 2001. [Google Scholar]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Milton, K.A. The Casimir effect: Recent controversies and progress. J. Phys. A Math. Gen. 2004, 37, R209–R277. [Google Scholar] [CrossRef]
- Genet, C.; Lambrecht, A.; Reynaud, S. The Casimir effect in the nanoworld. Eur. Phys. J. Spec. Top. 2008, 160, 183–193. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Control of the Casimir force using semiconductor test bodies. Int. J. Mod. Phys. B 2011, 25, 171–230. [Google Scholar] [CrossRef]
- Rodriguez, A.W.; Capasso, F.; Johnson, S.G. The Casimir effect in microstructured geometries. Nat. Photonics 2011, 5, 211–221. [Google Scholar] [CrossRef]
- Farrokhabadi, A.; Abadian, N.; Kanjouri, F.; Abadyan, M. Casimir force-induced instability in freestanding nanotweezers and nanoactuators made of cylindrical nanowires. Int. J. Mod. Phys. B 2014, 28, 1450129. [Google Scholar] [CrossRef]
- Farrokhabadi, A.; Mokhtari, J.; Rach, R.; Abadyan, M. Modeling the influence of the Casimir force on the pull-in instability of nanowire-fabricated nanotweezers. Int. J. Mod. Phys. B 2015, 29, 1450245. [Google Scholar] [CrossRef]
- Sergey, D.O.; Sáez-Gómez, D.; Xambó-Descamps, S. (Eds.) Cosmology, Quantum Vacuum and Zeta Functions; Number 137 in Springer Proceedings in Physics; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-19759-8/978-3-642-19760-4. [Google Scholar] [CrossRef]
- Cugnon, J. The Casimir Effect and the Vacuum Energy: Duality in the Physical Interpretation. Few-Body Syst. 2012, 53, 181–188. [Google Scholar] [CrossRef]
- Adler, R.J.; Casey, B.; Jacob, O.C. Vacuum catastrophe: An elementary exposition of the cosmological constant problem. Am. J. Phys. 1995, 63, 620–626. [Google Scholar] [CrossRef]
- Elizalde, E. Quantum vacuum fluctuations and the cosmological constant. J. Phys. A Math. Gen. 2007, 40, 6647. [Google Scholar] [CrossRef]
- Jaffe, R.L. Casimir effect and the quantum vacuum. Phys. Rev. D 2005, 72, 021301. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Milonni, P.W. The Quantum Vacuum; Academic: San Diego, CA, USA, 1994. [Google Scholar]
- Lamoreaux, S.K. The Casimir force: Background, experiments, and applications. Rep. Prog. Phys. 2005, 68, 201–236. [Google Scholar] [CrossRef]
- Nikolic, H. Proof that Casimir force does not originate from vacuum energy. arXiv 2016, arXiv:1605.04143. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D.J.; Iannuzzi, D. Tuning the Mass of Chameleon Fields in Casimir Force Experiments. Phys. Rev. Lett. 2010, 104, 241101. [Google Scholar] [CrossRef]
- Haghmoradi, H.; Fischer, H.; Bertolini, A.; Galić, I.; Intravaia, F.; Pitschmann, M.; Schimpl, R.A.; Sedmik, R.I.P. Force Metrology with Plane Parallel Plates: Final Design Review and Outlook. Physics 2024, 6, 690–741. [Google Scholar] [CrossRef]
- Almasi, A.; Brax, P.; Iannuzzi, D.; Sedmik, R.I.P. Force sensor for chameleon and Casimir force experiments with parallel-plate configuration. Phys. Rev. D 2015, 91, 102002. [Google Scholar] [CrossRef]
- Fisher, M.E.; de Gennes, P.G. Phénomènes aux parois dans un mélange binaire critique. In Simple Views on Condensed Matter; World Scientific: Singapore, 1978; pp. 207–209. [Google Scholar]
- Maciołek, A.; Dietrich, S. Collective behavior of colloids due to critical Casimir interactions. Rev. Mod. Phys. 2018, 90, 045001. [Google Scholar] [CrossRef]
- Dantchev, D.; Dietrich, S. Critical Casimir effect: Exact results. Phys. Rep. 2023, 1005, 1–130. [Google Scholar] [CrossRef]
- Gambassi, A.; Dietrich, S. Critical Casimir forces in soft matter. Soft Matter 2024, 20, 3212–3242. [Google Scholar] [CrossRef] [PubMed]
- Dantchev, D. On Casimir and Helmholtz Fluctuation-Induced Forces in Micro- and Nano-Systems: Survey of Some Basic Results. Entropy 2024, 26, 499. [Google Scholar] [CrossRef]
- Garcia, R.; Chan, M.H.W. Critical Fluctuation-Induced Thinning of 4He Films near the Superfluid Transition. Phys. Rev. Lett. 1999, 83, 1187–1190. [Google Scholar] [CrossRef]
- Garcia, R.; Chan, M.H.W. Critical Casimir Effect near the 3He-4He Tricritical Point. Phys. Rev. Lett. 2002, 88, 086101. [Google Scholar] [CrossRef] [PubMed]
- Ganshin, A.; Scheidemantel, S.; Garcia, R.; Chan, M.H.W. Critical Casimir Force in 4He Films: Confirmation of Finite-Size Scaling. Phys. Rev. Lett. 2006, 97, 075301. [Google Scholar] [CrossRef]
- Soyka, F.; Zvyagolskaya, O.; Hertlein, C.; Helden, L.; Bechinger, C. Critical Casimir Forces in Colloidal Suspensions on Chemically Patterned Surfaces. Phys. Rev. Lett. 2007, 101, 208301. [Google Scholar] [CrossRef]
- Hertlein, C.; Helden, L.; Gambassi, A.; Dietrich, S.; Bechinger, C. Direct measurement of critical Casimir forces. Nature 2008, 451, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Nellen, U.; Helden, L.; Bechinger, C. Tunability of critical Casimir interactions by boundary conditions. EPL 2009, 88, 26001. [Google Scholar] [CrossRef]
- Zvyagolskaya, O.; Archer, A.J.; Bechinger, C. Criticality and phase separation in a two-dimensional binary colloidal fluid induced by the solvent critical behavior. EPL 2011, 96, 28005. [Google Scholar] [CrossRef]
- Tröndle, M.; Zvyagolskaya, O.; Gambassi, A.; Vogt, D.; Harnau, L.; Bechinger, C.; Dietrich, S. Trapping colloids near chemical stripes via critical Casimir forces. Mol. Phys. 2011, 109, 1169–1185. [Google Scholar] [CrossRef]
- Paladugu, S.; Callegari, A.; Tuna, Y.; Barth, L.; Dietrich, S.; Gambassi, A.; Volpe, G. Nonadditivity of critical Casimir forces. Nat. Comm. 2016, 7, 11403. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, F.; Magazzù, A.; Callegari, A.; Biancofiore, L.; Cichos, F.; Volpe, G. Microscopic Engine Powered by Critical Demixing. Phys. Rev. Lett. 2018, 120, 068004. [Google Scholar] [CrossRef] [PubMed]
- Magazzù, A.; Callegari, A.; Staforelli, J.P.; Gambassi, A.; Dietrich, S.; Volpe, G. Controlling the dynamics of colloidal particles by critical Casimir forces. Soft Matter 2019, 15, 2152–2162. [Google Scholar] [CrossRef]
- Schmidt, F.; Callegari, A.; Daddi-Moussa-Ider, A.; Munkhbat, B.; Verre, R.; Shegai, T.; Käll, M.; Löwen, H.; Gambassi, A.; Volpe, G. Tunable critical Casimir forces counteract Casimir–Lifshitz attraction. Nat. Phys. 2023, 19, 271–278. [Google Scholar] [CrossRef]
- Nowakowski, P.; Bafi, N.F.; Volpe, G.; Kondrat, S.; Dietrich, S. Critical Casimir levitation of colloids above a bull’s-eye pattern. J. Chem. Phys. 2024, 161, 214114. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Nowakowski, P.; Bafi, N.F.; Midtvedt, B.; Schmidt, F.; Verre, R.; Käll, M.; Dietrich, S.; Kondrat, S.; Volpe, G. Nanoalignment by Critical Casimir Torques. Nat. Commun. 2024, 15, 5086. [Google Scholar] [CrossRef]
- Barber, M.N. Finite-size Scaling. In Phase Transitions and Critical Phenomena; Domb, C., Lebowitz, J.L., Eds.; Academic: London, UK, 1983; Chapter 2; Volume 8, pp. 146–266. [Google Scholar]
- Binder, K. Critical Behaviour at Surfaces. In Phase Transitions and Critical Phenomena; Domb, C., Lebowitz, J.L., Eds.; Academic: London, UK, 1983; Chapter 1; Volume 8, pp. 1–145. [Google Scholar]
- Privman, V. (Ed.) Finite-Size Scaling Theory. In Finite Size Scaling and Numerical Simulations of Statistical Systems; World Scientific: Singapore, 1990; p. 1. [Google Scholar]
- Brankov, J.G.; Dantchev, D.M.; Tonchev, N.S. The Theory of Critical Phenomena in Finite-Size Systems—Scaling and Quantum Effects; World Scientific: Singapore, 2000. [Google Scholar]
- Evans, R. Microscopic theories of simple fluids and their interfaces. In Liquids at Interfaces; Charvolin, J., Joanny, J., Zinn-Justin, J., Eds.; Les Houches Session; Elsevier: Amsterdam, The Netherlands, 1990; Volume XLVIII. [Google Scholar]
- Krech, M. Casimir Effect in Critical Systems; World Scientific: Singapore, 1994. [Google Scholar]
- Krech, M.; Dietrich, S. Free energy and specific heat of critical films and surfaces. Phys. Rev. A 1992, 46, 1886–1921. [Google Scholar] [CrossRef]
- Dantchev, D.; Krech, M. Critical Casimir force and its fluctuations in lattice spin models: Exact and Monte Carlo results. Phys. Rev. E 2004, 69, 046119. [Google Scholar] [CrossRef]
- Kastening, B.; Dohm, V. Finite-size effects in film geometry with nonperiodic boundary conditions: Gaussian model and renormalization-group theory at fixed dimension. Phys. Rev. E 2010, 81, 061106. [Google Scholar] [CrossRef]
- Diehl, H.W.; Rutkevich, S.B. Fluctuation-induced forces in confined ideal and imperfect Bose gases. Phys. Rev. E 2017, 95, 062112. [Google Scholar] [CrossRef]
- Dantchev, D.; Rudnick, J. Manipulation and amplification of the Casimir force through surface fields using helicity. Phys. Rev. E 2017, 95, 042120. [Google Scholar] [CrossRef]
- Gross, M. Dynamics and steady states of a tracer particle in a confined critical fluid. J. Stat. Mech. 2021, 2021, 063209. [Google Scholar] [CrossRef]
- Gross, M.; Gambassi, A.; Dietrich, S. Fluctuations of the critical Casimir force. Phys. Rev. E 2021, 103, 062118. [Google Scholar] [CrossRef] [PubMed]
- Krech, M. Casimir forces in binary liquid mixtures. Phys. Rev. E 1997, 56, 1642–1659. [Google Scholar] [CrossRef]
- Parry, A.O.; Evans, R. Novel phase behavior of a confined fluid or Ising magnet. Physica A 1992, 181, 250. [Google Scholar] [CrossRef]
- Gambassi, A.; Dietrich, S. Critical dynamics in thin films. J. Stat. Phys. 2006, 123, 929–1005. [Google Scholar] [CrossRef]
- Dantchev, D.; Schlesener, F.; Dietrich, S. Interplay of critical Casimir and dispersion forces. Phys. Rev. E 2007, 76, 011121. [Google Scholar] [CrossRef]
- Zandi, R.; Shackell, A.; Rudnick, J.; Kardar, M.; Chayes, L.P. Thinning of superfluid films below the critical point. Phys. Rev. E 2007, 76, 030601. [Google Scholar] [CrossRef]
- Vasilyev, O.; Maciòłek, A.; Dietrich, S. Critical Casimir forces for Ising films with variable boundary fields. Phys. Rev. E 2011, 84, 041605. [Google Scholar] [CrossRef]
- Mohry, T.F.; Kondrat, S.; Maciolek, A.; Dietrich, S. Critical Casimir interactions around the consolute point of a binary solvent. Soft Matter 2014, 10, 5510–5522. [Google Scholar] [CrossRef]
- Dantchev, D.M.; Vassilev, V.M.; Djondjorov, P.A. Exact results for the behavior of the thermodynamic Casimir force in a model with a strong adsorption. J. Stat. Mech. Theory Exp. 2016, 2016, 093209. [Google Scholar] [CrossRef]
- Gross, M.; Vasilyev, O.; Gambassi, A.; Dietrich, S. Critical adsorption and critical Casimir forces in the canonical ensemble. Phys. Rev. E 2016, 94, 022103. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.H. Table of Integrals, Series, and Products; Academic: New York, NY, USA, 2007. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; NIST and Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ma, S.K. Modern Theory of Critical Phenomena; Advanced Book Classics; Perseus: Cambridge, MA, USA, 2000. [Google Scholar]
- Privman, V. (Ed.) Finite Size Scaling and Numerical Simulations of Statistical Systems; World Scientific: Singapore, 1990. [Google Scholar]
- Gelfand, I.M.; Fomin, S.V. Calculus of Variations; Revised English Edition Translated and Edited by Richard A. Silverman; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics; Wiley-VCH: Weinheim, Germany, 1989; Volume 1. [Google Scholar]
- Dickey, L.A. On the Variation of a Functional when the Boundary of the Domain is not Fixed. Lett. Math. Phys. 2007, 83, 33–40. [Google Scholar] [CrossRef]
- Indekeu, J.O.; Nightingale, M.P.; Wang, W.V. Finite-size interaction amplitudes and their universality: Exact, mean-field, and renormalization-group results. Phys. Rev. B 1986, 34, 330–342. [Google Scholar] [CrossRef]
- Schlesener, F.; Hanke, A.; Dietrich, S. Critical Casimir forces in colloidal suspensions. J. Stat. Phys. 2003, 110, 981–1013. [Google Scholar] [CrossRef]
- Dantchev, D.; Vassilev, V.M.; Djondjorov, P.A. Analytical results for the Casimir force in a Ginzburg–Landau type model of a film with strongly adsorbing competing walls. Physica A 2018, 510, 302–315. [Google Scholar] [CrossRef]
- Dantchev, D.; Vassilev, V. ϕ4 model under Dirichlet-Neumann boundary conditions. J. Phys. Conf. Ser. 2024, 2910, 012011. [Google Scholar] [CrossRef]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis; Cambridge University Press: London, UK, 1963. [Google Scholar]
- Krech, M.; Dietrich, S. Finite-size scaling for critical films. Phys. Rev. Lett. 1991, 66, 345–348. [Google Scholar] [CrossRef]
- Dantchev, D.; Rudnick, J. Exact expressions for the partition function of the one-dimensional Ising model in the fixed-M ensemble. Phys. Rev. E 2022, 106, L042103. [Google Scholar] [CrossRef]
- Dantchev, D. Fluctuation-induced Interactions in Micro- and Nano-systems: Survey of Some Basic Results. arXiv 2023, arXiv:2307.09990. [Google Scholar] [CrossRef]
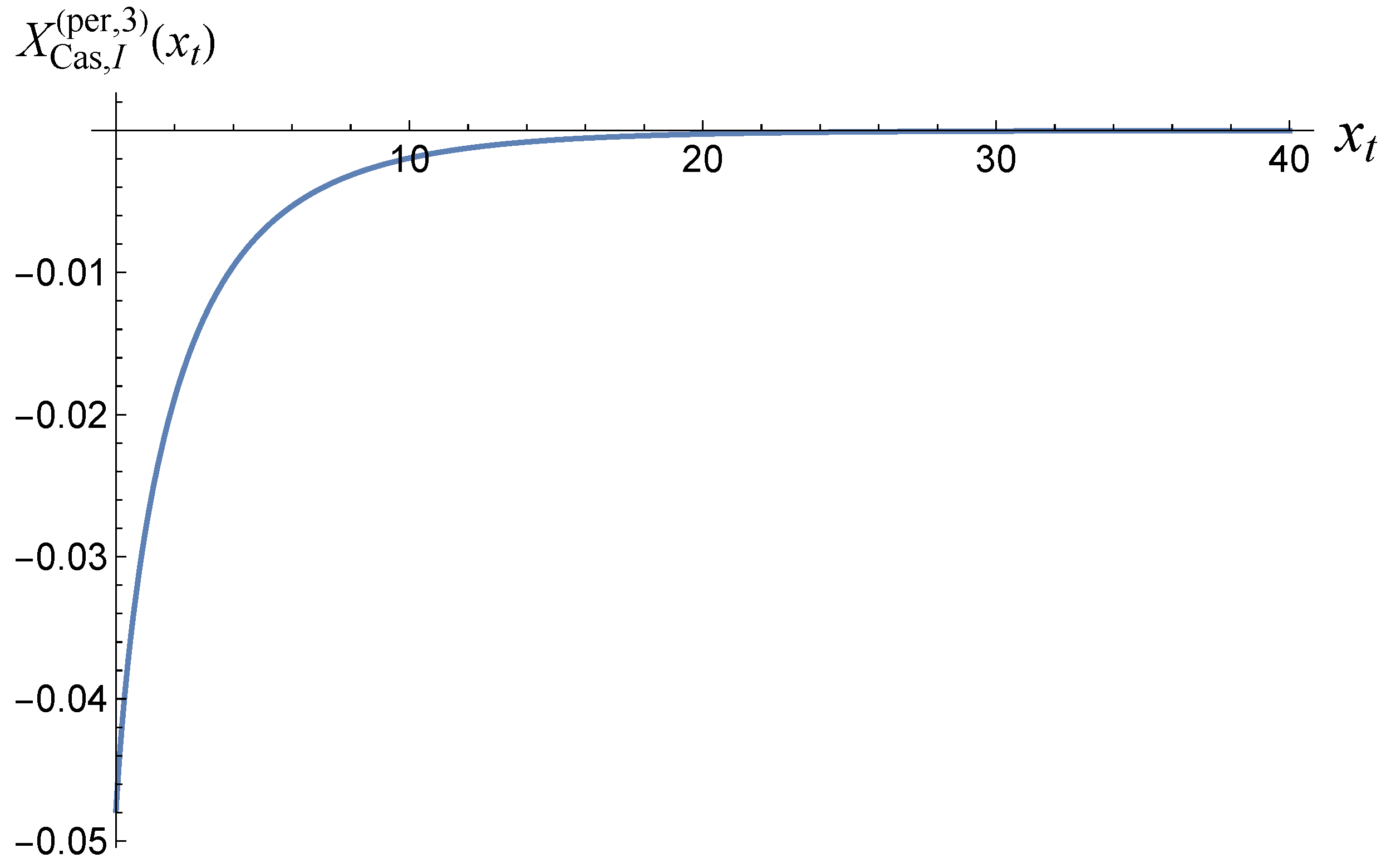







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dantchev, D.; Vassilev, V.; Rudnick, J. Gaussian Versus Mean-Field Models: Contradictory Predictions for the Casimir Force Under Dirichlet–Neumann Boundary Conditions. Entropy 2025, 27, 468. https://doi.org/10.3390/e27050468
Dantchev D, Vassilev V, Rudnick J. Gaussian Versus Mean-Field Models: Contradictory Predictions for the Casimir Force Under Dirichlet–Neumann Boundary Conditions. Entropy. 2025; 27(5):468. https://doi.org/10.3390/e27050468
Chicago/Turabian StyleDantchev, Daniel, Vassil Vassilev, and Joseph Rudnick. 2025. "Gaussian Versus Mean-Field Models: Contradictory Predictions for the Casimir Force Under Dirichlet–Neumann Boundary Conditions" Entropy 27, no. 5: 468. https://doi.org/10.3390/e27050468
APA StyleDantchev, D., Vassilev, V., & Rudnick, J. (2025). Gaussian Versus Mean-Field Models: Contradictory Predictions for the Casimir Force Under Dirichlet–Neumann Boundary Conditions. Entropy, 27(5), 468. https://doi.org/10.3390/e27050468





