Assessment of Energy Arbitrage Using Energy Storage Systems: A Wind Park’s Perspective

Abstract

With the growing application of green energy, the importance of effectively handling the volatile nature of these energy sources is also growing in order to ensure economic and operational viability. Accordingly, the main contribution of this work is to evaluate the revenue potential for wind parks with integrated storage systems in the day-ahead electricity markets using genetic algorithm. It is achieved by the concept of flexible charging–discharging of the Energy Storage System (ESS), taking advantage of the widespread electricity prices that are predicted using a feedforward-neural-network-based forecasting algorithm. In addition, the reactive power restrictions posed by grid code that are to be followed by the wind park are also considered as one of the constraints. Moreover, the profit obtained with a Battery Energy Storage System (BESS) is compared with that of a Thermal Energy Storage System (TESS). The proposed method gave more profitable results when utilizing BESS for energy arbitrage in day-ahead electricity markets than with TESS. Moreover, the availability of ESS at wind park has reduced the wind power curtailment.

1. Introduction

Increasing the penetration of Renewable Energy Sources (RES) is of high importance, as many countries have already set their goals for increasing RES share in the energy mix [1,2]. The technical and economical analysis of both standalone and grid-connected RES is presented in [3,4]. Climatic conditions highly influence the wind farm output that often causes voltage and frequency deviations in the connected power grid. Using the governor actions to solve these instability issues due to either shortage or surplus wind power would be detrimental to speed-control systems [5]. For example, in Denmark, 10% of hourly small variations are most common for wind farms, but up to 30% of hourly fluctuations still occur once in 1.1 years [6]. Energy storage systems not only enable the effective integration of widespread RES into power systems, but also provide various services including load shifting, energy management, frequency regulation, wind power smoothing, or energy arbitrage to the power grid. Among various Energy Storage System (ESS) technologies, Battery Energy Storage System (BESS) turned out to be a suitable choice for integration of wind farms and for maximizing profit [7]. There has been a large interest towards investing in BESS for a decade; for example, Tesla completed installation of a 129-MWh, grid-scale, lithium-ion battery connected to Neoen’s Hornsdale Wind Farm near Jamestown, South Australia in 2017 [8]. Further, ABB won an order from DONG Energy, the leading Denmark-based sustainable energy group, to deliver a 2-MegaWatt BESS to support the integration and transmission of power from the Burbo Bank offshore wind farm near Liverpool, UK [9].

Study of Literature: Battery Energy Storage System (BESS) and Thermal Energy Storage System (TESS)

The Energy Storage System (ESS) plays a key role, even in the reserve market; however, cross border and intraday trade have lessened the potential for ESS in the Nordic intraday market [10], resulting in a lower return on investment compared to the day-ahead market. The most significant revenue stream for BESS is energy arbitrage in short-term electricity markets, such as the day-ahead electricity market. In general, the arbitrage is a transaction that generates revenue by using price differences over a period, where the energy is stored during the low-demand periods or low energy prices and dispatches during high-demand periods or high energy prices [11]. For storage units, real-time arbitrage is a major source of revenue, but the uncertain nature of prices pose difficulties in designing good strategies. The difficulties arise from the fact that the future electricity prices are unknown, highly stochastic, and difficult to forecast as well [12]. In general, the demand dynamics dictate the price dynamics in a cyclical pattern, which can be daily, weekly, seasonal, and with some unpredictable factors. Application of appropriate optimization methods would maximize the returns from the combination of wind farms and ESS.

The general solutions that can be employed for handling the intermittency of the wind power systems include flexibility technologies such as demand response technologies [13], energy storage technologies [14], etc. Several research works demonstrated that the effective coordination of Wind and ESS can handle the future fluctuations in wind power generation [15]. In [16], BESS is used to reduce the shortfalls of load, and reserves are reduced along with a decrease in wind power curtailment in day-ahead scheduling. It is assumed that the BESS is a system asset operated by the system operator. A comprehensive analysis of the fallouts of grid-scale ESS in a real thermal power system under a centralized spot market is carried out in [17]. The ESS is employed to provide energy arbitrage, and primary and secondary reserves. A novel wind dispatch control scheme is proposed in [18], where the major decision lies in discharging the BESS during peak price times and storing it at off-peak periods in agreement with the Australian National Electricity Market. Further, the price arbitrage-based feasibility study is carried out for BESS in relation to a RES park in [19]. In the literature, several tools have been developed to analyze the economic viability of the wind-storage systems [20]. The storage technologies used for integrating renewable generation are not only in the form of electrical energy, but also chemical and thermal energy [21]. Thermal energy storage systems, especially with latent heat storage methods, have also been proven to be a competing energy dispatcher, due to their large-scale, being environmentally friendly, and long life [22]. In TESS technologies, latent heat storage is preferred over sensible due to its high storage capacities. The molten-salt-based phase change material (PCM) is used for energy storage in the form of latent heat at high temperatures due to its recognition as the best heat transfer fluid (HTF) in Thermal Energy Storage System (TESS) [23] and the cost of molten salt being low. In countries such as Denmark, where more than 60% of heating in Danish houses is supplied by district heating and, in addition, high wind power penetration, a considerable amount of wind energy can be used to support DH system in low electricity price periods [24]. For half of the concentrated solar power (CSP) throughout the world, TESS is used as a viable storage [25]. Moreover, thermal energy present in the solar irradiance can be stored in the TESS and used to meet the heat load [26].

The present work prioritizes the use of battery and thermal energy storage systems for maximizing the profit of the wind farm operator obtained by selling the wind energy through energy arbitrage. The problem is formulated as a maximization function that measures the economic benefits obtained from the dispatched power from the wind farm against the cost of ESS. Both BESS and TESS types are considered and their effect on the wind park’s profit is evaluated. Considering the point of common connection (PCC) node prices, the ESS is scheduled for either charging/discharging. According to the grid codes of various countries, for maintaining power factor at the PCC as a function of voltage, the wind farms not only supply active power but also reactive power into the grid [27]. Accordingly, the reactive power compensation at the PCC is considered one of the constraints, which is a regulatory imposition by the Transmission System Operator (TSO) to be followed by the wind park operator for injecting its power production into the grid. The modeled wind farm is used to find the reactive power set points and passed onto optimization routine in the form of a constraint. This is an important aspect, as in the process of maintaining the reactive power at the PPC and within wind farm, there can be a possibility to adjust the real power output of the wind farm, which has a direct effect on energy sold to the grid, thereby on the hourly profit. However, the wind turbine dynamics are not considered in this work, as the time scale is hourly precision. The dynamics, including electrical converter controls and turbine mechanical controls, is a study of a seconds or less time range but this is out of the scope of present work. The advantage of this work is that both the performances of BESS and TESS are compared with respect to the wind park’s revenue. The novelty of this work lies in considering the energy storage arbitrage along with grid code fulfillment in terms of reactive power response for finding a trade-off solution to maximize the revenue generated by selling wind energy to the grid. In addition, the neural network model proposed in this work for forecasting the electricity price is compared with the methods that are proposed in literature [28,29] and were revealed to be better.

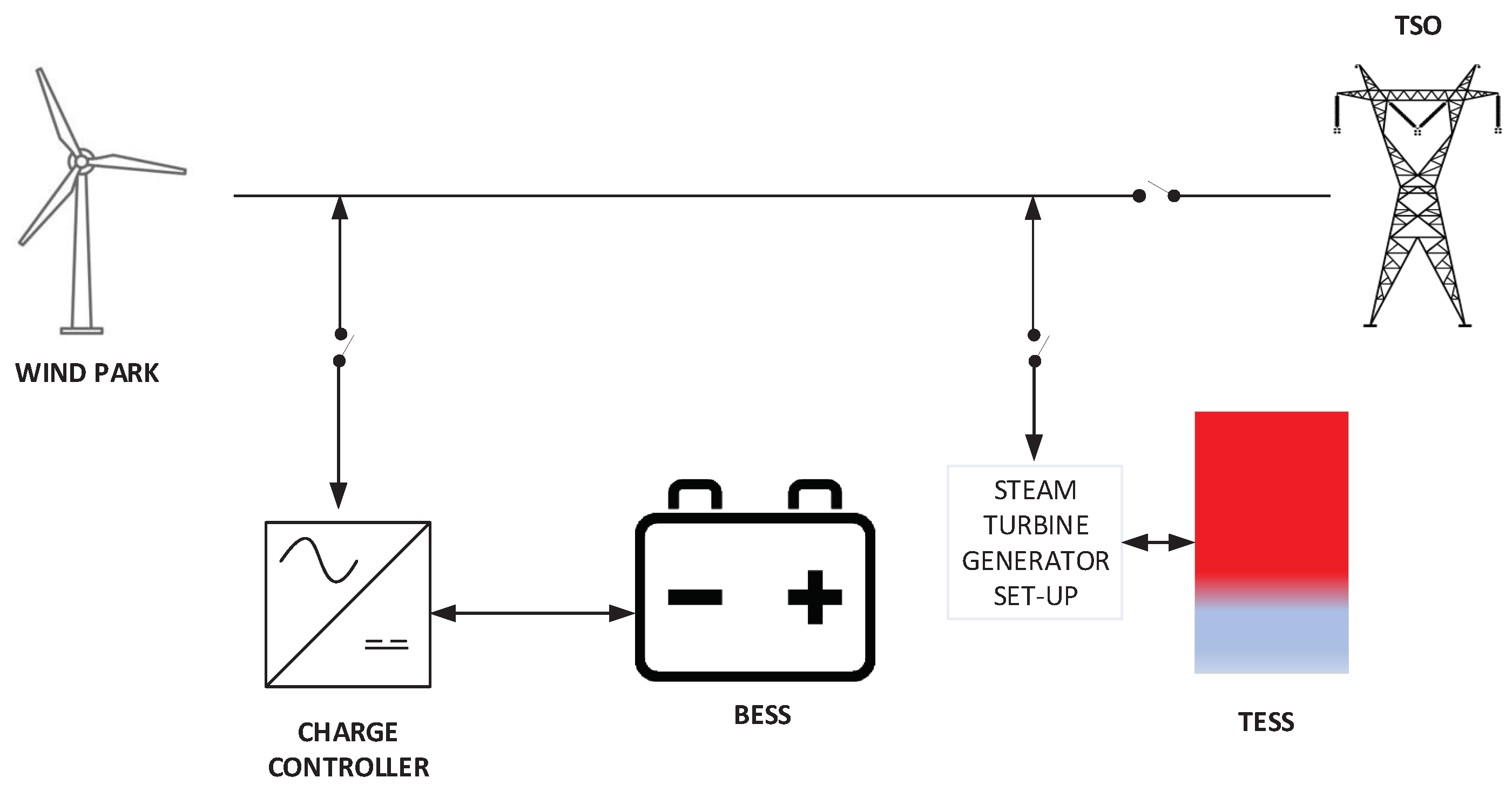
Figure 1 shows the generic wind park model with the ESS. The ESS (either battery or thermal) is installed at the wind park site and connected to the main grid through a charge controller/inverter. The energy capacity of ESS describes the energy stored in the battery for a given hour and the power that can be supplied or stored under the rated charge/discharge time interval. The selected power and energy rating are given in the wind park modeling section. The details of the BESS and TESS mathematical models are described in the following subsections.

2. Battery Energy Storage Systems

There are several BESS models reported in the literature. The charging/discharging process for both the long-term and short-term applications is illustrated in [30]. The present work considers the long-term operation (e.g., over hours/days) for BESS/TESS charging and discharging processes, which is relevant for energy arbitrage applications. Besides this, a numerical model in [31] is adapted for charge/discharge for BESS modeling, as given in Equation (1).The equation gives the state of charge (SoC) at any time step k with respect to charge ($P_{ch,BESS}$) and discharge ($P_{dch,BESS}$) instances corresponding to given charge (${\eta }_{ch}$)/discharge (${\eta }_{dch}$) efficiencies. The SoC is having upper limit ($SO{C}_{max}$) and lower limit ($SO{C}_{min}$) and the SoC for any time interval ($\Delta t$) are limited by charge ($r_{ch}$)/discharge ($r_{dch}$) rates.

$$\begin{array}{cc}\hfill SoC(k+1)& = SoC\left(k\right) + \frac{P_{ch,k}{\eta }_{ch,BESS}\Delta t}{E_{BESS,k}}\hfill \\ \hfill SoC(k+1)& = SoC\left(k\right) - \frac{P_{dch,k}{\eta }_{dch,BESS}\Delta t}{E_{BESS,k}}\hfill \\ \hfill & So{C}_{min} \le SoC\left(k\right) \le So{C}_{max}\hfill \\ \hfill & r_{ch} \le SoC(k+1) - SoC\left(k\right) \le r_{dch}\hfill \end{array}$$

(1)

3. Thermal Energy Storage Systems

Thermal energy storage systems are considered for wind parks due to many factors including cost effectiveness, large-scale potential, and environmental friendliness. The most widespread configuration of TESS is the two-tank sensible heat system with Solar salt as Heat Transfer Fluid (HTF) and a storage medium due to its high thermal efficiency and strong operability [32]. The molten-salt-based TESS system is one of the best HTFs due to its low cost, which makes it economically attractive. The present work considers a thermal storage model proposed by Stiesdal, currently under development [33], which is basically a two-tank model with a compressor connected to a generator with a governor system. End-use TESS stores electricity from off-peak periods in the form of heat using hot or cold storage tanks in underground aquifers, water or ice tanks, molten salts, or other storage materials. Heat losses would be there, which can be considered in cost calculation. In the present model, the associated delays are due to the ramping time of the generator dynamic system. The state of energy (SoE) that is stored at any time step k is derived from the total thermal energy ($E_{cap}$) and current energy ($E_k$) available in the TESS. The binary variable ($u_k$) is used to avoid simultaneous charge/discharge and ($l_k$) is accounting for the internal losses within the thermal storage tank. are given in Equation (2):

$$\begin{array}{cc}\hfill E(k+1)& = (1 - u_k{l}_k)E\left(k\right) + {\eta }_{ch,BESS}{P}_{ch,k}\Delta t - \frac{P_{dch,k}}{{\eta }_{dch,BESS}}\Delta t\hfill \\ \hfill SoE\left(k\right)& = \frac{E\left(k\right)}{E_{cap}}\hfill \end{array}$$

(2)

The power capacity ($P_{cap}$) of both the thermal and battery storage systems is used in formulating the charge and discharge constraints, which are given in Equation (3):

$$\begin{array}{c}\hfill P_{ch,k} \le u_k{P}_{cap}\\ \hfill P_{dch,k} \le (1 - u_k)P_{cap}\end{array}$$

(3)

Unlike BESS, the thermal storage systems have a ramp constraint, expressed in terms of SoE, which is given in Equation (3). Further, the constraint on the minimum energy ($E_{min}$) and maximum energy ($E_{max}$) that TESS can handle is given in Equation (4):

$$\begin{array}{cc}\hfill & -R_k\Delta t \le SoE(k+1) - SoE\left(k\right) \le R_k\Delta t\hfill \\ \hfill & So{E}_{min} \le SoE\left(k\right) \le So{E}_{max}\hfill \\ \hfill & E_{min} \le E_k \le E_{max}\hfill \end{array}$$

(4)

In the present work, the ramp rate ($R_k$) is seen as rate at which the dispatch of power takes place from TESS to grid.

4. Problem Statement and Optimization Formulation

The optimization formulation was solved using a Genetic Algorithm (GA) due to its parallel optimization capability, thereby giving a group of solutions at once. In addition, the conventional optimization solvers might end up in local minima and oscillation effects, thereby failing to arrive at global optima. The Darwinian principle of natural evolution was adapted in GA involving a population, which finds the solution for a given problem [34]. In comparison with other global search algorithms, GA proves to be superior over global convergence. This method solves the problem by considering an appropriate selection of mutation and cross-over operators, thereby updating the individual population in each iteration [35].

The objective is to maximize the revenue of the wind park, as shown in Equation (5), using intelligent charging/discharging based on predicted electricity prices for relevant constraints on storage systems including their SoC limits, ramp rates for thermal storage, charge/discharge rates and reactive power limits (($Q_{min}$), ($Q_{max}$)). The power management strategy for ESS ($P_{ESS,i}$) is based on given wind production profiles ($P_{W,i}$) and forecasted electricity prices ($E_{pr,i}$) by the maximization optimization of the revenue.

$$\begin{array}{c}\hfill Max\sum _{i=1}^{24}{E}_{pr,i}(P_{W,i}+P_{ESS,i})\\ \hfill Constraints\\ \hfill & Equation\left(1\right) - BESS\hfill \\ \hfill & Equations\left(2\right) - \left(4\right) - TESS\hfill \\ \hfill & Q_{min} \le Q_{i,W} \le Q_{max}\hfill \end{array}$$

(5)

From the above formulation, the revenue obtained by selling energy from both wind and ESS ($E_{ESS}$) to the grid is obtained. The net profit is obtained from the difference of revenue and the costs that is given in Equation (6). Since the focus of this paper is on energy storage facility, the corresponding capital costs of both the wind farm and converters are assumed to be constant. This equation describes the costs of both the TESS and BESS, whereas the cost of storing energy is comparatively less than that of the cost of operating for the TESS system. This is due to the fact that the TESS consists of a steam turbine along with a generator for generating electricity from thermal form. So, the operating cost of TESS is assumed to be high compared with BESS.

$$Profit = \alpha P_{sold} - \beta P_{ESS} - \gamma E_{ESS}$$

(6)

In this study, it is considered that the predicted values of wind speed profiles are already available and electricity prices are forecasted from historical data using neural networks. The real data for a period of two years (2018–2019) corresponding to wind speed profiles of the wind farm under study and electricity nodal pricing is provided by our project partners. The forecasting is carried out only for electricity prices, with price being the main decision maker in the profit maximization.

The simulation model is as shown in Figure 2, illustrating the neural-network-based forecasting model for day-ahead electricity prices. The input for the model contains hour of the day, day of the week, and time of year, which are used deterministically, and this dataset is divided into a training set to train the neural network for day-ahead price forecasting. The other dataset is the test set to validate the accuracy of the forecast model. The model accuracy for the given sample periods is computed with the Mean Absolute Error (MAE) and Mean Absolute Percent Error (MAPE) metrics. The forecasting toolbox available in Matlab is used to carry out the prediction algorithm.

Once the day-ahead electricity prices are forecasted, the GA-based optimization is carried out for two cases, (1) BESS and (2) TESS, and the working flowchart is as shown in Figure 3. The optimization formulation given in Equation (5) is solved once for BESS and once for TESS. Within the GA optimization routine, the control goes to the DIgSILENT (power flow program) routine to simulate the total wind farm model and obtain the values of reactive power to be inserted in the Matlab routine. In the profit maximization, along with constraints of BESS and TESS, meeting the reactive power requirements is also formulated as one of the constraints.

5. DIgSILENT Model of Wind Park

The DIgSILENT model of the wind farm illustrating the basic load flow results is shown in Figure 4. This model is one of the examples within the software, and the original wind farm under study is modeled in the same way. However, it is not shown here due to data protection policy. Parameters such as copper losses and short circuit voltage are calculated [36].

A fully rated converter-based wind turbine generator of 3.45 MW model is used to model the wind turbines. The maximum real power output of the park is around 197 MW. The reactive response to be seen at the PCC, which is a 345 kV connection that is governed by the Vestas Power Plant Controller (PPC) utilizing the capabilities of the turbines. As ordered by the TSO, the park controller sends the set points for real and reactive powers either directly to wind turbine units or through a cluster controller that is commonly used in large wind parks [37]. When reactive power supply is insufficient, the PPC will operate the capacitor bank installed at the wind park site, thereby avoiding drawing reactive power from the grid, which would otherwise have led to grid code violations [38]. The bank is sized into two steps of 12.6 MVar each-total 25.2 MVar compensation. The real data of wind speed profiles are given as input to the DIgSILENT models of wind turbines and the load flow simulations are carried out for determining the total wind park production at the PCC for a month, as shown in Figure 5.

The active power injection of the wind turbines mainly depends on the wind speed. The real power production at PCC and real power losses within the wind park with respect to wind sweep speeds are shown in Figure 6.

Reactive Power Capability

The concept of capability curve is used to determine the active and reactive powers that can be delivered by a wind farm. The real power–reactive power (PQ) diagrams depict the performance of the individual turbines or wind farm as a whole based on the limits of active and reactive powers. It is possible to control the reactive power at PCC with the park controller on-site. The reactive power capability of the wind park without and with park controller are analyzed and the results are represented as Case 1 and Case 2, respectively. The reference curve for reactive power capability (red color) of the wind park for a given reactive power requirement (blue color) without a park controller system is shown in Figure 7. The active power is swept from the starting value to maximum using two cases, i.e., $Q_{min}$ and ($Q_{max}$) correspond to reactive power for underexcited and overexcited cases, respectively. This is formulated as a constraint in the optimization problem given in Equation (5). The DIgSILENT output is given in

Table 1. Simulation results from the DIgSILENT model without PPC set points.

At Maximum Active Power	Requirement (Mvar)	Capability (Mvar)	Mismatch (Mvar)
Underexcited	−58.99	−41.59	17.41
Overexcited	58.99	41.37	17.62

. In Figure 7, the blue curve (requirement of reactive power) is exceeding the red curve (capability of the wind park) for both underexcited (left side of origin) and overexcited (right side of origin) cases.

It can be seen from both Figure 7 and the DIgSILENT output data in Table 1 that the wind park is unable to meet the required reactive power in few operating conditions. For overexcited case, the reactive power requirement is 58.99 MVar, whereas the wind park capability is only 41.37 MVar. Likewise, during underexcited cases, the wind park could not meet the required reactive power. Therefore, the park controller is made responsible for meeting the reactive power requirement either by switching the capacitor bank or modifying the active power output of the wind park.

The modified reactive power capability of the wind park by park controller in accordance with the reference (blue color) is as shown in Figure 8. The capacitor bank is switched on by PPC in order to meet the reactive power requirement. The park controller present in the wind farm switches ON the capacitor bank of 25.2 MVar in two steps depending on the reactive power requirement at the PCC. It can be observed from the DIgSILENT report that the capability is increased to 82.58 Mvar for underexcited and 83.14 Mvar for overexcited cases compared with the results obtained without park controller. As can be observed from Figure 8, the blue curve (requirement) is well within the red curve (capability of the wind park) for both underexcited (left side of origin) and overexcited (right side of origin) cases. The DIgSILENT output is given in

Table 2. Simulation results from the DIgSILENT model after correction using PPC set points.

At Maximum Active Power	Requirement (Mvar)	Capability (Mvar)	Margin (Mvar)
Underexcited	−58.99	−82.58	23.5941
Overexcited	58.99	83.11	24.15

. The PPC finds new active and reactive power set points, thereby operating the capacitor bank in order to meet the reactive power requirements. It can be seen from the results that there is a fair margin between capability and requirements, enabling the wind park to accommodate any future rise in reactive power requirement.

Table 3. Simulated results for PQ-analysis before/after PPC operation.

Dataset	Simulated Results
	Before PPC Operation (Case 1)	After PPC Operation (Case 2)
Max. cable loading	53.315%	55.022%
Max. transformer loading	100.00%	99.974%
Max. voltage inside power plant	1.022 p.u.	1.095 p.u.
Min. voltage inside power plant	0.952 p.u.	1.023 p.u.
Max. voltage at generation unit terminals	1.001 p.u.	1.071 p.u.
Min. voltage at generation unit terminals	0.960 p.u.	1.034 p.u.
Max. voltage at shunt terminal	0.953 p.u.	1.024 p.u.
Min. voltage at shunt terminal	0.952 p.u.	1.023 p.u.

presents the simulation results for PQ-analysis carried on the wind park before and after PPC operation. It can be observed from the PQ-analysis results, that the maximum and minimum voltage at shunt terminal are above 1 p.u. in Case 2 and are higher than in Case 1 because the capacitor bank is switched ON, thereby injecting reactive power. Further, in Case 1, the transformer should be loaded to 100%, whereas it is only loaded to 99.9%, showing that the real power production of wind park is also reduced to meet the reactive power requirement. This reduction in active power is significantly lower for both cases, but may be significant during fault disturbances within or outside the wind farm. This is not of main interest for this work. The DIgSILENT model is used to simulate the system and obtain the operating points for the later optimization problem that will be solved in Matlab, where a cosimulation between Matlab and DIgSILENT is established.

6. Simulations Results

The performance of the profit maximization algorithm is validated for various seasons where electricity prices are widespread, and the comparative analysis is shown for both BESS and TESS. The power and energy ratings, SoC/SoE limits, and ramp rates for both the storage models are given in

Table 4. Parameters of storage systems.

Parameters	BESS	TESS
Power (MW)	197	197
Energy (MWh)	250	250
SoC limits (%)	20–90	0–95
Round trip efficiency (%)	75–90	65–75
Ramp rate	No delay	3 MW/min [40]
BESS capital Cost	116 $/kWh	100 $/100l
BESS maintenance Cost	29 $/kWh/year	1 $/100l
$\alpha$	0.065 $/kWh	0.065 $/kWh
$\beta$	0.0116 $/kW/h	–
$\gamma$	0.0099 $/kWh/h	–

. Considering the hourly time-steps, the response time of BESS is only from 20 ms-s [39], where BESS characteristics show no delay in terms of ramp rate. In addition, the amortized cost parameters are taken from [6] for the present work. Considering the BESS costs, the investment cost is $29 million for a battery cost of $116\$$/kWh. This can be recovered in a span of 3–4 years with the proposed energy arbitrage solution for the wind farm.

The ability of deep learning regarding the input–output relationship for a given input data makes neural networks preferable over linear regression techniques. Figure 9 shows the electricity price results obtained from the forecasting algorithm. The residuals plot shows the estimated error between actual data and modeled data. The forecasting algorithm is based on Neural Network (NN)-based regression. The simple linear regression uses an approach where a line is used to best fit the given data for minimizing the error. However, when the data is scattered, this approach leads to either overfitting or underfitting. Even though the overfitting problem is also an issue in neural networks, in this work, it is handled by decreasing the complexity of the model through strategically reducing the number of neurons. There are many methods to resolve this problem, but this solution came out to be feasible for handling the present formulation. A three-layer feedforward neural network is used for forecasting the day-ahead electricity prices of hourly interval. The NN model consists of an input layer, hidden layer with 10 neurons, and output layer connected by weight functions. These weight functions are adjusted to better fit the model, thereby reducing the error. The model considers inputs including historical hourly prices, temperature, and holidays. The predictor matrix contains information about hour of the day, day in a week, previous day’s average price, and price from the same hour on the previous day. Then, this whole data is split into training for building the model and test data for forecasting the prices using estimated parameters from the training data set. The MAPE for a day is as given in Equation (7):

$$\begin{array}{c}\hfill MAPE = \frac{1}{24}\sum _{i=1}^{24}\frac{P_{i,actual}-P_{i,model}}{{\overline{P}}_{actual}}\\ \hfill {\overline{P}}_{actual} = \frac{1}{24}\sum _{i=1}^{24}{P}_{i,actual}\end{array}$$

(7)

It can be observed from Figure 9 that the model is able to predict the electricity prices using the historical data, where the model is able to track the actual data. There exists large MAE during the large peaks for certain periods, this is due to the fact that sometimes the NN model could not capture the sudden uncertainty in the electricity prices, which has no relation with the historical data. This uncertainty in electricity price can be caused by the demand, as electricity price is sensitive to load changes. The average MAPE is 6.89%, MAE is 5.27 MWh, and Daily Peak MAPE is 6.33% for the considered data set. The MAE provides information about the deviation in the estimated model and predicted model—the less the deviation, the better the predicted model. The average MAPE result obtained from the proposed NN model is 6.89%.

Table 5. Comparison of proposed ANN results with literature.

References	Methods	MAPE for a Day
[28]	Selected 8 days for year 2010	7.81% (Average value)
[29]	Selected 4, 8, and 12 neurons for hidden layer	23.3% (Best value)
Proposed method	Selected 10 days for year 2019 with 10 hidden neurons	6.89% (Average value)

shows the comparison of the results from the proposed method with the results from the literature. It is to be noted that the MAPE obtained from the proposed method is lower, which shows the effectiveness of the proposed method. Figure 10 shows the daily forecast results corresponding to various seasons. The MAPE came out to be higher in the fall season, i.e., 7.05%, as shown in Figure 10c; it is worth noticing that the prediction is quite good during morning and evenings. However, the inaccuracy exists, especially during higher price ranges caused due to the uncertainty in the power demand. For the winter season, as shown in Figure 10d, the ANN forecast price is almost same as the actual price from morning till evening, this is due to the fact that the training data has better accuracy that could lead to increased efficiency in the forecasting.

The predicted electricity prices and the simulated wind production profiles are given as known variables and the ESS charge/discharge strategies are decision variables in the GA optimization routine. As a first step, GA initializes the population and creates the next generation, including elite children with better fitness function, cross-over children from a pair of parents, and mutated children with random changes of same parent. The cross-over generation extracts the best features from the different populations and mutation helps in adding diversity—this way, GA generates superior individuals with a better fitness function that increases the maximum likelihood. For these heuristic algorithms, the initial population plays a significant role in finding the feasible solution. The convergence of objective/fitness function for four days corresponding to four seasons is shown in Figure 11, Figure 12, Figure 13 and Figure 14. The selection function provides information about the selection of offspring from the cross-over and mutation of parents/individuals from the population of 200. The GA tool in Matlab is a minimization algorithm, however, the present study is a maximization problem. Accordingly, the objective function is given as a negative function, as is the negative value for the fitness function. The day in July could capture more profit compared to other seasonal days, which is a positive outcome from energy arbitrage using BESS. Further, the number of iterations that are needed by GA to meet the stopping criteria are different.

The results obtained from GA are shown in Figure 15a,b for the SoC (BESS: min—20% and max—90%) and SoE (TESS: min—0% and max—95%) of both the BESS and TESS, respectively. The depth of discharge is different for the two storage systems, which can be observed from charge and discharge profiles as shown in Figure 16 and Figure 17. The thermal storage system discharges fully to zero, whereas the battery storage system’s minimum discharge limit is 20% of the total capacity. Internal losses are comparatively higher in the thermal storage system than in BESS, as can be seen from the negative axes of Figure 16 and Figure 17. Even though the TESS could charge up to 180 MW, due to more internal heat losses, it could only discharge 150 MW at any given time interval.

The optimal fitness function values, which is the profit that is obtained without ESS and with BESS/TESS, for the year 2019 are given in

Table 6. GA results: Profit obtained for cases without and with ESS.

Without ESS (Million $)	BESS (Million $)	TESS (Million $)
14.2	42.5	38.6

. It is to be noticed that the profit obtained from BESS is more than that in the TESS case. Nevertheless, if the objective is a trade-off between being ecologically friendly and maximizing the profit along with leveled costs, then TESS could be a better solution in spite of P2X losses.

Without the introduction of ESS, the wind farm is subjected to curtailment due to wind speed prediction errors, reactive power restrictions, etc. In this study, the curtailment of wind power for the year 2019 is compared for three cases (No ESS, BESS, and TESS), given in

Table 7. Wind power curtailment without and with ESS.

Without ESS (GW)	BESS (GW)	TESS (GW)
79.94	43.58	60.55

. It can be observed that the curtailment is less in the presence of BESS than with TESS case. This is due to the fact that there exists operational delays, including ramp rate charge/discharge for TESS, which is negligible in BESS.

7. Discussion and Conclusions

Grid-scalable energy storage systems, including BESS and TESS, are utilized to study their impact on wind park owner’s revenue through selling power to the grid, taking advantage of the price arbitrage. The thermal storage system behavior is different to the BESS system, which is due to the ramp rate constraints and the higher operating losses. Even though the depth of discharge of TESS is more than that of BESS, due to internal heat losses in the conversion of heat to electricity, BESS gives more profit than TESS. In this work, the energy from the TESS is used to produce electrical energy, thereby selling to the grid. Whereas, there can be other option of meeting heat demand with the TESS. The main conclusions can be summarized as follows.

• The present work deals with a real-world project, proposing an optimal strategy that helps the wind park owner to invest in large-scale ESS in order to prudently sell wind energy into the grid along with adhering to grid code requirements, thereby maximizing the profit.
• The proposed forecasting algorithm using feedforward neural network obtained better results compared to the results from the literature. The overfitting problem of the NN is handled by strategically reducing the model complexity by decreasing the number of hidden neurons.
• Profit maximization by GA mainly depends upon the accuracy of the electricity price and wind power forecasting, which are inputs to the optimization problem. In this work, the electricity price is considered as a major factor, so NN-based regression analysis is performed to have better prediction values. Furthermore, the mean absolute error is only 6.89% with the proposed NN model, which shows the accuracy of the predicted model regarding the profit.
• The utilization of wind energy (reduced curtailment) is much better in BESS than in TESS because of the ramp rate constraint and also significant power to heat and heat-to-power losses. However, with respect to the cost associated with operation and maintenance, TESS would be in high competition to become the first choice for a wind park operator.
• The reactive power support is provided by the wind farm, whereas the ESS is only responsible for real power charge/discharge with respect to electricity prices.
• The integrated system either with the BESS or the TESS gives better revenue to wind park owners when compared to the case where there is no ESS facility.
• The BESS of large capacity will be a better option for short-term or long-term energy arbitrage, i.e., in day-ahead electricity markets. However, the cost is a major factor in this decision.
• Further, balancing markets and reserves could also be possible marketplaces for energy arbitrage with ESS.