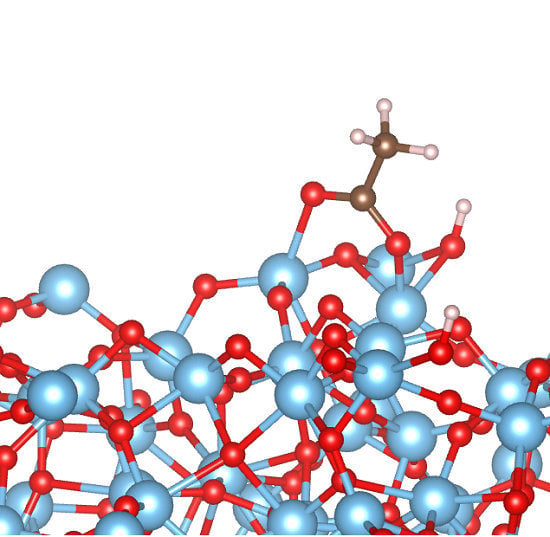
A Density Functional Tight Binding Study of Acetic Acid Adsorption on Crystalline and Amorphous Surfaces of Titania
Abstract
:1. Introduction
2. Theoretical and Computational Methods
3. Results and Discussion
3.1. TiO2 Bulk and Surfaces

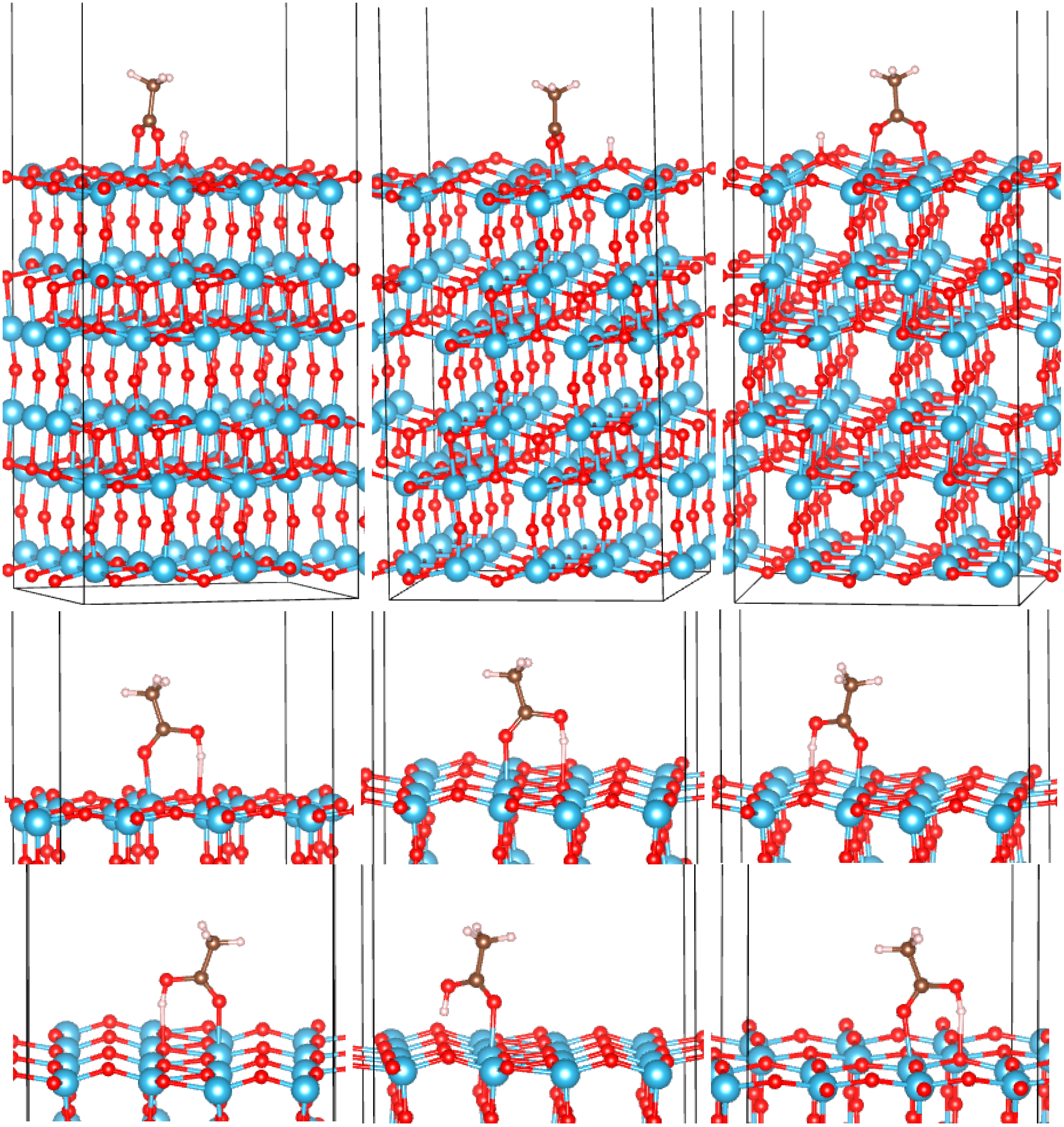
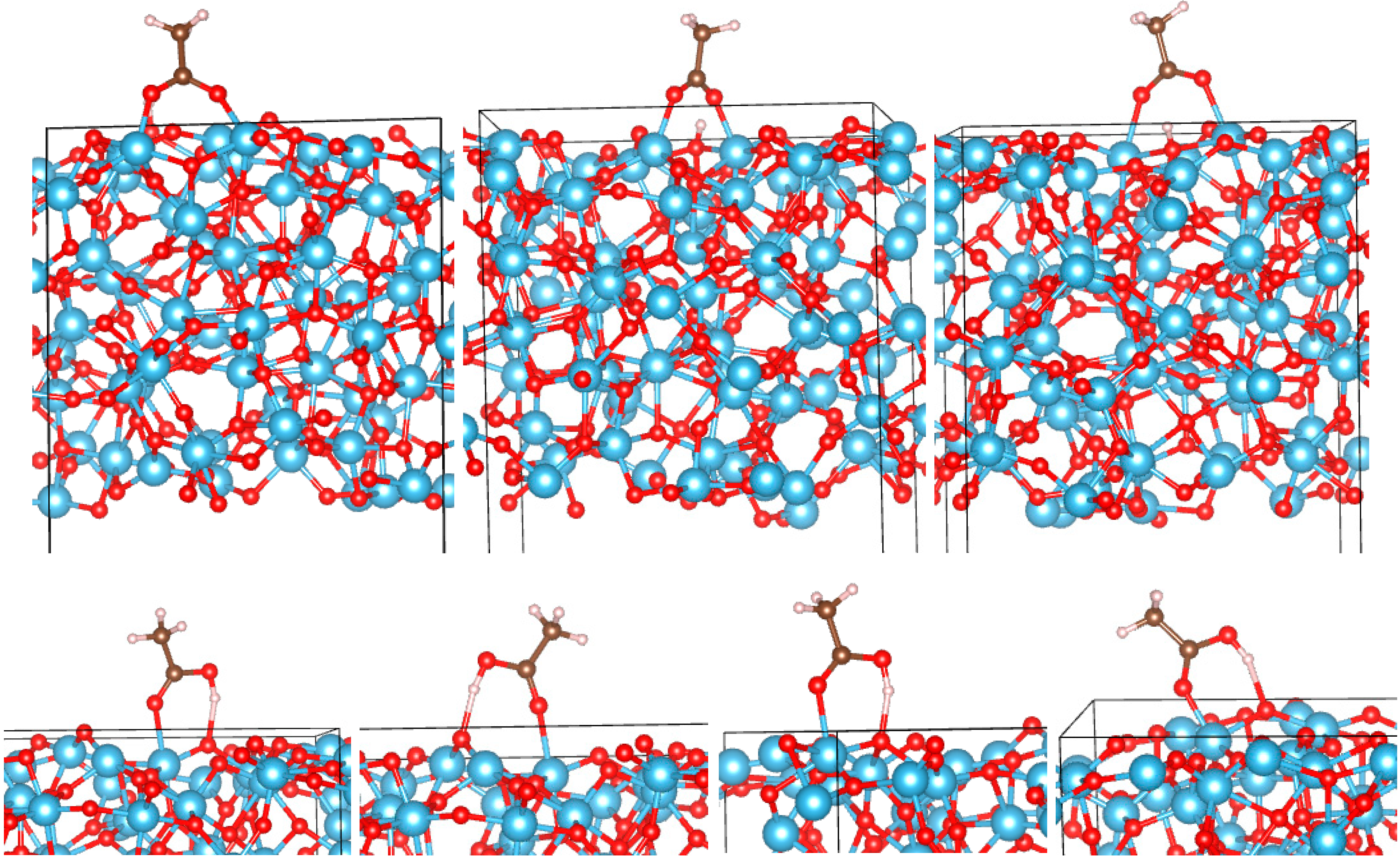
3.2. Adsorption Configurations of AcOH and Energetics

| System | Eads, eV | q, |e| | Omol-Ti, Å | Omol-Ti/H-Osurf, Å |
|---|---|---|---|---|
| Anatase (101) | ||||
| BB | −1.93 | −0.12 | 2.22 | 2.22 |
| M1 | −0.93 | 0.16 | 2.26 | 1.62 |
| M2 | −1.06 | 0.17 | 2.26 | 1.62 |
| Rutile (110) | ||||
| BB | −2.49 | −0.11 | 2.21 | 2.21 |
| M1 | −1.04 | 0.17 | 2.26 | 1.60 |
| M2B | −1.11 | 0.34 | 2.27 | 2.29 |
| B (001) | ||||
| BB1 | −0.74 | −0.17 | 2.24 | 2.25 |
| BB2 | −0.41 | −0.18 | 2.25 | 2.25 |
| BB3 | −1.07 | −0.16 | 2.23 | 2.24 |
| M1 | −0.78 | 0.17 | 2.27 | 1.83 |
| M2 | −0.79 | 0.18 | 2.27 | 1.87 |
| M3 | −0.86 | 0.19 | 2.27 | 1.97 |
| M4 | −0.70 | 0.17 | 2.27 | 1.87 |
| M5 | −0.79 | 0.19 | 2.27 | 2.08 |
| M6 | −0.75 | 0.18 | 2.27 | 1.86 |
| a-TiO2 | ||||
| top BB1 | −2.60 | 0.03 | 1.93 | 2.25 |
| top BB2 | −3.56 | 0.00 | 1.94 | 2.24 |
| top BB3 | −2.96 | −0.03 | 1.93 | 2.27 |
| top M1 | −2.20 | 0.33 | 1.96 | 1.60 |
| top M2 | −2.40 | 0.35 | 1.95 | 1.60 |
| top M3 | −2.38 | 0.35 | 1.95 | 1.63 |
| top M4 | −0.97 | 0.18 | 2.26 | 1.63 |
| top M5 | −0.80 | 0.16 | 2.26 | 1.62 |
| bottom BB1 | −4.43 | 0.04 | 1.91 | 1.95 |
| bottom BB2 | −4.92 | 0.08 | 1.97 | 2.00 |
| bottom BB3 | −0.28 | −0.07 | 2.21 | 2.22 |
| bottom M1 | −1.18 | 0.18 | 2.25 | 1.69 |
| bottom M2 | −0.84 | 0.14 | 2.25 | 1.63 |
| bottom M3 | −1.53 | 0.19 | 2.23 | 1.62 |
| bottom M4 | −1.83 | 0.14 | 1.93 | 1.77 |


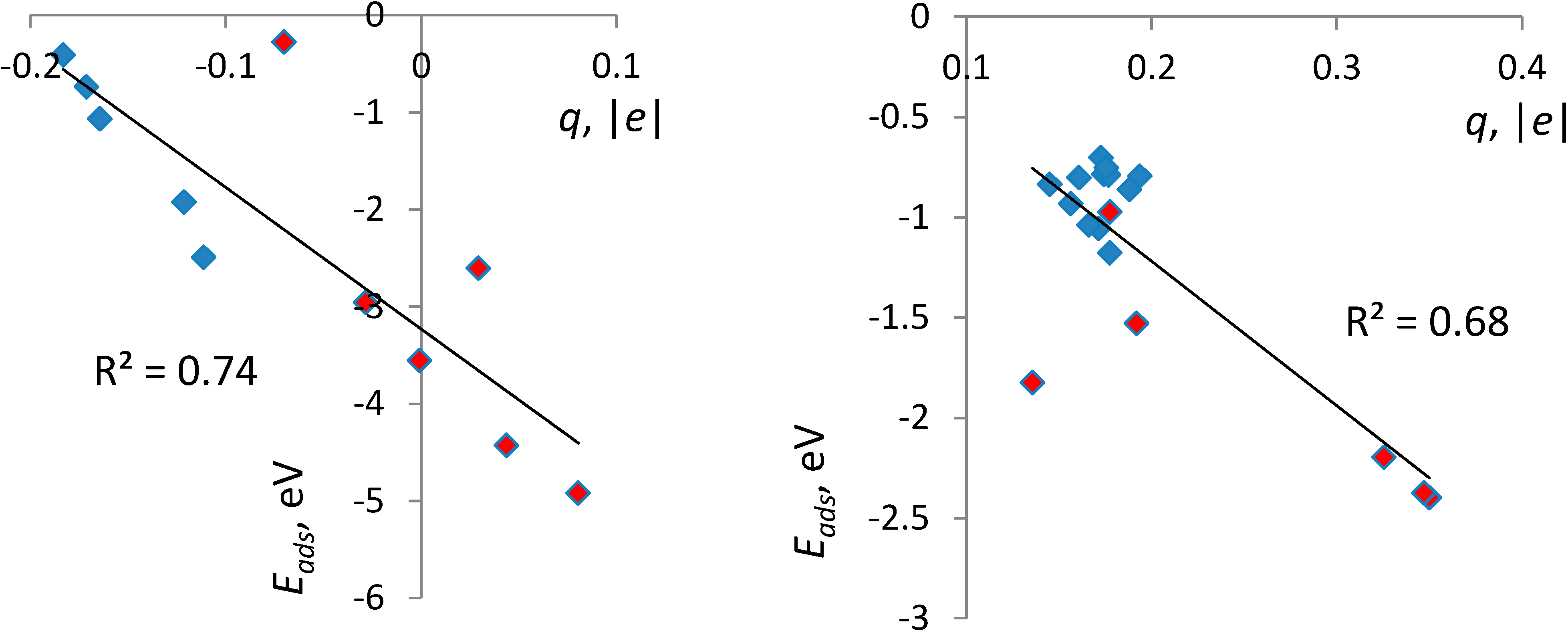
3.3. Correlates of Adsorption Strength
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sorescu, D.C.; Civiš, S.; Jordan, K.D. Mechanism of oxygen exchange between CO2 and TiO2(101) anatase. J. Phys. Chem. C 2014, 118, 1628–1639. [Google Scholar] [CrossRef]
- Müller, K.; Lu, D.; Senanayake, S.D.; Starr, D.E. Monoethanolamine adsorption on TiO2(110): Bonding, structure, and implications for use as a model solid-supported CO2 capture material. J. Phys. Chem. C 2013, 118, 1576–1586. [Google Scholar] [CrossRef]
- Drew, K.; Girishkumar, G.; Vinodgopal, K.; Kamat, P.V. Boosting fuel cell performance with a semiconductor photocatalyst: TiO2/Pt-Ru hybrid catalyst for methanol oxidation. J. Phys. Chem. B 2005, 109, 11851–11857. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, J.; Zhou, B.; Chen, H.; Wang, Z.; Cai, W. A TiO2-nanotube-array-based photocatalytic fuel cell using refractory organic compounds as substrates for electricity generation. Chem. Commun. 2011, 47, 10314–10316. [Google Scholar] [CrossRef]
- Upadhyaya, H.M.; Senthilarasu, S.; Hsu, M.-H.; Kumar, D.K. Recent progress and the status of dye-sensitised solar cell (DSSC) technology with state-of-the-art conversion efficiencies. Sol. Energy Mater. Sol. Cells 2013, 119, 291–295. [Google Scholar] [CrossRef]
- Ning, Z.; Fu, Y.; Tian, H. Improvement of dye-sensitized solar cells: What we know and what we need to know. Energy Environ. Sci. 2010, 3, 1170–1181. [Google Scholar] [CrossRef]
- Jung, H.S.; Lee, J.-K. Dye sensitized solar cells for economically viable photovoltaic systems. J. Phys. Chem. Lett. 2013, 4, 1682–1693. [Google Scholar] [CrossRef]
- Hagfeldt, A.; Boschloo, G.; Sun, L.; Kloo, L.; Pettersson, H. Dye-sensitized solar cells. Chem. Rev. 2010, 110, 6595–6663. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Mora-Sero, I.; de Angelis, F.; Bisquert, J.; Wang, P. Titanium dioxide for photovoltaic applications. Chem. Rev. 2014, 114, 10095–10130. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometallic halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-S.; Lee, C.-R.; Im, J.-H.; Lee, K.-B.; Moehl, T.; Marchioro, A.; Moon, S.-J.; Humphry-Baker, R.; Yum, J.-H.; Moser, J.E.; et al. Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. Rep. 2012, 2, 591. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Kim, M.G.; Lee, J.Y.; Chi, J. Green energy storage materials: Nanostructured TiO2 and Sn-based anodes for lithium-ion batteries. Energy Environ. Sci. 2009, 2, 818–837. [Google Scholar] [CrossRef]
- Yang, Z.; Choi, D.; Kerisit, S.; Rosso, K.M.; Wang, D.; Zhang, J.; Graff, G.; Liu, J. Nanostructures and lithium electrochemical reactivity of lithium titanites and titanium oxides: A review. J. Power Sources 2009, 192, 588–598. [Google Scholar] [CrossRef]
- Liu, S.; Hu, J.J.; Yan, N.F.; Pan, G.L.; Li, G.R.; Gao, X.P. Aluminum storage behavior of anatase TiO2 nanotube arrays in aqueous solution for aluminum ion batteries. Energy Environ. Sci. 2012, 5, 9743–9746. [Google Scholar] [CrossRef]
- Dylla, A.G.; Henkelman, G.; Stevenson, K.J. Lithium insertion in nanostructured TiO2(B) architectures. Acc. Chem. Res. 2013, 46, 1104–1112. [Google Scholar] [CrossRef] [PubMed]
- Myung, S.-T.; Kikuchi, M.; Yoon, C.S.; Yashiro, H.; Kim, S.-J.; Sun, Y.-K.; Scrosati, B. Black anatase titania enabling ultra high cycling rates for rechargeable lithium batteries. Energy Environ. Sci. 2013, 6, 2609–2614. [Google Scholar] [CrossRef]
- Li, W.; Wang, F.; Feng, S.; Wang, J.; Sun, Z.; Li, B.; Li, Y.; Yang, J.; Elzatahry, A.; Xia, Y.; et al. Sol–gel design strategy for ultradispersed TiO2 nanoparticles on graphene for high-performance lithium ion batteries. J. Am. Chem. Soc. 2013, 135, 18300–18303. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-T.; Ali, G.; Chung, K.Y.; Yoon, C.S.; Yashiro, H.; Sun, Y.-K.; Lu, J.; Amine, K.; Myung, S.-T. Anatase titania nanorods as an intercalation anode material for rechargeable sodium batteries. Nano Lett. 2014, 14, 416–422. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Zhang, R.Q.; Ng, A.M.C.; Djurisic, A.B.; Chan, H.T.; Chan, W.K.; Tong, S.Y. Splitting water on metal oxide surfaces. J. Phys. Chem. C 2011, 115, 19710–19715. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, Y.-G.; Li, J.; Zhuang, J.; Wang, X. Surface-specific interaction by structure-match confined pure high-energy facet of unstable TiO2(B) polymorph. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef]
- Niu, M.; Cheng, D.; Cao, D. Fluorite TiO2(111) surface phase for enhanced visible-light solar energy conversion. J. Phys. Chem. C 2014, 118, 20107–20111. [Google Scholar] [CrossRef]
- Vittadini, A.; Casarin, M.; Selloni, A. Structure and stability of TiO2-B surfaces: A Density Functional study. J. Phys. Chem. C 2009, 113, 18973–18977. [Google Scholar] [CrossRef]
- Perron, H.; Domain, C.; Roques, J.; Drot, R.; Simoni, E.; Catalette, H. Optimisation of accurate rutile TiO2 (110), (100), (101) and (001) surface models from periodic DFT calculations. Theor. Chem. Acc. 2007, 117, 565–574. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, G.; Fujisawa, J.-I.; Segawa, H.; Yamashita, K. Unraveling the adsorption mechanism of aromatic and aliphatic diols on TiO2 surface: a density functional theory analysis. Phys. Chem. Chem. Phys. 2013, 15, 9761–9767. [Google Scholar] [CrossRef] [PubMed]
- Heckel, W.; Elsner, B.A.M.; Schulz, C.; Müller, S. The role of hydrogen on the adsorption behavior of carboxylic acid on TiO2 surfaces. J. Phys. Chem. C 2014, 118, 10771–10779. [Google Scholar] [CrossRef]
- Manzhos, S.; Segawa, H.; Yamashita, K. The effect of ligand substitution and water co-adsorption on the adsorption dynamics and energy level matching of amino-phenyl acid dyes on TiO2. Phys. Chem. Chem. Phys. 2012, 14, 1749–1755. [Google Scholar] [CrossRef] [PubMed]
- O’Rurke, C.; Bowler, D.R. Adsorption of thiophene-conjugated sensitizers on TiO2 anatase (101). J. Phys. Chem. C 2010, 114, 20240–20248. [Google Scholar] [CrossRef]
- Pastore, M.; de Angelis, F. Aggregation of organic dyes on TiO2 in dye-sensitized solar cells models: an ab initio investigation. ACS Nano 2010, 4, 556–562. [Google Scholar] [CrossRef] [PubMed]
- De Angelis, F.; Fantacci, S.; Gebauer, R. Simulating dye-sensitized TiO2 heterointerfaces in explicit solvent: Absorption spectra, energy levels, and dye desorption. J. Phys. Chem. Lett. 2011, 2, 813–817. [Google Scholar] [CrossRef]
- Spreafico, C.; Schiffmann, F.; VandeVondele, J. Structure and mobility of acetic acid at the anatase (101)/acetonitrile interface. J. Phys. Chem. C 2014, 118, 6251–6260. [Google Scholar] [CrossRef]
- Anselmi, C.; Mosconi, E.; Pastore, M.; Ronca, E.; de Angelis, F. Adsorption of organic dyes on TiO2 surfaces in dye-sensitized solar cells: interplay of theory and experiment. Phys. Chem. Chem. Phys. 2012, 14, 15963–15974. [Google Scholar] [CrossRef] [PubMed]
- Vittadini, A.; Selloni, A.; Rotzinger, F.P.; Gra1tzel, M. Formic acid adsorption on dry and hydrated TiO2 Anatase (101) surfaces by DFT calculations. J. Phys. Chem. B 2000, 104, 1300–1306. [Google Scholar] [CrossRef]
- Agosta, L.; Zollo, G.; Arcangeli, C.; Buonocore, F.; Gala, F.; Celino, M. Water driven adsorption of amino acids on the (101) anatase TiO2 surface: An ab initio study. Phys. Chem. Chem. Phys. 2015, 17, 1556–1561. [Google Scholar] [CrossRef] [PubMed]
- Coropceanu, V.; Cornil, J.; da Silva Filho, D.A.; Olivier, Y.; Silbey, R.; Brédas, J.L. Charge transport in organic semiconductors. Chem. Rev. 2007, 107, 926–952. [Google Scholar] [CrossRef]
- Borghols, W.J.H.; Wagemaker, M.; Lafont, U.; Kelder, E.M.; Mulder, F.M. Impact of nanosizing on lithiated rutile TiO2. Chem. Mater. 2008, 20, 2949–2955. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Arrouvel, C.; Gentili, V.; Parker, S.C.; Saiful Islam, M.; Bruce, P. Lithium coordination sites in LixTiO2(B): A structural and computational study. Chem. Mater. 2010, 22, 6426–6432. [Google Scholar] [CrossRef]
- Borghols, W.J.H.; Lützenkirchen-Hecht, D.; Haake, U.; van Eck, E.R.H.; Muldera, F.M.; Wagemaker, M. The electronic structure and ionic diffusion of nanoscale LiTiO2 anatase. Phys. Chem. Chem. Phys. 2009, 11, 5742–5748. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Wei, S.-H.; Kim, Y.-H. First-principles theory of electrochemical capacitance of nanostructured materials: Dipole-assisted subsurface intercalation of lithium in pseudocapacitive TiO2 anatase nanosheets. J. Phys. Chem. C 2011, 115, 4909–4915. [Google Scholar] [CrossRef]
- Sushko, M.L.; Rosso, K.M.; Liu, J. Mechanism of Li+/electron conductivity in rutile and anatase TiO2 nanoparticles. J. Phys. Chem. C 2010, 114, 20277–20283. [Google Scholar] [CrossRef]
- Eithiraj, R.D.; Geethalakshmi, K.R. Suitability of amorphous TiO2 nanoparticles as a photoelectrode in dye sensitized solar cells: A DFT–TDDFT study. Chem. Phys. Lett. 2013, 585, 138–142. [Google Scholar] [CrossRef]
- Tang, X.; Liu, X.; Zhang, L.; Xing, Y.; Tian, Y. Low crystallinity TiO2 film with inherent low oxygen vacancy for sensitized solar cells. Chem. Phys. 2014, 441, 121–127. [Google Scholar] [CrossRef]
- Kakuta, N.; Oku, T.; Suzuki, A.; Kikuchi, K.; Kikuchi, S. Effect of an amorphous TiO2 addition on dye-sensitized solar cells with organic dyes. J. Ceram. Process. Res. 2012, 13, 28–31. [Google Scholar]
- Xiong, H.; Slater, M.D.; Balasubramanian, M.; Johnson, C.S.; Rajh, T. Amorphous TiO2 nanotube anode for rechargeable sodium ion batteries. J. Phys. Chem. Lett. 2011, 2, 2560–2565. [Google Scholar] [CrossRef]
- Borghols, W.J.H.; Lützenkirchen-Hecht, D.; Haake, U.; Chan, W.; Lafont, U.; Kelder, E.M.; van Eck, E.R.H.; Kentgens, A.P.M.; Mulder, F.M.; Wagemaker, M. Lithium storage in amorphous TiO2 nanoparticles. J. Electrochem. Soc. 2010, 157, A582–A588. [Google Scholar] [CrossRef]
- Hibino, M.; Abe, K.; Mochizuki, M.; Miyayama, M. Amorphous titanium oxide electrode for high-rate discharge and charge. J. Power Sources 2004, 126, 139–143. [Google Scholar] [CrossRef]
- Sun, X.; Xie, M.; Travis, J.J.; Wang, G.; Sun, H.; Lian, J.; George, S.M. Pseudocapacitance of amorphous TiO2 thin films anchored to graphene and carbon nanotubes using atomic layer deposition. J. Phys. Chem. C 2013, 117, 22497–22508. [Google Scholar] [CrossRef]
- Hai-Tao, F.; Min, L.; Da-Wei, W.; Tao, S.; Dong-Sheng, G.; Feng, L.; Jigang, Z.; Tsun-Kong, S.; Hui-Ming, C. Comparison of the rate capability of nanostructured amorphous and anatase TiO2 for lithium insertion using anodic TiO2 nanotube arrays. Nanotechnology 2009, 20. [Google Scholar] [CrossRef] [PubMed]
- Yildirim, H.; Greeley, J.P.; Sankaranarayanan, S.K.R.S. Localized order–disorder transitions induced by Li segregation in amorphous TiO2 nanoparticles. ACS Appl. Mater. Interfaces 2014, 6, 18962–18970. [Google Scholar] [CrossRef] [PubMed]
- Kaur, K.; Singh, C.V. Amorphous TiO2 as a photocatalyst for hydrogen production: A DFT study of structural and electronic properties. Energy Procedia 2012, 29, 291–299. [Google Scholar] [CrossRef]
- Legrain, F.; Malyi, O.; Manzhos, S. Insertion energetics of lithium, sodium, and magnesium in crystalline and amorphous titanium dioxide: A comparative first-principles study. J. Power Sources 2015, 278, 197–202. [Google Scholar] [CrossRef]
- Legrain, F.; Malyi, O.; Manzhos, S. Comparative ab initio study of lithium storage in amorphous and crystalline TiO2. In Proceedings of the 14th Asian Conference on Solid State Ionics, Singapore, Singapore, 24–27 June 2014.
- Prasai, B.; Cai, B.; Underwood, M.K.; Lewis, J.P.; Drabold, D.A. Properties of amorphous and crystalline titanium dioxide from first principles. J. Mater. Sci. 2012, 47, 7515–7521. [Google Scholar] [CrossRef]
- Dolgonos, G. Self-consistent-charge density-functional tight-binding molecular dynamics simulations of amorphous TiO2 growth. Surf. Sci. 2014, 621, 51–54. [Google Scholar] [CrossRef]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a sparse matrix-based implementation of the DFTB method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- Gemming, S.; Enyashin, A.; Frenzel, J.; Seifert, G. Adsorption of nucleotides on the rutile (110) surface. Int. J. Mater. Res. 2010, 101, 758–764. [Google Scholar] [CrossRef]
- Zhu, T.; Gao, S.-P. The stability, electronic structure, and optical property of TiO2 polymorphs. J. Phys. Chem. C 2014, 118, 11385–11396. [Google Scholar] [CrossRef]
- Burdett, J.K.; Hughbanks, T.; Miller, G.J.; Richardson, J.W.; Smith, J.V. Structural-electronic relationships in inorganic solids: Powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K. J. Am. Chem. Soc. 1987, 109, 3639–3646. [Google Scholar] [CrossRef]
- Horn, M.; Schwerdtfeger, C.F.; Meagher, E.P. Refinement of the structure of anatase at several temperatures. Z. Kristallogr. 1972, 136, 273–281. [Google Scholar] [CrossRef]
- Asahi, R.; Taga, Y.; Mannstadt, W.; Freeman, A.J. Electronic and optical properties of anatase TiO2. Phys. Rev. B 2000, 61, 7459–7465. [Google Scholar] [CrossRef]
- Labat, F.; Baranek, P.; Domain, C.; Minot, C.; Adamo, C. Density functional theory analysis of the structural and electronic properties of TiO2 rutile and anatase polytypes: Performances of different exchange-correlation functionals. J. Chem. Phys. 2007, 126, 154703–12. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Berger, H.; Schmid, P.E.; Lévy, F.; Burri, G. Photoluminescence in TiO2 anatase single crystals. Solid State Commun. 1993, 87, 847–850. [Google Scholar] [CrossRef]
- Dolgonos, G.; Aradi, B.; Moreira, N.H.; Frauenheim, T. An improved self-consistent-charge Density-Functional Tight-Binding (SCC-DFTB) set of parameters for simulation of bulk and molecular systems involving titanium. J. Chem. Theory Comput. 2010, 6, 266–278. [Google Scholar] [CrossRef]
- Tezuka, Y.; Shin, S.; Lshii, T.; Ejima, T.; Suzuki, S.; Sato, S. Photoemission and Bremsstrahlung Isochromat spectroscopy studies of TiO2 (Rutile) and SrTiO3. J. Phys. Soc. Jpn. 1994, 63, 347–357. [Google Scholar] [CrossRef]
- Pascual, J.; Camassel, J.; Mathieu, H. Resolved quadrupolar transition in TiO2. Phys. Rev. Lett. 1977, 39, 1490–1493. [Google Scholar] [CrossRef]
- Pascual, J.; Camassel, J.; Mathieu, H. Fine structure in the intrinsic absorption edge of TiO2. Phys. Rev. B 1978, 18, 5606–5614. [Google Scholar] [CrossRef]
- CRC Handbook of Chemistry and Physics, 67th ed.; CRC: Cleveland, OH, USA, 1986.
- Chase, M.W.; Davies, C.A.; Downey, J.R.; Frurip, D.J.; McDonald, R.A.; Syverud, A.N. JANAF Thermodynamical Tables, 3rd ed. J. Phys. Chem. Ref. Data 1985, 14 (Suppl. 1), 1680. [Google Scholar]
- Hamad, B.A. First-principle calculations of structural and electronic properties of rutile-phase dioxides (MO2), M = Ti, V, Ru, Ir and Sn. Eur. Phys. J. B 2009, 70, 163–169. [Google Scholar] [CrossRef]
- Lazzeri, M.; Vittadini, A.; Selloni, A. Structure and energetics of stoichiometric TiO2 anatase surfaces. Phys. Rev. B 2001, 63, 155409. [Google Scholar] [CrossRef]
- Yang, H.G.; Sun, C.H.; Qiao, S.Z.; Zou, J.; Liu, G.; Smith, S.C.; Cheng, H.M.; Lu, G.Q. Anatase TiO2 single crystals with a large percentage of reactive facets. Nature 2008, 453, 638–641. [Google Scholar] [CrossRef] [PubMed]
- Yahia, M.B.; Lemoigno, F.; Beuvier, T.; Filhol, J.-S.; Richard-Plouet, M.; Brohan, L.; Doublet, M.-L. Updated references for the structural, electronic, and vibrational properties of TiO2(B) bulk using first-principles density functional theory calculations. J. Chem. Phys. 2009, 130, 204501–204511. [Google Scholar] [CrossRef] [PubMed]
- Betz, G.; Tributsch, H.; Marchand, R. Hydrogen insertion (intercalation) and light induced proton exchange at TiO2(B) -electrodes. J. Appl. Electrochem. 1984, 14, 315–322. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B: Condens. Matter. 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mat. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhoff, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17978. [Google Scholar] [CrossRef]
- Chan, M.; Carrington, T.; Manzhos, S. Anharmonic vibrations of the carboxyl group in acetic acid on TiO2: implications for adsorption mode assignment in dye-sensitized solar cells. Phys. Chem. Chem. Phys. 2013, 15, 10028–10034. [Google Scholar] [CrossRef] [PubMed]
- Soler, J.M.; Artacho, E.; Dale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys.: Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. CP2K: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Lippert, G.; Hutter, J.; Parrinello, M. A hybrid Gaussian and plane wave Density Functional scheme. Mol. Phys. 1997, 92, 477–487. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Tao, J.; Luttrell, T.; Bylsma, J.; Batzill, M. Adsorption of acetic acid on rutile TiO2(110) vs. (011)-2 × 1 surfaces. J. Phys. Chem. C 2011, 115, 3434–3442. [Google Scholar] [CrossRef]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzhos, S.; Giorgi, G.; Yamashita, K. A Density Functional Tight Binding Study of Acetic Acid Adsorption on Crystalline and Amorphous Surfaces of Titania. Molecules 2015, 20, 3371-3388. https://doi.org/10.3390/molecules20023371
Manzhos S, Giorgi G, Yamashita K. A Density Functional Tight Binding Study of Acetic Acid Adsorption on Crystalline and Amorphous Surfaces of Titania. Molecules. 2015; 20(2):3371-3388. https://doi.org/10.3390/molecules20023371
Chicago/Turabian StyleManzhos, Sergei, Giacomo Giorgi, and Koichi Yamashita. 2015. "A Density Functional Tight Binding Study of Acetic Acid Adsorption on Crystalline and Amorphous Surfaces of Titania" Molecules 20, no. 2: 3371-3388. https://doi.org/10.3390/molecules20023371
APA StyleManzhos, S., Giorgi, G., & Yamashita, K. (2015). A Density Functional Tight Binding Study of Acetic Acid Adsorption on Crystalline and Amorphous Surfaces of Titania. Molecules, 20(2), 3371-3388. https://doi.org/10.3390/molecules20023371