High-Pressure Design of Advanced BN-Based Materials
Abstract
:1. Introduction
2. Advanced BN Precursors
2.1. Pyrolytic BN
2.2. Turbostratic BN
2.3. BN Nanoparticles
3. New Advanced B–N Materials
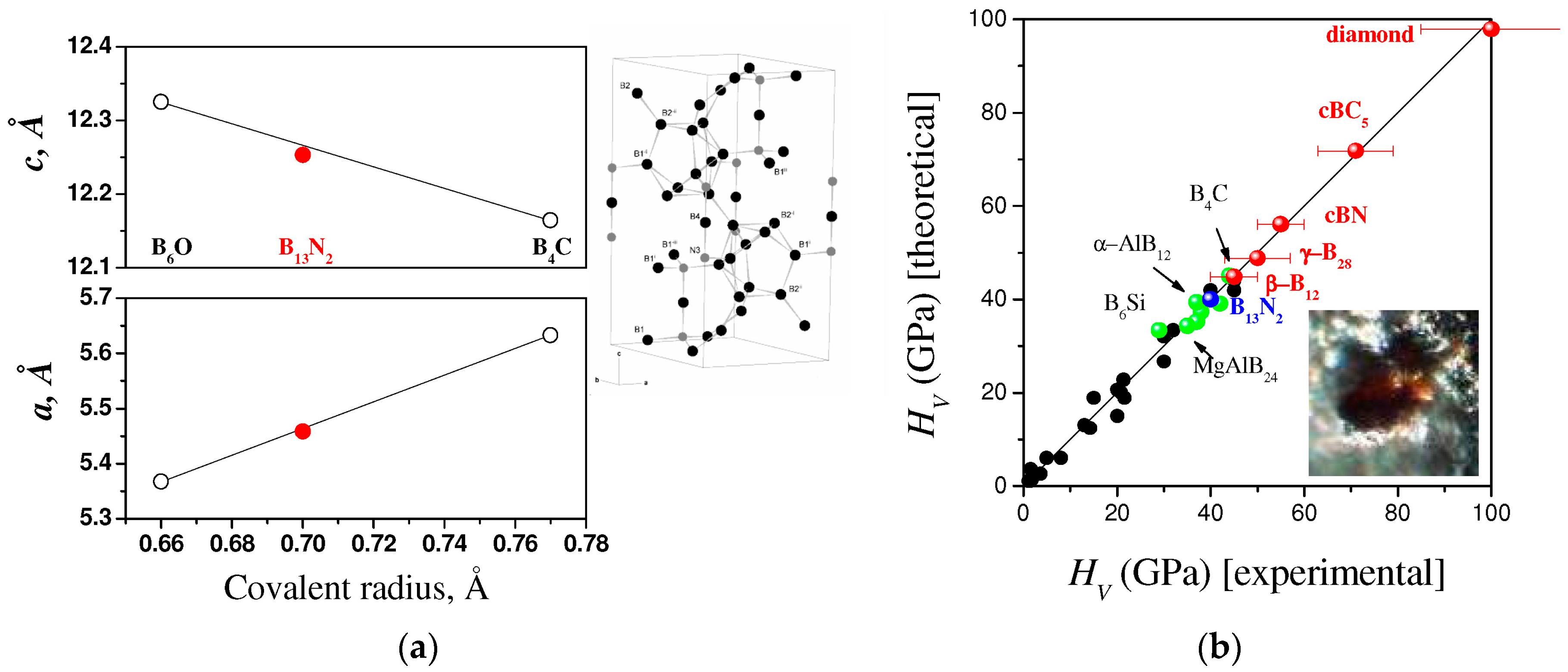
3.1. Boron Subnitrides
3.2. cBN-wBN Nanocomposites
3.3. Nano-cBN
4. Thermodynamics and Phase Diagrams of the B–N System
4.1. p-V-T Equations of State of BN
4.2. Equilibrium Phase Diagram of BN
4.3. Phase Diagrams of the B–BN System
5. Kinetics of BN Phase Transformations
5.1. Kinetics of Direct hBN-to-cBN Phase Transformation
5.2. Mechanism of Direct tBN-to-cBN Phase Transformation: Reconstructive Features and Thermal Activation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Balmain, W.H. Bemerkungen über die Bildung von Verbindungen des Bors und Siliciums mit Stickstoff und gewissen Metallen. J. Prakt. Chem. 1842, 27, 422–430. [Google Scholar] [CrossRef]
- Wentorf, H.R., Jr. Cubic form of boron nitride. Chem. Phys. 1957, 26, 956–960. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Petrusha, I.A.; Svirid, A.A. High pressure produced textured wurtzitic BN with unusually low thermal stability. High Press. Res. 1994, 12, 347–351. [Google Scholar] [CrossRef]
- Oganov, A.R.; Chen, J.; Gatti, C.; Ma, Y.; Ma, Y.; Glass, C.W.; Liu, Z.; Yu, T.; Kurakevych, O.O.; Solozhenko, V.L. Ionic high-pressure form of elemental boron. Nature 2009, 457, 863–867. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Kurakevych, O.O.; Oganov, A.R. On the hardness of a new boron phase, orthorhombic g-B28. J. Superhard Mater. 2008, 30, 428–429. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; Solozhenko, V.L. Crystal structure of dense pseudo-cubic boron allotrope, pc-B52, by powder X-ray diffraction. J. Superhard Mater. 2013, 35, 60–63. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Andrault, D.; le Godec, Y.; Mezouar, M. Ultimate metastable solubility of boron in diamond: Synthesis of superhard diamond-like BC5. Phys. Rev. Lett. 2009, 102, 015506. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Andrault, D.; Fiquet, G.; Mezouar, M.; Rubie, D.C. Synthesis of superhard cubic BC2N. Appl. Phys. Lett. 2001, 78, 1385–1387. [Google Scholar] [CrossRef]
- Kurakevych, O.O. Superhard phases of simple substances and binary compounds of the B–C–N–O system: From diamond to the latest results (a Review). J. Superhard Mater. 2009, 31, 139–157. [Google Scholar] [CrossRef]
- Zheng, M.; Liu, Y.; Wang, P.; Xiao, Y. Synthesis and formation mechanism of cubic boron nitride nanorods in lithium bromide molten salt. Mater. Lett. 2013, 91, 206–208. [Google Scholar] [CrossRef]
- Taniguchi, T.; Teraji, T.; Koizumi, S.; Watanabe, K.; Yamaoka, S. Appearance of n-Type Semiconducting Properties of cBN Single Crystals Grown at High Pressure. Jpn. J. Appl. Phys. 2002, 41, L109. [Google Scholar] [CrossRef]
- Lei, W.; Zhang, H.; Wu, Y.; Zhang, B.; Liu, D.; Qin, S.; Liu, Z.; Liu, L.; Ma, Y.; Chen, Y. Oxygen-doped boron nitride nanosheets with excellent performance in hydrogen storage. Nano Energy 2014, 6, 219–224. [Google Scholar] [CrossRef]
- Akinwande, D.; Petrone, N.; Hone, J. Two-dimensional flexible nanoelectronics. Nat. Commun. 2014, 5, 5678. [Google Scholar] [CrossRef] [PubMed]
- Lei, W.; Portehault, D.; Dimova, R.; Antonietti, M. Boron Carbon Nitride Nanostructures from Salt Melts: Tunable Water-Soluble Phosphors. J. Amer. Chem. Soc. 2011, 133, 7121–7127. [Google Scholar] [CrossRef] [PubMed]
- Portehault, D.; Giordano, C.; Gervais, C.; Senkovska, I.; Kaskel, S.; Sanchez, C.; Antonietti, M. High-Surface-Area Nanoporous Boron Carbon Nitrides for Hydrogen Storage. Adv. Funct. Mater. 2010, 20, 1827–1833. [Google Scholar] [CrossRef]
- Yu, J.; Chen, Y.; Elliman, R.G.; Petravic, M. Isotopically Enriched 10BN Nanotubes. Adv. Mater. 2006, 18, 2157–2160. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Bouvier, P. First and second order Raman scattering of B6O. J. Raman Spectr. 2009, 40, 1078–1081. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O. Chemical interaction in the B–BN system at high pressures and temperatures. Synthesis of novel boron subnitrides. J. Solid State Chem. 2009, 182, 1359–1364. [Google Scholar] [CrossRef]
- Kim, E.; Pang, T.; Utsumi, W.; Solozhenko, V.L.; Zhao, Y.S. Cubic phases of BC2N: A first-principles study. Phys. Rev. B 2007, 75, 184115. [Google Scholar] [CrossRef]
- Ganguly, S.; Kazem, N.; Carter, D.; Kauzlarich, S.M. Colloidal Synthesis of an Exotic Phase of Silicon: The BC8 Structure. J. Am. Chem. Soc. 2014, 136, 1296–1299. [Google Scholar] [CrossRef] [PubMed]
- Irifune, T.; Kurio, A.; Sakamoto, S.; Inoue, T.; Sumiya, H. Ultrahard polycrystalline diamond from graphite. Nat. Mater. 2003, 421, 599–600. [Google Scholar] [CrossRef] [PubMed]
- Mukhanov, V.A.; Sokolov, P.S.; Solozhenko, V.L. On melting of B4C boron carbide under pressure. J. Superhard Mater. 2012, 34, 211–213. [Google Scholar] [CrossRef]
- Sharupin, B.N.; Kravchik, A.E.; Efremenko, M.M.; Mametev, R.Y.; Tupitsina, E.V.; Osmakov, A.S. Analysis of the structure of pyrolytic boron-nitride. J. Appl. Chem. USSR 1990, 63, 1569–1572. [Google Scholar]
- Kurdyumov, A.V. Packing defects in graphite-like bornitride. Kristallografiya 1975, 20, 969–973. [Google Scholar]
- Kurdyumov, A.V.; Solozhenko, V.L.; Zelyavski, W.B. Lattice parameters of boron nitride polymorphous modifications as a function of their crystal-structure perfection. J. Appl. Crystallogr. 1995, 28, 540–545. [Google Scholar] [CrossRef]
- Franklin, R.E. The structure of graphitic carbons. Acta Crystallogr. 1951, 4, 253–261. [Google Scholar] [CrossRef]
- Lei, W.; Mochalin, V.N.; Liu, D.; Qin, S.; Gogotsi, Y.; Chen, Y. Boron nitride colloidal solutions, ultralight aerogels and freestanding membranes through one-step exfoliation and functionalization. Nat. Commun. 2015, 6, 8849. [Google Scholar] [CrossRef] [PubMed]
- Lei, W.; Liu, D.; Chen, Y.C. Highly Crumpled Boron Nitride Nanosheets as adsorbents: Scalable solvent-less production. Adv. Mater. Interface 2015, 2, 1400529. [Google Scholar] [CrossRef]
- Condon, J.B.; Holcombe, C.E.; Johnson, D.H.; Steckel, L.M. The kinetics of the boron plus nitrogen reaction. Inorg. Chem. 1976, 15, 2173–2179. [Google Scholar] [CrossRef]
- Bauer, J.D.; Back, C.A.; Castor, J.I.; Dykema, P.G.; Hammel, B.A.; Lee, R.W.; Nash, J.K.; Seely, J.F.; Feldman, U.; Brown, C.M. Simulation and analysis of an x-ray-heated boron nitride foil. Phys. Rev. E 1995, 52, 6736–6752. [Google Scholar] [CrossRef]
- Hubert, H.; Garvie, L.A.J.; Buseck, P.R.; Petuskey, W.T.; McMillan, P.F. High-pressure, high-temperature syntheses in the B–C–N–O system. I. Preparation and Characterization. J. Solid State Chem. 1997, 133, 356–364. [Google Scholar] [CrossRef]
- An, Q.; Reddy, K.M.; Dong, H.; Chen, M.-W.; Oganov, A.R.; Goddard, W.A. Nanotwinned Boron Suboxide (B6O): New Ground State of B6O. Nano Lett. 2016, 16, 4236–4242. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Oganov, A.R.; Wang, Q.; Wang, S.-N.; Wang, Z.; Zhang, J.; Esfahani, M.M.D.; Zhou, X.-F.; Wu, F.; Zhu, Q. Prediction of a new ground state of superhard compound B6O at ambient conditions. Sci. Rep. 2016, 6, 31288. [Google Scholar] [CrossRef] [PubMed]
- Kurakevych, O.O.; Solozhenko, V.L. Rhombohedral boron subnitride, B13N2, by X-ray powder diffraction. Acta Crystallogr. C 2007, 63, i80–i82. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Kurakevych, O.O. New boron subnitride B13N2: HP-HT synthesis, structure and equation of state. J. Phys. Conf. Ser. 2008, 121, 062001. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; le Godec, Y.; Hammouda, T.; Goujon, C. Comparison of solid-state crystallization of boron polymorphs at ambient and high pressures. High Press. Res. 2012, 32, 30–38. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O. Equilibrium p-T phase diagram of boron: Experimental study and thermodynamic analysis. Sci. Rep. 2013. [Google Scholar] [CrossRef] [PubMed]
- Ploog, K.; Schmidt, H.; Amberger, E.; Will, G.; Kossubutzki, K.H. B48B2C2 and B48B2N2, two non-metal borides with structure of so-called I-tetragonal boron. J. Less Commun. Met. 1972, 29, 161–169. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; Zhu, M.; Zhu, J.; Yan, H. Synthesis of B50N2 nanorods by electrolysis of organic solutions. Electrochem. Commun. 2006, 8, 1211–1214. [Google Scholar] [CrossRef]
- Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. Thermodynamic Model of Hardness: Particular Case of Boron-Rich Solids. J. Superhard Mater. 2010, 32, 167–176. [Google Scholar] [CrossRef]
- Gou, H.Y.; Zhang, J.W.; Gao, F.M. First-principles calculations of boron-rich compounds of B13N2 and B12C2X (X = Si, Ge). J. Phys. Cond. Matter 2008, 20, 505211. [Google Scholar] [CrossRef]
- Dubrovinskaia, N.; Solozhenko, V.L.; Miyajima, N.; Dmitriev, V.; Kurakevych, O.O.; Dubrovinsky, L. Superhard nanocomposite of dense polymorphs of boron nitride: Noncarbon material has reached diamond hardness. Appl. Phys. Lett. 2007, 90, 101912. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; le Godec, Y.; Crichton, W.A.; Guignard, J.; Strobel, T.A.; Zhang, H.; Liu, H.; Coelho Diogo, C.; Polian, A.; Menguy, N.; et al. Synthesis of bulk BC8 silicon allotrope by direct transformation and reduced-pressure chemical pathways. Inorg. Chem. 2016. [Google Scholar] [CrossRef] [PubMed]
- Kurdyumov, A.V.; Pilyankevich, A.N. Phase Transformations in Carbon and Boron Nitride; Naukova Dumka: Kiev, Ukraine, 1979. [Google Scholar]
- Schiøtz, J.; Jacobsen, K.W. A maximum in the strength of nanocrystalline copper. Science 2003, 301, 1357–1359. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Xu, B.; Yu, D.; Ma, Y.; Wang, Y.; Jiang, Y.; Hu, W.; Tang, C.; Gao, Y.; Luo, K.; et al. Ultrahard nanotwinned cubic boron nitride. Nature 2013, 493, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Dubrovinskaia, N.; Dubrovinsky, L. Controversy about ultrahard nanotwinned cBN. Nature 2013, 502, E1–E2. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Sun, H.; Chen, C. Large indentation strain-stiffening in nanotwinned cubic boron nitride. Nat. Commun. 2014, 5, 4965. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Kurakevych, O.O.; le Godec, Y. Creation of Nanostuctures by Extreme Conditions: High-Pressure Synthesis of Ultrahard Nanocrystalline Cubic Boron Nitride. Adv. Mater. 2012, 24, 1540–1544. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Chernyshev, V.V.; Fetisov, G.V.; Rybakov, V.B.; Petrusha, I.A. Structure-Analysis of the Cubic Boron-Nitride Crystals. J. Phys. Chem. Solids 1990, 51, 1011–1012. [Google Scholar] [CrossRef]
- Anderson, O.; Oda, H.; Chopelas, A.; Isaak, D. A thermodynamic theory of the Grueneisen ratio at extreme conditions: MgO as an example. Phys. Chem. Miner. 1993, 19, 369–380. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; Solozhenko, V.L. Thermoelastic equation of state of boron suboxide B6O up to 6 GPa and 2700 K: Simplified Anderson-Grüneisen model and thermodynamic consistency. J. Superhard Mater. 2014, 36, 270–278. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; le Godec, Y.; Solozhenko, V.L. Equations of state of novel solids synthesized under extreme pressure-temperature conditions. J. Phys. Conf. Ser. 2015, 653, 012080. [Google Scholar] [CrossRef] [Green Version]
- Kurakevych, O.O.; le Godec, Y.; Strobel, T.A.; Kim, D.Y.; Crichton, W.A.; Guignard, J. High-pressure and high-temperature stability of antifluorite Mg2C by in situ X-ray diffraction and ab initio calculations. J. Phys. Chem. C 2014, 118, 8128–8133. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; Solozhenko, V.L. Experimental study and critical review of structural, thermodynamic and mechanical properties of superhard refractory boron suboxide B6O. J. Superhard Mater. 2011, 33, 421–428. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; le Godec, Y.; Brazhkin, V.V. Thermodynamically consistent p-T phase diagram of boron oxide B2O3 by in situ probing and thermodynamic analysis. J. Phys. Chem. C 2015, 119, 20600–20605. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Solozhenko, E.G. On the compressibility of graphite-like boron nitride. J. Superhard Mater. 1999, 21, 83–84. [Google Scholar]
- Solozhenko, V.L.; Peun, T. Compression and thermal expansion of hexagonal graphite-like boron nitride up to 7 GPa and 1800 K. J. Phys. Chem. Solids 1997, 58, 1321–1323. [Google Scholar] [CrossRef]
- Datchi, F.; Dewaele, A.; Godec, Y.L.; Loubeyre, P. Equation of state of cubic boron nitride at high pressures and temperatures. Phys. Rev. B 2007, 75, 214104–214109. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; Solozhenko, V.L. 300-K equation of state of rhombohedral boron subnitride, B13N2. Solid State Commun. 2009, 149, 2169–2171. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Turkevich, V.Z.; Turkevich, D.V. Phase diagram of the B–BN system at 5 GPa. J. Phys. Chem. B 2010, 114, 5819–5822. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Hausermann, D.; Mezouar, M.; Kunz, M. Equation of state of wurtzitic boron nitride to 66 GPa. Appl. Phys. Lett. 1998, 72, 1691–1693. [Google Scholar] [CrossRef]
- Le Godec, Y.; Kurakevych, O.O.; Munsch, P.; Garbarino, G.; Mezouar, M.; Solozhenko, V.L. Effect of nanostructuration on compressibility of cubic BN. J. Superhard Mater. 2012, 34, 336–338. [Google Scholar] [CrossRef]
- Bundy, F.P.; Wentorf, R.H., Jr. Direct Transformation of hexagonal boron nitride to denser forms. J. Chem. Phys. 1963, 38, 1144–1149. [Google Scholar] [CrossRef]
- Wentorf, R.H., Jr. Condensed systems at high pressures. J. Phys. Chem. 1959, 63, 1934–1940. [Google Scholar] [CrossRef]
- Corrigan, F.R.; Bundy, F.P. Direct transitions among the allotropic forms of boron nitride at high pressures and temperatures. J. Chem. Phys. 1975, 63, 3812–3820. [Google Scholar] [CrossRef]
- Solozhenko, V.L. On the phase diagram of boron nitride. Dokl. Phys. Chem. 1988, 301, 147–149. [Google Scholar]
- Solozhenko, V.L.; Turkevich, V.Z.; Holzapfel, W.B. Refined phase diagram of boron nitride. J. Phys. Chem. B 1999, 103, 2903–2905. [Google Scholar] [CrossRef]
- Solozhenko, V.L. Thermodynamics of dense boron nitride modifications and a new phase P,T diagram for BN. Thermochim. Acta 1993, 218, 221–227. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Will, G.; Elf, F. Isothermal compression of hexagonal graphite-like boron nitride up to 12 GPa. Solid State Commun. 1995, 96, 1–3. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Will, G.; Hupen, H.; Elf, F. Isothermal compression of rhombohedral boron nitride up to 14 GPa. Solid State Commun. 1994, 90, 65–67. [Google Scholar] [CrossRef]
- Glushko, V.P. Thermodynamic Properties of Individual Substances; Nauka: Moscow, Russia, 1981; Volume 3. [Google Scholar]
- Vinogradov, V.L.; Kostanovsky, A.V. Determination of melting parameters for boron nitride. Teplofiz. Vys. Temp. 1991, 29, 1112–1120. [Google Scholar]
- Gustafson, P. An evaluation of the thermodynamic properties and the P, T phase diagram of carbon. Carbon 1986, 24, 169–176. [Google Scholar] [CrossRef]
- Zerr, A.; Serghiou, G.; Boehler, R. 5th NIRIM International Symposium on Advanced Materials, 1998; NIRIM: Tsukuba, Japan, 1998; p. 5. [Google Scholar]
- Solozhenko, V.L.; Kurakevych, O.O.; Turkevich, V.Z.; Turkevich, D.V. Phase Diagram of the B–B2O3 System at 5 GPa: Experimental and Theoretical Studies. J. Phys. Chem. B 2008, 112, 6683–6687. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Turkevich, V.Z.; Kurakevych, O.O.; Turkevich, D.V.; Taniguchi, T. Phase Equilibria in the B–BN-B2O3 System at 5 GPa. J. Phys. Chem. C 2013, 117, 18642–18647. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; le Godec, Y.; Klotz, S.; Mezouar, M.; Turkevich, V.Z.; Besson, J.M. In situ studies of boron nitride crystallization from BN solutions in supercritical N-H fluid at high pressures and temperatures. Phys. Chem. Chem. Phys. 2002, 4, 5386–5393. [Google Scholar] [CrossRef]
- Solozhenko, V.L. Synchrotron radiation studies of the kinetics of cBN crystallization in the NH4F-BN system. Phys. Chem. Chem. Phys. 2002, 4, 1033–1035. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Turkevich, V.Z.; Novikov, N.V.; Petitet, J.P. On the cubic boron nitride crystallization in fluid systems. Phys. Chem. Chem. Phys. 2004, 6, 3900–3902. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Turkevich, V.Z.; Holzapfel, W.B. On nucleation of cubic boron nitride in the BN-MgB2 system. J. Phys. Chem. B 1999, 103, 8137–8140. [Google Scholar] [CrossRef]
- Mazurenko, A.M.; Leusenko, A.A.; Rakitskii, E.B.; Dobryanskii, V.M.; Rakitskaya, L.I. Kinetics of the transformation of pyrolytic boron nitride into cubic. Inorg. Mater. 1990, 26, 1045–1047. [Google Scholar]
- Sirota, N.N.; Mazurenko, A.M. Kinetics of transformation of graphite-like boron nitride into a cubic modification. Rep. Acad. Sci. USSR 1978, 241, 884–887. [Google Scholar]
- Solozhenko, V.L.; Kurakevych, O.O.; Sokolov, P.S.; Baranov, A.N. Kinetics of the wurtzite-to-rock-salt phase transformation in ZnO at high pressure. J. Phys. Chem. A 2011, 115, 4354–4358. [Google Scholar] [CrossRef] [PubMed]
- Avrami, M. Kinetics of phase change. II. Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Kurakevych, O.O. Restricted growth of solid phase from solution. Mater. Chem. Phys. 2007, 105, 401–407. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Saüren. Z. Physik. Chem. 1889, 4, 226. [Google Scholar]
- Merkle, R.; Maier, J. On the Tammann–Rule. Z. Anorg. Allg. Chem. 2005, 631, 1163–1166. [Google Scholar] [CrossRef]
- Britun, V.F.; Kurdyumov, A.V. Mechanisms of martensitic transformations in boron nitride and conditions of their development. High Press. Res. 2000, 17, 101–111. [Google Scholar] [CrossRef]
- Dub, S.N.; Petrusha, I.A. Mechanical properties of polycrystalline cBN obtained from pyrolytic gBN by direct transformation technique. High Press. Res. 2006, 26, 71–77. [Google Scholar] [CrossRef]
- Ueno, M.; Hasegawa, K.; Oshima, R.; Onodera, A.; Shimomura, O.; Takemura, K.; Nakae, H.; Matsuda, T.; Hirai, T. Room-temperature transition of rhombohedral-type boron nitride under high static pressure. Phys. Rev. B 1992, 45, 10226–10230. [Google Scholar] [CrossRef]
- Meng, Y.; Mao, H.-K.; Eng, P.J.; Trainor, T.P.; Newville, M.; Hu, M.Y.; Kao, C.; Shu, J.; Hausermann, D.; Hemley, R.J. The formation of sp3 bonding in compressed BN. Nat. Mater. 2004, 3, 111–114. [Google Scholar] [CrossRef] [PubMed]
- Solozhenko, V.L.; Kurakevych, O.O.; Kuznetsov, A.Y. Raman scattering from turbostratic graphite-like BC4 under pressure. J. Appl. Phys. 2007, 102, 063509. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Solozhenko, E.G.; Chen, J.; Parise, J.B. Equation of state of graphite-like BC. Solid State Commun. 2006, 137, 268–271. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O. Reversible pressure-induced structure changes in turbostratic BN–C solid solutions. Acta Crystallogr. B 2005, 61, 498–503. [Google Scholar] [CrossRef] [PubMed]








| B–N phase | Fitted Parameters 1 | Fixed Parameters 1 |
|---|---|---|
| cBN [60] | B0 = 390; B0’ = 3.35; δ = 3; a = 1 × 10−6; b = 5 × 10−9 | |
| wBN [63] | B0 = 375; B0’ = 4.9; δ = 3; a = 1 × 10−6; b = 5 × 10−9 | |
| nano-cBN [64] | B0 = 375; B0’ = 2.3; δ = 3; a = 1 × 10−6; b = 5 × 10−9 | |
| hBN [59] | δ = 2.5; a = 4.1 × 10−5 | B0 = 36.7; B0’ = 5.6; b = 0 |
| tBN [58] | B0 = 17.2; B0’ = 11.4 | |
| B13N2 [53] | B0 = 200; B0’ = 4; δ = 5.5; a = 1.4 × 10−5; b = 5 × 10−9 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurakevych, O.O.; Solozhenko, V.L. High-Pressure Design of Advanced BN-Based Materials. Molecules 2016, 21, 1399. https://doi.org/10.3390/molecules21101399
Kurakevych OO, Solozhenko VL. High-Pressure Design of Advanced BN-Based Materials. Molecules. 2016; 21(10):1399. https://doi.org/10.3390/molecules21101399
Chicago/Turabian StyleKurakevych, Oleksandr O., and Vladimir L. Solozhenko. 2016. "High-Pressure Design of Advanced BN-Based Materials" Molecules 21, no. 10: 1399. https://doi.org/10.3390/molecules21101399
APA StyleKurakevych, O. O., & Solozhenko, V. L. (2016). High-Pressure Design of Advanced BN-Based Materials. Molecules, 21(10), 1399. https://doi.org/10.3390/molecules21101399






