Continuous Monitoring of Shelf Lives of Materials by Application of Data Loggers with Implemented Kinetic Parameters
Abstract
:1. Introduction
2. Results and Discussion
2.1. Experimental
2.2. Kinetic Analysis
2.2.1. Determination of the Reaction Rate and Kinetic Triplets
2.2.2. Propellants: Application of Kinetic Analyses for Shelf Life Predictions
- -
- -
- Middle section: Long-term prediction of the reaction course according to the best model containing prediction bands with 95% confidence. The empty circles indicate the results of the additional experiments not used during the kinetic analysis which were applied for the verification of the simulations. The plot additionally contains the simulated course of the reaction at a lower temperature (50 °C) with one experimental point.
- -
- Bottom section: Comparison of the prediction of the reaction course at 20 °C over 10 years and for climatic category A1 (diurnal seasonal storage according to [10] using the best, 0th, and 1st order models.
2.2.3. Pharmaceuticals
The Peculiarities of the Application of Kinetics for the Evaluation of the Shelf Life
Shelf Life Evaluation Criteria Derived from the Arrhenius Equation
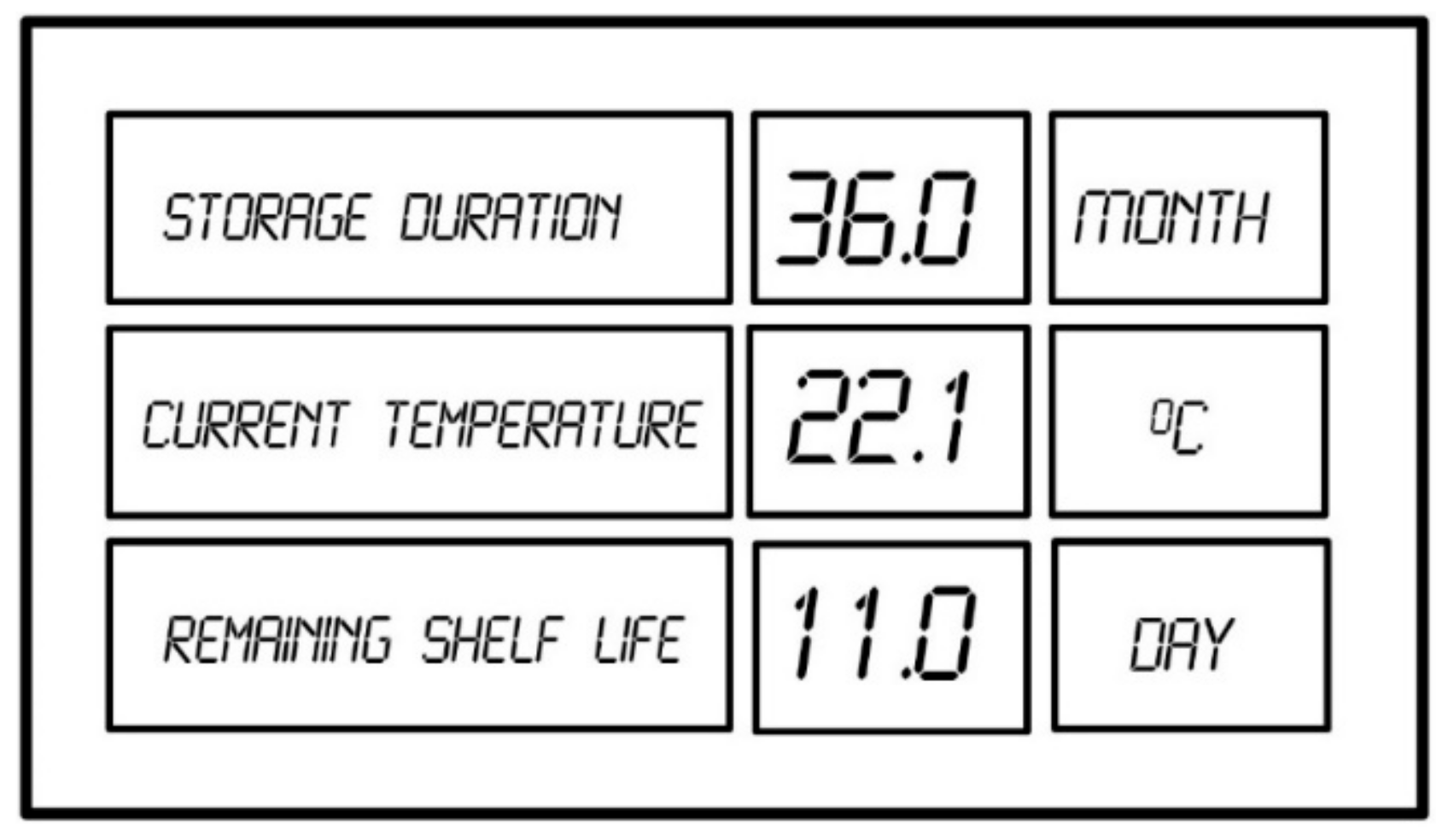
2.3. Continuous Shelf-Life Estimation by Using Data Logger
2.4. Basic Technical Information about the Application of Data Loggers with Implemented Kinetic Data
3. Materials and Methods
3.1. Propellant
3.1.1. Analytical Methods
Pressure Firing (PF)
Gas Evolution (VST)
Ultra-Performance Liquid Chromatography (UPLC)
Heat Flow Calorimetry (HFC)
3.2. Vaccine
3.2.1. Stability Monitoring
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cargosense Homepage. Available online: http://www.cargosense.com/supply-chain-intelligence-the-internet-of-things-iot-and-its-impact-on-healthcare-logistics/ (accessed on 24 April 2019).
- Roduit, B.; Hartmann, M.; Folly, P.; Sarbach, A.; Baltensperger, R. Prediction of thermal stability of materials by modified kinetic and model selection approaches based on limited amount of experimental points. Thermochim. Acta 2014, 579, 31–39. [Google Scholar] [CrossRef]
- Brown, M.E.; Maciejewski, M.; Vyazovkin, S.; Nomen, R.; Sempere, J.; Burnham, A.; Opfermann, J.; Strey, R.; Anderson, H.L.; Kemmler, A.; et al. Computational aspects of kinetic analysis. Part A: The ICTAC kinetics project-data, methods and results. Thermochim. Acta 2000, 355, 125–143. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- AKTS-Thermokinetics Software Version 5.1. Available online: http://www.akts.com (accessed on 13 January 2019).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bohn, M.A. Assessment of description quality of models by information theoretical criteria based on Akaike and Schwarz-Bayes applied with stability data of energetic materials. In Proceedings of the 46th International Annual Conference of ICT on “Energetic Materials—Performance, Safety and System Applications”, Karlsruhe, Germany, 23–26 June 2015; pp. 6.1–6.23. [Google Scholar]
- De Klerk, W.P.C. Assessment of Stability of propellants and safe lifetimes. Propellants Explos. Pyrotech. 2015, 40, 388–393. [Google Scholar] [CrossRef]
- NATO AOP-48. Explosives, Nitrocellulose Based Propellants—Stability Test Procedures and Requirements Using Stabilizer Depletion, 2nd ed.; North Atlantic Treaty Organization: Brussels, Belgium; Military Agency for Standardization: Brussels, Belgium, 2008. [Google Scholar]
- NATO STANAG 4582. Explosives, Nitrocellulose-Based Propellants, Stability Test Procedure and Requirements Using Heat Flow Calorimetry; Military Agency for Standardization: Brussels, Belgium; North Atlantic Treaty Organization: Brussels, Belgium, 2004. [Google Scholar]
- Carstensen, J.T.; Rhodes, C.T. Drug Stability, Principles and Practices, 3rd ed.; CT Informa Healthcare: New York, NY, USA, 2007. [Google Scholar]
- Kartoglu, U.; Milstein, J. Tools and approaches to ensure of vaccines throughout the cold chain. Expert Rev. Vaccines 2014, 13, 843–854. [Google Scholar] [CrossRef]
- Waterman, K.C. Understanding and predicting pharmaceutical product shelf life. In Handbook of Stability Testing in Pharmaceutical Development; Huynh-Ba, K., Ed.; Springer: New York, NY, USA, 2000; pp. 115–135. [Google Scholar]
- Waterman, K.C.; Adami, R.C. Accelerated aging: Prediction of chemical stability of pharmaceuticals. Int. J. Pharm. 2005, 293, 101–125. [Google Scholar] [CrossRef] [PubMed]
- Waterman, K.C.; Carella, A.J.; Gumkowski, M.J.; Lukulay, P.; MacDonald, B.C.; Roy, M.C.; Shamblin, S.L. Improved protocol and data analysis for accelerated shelf life estimation of solid dosage forms. Pharm. Res. 2007, 24, 780–790. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, L. One- and two-stage Arrhenius model for pharmaceutical shelf life prediction. J. Biopharm. Stat. 2015, 25, 307–316. [Google Scholar] [CrossRef]
- Fu, M.; Perlman, M.; Lu, Q.; Varga, C. Pharmaceutical solid-state kinetic stability investigation by using moisture modified Arrhenius equation and JMP Statistical software. J. Pharm. Biomed. Anal. 2015, 107, 370–377. [Google Scholar] [CrossRef]
- Almalik, O.; Nijhuis, M.B.; van den Heuvel, E.R. Combined statistical analyses for long-term stability data with multiple storage conditions: A simulation study. J. Biopharm. Stat. 2014, 24, 493–506. [Google Scholar] [CrossRef] [PubMed]
- Faya, P.; Seaman, J.W., Jr.; Stamey, J.D. Using accelerated drug stability results to inform long-term studies in shelf life determination. Stat. Med. 2018, 37, 2599–2615. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.R.; Kona, R.; Faustino, P.J.; Gupta, A.; Taylor, J.S.; Porter, D.A.; Khan, M. United States Food and Drug Administration and Department of Defense shelf life extension program of pharmaceutical products: Progress and promise. J. Pharm. Sci. 2014, 103, 1331–1336. [Google Scholar] [CrossRef] [PubMed]
- Clénet, D.; Imbert, F.; Probeck, P.; Rahman, N.; Ausar, A.F. Advanced kinetic analysis as a tool for formulation development and prediction of vaccine stability. J. Pharm. Sci. 2014, 103, 3055–3062. [Google Scholar] [CrossRef] [PubMed]
- Clénet, D. Accurate prediction of vaccine stability under real storage conditions and during temperature excursions. Eur. J. Pharm. Biopharm. 2018, 125, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Clancy, D.; Hodnett, N.; Orr, R.; Owen, M.; Peterson, J. Kinetic model development for accelerated stability studies. AAPS PharmSciTech 2017, 18, 1158–1176. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Guidelines on Stability Evaluation of Vaccines. WHO/BS/06.249-Final. 2006. Available online: https://www.who.int/biologicals/publications/trs/areas/vaccines/stability/en/ (accessed on 11 January 2019).
- Controlled Temperature Chain Working Group. Controlled Temperature Chain: Strategic Roadmap for Priority Vaccines 2017–2020; World Health Organization: Geneva, Switzerland, 2017; Available online: https://www.who.int/immunization/programmes_systems/supply_chain/ctc_strategic_roadmap_priority_vaccines.pdf (accessed on 13 December 2018).
- World Health Organization. WHO PQS Prequalified Devices and Equipment, E006 Temperature Monitoring Devices. Available online: http://www.who.int/immunization/documents/financing/who_ivb_15.04/en/ (accessed on 11 January 2019).
- WHO. Controlled Temperature Chain (CTC); World Health Organization (WHO): Geneva, Switzerland, 2016; Available online: http://www.who.int/immunization/programmes_systems/supply_chain/ctc/en/ (accessed on 19 December 2018).
- Haynes, J.D. Worldwide virtual temperatures for product stability testing. J. Pharm. Sci. 1971, 60, 927–929. [Google Scholar] [CrossRef]
- Seevers, R.H.; Hoffer, J.; Harber, P.; Ulrich, D.A.; Bishara, R. The use of Mean Kinetic temperature (MKT) in the handling, storage and distribution of temperature sensitive pharmaceuticals. Pharm. Outsourcing 2009, 10, 12–17. Available online: https://studylib.net/doc/8854836/the-use-of-mean-kinetic-temperature--mkt-, (accessed on 15 December 2018).
- Tong, C.; Lock, A. A computational procedure for Mean Kinetic Temperature using unequally spaced data. In Proceedings of the Joint Statistical Meeting 2015, Biopharmaceutical Section, Seattle, WA, USA, 8–13 August 2015; pp. 2065–2070. [Google Scholar]
- Health Products Regulatory Authority (HPRA). Guide to Control and Monitoring of Storage and Transportation Temperature Conditions for Medicinal Products and Active Substances IA-G0011-2.2017. Available online: https://www.hpra.ie/docs/default-source/publications-forms/guidance-documents/ia-g0011-guide-to-control-and-monitoring-of-storage-and-transportation-conditions-v2.pdf (accessed on 15 December 2018).
- Okeke, C.C.; Bailey, L.C.; Medwick, T.; Grady, L.T. Temperature fluctuations during mail order shipments of pharmaceutical articles using Mean Kinetic temperature approach. Pharm. Forum 1997, 23, 4155–4182. [Google Scholar]
- Okeke, C.C.; Bailey, L.C.; Lindauer, R.F.; Medwick, T.; Grady, L.T. Evaluation of the physical and chemical stability of some drugs when exposed to temperature fluctuations during shipment. Pharm. Forum 1998, 24, 7064–7073. [Google Scholar]
- Kumru, O.S.; Joshi, S.B.; Smith, D.E.; Middaugh, C.R.; Prusik, T.; Volkin, D.B. Vaccine instability in the cold chain: Mechanisms, analysis and formulation strategies. Biologicals 2014, 42, 237–250. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Pritchard, E.; Hu, X.; Valentin, T.; Panilaitis, B.; Omenetto, F.G.; Kaplan, D.L. Stabilization of vaccines and antibiotics in silk and eliminating the cold chain. Proc. Natl. Acad. Sci. USA 2012, 109, 11981–11986. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watzky, M.A.; Morris, A.M.; Ross, E.D.; Finke, R.G. Fitting yeast and mammalianprion aggregation kinetic data with the Finke-Watzky two-step model of nucleation and autocatalytic growth. Biochemistry 2008, 47, 10790–10800. [Google Scholar] [CrossRef] [PubMed]
- Morris, A.M.; Watzky, M.A.; Finke, R.G. Protein aggregation kinetics, mechanism and curve-fitting: A review of the literature. Biochim. Biophys. Acta 2009, 1794, 375–397. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.E.; Glass, B.D. Pharmaceutical application of the Prout-Tompkins rate equation. Int J. Pharm. 1999, 190, 129–137. [Google Scholar] [CrossRef]
- Ammann, C. A mathematical approach to assessing temperature excursions in temperature-controlled chains. Eur. J. Parenter. Pharm. Sci. 2008, 13, 57–59. [Google Scholar]
- Capen, R.; Christopher, D.; Forenzo, P.; Ireland, C.; Liu, O.; Lyapustina, S.; O’Neill, J.; Patterson, N.; Quinlan, M.; Sandell, D.; et al. On the shelf life of pharmaceutical products. AAPS PharmSciTech 2012, 13, 911–918. [Google Scholar] [CrossRef]
- Madakam, S.; Ramaswamy, R.; Tripathi, S. Internet of Things (IoT): A literature review. J. Comp. Commun. 2015, 3, 164–173. [Google Scholar] [CrossRef]
- Proceedings of the GloTs 2017: Global Internet of Things Summit, Geneva, Switzerland, 6–9 June 2017. Available online: https://ieeexplore.ieee.org/xpl/mostRecentIssue.jsp?punumber=8011434 (accessed on 13 March 2019).
- Tsang, Y.P.; Choy, K.L.; Wu, C.H.; Ho, G.T.S.; Lam, H.Y.; Koo, P.S. An IoT-based cargo monitoring system for enhancing operational effectiveness under a cold chain environment. Int. J. Eng. Bus. Manag. 2017, 9, 1–13. [Google Scholar] [CrossRef]
- Salunkhe, P.G.; Nerkar, R. IoT driven smart system for best cold chain application. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, Maharashtra, India, 22–24 December 2016; pp. 64–67. Available online: https://ieeexplore.ieee.org/document/7955270 (accessed on 20 January 2019).
- Monteleone, S.; Sampalo, M.; Maia, R.F. A novel deployment of smart Cold Chain system using 2g-RFID-Sys temperature monitoring in medicine Cold Chain based on Internet of Things. In Proceedings of the 2017 IEE International Conference on Service Operations and Logistics, and Informatics (SOLI), Bari, Italy, 18–20 September 2017; pp. 205–210. Available online: https://ieeexplore.ieee.org/document/8120995 (accessed on 20 January 2019).
- Mohsin, A.; Yellampalli, S.S. IoT based cold chain logistics monitoring. In Proceedings of the International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; pp. 1971–1974. Available online: https://ieeexplore.ieee.org/document/8392059 (accessed on 15 January 2019).
- Ping, H.; Wang, J.; Ma, Z.; Du, Y. Mini-review of application of IoT technology in monitoring agricultural products quality and safety. Int. J. Agric. Biol. Eng. 2018, 11, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Corradini, M.G. Shelf Life of Food products: From open Labeling to real-time measurements. Annu. Rev. Food Sci. Technol. 2018, 9, 251–269. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.mckinsey.com/industries/high-tech/our-insights/the-internet-of-things (accessed on 15 January 2019).
- Yuen, J.S.M.; Choy, K.I.; Lam, H.Y.; Tsang, Y.P. An Intelligent-Internet of Things (IoT) outbound Logistic knowledge management system for handling temperature sensitive products. Int. J. Knowl. Syst. Sci. 2018, 9, 23–40. [Google Scholar] [CrossRef]
- Allison, L.M.C.; Mann, G.F.; Perkins, F.T.; Zuckerman, A.J. An accelerated stability test procedure for lyophilized measles vaccines. J. Biol. Stand. 1981, 9, 185–194. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are available from the authors. |












| wAIC (%) | wBIC (%) | No. of param. | No. of data | RSS | E (kJ·mol−1) | Ln(A*s) (-) | n (-) | m (-) | Yinit | Yend | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PF | 78.59 | 82.22 | 2 | 15 | 6.66 × 104 | 206.5 | 58.30 | 3 | 0 | 3599 | 5000 |
| 12.31 | 8.25 | 3 | 15 | 6.61 × 104 | 202.8 | 56.95 | 2.85 | 0 | 3599 | 5000 | |
| 9.09 | 9.51 | 2 | 15 | 8.88 × 104 | 179.5 | 48.52 | 2 | 0 | 3599 | 5000 | |
| ~0 | ~0 | 2 | 15 | 2.15 × 105 | 147.4 | 36.96 | 1 | 0 | 3599 | 5000 | |
| ~0 | ~0 | 2 | 15 | 9.81 × 1013 | 129.0 | 30.19 | 0 | 0 | 3599 | 5000 | |
| VST | 59.1 | 56.46 | 3 | 14 | 1.37 × 10−1 | 143.1 | 35.30 | 0 | 0.20 | 0.34 | 5 |
| 25.67 | 24.53 | 3 | 14 | 1.54 × 10−1 | 141.6 | 34.10 | –1.33 | 0 | 0.34 | 5 | |
| 9.66 | 12.42 | 2 | 14 | 2.36 × 10−1 | 146.9 | 36.16 | 0 | 0 | 0.34 | 5 | |
| 5.15 | 6.06 | 4 | 14 | 1.35 × 10−1 | 144.0 | 35.88 | 0.57 | 0.27 | 0.34 | 5 | |
| ~0 | ~0 | 2 | 14 | 3.75 × 10−1 | 150.9 | 37.72 | 1 | 0 | 0.34 | 5 | |
| ~0 | ~0 | 2 | 14 | 5.47 × 10−1 | 154.7 | 39.18 | 2 | 0 | 0.34 | 5 | |
| ~0 | ~0 | 2 | 14 | 7.33 × 10−1 | 158.4 | 40.61 | 3 | 0 | 0.34 | 5 | |
| UPLC | 55.51 | 48.10 | 3 | 14 | 9.62 × 10−3 | 145.8 | 37.13 | 0.62 | 0 | 0.61 | 0 |
| 44.47 | 51.88 | 2 | 14 | 1.32 × 10−2 | 148.2 | 38.16 | 1 | 0 | 0.61 | 0 | |
| ~0 | ~0 | 2 | 14 | 4.05 × 10−2 | 157.6 | 41.89 | 2 | 0 | 0.61 | 0 | |
| ~0 | ~0 | 2 | 14 | 7.37 × 10−2 | 169.1 | 46.31 | 3 | 0 | 0.61 | 0 | |
| ~0 | ~0 | 2 | 14 | 6.71 × 10−1 | 150.0 | 38.27 | 0 | 0 | 0.61 | 0 | |
| HFC | 99.59 | 98.68 | 4 | 28 | 6.71 × 102 | 138.6 | 30.50 | −4.79 | 0.25 | 0 | 4000 |
| 0.40 | 1.31 | 3 | 28 | 1.10 × 103 | 137.6 | 30.80 | 0 | 0.37 | 0 | 4000 | |
| ~0 | ~0 | 3 | 28 | 1.83 × 103 | 143.3 | 30.84 | –12.40 | 0 | 0 | 4000 | |
| ~0 | ~0 | 2 | 28 | 1.92 × 104 | 164.8 | 38.43 | 0 | 0 | 0 | 4000 | |
| ~0 | ~0 | 2 | 28 | 2.13 × 104 | 166.5 | 38.03 | 1 | 0 | 0 | 4000 | |
| ~0 | ~0 | 2 | 28 | 2.37 × 104 | 168.2 | 39.63 | 2 | 0 | 0 | 4000 | |
| ~0 | ~0 | 2 | 28 | 2.58 × 104 | 169.9 | 40.23 | 3 | 0 | 0 | 4000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roduit, B.; Luyet, C.A.; Hartmann, M.; Folly, P.; Sarbach, A.; Dejeaifve, A.; Dobson, R.; Schroeter, N.; Vorlet, O.; Dabros, M.; et al. Continuous Monitoring of Shelf Lives of Materials by Application of Data Loggers with Implemented Kinetic Parameters. Molecules 2019, 24, 2217. https://doi.org/10.3390/molecules24122217
Roduit B, Luyet CA, Hartmann M, Folly P, Sarbach A, Dejeaifve A, Dobson R, Schroeter N, Vorlet O, Dabros M, et al. Continuous Monitoring of Shelf Lives of Materials by Application of Data Loggers with Implemented Kinetic Parameters. Molecules. 2019; 24(12):2217. https://doi.org/10.3390/molecules24122217
Chicago/Turabian StyleRoduit, Bertrand, Charles Albert Luyet, Marco Hartmann, Patrick Folly, Alexandre Sarbach, Alain Dejeaifve, Rowan Dobson, Nicolas Schroeter, Olivier Vorlet, Michal Dabros, and et al. 2019. "Continuous Monitoring of Shelf Lives of Materials by Application of Data Loggers with Implemented Kinetic Parameters" Molecules 24, no. 12: 2217. https://doi.org/10.3390/molecules24122217
APA StyleRoduit, B., Luyet, C. A., Hartmann, M., Folly, P., Sarbach, A., Dejeaifve, A., Dobson, R., Schroeter, N., Vorlet, O., Dabros, M., & Baltensperger, R. (2019). Continuous Monitoring of Shelf Lives of Materials by Application of Data Loggers with Implemented Kinetic Parameters. Molecules, 24(12), 2217. https://doi.org/10.3390/molecules24122217





