Adsorption of Azo Dye Methyl Orange from Aqueous Solutions Using Alkali-Activated Polypyrrole-Based Graphene Oxide
Abstract
:1. Introduction
2. Results and Discussion
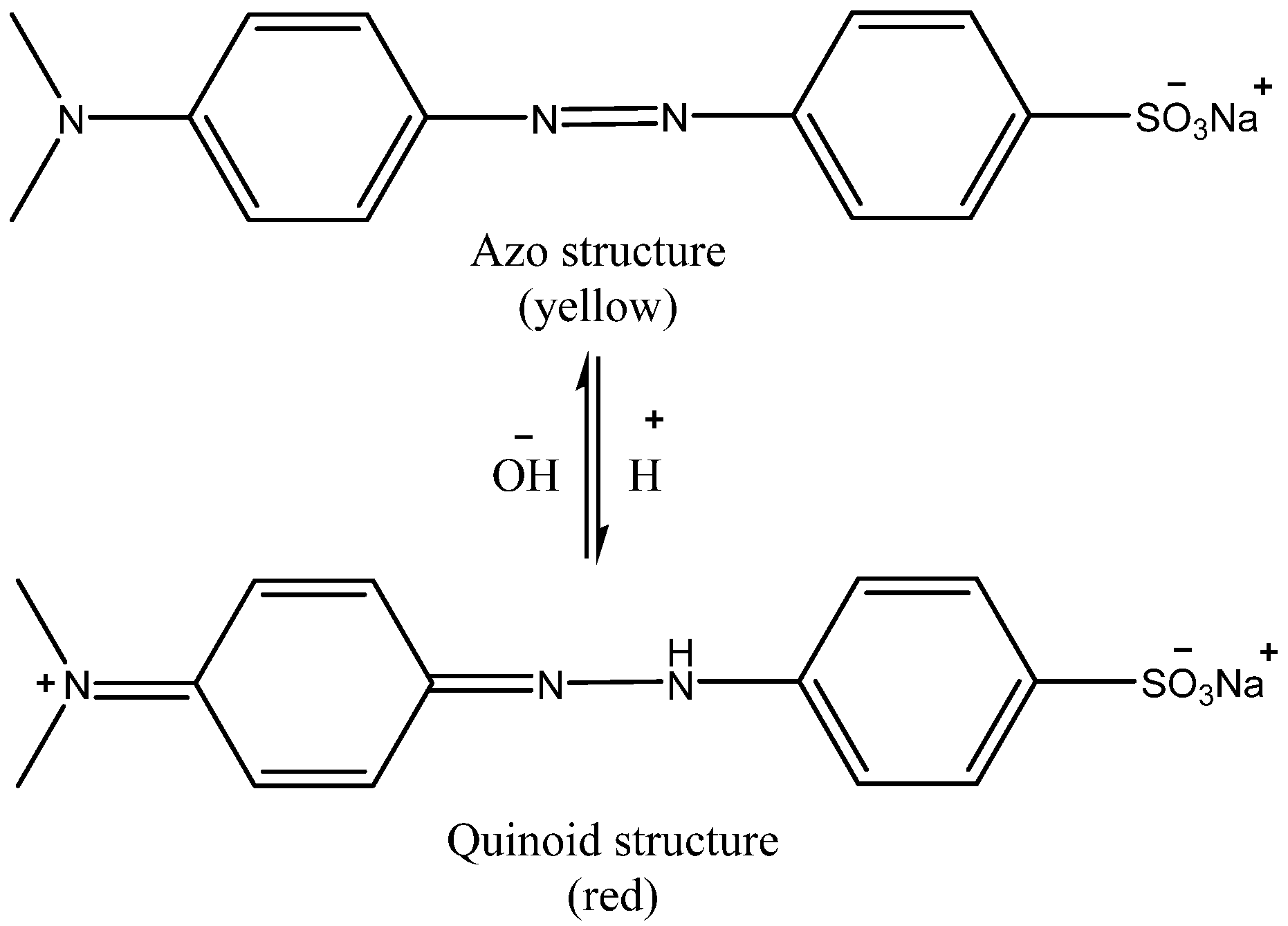
2.1. Characterization of the Adsorbent
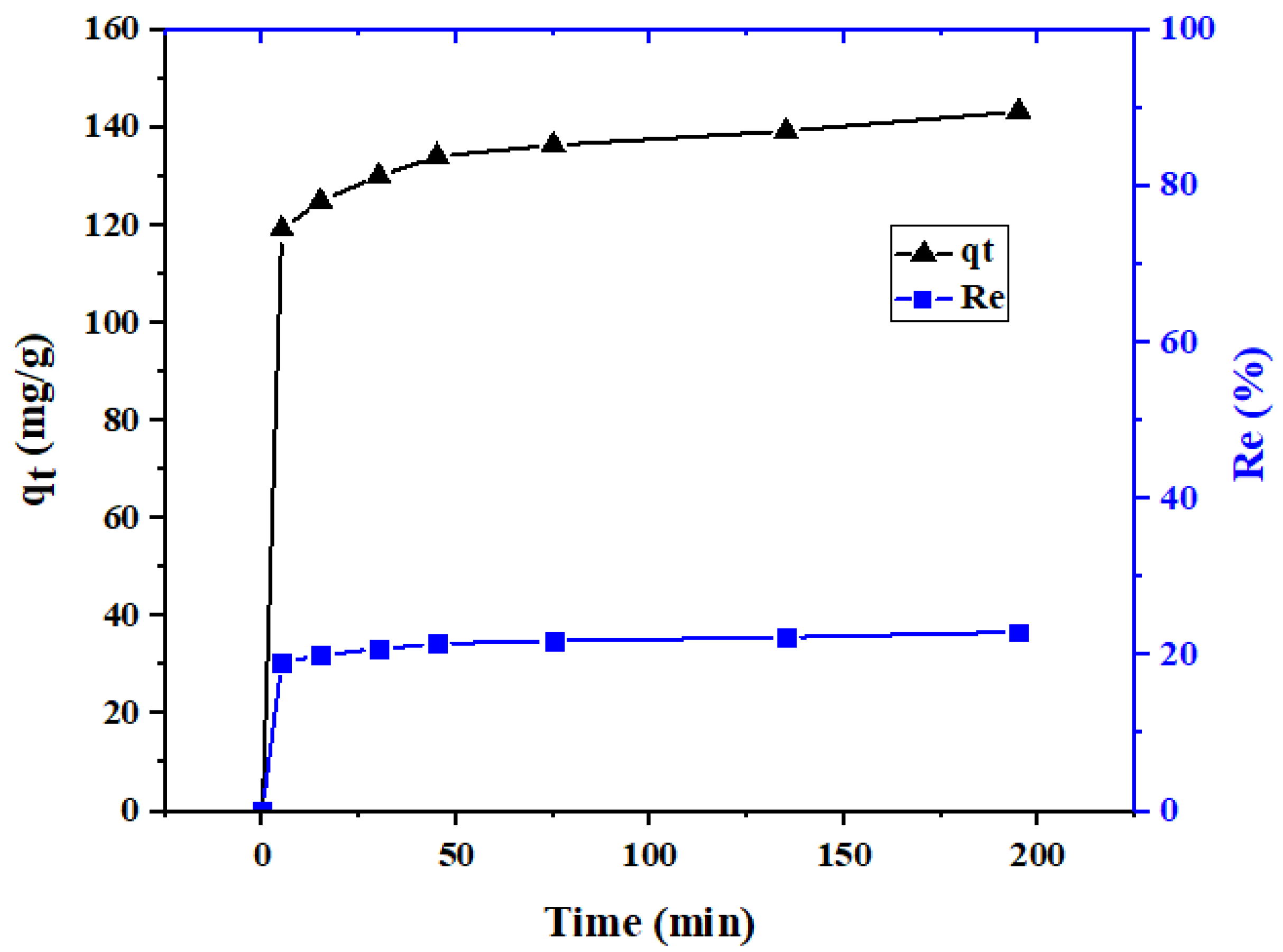
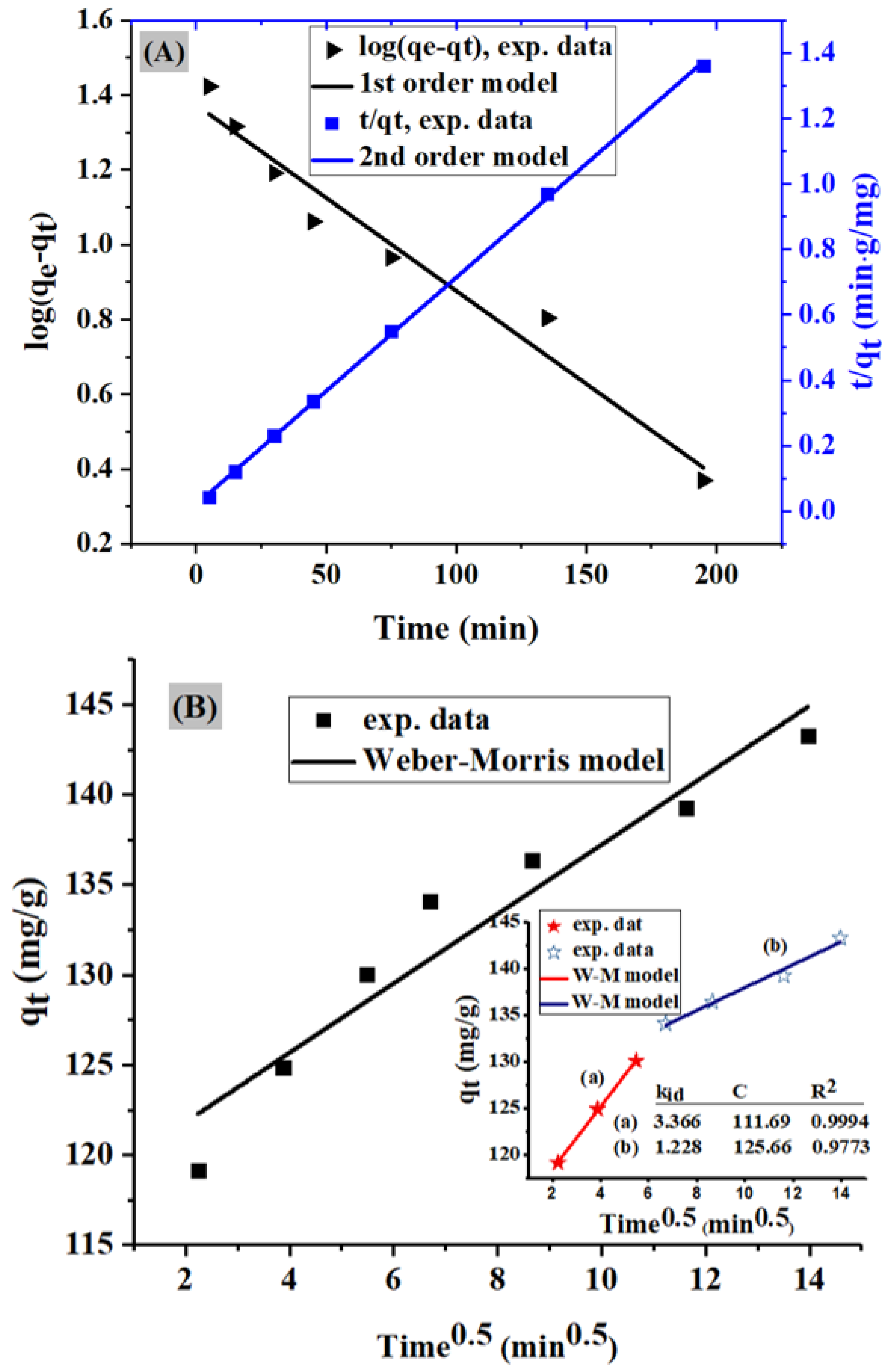
2.2. Adsorption Kinetic
2.3. Adsorption Isotherms
2.4. Adsorption Thermodynamics
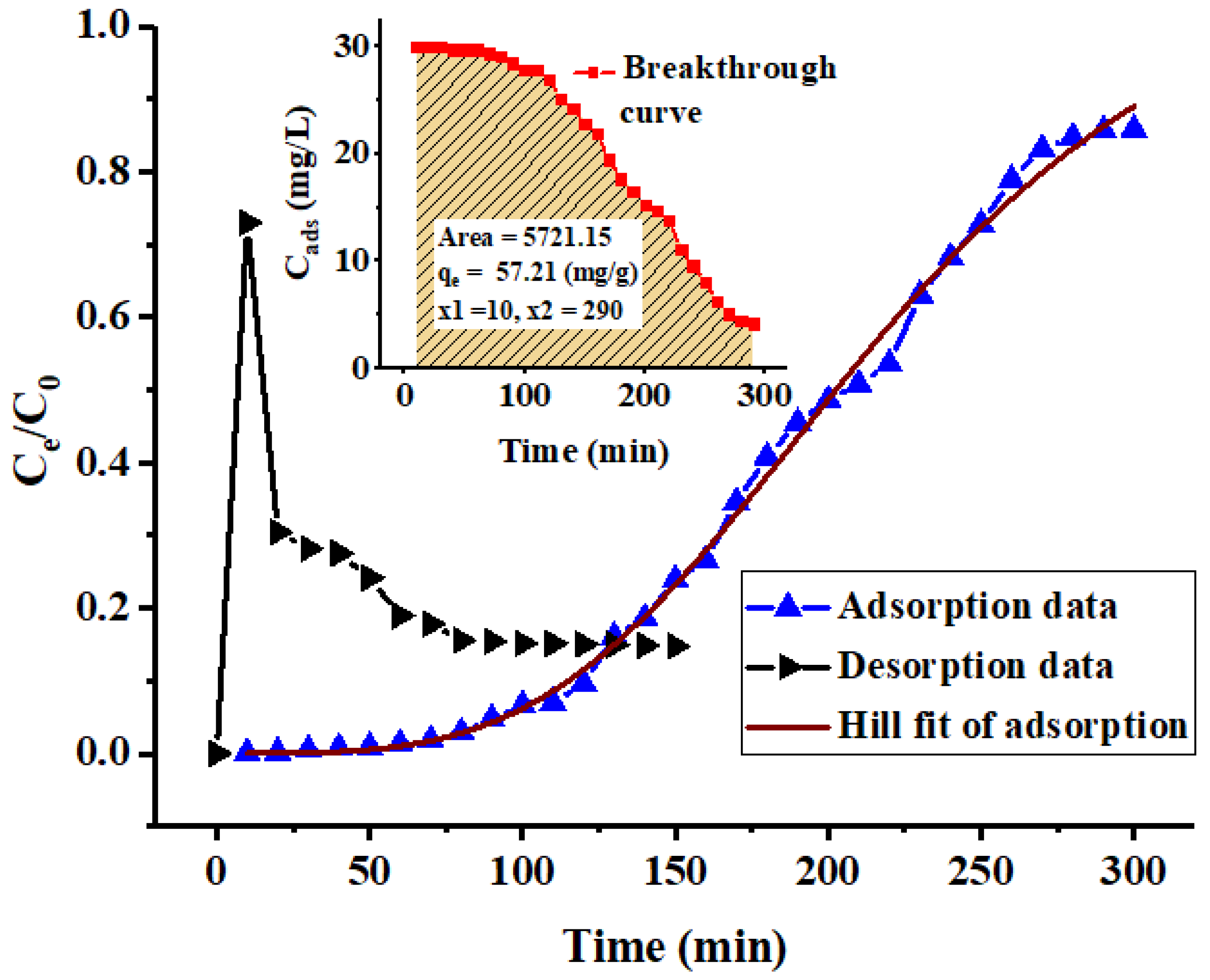
2.5. Column Behavior
3. Materials and Methods
3.1. Materials
3.2. Adsorbent
3.3. Adsorbate
3.4. Batch Adsorption Studies
3.4.1. Batch Adsorption Experiments
3.4.2. Adsorption Data Evaluation
3.5. Column Adoption Studies
3.5.1. Column Experimental Set-Up
3.5.2. Column Data Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hildenbrand, S.; Schmahl, F.; Wodarz, R.; Kimmel, R.; Dartsch, P. Azo dyes and carcinogenic aromatic amines in cell cultures. Int. Arch. Occup. Environ. Health 1999, 72, M052–M056. [Google Scholar] [CrossRef]
- Huang, J.-H.; Huang, K.-L.; Liu, S.-Q.; Wang, A.-T.; Yan, C. Adsorption of Rhodamine B and methyl orange on a hypercrosslinked polymeric adsorbent in aqueous solution. Colloids Surf. A Physicochem. Eng. Asp. 2008, 330, 55–61. [Google Scholar] [CrossRef]
- Akansha, K.; Chakraborty, D.; Sachan, S.G. Decolorization and degradation of methyl orange by Bacillus stratosphericus SCA1007. Biocatal. Agric. Biotechnol. 2019, 18, 101044. [Google Scholar] [CrossRef]
- Alghamdi, A.A.; Al-Odayni, A.-B.; Saeed, W.S.; Al-Kahtani, A.; Alharthi, F.A.; Aouak, T. Efficient Adsorption of Lead (II) from Aqueous Phase Solutions Using Polypyrrole-Based Activated Carbon. Materials 2019, 12, 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Zou, W.; Zou, L.; He, X.; Song, J.; Han, R. Adsorption of methylene blue and methyl orange from aqueous solution by iron oxide-coated zeolite in fi xed bed column: Predicted curves. Desalin. Water Treat. 2010, 22, 258–264. [Google Scholar] [CrossRef]
- Chen, D.; Chen, J.; Luan, X.; Ji, H.; Xia, Z. Characterization of anion–cationic surfactants modified montmorillonite and its application for the removal of methyl orange. Chem. Eng. J. 2011, 171, 1150–1158. [Google Scholar] [CrossRef]
- Deliyanni, E.A.; Kyzas, G.Z.; Triantafyllidis, K.S.; Matis, K.A. Activated carbons for the removal of heavy metal ions: A systematic review of recent literature focused on lead and arsenic ions. Open Chem. 2015, 13, 699–708. [Google Scholar] [CrossRef]
- Alghamdi, A.; Alshahrani, A.; Khdary, N.; Alharthi, F.; Alattas, H.; Adil, S. Enhanced CO2 adsorption by nitrogen-doped graphene oxide sheets (N-GOs) prepared by employing polymeric precursors. Materials 2018, 11, 578. [Google Scholar] [CrossRef]
- Sevilla, M.; Valle-Vigón, P.; Fuertes, A.B. N-doped polypyrrole-based porous carbons for CO2 capture. Adv. Funct. Mater. 2011, 21, 2781–2787. [Google Scholar] [CrossRef]
- Ahmad, Z.; Choudhary, M.A.; Mehmood, A.; Wakeel, R.; Akhtar, T.; Rafiq, M.A. Synthesis of polypyrrole nano/microspheres using cobalt (III) as an oxidizing agent and its ammonia sensing behavior. Macromol. Res. 2016, 24, 596–601. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Wang, H.; Wang, Y.; Liang, M.; Xue, S. Nitrogen-doped graphene as a cathode material for dye-sensitized solar cells: Effects of hydrothermal reaction and annealing on electrocatalytic performance. RSC Adv. 2015, 5, 10430–10439. [Google Scholar] [CrossRef]
- Islam, M.S.; Ang, B.C.; Gharehkhani, S.; Afifi, A.B.M. Adsorption capability of activated carbon synthesized from coconut shell. Carbon Lett. 2016, 20, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Harikumar, P.; Joseph, L.; Dhanya, A. Photocatalytic degradation of textile dyes by hydrogel supported titanium dioxide nanoparticles. J. Environ. Eng. Ecol. Sci. 2013, 2, 2. [Google Scholar]
- Youssef, N.A.; Shaban, S.A.; Ibrahim, F.A.; Mahmoud, A.S. Degradation of methyl orange using Fenton catalytic reaction. Egypt. J. Pet. 2016, 25, 317–321. [Google Scholar] [CrossRef] [Green Version]
- Ai, L.; Jiang, J.; Zhang, R. Uniform polyaniline microspheres: A novel adsorbent for dye removal from aqueous solution. Synth. Metals 2010, 160, 762–767. [Google Scholar] [CrossRef]
- Rengaraj, S.; Kim, Y.; Joo, C.K.; Yi, J. Removal of copper from aqueous solution by aminated and protonated mesoporous aluminas: Kinetics and equilibrium. J. Colloid Interface Sci. 2004, 273, 14–21. [Google Scholar] [CrossRef]
- Haitham, K.; Razak, S.; Nawi, M. Kinetics and isotherm studies of methyl orange adsorption by a highly recyclable immobilized polyaniline on a glass plate. Arab. J. Chem. 2014. [Google Scholar] [CrossRef]
- Başar, C.A. Applicability of the various adsorption models of three dyes adsorption onto activated carbon prepared waste apricot. J. Hazard. Mater. 2006, 135, 232–241. [Google Scholar] [CrossRef]
- Krika, F.; Benlahbib, O.e.F. Removal of methyl orange from aqueous solution via adsorption on cork as a natural and low-coast adsorbent: Equilibrium, kinetic and thermodynamic study of removal process. Desalin. Water Treat. 2015, 53, 3711–3723. [Google Scholar] [CrossRef]
- Yang, S.; Pyle, D. The adsorption kinetics of cephalosporin-c on non-ionic polymeric macropore Amberlite XAD-16 resin. J. Chem. Technol. Biotechnol. 1999, 74, 216–220. [Google Scholar] [CrossRef]
- Xu, R.; Mao, J.; Peng, N.; Luo, X.; Chang, C. Chitin/clay microspheres with hierarchical architecture for highly efficient removal of organic dyes. Carbohydr. Polym. 2018, 188, 143–150. [Google Scholar] [CrossRef] [PubMed]
- Albroomi, H.; Elsayed, M.; Baraka, A.; Abdelmaged, M. Batch and fixed-bed adsorption of tartrazine azo-dye onto activated carbon prepared from apricot stones. Appl. Water Sci. 2017, 7, 2063–2074. [Google Scholar] [CrossRef]
- Landry, K.A.; Boyer, T.H. Fixed bed modeling of nonsteroidal anti-inflammatory drug removal by ion-exchange in synthetic urine: Mass removal or toxicity reduction? Environ. Sci. Technol. 2017, 51, 10072–10080. [Google Scholar] [CrossRef] [PubMed]
- Annadurai, G.; Juang, R.-S.; Lee, D.-J. Use of cellulose-based wastes for adsorption of dyes from aqueous solutions. J. Hazard. Mater. 2002, 92, 263–274. [Google Scholar] [CrossRef]
- Qin, Q.; Ma, J.; Liu, K. Adsorption of anionic dyes on ammonium-functionalized MCM-41. J. Hazard. Mater. 2009, 162, 133–139. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, J.; Wu, J.; Dai, G. Isotherm, thermodynamic, kinetics and adsorption mechanism studies of methyl orange by surfactant modified silkworm exuviae. J. Hazard. Mater. 2011, 192, 246–254. [Google Scholar] [CrossRef]
- Khan, T.A.; Rahman, R.; Khan, E.A. Adsorption of malachite green and methyl orange onto waste tyre activated carbon using batch and fixed-bed techniques: Isotherm and kinetics modeling. Model. Earth Syst. Environ. 2017, 3, 38. [Google Scholar] [CrossRef]
- Mittal, A.; Malviya, A.; Kaur, D.; Mittal, J.; Kurup, L. Studies on the adsorption kinetics and isotherms for the removal and recovery of Methyl Orange from wastewaters using waste materials. J. Hazard. Mater. 2007, 148, 229–240. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Edokpayi, J.; Odiyo, J.; Msagati, T.; Popoola, E. A Novel Approach for the removal of lead (II) ion from wastewater using mucilaginous leaves of diceriocaryum eriocarpum plant. Sustainability 2015, 7, 14026–14041. [Google Scholar] [CrossRef]
- Moyo, M.; Chikazaza, L. Bioremediation of lead (II) from polluted wastewaters employing sulphuric acid treated maize tassel biomass. Am. J. Anal. Chem. 2013, 4, 689. [Google Scholar] [CrossRef]
- Freundlich, H.; Heller, W. The adsorption of cis-and trans-azobenzene. J. Am. Chem. Soc. 1939, 61, 2228–2230. [Google Scholar] [CrossRef]
- Gong, R.; Ye, J.; Dai, W.; Yan, X.; Hu, J.; Hu, X.; Li, S.; Huang, H. Adsorptive removal of methyl orange and methylene blue from aqueous solution with finger-citron-residue-based activated carbon. Indust. Eng. Chem. Res. 2013, 52, 14297–14303. [Google Scholar] [CrossRef]
- Li, Q.; Yue, Q.-Y.; Su, Y.; Gao, B.-Y.; Sun, H.-J. Equilibrium, thermodynamics and process design to minimize adsorbent amount for the adsorption of acid dyes onto cationic polymer-loaded bentonite. Chem. Eng. J. 2010, 158, 489–497. [Google Scholar] [CrossRef]
- Banerjee, S.; Chattopadhyaya, M. Adsorption characteristics for the removal of a toxic dye, tartrazine from aqueous solutions by a low cost agricultural by-product. Arab. J. Chem. 2017, 10, S1629–S1638. [Google Scholar] [CrossRef] [Green Version]
- Aljeboree, A.M.; Alshirifi, A.N.; Alkaim, A.F. Kinetics and equilibrium study for the adsorption of textile dyes on coconut shell activated carbon. Arab. J. Chem. 2017, 10, S3381–S3393. [Google Scholar] [CrossRef] [Green Version]
- Lagegren, S.; Svenska, B. Zur theorie der sogenannten adsorption geloester stoffe. Vaternskapsakad Handlingar 1898, 24, 1–39. [Google Scholar]
- Ho, Y.-S.; McKay, G. Pseudo-second order model for sorption processes. Process. Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Kinetics of adsorption on carbon from solution. J. Sanitary Eng. Div. 1963, 89, 31–60. [Google Scholar]
- Guo, J.; Song, Y.; Ji, X.; Ji, L.; Cai, L.; Wang, Y.; Zhang, H.; Song, W. Preparation and Characterization of Nanoporous Activated Carbon Derived from Prawn Shell and Its Application for Removal of Heavy Metal Ions. Materials 2019, 12, 241. [Google Scholar] [CrossRef]
- Lin, X.; Li, R.; Wen, Q.; Wu, J.; Fan, J.; Jin, X.; Qian, W.; Liu, D.; Chen, X.; Chen, Y. Experimental and modeling studies on the sorption breakthrough behaviors of butanol from aqueous solution in a fixed-bed of KA-I resin. Biotechnol. Bioprocess Eng. 2013, 18, 223–233. [Google Scholar] [CrossRef]
- Goutelle, S.; Maurin, M.; Rougier, F.; Barbaut, X.; Bourguignon, L.; Ducher, M.; Maire, P. The Hill equation: A review of its capabilities in pharmacological modelling. Fundam. Clin. Pharmacol. 2008, 22, 633–648. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds KOH-activated polypyrrole-based graphene oxide (PACK) are available from the authors. |
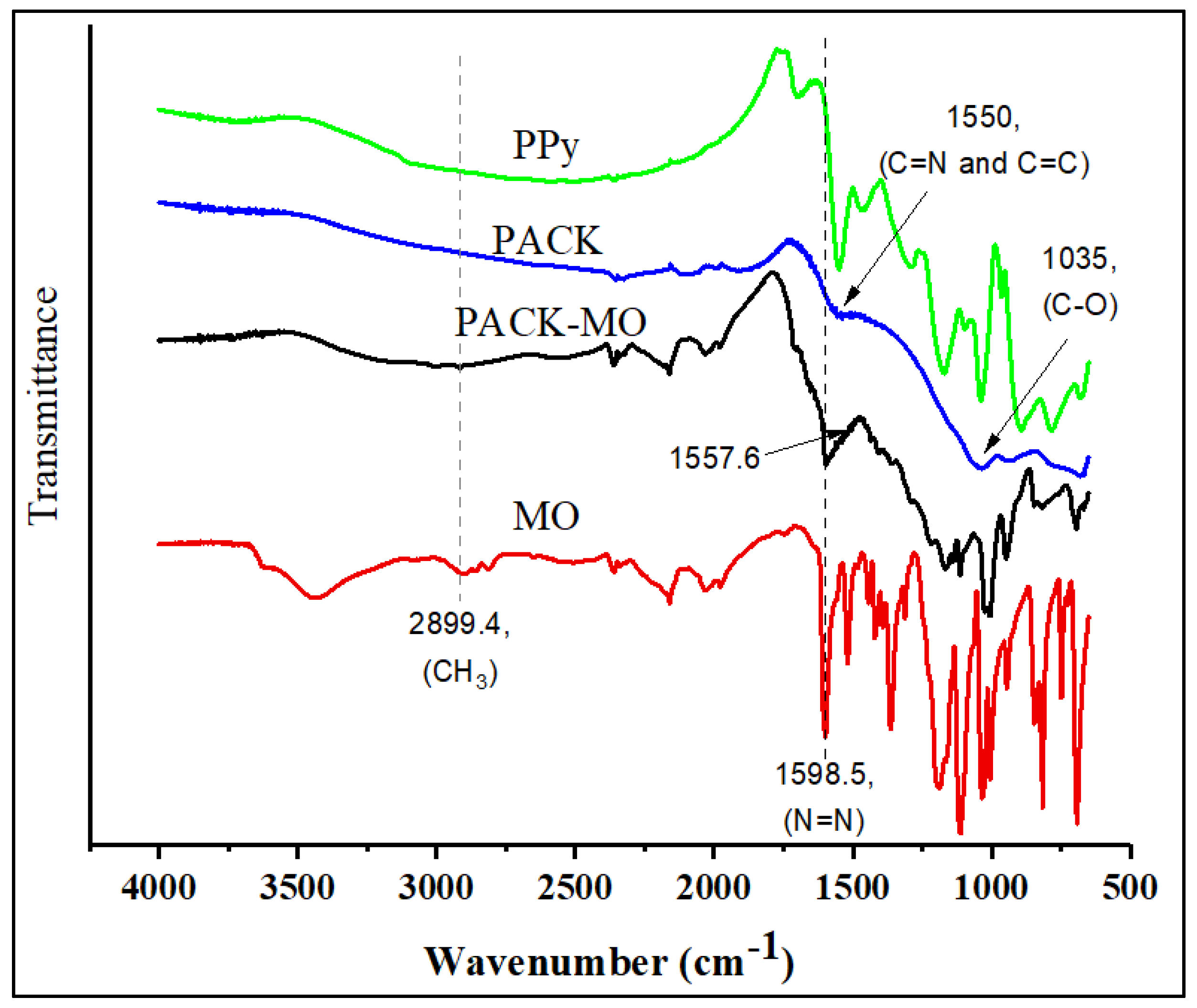

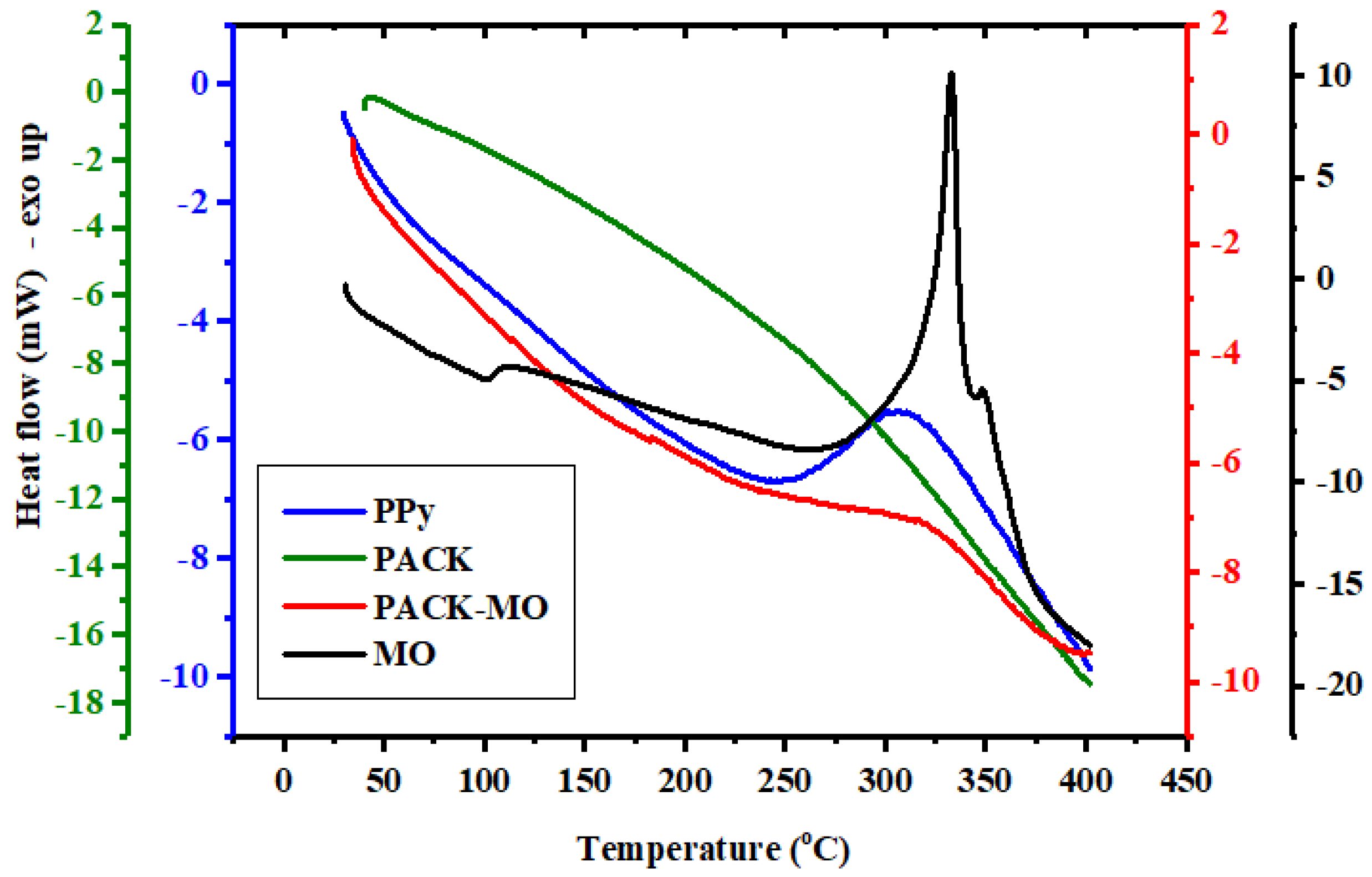
| Material | Step | TGA, T (°C) | DTG, T (°C) | Mass Loss (%) | Notes |
|---|---|---|---|---|---|
| PACK | 1 | 25–95 | 64 | 5.6 | Moisture, volatiles |
| 2 | 95–336 | 296 | 8.6 | Total mass loss = 48.2%, Residue = 51.8% | |
| 3 | 336–820 | 767 | 25.2 | ||
| 4 | 820–1000 | - | gradual | ||
| PACK–MO | 1 | 25–95 | 51 | 2.1 | Moisture, volatiles |
| 2 | 95–265 | 199 | 19.1 | Total mass loss = 61.1%, Residue = 38.1% | |
| 3 | 265–445 | 360 | 15.6 | ||
| 4 | 445–1000 | 720 | gradual |
| qe. Exp. (mg/g) | Pseudo-First-Order | Pseudo-Second-Order | Intra-Particle Diffusion | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| qe (mg/g) | k1 (min−1) | R2 | qe (mg/g) | k2 (g/(mg·min)) | R2 | h (mg/(g·min)) | kid (mg/(g·min0.5)) | C (mg/g) | R2 | |
| 143.38 | 23.67 | 0.0115 | 0.9639 | 143.89 | 0.0025 | 0.9996 | 51.71 | 1.925 | 117.98 | 0.9303 |
| T (K) | Langmuir | Freundlich | Temkin | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| qm (mg/g) | KL (L/mg) | RL (C0 (mg/L) = 100, 200, 300, 500) | R2 | KF (mg/g) (L/mg)1/n | 1/n | R2 | A (g/mg) | KT (J/mol) | B | R2 | |
| 298 | 520.8 | 0.323 | 0.030, 0.015, 0.010, 0.006 | 0.9951 | 221.8 | 0.176 | 0.9979 | 245.58 | 53.69 | 46.15 | 0.9347 |
| 308 | 512.8 | 0.263 | 0.037, 0.019, 0.013, 0.008 | 0.9961 | 205.6 | 0.185 | 0.9915 | 134.11 | 53.61 | 47.77 | 0.9229 |
| 318 | 497.5 | 0.244 | 0.039, 0.020, 0.013, 0.008 | 0.9962 | 198.9 | 0.183 | 0.9938 | 124.03 | 56.72 | 46.61 | 0.9322 |
| Co (mg/L) | T (K) | lnK0 | ΔG° (kJ/mol) | ΔH° (kJ/mol) | ΔS° (J/mol·K) | R2 |
|---|---|---|---|---|---|---|
| 100 | 298 | 8.1962 | −20.31 | −27.61 | −24.87 | 0.9521 |
| 308 | 7.6851 | −19.68 | ||||
| 318 | 7.5027 | −19.84 | ||||
| 200 | 298 | 4.7303 | −11.72 | −29.27 | −59.48 | 0.8911 |
| 308 | 4.1101 | −10.52 | ||||
| 318 | 3.9995 | −10.57 | ||||
| 300 | 298 | 3.0944 | −7.667 | −7.974 | −0.85 | 0.8479 |
| 308 | 3.0573 | −7.829 | ||||
| 318 | 2.8881 | −7.636 | ||||
| 500 | 298 | 1.6840 | −4.172 | −9.210 | −16.844 | 0.9849 |
| 308 | 1.5821 | −4.051 | ||||
| 318 | 1.4489 | −3.831 |
| qe. Exp. (mg/g) | Thomas | Yoon–Nelson | 3-PL Hill | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| KTh (L/(mg·min)) | qe (mg/g) | R2 | KYN (L/(mg·min)) | τ (min) | R2 | c | b | α | R2 | |
| 57.21 | 0.858 | 69.71 | 0.9676 | 0.0286 | 209.12 | 0.9676 | 219.8 | 1.17 | 3.67 | 0.9968 |
| Adsorbent | qm (mg/L) | Adsorption Conditions | Reference | Source Type | Reusability | |||
|---|---|---|---|---|---|---|---|---|
| Co (mg/L) | pH | T (°C) | Adsorbent Dosage (g/L) | |||||
| Polyaniline microspheres | 154.6 | - | - | RT | 2.0 | [15] | Synthetic | - |
| Banana peels | 21.0 | 100 | 5.7 | 30 | 1.0 | [24] | Agriculture | - |
| Orange peels | 20.5 | 100 | 5.7 | 30 | 1.0 | [24] | Agriculture | - |
| Hyper crosslinked polymer | 70.9 | 100 | - | 20 | 2.5 | [2] | Synthetic | - |
| NH3+-MCM-41 | 366.6 | 98.2 | 5.6 | 24.5 | 0.5 | [25] | Synthetic | - |
| PANI/CPL | 333.3 | 50 | 4.0 | - | 2.0 | [26] | Synthetic | - |
| Organo-modified silkworm exuviae (MSE) | 87.03 | 300 | - | 30 | 2.0 | [26] | Biosource waste | 17.25% |
| surfactants modified montmorillonite | 128.21 | 120 | - | 30 | 2.0 | [6] | Modified-Natural source | 11.5% |
| PACK | 520.8 | 100–500 | 6.5 | 25 | 0.8 | This work | Synthetic | - |
| Adsorbent | Column Conditions | qe (mg/g) | R2 | Reference | Regeneration | |||
|---|---|---|---|---|---|---|---|---|
| C0 (mg/L) | pH | Flow Rate (mL/min) | Bed (cm) | |||||
| Iron oxide-coated zeolite (IOCZ) | 30 | 2.5 | 11 | 6 | 0.334 | 0.772 | [5] | - |
| Waste tyre activated carbon (WTAC) | 40 | - | 3 | 1.5 | 6.89 | 0.983 | [27] | 89% |
| De-oiled Soya | 33 | 6.5 | 0.5 | 1 g | 3.5 | - | [28] | 93% |
| PACK | 30 | 6.5 | 1.1 | 0.7 | 69.1 | 0.9676 | This work | 73% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, A.A.; Al-Odayni, A.-B.; Saeed, W.S.; Almutairi, M.S.; Alharthi, F.A.; Aouak, T.; Al-Kahtani, A. Adsorption of Azo Dye Methyl Orange from Aqueous Solutions Using Alkali-Activated Polypyrrole-Based Graphene Oxide. Molecules 2019, 24, 3685. https://doi.org/10.3390/molecules24203685
Alghamdi AA, Al-Odayni A-B, Saeed WS, Almutairi MS, Alharthi FA, Aouak T, Al-Kahtani A. Adsorption of Azo Dye Methyl Orange from Aqueous Solutions Using Alkali-Activated Polypyrrole-Based Graphene Oxide. Molecules. 2019; 24(20):3685. https://doi.org/10.3390/molecules24203685
Chicago/Turabian StyleAlghamdi, Abdulaziz Ali, Abdel-Basit Al-Odayni, Waseem Sharaf Saeed, Mohammed S. Almutairi, Fahad A. Alharthi, Taieb Aouak, and Abdullah Al-Kahtani. 2019. "Adsorption of Azo Dye Methyl Orange from Aqueous Solutions Using Alkali-Activated Polypyrrole-Based Graphene Oxide" Molecules 24, no. 20: 3685. https://doi.org/10.3390/molecules24203685
APA StyleAlghamdi, A. A., Al-Odayni, A.-B., Saeed, W. S., Almutairi, M. S., Alharthi, F. A., Aouak, T., & Al-Kahtani, A. (2019). Adsorption of Azo Dye Methyl Orange from Aqueous Solutions Using Alkali-Activated Polypyrrole-Based Graphene Oxide. Molecules, 24(20), 3685. https://doi.org/10.3390/molecules24203685










