Mechanical Respond and Failure Mode of Large Size Honeycomb Sandwiched Composites under In-Plane Shear Load
Abstract
:1. Introduction
2. Material and Specimens
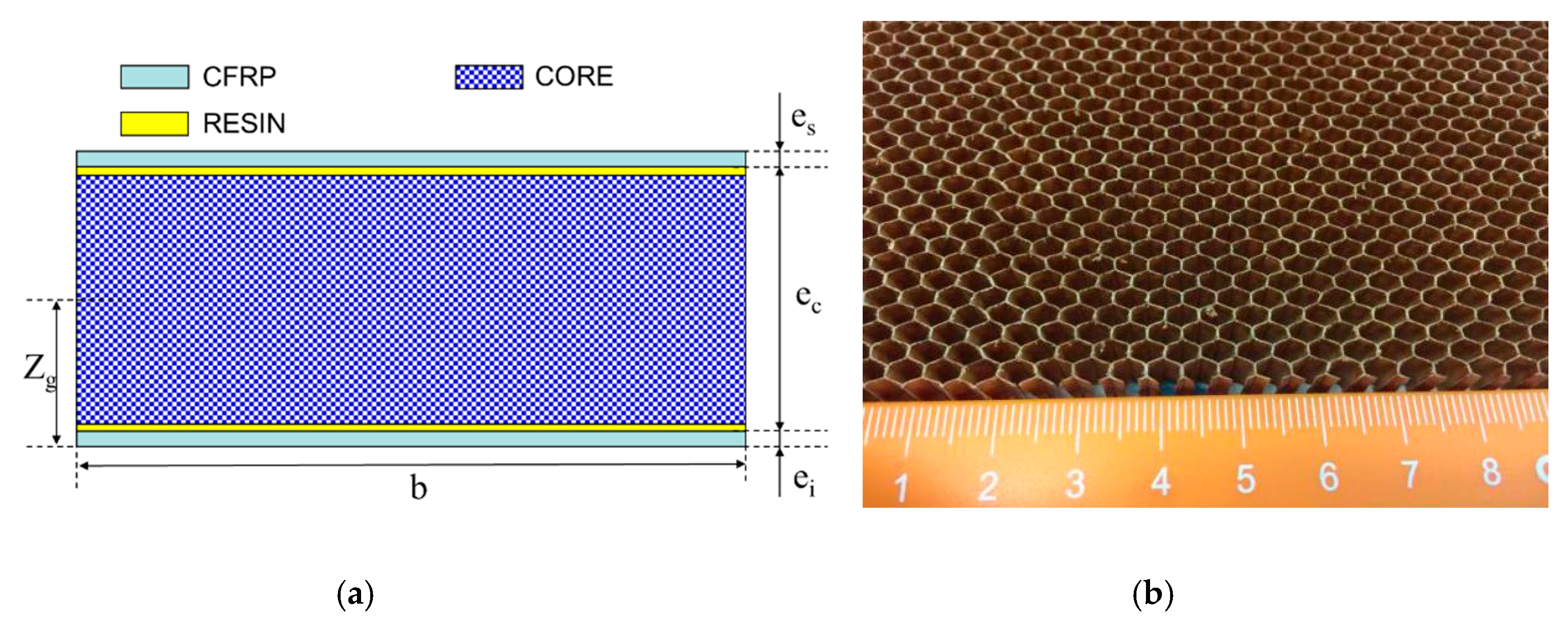
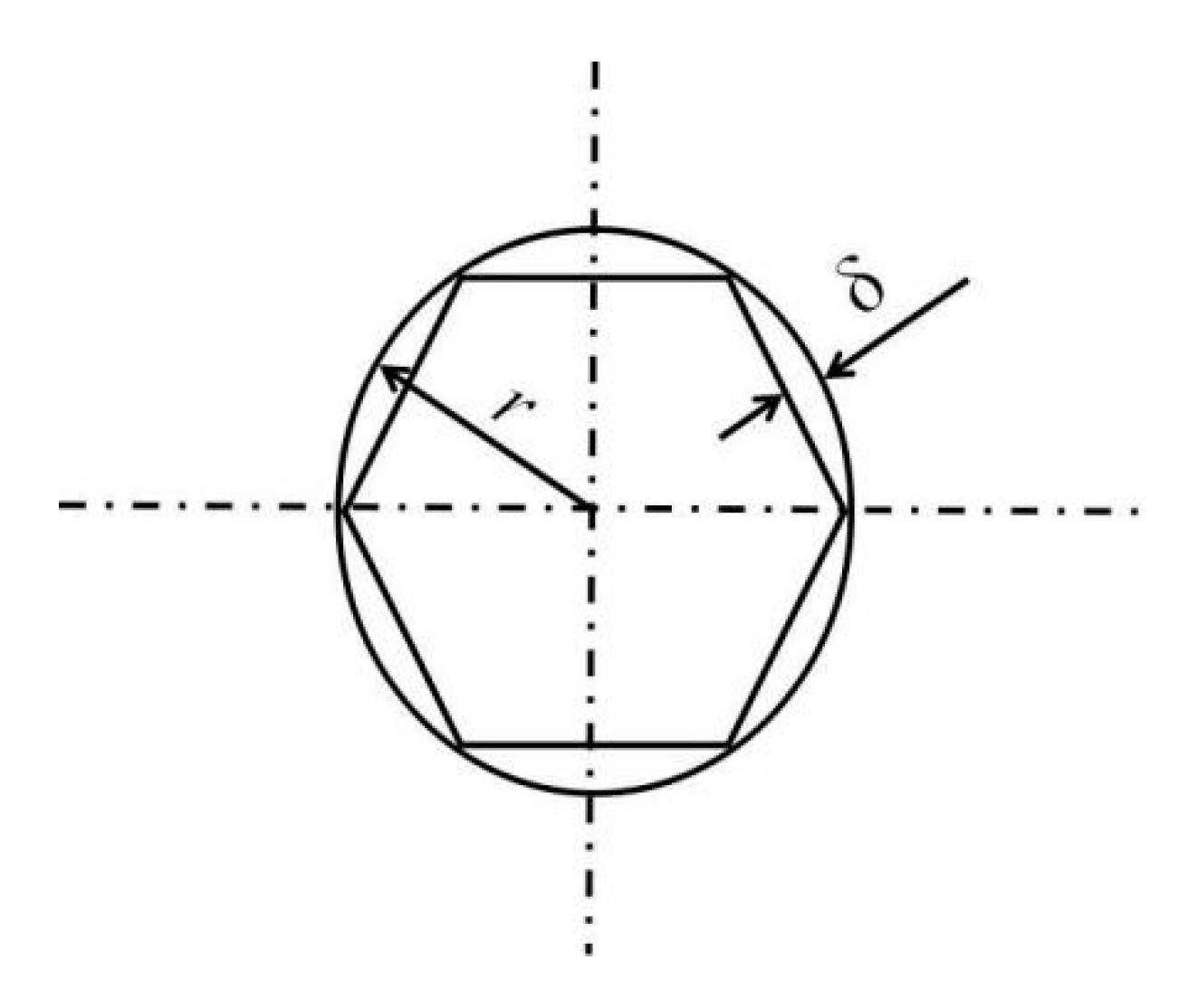
2.1. CFRP Skin and Honeycomb Core
2.2. Manufacturing Process
2.3. Dimension Design of Sandwich Panel
3. Experimental
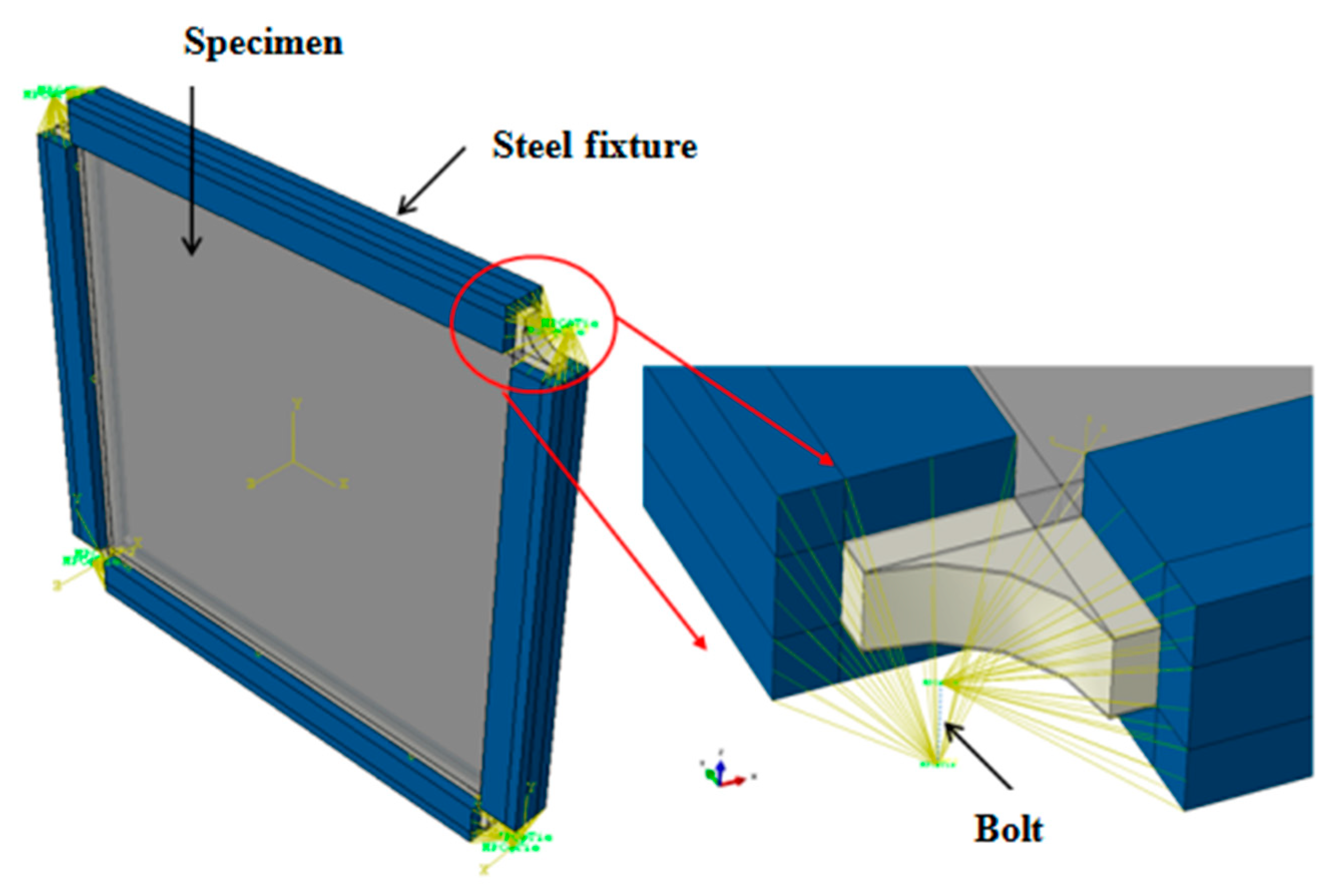
3.1. Shear Test Fixture
3.2. Test Equipment
4. Theoretical analysis
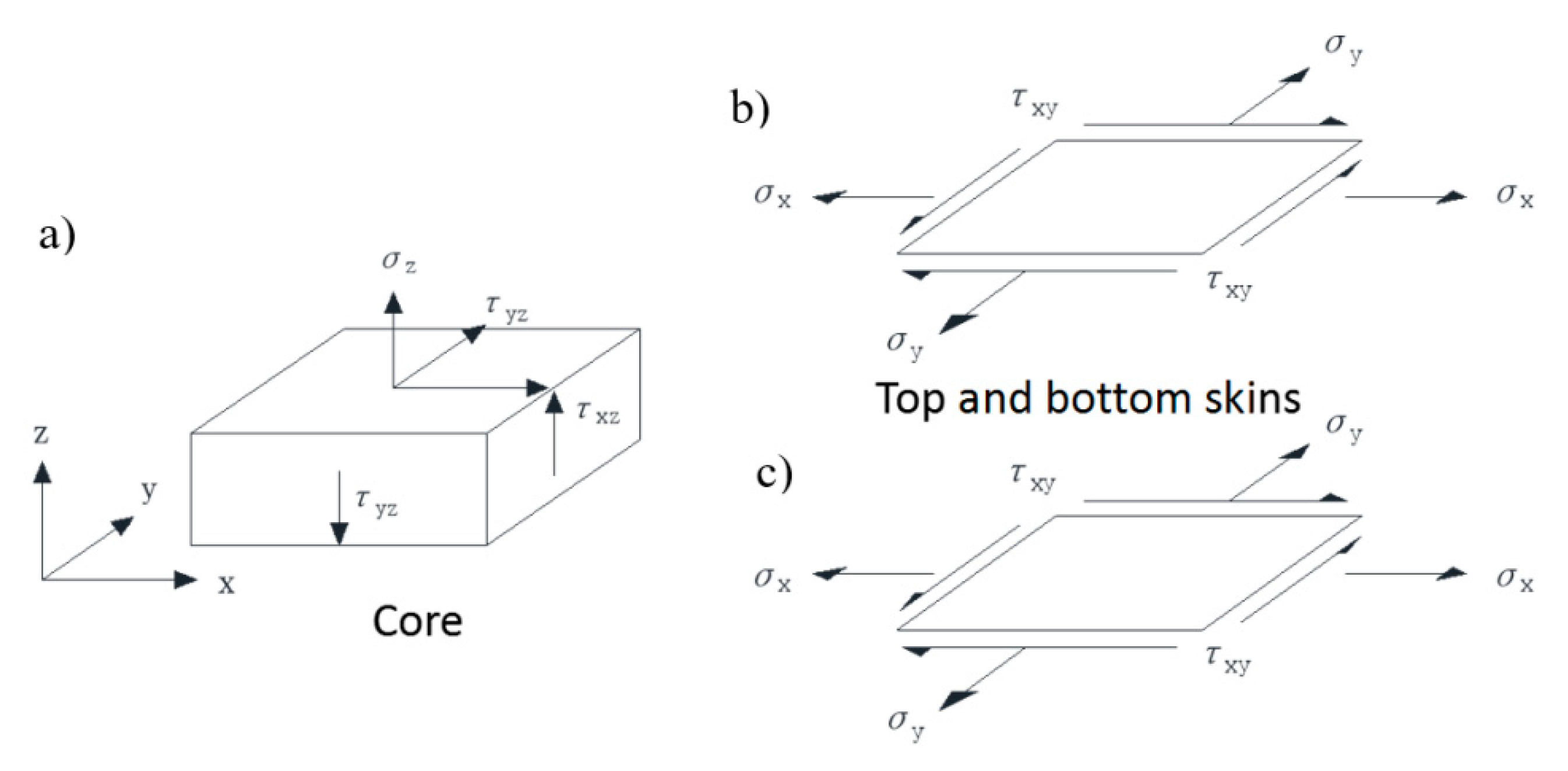
4.1. Assumptions
4.2. Equivalent Stiffness of Honeycomb Sandwich Composite Structure
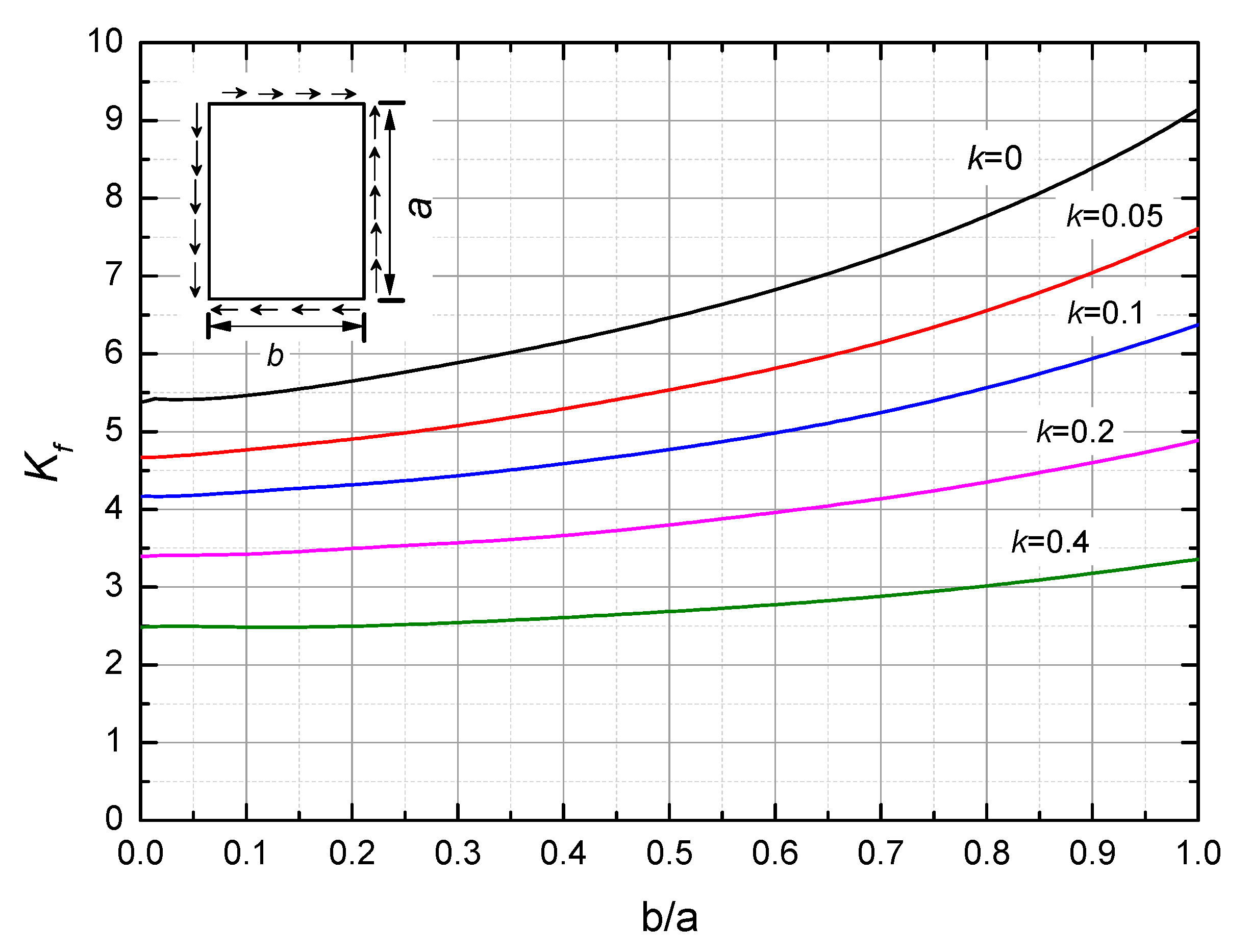
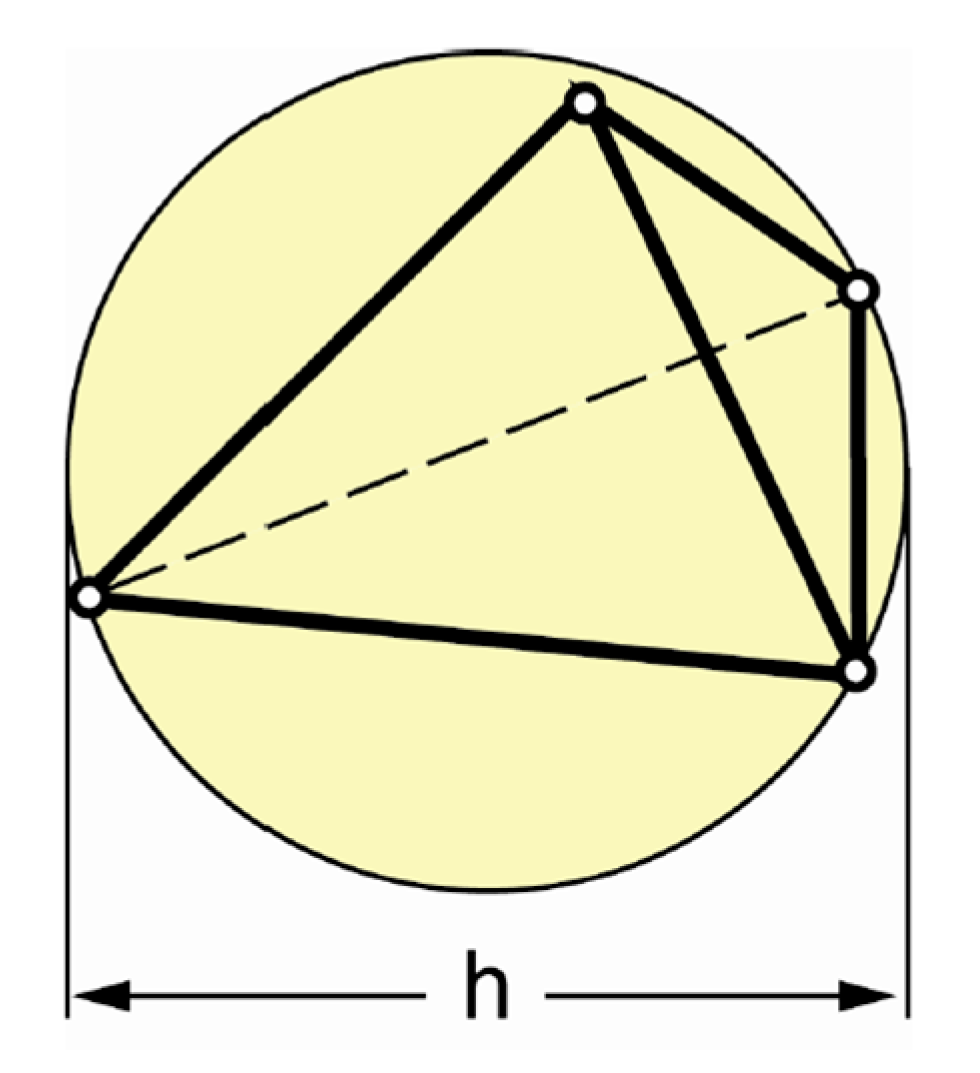
4.3. Buckling of Honeycomb Sandwich Composite Structure
5. Finite Element Model
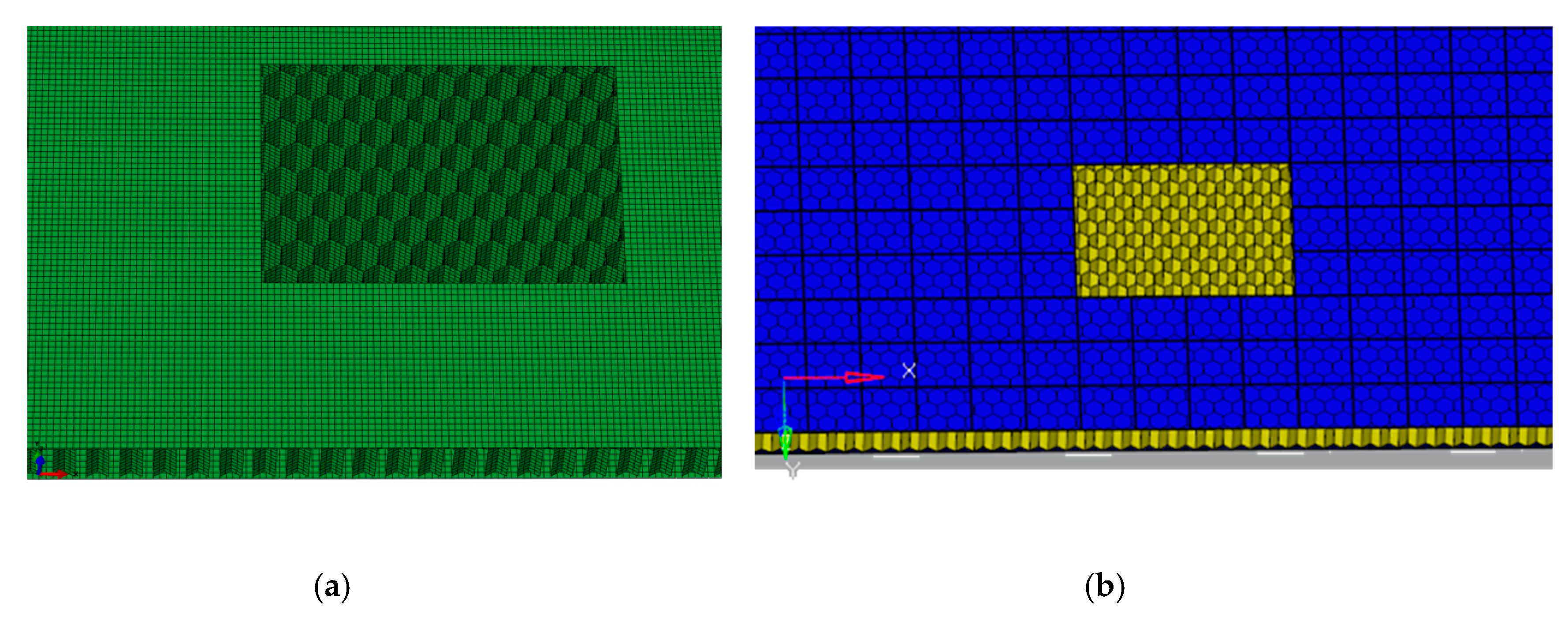
5.1. Mesh
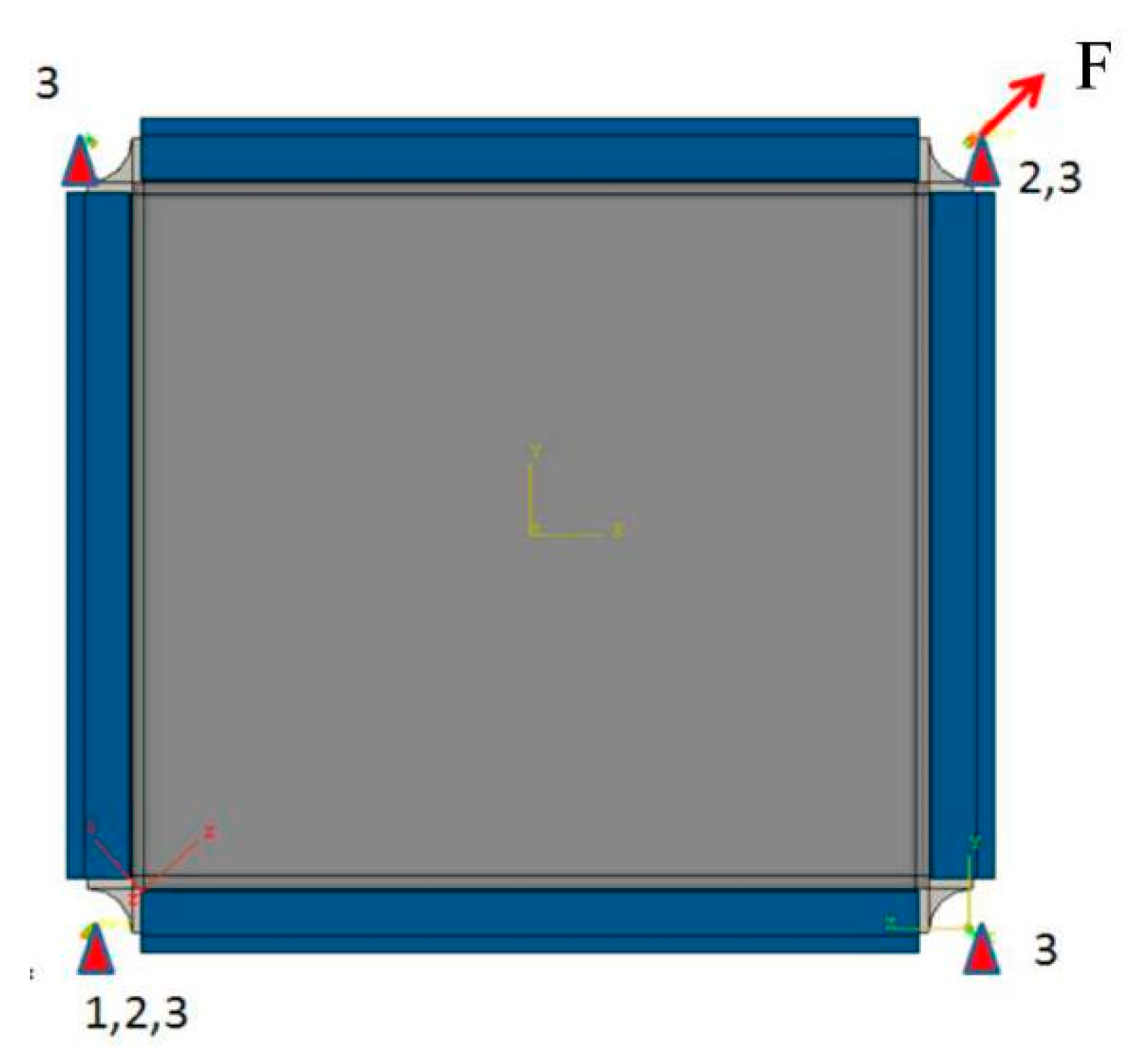
5.2. Boundary Conditions
5.3. Material Constitutive
5.4. Buckling Load Analysis
6. Results and Discussion
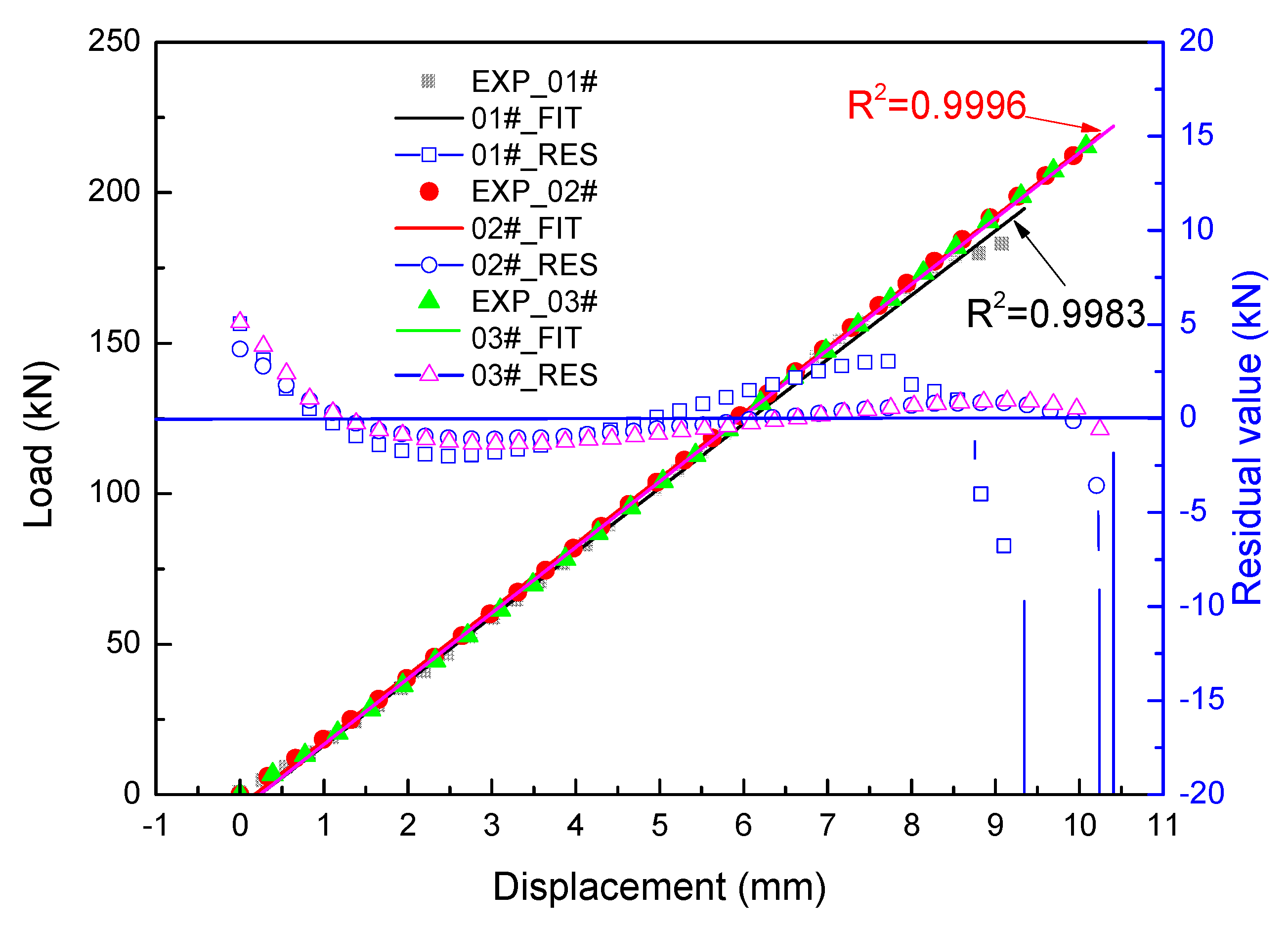
6.1. Load-Displacement Curves
6.2. Strain Analysis
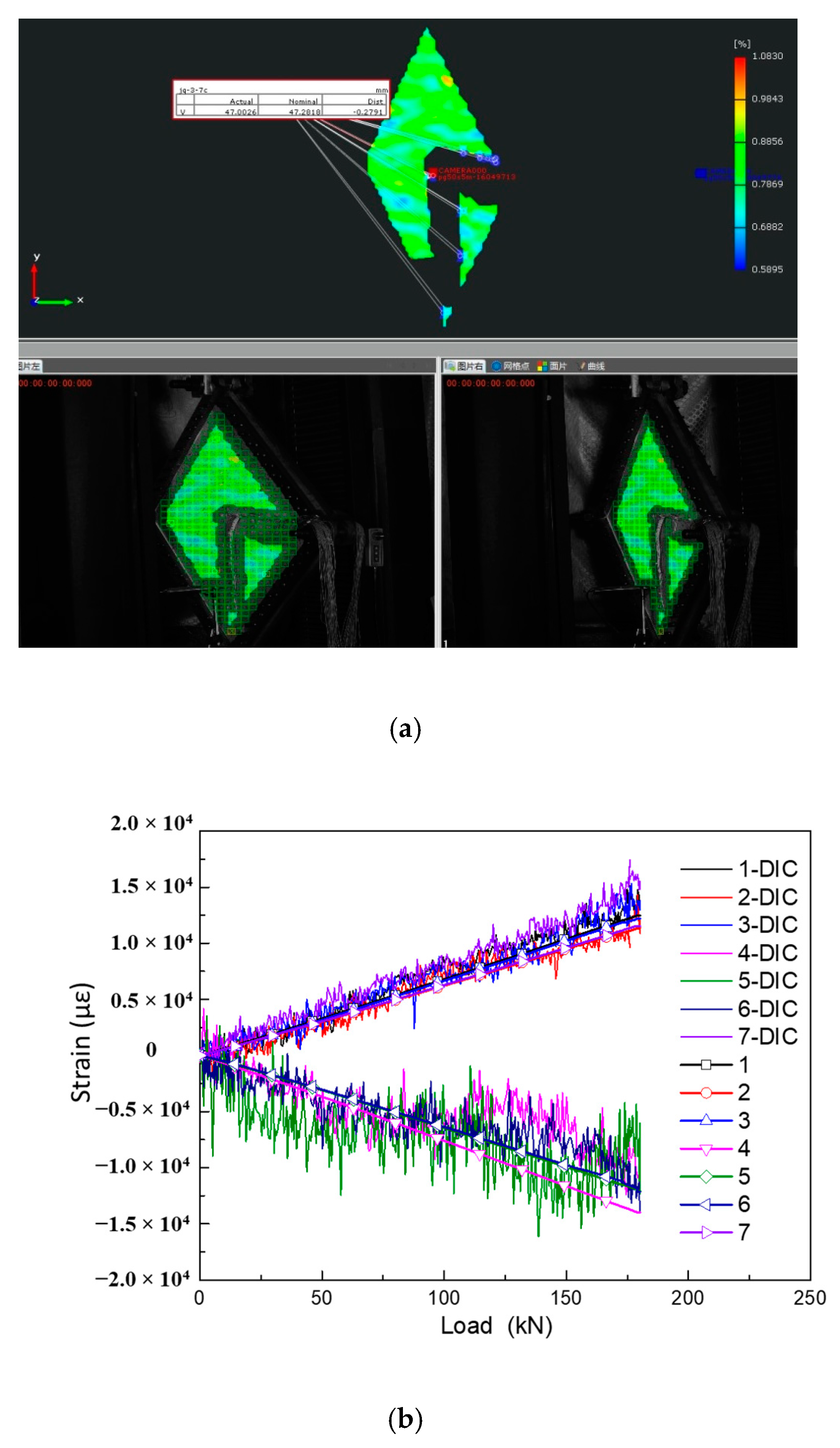
6.2.1. Strain Data
6.2.2. Strain Discreteness
6.2.3. Comparison of Theoretical Prediction and Experimental Results
6.2.4. DIC Strain Filed
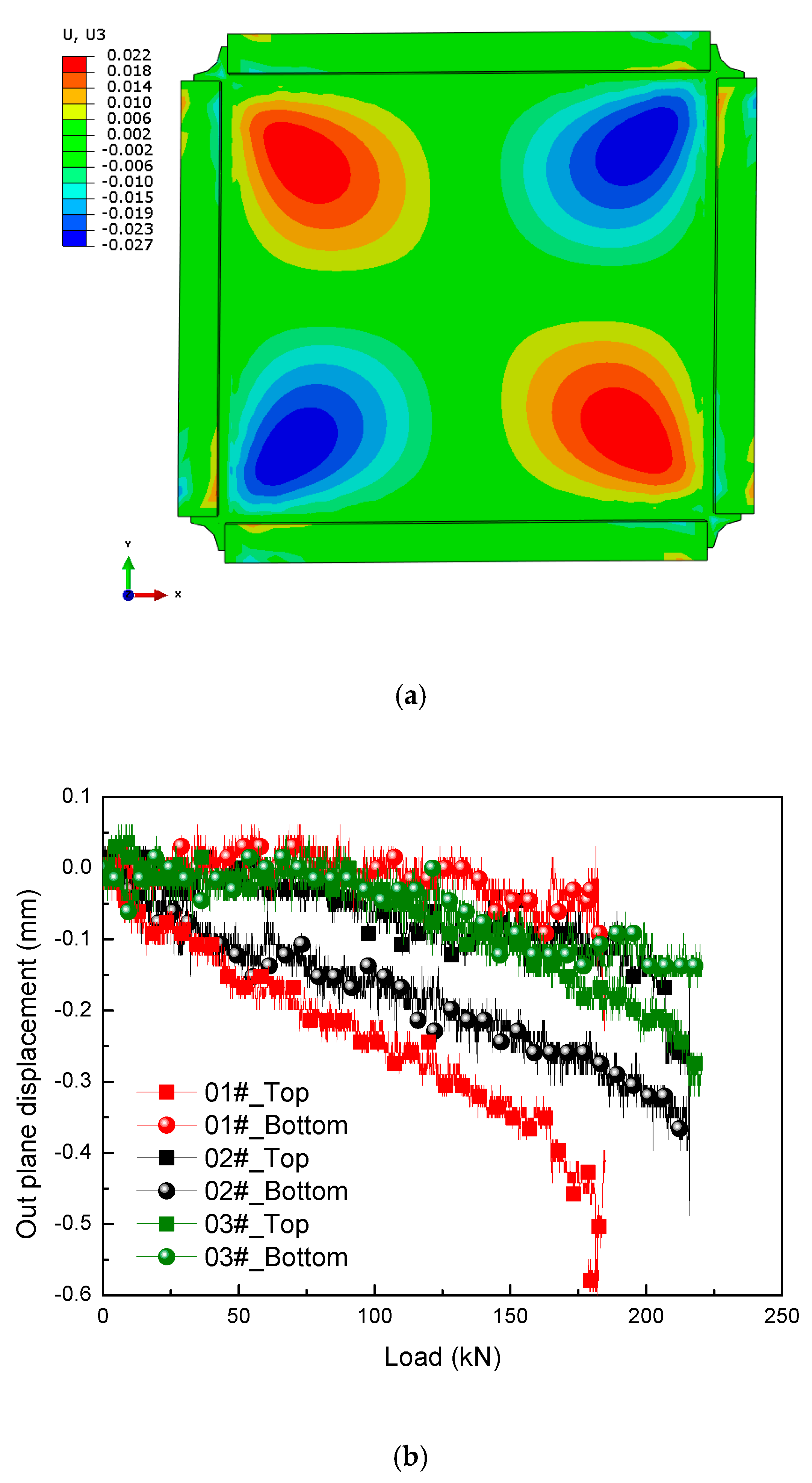
6.3. Out-of-Plane Displacement Analysis
6.4. Strain Field Distribution
6.5. Buckling and Failure Mode Characteristics
7. Conclusions
- The experimental displacement and strain data show good repeatability and symmetry, which confirms the rationality of the experiment design for the large-scale sandwiched structure.
- The honeycomb sandwich composite shows linear response under in-plane shear load until final failure. The average failure load reaches 205.68 kN, and the maximum shear strain monitored on the composite plate is up to 16,115 με.
- Local wrinkling occurs at the corner or diagonal tension direction before overall buckling appears due to the manufacture quality assurance problem for the such large size honeycomb sandwich composite.
- The out-of-plane displacement filed distribution under pure shear loading had approximately symmetric deformation at the corners. The ability to transfer shear force for the sandwich structure mainly depends on the harmonious deformation between the top and bottom skins.
- A relatively uniform shear strain field was generated, in which the strain gradually increased from the corners to the middle.
- The results of the finite element method and theoretical analysis method were verified by comparing shear load vs. displacement curves, load vs. strain curves, and strain field distribution with experimental results.
- By comparing the experimental, FEM, and theoretical results, it can be concluded that the theoretical analysis method is relatively conservative, and the FEM method is more accurate in the case of deformation and strain. The results predicted by h element and p element methods are very close.
- The overall buckling loads obtained by the three methods are similar. Experiment results were relatively low because local failure occurs in advance. However, the FEM method and the theoretical analysis method can verify each other.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wahl, L.; Maas, S.; Waldmann, D.; Zürbes, A.; Frères, P. Shear stresses in honeycomb sandwich plates: Analytical solution, finite element method and experimental verification. J. Sandw. Struct. Mater. 2012, 14, 449–468. [Google Scholar] [CrossRef]
- Farooq, U.; Ahmad, M.S.; Rakha, S.A. Interfacial Mechanical Performance of Composite Honeycomb Sandwich Panels for Aerospace Applications. Arab. J. Sci. Eng. 2017, 42, 1775–1782. [Google Scholar] [CrossRef]
- Vitale, J.P.; Francucci, G.; Xiong, J.; Stocchi, A. Failure mode maps of natural and synthetic fiber reinforced composite sandwich panels. Compos. Part A Appl. Sci. Manuf. 2017, 94, 217–225. [Google Scholar] [CrossRef]
- Wang, J.; Waas, A.M.; Wang, H. Experimental and numerical study on the low-velocity impact behavior of foam-core sandwich panels. Compos. Struct. 2013, 96, 298–311. [Google Scholar] [CrossRef]
- Vogel, J.; Keller, J.; Sviridov, A.; Feige, H.J.; Kreyssig, K.; Auersperg, J. Characterisation of Strength Behaviour of Aluminium Foam Sandwiches Under Static Load. Strain 2011, 47, 234–242. [Google Scholar] [CrossRef]
- Xu, A.; Vodenitcharova, T.; Kabir, K.; Flores-Johnson, E.A.; Hoffman, M. Finite element analysis of indentation of aluminium foam and sandwich panels with aluminium foam core. Mater. Sci. Eng. A 2014, 599, 125–133. [Google Scholar] [CrossRef]
- Birman, V.; Kardomateas, G.A. Review of current trends in research and applications of sandwich structures. Compos. Part B Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Lee, W.-J.; Baek, S.-M.; Kim, S.-Y. Design of electromagnetic wave absorbing sandwich composite for secondary bonding application. J. Electromagn. Waves Appl. 2019, 33, 625–636. [Google Scholar] [CrossRef]
- Balázs, D.Á.; Nyikes, Z.; Kovács, T. Building Protection with Composite Materials Application. Key Eng. Mater. 2017, 755, 286–291. [Google Scholar] [CrossRef]
- Irfan, S.; Siddiqui, F. A review of recent advancements in finite element formulation for sandwich plates. Chin. J. Aeronaut. 2019, 32. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Mei, J. Investigation on manufacturing and mechanical behavior of all-composite sandwich structure with Y-shaped cores. Compos. Sci. Technol. 2018, 159, 87–102. [Google Scholar] [CrossRef]
- Mei, J.; Liu, J.; Liu, J. A novel fabrication method and mechanical behavior of all-composite tetrahedral truss core sandwich panel. Compos. Part A Appl. Sci. Manuf. 2017, 102, 28–39. [Google Scholar] [CrossRef]
- Belardi, W.; De Lucia, F.; Poletti, F.; Sazio, P.J. Composite material hollow antiresonant fibers. Opt. Lett. 2017, 42, 2535–2538. [Google Scholar] [CrossRef]
- Junqi, Z.; Longquan, L.; Hai, W. Test of composite honeycomb sandwich structure with thin facesheets subject to impact load. Acta Mater. Compos. Sin. 2014, 31, 1063–1071. [Google Scholar]
- Abbadi, A.; Koutsawa, Y.; Carmasol, A. Experimental and numerical characterization of honeycomb sandwich composite panels. Simul. Model. Pract. Theory 2009, 17, 1533–1547. [Google Scholar] [CrossRef]
- Lin, L.X.; Mou, H.L.; Ren, J. The Static Strength Reliability Analysis of Composite Aircraft Structures. Appl. Mech. Mater. 2014, 488, 1215–1218. [Google Scholar] [CrossRef]
- Chi, H.E.C.; Lin, K.Y. Numerical Analysis of Fastener Delamination/Disbond Arrest Mechanism in Aircraft Composite Structures. J. Aircr. 2012, 49, 630–635. [Google Scholar]
- Liu, J.; Xiang, L.; Kan, T. The effect of temperature on the bending properties and failure mechanism of composite truss core sandwich structures. Compos. Part A Appl. Sci. Manuf. 2015, 79, 146–154. [Google Scholar] [CrossRef]
- Wang, B.; Wu, L.; Ma, L.; Sun, Y.; Du, S. Mechanical behavior of the sandwich structures with carbon fiber-reinforced pyramidal lattice truss core. Mater. Des. 2010, 31, 2659–2663. [Google Scholar] [CrossRef]
- Qi, G.; Ma, L. Experimental investigation of composite pyramidal truss core sandwich panels with lightweight inserts. Compos. Struct. 2018, 187, 336–343. [Google Scholar] [CrossRef]
- Wang, S.L.; Zhang, L.H.; Li, X. Introduction of All Composite General Aircraft in Structure Design and Process. Sci. Technol. Vis. 2014, 15, 71–72. [Google Scholar]
- Classen, M.; Herbrand, M. Shear behavior of composite dowels in transversely cracked concrete. Struct. Concr. 2015, 16, 195–206. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, Y.; Chen, Z. Experimental seismic behavior of innovative composite shear walls. J. Constr. Steel Res. 2016, 116, 218–232. [Google Scholar] [CrossRef]
- Ma, P.; Zhang, F.; Jiang, G.; Gao, Z.; Xia, D. Transverse impact characterization of carbon woven fabric-foam sandwich composites with carbon nanotubes. Fibers Polym. 2014, 15, 1560–1566. [Google Scholar] [CrossRef]
- Dong, H.; Cao, W.; Wu, H.; Qiao, Q.; Yu, C. Experimental and analytical study on seismic behavior of steel-concrete multienergy dissipation composite shear walls. Earthq. Eng. Eng. Vib. 2015, 14, 125–139. [Google Scholar] [CrossRef]
- Holomek, J.; Bajer, M.; Barnat, J.; Vild, M. Shear Tests of Composite Slabs, Experimental and Numerical Investigation. Adv. Mater. Res. 2014, 923, 217–220. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, W.; Hu, Z. Experimental and Numerical Analysis of the Mechanical Behaviors of Large Scale Composite C-Beams Fastened with multi-Bolt Joints under four-point Bending Load. Compos. Part B 2019, 164, 168–178. [Google Scholar] [CrossRef]
- Thornton, C.; Zhang, L. Numerical Simulations of the Direct Shear Test. Chem. Eng. Technol. 2010, 26, 153–156. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Yin, X.; Liu, Y.; He, Z.; Zhang, J. Effects of porosity on in-plane and interlaminar shear strengths of two-dimensional carbon fiber reinforced silicon carbide composites. Mater. Des. 2016, 98, 120–127. [Google Scholar] [CrossRef]
- Kolanu, N.R.; Raju, G.; Ramji, M. Damage assessment studies in CFRP composite laminate with cut-out subjected to in-plane shear loading. Compos. Part B Eng. 2019, 166, 257–271. [Google Scholar] [CrossRef]
- Cela Greven, B.; Gross-Barsnick, S.; Koppitz, T.; Conradt, R.; Smeacetto, F.; Ventrella, A.; Ferraris, M. Torsional shear strength of novel glass-ceramic composite sealants for solid oxide fuel cell stacks. Int. J. Appl. Ceram. Technol. 2018, 15, 286–295. [Google Scholar] [CrossRef]
- Tan, W.; Falzon, B.G. Modelling the nonlinear behaviour and fracture process of AS4/PEKK thermoplastic composite under shear loading. Compos. Sci. Technol. 2016, 126, 60–77. [Google Scholar] [CrossRef]
- Jung, W.-Y.; Han, S.-C. Shear buckling responses of laminated composite shells using a modified 8-node ANS shell element. Compos. Struct. 2014, 109, 119–129. [Google Scholar] [CrossRef]
- Chen, Q.; Qiao, P. Shear buckling of rotationally-restrained composite laminated plates. Thin-Walled Struct. 2015, 94, 147–154. [Google Scholar] [CrossRef]
- Mahi, A.; Bedia, E.A.A.; Tounsi, A. A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates. Appl. Math. Model. 2015, 39, 2489–2508. [Google Scholar] [CrossRef]
- Fan, X.M.; Wang, J.F.; Duan, C.J. Study on Automobile Body Performance of Honeycomb Sandwich Composite Material. Adv. Mater. Res. 2012, 567, 146–149. [Google Scholar] [CrossRef]
- Kim, H.G.; Kim, Y.J.; Shin, H.J. A Study on the Bending Analysis of the Al Honeycomb Core Sandwich Composite Panel Bearing Large Bending Load. Adv. Mater. Res. 2013, 702, 245–252. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Saleemi, S.; Zhang, Y. Bending properties and failure mechanisms of three-dimensional hybrid woven spacer composites with glass and carbon fibers. Text. Res. J. 2019, 89, 4502–4511. [Google Scholar] [CrossRef]
- Prakash, A.A.; Guptha, J.; Sharma, R. Influence of Cell Size on the Core Shear Properties of FRP Honeycomb Sandwich Panels. Adv. Manuf. Process. 2012, 27, 169–176. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, Z.D.; Gao, L.M. Investigation on In-plane Shear Behavior of Large-Size Composite Plates with Multi-bolt Joints. Compos. Struct. 2020, 232. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Liu, W. Post-buckling progressive damage of CFRP laminates with a large-sized elliptical cutout subjected to shear loading. Compos. Struct. 2015, 128, 313–321. [Google Scholar] [CrossRef]
- Wan, Y.; Zhang, F.; Liu, C. Overall buckling of typical thin-wall sandwich composites applied on the aircraft. Acta Mater. Compos. Sin. 2018, 35, 2235–2245. [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Li, S.L. Composite materials workbook; Aviation Industry Press: Beijing, China, 1988. [Google Scholar]
- Carlsson, L.; Kardomateas, G. Structural and Failure Mechanics of Sandwich Composites; Springer Science and Business Media LLC: Berlin, Germany, 2011. [Google Scholar]
- Xie, S. Aircraft Design Manual Book, 9th ed.; Aviation Industry Press: Beijing, China, 2001. [Google Scholar]
- Zhang, F.; Mohmmed, R.; Sun, B.; Gu, B. Damage Behaviors of Foam Sandwiched Composite Materials Under Quasi-Static Three-point Bending. Appl. Compos. Mater. 2013, 20, 1231–1246. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are available from the authors. |










| Property | CFRP Skin | Nomex Honeycomb Core |
|---|---|---|
| Longitudinal stiffness, E11 (GPa) | 36.65 | 0.015 |
| Transverse stiffness, E22 (GPa) | 36.65 | 0.015 |
| Out-of-plane stiffness, E33 (GPa) | 10.16 | 0.175 |
| Poisson’s ratio, ν11 | 0.04 | 0.4 |
| Poisson’s ratio, ν13 | 0.31 | 0.1 |
| Poisson’s ratio, ν23 | 0.31 | 0.1 |
| Shear modulus, G12 (GPa) | 4.21 | 0.113 |
| Shear modulus, G13 (GPa) | 4.23 | 0.077 |
| Shear modulus, G23 (GPa) | 4.23 | 0.077 |
| Longitudinal tensile strength, Xt (MPa) | 676 | -- |
| Longitudinal compressive strength, Xc (MPa) | 230 | 2.17 |
| Transverse tensile strength, Yt (MPa) | 676 | -- |
| Transverse compressive strength, Yc (MPa) | 230 | -- |
| Longitudinal shear strength, S12 (MPa) | 50 | 1.48 |
| Transverse shear strength, S23 (MPa) | 75 | 0.84 |
| Density, ρ (kg/m3) | 1532 | 48 |
| Axial Stiffness K1/(1010N·mm−1) | Shear Stiffness K2/(1010N·mm−1) | Shear Stiffness K3/(1010N·mm−1) | Rotational Stiffness K4/(1010N·rad−1) | Bending Stiffness K5/(1010N·rad−1) | Bending Stiffness K6/(1010N·rad−1) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 1 |
| Specimen | 01# | 02# | 03# |
|---|---|---|---|
| Shear (με) | 16,343 | 15,886 | 16,118 |
| Failure load (kN) | 185.56 | 210.63 | 220.84 |
| Method | Failure Load/N |
|---|---|
| Experiment | 205,681 |
| FEM_h ele | 279,954 |
| FEM_p ele | 277,805 |
| Theoretical analysis | 260,433 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.-N.; Wang, B.; Liu, C.; Zhang, G.; Wan, Y.; Zhang, F. Mechanical Respond and Failure Mode of Large Size Honeycomb Sandwiched Composites under In-Plane Shear Load. Molecules 2019, 24, 4248. https://doi.org/10.3390/molecules24234248
Wang M-N, Wang B, Liu C, Zhang G, Wan Y, Zhang F. Mechanical Respond and Failure Mode of Large Size Honeycomb Sandwiched Composites under In-Plane Shear Load. Molecules. 2019; 24(23):4248. https://doi.org/10.3390/molecules24234248
Chicago/Turabian StyleWang, Mo-Nan, Baoqin Wang, Changxi Liu, Guangxin Zhang, Yumin Wan, and Fa Zhang. 2019. "Mechanical Respond and Failure Mode of Large Size Honeycomb Sandwiched Composites under In-Plane Shear Load" Molecules 24, no. 23: 4248. https://doi.org/10.3390/molecules24234248






