The Halogen-Bond Nature in Noble Gas–Dihalogen Complexes from Scattering Experiments and Ab Initio Calculations
Abstract
:1. Introduction
2. Results and Discussion
2.1. Scattering Results
2.2. Interaction Potential Components
2.3. Ab Initio Potential Energy Surfaces
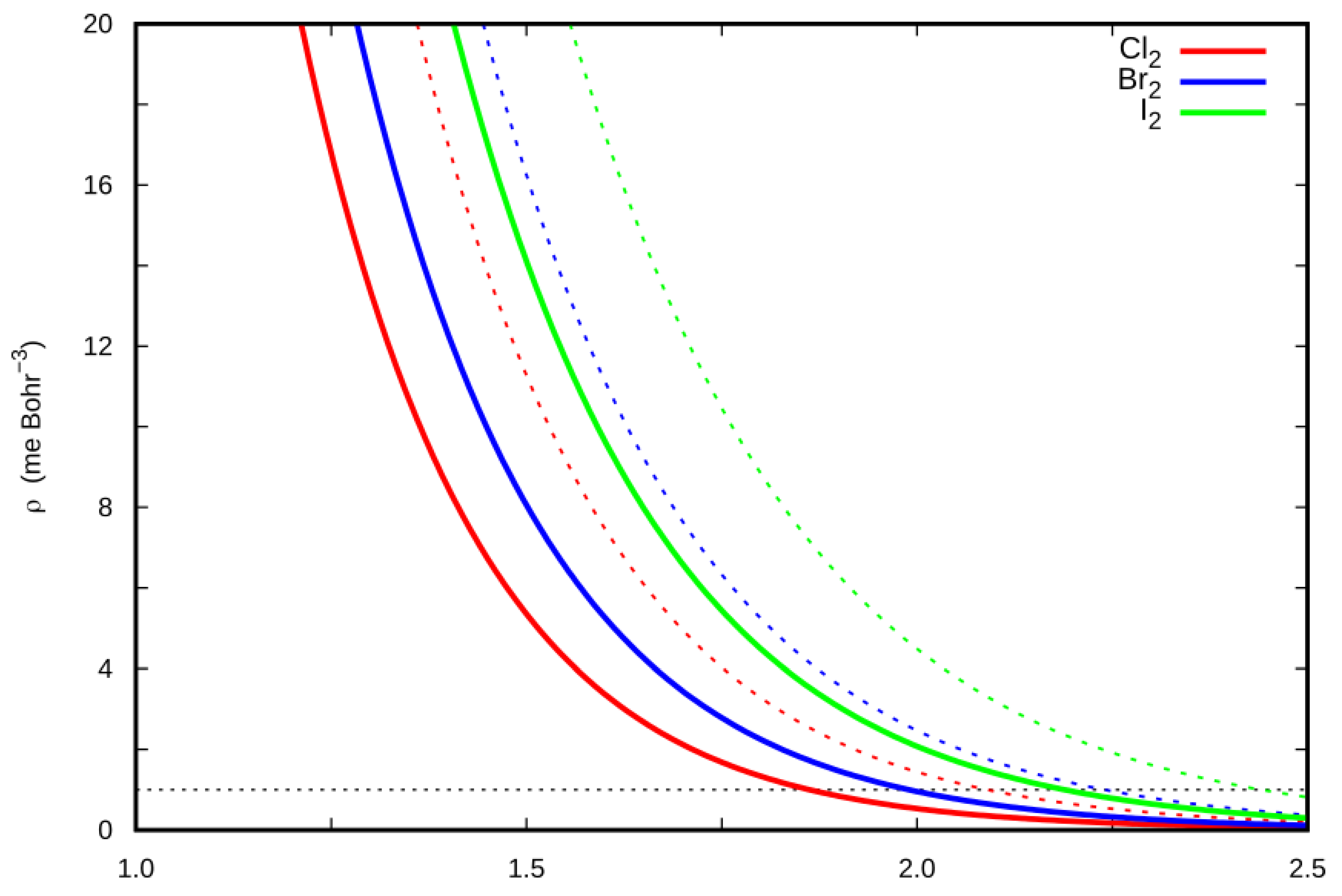
2.4. Halogen Polar Flattening in the Ng–X2 Complexes
2.5. Charge Displacement Analysis
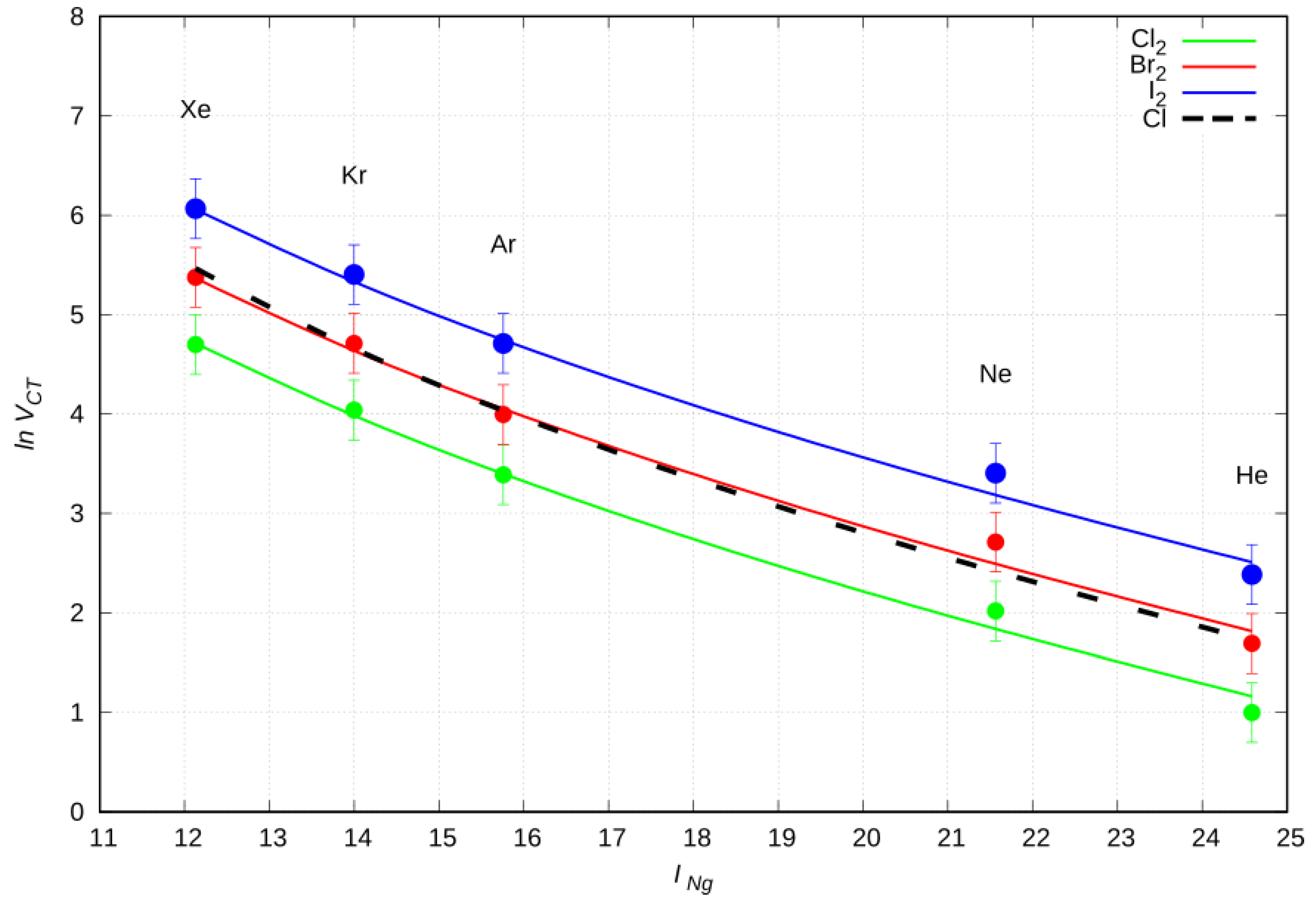
2.6. CT Dependence on the First Ionization Potential
2.7. CT Proportional Constant
3. Materials and Methods
3.1. Phenomenological Approach
3.2. Computational Details
3.3. Charge Displacement Function
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (iupac recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Han, Z.M.; Czap, G.; Chiang, C.L.; Xu, C.; Wagner, P.J.; Wei, X.Y.; Zhang, Y.X.; Wu, R.Q.; Ho, W. Imaging the halogen bond in self-assembled halogenbenzenes on silver. Science 2017, 358, 206–210. [Google Scholar] [CrossRef] [PubMed]
- Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef] [PubMed]
- Rohrbacher, A.; Halberstadt, N.; Janda, K.C. The Dynamics of Noble Gas-Halogen Molecules and Clusters. Annu. Rev. Phys. Chem. 2000, 51, 405–433. [Google Scholar] [CrossRef] [PubMed]
- Beswick, J.A.; Halberstadt, N.; Janda, K.C. Structure and Dynamics of Noble Gas-Halogen and Noble Gas Ionic Clusters: When Theory Meets Experiment. Chem. Phys. 2012, 399, 4–16. [Google Scholar] [CrossRef]
- Wei, J.; Makarem, C.; Reinitz, A.L.; Darr, J.P.; Loomis, R.A. Accurate Measurement of the T-Shaped And Linear Ar··· I2(X, ν″=0) Binding Energies Using Vibronic-Specific I2(B, ν) Fragment Velocity-Map Imaging. Chem. Phys. 2012, 399, 172–179. [Google Scholar] [CrossRef]
- Delgado-Tellez, L.; Valdes, A.; Prosmiti, R.; Villarreal, P.; Delgado-Barrio, G. Ab Initio Characterization of the Ne-I2 Van Der Waals Complex: Intermolecular Potentials and Vibrational Bound States. J. Chem. Phys. 2011, 134, 21. [Google Scholar] [CrossRef]
- Baturo, V.V.; Lukashov, S.S.; Poretsky, S.A.; Pravilov, A.M. The RgI2 (Ion-Pair States) van der Waals Complexes. Eur. Phys. J. D 2017, 71, 227. [Google Scholar] [CrossRef]
- Legon, A.C. The Halogen Bond: An Interim Perspective. Phys. Chem. Chem. Phys. 2010, 12, 7736–7747. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Mathematical modeling and physical reality in noncovalent interactions. J. Mol. Modeling 2015, 21, 3. [Google Scholar] [CrossRef]
- Shields, Z.P.; Murray, J.S.; Politzer, P. Directional Tendencies of Halogen and Hydrogen Bonds. Int. J. Quantum Chem. 2010, 110, 2823–2832. [Google Scholar] [CrossRef]
- Pirani, F.; Cappelletti, D.; Falcinelli, S.; Cesario, D.; Nunzi, F.; Belpassi, L.; Tarantelli, F. Selective Emergence of Halogen Bond in Ground and Excited States of Noble-Gas—Chlorine Systems. Angew. Chem. Int. Ed. 2019, 58, 4195–4199. [Google Scholar] [CrossRef] [PubMed]
- Nunzi, F.; Cesario, D.; Belpassi, L.; Tarantelli, F.; Roncaratti, L.F.; Falcinelli, S.; Cappelletti, D.; Pirani, F. Insight into The Halogen-Bond Nature Of Noble Gas-Chlorine Systems By Molecular Beam Scattering Experiments, Ab Initio Calculations And Charge Displacement Analysis. Phys. Chem. Chem. Phys. 2019, 21, 7330–7340. [Google Scholar] [CrossRef] [PubMed]
- De Santis, M.; Nunzi, F.; Cesario, D.; Belpassi, L.; Tarantelli, F.; Cappelletti, D.; Pirani, F. Cooperative Role of Halogen And Hydrogen Bonding In The Stabilization Of Water Adducts With Apolar Molecules. New J. Chem. 2018, 42, 10603–10614. [Google Scholar] [CrossRef]
- Cappelletti, D.; Aquilanti, V.; Bartocci, A.; Nunzi, F.; Tarantelli, F.; Belpassi, L.; Pirani, F. Interaction of O2 with CH4, CF4, and CCl4 by Molecular Beam Scattering Experiments and Theoretical Calculations. J. Phys. Chem. A 2016, 120, 5197–5207. [Google Scholar] [CrossRef]
- Cappelletti, D.; Ronca, E.; Belpassi, L.; Tarantelli, F.; Pirani, F. Revealing Charge-Transfer Effects in Gas-Phase Water Chemistry. Acc. Chem. Res. 2012, 45, 1571–1580. [Google Scholar] [CrossRef]
- Cappelletti, D.; Cinti, A.; Nicoziani, A.; Falcinelli, S.; Pirani, F. Molecular Beam Scattering Experiments as a Sensitive Probe of the Interaction in Bromine-Noble Gas Complexes. Front. Chem. 2019, 7, 10. [Google Scholar] [CrossRef]
- Pirani, F.; Vecchiocattivi, F. A Fast and Accurate Semiclassical Calculation of the Total Elastic Cross Section In The Glory Energy Range. Mol. Phys. 1982, 45, 1003–1013. [Google Scholar] [CrossRef]
- Pirani, F.; Brizi, S.; Roncaratti, L.F.; Casavecchia, P.; Cappelletti, D.; Vecchiocattivi, F. Beyond the Lennard-Jones Model: A Simple and Accurate Potential Function Probed by High Resolution Scattering Data Useful For Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2008, 10, 5489–5503. [Google Scholar] [CrossRef]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen Bonding: The σ-hole. J. Mol. Modeling 2007, 13, 291–296. [Google Scholar] [CrossRef]
- Riley, K.E.; Murray, J.S.; Fanfrlik, J.; Rezac, J.; Sola, R.J.; Concha, M.C.; Ramos, F.M.; Politzer, P. Halogen bond tunability II: The varying roles of electrostatic and dispersion contributions to attraction in halogen bonds. J. Mol. Modeling 2013, 19, 4651–4659. [Google Scholar] [CrossRef] [PubMed]
- Belpassi, L.; Infante, I.; Tarantelli, F.; Visscher, L. The Chemical Bond Between Au(I) and the Noble Gases. Comparative Study of NgAuF And NgAu+ (Ng = Ar, Kr, Xe) By Density Functional and Coupled Cluster Methods. J. Am. Chem. Soc. 2008, 130, 1048–1060. [Google Scholar] [CrossRef] [PubMed]
- Bistoni, G.; Belpassi, L.; Tarantelli, F.; Pirani, F.; Cappelletti, D. Charge-Displacement Analysis of the Interaction in the Ammonia-Noble Gas Complexes. J. Phys Chem 2011, 115, 14657–14666. [Google Scholar] [CrossRef] [PubMed]
- Nunzi, F.; Cesario, D.; Pirani, F.; Belpassi, L.; Frenking, G.; Grandinetti, F.; Tarantelli, F. Helium Accepts Back-Donation In Highly Polar Complexes: New Insights into the Weak Chemical Bond. J. Phys. Chem. Lett. 2017, 8, 3334–3340. [Google Scholar] [CrossRef] [PubMed]
- Nunzi, F.; Cesario, D.; Pirani, F.; Belpassi, L.; Tarantelli, F. Modelling Charge Transfer in Weak Chemical Bonds: Insights from the Chemistry of Helium. Chemphyschem 2018, 19, 1476–1485. [Google Scholar] [CrossRef]
- Aquilanti, V.; Cappelletti, D.; Lorent, V.; Luzzatti, E.; Pirani, F. The Ground and Lowest Excited-States of XeCl By Atomic-Beam Scattering. Chem. Phys. Lett. 1992, 192, 153–160. [Google Scholar] [CrossRef]
- Pirani, F.; Giulivi, A.; Cappelletti, D.; Aquilanti, V. Coupling by Charge Transfer: Role In Bond Stabilization For Open-Shell Systems And Ionic Molecules And In Harpooning And Proton Attachment Processes. Mol. Phys. 2000, 98, 1749–1762. [Google Scholar] [CrossRef]
- Weast, R.C.; Astle, M.J.; Beyer, W.H. CRC Handbook of Chemistry and Physics; CRC press: Boca Raton, FL, USA, 1988; Volume 69. [Google Scholar]
- Wang, C.; Danovich, D.; Mo, Y.; Shaik, S. On the Nature of the Halogen Bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. [Google Scholar] [CrossRef]
- Olney, T.N.; Cann, N.M.; Cooper, G.; Brion, C.E. Absolute scale determination for photoabsorption spectra and the calculation of molecular properties using dipole sum rules. Chem. Phys. 1997, 223, 59–98. [Google Scholar] [CrossRef]
- Cappelletti, D.; Bartocci, A.; Grandinetti, F.; Falcinelli, S.; Belpassi, L.; Tarantelli, F.; Pirani, F. Experimental Evidence of Chemical Components in the Bonding of Helium and Neon with Neutral Molecules. Chem. A Eur. J. 2015, 21, 6234–6240. [Google Scholar] [CrossRef]
- Bartocci, A.; Belpassi, L.; Cappelletti, D.; Falcinelli, S.; Grandinetti, F.; Tarantelli, F.; Pirani, F. Catching the Role of Anisotropic Electronic Distribution and Charge Transfer in Halogen Bonded Complexes of Noble Gases. J. Chem. Phys. 2015, 142, 184304. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schutz, M. Molpro: A General-Purpose Quantum Chemistry Program Package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Headgordon, M. A 5th-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure, Constants of Diatomic Molecules, Vol. IV; Van Nostrand: New York, NY, USA, 1979. [Google Scholar]
- Le Roy, R.J.; Bernstein, R.B. Dissociation Energies and Long-Range Potentials of Diatomic Molecules from Vibrational Spacings: The Halogens. J. Mol. Spectrosc. 1971, 37, 109–130. [Google Scholar] [CrossRef] [Green Version]
- Jansen, H.B.; Ros, P. Non-Empirical Molecular Orbital Calculations on the Protonation of Carbon Monoxide. Chem. Phys. Lett. 1991, 3, 140–143. [Google Scholar] [CrossRef]
- Liu, B.; McLean, A.D. Accurate Calculation of the Attractive Interaction of Two Ground State Helium Atoms. J. Chem. Phys. 1973, 59, 4557–4558. [Google Scholar] [CrossRef] [Green Version]
Sample Availability: Samples of the compounds are not available from the authors. |







| Vsph | Vlin | Vperp | ||||
|---|---|---|---|---|---|---|
| Rm | Em | Rm | Em | Rm | Em | |
| He–Cl2 | 4.16 | 3.23 | 4.27 | 5.93 | 3.39 | 6.15 |
| Ne–Cl2 | 4.16 | 6.98 | 4.29 | 12.21 | 3.44 | 12.10 |
| Ar–Cl2 | 4.33 | 17.99 | 4.53 | 27.01 | 3.70 | 27.12 |
| Kr–Cl2 | 4.43 | 23.01 | 4.61 | 34.67 | 3.83 | 32.78 |
| Xe–Cl2 | 4.56 | 27.77 | 4.73 | 41.45 | 4.00 | 37.71 |
| He–Br2 | 4.41 | 3.24 | 4.51 | 6.51 | 3.50 | 6.43 |
| Ne–Br2 | 4.40 | 7.29 | 4.52 | 14.09 | 3.54 | 13.22 |
| Ar–Br2 | 4.57 | 18.42 | 4.75 | 30.03 | 3.81 | 29.28 |
| Kr–Br2 | 4.61 | 25.69 | 4.77 | 43.92 | 3.88 | 38.91 |
| Xe–Br2 | 4.73 | 32.24 | 4.86 | 55.02 | 4.04 | 46.18 |
| He–I2 | 4.85 | 2.76 | 4.95 | 5.54 | 3.79 | 5.54 |
| Ne–I2 | 4.80 | 6.46 | 4.90 | 13.21 | 3.78 | 12.21 |
| Ar–I2 | 4.88 | 19.20 | 5.04 | 34.66 | 3.94 | 32.98 |
| Kr–I2 | 4.93 | 26.34 | 5.05 | 49.82 | 4.02 | 43.19 |
| Xe–I2 | 5.02 | 34.64 | 5.11 | 65.77 | 4.16 | 54.26 |
| Vsph | Vlin | Vperp | ||||
|---|---|---|---|---|---|---|
| Rm | Em | Rm | Em | Rm | Em | |
| He–Cl2 | 4.37 | 2.69 | 4.82 | 3.24 | 3.37 | 5.79 |
| Ne–Cl2 | 4.40 | 5.52 | 4.84 | 6.77 | 3.41 | 11.59 |
| Ar–Cl2 | 4.58 | 14.45 | 5.00 | 17.60 | 3.67 | 27.37 |
| Kr–Cl2 | 4.68 | 18.66 | 5.10 | 22.68 | 3.78 | 34.18 |
| Xe–Cl2 | 4.82 | 23.18 | 5.25 | 28.11 | 3.95 | 40.61 |
| He–Br2 | 4.57 | 2.67 | 5.03 | 3.15 | 3.61 | 5.37 |
| Ne–Br2 | 4.58 | 5.66 | 5.03 | 6.77 | 3.63 | 11.21 |
| Ar–Br2 | 4.73 | 16.01 | 5.16 | 19.24 | 3.82 | 29.41 |
| Kr–Br2 | 4.81 | 21.25 | 5.24 | 25.43 | 3.92 | 38.03 |
| Xe–Br2 | 4.93 | 27.14 | 5.35 | 32.51 | 4.07 | 46.35 |
| He–I2 | 5.12 | 2.13 | 5.62 | 2.85 | 3.83 | 4.88 |
| Ne–I2 | 5.10 | 4.66 | 5.59 | 6.32 | 3.82 | 10.62 |
| Ar–I2 | 5.19 | 14.69 | 5.66 | 20.05 | 3.94 | 31.73 |
| Kr–I2 | 5.26 | 20.15 | 5.73 | 27.30 | 4.02 | 42.49 |
| Xe–I2 | 5.35 | 26.94 | 5.83 | 36.42 | 4.14 | 55.01 |
| INg (eV) (a) | ||||
|---|---|---|---|---|
| He | 24.587 | Cl | 3.621 | 3430 |
| Ne | 21.564 | Cl2 | 2.38 ± 0.1 | 1300 |
| Ar | 15.759 | Br2 | 2.55 ± 0.1 | 2500 |
| Kr | 13.999 | I2 | 2.55 ± 0.05 | 5000 |
| Xe | 12.130 |
| rm|| | ε || | rm⊥ | ε ⊥ | ACT | A3B | |
|---|---|---|---|---|---|---|
| He–Cl2 | 3.39 | 4.47 | 3.55 | 2.93 | 310,000 | 22,000 |
| Ne–Cl2 | 3.44 | 8.76 | 3.60 | 5.76 | 450,000 | 61,000 |
| Ar–Cl2 | 3.68 | 19.70 | 3.85 | 13.00 | 700,000 | 240,000 |
| Kr–Cl2 | 3.79 | 24.40 | 3.98 | 15.70 | 830,000 | 460,000 |
| Xe–Cl2 | 3.94 | 28.20 | 4.14 | 18.10 | 970,000 | 890,000 |
| He–Br2 | 3.53 | 4.71 | 3.71 | 3.02 | 620,000 | 44,000 |
| Ne–Br2 | 3.57 | 9.66 | 3.75 | 6.21 | 900,000 | 120,000 |
| Ar–Br2 | 3.80 | 21.30 | 4.00 | 13.90 | 1,400,000 | 440,000 |
| Kr–Br2 | 3.87 | 28.90 | 4.07 | 18.40 | 1,660,000 | 900,000 |
| Xe–Br2 | 4.01 | 34.50 | 4.23 | 21.90 | 1,900,000 | 1,750,000 |
| He–I2 | 3.81 | 4.00 | 4.06 | 2.59 | 1,550,000 | 88,000 |
| Ne–I2 | 3.81 | 8.76 | 4.05 | 5.70 | 2,250,000 | 244,000 |
| Ar–I2 | 3.95 | 23.60 | 4.20 | 15.50 | 3,500,000 | 900,000 |
| Kr–I2 | 4.03 | 30.90 | 4.28 | 20.30 | 4,150,000 | 1,800,000 |
| Xe–I2 | 4.16 | 38.60 | 4.41 | 25.60 | 4,750,000 | 3,500,000 |
| rm|| | ε|| | rm⊥ | ε⊥ | ACT | A3B | |
|---|---|---|---|---|---|---|
| He–Cl2 | 3.62 | 3.03 | 3.58 | 2.88 | 0 | 0 |
| Ne–Cl2 | 3.64 | 6.32 | 3.62 | 5.73 | 0 | 0 |
| Ar–Cl2 | 3.81 | 16.30 | 3.87 | 13.40 | 0 | 0 |
| Kr–Cl2 | 3.91 | 20.90 | 3.98 | 16.70 | 0 | 0 |
| Xe–Cl2 | 4.06 | 25.70 | 4.14 | 19.80 | 0 | 0 |
| He–Br2 | 3.83 | 2.92 | 3.81 | 2.66 | 0 | 0 |
| Ne–Br2 | 3.83 | 6.27 | 3.83 | 5.53 | 0 | 0 |
| Ar–Br2 | 3.96 | 17.70 | 4.02 | 14.40 | 0 | 0 |
| Kr–Br2 | 4.04 | 23.30 | 4.11 | 18.60 | 0 | 0 |
| Xe–Br2 | 4.16 | 29.60 | 4.26 | 22.60 | 0 | 0 |
| He–I2 | 4.12 | 2.70 | 4.12 | 2.40 | 0 | 0 |
| Ne–I2 | 4.09 | 6.00 | 4.11 | 5.20 | 0 | 0 |
| Ar–I2 | 4.16 | 19.00 | 4.23 | 15.40 | 0 | 0 |
| Kr–I2 | 4.23 | 25.80 | 4.31 | 20.60 | 0 | 0 |
| Xe–I2 | 4.33 | 34.30 | 4.42 | 26.60 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunzi, F.; Di Erasmo, B.; Tarantelli, F.; Cappelletti, D.; Pirani, F. The Halogen-Bond Nature in Noble Gas–Dihalogen Complexes from Scattering Experiments and Ab Initio Calculations. Molecules 2019, 24, 4274. https://doi.org/10.3390/molecules24234274
Nunzi F, Di Erasmo B, Tarantelli F, Cappelletti D, Pirani F. The Halogen-Bond Nature in Noble Gas–Dihalogen Complexes from Scattering Experiments and Ab Initio Calculations. Molecules. 2019; 24(23):4274. https://doi.org/10.3390/molecules24234274
Chicago/Turabian StyleNunzi, Francesca, Benedetta Di Erasmo, Francesco Tarantelli, David Cappelletti, and Fernando Pirani. 2019. "The Halogen-Bond Nature in Noble Gas–Dihalogen Complexes from Scattering Experiments and Ab Initio Calculations" Molecules 24, no. 23: 4274. https://doi.org/10.3390/molecules24234274
APA StyleNunzi, F., Di Erasmo, B., Tarantelli, F., Cappelletti, D., & Pirani, F. (2019). The Halogen-Bond Nature in Noble Gas–Dihalogen Complexes from Scattering Experiments and Ab Initio Calculations. Molecules, 24(23), 4274. https://doi.org/10.3390/molecules24234274








