Modeling Physico-Chemical ADMET Endpoints with Multitask Graph Convolutional Networks
Abstract
:1. Introduction
2. Results and Discussion
2.1. Datasets Sizes and Overlaps
2.2. Performance of Single Task Models
2.3. Performance in Multitask Setting
2.4. Effect of Helper Tasks
2.5. General Solubility Equation
2.6. Performance in Time Splits
3. Materials and Methods
3.1. Dataset
3.2. Model Validation
3.2.1. Data Splits
3.2.2. Performance Measures
3.3. Machine Learning Models
3.3.1. Random Forest
3.3.2. Fully-Connected Single Task Network
3.3.3. Fully-Connected Multitask Network
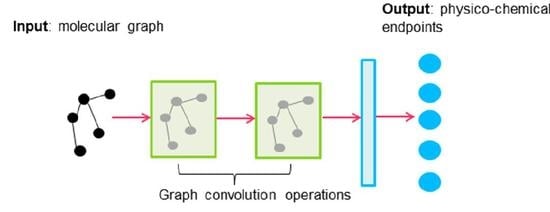
3.3.4. Graph Convolutions
- -
- 75 input atomic features (see Figure S1 for details);
- -
- two graph convolution steps with a feature dimension of 128 each, with ReLU activation functions; and
- -
- a dense layer with 256 units and ReLU activation functions.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Waring, M.J.; Arrowsmith, J.; Leach, A.R.; Leeson, P.D.; Mandrell, S.; Owen, R.M.; Pairaudeau, G.; Pennie, W.D.; Pickett, S.D.; Wang, J.; et al. An analysis of the attrition of drug candidates from four major pharmaceutical companies. Nat. Rev. Drug Discov. 2015, 14, 475–486. [Google Scholar] [CrossRef] [PubMed]
- Gleeson, M.P.; Hersey, A.; Montanari, D.; Overington, J. Probing the links between in vitro potency, ADMET and physicochemical parameters. Nat. Rev. Drug Discov. 2011, 10, 197–208. [Google Scholar] [CrossRef] [PubMed]
- Zang, Q.; Mansouri, K.; Williams, A.J.; Judson, R.S.; Allen, D.G.; Casey, W.M.; Kleinstreuer, N.C. In Silico Prediction of Physicochemical Properties of Environmental Chemicals Using Molecular Fingerprints and Machine Learning. J. Chem. Inf. Model. 2017, 57, 36–49. [Google Scholar] [CrossRef] [PubMed]
- Watkins, M.; Sizochenko, N.; Rasulev, B.; Leszczynski, J. Estimation of melting points of large set of persistent organic pollutants utilizing QSPR approach. J. Mol. Model. 2016, 22, 55. [Google Scholar] [CrossRef] [PubMed]
- Tetko, I.V.; Lowe, D.M.; Williams, A.J. The development of models to predict melting and pyrolysis point data associated with several hundred thousand compounds mined from PATENTS. J. Cheminform. 2016, 8, 2. [Google Scholar] [CrossRef] [Green Version]
- Bhhatarai, B.; Teetz, W.; Liu, T.; Öberg, T.; Jeliazkova, N.; Kochev, N.; Pukalov, O.; Tetko, I.V.; Kovarich, S.; Papa, E.; et al. CADASTER QSPR Models for Predictions of Melting and Boiling Points of Perfluorinated Chemicals. Mol. Inform. 2011, 30, 189–204. [Google Scholar] [CrossRef]
- Ghafourian, T.; Amin, Z. QSAR models for the prediction of plasma protein binding. Bioimpacts 2013, 3, 21–27. [Google Scholar]
- Cheng, T.; Li, Q.; Wang, Y.; Bryant, S.H. Binary Classification of Aqueous Solubility Using Support Vector Machines with Reduction and Recombination Feature Selection. J. Chem. Inf. Model. 2011, 51, 229–236. [Google Scholar] [CrossRef]
- Fioressi, S.E.; Bacelo, D.E.; Rojas, C.; Aranda, J.F.; Duchowicz, P.R. Conformation-independent quantitative structure-property relationships study on water solubility of pesticides. Ecotoxicol. Environ. Saf. 2019, 171, 47–53. [Google Scholar] [CrossRef]
- Sun, H.; Shah, P.; Nguyen, K.; Yu, K.R.; Kerns, E.; Kabir, M.; Wang, Y.; Xu, X. Predictive models of aqueous solubility of organic compounds built on A large dataset of high integrity. Bioorg. Med. Chem. 2019, 27, 3110–3114. [Google Scholar] [CrossRef]
- Bergström, C.A.S.; Larsson, P. Computational prediction of drug solubility in water-based systems: Qualitative and quantitative approaches used in the current drug discovery and development setting. Int. J. Pharm. 2018, 540, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Nigsch, F.; Bender, A.; van Buuren, B.; Tissen, J.; Nigsch, E.; Mitchell, J.B.O. Melting Point Prediction Employing k-Nearest Neighbor Algorithms and Genetic Parameter Optimization. J. Chem. Inf. Model. 2006, 46, 2412–2422. [Google Scholar] [CrossRef] [PubMed]
- Chinta, S.; Rengaswamy, R. Machine Learning Derived Quantitative Structure Property Relationship (QSPR) to Predict Drug Solubility in Binary Solvent Systems. Ind. Eng. Chem. Res. 2019, 58, 3082–3092. [Google Scholar] [CrossRef]
- Kratochwil, N.A.; Huber, W.; Müller, F.; Kansy, M.; Gerber, P.R. Predicting plasma protein binding of drugs: A new approach. Biochem. Pharmacol. 2002, 64, 1355–1374. [Google Scholar] [CrossRef]
- Merck Molecular Activity Challenge | Kaggle. Available online: https://www.kaggle.com/c/MerckActivity (accessed on 20 December 2019).
- Dahl, G.E.; Jaitly, N.; Salakhutdinov, R. Multi-task Neural Networks for QSAR Predictions. arXiv 2014, arXiv:1406.1231. [Google Scholar]
- Ma, J.; Sheridan, R.P.; Liaw, A.; Dahl, G.E.; Svetnik, V. Deep Neural Nets as a Method for Quantitative Structure–Activity Relationships. J. Chem. Inf. Model. 2015, 55, 263–274. [Google Scholar] [CrossRef] [PubMed]
- Caruana, R. Multitask Learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Kearnes, S.; Goldman, B.; Pande, V. Modeling Industrial ADMET Data with Multitask Networks. arXiv 2016, arXiv:1606.08793. [Google Scholar]
- Rogers, D.; Hahn, M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. arXiv arXiv:1312.6203, 2013.
- Henaff, M.; Bruna, J.; LeCun, Y. Deep Convolutional Networks on Graph-Structured Data. arXiv 2015, arXiv:1506.05163. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Duvenaud, D.; Maclaurin, D.; Aguilera-Iparraguirre, J.; Gómez-Bombarelli, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional Networks on Graphs for Learning Molecular Fingerprints. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Feinberg, E.N.; Sheridan, R.; Joshi, E.; Pande, V.S.; Cheng, A.C. Step Change Improvement in ADMET Prediction with PotentialNet Deep Featurization. arXiv 2019, arXiv:1903.11789. [Google Scholar]
- Feinberg, E.N.; Sur, D.; Wu, Z.; Husic, B.E.; Mai, H.; Li, Y.; Sun, S.; Yang, J.; Ramsundar, B.; Pande, V.S. PotentialNet for Molecular Property Prediction. ACS Cent. Sci. 2018, 4, 1520–1530. [Google Scholar] [CrossRef] [PubMed]
- Hughes, L.D.; Palmer, D.S.; Nigsch, F.; Mitchell, J.B.O. Why Are Some Properties More Difficult To Predict than Others? A Study of QSPR Models of Solubility, Melting Point, and Log P. J. Chem. Inf. Model. 2008, 48, 220–232. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Cahya, S.; Combs, S.A.; Nicolaou, C.A.; Wang, J.; Desai, P.V.; Shen, J. Exploring Tunable Hyperparameters for Deep Neural Networks with Industrial ADME Data Sets. J. Chem. Inf. Model. 2019, 59, 1005–1016. [Google Scholar] [CrossRef]
- Jain, N.; Yalkowsky, S.H. Estimation of the aqueous solubility I: Application to organic nonelectrolytes. J. Pharm. Sci. 2001, 90, 234–252. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv 2015, arXiv:1502.01852. [Google Scholar]
- Ramsundar, B.; Eastman, P.; Walters, P.; Pande, V.; Leswing, K.; Wu, Z. Deep Learning for the Life Sciences; O’Reilly Media Inc: Sebastopol, CA, USA, 2019. [Google Scholar]



| Endpoint | Code | # Compounds | Data Transformation | Helper Task |
|---|---|---|---|---|
| LogD (pH7.5) | LOD | 76,548 | none | no |
| LogD (pH2.3) | LOA | 236,280 | none | no |
| Membrane affinity | LOM | 64,506 | log10 | no |
| Human serum albumin binding | LOH | 61,398 | log10 | no |
| Melting point | LMP | 90,589 | none | no |
| Solubility (DMSO) | LOO | 38,841 | log10(mol/L) | no |
| Solubility (powder) | LOP | 2334 | log10(mol/L) | no |
| Solubility (nephelometry) | LON | 88,301 | log10(mol/L) | yes |
| Solubility (DMSO not fully dissolved) | LOX | 7392 | log10(mol/L) | yes |
| Solubility (no assay annotation) | LOQ | 50,016 | log10(mol/L) | yes |
| Random Forest | STNN a | STNN Graph Conv b | MTNN c | MTNN Graph Conv d | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | Spearman | R2 | Spearman | R2 | Spearman | R2 | Spearman | R2 | Spearman | |
| LOD e | 0.63 | 0.81 | 0.78 | 0.89 | 0.87 | 0.94 | 0.75 | 0.88 | 0.88 | 0.94 |
| LOA f | 0.49 | 0.76 | 0.72 | 0.89 | 0.94 | 0.97 | 0.64 | 0.86 | 0.91 | 0.96 |
| LOM g | 0.43 | 0.68 | 0.53 | 0.75 | 0.64 | 0.80 | 0.51 | 0.75 | 0.71 | 0.84 |
| LOH h | 0.39 | 0.65 | 0.49 | 0.73 | 0.56 | 0.76 | 0.49 | 0.73 | 0.65 | 0.82 |
| LMP i | 0.39 | 0.63 | 0.31 | 0.66 | 0.51 | 0.71 | 0.35 | 0.64 | 0.51 | 0.73 |
| LOO j | 0.43 | 0.66 | 0.47 | 0.69 | 0.47 | 0.73 | 0.49 | 0.71 | 0.59 | 0.77 |
| LOP k | 0.09 | 0.49 | 0.03 | 0.48 | −0.17 | 0.59 | 0.32 | 0.64 | 0.56 | 0.76 |
| LON l | 0.50 | 0.69 | 0.53 | 0.74 | 0.59 | 0.75 | 0.54 | 0.73 | 0.68 | 0.83 |
| LOX m | 0.33 | 0.61 | 0.37 | 0.64 | 0.33 | 0.65 | 0.48 | 0.72 | 0.58 | 0.78 |
| LOQ n | 0.46 | 0.70 | 0.51 | 0.74 | 0.58 | 0.77 | 0.53 | 0.75 | 0.69 | 0.85 |
| R2 | Spearman | |
|---|---|---|
| LOD a | 0.87 (−0.01) | 0.94 |
| LOA b | 0.92 (+0.01) | 0.96 |
| LOM c | 0.71 | 0.84 |
| LOH d | 0.65 | 0.83 (+0.01) |
| LMP e | 0.52 (+0.01) | 0.73 |
| LOO f | 0.57 (−0.02) | 0.76 (−0.01) |
| LOP g | 0.56 | 0.74 (−0.02) |
| R2 | Spearman | RMSE | Test Set Size | |
|---|---|---|---|---|
| LOD a | 0.87 | 0.93 | 0.33 | 32,794 |
| LOA b | 0.91 | 0.96 | 0.35 | 46,481 |
| LOM c | 0.69 | 0.86 | 0.49 | 197 |
| LOH d | 0.55 | 0.78 | 0.61 | 614 |
| LMP e | 0.35 | 0.59 | 45 °C | 55 |
| LOO f | 0.48 | 0.74 | 0.90 | 22,803 |
| LOP g | 0.54 | 0.75 | 0.84 | 935 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montanari, F.; Kuhnke, L.; Ter Laak, A.; Clevert, D.-A. Modeling Physico-Chemical ADMET Endpoints with Multitask Graph Convolutional Networks. Molecules 2020, 25, 44. https://doi.org/10.3390/molecules25010044
Montanari F, Kuhnke L, Ter Laak A, Clevert D-A. Modeling Physico-Chemical ADMET Endpoints with Multitask Graph Convolutional Networks. Molecules. 2020; 25(1):44. https://doi.org/10.3390/molecules25010044
Chicago/Turabian StyleMontanari, Floriane, Lara Kuhnke, Antonius Ter Laak, and Djork-Arné Clevert. 2020. "Modeling Physico-Chemical ADMET Endpoints with Multitask Graph Convolutional Networks" Molecules 25, no. 1: 44. https://doi.org/10.3390/molecules25010044
APA StyleMontanari, F., Kuhnke, L., Ter Laak, A., & Clevert, D.-A. (2020). Modeling Physico-Chemical ADMET Endpoints with Multitask Graph Convolutional Networks. Molecules, 25(1), 44. https://doi.org/10.3390/molecules25010044