Small Molecules, Non-Covalent Interactions, and Confinement
Abstract
:1. Introduction
2. Porous Host Materials
2.1. Microporous Materials as Hosts
2.2. Mesoporous Silica Materials as Hosts
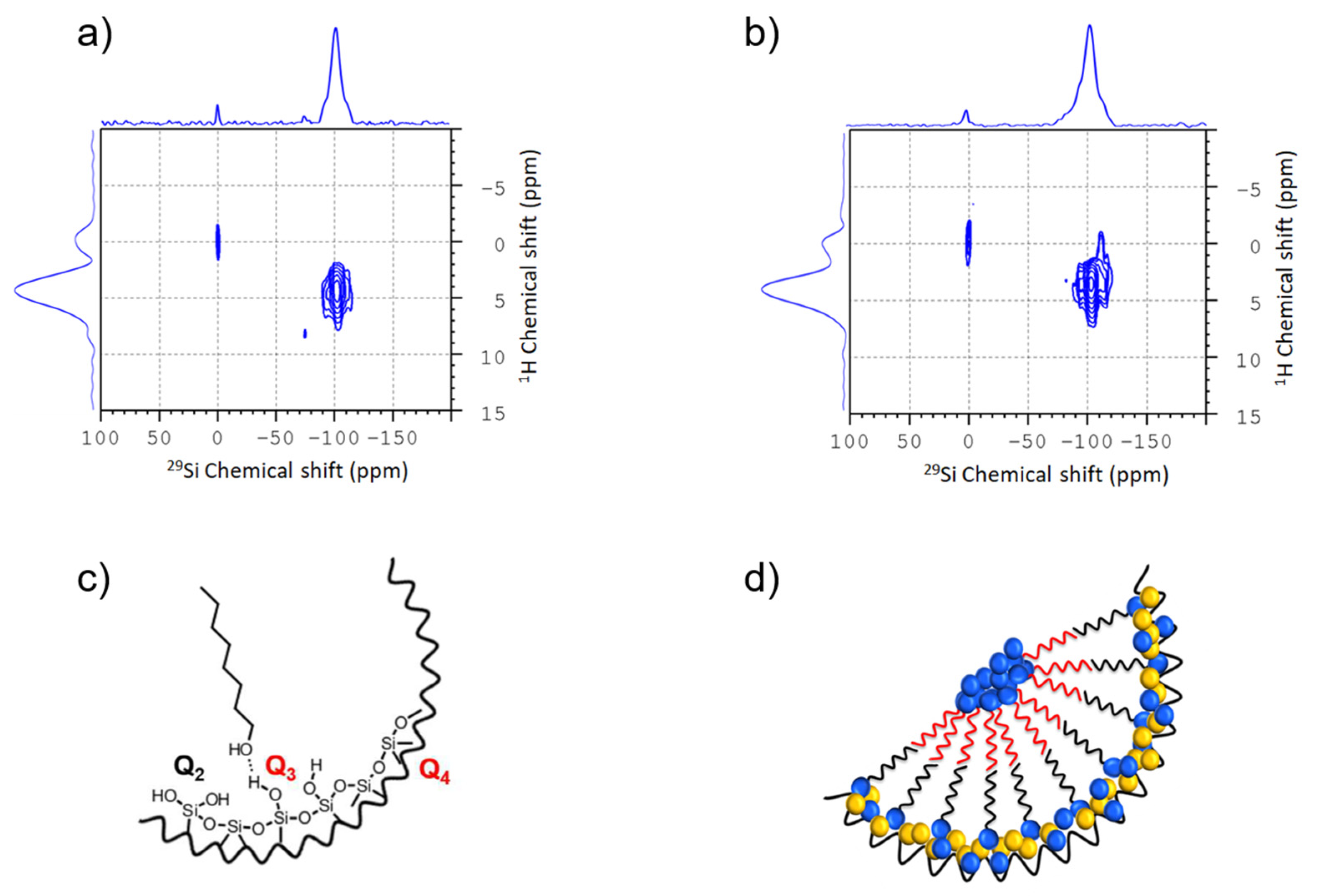
2.3. Preparation and Chemical Functionalization of Mesoporous Silica; NMR Characterization
3. Simple Liquids in Confinement
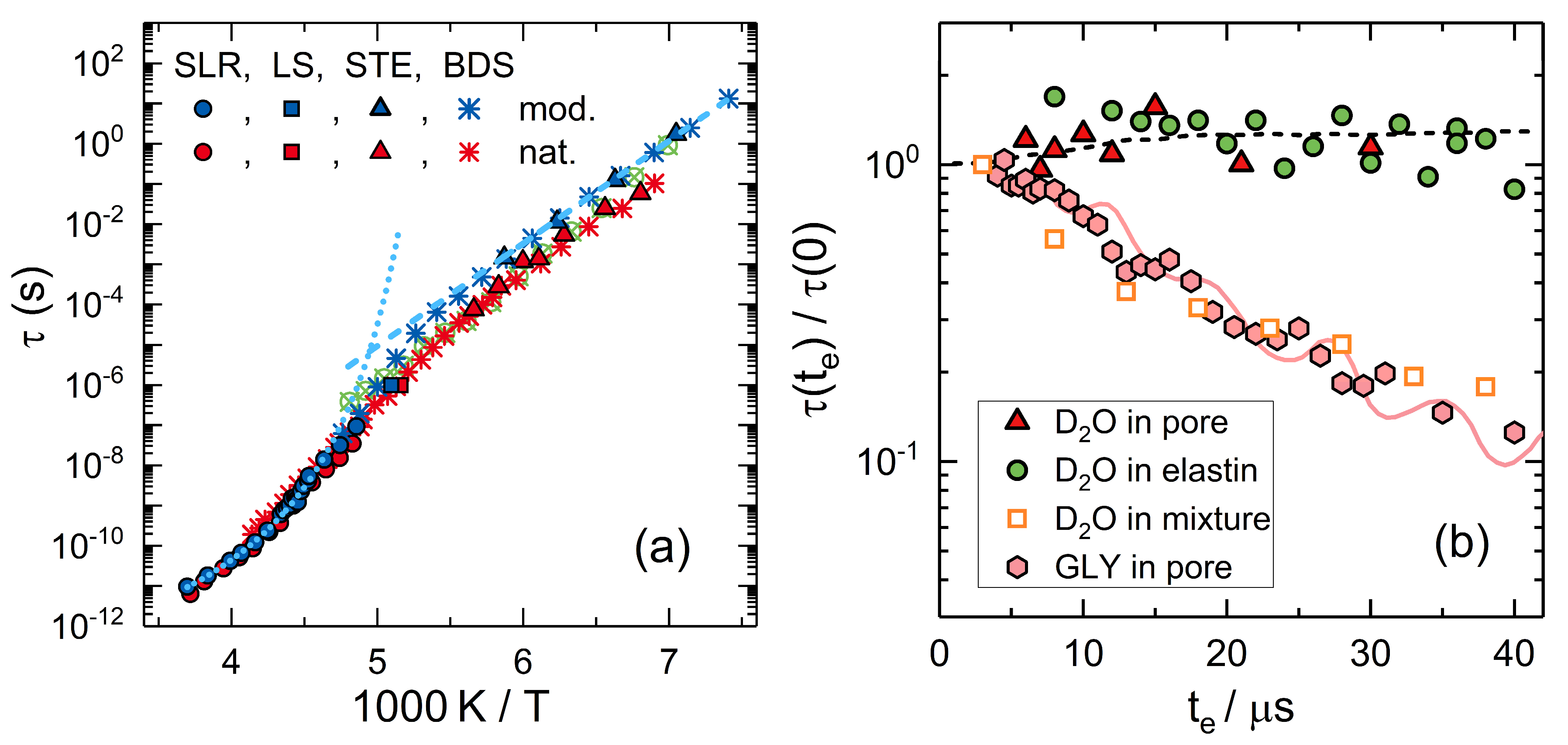
3.1. Water inside Mesoporous Silica
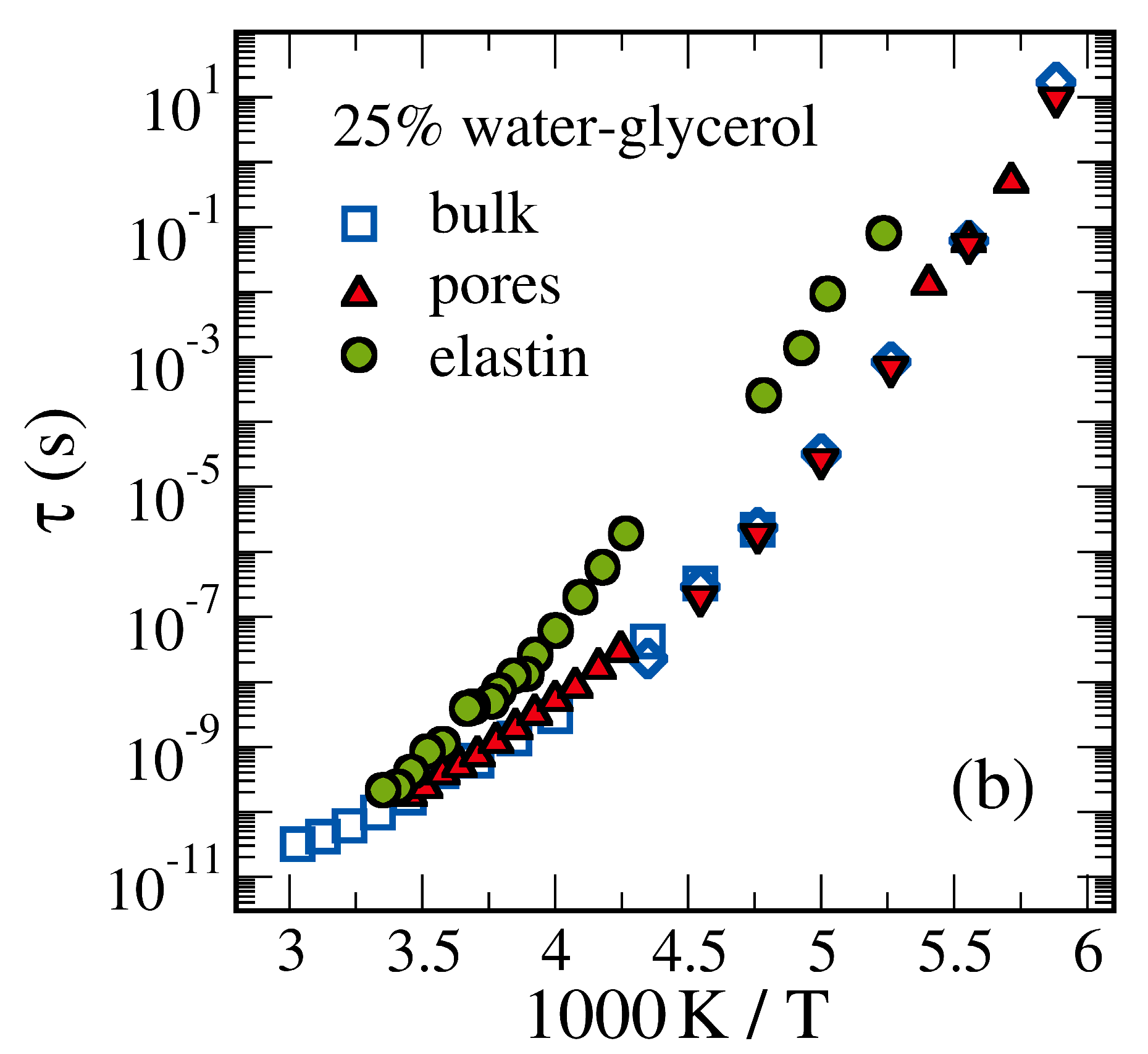
3.2. Glycerol inside Mesoporous Silica
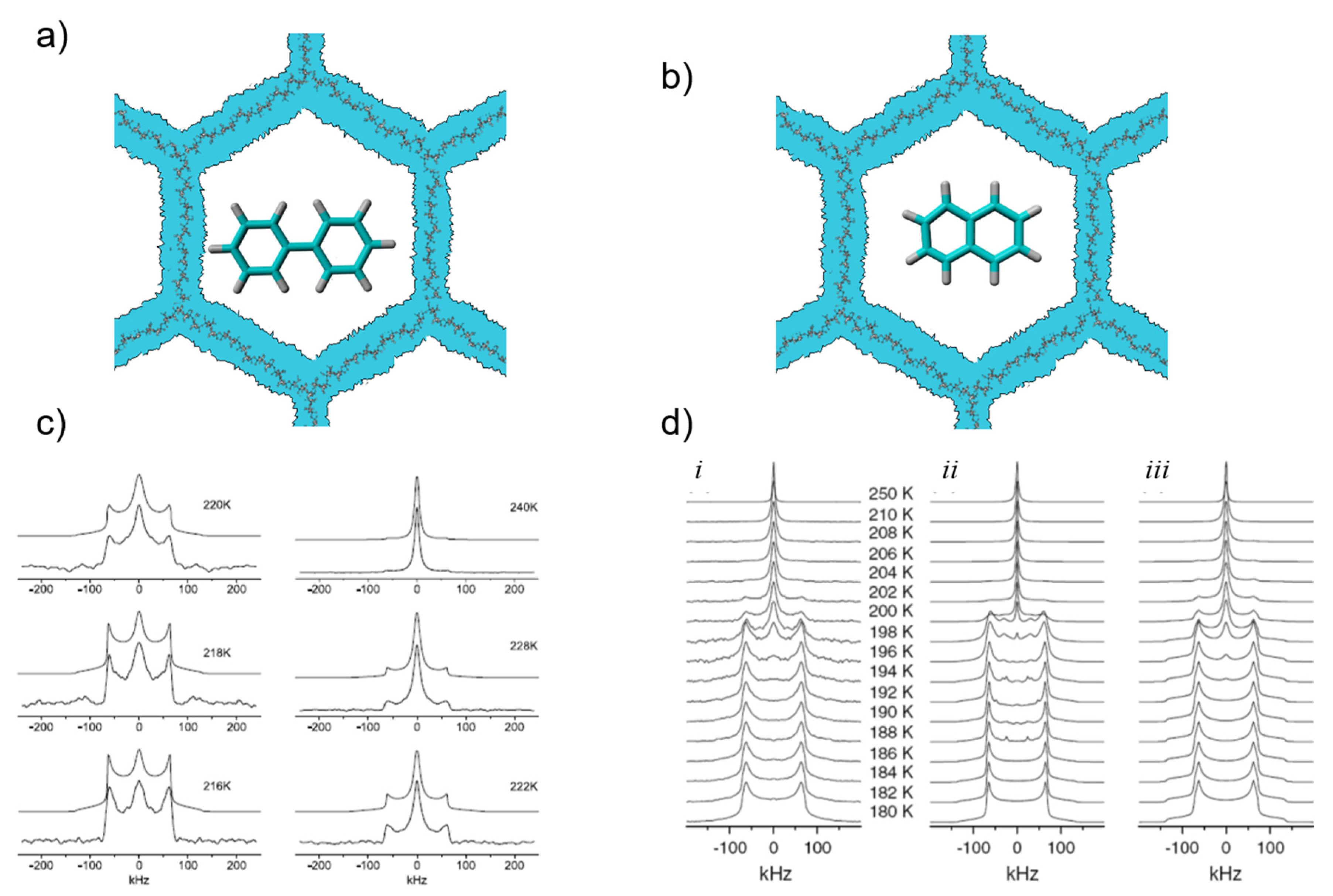
3.3. Benzene, Biphenyl, and Naphthalene inside Mesoporous Silica
3.4. Pyridine inside Mesoporous Silica
4. Complex Liquids in Confinement
4.1. Confined Water-Octanol Mixtures
4.2. Water-Isobutyric Acid (IBA) Mixtures in Experiment and Simulation
4.3. Confined Water-Glycol Mixtures
4.4. Glass Transition of Confined Water-Alcohol Mixtures
4.5. Ionic Liquids and Surfactants in Confinement as Nonconventional Solvents
5. Summary and Outlook
Funding
Conflicts of Interest
References
- Le Page, M.; Beau, R.; Duchene, J. Porous Silica Particles Containing a Crystallized Phase and Method. U.S. Patent Application No. 3,493,341, 3 February 1970. [Google Scholar]
- Chiola, V.; Ritsko, J.E.; Vanderpool, C.D. Process for Producing Low-Bulk Density Silica. U.S. Patent Application No. 3,556,725, 19 January 1971. [Google Scholar]
- Beck, J.; Vartuli, J.; Roth, W.; Leonowicz, M.; Kresge, C.; Schmitt, K.; Chu, C.; Olson, D.; Sheppard, E. A new family of mesoporous molecular sieves prepared with liquid crystal templates. J. Am. Chem. Soc. 1992, 114, 10834–10843. [Google Scholar] [CrossRef]
- Zhao, D.Y.; Huo, Q.S.; Feng, J.L.; Chmelka, B.F.; Stucky, G.D. Nonionic triblock and star diblock copolymer and oligomeric surfactant syntheses of highly ordered, hydrothermally stable, mesoporous silica structures. J. Am. Chem. Soc. 1998, 120, 6024–6036. [Google Scholar] [CrossRef]
- Zhao, D.Y.; Feng, J.L.; Huo, Q.S.; Melosh, N.; Fredrickson, G.H.; Chmelka, B.F.; Stucky, G.D. Triblock copolymer syntheses of mesoporous silica with periodic 50 to 300 angstrom pores. Science 1998, 279, 548–552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sayari, A.; Hamoudi, S. Periodic mesoporous silica-based organic-inorganic nanocomposite materials. Chem. Mater. 2001, 13, 3151–3168. [Google Scholar] [CrossRef]
- Linssen, T.; Cassiers, K.; Cool, P.; Vansant, E. Mesoporous templated silicates: An overview of their synthesis, catalytic activation and evaluation of the stability. Adv. Colloid Interface Sci. 2003, 103, 121–147. [Google Scholar] [CrossRef]
- Selvam, P.; Bhatia, S.K.; Sonwane, C.G. Recent advances in processing and characterization of periodic mesoporous MCM-41 silicate molecular sieves. Ind. Eng. Chem. Res. 2001, 40, 3237–3261. [Google Scholar] [CrossRef]
- Schreiber, A.; Ketelsen, I.; Findenegg, G.H. Melting and freezing of water in ordered mesoporous silica materials. Phys. Chem. Chem. Phys. 2001, 3, 1185–1195. [Google Scholar] [CrossRef]
- Schüth, F.; Schmidt, W. Microporous and mesoporous materials. Adv. Mater. 2002, 14, 629–638. [Google Scholar] [CrossRef]
- Vinu, A.; Hossain, K.Z.; Ariga, K. Recent advances in functionalization of mesoporous silica. J. Nanosci. Nanotechno. 2005, 5, 347–371. [Google Scholar] [CrossRef]
- Wang, X.; Lin, K.S.K.; Chan, J.C.C.; Cheng, S. Direct synthesis and catalytic applications of ordered large pore aminopropyl-functionalized SBA-15 mesoporous materials. J. Phys. Chem. B 2005, 109, 1763–1769. [Google Scholar] [CrossRef]
- Vinu, A.; Miyahara, M.; Ariga, K. Assemblies of biomaterials in mesoporous media. J. Nanosci. Nanotechno. 2006, 6, 1510–1532. [Google Scholar] [CrossRef] [PubMed]
- Morey, M.; Davidson, A.; Stucky, G. Silica-based, cubic mesostructures: Synthesis, characterization and relevance for catalysis. J. Porous Mater. 1998, 5, 195–204. [Google Scholar] [CrossRef]
- Chen, H.-T.; Huh, S.; Wiench, J.W.; Pruski, M.; Lin, V.S.-Y. Dialkylaminopyridine-functionalized mesoporous silica nanosphere as an efficient and highly stable heterogeneous nucleophilic catalyst. J. Am. Chem. Soc. 2005, 127, 13305–13311. [Google Scholar] [CrossRef] [PubMed]
- Ghiaci, M.; Dokhaie, Z.; Farrokhpour, H.; Buntkowsky, G.; Breitzke, H. SBA-15 supported imidazolium ionic liquid through different linkers as sustainable catalyst for synthesis of cyclic carbonates: A kinetic study and Theoretical DFT calculations. Ind. Eng. Chem. Res. 2020, 59, 12632–12644. [Google Scholar]
- Grünberg, A.; Breitzke, H.; Buntkowsky, G. Solid state NMR of immobilized catalysts and nanocatalysts. Spectrosc. Prop. Inorg. Organomet. Compd. 2012, 43, 289–323. [Google Scholar]
- Mellaerts, R.; Jammaer, J.A.G.; Van Speybroeck, M.; Chen, H.; Van Humbeeck, J.; Augustijns, P.; Van den Mooter, G.; Martens, J.A. Physical state of poorly water soluble therapeutic molecules loaded into SBA-15 ordered mesoporous silica carriers: A case study with itraconazole and ibuprofen. Langmuir 2008, 24, 8651–8659. [Google Scholar] [CrossRef]
- Ukmar, T.; Cendak, T.; Mazaj, M.; Kaucic, V.; Mali, G. Structural and dynamical properties of indomethacin molecules embedded within the mesopores of SBA-15: A solid-state NMR view. J. Phys. Chem. C 2012, 116, 2662–2671. [Google Scholar] [CrossRef]
- Vallet-Regi, M.; Ramila, A.; Del Real, R.; Pérez-Pariente, J. A new property of MCM-41: Drug delivery system. Chem. Mater. 2001, 13, 308–311. [Google Scholar] [CrossRef]
- Hall, S.R.; Walsh, D.; Green, D.; Oreffo, R.; Mann, S. A novel route to highly porous bioactive silica gels. J. Mater. Chem. 2003, 13, 186–190. [Google Scholar] [CrossRef]
- de Oliveira, M.; Seeburg, D.; Weiß, J.; Wohlrab, S.; Buntkowsky, G.; Bentrup, U.; Gutmann, T. Structural characterization of vanadium environments in MCM-41 molecular sieve catalysts by solid state 51V NMR. Catal. Sci. Tech. 2019, 9, 6180–6190. [Google Scholar] [CrossRef]
- Gedat, E.; Schreiber, A.; Albrecht, J.; Shenderovich, I.; Findenegg, G.; Limbach, H.-H.; Buntkowsky, G. 2H- solid state NMR study of benzene-d6 confined in mesoporous silica SBA-15. J. Phys. Chem. B 2002, 106, 1977. [Google Scholar] [CrossRef]
- Medick, P.; Blochowicz, T.; Vogel, M.; Roessler, E. Comparing the dynamical heterogeneities in binary glass formers and in a glass former embedded in a zeolite - a (2) hnmr study. J. Non Cryst. Solids 2002, 307, 565–572. [Google Scholar] [CrossRef]
- Dosseh, G.; Xia, Y.; Alba-Simionesco, C. Cyclohexane and benzene confined in MCM-41 and SBA-15: Confinement effects on freezing and melting. J. Phys. Chem. 2003, 107, 6445. [Google Scholar] [CrossRef]
- Lusceac, S.A.; Koplin, C.; Medick, P.; Vogel, M.; Brodie-Linder, N.; LeQuellec, C.; Alba-Simionesco, C.; Roessler, E.A. Type a versus type b glass formers: NMR relaxation in bulk and confining geometry. J. Phys. Chem. B 2004, 108, 16601–16605. [Google Scholar] [CrossRef]
- Alba-Simionesco, C.; Coasne, B.; Dosseh, G.; Dudziak, G.; Gubbins, K.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Effects of confinement on freezing and melting. J. Phys. Condens. Matter 2006, 18, R15. [Google Scholar] [CrossRef]
- Kiwilsza, A.; Pajzderska, A.; Gonzalez, M.A.; Mielcarek, J.; Wąsicki, J. Qens and NMR study of water dynamics in SBA-15 with a low water content. J. Phys. Chem. C 2015, 119, 16578–16586. [Google Scholar] [CrossRef]
- Krzyżak, A.T.; Habina, I. Low field 1H NMR characterization of mesoporous silica MCM-41 and SBA-15 filled with different amount of water. Microporous Mesoporous Mater. 2016, 231, 230–239. [Google Scholar] [CrossRef]
- Brilmayer, R.; Kübelbeck, S.; Khalil, A.; Brodrecht, M.; Kunz, U.; Kleebe, H.-J.; Buntkowsky, G.; Baier, G.; Andrieu-Brunsen, A. Influence of nanoconfinement on the pka of polyelectrolyte functionalized silica mesopores. Adv. Mater. Interfaces 2020, 7, 1901914. [Google Scholar] [CrossRef]
- Nordberg, M.E. Properties of some vycor-brand glasses. J. Am. Ceram. Soc. 1944, 27, 299–305. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.E.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Phase separation in confined systems. Rep. Prog. Phys. 1999, 62, 1573–1659. [Google Scholar] [CrossRef] [Green Version]
- Ciesla, U.; Schüth, F. Ordered mesoporous materials. Microporous Mesoporous Mater. 1999, 27, 131. [Google Scholar] [CrossRef]
- Yokoi, T.; Yoshitake, H.; Tatsumi, T. Synthesis of amino-functionalized MCM-41 via direct co-condensation and post-synthesis grafting methods using mono-, di- and tri-amino-organoalkoxysilanes. J. Mater. Chem. 2004, 14, 951–957. [Google Scholar] [CrossRef]
- Hemminger, W.F.; Cammenga, H.K. Methoden der Thermischen Analyse; Springer: Berlin, Germany, 1989. [Google Scholar]
- Grünberg, B.; Emmler, T.; Gedat, E.; Shenderovich, I.; Findenegg, G.H.; Limbach, H.H.; Buntkowsky, G. Hydrogen bonding of water confined in mesoporous silica MCM-41 and SBA-15 studied by h-1 solid-state NMR. Chem. Eur. J. 2004, 10, 5689–5696. [Google Scholar] [CrossRef] [PubMed]
- Masierak, W.; Emmler, T.; Gedat, E.; Schreiber, A.; Findenegg, G.H.; Buntkowsky, G. Microcrystallization of benzene-d6 in mesoporous silica revealed by 2H-solid state NMR. J. Phys. Chem. B 2004, 108, 18890–18896. [Google Scholar] [CrossRef]
- Vyalikh, A.; Emmler, T.; Gedat, E.; Shenderovich, I.; Findenegg, G.H.; Limbach, H.H.; Buntkowsky, G. Evidence of microphase separation in controlled pore glasses. Solid State Nucl. Mag. Res. 2005, 28, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Buntkowsky, G.; Breitzke, H.; Adamczyk, A.; Roelofs, F.; Emmler, T.; Gedat, E.; Grünberg, B.; Xu, Y.; Limbach, H.H.; Shenderovich, I.; et al. Structural and dynamical properties of guest molecules confined in mesoporous silica materials revealed by NMR. Phys. Chem. Chem. Phys. 2007, 9, 4843–4853. [Google Scholar] [PubMed]
- Vyalikh, A.; Emmler, T.; Gruenberg, B.; Xu, Y.; Shenderovich, I.; Findenegg, G.H.; Limbach, H.H.; Buntkowsky, G. Hydrogen bonding of water confined in controlled-pore glass 10–75 studied by h-1-solid state NMR. Z. Phys. Chem. 2007, 221, 155–168. [Google Scholar] [CrossRef]
- Schoen, M.; Klapp, S. Nanoconfined fluids: Soft matter between two and three dimensions. Rev. Comput. Chem. 2007, 24, 1–517. [Google Scholar]
- Vyalikh, A.; Emmler, T.; Shenderovich, I.; Zeng, Y.; Findenegg, G.H.; Buntkowsky, G. H-2-solid state NMR and dsc study of isobutyric acid in mesoporous silica materials. Phys. Chem. Chem. Phys. 2007, 9, 2249–2257. [Google Scholar] [CrossRef]
- Amadeu, N.d.S.; Gruenberg, B.; Frydel, J.; Werner, M.; Limbach, H.-H.; Breitzke, H.; Buntkowsky, G. Melting of low molecular weight compounds in confinement observed by h-2-solid state NMR: Biphenyl, a case study. Z. Phys. Chem. 2012, 226, 1169–1185. [Google Scholar] [CrossRef]
- Kahse, M.; Werner, M.; Zhao, S.; Hartmann, M.; Buntkowsky, G.; Winter, R. Stability, hydration, and thermodynamic properties of rnase a confined in surface-functionalized SBA-15 mesoporous molecular sieves. J. Phys. Chem. C 2014, 118, 21523–21531. [Google Scholar] [CrossRef]
- Sattig, M.; Reutter, S.; Fujara, F.; Werner, M.; Buntkowsky, G.; Vogel, M. NMR studies on the temperature-dependent dynamics of confined water. Phys. Chem. Chem. Phys. 2014, 16, 19229–19240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Werner, M.; Rothermel, N.; Breitzke, H.; Gutmann, T.; Buntkowsky, G. Recent advances in solid state NMR of small molecules in confinement. Isr. J. Chem. 2014, 54, 60–73. [Google Scholar] [CrossRef]
- Werner, M.; Heil, A.; Rothermel, N.; Breitzke, H.; Groszewicz, P.B.; Thankamony, A.S.; Gutmann, T.; Buntkowsky, G. Synthesis and solid state NMR characterization of novel peptide/silica hybrid materials. Solid State Nucl. Mag. Res. 2015, 72, 73–78. [Google Scholar] [CrossRef] [PubMed]
- Treacy, M.M.; Higgins, J.B.; von Ballmoos, R. Collection of Simulated XRD Powder Patterns for Zeolites; Elsevier: London, UK, 1996. [Google Scholar]
- Marler, B.; Oberhagemann, U.; Vortmann, S.; Gies, H. Influence of the sorbate type on the XRD peak intensities of loaded MCM-41. Microporous Mater. 1996, 6, 375–383. [Google Scholar] [CrossRef]
- Yao, M.; Baird, R.; Kunz, F.; Hoost, T. An XRD and tem investigation of the structure of alumina-supported ceria–zirconia. J. Catal. 1997, 166, 67–74. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The determination of pore volume and area distributions in porous substances. I. Computations from nitrogen isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar]
- Höhne, G.; Hemminger, W.F.; Flammersheim, H.-J. Differential Scanning Calorimetry; Springer: Berlin, Germany, 2013. [Google Scholar]
- Freude, D.; Kärger, J. NMR techniques. Handbook Porous Solids 2002, 1, 465–504. [Google Scholar]
- Koller, H.; Weiß, M. Solid state NMR of porous materials. In Solid State NMR; Springer: Berlin, Germany, 2011; pp. 189–227. [Google Scholar]
- Haouas, M.; Martineau, C.; Taulelle, F. Quadrupolar NMR of Nanoporous Materials; Emagres: Orense, Spain, 2007. [Google Scholar]
- Gutmann, T.; Groszewicz, P.B.; Buntkowsky, G. Solid-State NMR of Nanocrystals. Ann. Rep. NMR Spectrosc. 2019, 97, 1–82. [Google Scholar]
- Faivre, C.; Bellet, D.; Dolino, G. Phase transitions of fluids confined in porous silicon: A differential calorimetry investigation. Eur. Phys. J. B Condens. Matter Complex Syst. 1999, 7, 19–36. [Google Scholar] [CrossRef]
- Alcoutlabi, M.; McKenna, G.B. Effects of confinement on material behaviour at the nanometre size scale. J. Phys. Condens. Matter 2005, 17, R461. [Google Scholar] [CrossRef]
- Kaerger, J.; Pfeifer; Heink, W. Principles and application of self-diffusion measurements by nuclear magnetic resonance. Adv. Magn. Opt. Res. 1988, 12, 1–89. [Google Scholar]
- Kaerger, J.; Freude, D. In situ studies of catalytic reactions in zeolites by means of PFG and MAS NMR techniques. Prog. Zeolite Microporous Mater. Pts a-C 1997, 105, 551–558. [Google Scholar]
- Kaerger, J.; Freude, D. Mass transfer in micro- and mesoporous materials. Chem. Eng. Technol. 2002, 25, 769–778. [Google Scholar]
- Kärger, J.; Freude, D.; Haase, J. Diffusion in nanoporous materials: Novel insights by combining MAS and PFG NMR. Processes 2018, 6, 147. [Google Scholar] [CrossRef] [Green Version]
- Kaerger, J.; Valiullin, R. Mass transfer in mesoporous materials: The benefit of microscopic diffusion measurement. Chem. Soc. Rev. 2013, 42, 4172–4197. [Google Scholar] [CrossRef]
- Findenegg, G.H.; Jaehnert, S.; Akcakayiran, D.; Schreiber, A. Freezing and melting of water confined in silica nanopores. ChemPhysChem 2008, 9, 2651–2659. [Google Scholar] [CrossRef]
- Geppi, M.; Borsacchi, S.; Mollica, G.; Veracini, C.A. Applications of solid-state NMR to the study of organic/inorganic multicomponent materials. Appl. Spectr. Rev. 2009, 44, 1–89. [Google Scholar] [CrossRef]
- Vogel, M. NMR studies on simple liquids in confinement. Eur. Phys. J. 2010, 189, 47–64. [Google Scholar] [CrossRef]
- Ishii, Y.; Tycko, R. Sensitivity enhancement in solid state 15N NMR by indirect detection with high-speed magic angle spinning. J. Magn. Reson. 2000, 142, 199–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, K.; Wiench, J.W.; Lin, V.S.Y.; Pruski, M. Indirectly detected through-bond chemical shift correlation NMR spectroscopy in solids under fast MAS: Studies of organic-inorganic hybrid materials. J. Magn. Reson. 2009, 196, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Mao, K.; Pruski, M. Directly and indirectly detected through-bond heteronuclear correlation solid-state NMR spectroscopy under fast MAS. J. Magn. Reson. 2009, 201, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.; Mao, K.; Wang, S.G.; Lin, V.S.Y.; Pruski, M. Molecular ordering of mixed surfactants in mesoporous silicas: A solid-state NMR study. Solid State Nucl. Mag. Res. 2011, 39, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Hsin, T.M.; Chen, S.; Guo, E.; Tsai, C.H.; Pruski, M.; Lin, V.S.Y. Calcium containing silicate mixed oxide-based heterogeneous catalysts for biodiesel production. Top. Catal. 2010, 53, 746–754. [Google Scholar] [CrossRef]
- Maly, T.; Debelouchina, G.T.; Bajaj, V.S.; Hu, K.; Joo, C.; Mak-Jurkauskas, M.L.; Sirigiri, J.R.; Wel, P.C.A.v.d.; Herzfeld, J.; Temkin, R.J.; et al. Dynamic nuclear polarization at high magnetic fields. J. Chem. Phys. 2008, 128, 052211. [Google Scholar] [CrossRef] [Green Version]
- Hovav, Y.; Feintuch, A.; Vega, S. Theoretical aspects of dynamic nuclear polarization in the solid state - spin temperature and thermal mixing. Phys. Chem. Chem. Phys. 2013, 15, 188–203. [Google Scholar] [CrossRef]
- Mentink-Vigier, F.; Akbey, U.; Hovav, Y.; Vega, S.; Oschkinat, H.; Feintuch, A. Fast passage dynamic nuclear polarization on rotating solids. J. Magn. Reson. 2012, 224, 13–21. [Google Scholar] [CrossRef]
- Hovav, Y.; Feintuch, A.; Vega, S. Theoretical aspects of dynamic nuclear polarization in the solid state - the cross effect. J. Magn. Reson. 2012, 214, 29–41. [Google Scholar] [CrossRef]
- Overhauser, A.W. Polarization of nuclei in metals. Phys. Rev. 1953, 92, 411–415. [Google Scholar] [CrossRef]
- Carver, T.P.; Slichter, C.P. Polarization of nuclear spins in metals. Phys.Rev. 1953, 92, 212–213. [Google Scholar] [CrossRef]
- Carver, T.P.; Slichter, C.P. Experimental verification of the overhauser nuclear polarization effect. Phys.Rev. 1956, 102, 975–980. [Google Scholar] [CrossRef]
- Wind, R.A.; Duijvestijn, M.J.; Vanderlugt, C.; Manenschijn, A.; Vriend, J. Applications of dynamic nuclear-polarization in c-13 NMR in solids. Prog. Nucl. Magn. Reson. Spectrosc. 1985, 17, 33–67. [Google Scholar] [CrossRef]
- Becerra, L.R.; Gerfen, G.J.; Temkin, R.J.; Singel, D.J.; Griffin, R.G. Dynamic nuclear polarization with a cyclotron resonance maser at 5 T. Phys. Rev. Lett. 1993, 71, 3561. [Google Scholar] [CrossRef] [PubMed]
- Thankamony, A.S.; Knoche, S.; Drochner, A.; Pandurang, J.A.; Sigurdsson, S.T.; Vogel, H.; Etzold, B.J.M.; Gutmann, T.; Buntkowsky, G. Characterization of V-Mo-W Mixed Oxide Catalyst Surface Species by 51V Solid-State Dynamic Nuclear Polarization NMR. J. Phys. Chem. C 2017, 121, 20857–20864. [Google Scholar] [CrossRef]
- Kiesewetter, M.K.; Michaelis, V.K.; Walish, J.J.; Griffin, R.G.; Swager, T.M. High field dynamic nuclear polarization NMR with surfactant sheltered biradicals. J. Phys. Chem. B 2014, 118, 1825–1830. [Google Scholar] [CrossRef]
- Thankamony, A.S.L.; Wittmann, J.J.; Kaushik, M.; Corzilius, B. Dynamic nuclear polarization for sensitivity enhancement in modern solid-state NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 102, 120–195. [Google Scholar] [CrossRef]
- Lesage, A.; Lelli, M.; Gajan, D.; Caporini, M.A.; Vitzthum, V.; Mieville, P.; Alauzun, J.; Roussey, A.; Thieuleux, C.; Mehdi, A.; et al. Surface enhanced NMR spectroscopy by dynamic nuclear polarization. J. Am. Chem. Soc. 2010, 132, 15459–15461. [Google Scholar] [CrossRef] [Green Version]
- Gajan, D.; Levine, D.; Zocher, E.; Coperet, C.; Lesage, A.; Emsley, L. Probing surface site heterogeneity through 1d and inadequate p-31 solid state NMR spectroscopy of silica supported pme3-au(i) adducts. Chem. Sci. 2011, 2, 928–931. [Google Scholar] [CrossRef]
- Lelli, M.; Gajan, D.; Lesage, A.; Caporini, M.A.; Vitzthum, V.; Mieville, P.; Heroguel, F.; Rascon, F.; Roussey, A.; Thieuleux, C.; et al. Fast characterization of functionalized silica materials by silicon-29 surface-enhanced NMR spectroscopy using dynamic nuclear polarization. J. Am. Chem. Soc. 2011, 86–121. [Google Scholar] [CrossRef] [Green Version]
- Conley, M.P.; Drost, R.M.; Baffert, M.; Gajan, D.; Elsevier, C.; Franks, W.T.; Oschkinat, H.; Veyre, L.; Zagdoun, A.; Rossini, A.; et al. A well-defined pd hybrid material for the z-selective semihydrogenation of alkynes characterized at the molecular level by DNP sens. Chem. Eur. J. 2013, 19, 12234–12238. [Google Scholar] [CrossRef] [PubMed]
- Conley, M.P.; Rossini, A.J.; Comas-Vives, A.; Valla, M.; Casano, G.; Ouari, O.; Tordo, P.; Lesage, A.; Emsley, L.; Coperet, C. Silica-surface reorganization during organotin grafting evidenced by sn-119 DNP sens: A tandem reaction of gem-silanols and strained siloxane bridges. Phys. Chem. Chem. Phys. 2014, 16, 17822–17827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valla, M.; Rossini, A.J.; Caillot, M.; Chizallet, C.; Raybaud, P.; Digne, M.; Chaumonnot, A.; Lesage, A.; Emsley, L.; van Bokhoven, J.A.; et al. Atomic description of the interface between silica and alumina in aluminosilicates through dynamic nuclear polarization surface-enhanced NMR spectroscopy and first-principles calculations. J. Am. Chem. Soc. 2015, 137, 10710–10719. [Google Scholar] [CrossRef]
- Ong, T.C.; Liao, W.C.; Mougel, V.; Gajan, D.; Lesage, A.; Emsley, L.; Coperet, C. Atomistic description of reaction intermediates for supported metathesis catalysts enabled by DNP sens. Angew. Chem. Int. Ed. 2016, 55, 4743–4747. [Google Scholar] [CrossRef] [PubMed]
- Delley, M.F.; Lapadula, G.; Nunez-Zarur, F.; Comas-Vives, A.; Kalendra, V.; Jeschke, G.; Baabe, D.; Walter, M.D.; Rossini, A.J.; Lesage, A.; et al. Local structures and heterogeneity of silica-supported m(iii) sites evidenced by epr, ir, NMR, and luminescence spectroscopies. J. Am. Chem. Soc. 2017, 139, 8855–8867. [Google Scholar] [CrossRef]
- Liao, W.C.; Ong, T.C.; Gajan, D.; Bernada, F.; Sauvee, C.; Yulikov, M.; Pucino, M.; Schowner, R.; Schwarzwalder, M.; Buchmeiser, M.R.; et al. Dendritic polarizing agents for DNP sens. Chem. Sci. 2017, 8, 416–422. [Google Scholar] [CrossRef] [Green Version]
- Pump, E.; Bendjeriou-Sedjerari, A.; Viger-Gravel, J.; Gajan, D.; Scotto, B.; Samantaray, M.K.; Abou-Hamad, E.; Gurinov, A.; Almaksoud, W.; Cao, Z.; et al. Predicting the DNP-sens efficiency in reactive heterogeneous catalysts from hydrophilicity. Chem. Sci. 2018, 9, 4866–4872. [Google Scholar] [CrossRef] [Green Version]
- Azais, T.; Von Euw, S.; Ajili, W.; Auzoux-Bordenave, S.; Bertani, P.; Gajan, D.; Emsley, L.; Nassif, N.; Lesage, A. Structural description of surfaces and interfaces in biominerals by DNP sens. Solid State Nucl. Mag. Res. 2019, 102, 2–11. [Google Scholar] [CrossRef] [Green Version]
- Eisenschmidt, T.C.; Kirss, R.U.; Deutsch, P.P.; Hommeltoft, S.I.; Eisenberg, R.; Bargon, J. Para hydrogen induced polarization in hydrogenation reactions. J. Am. Chem. Soc. 1987, 109, 8089–8091. [Google Scholar] [CrossRef]
- Bowers, C.R.; Weitekamp, D.P. Transformation of symmetrization order to nuclear-spin magnetization by chemical reaction and nuclear magnetic resonance. Phys. Rev. Lett. 1986, 57, 2645–2648. [Google Scholar] [CrossRef] [Green Version]
- Bowers, C.R.; Jones, D.H.; Kurur, N.D.; Labinger, J.A.; Pravica, M.G.; Weitekamp, D.P. Pasadena and altadena. Adv. Magn. Res. 1990, 15, 269. [Google Scholar]
- Henning, H.; Dyballa, M.; Scheibe, M.; Klemm, E.; Hunger, M. In situ cf MAS NMR study of the pairwise incorporation of parahydrogen into olefins on rhodium-containing zeolites y. Chem. Phys. Lett. 2013, 555, 258–262. [Google Scholar] [CrossRef]
- Hunger, M. In situ NMR spectroscopy in heterogeneous catalysis. Catal. Today 2004, 97, 3–12. [Google Scholar] [CrossRef]
- Arzumanov, S.S.; Stepanov, A.G. Parahydrogen-induced polarization detected with continuous flow MAS NMR. J. Phys. Chem. C 2013, 117, 2888–2892. [Google Scholar] [CrossRef]
- Heinze, M.T.; Zill, J.C.; Matysik, J.; Einicke, W.D.; Gläser, R.; Stark, A. Solid–ionic liquid interfaces: Pore filling revisited. Phys. Chem. Chem. Phys. 2014, 16, 24359–24372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fraissard, J.; Jameson, C.; Saam, B.; Brunner, E.; Hersman, W.; Goodson, B.; Meersmann, T.; Fujiwara, H.; Wang, L.-Q.; Sozzani, P. Hyperpolarized Xenon-129 Magnetic Resonance: Concepts, Production, Techniques and Applications; Royal Society of Chemistry: London, UK, 2015. [Google Scholar]
- Yang, Y.; Beele, B.; Bluemel, J. Easily immobilized di- and tetraphosphine linkers: Rigid scaffolds that prevent interactions of metal complexes with oxide supports. J. Am. Chem. Soc. 2008, 130, 3771–3773. [Google Scholar] [CrossRef]
- Bluemel, J. Linkers and catalysts immobilized on oxide supports: New insights by solid-state NMR spectroscopy. Coord. Chem. Rev. 2008, 252, 2410–2423. [Google Scholar] [CrossRef]
- Gutmann, T.; Grünberg, A.; Rothermel, N.; Werner, M.; Srour, M.; Abdulhussain, S.; Tan, S.; Xu, Y.; Breitzke, H.; Buntkowsky, G. Solid-state NMR concepts for the investigation of supported transition metal catalysts and nanoparticles. Solid State Nucl. Mag. Res. 2013, 55, 1–11. [Google Scholar] [CrossRef]
- Motokura, K.; Itagaki, S.; Iwasawa, Y.; Miyaji, A.; Baba, T. Silica-supported aminopyridinium halides for catalytic transformations of epoxides to cyclic carbonates under atmospheric pressure of carbon dioxide. Green Chem. 2009, 11, 1876–1880. [Google Scholar] [CrossRef]
- Gath, J.; Hoaston, G.L.; Vold, R.L.; Berthoud, R.; Coperet, C.; Grellier, M.; Sabo-Etienne, S.; Lesage, A.; Emsley, L. Motional heterogeneity in single-site silica-supported species revealed by deuteron NMR. Phys. Chem. Chem. Phys. 2009, 11, 6962–6971. [Google Scholar] [CrossRef]
- Wang, Q.; Jordan, E.; Shantz, D.F. H-2 NMR studies of simple organic groups covalently attached to ordered mesoporous silica. J. Phys. Chem. C 2009, 113, 18142–18151. [Google Scholar] [CrossRef]
- Kandel, K.; Althaus, S.M.; Peeraphatdit, C.; Kobayashi, T.; Trewyn, B.G.; Pruski, M.; Slowing, I.I. Substrate inhibition in the heterogeneous catalyzed aldol condensation: A mechanistic study of supported organocatalysts. J. Catal. 2012, 291, 63–68. [Google Scholar] [CrossRef]
- Kandel, K.; Althaus, S.M.; Peeraphatdit, C.; Kobayashi, T.; Trewyn, B.G.; Pruski, M.; Slowing, I.I. Solvent-induced reversal of activities between two closely related heterogeneous catalysts in the aldol reaction. ACS Catal. 2013, 3, 265–271. [Google Scholar] [CrossRef] [Green Version]
- Jayanthi, S.; Frydman, V.; Vega, S. Dynamic deuterium magic angle spinning NMR of a molecule grafted at the inner surface of a mesoporous material. J. Phys. Chem. B 2012, 116, 10398–10405. [Google Scholar] [CrossRef]
- Sundaresan, J.; Werner, M.; Yeping, X.; Buntkowsky, G.; Vega, S. Restricted dynamics of a deuterated linker grafted on SBA-15 revealed by deuterium MAS NMR. J. Phys. Chem. C 2013, 117, 13114–13121. [Google Scholar]
- Jayanthi, S.; Kababya, S.; Schmidt, A.; Vega, S. Deuterium MAS NMR and local molecular dynamic model to study adsorption–desorption kinetics of a dipeptide at the inner surfaces of SBA-15. J. Phys. Chem. C 2016, 120, 2797–2806. [Google Scholar] [CrossRef]
- Keifer, P.A.; Baltusis, L.; Rice, D.M.; Tymiak, A.A.; Shoolery, J.N. A comparison of NMR spectra obtained for solid-phase-synthesis resins using conventional high-resolution, magic-angle-spinning, and high-resolution magic-angle-spinning probes. J. Magn. Reson. Ser. A 1996, 119, 65–75. [Google Scholar] [CrossRef]
- Bluemel, J. Reactions of ethoxysilanes with silica: A solid-state NMR study. J. Am. Chem. Soc. 1995, 117, 2112–2113. [Google Scholar] [CrossRef]
- Merckle, C.; Haubrich, S.; Bluemel, J. Immobilized rhodium hydrogenation catalysts. J. Organomet. Chem. 2001, 627, 44–54. [Google Scholar] [CrossRef]
- Merckle, C.; Bluemel, J. Improved rhodium hydrogenation catalysts immobilized on silica. Top. Catal. 2005, 34, 5–15. [Google Scholar] [CrossRef]
- Brenna, S.; Posset, T.; Furrer, J.; Blümel, J. 14n NMR and two-dimensional suspension 1H and 13C hrmas NMR spectroscopy of ionic liquids immobilized on silica. Chem. A Eur. J. 2006, 12, 2880–2888. [Google Scholar] [CrossRef] [PubMed]
- Beele, B.; Guenther, J.; Perera, M.; Stach, M.; Oeser, T.; Bluemel, J. New linker systems for superior immobilized catalysts. New J. Chem. 2010, 34, 2729–2731. [Google Scholar] [CrossRef]
- Posset, T.; Guenther, J.; Pope, J.; Oeser, T.; Bluemel, J. Immobilized sonogashira catalyst systems: New insights by multinuclear hrmas NMR studies. Chem. Commun. 2011, 47, 2059–2061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cluff, K.J.; Schnellbach, M.; Hilliard, C.R.; Bluemel, J. The adsorption of chromocene and ferrocene on silica: A solid-state NMR study. J. Organomet. Chem. 2013, 744, 119–124. [Google Scholar] [CrossRef]
- Hilliard, C.R.; Kharel, S.; Cluff, K.J.; Bhuvanesh, N.; Gladysz, J.A.; Bluemel, J. Structures and unexpected dynamic properties of phosphine oxides adsorbed on silica surfaces. Chem. A Eur. J. 2014, 20, 17292–17295. [Google Scholar] [CrossRef]
- Kharel, S.; Cluff, K.J.; Bhuvanesh, N.; Gladysz, J.A.; Bluemel, J. Structures and dynamics of secondary and tertiary alkylphosphine oxides adsorbed on silica. Chem. Asian J. 2019, 14, 2704–2711. [Google Scholar] [CrossRef]
- Hubbard, P.J.; Benzie, J.W.; Bakhmutov, V.I.; Blümel, J. Ferrocene adsorbed on silica and activated carbon surfaces: A solid-state NMR study of molecular dynamics and surface interactions. Organometallics 2020, 39, 1080–1091. [Google Scholar] [CrossRef]
- Saint-Arroman, R.P.; Chabanas, M.; Baudouin, A.; Coperet, C.; Basset, J.H.; Lesage, A.; Emsley, L. Characterization of surface organometallic complexes using high resolution 2d solid-state NMR spectroscopy. Application to the full characterization of a silica supported metal carbyne: =sio-mo(=-bu-t(ch2-bu-t)(2). J. Am. Chem. Soc. 2001, 123, 3820–3821. [Google Scholar] [CrossRef]
- Rataboul, F.; Chabanas, M.; de Mallmann, A.; Coperet, C.; Thivolle-Cazat, J.; Basset, J.M. Hydrogenolysis of cycloalkanes on a tantalum hydride complex supported on silica and insight into the deactivation pathway by the combined use of id solid-state NMR and exafs spectroscopies. Chem. Eur. J. 2003, 9, 1426–1434. [Google Scholar] [CrossRef]
- Blanc, F.; Basset, J.M.; Coperet, C.; Sinha, A.; Tonzetich, Z.J.; Schrock, R.R.; Solans-Monfort, X.; Clot, E.; Eisenstein, O.; Lesage, A.; et al. Dynamics of silica-supported catalysts determined by combining solid-state NMR spectroscopy and dft calculations. J. Am. Chem. Soc. 2008, 130, 5886–5900. [Google Scholar] [CrossRef]
- Kerber, R.N.; Kermagoret, A.; Callens, E.; Florian, P.; Massiot, D.; Lesage, A.; Coperet, C.; Delbecq, F.; Rozanska, X.; Sautet, P. Nature and structure of aluminum surface sites grafted on silica from a combination of high-field aluminum-27 solid-state NMR spectroscopy and first-principles calculations. J. Am. Chem. Soc. 2012, 134, 6767–6775. [Google Scholar] [CrossRef] [PubMed]
- Conley, M.; Coperet, C.; Andersen, R. Nature of secondary interactions in molecular and silica-supported organolutetium complexes from solid-state NMR spectroscopy. Abstr. Papers Am. Chem. Soc. 2016, 251, 1155. [Google Scholar]
- Conley, M.P.; Lapadula, G.; Sanders, K.; Gajan, D.; Lesage, A.; del Rosa, I.; Maron, L.; Lukens, W.W.; Coperet, C.; Andersen, R.A. The nature of secondary interactions at electrophilic metal sites of molecular and silica-supported organolutetium complexes from solid-state NMR spectroscopy. J. Am. Chem. Soc. 2016, 138, 3831–3843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Estes, D.P.; Gordon, C.P.; Fedorov, A.; Liao, W.C.; Ehrhorn, H.; Bittner, C.; Zier, M.L.; Bockfeld, D.; Chan, K.W.; Eisenstein, O.; et al. Molecular and silica-supported molybdenum alkyne metathesis catalysts: Influence of electronics and dynamics on activity revealed by kinetics, solid-state NMR, and chemical shift analysis. J. Am. Chem. Soc. 2017, 139, 17597–17607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crisci, A.J.; Tucker, M.H.; Dumesic, J.A.; Scott, S.L. Bifunctional solid catalysts for the selective conversion of fructose to 5-hydroxymethylfurfural. Top. Catal. 2010, 53, 1185–1192. [Google Scholar] [CrossRef] [Green Version]
- Crisci, A.J.; Tucker, M.H.; Lee, M.-Y.; Jang, S.G.; Dumesic, J.A.; Scott, S.L. Acid-functionalized SBA-15-type silica catalysts for carbohydrate dehydration. ACS Catal. 2011, 1, 719–728. [Google Scholar] [CrossRef]
- Alamillo, R.; Crisci, A.J.; Gallo, J.M.R.; Scott, S.L.; Dumesic, J.A. A tailored microenvironment for catalytic biomass conversion in inorganic–organic nanoreactors. Angew. Chem. 2013, 125, 10539–10541. [Google Scholar] [CrossRef]
- Sievers, C.; Noda, Y.; Qi, L.; Albuquerque, E.M.; Rioux, R.M.; Scott, S.L. Phenomena affecting catalytic reactions at solid–liquid interfaces. ACS Catal. 2016, 6, 8286–8307. [Google Scholar] [CrossRef]
- Goldsmith, B.R.; Peters, B.; Johnson, J.K.; Gates, B.C.; Scott, S.L. Beyond ordered materials: Understanding catalytic sites on amorphous solids. ACS Catal. 2017, 7, 7543–7557. [Google Scholar] [CrossRef]
- Moon, H.; Han, S.; Scott, S.L. Tuning molecular adsorption in SBA-15-type periodic mesoporous organosilicas by systematic variation of their surface polarity. Chem. Sci. 2020, 11, 3702–3712. [Google Scholar] [CrossRef]
- Trebosc, J.; Wiench, J.W.; Huh, S.; Lin, V.S.Y.; Pruski, M. Studies of organically functionalized mesoporous silicas using heteronuclear solid-state correlation NMR spectroscopy under fast magic angle spinning. J. Am. Chem. Soc. 2005, 127, 7587–7593. [Google Scholar] [CrossRef] [PubMed]
- Mao, K.; Kobayashi, T.; Wiench, J.W.; Chen, H.T.; Tsai, C.H.; Lin, V.S.Y.; Pruski, M. Conformations of silica-bound (pentafluorophenyl)propyl groups determined by solid-state NMR spectroscopy and theoretical calculations. J. Am. Chem. Soc. 2010, 132, 12452–12457. [Google Scholar] [CrossRef] [PubMed]
- Hara, K.; Akahane, S.; Wiench, J.W.; Burgin, B.R.; Ishito, N.; Lin, V.S.Y.; Fukuoka, A.; Pruski, M. Selective and efficient silylation of mesoporous silica: A quantitative assessment of synthetic strategies by solid-state NMR. J. Phys. Chem. C 2012, 116, 7083–7090. [Google Scholar] [CrossRef]
- Kobayashi, T.; Singappuli-Arachchige, D.; Wang, Z.R.; Slowing, I.I.; Pruski, M. Spatial distribution of organic functional groups supported on mesoporous silica nanoparticles: A study by conventional and DNP-enhanced si-29 solid-state NMR. Phys. Chem. Chem. Phys. 2017, 19, 1781–1789. [Google Scholar] [CrossRef] [PubMed]
- Perras, F.; Kobayashi, T.; Pruski, M. Studies of silica- and alumina-supported catalysts by dynamic nuclear polarization solidstate NMR. Abstr. Papers Am. Chem. Soc. 2017, 253, 1155. [Google Scholar]
- Kobayashi, T.; Singappuli-Arachchige, D.; Slowing, I.I.; Pruski, M. Spatial distribution of organic functional groups supported on mesoporous silica nanoparticles (2): A study by h-1 triple-quantum fast-MAS solid-state NMR. Phys. Chem. Chem. Phys. 2018, 20, 22203–22209. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T.; Pruski, M. Spatial distribution of silica-bound catalytic organic functional groups can now be revealed by conventional and DNP-enhanced solid-state NMR methods. ACS Catal. 2019, 9, 7238–7249. [Google Scholar] [CrossRef] [Green Version]
- Adamczyk, A.; Xu, Y.; Walaszek, B.; Roelofs, F.; Pery, T.; Pelzer, K.; Philippot, K.; Chaudret, B.; Limbach, H.H.; Breitzke, H.; et al. Solid state and gas phase NMR studies of immobilized catalysts and catalytic active nanoparticles. Top. Catal. 2008, 48, 75–83. [Google Scholar] [CrossRef]
- Gutmann, T.; Ratajczyk, T.; Xu, Y.P.; Breitzke, H.; Grunberg, A.; Dillenberger, S.; Bommerich, U.; Trantzschel, T.; Bernarding, J.; Buntkowsky, G. Understanding the leaching properties of heterogenized catalysts: A combined solid-state and phip NMR study. Solid State Nucl. Mag. Res. 2010, 38, 90–96. [Google Scholar] [CrossRef]
- Grunberg, A.; Gutmann, T.; Rothermel, N.; Xu, Y.P.; Breitzke, H.; Buntkowsky, G. Immobilization and characterization of rucl2(pph3)(3) mesoporous silica SBA-3. Z. Phys. Chem. 2013, 227, 901–915. [Google Scholar] [CrossRef]
- Srour, M.; Hadjiali, S.; Sauer, G.; Brunnengräber, K.; Breitzke, H.; Xu, Y.; Weidler, H.; Limbach, H.-H.; Gutmann, T.; Buntkowsky, G. Synthesis and solid-state NMR characterization of a novel, robust, pyridyl-based immobilized Wilkinson’s type catalyst with high catalytic performance. ChemCatChem 2016, 8, 3409–3416. [Google Scholar] [CrossRef]
- Abdulhussain, S.; Breitzke, H.; Ratajczyk, T.; Grunberg, A.; Srour, M.; Arnaut, D.; Weidler, H.; Kunz, U.; Kleebe, H.J.; Bommerich, U.; et al. Synthesis, solid-state NMR characterization, and application for hydrogenation reactions of a novel wilkinson’s-type immobilized catalyst. Chem. Eur. J. 2014, 20, 1159–1166. [Google Scholar] [CrossRef] [PubMed]
- Gutmann, T.; Alkhagani, S.; Rothermel, N.; Limbach, H.H.; Breitzke, H.; Buntkowsky, G. P-31-solid-state NMR characterization and catalytic hydrogenation tests of novel heterogenized iridium-catalysts. Z. Phys. Chem. 2017, 231, 653–669. [Google Scholar] [CrossRef]
- Liu, J.Q.; Groszewicz, P.B.; Wen, Q.B.; Thankamony, A.S.L.; Zhang, B.; Kunz, U.; Sauer, G.; Xu, Y.P.; Gutmann, T.; Buntkowsky, G. Revealing structure reactivity relationships in heterogenized dirhodium catalysts by solid-state NMR techniques. J. Phys. Chem. C 2017, 121, 17409–17416. [Google Scholar] [CrossRef]
- Folliet, N.; Gervais, C.; Costa, D.; Laurent, G.; Babonneau, F.; Stievano, L.; Lambert, J.-F.; Tielens, F. A molecular picture of the adsorption of glycine in mesoporous silica through NMR experiments combined with dft-d calculations. J. Phys. Chem. C 2013, 117, 4104–4114. [Google Scholar] [CrossRef]
- Azaïs, T.; Laurent, G.; Panesar, K.; Nossov, A.; Guenneau, F.; Sanfeliu Cano, C.; Tourné-Péteilh, C.; Devoisselle, J.-M.; Babonneau, F. Implication of water molecules at the silica–ibuprofen interface in silica-based drug delivery systems obtained through incipient wetness impregnation. J. Phys. Chem. C 2017, 121, 26833–26839. [Google Scholar] [CrossRef]
- Tielens, F.; Folliet, N.; Bondaz, L.; Etemovic, S.; Babonneau, F.; Gervais, C.; Azaïs, T. Molecular picture of the adsorption of ibuprofen and benzoic acid on hydrated amorphous silica through dft-d calculations combined with solid-state NMR experiments. J. Phys. Chem. C 2017, 121, 17339–17347. [Google Scholar] [CrossRef] [Green Version]
- Klimavicius, V.; Dagys, L.; Chizhik, V.; Balevicius, V. Cp MAS kinetics study of ionic liquids confined in mesoporous silica: Convergence of non-classical and classical spin coupling models. Appl. Magn. Res. 2017, 48, 673–685. [Google Scholar] [CrossRef]
- Riedel, E.; Janiak, C. Anorganische Chemie, 7th ed.; Walter De Gruyter: Berlin, Germany, 2007. [Google Scholar]
- Zhang, C.; Lively, R.P.; Zhang, K.; Johnson, J.R.; Karvan, O.; Koros, W.J. Unexpected molecular sieving properties of zeolitic imidazolate framework-8. J. Phys. Chem. Let. 2012, 3, 2130–2134. [Google Scholar] [CrossRef]
- Cejka, J.; Van Bekkum, H.; Corma, A.; Schüth, F. Introduction to Zeolite Science and Practice. In Studies in Surface Science and Catalysis 168; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Shantz, D.F.; Fild, C.; Koller, H.; Lobo, R.F. Guest-host interactions in as-made al-zsm-12: Implications for the synthesis of zeolite catalysts. J. Phy. Chem. B 1999, 103, 10858–10865. [Google Scholar] [CrossRef]
- Shantz, D.F.; Lobo, R.F. Guest-host interactions in zeolites as studied by NMR spectroscopy: Implications in synthesis, catalysis and separations. Top. Catal. 1999, 9, 1–11. [Google Scholar] [CrossRef]
- Wang, B.; Côté, A.P.; Furukawa, H.; O’Keeffe, M.; Yaghi, O.M. Colossal cages in zeolitic imidazolate frameworks as selective carbon dioxide reservoirs. Nature 2008, 453, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Kärger, J.; Pfeifer, H. N.M.R. Self-diffusion studies in zeolite science and technology. Zeolites 1987, 7, 90–107. [Google Scholar] [CrossRef]
- Kärger, J.; Vasenkov, S.; Auerbach, S.M. Diffusion in zeolites. In Handbook of Zeolite Science and Technology; Auerbach, S.M., Carrado, K.A., Eds.; Marcel Dekker: New York, NY, USA, 2003; pp. 458–560. [Google Scholar]
- Nishchenko, A.M.; Kolokolov, D.I.; Gabrienko, A.A.; Stepanov, A.G. Mobility of tert-butyl alcohol in mfi framework type studied by deuterium NMR. J. Phys. Chem. C 2012, 116, 8956–8963. [Google Scholar] [CrossRef]
- Lalowicz, Z.T.; Stoch, G.; Birczynski, A.; Punkkinen, M.; Ylinen, E.E.; Krzystyniak, M.; Gora-Marek, K.; Datka, J. Translational and rotational mobility of methanol-d(4) molecules in nax and nay zeolite cages: A deuteron NMR investigation. Solid State Nucl. Mag. Res. 2012, 45, 66–74. [Google Scholar] [CrossRef]
- Stoch, G.; Ylinen, E.E.; Birczynski, A.; Lalowicz, Z.T.; Gora-Marek, K.; Punkkinen, M. Deuteron spin-lattice relaxation in the presence of an activation energy distribution: Application to methanols in zeolite nax. Solid State Nucl. Mag. Res. 2013, 49, 33–41. [Google Scholar] [CrossRef]
- Arzumanov, S.S.; Kolokolov, D.I.; Freude, D.; Stepanov, A.G. Methane mobility in ag/h-zsm-5 zeolite in the presence of ethene: A view based on PFG 1H MAS NMR analysis of methane diffusivity. J. Phys.Chem. C 2015, 119, 18481–18486. [Google Scholar] [CrossRef]
- Kärger, J.; Caro, J.; Cool, P.; Coppens, M.O.; Jones, D.; Kapteijn, F.; Rodríguez-Reinoso, F.; Stöcker, M.; Theodorou, D.; Vansant, E.F.; et al. Benefit of microscopic diffusion measurement for the characterization of nanoporous materials. Chem. Eng. Technol. 2009, 32, 1494–1511. [Google Scholar] [CrossRef]
- Karger, J. Transport phenomena in nanoporous materials. ChemPhysChem 2015, 16, 24–51. [Google Scholar] [CrossRef]
- Naumov, S.; Valiullin, R.; Kärger, J.; Pitchumani, R.; Coppens, M.-O. Tracing pore connectivity and architecture in nanostructured silica SBA-15. Microporous Mesoporous Mater. 2008, 110, 37–40. [Google Scholar] [CrossRef]
- Gutsze, A.; Masierak, W.; Geil, B.; Kruk, D.; Pahlke, H.; Fujara, F. On the problem of field-gradient NMR measurements of intracrystalline diffusion in small crystallites--water in naa zeolites as an example. Solid State Nucl Magn Reson 2005, 28, 244–249. [Google Scholar] [CrossRef] [PubMed]
- Pahlke, H.; Lusceac, S.A.; Geil, B.; Fujara, F. NMR study of local and long range dynamics of adsorbed water in zeolite nay(br). Z. Phys. Chem. 2012, 226, 1093–1114. [Google Scholar] [CrossRef]
- Krylova, E.A.; Shelyapina, M.G.; Nowak, P.; Harańczyk, H.; Chislov, M.; Zvereva, I.A.; Privalov, A.F.; Becher, M.; Vogel, M.; Petranovskii, V. Mobility of water molecules in sodium- and copper-exchanged mordenites: Thermal analysis and 1 h NMR study. Microporous Mesoporous Mater. 2018, 265, 132–142. [Google Scholar] [CrossRef]
- Brodrecht, M.; Breitzke, H.; Gutmann, T.; Buntkowsky, G. Biofunctionalization of nano channels by direct in-pore solid-phase peptide synthesis. Chem. Eur. J. 2018, 24, 17814–17822. [Google Scholar] [CrossRef]
- Brodrecht, M.; Kumari, B.; Breitzke, H.; Gutmann, T.; Buntkowsky, G. Chemically modified silica materials as model systems for the characterization of water-surface interactions. Z. Phys. Chem. 2018, 232, 1127–1146. [Google Scholar] [CrossRef]
- Brodrecht, M.; Kunnari, B.; Thankamony, A.S.S.L.; Breitzke, H.; Gutmann, T.; Buntkowsky, G. Structural insights into peptides bound to the surface of silica nanopores. Chem. Eur. J. 2019, 25, 5214–5221. [Google Scholar] [CrossRef]
- Schottner, S.; Brodrecht, M.; Uhlein, E.; Dietz, C.; Breitzke, H.; Tietze, A.A.; Buntkowsky, G.; Gallei, M. Amine-containing block copolymers for the bottom-up preparation of functional porous membranes. Macromolecules 2019, 52, 2631–2641. [Google Scholar] [CrossRef]
- Grün, M.; Unger, K.K.; Matsumoto, A.; Tsutsumi, K. Novel pathways for the preparation of mesoporous MCM-41 materials: Control of porosity and morphology. Microporous Mesoporous Mater. 1999, 27, 207–216. [Google Scholar] [CrossRef]
- Buntkowsky, G.; Vogel, M.; Winter, R. Properties of hydrogen-bonded liquids at interfaces. Z. Phys. Chem. 2018, 232, 937–972. [Google Scholar] [CrossRef]
- Weigler, M.; Brodrecht, M.; Breitzke, H.; Dietrich, F.; Sattig, M.; Buntkowsky, G.; Vogel, M. 2H NMR studies on water dynamics in functionalized mesoporous silica. Z. Phys. Chem. 2018, 232, 1041–1058. [Google Scholar] [CrossRef]
- Richert, R. Dynamics of nanoconfined supercooled liquids. Annu. Rev. Phys. Chem. 2011, 62, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Brodrecht, M.; Klotz, E.; Lederle, C.; Breitzke, H.; Stühn, B.; Vogel, M.; Buntkowsky, G. A combined solid-state NMR, dielectric spectroscopy and calorimetric study of water in lowly hydrated MCM-41 samples. Z. Phys. Chem. 2018, 232, 1003–1016. [Google Scholar] [CrossRef]
- Sumper, M.; Brunner, E. Silica biomineralisation in diatoms: The model organism thalassiosira pseudonana. Chembiochem 2008, 9, 1187–1194. [Google Scholar] [CrossRef] [PubMed]
- Poulsen, N.; Sumper, M.; Kröger, N. Biosilica formation in diatoms: Characterization of native silaffin-2 and its role in silica morphogenesis. Proc. Natl. Acad. Sci. USA 2003, 100, 12075–12080. [Google Scholar] [CrossRef] [Green Version]
- Brunner, E.; Groger, C.; Lutz, K.; Richthammer, P.; Spinde, K.; Sumper, M. Analytical studies of silica biomineralization: Towards an understanding of silica processing by diatoms. Appl. Microbiol. Biotechnol. 2009, 84, 607–616. [Google Scholar] [CrossRef]
- Almqvist, N.; Delamo, Y.; Smith, B.L.; Thomson, N.H.; Bartholdson, A.; Lal, R.; Brzezinski, M.; Hansma, P.K. Micromechanical and structural properties of a pennate diatom investigated by atomic force microscopy. J. Microsc. 2001, 202 Pt 3, 518–532. [Google Scholar] [CrossRef]
- Mann, S. Biomineralization: Principles and Concepts in Bioinorganic Materials Chemistry; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Nassif, N.; Livage, J. From diatoms to silica-based biohybrids. Chem. Soc. Rev. 2011, 40, 849–859. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, M.; Kostrov, X. Immobilization of enzymes on porous silicas - benefits and challenges. Chem. Soc. Rev. 2013, 42, 6277–6289. [Google Scholar] [CrossRef]
- Zhou, Z.; Piepenbreier, F.; Marthala, V.R.R.; Karbacher, K.; Hartmann, M. Immobilization of lipase in cage-type mesoporous organosilicas via covalent bonding and crosslinking. Catal. Today 2014, 243, 173–183. [Google Scholar] [CrossRef]
- Matlahov, I.; Geiger, Y.; Goobes, G. Trapping rnase a on MCM41 pores: Effects on structure stability, product inhibition and overall enzymatic activity. Phys. Chem. Chem. Phys. 2014, 16, 9031–9038. [Google Scholar] [CrossRef]
- Duer, M.J. The contribution of solid-state NMR spectroscopy to understanding biomineralization: Atomic and molecular structure of bone. J. Magn. Reson. 2015, 253, 98–110. [Google Scholar] [CrossRef] [PubMed]
- Brodrecht, M.; Herr, K.; Bothe, S.; de Oliveira, M.; Gutmann, T.; Buntkowsky, G. Efficient building blocks for solid-phase peptide synthesis of spin labeled peptides for electron paramagnetic resonance and dynamic nuclear polarization applications. ChemPhysChem 2019, 20, 1475–1487. [Google Scholar] [CrossRef] [PubMed]
- Trautmann, C. Micro-and nanoengineering with ion tracks. In Ion Beams in Nanoscience and Technology; Hellborg, R., Whitlow., H.J., Eds.; Springer: Berlin, Germany, 2009; pp. 369–387. [Google Scholar]
- Kumari, B.; John, D.; Hoffmann, P.; Spende, A.; Toimil-Molares, M.E.; Trautmann, C.; Hess, C.; Ruff, P.; Stark, R.; Schulze, M.; et al. Surface enhanced DNP assisted solid-state NMR of functionalized sio2 coated polycarbonate membranes. Z. Phys. Chem. 2018, 232, 1173–1186. [Google Scholar] [CrossRef]
- Febles, M.; Perez-Hernandez, N.; Perez, C.; Rodriguez, M.L.; Foces-Foces, C.; Roux, M.V.; Morales, E.Q.; Buntkowsky, G.; Limbach, H.-H.; Martin, J.D. Distinct dynamic behaviors of water molecules in hydrated pores. J. Am. Chem. Soc. 2006, 128, 10008–10009. [Google Scholar] [CrossRef] [PubMed]
- Perez-Hernandez, N.; Trung Quan, L.; Febles, M.; Marco, C.; Limbach, H.-H.; Havenith, M.; Perez, C.; Victoria Roux, M.; Perez, R.; Martin, J.D. The mobility of water molecules through hydrated pores. J. Phys. Chem. C 2012, 116, 9616–9630. [Google Scholar] [CrossRef]
- Hassan, J. Analysis of h-2 NMR spectra of water molecules on the surface of nano-silica material MCM-41: Deconvolution of the signal into a lorentzian and a powder pattern line shapes. Phys. B Condens. Matter 2012, 407, 179–183. [Google Scholar] [CrossRef]
- Hassan, J.; Reardon, E.; Peemoeller, H. Correlation between deuterium NMR spectral components and MCM-41 pore surface hydration sites. Microporous Mesoporous Mater. 2009, 122, 121–127. [Google Scholar] [CrossRef]
- Niknam, M.; Liang, J.; Walia, J.; Peemoeller, H. Chemical exchange and spectral coalescence in low-hydration MCM-41 studied by proton NMR. Microporous Mesoporous Mater. 2012, 162, 136–142. [Google Scholar] [CrossRef]
- Weigler, M.; Winter, E.; Kresse, B.; Brodrecht, M.; Buntkowsky, G.; Vogel, M. Static field gradient NMR studies of water diffusion in mesoporous silica. Phys. Chem. Chem. Phys. 2020, 22, 13989–13998. [Google Scholar] [CrossRef]
- Kumari, B.; Brodrecht, M.; Breitzke, H.; Werner, M.; Grunberg, B.; Limbach, H.H.; Forg, S.; Sanjon, E.P.; Drossel, B.; Gutmann, T.; et al. Mixtures of alcohols and water confined in mesoporous silica: A combined solid-state NMR and molecular dynamics simulation study. J. Phys. Chem. C 2018, 122, 19540–19550. [Google Scholar] [CrossRef]
- Kumari, B.; Brodrecht, M.; Gutmann, T.; Breitzke, H.; Buntkowsky, G. Efficient referencing of fslg cpmas hetcor spectra using 2d h-1-h-1 MAS fslg. Appl. Magn. Res. 2019, 50, 1399–1407. [Google Scholar] [CrossRef]
- Edzes, H.T.; Samulski, E.T. Measurement of cross-relaxation effects in proton nmr spin-lattice relaxation of water in biological-systems - hydrated collagen and muscle. J. Magn. Reson. 1978, 31, 207–229. [Google Scholar] [CrossRef]
- Peemoeller, H. NMR spin grouping. Bull. Magn. Reson 1989, 11, 19–30. [Google Scholar]
- Kittaka, S.; Ishimaru, S.; Kuranishi, M.; Matsuda, T.; Yamaguchi, T. Enthalpy and interfacial free energy changes of water capillary condensed in mesoporous silica, MCM-41 and SBA-15. Phys. Chem. Chem. Phys. 2006, 8, 3223–3231. [Google Scholar] [CrossRef]
- Debenedetti, P.G. Supercooled and glassy water. J. Phys. Condens. Matter 2003, 15, 1669–1726. [Google Scholar]
- Mishima, O.; Stanley, H.E. The relationship between liquid, supercooled and glassy water. Nature 1998, 396, 329–335. [Google Scholar] [CrossRef]
- Cerveny, S.; Mallamace, F.; Swenson, J.; Vogel, M.; Xu, L. Confined water as model of supercooled water. Chem. Rev. 2016, 116, 7608–7625. [Google Scholar] [CrossRef]
- Chen, S.H.; Zhang, Y.; Lagi, M.; Chong, S.H.; Baglioni, P.; Mallamace, F. Evidence of dynamic crossover phenomena in water and other glass-forming liquids: Experiments, md simulations and theory. J. Phys. Condens. Matter 2009, 21, 504102. [Google Scholar] [CrossRef]
- Swenson, J.; Cerveny, S. Dynamics of deeply supercooled interfacial water. J. Phys. Condens. Matter 2015, 27, 033102. [Google Scholar] [CrossRef]
- Weigler, M.; Brodrecht, M.; Buntkowsky, G.; Vogel, M. Reorientation of deeply cooled water in mesoporous silica: NMR studies of the pore-size dependence. J. Phys. Chem. B 2019, 123, 2123–2134. [Google Scholar] [CrossRef]
- Sattig, M.; Vogel, M. Dynamic crossovers and stepwise solidification of confined water: A (2)h NMR study. J. Phys. Chem. Lett. 2014, 5, 174–178. [Google Scholar] [CrossRef] [PubMed]
- Lederle, C.; Sattig, M.; Vogel, M. Effects of partial crystallization on the dynamics of water in mesoporous silica. J. Phys. Chem. C 2018, 122, 15427–15434. [Google Scholar] [CrossRef]
- Yao, Y.; Fella, V.; Huang, W.; Zhang, K.A.I.; Landfester, K.; Butt, H.J.; Vogel, M.; Floudas, G. Crystallization and dynamics of water confined in model mesoporous silica particles: Two ice nuclei and two fractions of water. Langmuir 2019, 35, 5890–5901. [Google Scholar] [CrossRef] [PubMed]
- Demuth, D.; Sattig, M.; Steinrücken, E.; Weigler, M.; Vogel, M. 2H NMR studies on the dynamics of pure and mixed hydrogen-bonded liquids in confinement. Z. Phys. Chem. 2018, 232, 1059–1087. [Google Scholar] [CrossRef]
- Miyatou, T.; Ohashi, R.; Ida, T.; Kittaka, S.; Mizuno, M. An NMR study on the mechanisms of freezing and melting of water confined in spherically mesoporous silicas SBA-16. Phys. Chem. Chem. Phys. 2016, 18, 18555–18562. [Google Scholar] [CrossRef] [PubMed]
- Rosenstihl, M.; Kämpf, K.; Klameth, F.; Sattig, M.; Vogel, M. Dynamics of interfacial water. J. Non Cryst. Solids 2015, 407, 449–458. [Google Scholar] [CrossRef]
- Vogel, M. Origins of apparent fragile-to-strong transitions of protein hydration waters. Phys. Rev. Lett. 2008, 101, 225701. [Google Scholar] [CrossRef] [Green Version]
- Lusceac, S.A.; Vogel, M.R.; Herbers, C.R. 2H and 13C NMR studies on the temperature-dependent water and protein dynamics in hydrated elastin, myoglobin and collagen. Biochim. Biophys. Acta 2010, 1804, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Lusceac, S.A.; Rosenstihl, M.; Vogel, M.; Gainaru, C.; Fillmer, A.; Böhmer, R. NMR and dielectric studies of hydrated collagen and elastin: Evidence for a delocalized secondary relaxation. J. Non Cryst. Solids 2011, 357, 655–663. [Google Scholar] [CrossRef] [Green Version]
- Cerveny, S.; Schwartz, G.A.; Bergman, R.; Swenson, J. Glass transition and relaxation processes in supercooled water. Phys. Rev. Lett. 2004, 93, 245702. [Google Scholar] [CrossRef] [Green Version]
- Böhmer, R.; Diezemann, G.; Hinze, G.; Rössler, E. Dynamics of supercooled liquids and glassy solids. Prog. Nucl. Magn. Reson. Spectrosc. 2001, 39, 191–267. [Google Scholar] [CrossRef]
- Fujara, F.; Wefing, S.; Spiess, H.W. Dynamics of molecular reorientations: Analogies between quasielastic neutron scattering and deuteron NMR spin alignment. J. Chem. Phys. 1986, 84, 4579–4584. [Google Scholar] [CrossRef]
- Vogel, M.; Medick, P.; Rössler, E.A. Secondary relaxation processes in molecular glasses studied by nuclear magnetic resonance spectroscopy. Ann. Rep. NMR Spectrosc. 2005, 56, 231–299. [Google Scholar]
- Sjostrom, J.; Swenson, J.; Bergman, R.; Kittaka, S. Investigating hydration dependence of dynamics of confined water: Monolayer, hydration water and maxwell-wagner processes. J. Chem. Phys. 2008, 128, 154503. [Google Scholar] [CrossRef] [Green Version]
- Lusceac, S.A.; Gainaru, C.; Ratzke, D.A.; Graf, M.F.; Vogel, M. Secondary water relaxation in a water/dimethyl sulfoxide mixture revealed by deuteron nuclear magnetic resonance and dielectric spectroscopy. J. Phy. Chem. B 2011, 115, 11588–11596. [Google Scholar] [CrossRef]
- Vogel, M.; Rossler, E. Effects of various types of molecular dynamics on 1d and 2d (2)h NMR studied by random walk simulations. J. Magn. Reson. 2000, 147, 43–58. [Google Scholar] [CrossRef]
- Böhmer, R.; Hinze, G. Reorientations in supercooled glycerol studied by two-dimensional time-domain deuteron nuclear magnetic resonance spectroscopy. J. Chem. Phys. 1998, 109, 241–248. [Google Scholar] [CrossRef]
- Angell, C.A. Insights into phases of liquid water from study of its unusual glass-forming properties. Science 2008, 319, 582–587. [Google Scholar] [CrossRef] [Green Version]
- Amann-Winkel, K.; Böhmer, R.; Fujara, F.; Gainaru, C.; Geil, B.; Loerting, T. Colloquium: Water’s controversial glass transitions. Rev. Mod. Phys. 2016, 88, 011002. [Google Scholar] [CrossRef]
- Shephard, J.J.; Salzmann, C.G. Molecular reorientation dynamics govern the glass transitions of the amorphous ices. J. Phys. Chem. Lett. 2016, 7, 2281–2285. [Google Scholar] [CrossRef]
- Arndt, M.; Stannarius, R.; Gorbatschow, W.; Kremer, F. Dielectric investigations of the dynamic glass transition in nanopores. Phys. Rev. E 1996, 54, 5377–5390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elamin, K.; Jansson, H.; Kittaka, S.; Swenson, J. Different behavior of water in confined solutions of high and low solute concentrations. Phys. Chem. Chem. Phys. 2013, 15, 18437. [Google Scholar] [CrossRef] [PubMed]
- Geske, J.; Harrach, M.; Heckmann, L.; Horstmann, R.; Klameth, F.; Müller, N.; Pafong, E.; Wohlfromm, T.; Drossel, B.; Vogel, M. Molecular dynamics simulations of water, silica, and aqueous mixtures in bulk and confinement. Z. Phys. Chem. 2018, 232, 1187–1225. [Google Scholar] [CrossRef]
- Fillmer, A.; Gainaru, C.; Böhmer, R. Broadened dielectric loss spectra and reduced dispersion strength of viscous glycerol in a connective tissue protein. J. Non Cryst. Solids 2010, 356, 743–746. [Google Scholar] [CrossRef]
- Herbers, C.R.; Sauer, D.; Vogel, M. 2H NMR studies of glycerol dynamics in protein matrices. J. Chem. Phys. 2012, 136, 124511. [Google Scholar] [CrossRef]
- Gruenberg, B.; Gruenberg, A.; Limbach, H.-H.; Buntkowsky, G. Melting of naphthalene confined in mesoporous silica MCM-41. Appl. Magn. Res. 2013, 44, 189–201. [Google Scholar] [CrossRef]
- Ebener, M.; Vonfircks, G.; Günther, H. High-resolution solid-state MAS c-13 and h-1-nmr spectra of benzenoid aromatics adsorbed on alumina and silica - successful applications of 1d-pulse and 2d-pulse experiments from liquid-state nmr. Helv. Chim. Acta 1991, 74, 1296–1304. [Google Scholar] [CrossRef]
- Ebener, M.; Francke, V.; Günther, H. Solid state 13C MAS NMR as a tool for the study of reactions between compounds adsorbed on porous materials. Fresenius’ J. Anal. Chem. 1997, 357, 505–507. [Google Scholar] [CrossRef]
- von Fircks, G.; Hausmann, H.; Francke, V.; Günther, H. High-resolution solid state 19f and 15N MAS NMR spectra of fluoroaromatics and aromatic nitrogen heterocycles physisorbed on silica and alumina. J. Org. Chem. 1997, 62, 5074–5079. [Google Scholar] [CrossRef]
- Günther, H.; Oepen, S.; Ebener, M.; Francke, V. NMR study of adsorption techniques for organic compounds on silica surfaces. Magn. Reson. Chem. 1999, 37, 142–146. [Google Scholar] [CrossRef]
- Lee, J.A.; Rösner, H.; Corrigan, J.F.; Huang, Y. Phase transitions of naphthalene and its derivatives confined in mesoporous silicas. J. Phys. Chem. C 2011, 115, 4738–4748. [Google Scholar] [CrossRef]
- Azais, T.; Hartmeyer, G.; Quignard, S.; Laurent, G.; Babonneau, F. Solution state NMR techniques applied to solid state samples: Characterization of benzoic acid confined in MCM-41. J. Phys. Chem. C 2010, 114, 8884–8891. [Google Scholar] [CrossRef]
- Shenderovich, I.G.; Buntkowsky, G.; Schreiber, A.; Gedat, E.; Sharif, S.; Albrecht, J.; Golubev, N.S.; Findenegg, G.H.; Limbach, H.H. Pyridine-n-15 - a mobile NMR sensor for surface acidity and surface defects of mesoporous silica. J. Phys. Chem. B 2003, 107, 11924–11939. [Google Scholar] [CrossRef]
- Shenderovich, I.G.; Mauder, D.; Akcakayiran, D.; Buntkowsky, G.; Limbach, H.-H.; Findenegg, G.H. NMR provides checklist of generic properties for atomic-scale models of periodic mesoporous silicas. J. Phys. Chem. B 2007, 111, 12088–12096. [Google Scholar] [CrossRef] [PubMed]
- Gurinov, A.A.; Rozhkova, Y.A.; Zukal, A.; Cejka, J.; Shenderovich, I.G. Mutable lewis and bronsted acidity of aluminated SBA-15 as revealed by NMR of adsorbed pyridine-n-15. Langmuir 2011, 27, 12115–12123. [Google Scholar] [CrossRef] [PubMed]
- Lesnichin, S.B.; Kamdem, N.; Mauder, D.; Denisov, G.S.; Shenderovich, I.G. Studies of adsorption of 2,2 ‘-bipyridyl on the surface of highly regulated silica matrix of the MCM-41 type by means of n-15 NMR spectroscopy. Russ. J. Gen. Chem. 2010, 80, 2027–2031. [Google Scholar] [CrossRef]
- Ip, B.C.K.; Andreeva, D.V.; Buntkowsky, G.; Akcakayiran, D.; Findenegg, G.H.; Shenderovich, I.G. NMR study of proton transfer to strong bases on inner surfaces of MCM-41. Microporous Mesoporous Mater. 2010, 134, 22–28. [Google Scholar] [CrossRef]
- Gedat, E.; Schreiber, A.; Findenegg, G.H.; Shenderovich, I.; Limbach, H.H.; Buntkowsky, G. Stray field gradient NMR reveals effects of hydrogen bonding on diffusion coefficients of pyridine in mesoporous silica. Magn. Reson. Chem. 2001, 39, 149–157. [Google Scholar] [CrossRef]
- Shenderovich, I.; Denisov, G.S. Adduct under field—a qualitative approach to account for solvent effect on hydrogen bonding. Molecules 2020, 25, 436. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.-Y.; Watermann, T.; Sebastiani, D. Local microphase separation of a binary liquid under nanoscale confinement. J. Phys. Chem. B 2014, 118, 10207–10213. [Google Scholar] [CrossRef]
- Hermens, J.L.M.; de Bruijn, J.H.M.; Brooke, D.N. The octanol–water partition coefficient: Strengths and limitations. Environ. Toxicol. Chem. 2013, 32, 732–733. [Google Scholar] [CrossRef] [PubMed]
- Leo, A.; Hansch, C.; Elkins, D. Partition coefficients and their uses. Chem. Rev. 1971, 71, 525–616. [Google Scholar] [CrossRef]
- Harrach, M.F.; Drossel, B.; Winschel, W.; Gutmann, T.; Buntkowsky, G. Mixtures of isobutyric acid and water confined in cylindrical silica nanopores revisited: A combined solid-state NMR and molecular dynamics simulation study. J. Phys. Chem. C 2015, 119, 28961–28969. [Google Scholar] [CrossRef]
- van Rossum, B.J.; Förster, H.; de Groot, H.J.M. High-field and high-speed cp-MAS c-13 NMR heteronuclear dipolar-correlation spectroscopy of solids with frequency-switched lee-goldburg homonuclear decoupling. J. Magn. Reson. 1997, 124, 516–519. [Google Scholar] [CrossRef]
- Sattig, M.; Elamin, K.; Reuhl, M.; Swenson, J.; Vogel, M. Dynamics of dipgme–water mixtures in mesoporous silica. J. Phys. Chem. C 2017, 121, 6796–6806. [Google Scholar] [CrossRef]
- Schmitz, R.; Muller, N.; Ullmann, S.; Vogel, M. A molecular dynamics simulations study on ethylene glycol-water mixtures in mesoporous silica. J. Chem. Phys. 2016, 145, 104703. [Google Scholar] [CrossRef]
- Sauer, D.; Schuster, B.; Rosenstihl, M.; Schneider, S.; Talluto, V.; Walther, T.; Blochowicz, T.; Stuhn, B.; Vogel, M. Dynamics of water-alcohol mixtures: Insights from nuclear magnetic resonance, broadband dielectric spectroscopy, and triplet solvation dynamics. J. Chem. Phys. 2014, 140, 114503. [Google Scholar] [CrossRef]
- Sjostrom, J.; Mattsson, J.; Bergman, R.; Johansson, E.; Josefsson, K.; Svantesson, D.; Swenson, J. Dielectric secondary relaxation of water in aqueous binary glass-formers. Phys. Chem. Chem. Phys. 2010, 12, 10452–10456. [Google Scholar] [CrossRef] [Green Version]
- Wasserscheid, P.; Keim, W. Ionic liquids - new “solutions” for transition metal catalysis. Angew. Chem. Int. Ed. 2000, 39, 3772–3789. [Google Scholar] [CrossRef]
- Hardacre, C.; Holbrey, J.D.; Nieuwenhuyzen, M.; Youngs, T.G.A. Structure and solvation in ionic liquids. Acc. Chem. Res. 2007, 40, 1146–1155. [Google Scholar] [CrossRef]
- Poole, C.F.; Poole, S.K. Extraction of organic compounds with room temperature ionic liquids. J. Chromatogr. A 2010, 1217, 2268–2286. [Google Scholar] [CrossRef] [PubMed]
- Chiappe, C.; Pieraccini, D. Ionic liquids: Solvent properties and organic reactivity. J. Phys. Org. Chem. 2005, 18, 275–297. [Google Scholar] [CrossRef]
- Haumann, M.; Schoenweiz, A.; Breitzke, H.; Buntkowsky, G.; Werner, S.; Szesni, N. Solid-state NMR investigations of supported ionic liquid phase water-gas shift catalysts: Ionic liquid film distribution vs. Catal. Perform. Chem. Eng. Technol. 2012, 35, 1421–1426. [Google Scholar]
- Shylesh, S.; Hanna, D.; Werner, S.; Bell, A.T. Factors influencing the activity, selectivity, and stability of rh-based supported ionic liquid phase (silp) catalysts for hydroformylation of propene. ACS Catal. 2012, 2, 487–493. [Google Scholar] [CrossRef]
- Le Bideau, J.; Gaveau, P.; Bellayer, S.; Neouze, M.A.; Vioux, A. Effect of confinement on ionic liquids dynamics in monolithic silica ionogels: H-1 NMR study. Phys. Chem. Chem. Phys. 2007, 9, 5419–5422. [Google Scholar] [CrossRef]
- Rosa Castillo, M.; Fraile, J.M.; Mayoral, J.A. Structure and dynamics of 1-butyl-3-methylimidazolium hexafluorophosphate phases on silica and laponite clay: From liquid to solid behavior. Langmuir 2012, 28, 11364–11375. [Google Scholar] [CrossRef]
- Waechtler, M.; Sellin, M.; Stark, A.; Akcakayiran, D.; Findenegg, G.; Gruenberg, A.; Breitzke, H.; Buntkowsky, G. H-2 and f-19 solid-state NMR studies of the ionic liquid [c2py][bta]-d(10) confined in mesoporous silica materials. Phys. Chem. Chem. Phys. 2010, 12, 11371–11379. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Bothe, S.; Brodrecht, M.; Klimavicius, V.; Haro-Mares, N.B.; Gutmann, T.; Buntkowsky, G. Direct and indirect dynamic nuclear polarization transfer observed in mesoporous materials impregnated with nonionic surfactant solutions of polar polarizing agents. J. Phys. Chem. C 2020, 124, 5145–5156. [Google Scholar] [CrossRef]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buntkowsky, G.; Vogel, M. Small Molecules, Non-Covalent Interactions, and Confinement. Molecules 2020, 25, 3311. https://doi.org/10.3390/molecules25143311
Buntkowsky G, Vogel M. Small Molecules, Non-Covalent Interactions, and Confinement. Molecules. 2020; 25(14):3311. https://doi.org/10.3390/molecules25143311
Chicago/Turabian StyleBuntkowsky, Gerd, and Michael Vogel. 2020. "Small Molecules, Non-Covalent Interactions, and Confinement" Molecules 25, no. 14: 3311. https://doi.org/10.3390/molecules25143311
APA StyleBuntkowsky, G., & Vogel, M. (2020). Small Molecules, Non-Covalent Interactions, and Confinement. Molecules, 25(14), 3311. https://doi.org/10.3390/molecules25143311







