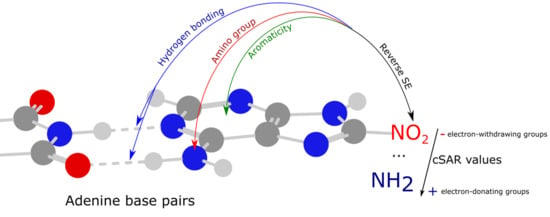
Mutual Relations between Substituent Effect, Hydrogen Bonding, and Aromaticity in Adenine-Uracil and Adenine-Adenine Base Pairs †
Abstract
:1. Introduction
- The classical substituent effect—i.e., how do substituents in various positions of adenine affect its amino group and individual hydrogen bonds?
- How do substituents affect the π-electron delocalization in adenine rings?
- How does the electronic structure of the substituents, estimated by cSAR(X), depend on the position and kind of a moiety to which they are attached? This means the estimation of the so-called reverse substituent effect.
- How do these characteristics depend on the nature of substituents—i.e., their electron-donating or electron-attracting properties?
- How do these characteristics differ from those estimated for monomers?
2. Methods
3. Results and Discussion
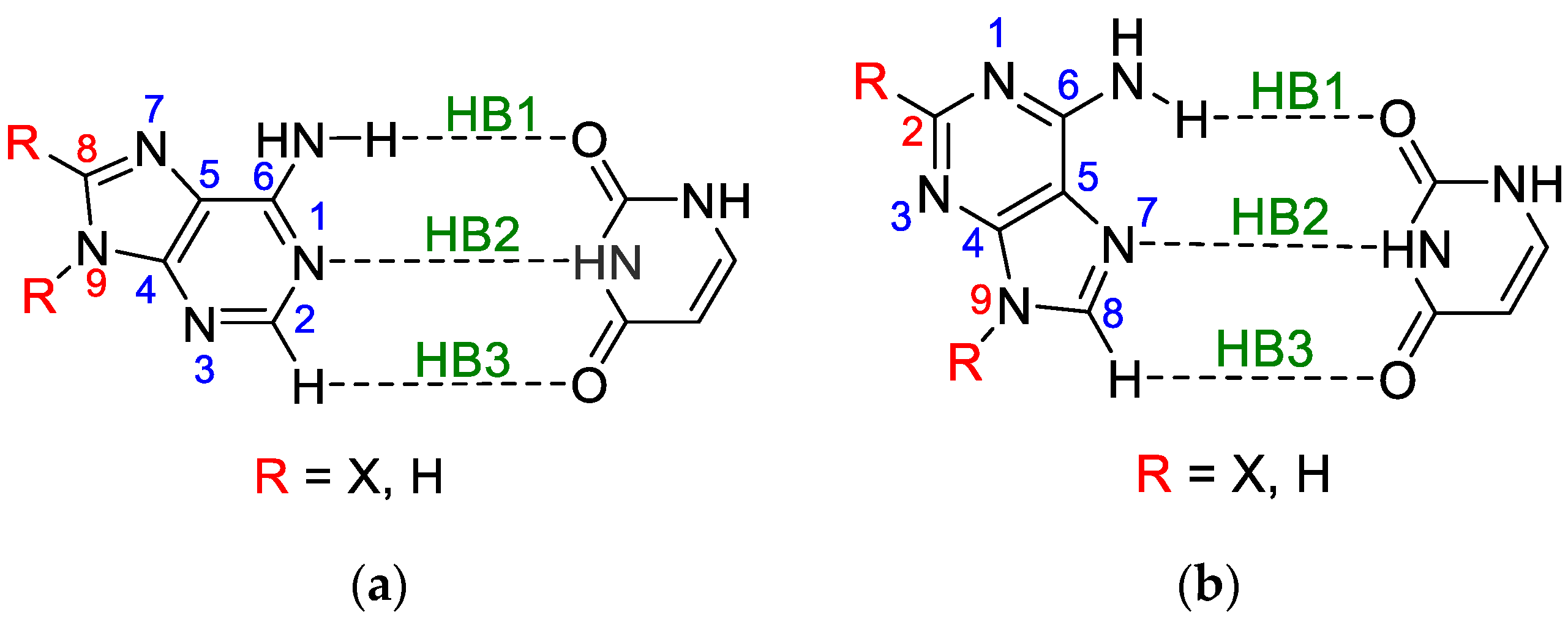
3.1. Classical Substituent Effect-Intramolecular Interactions
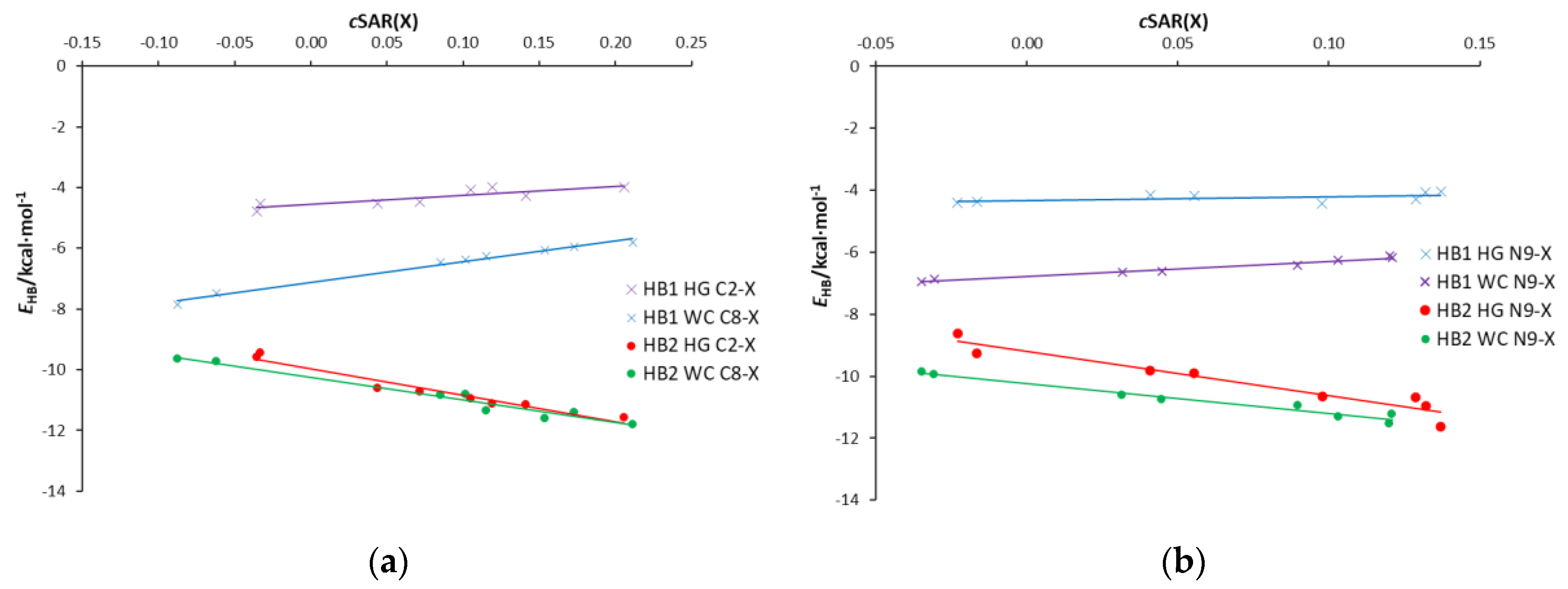
- The substituents at the C8 position in the five-membered adenine ring in the WC pair have a stronger influence on the electronic structure of NH2 involved in the H-bond than those attached to the C2 in the six-membered ring of the HG pair by the ratio of 0.219/0.183 = 1.20.
- The substituents attached to N9 in both pairs, WC and HG, affect the electronic structure of NH2 involved in the H-bond by almost the same extent, by the ratio (WC/HG) of 1.03.
- In all cases of adenine dimers, the effect of substitution at the C2 or C8 position is greater than that at N9 by an average ratio of 1.88.
3.2. Classical Substituent Effects-Intermolecular Interactions
- (HB1) NH⋯O, in which NH of the amino group is proton-donating towards the oxygen atom of uracil;
- (HB2) N⋯HN, in which the nitrogen atom of the adenine ring is proton accepting from the NH endo group in uracil;
- (HB3) a weak CH⋯O, where the C-H of the adenine ring, C2-H in WC and C8-H in HG, interacts with the carbonyl group of uracil.
3.3. Substituent Effect on the Transmitting Moiety
3.4. Reverse Substituent Effect
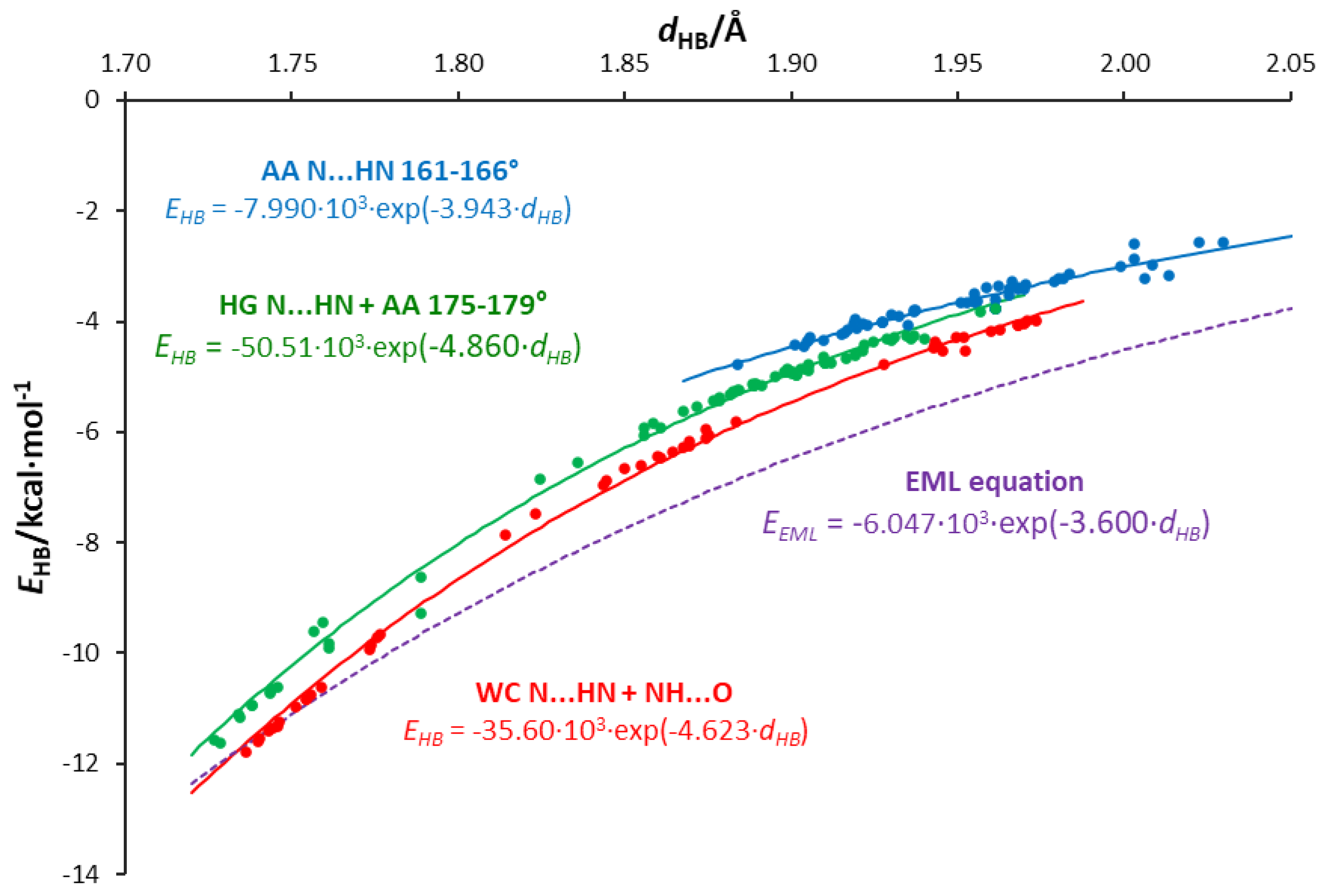
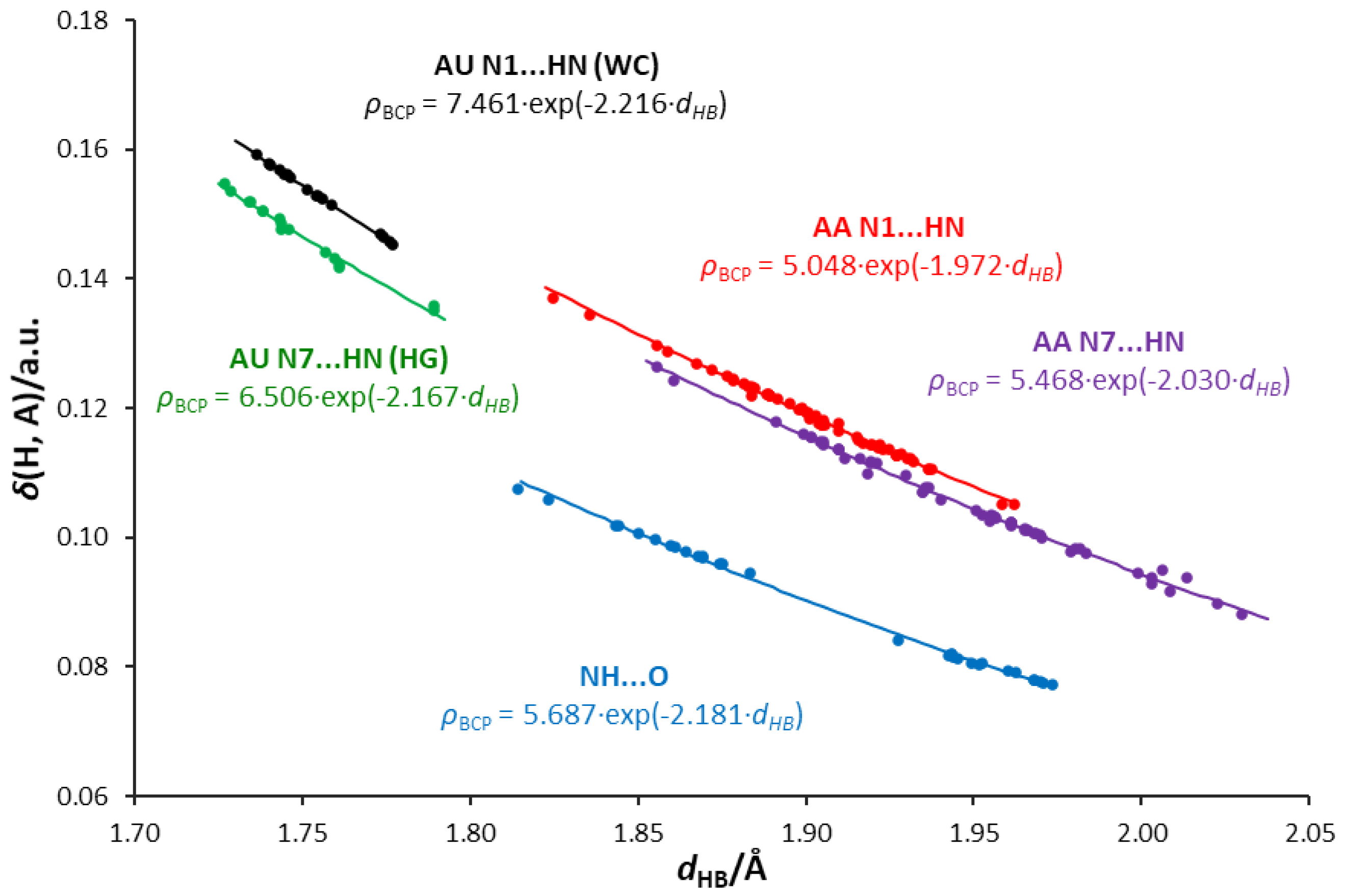
3.5. Interrelations between Hydrogen Bond Parameters
- NH⋯O, where the oxygen atom of the uracil molecule is the H-bond acceptor and adenine amino group is the H-bond donor.
- N1⋯HN, where the N1 acceptor atom is a part of a six-membered adenine ring.
- N7⋯HN, where the N7 acceptor atom is a part of a five-membered adenine ring.
4. Conclusions
- Hydrogen bond energies obtained by the NBO approach are smaller for a given length than those predicted by the EML equation for systems with an O⋯H single hydrogen bond. An exponential relation between the energy and H-bond length is proposed.
- The values of energy are dependent on the H-bond angle forced by the base pair geometry. The most favorable geometry is an anthracene-like system with two six-membered rings connected by two H-bonds. Base pairs of this geometry show the strongest H-bonding.
- Some of the H-bonds exhibit a partially covalent character, confirmed by positive values of the Laplacian and negative values of the total energy density at the bond critical point.
- Relations between the QTAIM parameters differentiate the type of acceptor atom—i.e., adenine N1, N7 atoms, and the uracil O carbonyl atom. The N1 acceptor atom of the six-membered ring forms H-bonds of higher covalent character than the N7 five-membered ring. Bonds formed by the carbonyl oxygen of uracil are less covalent in character, possibly due to the higher electronegativity and attraction of electrons.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Šponer, J.; Leszczynski, J.; Hobza, P. Structures and Energies of Hydrogen-Bonded DNA Base Pairs. A Nonempirical Study with Inclusion of Electron Correlation. J. Phys. Chem. 1996, 100, 1965–1974. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Bickelhaupt, F.M.; Snijders, J.G.; Baerends, E.J. Hydrogen Bonding in DNA Base Pairs: Reconciliation of Theory and Experiment. J. Am. Chem. Soc. 2000, 122, 4117–4128. [Google Scholar] [CrossRef] [Green Version]
- Šponer, J.; Jurečka, P.; Hobza, P. Accurate Interaction Energies of Hydrogen-Bonded Nucleic Acid Base Pairs. J. Am. Chem. Soc. 2004, 126, 10142–10151. [Google Scholar] [CrossRef] [PubMed]
- Poater, J.; Swart, M.; Bickelhaupt, F.M.; Fonseca Guerra, C. B-DNA Structure and Stability: The Role of Hydrogen Bonding, π–π Stacking Interactions, Twist-Angle, and Solvation. Org. Biomol. Chem. 2014, 12, 4691–4700. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Šponer, J.; Leszczynski, J.; Hobza, P. Electronic Properties, Hydrogen Bonding, Stacking, and Cation Binding of DNA and RNA Bases. Biopolymers 2001, 61, 3–31. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Bickelhaupt, F.M.; Saha, S.; Wang, F. Adenine Tautomers: Relative Stabilities, Ionization Energies, and Mismatch with Cytosine. J. Phys. Chem. A 2006, 110, 4012–4020. [Google Scholar] [CrossRef] [PubMed]
- Van der Wijst, T.; Fonseca Guerra, C.; Swart, M.; Bickelhaupt, F.M. Performance of Various Density Functionals for the Hydrogen Bonds in DNA Base Pairs. Chem. Phys. Lett. 2006, 426, 415–421. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Schwabe, T.; Mück-Lichtenfeld, C. Density Functional Theory with Dispersion Corrections for Supramolecular Structures, Aggregates, and Complexes of (Bio)Organic Molecules. Org. Biomol. Chem. 2007, 5, 741–758. [Google Scholar] [CrossRef]
- Poater, J.; Swart, M.; Fonseca Guerra, F.; Bickelhaupt, F.M. Selectivity in DNA Replication. Interplay of Steric Shape, Hydrogen Bonds, π-Stacking and Solvent Effects. Chem. Commun. 2011, 47, 7326. [Google Scholar] [CrossRef]
- Watson, J.D.; Crick, F.H.C. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef]
- Hoogsteen, K. The crystal and molecular structure of a hydrogen-bonded complex between 1-methylthymine and 9-methyladenine. Acta Cryst. 1963, 16, 907–916. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; van der Wijst, T.; Bickelhaupt, F.M. Substituent Effects on Hydrogen Bonding in Watson-Crick Base Pairs. A Theoretical Study. Struct. Chem. 2005, 16, 211–221. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; van der Wijst, T.; Bickelhaupt, F.M. Supramolecular Switches Based on the Guanine-Cytosine (GC) Watson-Crick Pair: Effect of Neutral and Ionic Substituents. Chem. Eur. J. 2006, 12, 3032–3042. [Google Scholar] [CrossRef] [PubMed]
- Fonseca Guerra, C.; van der Wijst, T.; Bickelhaupt, F.M. Nanoswitches Based on DNA Base Pairs: Why Adenine-Thymine is Less Suitable than Guanine-Cytosine. Chem. Phys. Chem. 2006, 7, 1971–1979. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, A.; Habibi Khorassani, S.M.; Delarami, H.; Esmaeeli, H. The Effect of CH3, F and NO2 Substituents on the Individual Hydrogen Bond Energies in the Adenine–Thymine and Guanine–Cytosine Base Pairs. J. Comput. Aided Mol. Des. 2010, 24, 409–416. [Google Scholar] [CrossRef]
- Nikolova, V.; Galabov, B. Effects of Structural Variations on the Hydrogen Bond Pairing between Adenine Derivatives and Thymine. Maced. J. Chem. Chem. Eng. 2015, 34, 159–167. [Google Scholar] [CrossRef] [Green Version]
- Jana, K.; Ganguly, B. In Silico Studies with Substituted Adenines to Achieve a Remarkable Stability of Mispairs with Thymine Nucleobase. New J. Chem. 2016, 40, 1807–1816. [Google Scholar] [CrossRef]
- Castro, A.C.; Swart, M. Fonseca Guerra, C. The Influence of Substituents and the Environment on the NMR Shielding Constants of Supramolecular Complexes Based on A–T and A–U Base Pairs. Phys. Chem. 2017, 19, 13496–13502. [Google Scholar]
- Jezuita, A.; Szatylowicz, H.; Krygowski, T.M. Impact of the Substituents on the Electronic Structure of the Four Most Stable Tautomers of Purine and Their Adenine Analogues. ACS Omega 2020, 5, 11570–11577. [Google Scholar] [CrossRef]
- Szatylowicz, H.; Marek, P.H.; Stasyuk, O.A.; Krygowski, T.M.; Solà, M. Substituted adenine quartets: Interplay between substituent effect, hydrogen bonding, and aromaticity. RSC Adv. 2020, 10, 23350–23358. [Google Scholar] [CrossRef]
- Saenger, W. Principles of Nucleic Acid Structure; Neidle, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Asensio, A.; Kobko, N.; Dannenberg, J.J. Cooperative Hydrogen-Bonding in Adenine−Thymine and Guanine−Cytosine Base Pairs. Density Functional Theory and Møller−Plesset Molecular Orbital Study. J. Phys. Chem. A 2003, 107, 6441–6443. [Google Scholar] [CrossRef]
- Grunenberg, J. Direct Assessment of Interresidue Forces in Watson-Crick Base Pairs Using Theoretical Compliance Constants. J. Am. Chem. Soc. 2004, 126, 16310–16311. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Matta, C.F.; Castillo, N.; Boyd, R.J. Extended Weak Bonding Interactions in DNA: π-Stacking (Base−Base), Base−Backbone, and Backbone-Backbone Interactions. J. Phys. Chem. B 2006, 110, 563–578. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Hua, W.; Li, S. Estimation on the Individual Hydrogen-Bond Strength in Molecules with Multiple Hydrogen Bonds. J. Phys. Chem. A 2007, 111, 2941–2945. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Popelier, P.L.A. Atoms in Molecules—An Introduction; Pearson Education: London, UK, 2000. [Google Scholar]
- Ebrahimi, A.; Habibi Khorassani, S.M.; Delarami, H. Estimation of individual binding energies in some dimers involving multiple hydrogen bonds using topological properties of electron charge density. Chem. Phys. 2009, 365, 18–23. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Valency and Bonding. A Natural Bond. Orbital Donor-Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Szatylowicz, H.; Sadlej-Sosnowska, N. Characterizing the Strength of Individual Hydrogen Bonds in DNA Base Pairs. J. Chem. Inf. Model. 2010, 50, 2151–2161. [Google Scholar] [CrossRef]
- Pandey, S.K.; Manogaran, D.; Manogaran, S.; Schaefer, H.F., III. Quantification of Hydrogen Bond Strength Based on Interaction Coordinates: A New Approach. J. Phys. Chem. A 2017, 121, 6090–6103. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Solà, M.; Duran, M.; Simon, S. On the Electron-Pair Nature of the Hydrogen Bond in the Framework of the Atoms in Molecules Theory. Chem. Phys. Lett. 2003, 369, 248–255. [Google Scholar] [CrossRef]
- Hammett, L.P. The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives. J. Am. Chem. Soc. 1937, 59, 96–103. [Google Scholar] [CrossRef]
- Hammett, L.P. Physical Organic Chemistry; McGraw-Hill Book Co. Inc.: New York, NY, USA, 1940. [Google Scholar]
- Sadlej-Sosnowska, N. On the Way to Physical Interpretation of Hammett Constants: How Substituent Active Space Impacts on Acidity and Electron Distribution in p-Substituted Benzoic Acid Molecules. Pol. J. Chem. 2007, 81, 1123–1134. [Google Scholar]
- Sadlej-Sosnowska, N. Substituent Active Region—A Gate for Communication of Substituent Charge with the Rest of a Molecule: Monosubstituted Benzenes. Chem. Phys. Lett. 2007, 447, 192–196. [Google Scholar] [CrossRef]
- Sadlej-Sosnowska, N.; Krygowski, T.M. Substituent effect on geometry of the NO and N(CH3)2 groups in para substituted derivatives of nitrosobenzene and N,N-dimethylaniline. Chem. Phys. Lett. 2009, 476, 191–195. [Google Scholar] [CrossRef]
- Stasyuk, O.A.; Szatylowicz, H.; Fonseca Guerra, C.; Krygowski, T.M. Theoretical Study of Electron-Attracting Ability of the Nitro Group: Classical and Reverse Substituent Effects. Struct. Chem. 2015, 26, 905–913. [Google Scholar] [CrossRef] [Green Version]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; J. Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Marek, P.H.; Szatylowicz, H.; Krygowski, T.M. Stacking of Nucleic Acid Bases: Optimization of the Computational Approach - the Case of Adenine Dimers. Struct. Chem. 2019, 30, 351–359. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-Functional Thermochemistry. V. Systematic Optimization of Exchange-Correlation Functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural Bond Orbital Analysis Program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Handgraaf, J.W.; Baerends, E.J.; Bickelhaupt, F.M. Voronoi Deformation Density (VDD) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD Methods for Charge Analysis. J. Comput. Chem. 2004, 25, 189–210. [Google Scholar] [CrossRef] [PubMed]
- Šponer, J.; Shukla, M.K.; Leszczynski, J. Computational modeling of DNA and RNA fragments. In Handbook of Computational Chemistry; Leszczynski, J., Ed.; Springer: Dordrecht, The Netherlands, 2012; pp. 1257–1275. [Google Scholar]
- Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Todd, A.; Keith, T.K. Gristmill Software, Overland Park KS, AIMAll (Version 19.10.12), USA, 2019. Available online: aim.tkgristmill.com (accessed on 11 August 2020).
- Kruszewski, J.; Krygowski, T.M. Definition of Aromaticity Basing on the Harmonic Oscillator Model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic Studies of Inter- and Intramolecular Interactions Reflected in Aromatic Character of Pi-Electron Systems. J. Chem. Inf. Model. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Palusiak, M.; Plonka, A.; Zachara–Horeglad, J.E. Relationship between substituent effect and aromaticity—Part III: Naphthalene as a transmitting moiety for substituent effect. J. Phys. Org. Chem. 2007, 20, 297–306. [Google Scholar] [CrossRef]
- Shahamirian, M.; Cyrański, M.K.; Krygowski, T.M. Conjugation Paths in Monosubstituted 1,2- and 2,3-Naphthoquinones. J. Phys. Chem. A 2011, 115, 12688–12694. [Google Scholar] [CrossRef]
- Koch, U.; Popelier, P.L.A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Palusiak, M.; Krygowski, T.M. Application of AIM Parameters at Ring Critical Points for Estimation of π-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings. Chem. Eur. J. 2007, 13, 7996–8006. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beiträge Zum Benzolproblem. Z. Phys. Chem. 1931, 70, 204–286. [Google Scholar]
- Hansch, C.; Leo, A.; Taft, R.W. A Survey of Hammett Substituent Constants and Resonance and Field Parameters. Chem. Rev. 1991, 91, 165–195. [Google Scholar] [CrossRef]
- Jeffrey, G.A. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Grabowski, S.J. Theoretical studies of strong hydrogen bonds. Annu. Rep. Prog. Chem. Sect. C 2006, 102, 131–165. [Google Scholar] [CrossRef]
- Rozas, I.; Alkorta, I.; Elguero, J. Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Sokalski, W.A.; Dyguda, E.; Leszczynski, J. Quantitative Classification of Covalent and Noncovalent H-Bonds. J. Phys. Chem. B 2006, 110, 6444–6446. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Calculation output files for all studied dimers are available from the authors. |



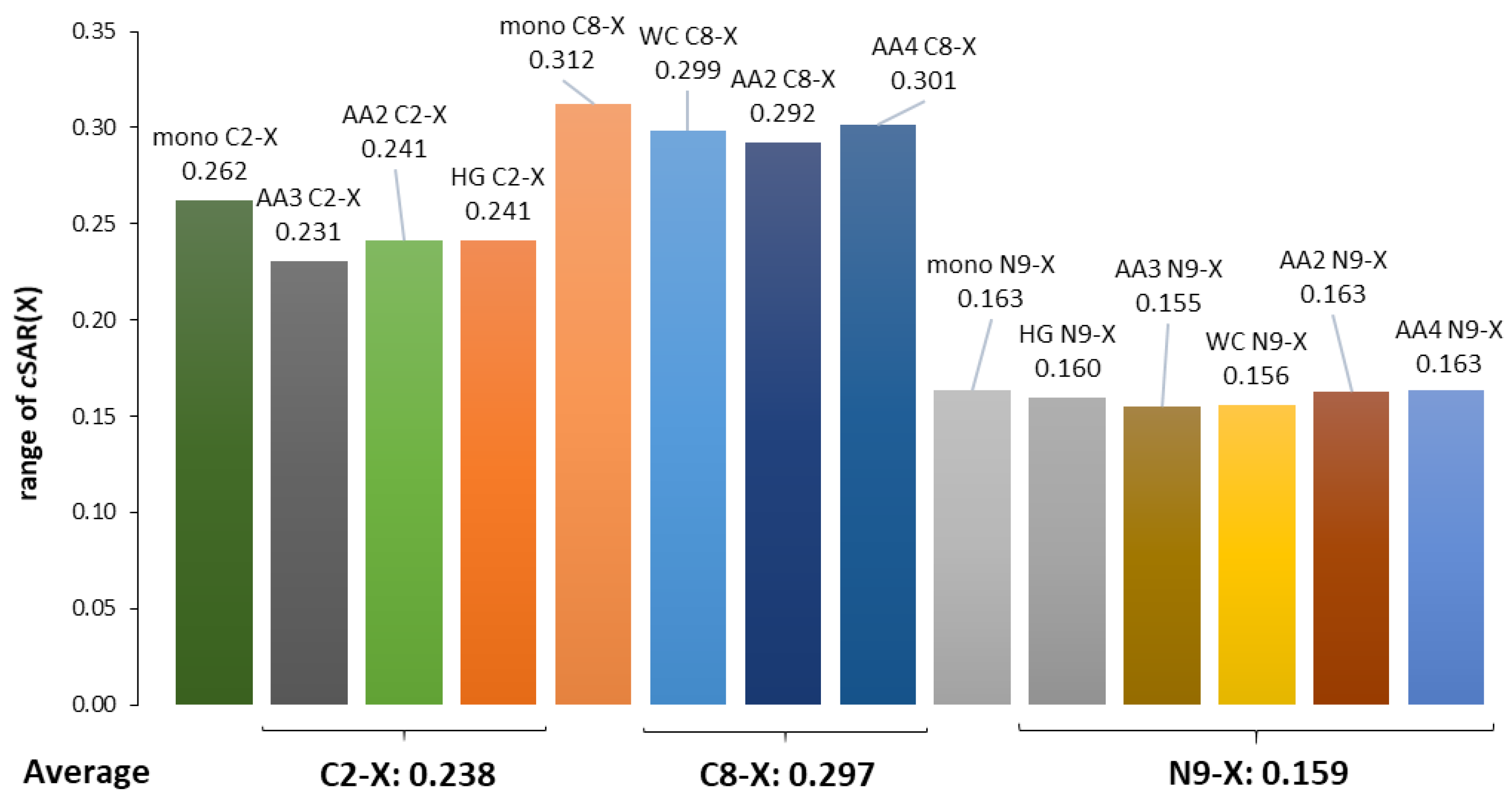

| a | R2 | |
|---|---|---|
| A-C2-X | −0.222 | 0.913 |
| HG C2-X | −0.183 | 0.882 |
| AA2 C2-X | −0.163 | 0.838 |
| AA3 C2-X | −0.184 | 0.824 |
| A-C8-X | −0.297 | 0.989 |
| WC C8-X | −0.219 | 0.991 |
| AA2 C8-X | −0.209 | 0.983 |
| AA4 C8-X | −0.167 | 0.875 |
| A-N9-X | −0.166 | 0.902 |
| HG N9-X | −0.084 | 0.817 |
| WC N9-X | −0.087 | 0.835 |
| AA2 N9-X | −0.100 | 0.883 |
| AA3 N9-X | −0.110 | 0.808 |
| AA4 N9-X | −0.079 | 0.813 |
| AA2 C2-X, C8-X | −0.176 | 0.890 |
| AA2 C2-X, C8-X | −0.201 | 0.947 |
| AA3 C2-X, C2-X | −0.182 | 0.818 |
| AA4 C8-X, C8-X | −0.236 | 0.994 |
| y = a∙cSAR(X) + b | y = EHB | y = dHB | y = ρBCP | y = δ(H,A) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Base Pair | HB | a | R2 | a | R2 | a | R2 | a | R2 |
| HG C2-X | 1 | 3.013 | 0.738 | 0.137 | 0.521 | −0.00757 | 0.526 | −0.0215 | 0.566 |
| 2 | −8.741 | 0.951 | −0.134 | 0.982 | 0.0172 | 0.984 | 0.0476 | 0.986 | |
| WC C8-X | 1 | 6.818 | 0.986 | 0.233 | 0.985 | −0.0175 | 0.980 | −0.0446 | 0.981 |
| 2 | −7.487 | 0.966 | −0.143 | 0.968 | 0.0179 | 0.967 | 0.0485 | 0.968 | |
| HG N9-X | 1 | 1.344 | 0.314 | 0.100 | 0.329 | −0.00620 | 0.400 | −0.0179 | 0.455 |
| 2 | −14.35 | 0.921 | −0.341 | 0.964 | 0.0402 | 0.971 | 0.104 | 0.980 | |
| WC N9-X | 1 | 4.927 | 0.971 | 0.182 | 0.929 | −0.0133 | 0.932 | −0.0343 | 0.934 |
| 2 | −9.655 | 0.967 | −0.194 | 0.972 | 0.0240 | 0.973 | 0.0645 | 0.970 | |
| y = a∙cSAR(X) + b | y = EHB | y = dHB | y = ρBCP | y = δ(H, A) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Base Pair | HB | a | R2 | a | R2 | a | R2 | a | R2 |
| AA2 C2-X | 1 | 3.589 | 0.811 | 0.200 | 0.825 | −0.0156 | 0.825 | −0.0426 | 0.835 |
| 2 | −3.794 | 0.987 | −0.193 | 0.993 | 0.0152 | 0.994 | 0.0439 | 0.994 | |
| AA2 C8-X | 1 | 6.036 | 0.987 | 0.260 | 0.992 | −0.0218 | 0.985 | −0.0571 | 0.986 |
| 2 | −3.036 | 0.963 | −0.161 | 0.958 | 0.0126 | 0.965 | 0.0369 | 0.964 | |
| AA3 C2-X | 1 | 2.172 | 0.433 | 0.137 | 0.223 | −0.0096 | 0.262 | −0.0261 | 0.291 |
| 2 | −4.843 | 0.762 | −0.276 | 0.579 | 0.0184 | 0.610 | 0.0547 | 0.672 | |
| AA4 C8-X | 1 | 7.362 | 0.990 | 0.284 | 0.993 | −0.0252 | 0.989 | −0.0426 | 0.835 |
| 2 | −3.998 | 0.976 | −0.189 | 0.976 | 0.0155 | 0.974 | 0.0439 | 0.994 | |
| AA2 N9-X | 1 | 1.925 | 0.472 | 0.122 | 0.687 | −0.0096 | 0.712 | −0.0267 | 0.718 |
| 2 | −6.930 | 0.978 | −0.370 | 0.986 | 0.0276 | 0.975 | 0.0834 | 0.968 | |
| AA3 N9-X | 1 | 1.187 | 0.187 | 0.097 | 0.501 | −0.0068 | 0.575 | −0.0187 | 0.491 |
| 2 | −5.778 | 0.792 | −0.413 | 0.943 | 0.0261 | 0.931 | 0.0831 | 0.908 | |
| AA4 N9-X | 1 | 5.128 | 0.963 | 0.220 | 0.960 | −0.0190 | 0.964 | −0.0495 | 0.961 |
| 2 | −4.715 | 0.949 | −0.225 | 0.967 | 0.0185 | 0.967 | 0.0529 | 0.968 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wieczorkiewicz, P.A.; Szatylowicz, H.; Krygowski, T.M. Mutual Relations between Substituent Effect, Hydrogen Bonding, and Aromaticity in Adenine-Uracil and Adenine-Adenine Base Pairs. Molecules 2020, 25, 3688. https://doi.org/10.3390/molecules25163688
Wieczorkiewicz PA, Szatylowicz H, Krygowski TM. Mutual Relations between Substituent Effect, Hydrogen Bonding, and Aromaticity in Adenine-Uracil and Adenine-Adenine Base Pairs. Molecules. 2020; 25(16):3688. https://doi.org/10.3390/molecules25163688
Chicago/Turabian StyleWieczorkiewicz, Paweł A., Halina Szatylowicz, and Tadeusz M. Krygowski. 2020. "Mutual Relations between Substituent Effect, Hydrogen Bonding, and Aromaticity in Adenine-Uracil and Adenine-Adenine Base Pairs" Molecules 25, no. 16: 3688. https://doi.org/10.3390/molecules25163688
APA StyleWieczorkiewicz, P. A., Szatylowicz, H., & Krygowski, T. M. (2020). Mutual Relations between Substituent Effect, Hydrogen Bonding, and Aromaticity in Adenine-Uracil and Adenine-Adenine Base Pairs. Molecules, 25(16), 3688. https://doi.org/10.3390/molecules25163688