Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds
Abstract
:1. Introduction
2. Methodological Aspects
3. Applications
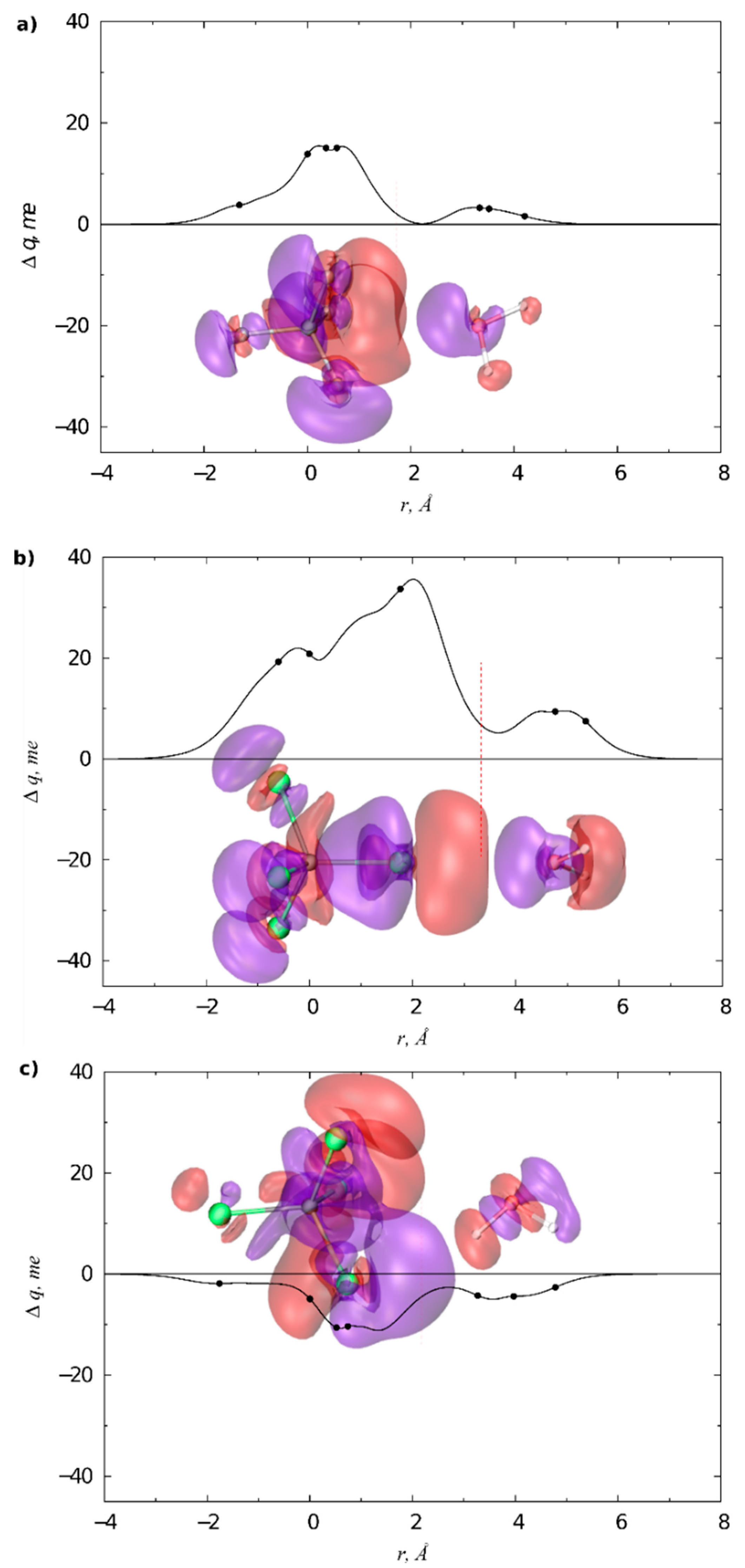
3.1. Gas Phase
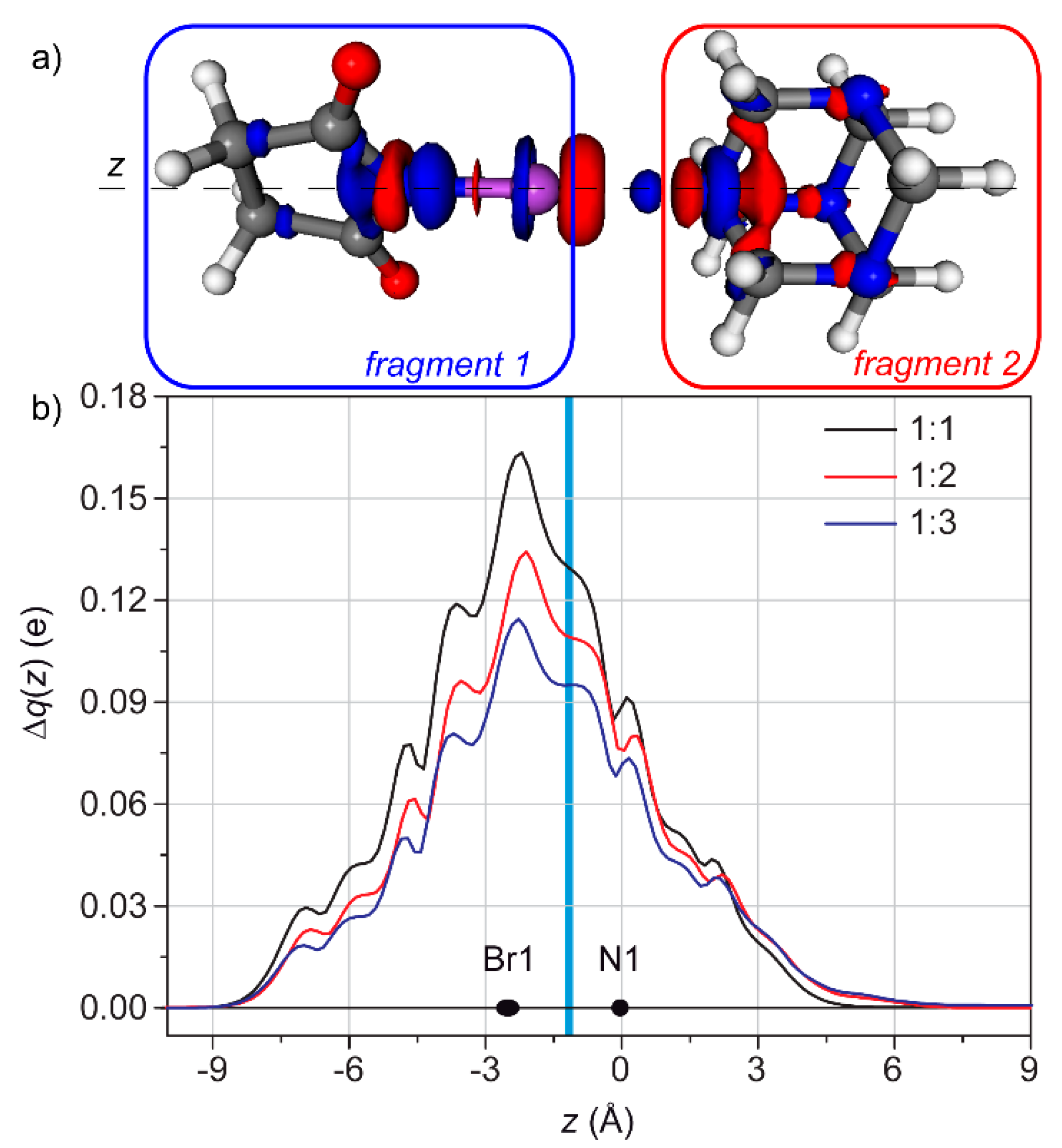
3.2. Condensed Phase
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Frenking, G.; Krapp, A. Unicorns in the World of Chemical Bonding Models. J. Comput. Chem. 2007, 28, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Gross, L.; Schuler, B.; Pavliček, N.; Fatayer, S.; Majzik, Z.; Moll, N.; Peña, D.; Meyer, G. Atomic Force Microscopy for Molecular Structure Elucidation. Angew. Chem. Int. Ed. 2018, 57, 3888–3908. [Google Scholar] [CrossRef]
- Freund, S.; Pawlak, R.; Moser, L.; Hinaut, A.; Steiner, R.; Marinakis, N.; Constable, E.C.; Meyer, E.; Housecroft, C.E.; Glatzel, T. Transoid-to-Cisoid Conformation Changes of Single Molecules on Surfaces Triggered by Metal Coordination. ACS Omega 2018, 3, 12851–12856. [Google Scholar] [CrossRef] [PubMed]
- Ebeling, D.; Zhong, Q.; Ahles, S.; Chi, L.; Wegner, H.A.; Schirmeisen, A. Chemical Bond Imaging Using Higher Eigenmodes of Tuning Fork Sensors in Atomic Force Microscopy. Appl. Phys. Lett. 2017, 110, 183102. [Google Scholar] [CrossRef]
- Iwata, K.; Yamazaki, S.; Mutombo, P.; Hapala, P.; Ondráček, M.; Jelínek, P.; Sugimoto, Y. Chemical Structure Imaging of a Single Molecule by Atomic Force Microscopy at Room Temperature. Nat. Commun. 2015, 6, 7766. [Google Scholar] [CrossRef] [PubMed]
- Von Hopffgarten, M.; Frenking, G. Energy Decomposition Analysis. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 43–62. [Google Scholar] [CrossRef]
- Popelier, P.L.A. The QTAIM Perspective of Chemical Bonding. In The Chemical Bond: Fundamental Aspects of Chemical Bonding; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2014; Volume 9783527333, pp. 271–308. [Google Scholar]
- Stone, A.J.; Misquitta, A.J. Charge-Transfer in Symmetry-Adapted Perturbation Theory. Chem. Phys. Lett. 2009, 473, 201–205. [Google Scholar] [CrossRef]
- Mo, Y.; Bao, P.; Gao, J. Energy Decomposition Analysis Based on a Block-Localized Wavefunction and Multistate Density Functional Theory. Phys. Chem. Chem. Phys. 2011, 13, 6760–6775. [Google Scholar] [CrossRef]
- Mitoraj, M.; Michalak, A. Natural Orbitals for Chemical Valence as Descriptors of Chemical Bonding in Transition Metal Complexes. J. Mol. Model. 2007, 13, 347–355. [Google Scholar] [CrossRef]
- Radoń, M. On the Properties of Natural Orbitals for Chemical Valence. Theory Chem. Acc. 2008, 120, 337–339. [Google Scholar] [CrossRef]
- Schneider, W.B.; Bistoni, G.; Sparta, M.; Saitow, M.; Riplinger, C.; Auer, A.A.; Neese, F. Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework. J. Chem. Theory Comput. 2016, 12, 4778–4792. [Google Scholar] [CrossRef] [PubMed]
- Belpassi, L.; Infante, I.; Tarantelli, F.; Visscher, L. The Chemical Bond between Au(I) and the Noble Gases. Comparative Study of NgAuF and NgAu+ (Ng = Ar, Kr, Xe) by Density Functional and Coupled Cluster Methods. J. Am. Chem. Soc. 2008, 130, 1048–1060. [Google Scholar] [CrossRef] [PubMed]
- Cappelletti, D.; Ronca, E.; Belpassi, L.; Tarantelli, F.; Pirani, F. Revealing Charge-Transfer Effects in Gas-Phase Water Chemistry. Acc. Chem. Res. 2012, 45, 1571–1580. [Google Scholar] [CrossRef] [PubMed]
- Belpassi, L.; Reca, M.L.; Tarantelli, F.; Roncaratti, L.F.; Pirani, F.; Cappelletti, D.; Faure, A.; Scribano, Y. Charge-Transfer Energy in the Water-Hydrogen Molecular Aggregate Revealed by Molecular-Beam Scattering Experiments, Charge Displacement Analysis, and Ab Initio Calculations. J. Am. Chem. Soc. 2010, 132, 13046–13058. [Google Scholar] [CrossRef]
- Ronca, E.; Belpassi, L.; Tarantelli, F. A Quantitative View of Charge Transfer in the Hydrogen Bond: The Water Dimer Case. ChemPhysChem 2014, 15, 2682–2687. [Google Scholar] [CrossRef]
- Nunzi, F.; Di Erasmo, B.; Tarantelli, F.; Cappelletti, D.; Pirani, F. The Halogen-Bond Nature in Noble Gas–Dihalogen Complexes from Scattering Experiments and Ab Initio Calculations. Molecules 2019, 24, 4274. [Google Scholar] [CrossRef] [Green Version]
- Pirani, F.; Cappelletti, D.; Falcinelli, S.; Cesario, D.; Nunzi, F.; Belpassi, L.; Tarantelli, F. Selective Emergence of the Halogen Bond in Ground and Excited States of Noble-Gas–Chlorine Systems. Angew. Chem. Int. Ed. 2019, 58, 4195–4199. [Google Scholar] [CrossRef]
- Ronca, E.; Pastore, M.; Belpassi, L.; Tarantelli, F.; De Angelis, F. Influence of the Dye Molecular Structure on the TiO2 Conduction Band in Dye-Sensitized Solar Cells: Disentangling Charge Transfer and Electrostatic Effects. Energy Environ. Sci. 2013, 6, 183–193. [Google Scholar] [CrossRef] [Green Version]
- Ronca, E.; Pastore, M.; Belpassi, L.; De Angelis, F.; Angeli, C.; Cimiraglia, R.; Tarantelli, F. Charge-Displacement Analysis for Excited States. J. Chem. Phys. 2014, 140, 054110. [Google Scholar] [CrossRef] [Green Version]
- Sorbelli, D.; Belpassi, L.; Tarantelli, F.; Belanzoni, P. Ligand Effect on Bonding in Gold(III) Carbonyl Complexes. Inorg. Chem. 2018, 57, 6161–6175. [Google Scholar] [CrossRef]
- Salvi, N.; Belpassi, L.; Tarantelli, F. On the Dewar-Chatt-Duncanson Model for Catalytic Gold(I) Complexes. Chem. A Eur. J. 2010, 16, 7231–7240. [Google Scholar] [CrossRef] [PubMed]
- Gaggioli, C.A.; Bistoni, G.; Ciancaleoni, G.; Tarantelli, F.; Belpassi, L.; Belanzoni, P. Modulating the Bonding Properties of N-Heterocyclic Carbenes (NHCs): A Systematic Charge-Displacement Analysis. Chem. A Eur. J. 2017, 23, 7558–7569. [Google Scholar] [CrossRef] [PubMed]
- Bartalucci, N.; Belpassi, L.; Marchetti, F.; Pampaloni, G.; Zacchini, S.; Ciancaleoni, G. Ubiquity of Cis-Halide → Isocyanide Direct Interligand Interaction in Organometallic Complexes. Inorg. Chem. 2018, 57, 14554–14563. [Google Scholar] [CrossRef] [PubMed]
- Ciancaleoni, G.; Belpassi, L.; Marchetti, F. Back-Donation in High-Valent D0 Metal Complexes: Does It Exist? The Case of NbV. Inorg. Chem. 2017, 56, 11266–11274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bistoni, G.; Rampino, S.; Scafuri, N.; Ciancaleoni, G.; Zuccaccia, D.; Belpassi, L.; Tarantelli, F. How π Back-Donation Quantitatively Controls the CO Stretching Response in Classical and Non-Classical Metal Carbonyl Complexes. Chem. Sci. 2016, 7, 1174–1184. [Google Scholar] [CrossRef] [Green Version]
- Ciancaleoni, G.; Biasiolo, L.; Bistoni, G.; Macchioni, A.; Tarantelli, F.; Zuccaccia, D.; Belpassi, L. Selectively Measuring Π Back-Donation in Gold(I) Complexes by NMR Spectroscopy. Chem. A Eur. J. 2015, 21, 2467–2473. [Google Scholar] [CrossRef]
- Marchione, D.; Izquierdo, M.A.; Bistoni, G.; Havenith, R.W.A.; Macchioni, A.; Zuccaccia, D.; Tarantelli, F.; Belpassi, L. 13C NMR Spectroscopy of N-Heterocyclic Carbenes Can Selectively Probe σ Donation in Gold(I) Complexes. Chem. A Eur. J. 2017, 23, 2722–2728. [Google Scholar] [CrossRef] [Green Version]
- Azzopardi, K.M.; Bistoni, G.; Ciancaleoni, G.; Tarantelli, F.; Zuccaccia, D.; Belpassi, L. Quantitative Assessment of the Carbocation/Carbene Character of the Gold–Carbene Bond. Dalton Trans. 2015, 44, 13999–14007. [Google Scholar] [CrossRef]
- Nunzi, F.; Cesario, D.; Pirani, F.; Belpassi, L.; Frenking, G.; Grandinetti, F.; Tarantelli, F. Helium Accepts Back-Donation in Highly Polar Complexes: New Insights into the Weak Chemical Bond. J. Phys. Chem. Lett. 2017, 8, 3334–3340. [Google Scholar] [CrossRef]
- Cesario, D.; Nunzi, F.; Belpassi, L.; Pirani, F.; Ronca, E.; Tarantelli, F. Chemical Bond Mechanism for Helium Revealed by Electronic Excitation. J. Phys. Chem. A 2019, 123, 6572–6577. [Google Scholar] [CrossRef]
- Ciancaleoni, G.; Santi, C.; Ragni, M.; Braga, A.L. Charge-Displacement Analysis as a Tool to Study Chalcogen Bonded Adducts and Predict Their Association Constants in Solution. Dalton Trans. 2015, 44, 20168–20175. [Google Scholar] [CrossRef] [PubMed]
- Ciancaleoni, G. Lewis Base Activation of Lewis Acid: A Detailed Bond Analysis. ACS Omega 2018, 3, 16292–16300. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novák, M.; Foroutan-Nejad, C.; Marek, R. Asymmetric Bifurcated Halogen Bonds. Phys. Chem. Chem. Phys. 2015, 17, 6440–6450. [Google Scholar] [CrossRef] [PubMed]
- Bora, P.L.; Novák, M.; Novotný, J.; Foroutan-Nejad, C.; Marek, R. Supramolecular Covalence in Bifurcated Chalcogen Bonding. Chem. A Eur. J. 2017, 23, 7315–7323. [Google Scholar] [CrossRef] [PubMed]
- Mitoraj, M.P.; Michalak, A. Theoretical Description of Halogen Bonding—An Insight Based on the Natural Orbitals for Chemical Valence Combined with the Extended-Transition—State Method (ETS-NOCV). J. Mol. Model. 2013, 19, 4681–4688. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buttarazzi, E.; Rosi, F.; Ciancaleoni, G. Influence of Halogen Bonding on Gold(i)—Ligand Bond Components and DFT Characterization of a Gold–Iodine Halogen Bond. Phys. Chem. Chem. Phys. 2019, 21, 20478–20485. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the Halogen Bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Halogen Bonding: An Interim Discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen Bonding: An Electrostatically-Driven Highly Directional Noncovalent Interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef]
- Brinck, T.; Borrfors, A.N. Electrostatics and Polarization Determine the Strength of the Halogen Bond: A Red Card for Charge Transfer. J. Mol. Model. 2019, 25, 125. [Google Scholar] [CrossRef] [Green Version]
- Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The Many Faces of Halogen Bonding: A Review of Theoretical Models and Methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
- Robertson, C.C.; Perutz, R.N.; Brammer, L.; Hunter, C.A. A Solvent-Resistant Halogen Bond. Chem. Sci. 2014, 5, 4179–4183. [Google Scholar] [CrossRef] [Green Version]
- Weinberger, C.; Hines, R.; Zeller, M.; Rosokha, S.V. Continuum of Covalent to Intermolecular Bonding in the Halogen-Bonded Complexes of 1,4-Diazabicyclo [2.2.2] Octane with Bromine-Containing Electrophiles. Chem. Commun. 2018, 54, 8060–8063. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction yet to Be Understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Eraković, M.; Cinčić, D.; Molčanov, K.; Stilinović, V. A Crystallographic Charge Density Study of the Partial Covalent Nature of Strong N⋅⋅⋅Br Halogen Bonds. Angew. Chem. Int. Ed. 2019, 58, 15702–15706. [Google Scholar] [CrossRef]
- Altun, A.; Neese, F.; Bistoni, G. Effect of Electron Correlation on Intermolecular Interactions: A Pair Natural Orbitals Coupled Cluster Based Local Energy Decomposition Study. J. Chem. Theory Comput. 2019, 15, 215–228. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Köster, A.M.; Jug, K. Chemical Valence from the Two-Particle Density Matrix. Theory Chim. Acta 1993, 85, 463–484. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Ozek, J. Modified Valence Indices from the Two-particle Density Matrix. Int. J. Quantum Chem. 1994, 51, 187–200. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Mrozek, J.; Michalak, A. Two-Electron Valence Indices from the Kohn-Sham Orbitals. Int. J. Quantum Chem. 1997, 61, 589–601. [Google Scholar] [CrossRef]
- Bistoni, G.; Rampino, S.; Tarantelli, F.; Belpassi, L. Charge-Displacement Analysis via Natural Orbitals for Chemical Valence: Charge Transfer Effects in Coordination Chemistry. J. Chem. Phys. 2015, 142, 084112. [Google Scholar] [CrossRef]
- Cooke, S.A.; Gerry, M.C.L. XeAuF. J. Am. Chem. Soc. 2004, 126, 17000–17008. [Google Scholar] [CrossRef] [PubMed]
- Evans, C.J.; Lesarri, A.; Gerry, M.C.L. Noble Gas-Metal Chemical Bonds. Microwave Spectra, Geometries, and Nuclear Quadrupole Coupling Constants of Ar-AuCl and Kr-AuCl. J. Am. Chem. Soc. 2000, 122, 6100–6105. [Google Scholar] [CrossRef]
- Nunzi, F.; Cesario, D.; Belpassi, L.; Tarantelli, F.; Roncaratti, L.F.; Falcinelli, S.; Cappelletti, D.; Pirani, F. Insight into the Halogen-Bond Nature of Noble Gas-Chlorine Systems by Molecular Beam Scattering Experiments: Ab Initio Calculations and Charge Displacement Analysis. Phys. Chem. Chem. Phys. 2019, 21, 7330–7340. [Google Scholar] [CrossRef] [PubMed]
- Pirani, F.; Brizi, S.; Roncaratti, L.F.; Casavecchia, P.; Cappelletti, D.; Vecchiocattivi, F. Beyond the Lennard-Jones Model: A Simple and Accurate Potential Function Probed by High Resolution Scattering Data Useful for Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2008, 10, 5489–5503. [Google Scholar] [CrossRef] [PubMed]
- Cappelletti, D.; Aquilanti, V.; Bartocci, A.; Nunzi, F.; Tarantelli, F.; Belpassi, L.; Pirani, F. Interaction of O2 with CH4, CF4, and CCl4 by Molecular Beam Scattering Experiments and Theoretical Calculations. J. Phys. Chem. A 2016, 120, 5197–5207. [Google Scholar] [CrossRef]
- De Santis, M.; Nunzi, F.; Cesario, D.; Belpassi, L.; Tarantelli, F.; Cappelletti, D.; Pirani, F. Cooperative Role of Halogen and Hydrogen Bonding in the Stabilization of Water Adducts with Apolar Molecules. New J. Chem. 2018, 42, 10603–10614. [Google Scholar] [CrossRef]
- Aragoni, M.C.; Arca, M.; Devillanova, F.A.; Isaia, F.; Lippolis, V. Adducts of S/Se Donors with Dihalogens as a Source of Information for Categorizing the Halogen Bonding. Cryst. Growth Des. 2012, 12, 2769–2779. [Google Scholar] [CrossRef]
- Brown, I.D. Bond Valence Theory: Part I, a New Twist to an Old Description of Chemical Bonding. J. Chem. Educ. 1976, 53, 100–101. [Google Scholar] [CrossRef]
- Brown, I.D. Bond Valence Theory: Part II, Examples. J. Chem. Educ. 1976, 53, 231. [Google Scholar] [CrossRef]
- Ciancaleoni, G.; Arca, M.; Caramori, G.F.; Frenking, G.; Schneider, F.S.S.; Lippolis, V. Bonding Analysis in Homo- and Hetero-Trihalide Species: A Charge Displacement Study. Eur. J. Inorg. Chem. 2016, 2016, 3804–3812. [Google Scholar] [CrossRef]
- Schneider, F.S.S.; Caramori, G.F.; Parreira, R.L.T.; Lippolis, V.; Arca, M.; Ciancaleoni, G. Bond Analysis in Dihalogen—Halide and Dihalogen—Dimethylchalcogenide Systems. Eur. J. Inorg. Chem. 2018, 2018, 1007–1015. [Google Scholar] [CrossRef]
- Turney, J.M.; Simmonett, A.C.; Parrish, R.M.; Hohenstein, E.G.; Evangelista, F.A.; Fermann, J.T.; Mintz, B.J.; Burns, L.A.; Wilke, J.J.; Abrams, M.L.; et al. Psi4: An Open-Source Ab Initio Electronic Structure Program. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 556–565. [Google Scholar] [CrossRef]
- Ciancaleoni, G.; Macchioni, A.; Rocchigiani, L.; Zuccaccia, C. A PGSE NMR Approach to the Characterization of Single and Multi-Site Halogen-Bonded Adducts in Solution. RSC Adv. 2016, 6, 80604–80612. [Google Scholar] [CrossRef] [Green Version]
- McDowell, S.A.C.; Joseph, J.A. Cooperative Effects of Noncovalent Bonds to the Br Atom of Halogen-Bonded H3NBrZ and HCNBrZ (Z F, Br) Complexes. J. Chem. Phys. 2012, 137, 074310. [Google Scholar] [CrossRef] [PubMed]
- George, J.; Deringer, V.L.; Dronskowski, R. Cooperativity of Halogen, Chalcogen, and Pnictogen Bonds in Infinite Molecular Chains by Electronic Structure Theory. J. Phys. Chem. A 2014, 118, 3193–3200. [Google Scholar] [CrossRef]
- Ciancaleoni, G. Cooperativity between Hydrogen- and Halogen Bonds: The Case of Selenourea. Phys. Chem. Chem. Phys. 2018, 20, 8506–8514. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Mousavian, P. Unusual Cooperativity Effects between Halogen Bond and Donor-Acceptor Interactions: The Role of Orbital Interaction. Chem. Phys. Lett. 2017, 678, 275–282. [Google Scholar] [CrossRef]
- Kelly, R.A.; Clavier, H.; Giudice, S.; Scott, N.M.; Stevens, E.D.; Bordner, J.; Samardjiev, I.; Hoff, C.D.; Cavallo, L.; Nolan, S.P. Determination of N-Heterocyclic Carbene (NHC) Steric and Electronic Parameters Using the [(NHC)Ir(CO)2Cl] System. Organometallics 2008, 27, 202–210. [Google Scholar] [CrossRef]
- Nelson, D.J.; Nolan, S.P. Quantifying and Understanding the Electronic Properties of N-Heterocyclic Carbenes. Chem. Soc. Rev. 2013, 42, 6723–6753. [Google Scholar] [CrossRef]
- Bistoni, G.; Belanzoni, P.; Belpassi, L.; Tarantelli, F. π Activation of Alkynes in Homogeneous and Heterogeneous Gold Catalysis. J. Phys. Chem. A 2016, 120, 5239–5247. [Google Scholar] [CrossRef]
- Rogachev, A.Y.; Hoffmann, R. Iodine (I2) as a Janus-Faced Ligand in Organometallics. J. Am. Chem. Soc. 2013, 135, 3262–3275. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Li, Q.; Li, H.B.; Li, W.; Cheng, J. How Do Organic Gold Compounds and Organic Halogen Molecules Interact? Comparison with Hydrogen Bonds. RSC Adv. 2015, 5, 12488–12497. [Google Scholar] [CrossRef]
- Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Kirina, Y.V.; Kukushkin, V.Y. Halogen Bonding between Metal Centers and Halocarbons. Chem. Commun. 2016, 52, 5565–5568. [Google Scholar] [CrossRef] [PubMed] [Green Version]





| Fragments | CT0 | CT1 | CT2 | CT3 | CTtot,back |
|---|---|---|---|---|---|
| [(SeU)Au]+…[NAC] | 0.359 | −0.049 | −0.030 | −0.013 | −0.092 |
| [SeU]…[Au(NAC)]+ | 0.346 | 0.024 | −0.021 | −0.016 | −0.037 |
| [(SeU)(ICF2CF3)Au]+…[NAC] | 0.372 | −0.040 | −0.030 | −0.010 | −0.080 |
| [(SeU)(ICF2CF3)]…[Au(NAC)]+ | 0.344 | 0.020 | −0.021 | −0.015 | −0.036 |
| [ICF2CF3]…[Au(SeU)(NAC)]+ | −0.039 | 0.005 | - | - | - |
| [(SeU)(NIS)Au]+…[NAC] | 0.375 | −0.044 | −0.027 | −0.010 | −0.081 |
| [SeU]…[Au(NIS)(NAC)]+ | 0.373 | 0.033 | −0.018 | −0.014 | −0.032 |
| [NIS]…[Au(SeU)(NAC)]+ | −0.106 | 0.024 | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciancaleoni, G.; Nunzi, F.; Belpassi, L. Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds. Molecules 2020, 25, 300. https://doi.org/10.3390/molecules25020300
Ciancaleoni G, Nunzi F, Belpassi L. Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds. Molecules. 2020; 25(2):300. https://doi.org/10.3390/molecules25020300
Chicago/Turabian StyleCiancaleoni, Gianluca, Francesca Nunzi, and Leonardo Belpassi. 2020. "Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds" Molecules 25, no. 2: 300. https://doi.org/10.3390/molecules25020300
APA StyleCiancaleoni, G., Nunzi, F., & Belpassi, L. (2020). Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds. Molecules, 25(2), 300. https://doi.org/10.3390/molecules25020300