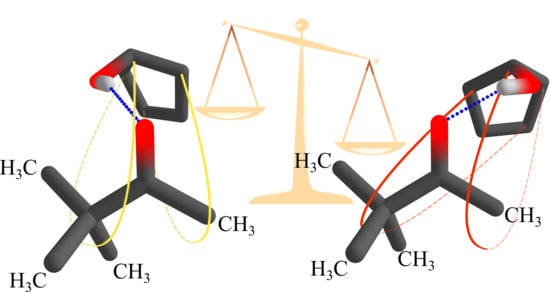
Pinacolone-Alcohol Gas-Phase Solvation Balances as Experimental Dispersion Benchmarks
Abstract
1. Introduction
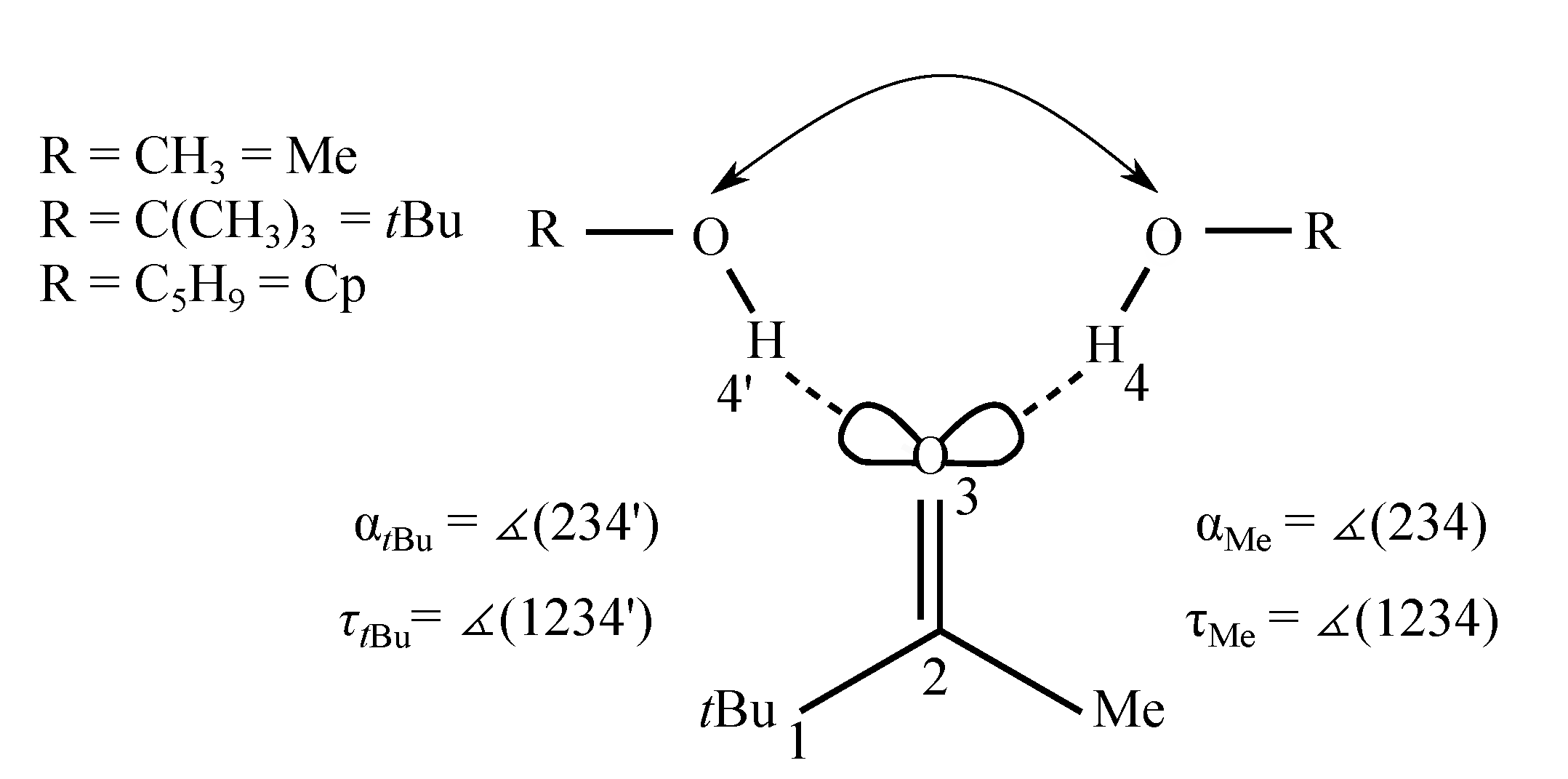
2. Results and Discussion
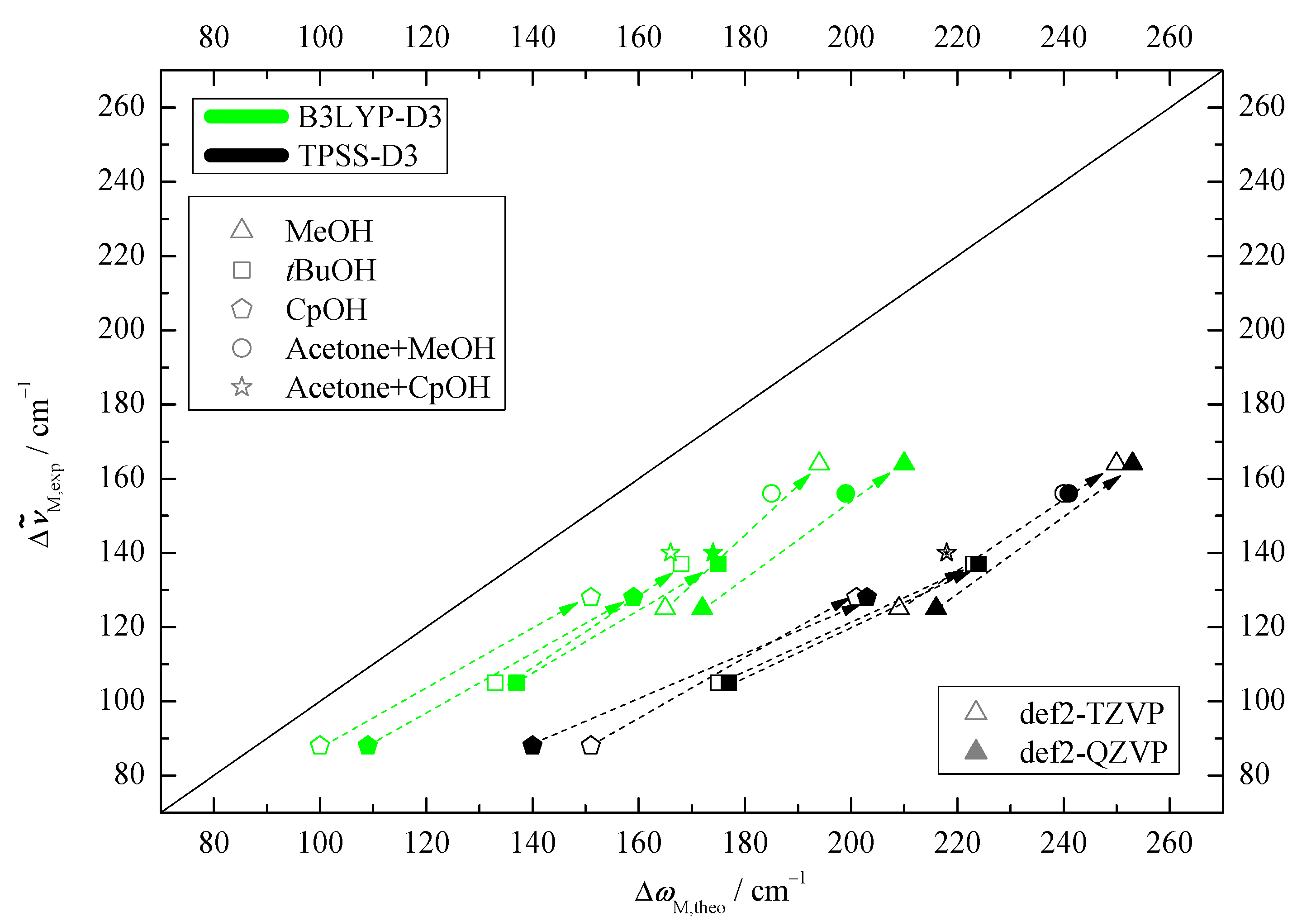
2.1. Density Functional Predictions
2.2. Experimental Results
2.3. DLPNO-CCSD(T) Check
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MeOH | Methanol |
| tBuOH | tert-Butyl alcohol |
| CpOH | Cyclopentanol |
| Pin | Pinacolone |
| ZPVE | Zero-point vibrational energy |
References
- Lommerse, J.P.M.; Price, S.L.; Taylor, R. Hydrogen bonding of carbonyl, ether, and ester oxygen atoms with alkanol hydroxyl groups. J. Comp. Chem. 1997, 18, 757–774. [Google Scholar] [CrossRef]
- Murray-Rust, P.; Glusker, J.P. Directional hydrogen bonding to sp2- and sp3-hybridized oxygen atoms and its relevance to ligand-macromolecule interactions. J. Am. Chem. Soc. 1984, 106, 1018–1025. [Google Scholar] [CrossRef]
- Derewenda, Z.S.; Lee, L.; Derewenda, U. The Occurence of C–H · · · O Hydrogen Bonds in Proteins. J. Mol. Biol. 1995, 252, 248–262. [Google Scholar] [CrossRef]
- Nikolova, E.N.; Stanfield, R.L.; Dyson, H.J.; Wright, P.E. CH···O Hydrogen Bonds Mediate Highly Specific Recognition of Methylated CpG Sites by the Zinc Finger Protein Kaiso. Biochemistry 2018, 57, 2109–2120. [Google Scholar] [CrossRef]
- Wagner, J.P.; Schreiner, P.R. London Dispersion in Molecular Chemistry–Reconsidering Steric Effects. Angew. Chem. Int. Ed. 2015, 54, 12274–12296. [Google Scholar] [CrossRef]
- Schnell, M.; Erlekam, U.; Bunker, P.R.; von Helden, G.; Grabow, J.U.; Meijer, G.; van der Avoird, A. Unraveling the internal dynamics of the benzene dimer: A combined theoretical and microwave spectroscopy study. Phys. Chem. Chem. Phys. 2013, 15, 10207–10223. [Google Scholar] [CrossRef][Green Version]
- Schwing, K.; Gerhards, M. Investigations on isolated peptides by combined IR/UV spectroscopy in a molecular beam—Structure, aggregation, solvation and molecular recognition. Int. Rev. Phys. Chem. 2016, 35, 569–677. [Google Scholar] [CrossRef]
- Shipman, S.T.; Neill, J.L.; Suenram, R.D.; Muckle, M.T.; Pate, B.H. Structure Determination of Strawberry Aldehyde by Broadband Microwave Spectroscopy: Conformational Stabilization by Dispersive Interactions. J. Phys. Chem. Lett. 2011, 2, 443–448. [Google Scholar] [CrossRef]
- Gottschalk, H.C.; Poblotzki, A.; Suhm, M.A.; Al-Mogren, M.M.; Antony, J.; Auer, A.A.; Baptista, L.; Benoit, D.M.; Bistoni, G.; Bohle, F.; et al. The furan microsolvation blind challenge for quantum chemical methods: First steps. J. Chem. Phys. 2018, 148, 014301. [Google Scholar] [CrossRef]
- Poblotzki, A.; Gottschalk, H.C.; Suhm, M.A. Tipping the Scales: Spectroscopic Tools for Intermolecular Energy Balances. J. Phys. Chem. Lett. 2017, 8, 5656–5665. [Google Scholar] [CrossRef]
- Zimmermann, C.; Gottschalk, H.C.; Suhm, M.A. Three-dimensional docking of alcohols to ketones: An experimental benchmark based on acetophenone solvation energy balances. Phys. Chem. Chem. Phys. 2020, 22, 2870–2877. [Google Scholar] [CrossRef]
- Burevschi, E.; Alonso, E.R.; Sanz, M.E. Binding Site Switch by Dispersion Interactions: Rotational Signatures of Fenchone–Phenol and Fenchone–Benzene Complexes. Chem. Eur. J. 2020, 26, 11327–11333. [Google Scholar] [CrossRef]
- Banerjee, P.; Pandey, P.; Bandyopadhyay, B. Stereo-preference of camphor for H-bonding with phenol, methanol and chloroform: A combined matrix isolation IR spectroscopic and quantum chemical investigation. Spectrochim. Acta Part A 2019, 209, 186–195. [Google Scholar] [CrossRef]
- Gottschalk, H.C.; Altnöder, J.; Heger, M.; Suhm, M.A. Control over the Hydrogen-Bond Docking Site in Anisole by Ring Methylation. Angew. Chem. Int. Ed. 2016, 55, 1921–1924. [Google Scholar] [CrossRef] [PubMed]
- Gottschalk, H.C.; Poblotzki, A.; Fatima, M.; Obenchain, D.A.; Pérez, C.; Antony, J.; Auer, A.A.; Baptista, L.; Benoit, D.M.; Bistoni, G.; et al. The first microsolvation step for furans: New experiments and benchmarking strategies. J. Chem. Phys. 2020, 152, 164303. [Google Scholar] [CrossRef] [PubMed]
- Altun, A.; Neese, F.; Bistoni, G. Local energy decomposition analysis of hydrogen-bonded dimers within a domain-based pair natural orbital coupled cluster study. Beilstein J. Org. Chem. 2018, 14, 919–929. [Google Scholar] [CrossRef]
- Schneider, W.B.; Bistoni, G.; Sparta, M.; Saitow, M.; Riplinger, C.; Auer, A.A.; Neese, F. Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework. J. Chem. Theory Comput. 2016, 12, 4778–4792. [Google Scholar] [CrossRef]
- Boese, A.D.; Jansen, G. ZMP-SAPT: DFT-SAPT using ab initio densities. J. Chem. Phys. 2019, 150, 154101. [Google Scholar] [CrossRef]
- Zhao, Y.; Nguyen, H.V.L.; Stahl, W.; Hougen, J.T. Unusual internal rotation coupling in the microwave spectrum of pinacolone. J. Mol. Spec. 2015, 318, 91–100. [Google Scholar] [CrossRef]
- Bende, A. Hydrogen bonding in the urea dimers and adenine–thymine DNA base pair: Anharmonic effects in the intermolecular H-bond and intramolecular H-stretching vibrations. Theor. Chem. Acc. 2010, 125, 253–268. [Google Scholar] [CrossRef]
- Kollipost, F.; Domanskaya, A.V.; Suhm, M.A. Microscopic Roots of Alcohol–Ketone Demixing: Infrared Spectroscopy of Methanol–Acetone Clusters. J. Phys. Chem. A 2015, 119, 2225–2232. [Google Scholar] [CrossRef]
- Carroll, P.B. Laboratory and Astronomical Rotational Spectroscopy. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2018. [Google Scholar] [CrossRef]
- Abraham, R.J.; Koniotou, R.; Sancassan, F. Conformational analysis. Part 39. A theoretical and lanthanide induced shift (LIS) investigation of the conformations of cyclopentanol and cis- and trans-cyclopentane-1,2-diol. J. Chem. Soc. Perkin Trans. 2002, 2, 2025–2030. [Google Scholar] [CrossRef]
- Karir, G.; Lüttschwager, N.O.B.; Suhm, M.A. Phenylacetylene as a gas phase sliding balance for solvating alcohols. Phys. Chem. Chem. Phys. 2019, 21, 7831–7840. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Pinski, P.; Becker, U.; Valeev, E.F.; Neese, F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Suhm, M.A.; Kollipost, F. Femtisecond single-mole infrared spectroscopy of molecular clusters. Phys. Chem. Chem. Phys. 2013, 15, 10702–10721. [Google Scholar] [CrossRef]
- Pracht, P.; Bohle, F.; Grimme, S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. A density-functional model of the dispersion interaction. J. Chem. Phys. 2005, 123, 154101. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D. A post-Hartree–Fock model of intermolecular interactions. J. Chem. Phys. 2005, 123, 024101. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D. A post-Hartree-Fock model of intermolecular interactions: Inclusion of higher-order corrections. J. Chem. Phys. 2006, 124, 174104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- TURBOMOLE V7.3 2018, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, Since 2007. Available online: http://www.turbomole.com (accessed on 30 October 2020).
- Furche, F.; Ahlrichs, R.; Hättig, C.; Klopper, W.; Sierka, M.; Weigend, F. Turbomole. WIREs Comput. Mol. Sci. 2014, 4, 91–100. [Google Scholar] [CrossRef]
- Ebata, T.; Fujii, A.; Mikami, N. Vibrational spectroscopy of small-sized hydrogen-bonded clusters and their ions. Int. Rev. Phys. Chem. 1998, 17, 331–361. [Google Scholar] [CrossRef]
Sample Availability: All compounds were obtained commercially and samples of the compounds are not available from the authors. |




| Donor | |||
|---|---|---|---|
| MeOH | 5.9–11.8 | 4.5–9.0 | 0.10–0.18 |
| tBuOH | 2.4–4.2 | 1.7–3.0 | 0.25–0.37 |
| CpOH | 5.5–7.3 | 3.4–4.4 | 0.18–0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimmermann, C.; Fischer, T.L.; Suhm, M.A. Pinacolone-Alcohol Gas-Phase Solvation Balances as Experimental Dispersion Benchmarks. Molecules 2020, 25, 5095. https://doi.org/10.3390/molecules25215095
Zimmermann C, Fischer TL, Suhm MA. Pinacolone-Alcohol Gas-Phase Solvation Balances as Experimental Dispersion Benchmarks. Molecules. 2020; 25(21):5095. https://doi.org/10.3390/molecules25215095
Chicago/Turabian StyleZimmermann, Charlotte, Taija L. Fischer, and Martin A. Suhm. 2020. "Pinacolone-Alcohol Gas-Phase Solvation Balances as Experimental Dispersion Benchmarks" Molecules 25, no. 21: 5095. https://doi.org/10.3390/molecules25215095
APA StyleZimmermann, C., Fischer, T. L., & Suhm, M. A. (2020). Pinacolone-Alcohol Gas-Phase Solvation Balances as Experimental Dispersion Benchmarks. Molecules, 25(21), 5095. https://doi.org/10.3390/molecules25215095