The Role of Titanium Dioxide on the Hydration of Portland Cement: A Combined NMR and Ultrasonic Study
Abstract
:1. Introduction
2. Experimental
2.1. Ultrasonic Section
2.2. NMR Section: Spin-Lattice Relaxation Time
2.3. NMR Section: Spin-Spin Relaxation Time and Diffusion Measurements
2.4. Materials
3. Results and Discussion
3.1. Vicat, Isothermal Calorimetry and DTA/TG Measurements
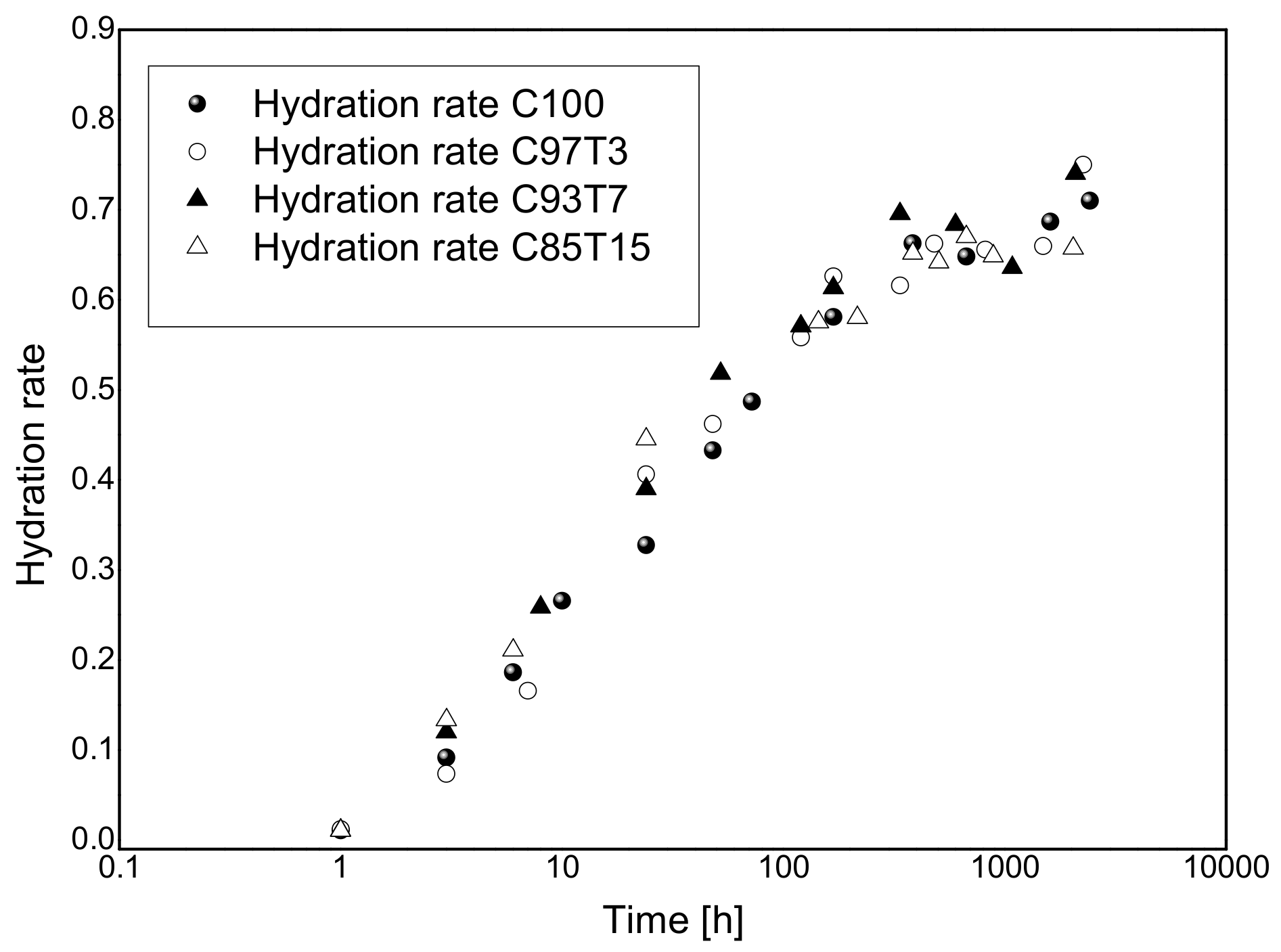
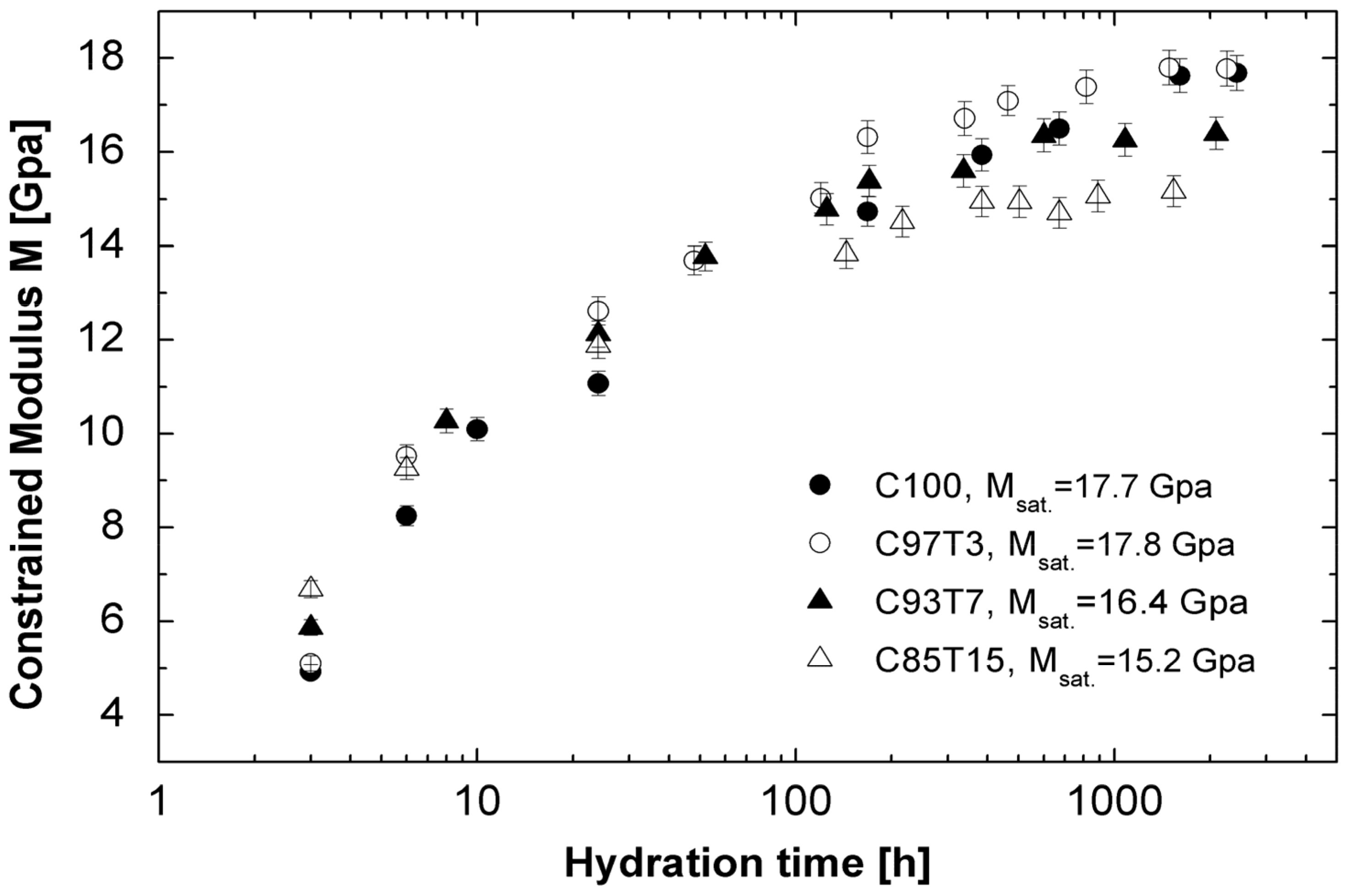
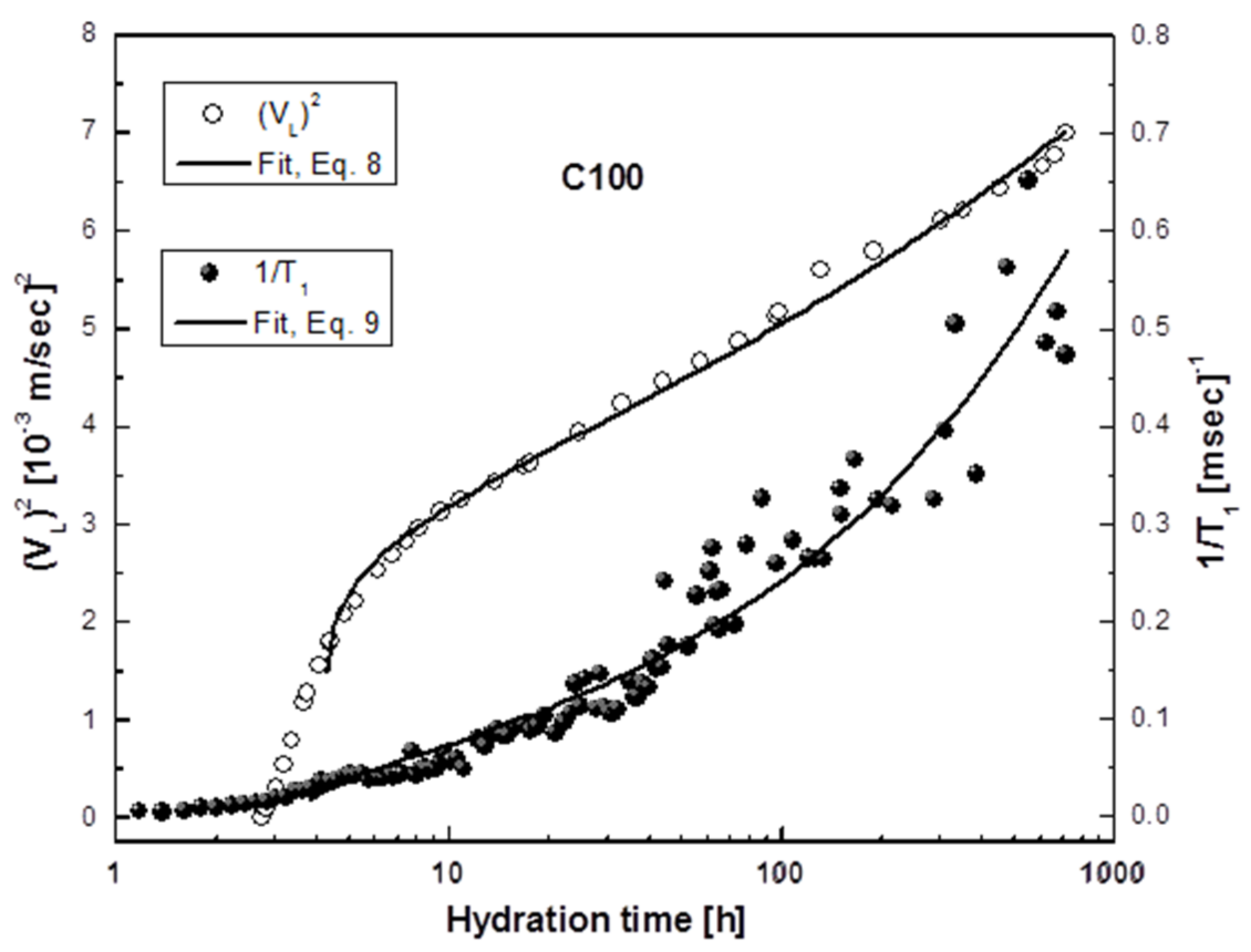
3.2. Ultrasonic Experiments
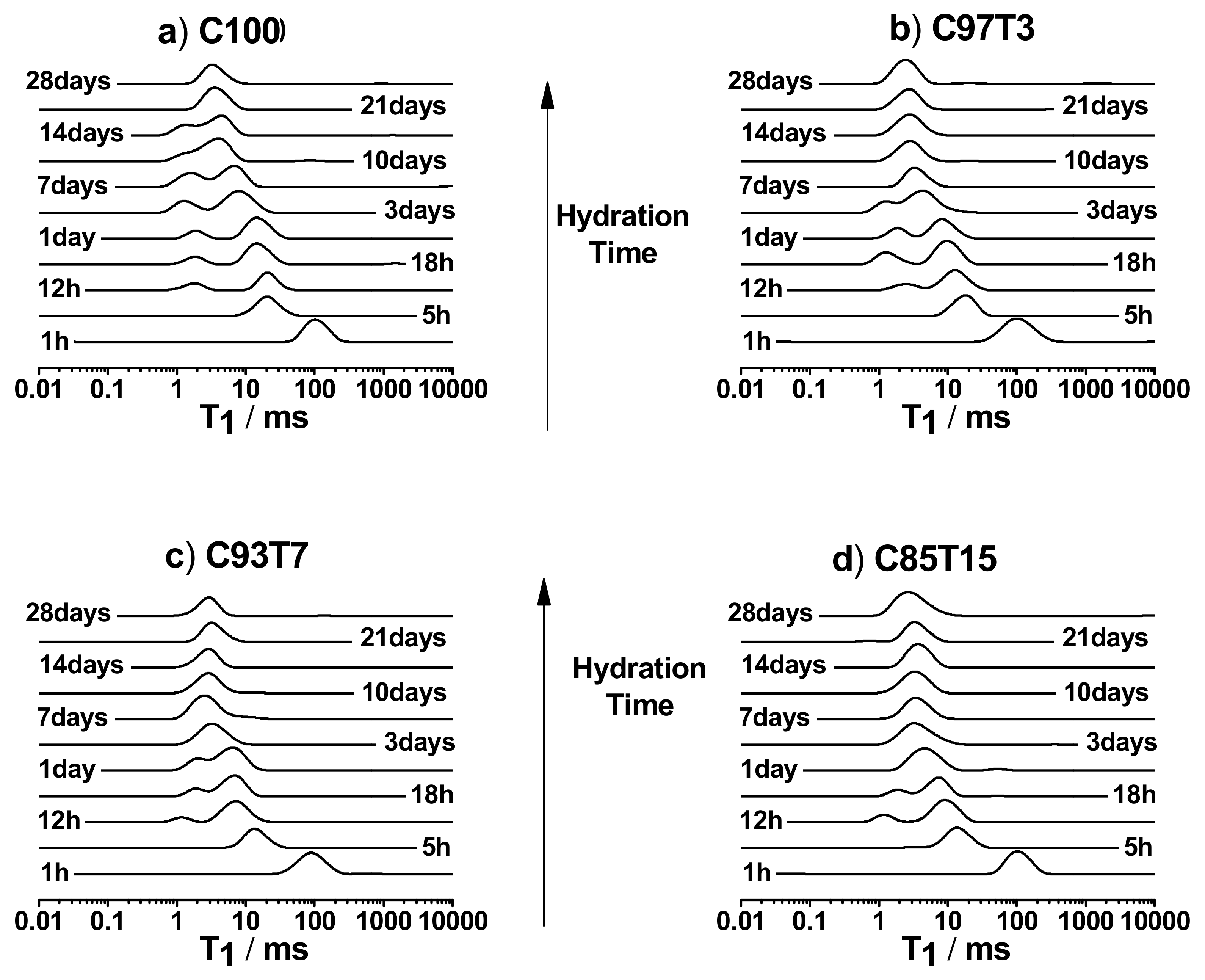
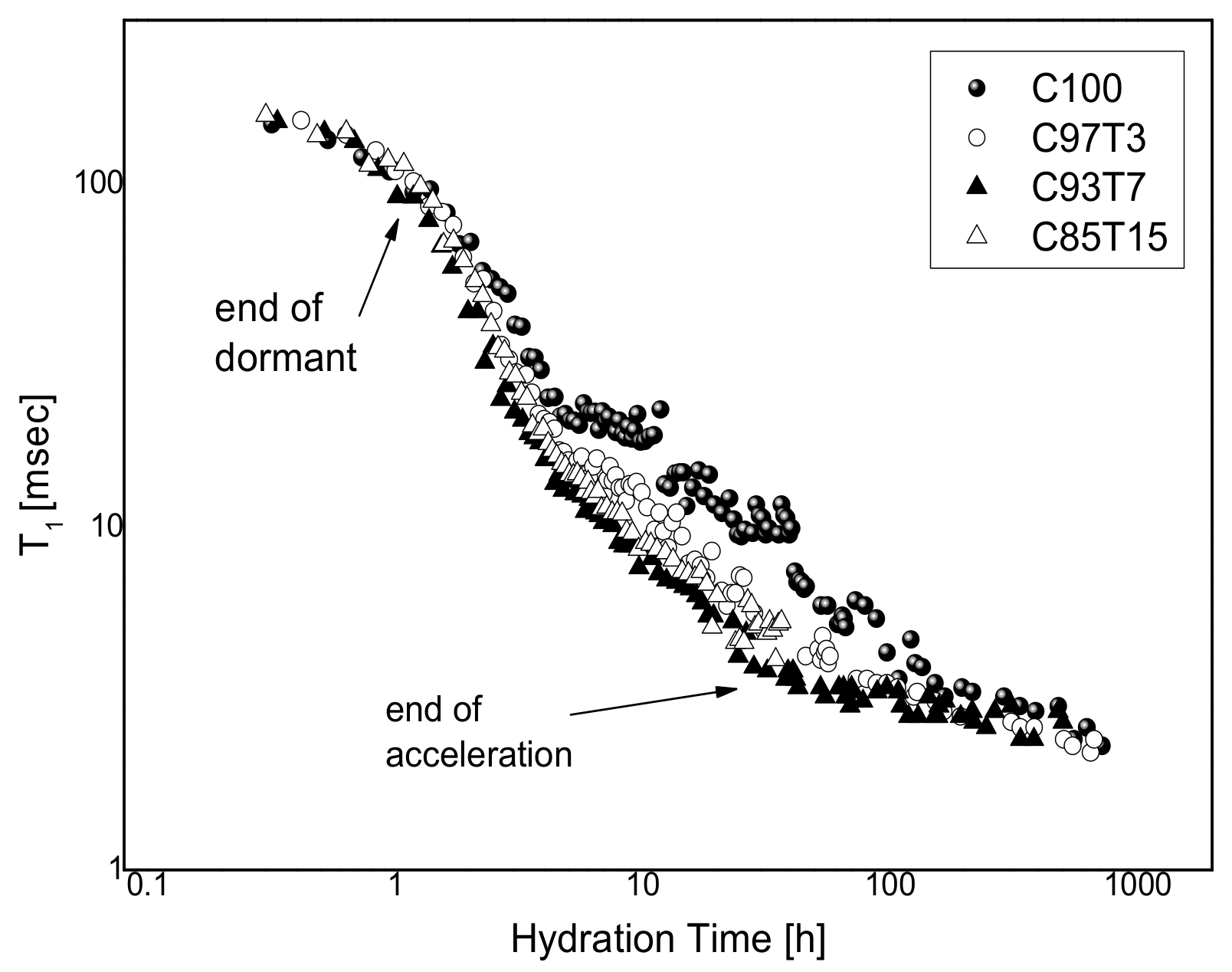
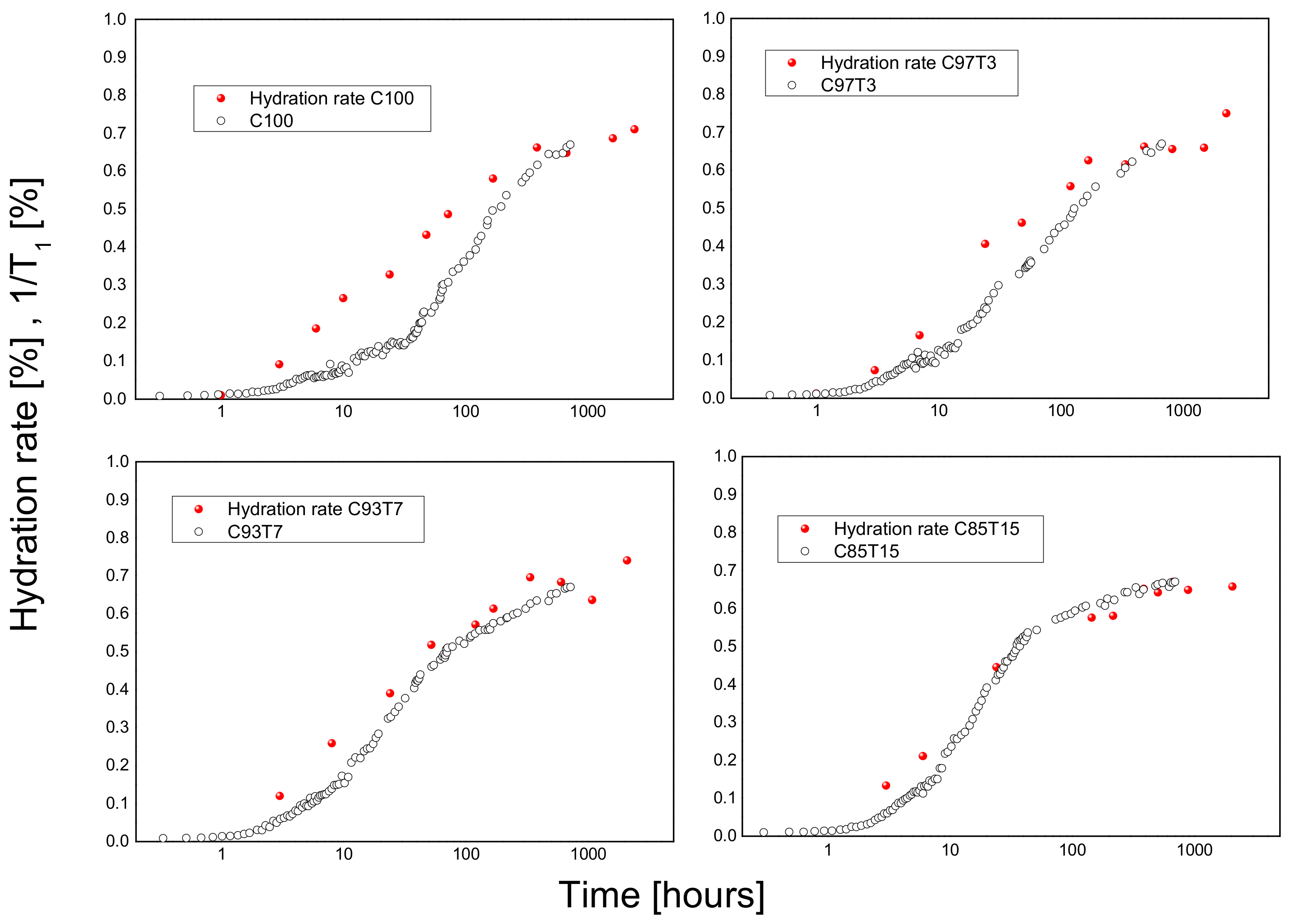
3.3. 1H-Spin–Lattice Relaxation Time (T1) Measurements
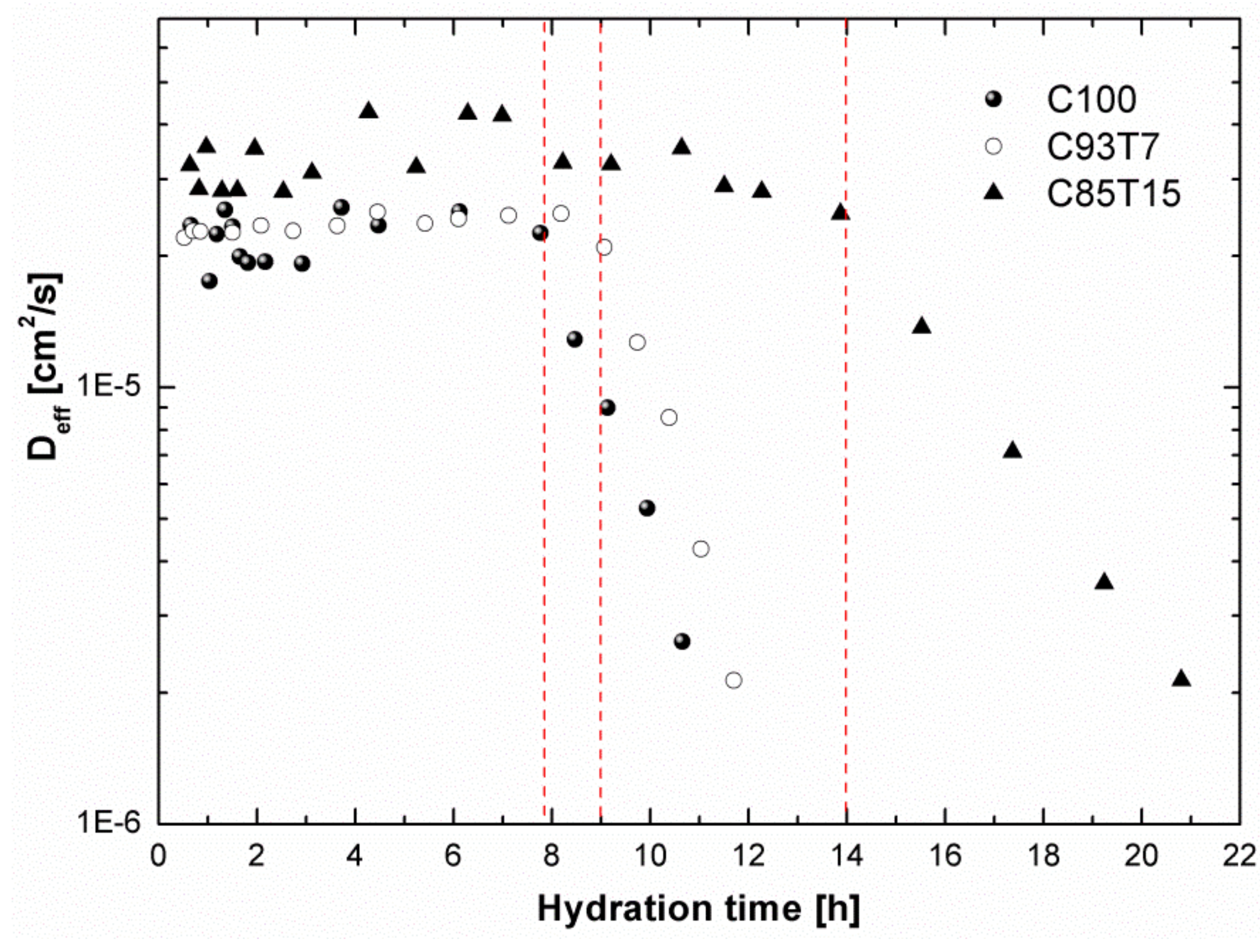
3.4. 1H-NMR Diffusion Measurements
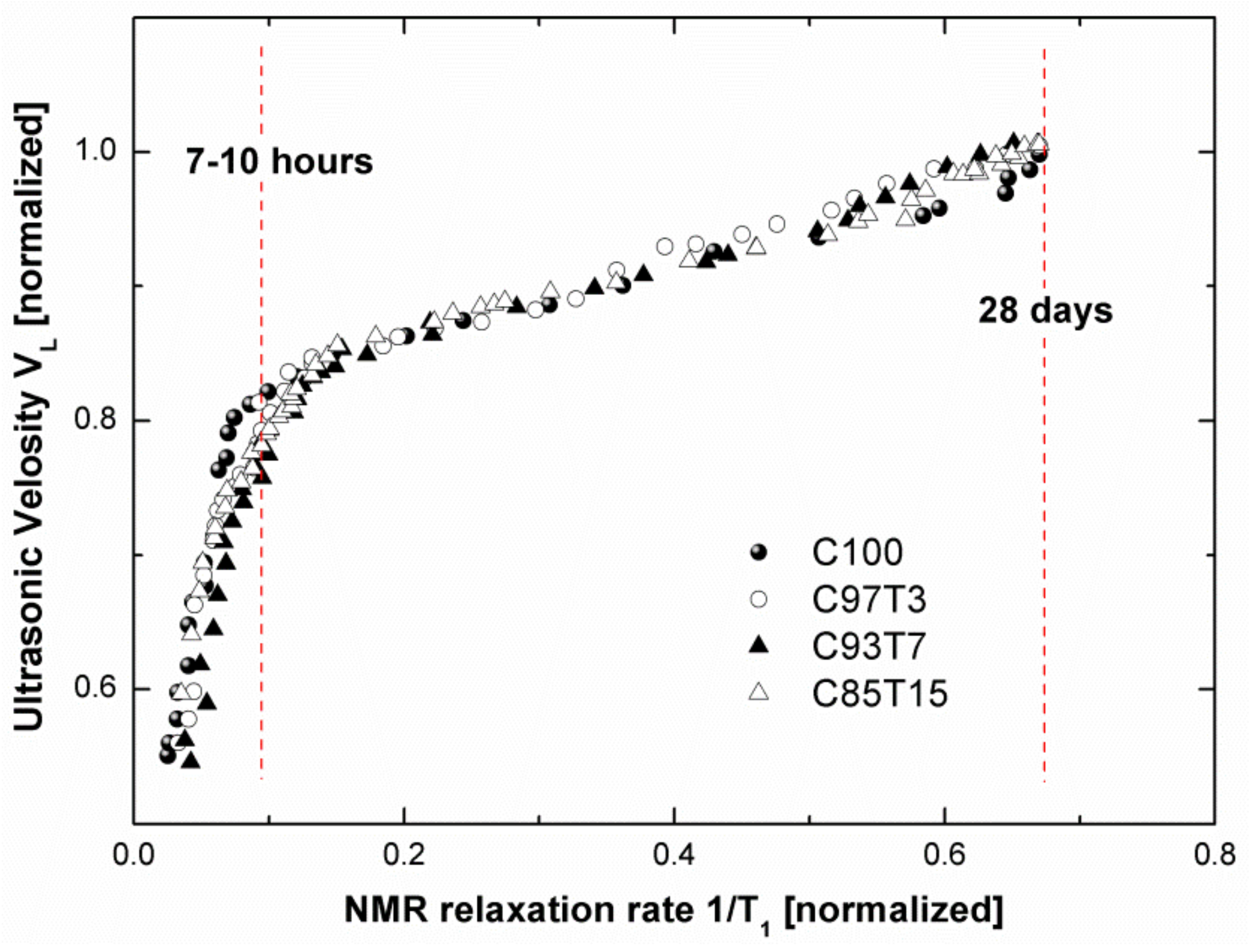
3.5. Correlation between NMR and Ultrasonic Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Competing Financial Interests
References
- Park, J.H.; Kim, S.; Bard, A.J. Novel carbon-doped TiO2 nanotube arrays with high aspect ratios for efficient solar water splitting. Nano Lett. 2006, 6, 24–28. [Google Scholar] [CrossRef] [PubMed]
- Nazeeruddin, M.K.; Kay, A.; Rodicio, I.; Humphry-Baker, R.; Mueller, E.; Liska, P.; Vlachopoulos, N.; Graetzel, M. Conversion of light to electricity by cis-X2bis(2,2′-bipyridyl-4,4′-dicarboxylate)ruthenium(II) charge-transfer sensitizers (X = Cl-, Br-, I-, CN-, and SCN-) on nanocrystalline titanium dioxide electrodes. J. Am. Chem. Soc. 1993, 115, 6382–6390. [Google Scholar] [CrossRef]
- Parkin, I.P.; Palgrave, R.G. Self-cleaning coatings. J. Mater. Chem. 2005, 17, 1689–1695. [Google Scholar] [CrossRef]
- Lackhoff, M.; Prieto, X.; Nestle, N.; Dehn, F.; Niessner, R. Photocatalytic activity of semiconductor-modified cement—Influence of semiconductor type and cement ageing. Appl. Catal. B-Environ. 2003, 43, 205–216. [Google Scholar] [CrossRef]
- Hüsken, G.; Hunger, M.; Ballari, M.M.; Brouwers, H.J.H. The effect of various process conditions on the photocatalytic degradation of NO. In NICOM3; Bittnar, Z., Bartos, P.J.M., Nemecek, J., Smilauer, V., Zeman, J., Eds.; Springer: Prague, Czech Republic, 2009; pp. 223–229. [Google Scholar]
- Fujishima, A.; Hashimoto, K.; Watanabe, T. TiO2 Photocatalysis, Fundamentals and Applications; BKC Inc.: Tokyo, Japan, 1999. [Google Scholar]
- VVallée, F.; Ruot, B.; Bonafous, L.; Guillot, L.; Pimpinelli, N.; Cassar, L.; Strini, A.; Mapelli, E.; Schiavi, L.; Gobin, C.; et al. Innovative self-cleaning and de-polluting facade surfaces. In Proceedings of the CIB World Building Congress, Toronto, Canada, 2–7 May 2004; pp. 1–7. [Google Scholar]
- Ballari, M.M.; Hunger, M.; Hüsken, G.; Brouwers, H.J.H. Heterogeneous Photocatalysis Applied to Concrete Pavement for Air Remediation. In NICOM3; Bittnar, Z., Bartos, P.J.M., Nemecek, J., Smilauer, V., Zeman, J., Eds.; Springer: Prague, Czech Republic, 2009; pp. 409–414. [Google Scholar]
- Guidebook on Non-Destructive Testing of Concrete Structures; International Atomic Energy Agency: Vienna, Austria, 2002.
- Jennings, H.M.; Bullard, J.W.; Thomas, J.J.; Andrade, J.E.; Chen, J.J.; Scherer, G.W. Characterization and Modeling of Pores and Surfaces in Cement Paste: Correlations to Processing and Properties. J. Adv. Concr. Technol. 2008, 6, 5–29. [Google Scholar] [CrossRef] [Green Version]
- Jehng, J.-Y.; Sprague, D.; Halperin, W. Pore structure of hydrating cement paste by magnetic resonance relaxation analysis and freezing. Magn. Reson. Imaging 1996, 14, 785–791. [Google Scholar] [CrossRef]
- Boguszyńska, J.; Tritt-Goc, J. 1H NMR Cryoporometry Study of the Melting Behavior of Water in White Cement. Z. Nat. A 2004, 59, 550–558. [Google Scholar] [CrossRef]
- Papavassiliou, G.; Milia, F.; Fardis, M.; Rumm, R.; Laganas, E. 1H Nuclear Magnetic Resonance Imaging of Water Diffusion in Hardened Cement Pastes. J. Am. Ceram. Soc. 1993, 76, 2109–2111. [Google Scholar] [CrossRef]
- Prado, P.J.; Balcom, B.J.; Beyea, S.D.; Bremner, T.W.; Armstrong, R.L.; Pishe, R.; Gratten-Bellew, P.E. Spatially resolved relaxometry and pore size distribution by single-point MRI methods: Porous media calorimetry. J. Phys. D Appl. Phys. 1998, 31, 2040. [Google Scholar] [CrossRef]
- Jaffer, S.; Lemaire, C.; Hansson, C.; Peemoeller, H. MRI: A complementary tool for imaging cement pastes. Cem. Concr. Res. 2007, 37, 369–377. [Google Scholar] [CrossRef]
- Friedemann, K.; Stallmach, F.; Kärger, J. NMR diffusion and relaxation studies during cement hydration—A non-destructive approach for clarification of the mechanism of internal post curing of cementitious materials. Cem. Concr. Res. 2006, 36, 817–826. [Google Scholar] [CrossRef]
- Nestle, N.; Galvosas, P.; Kärger, J. Liquid-phase self-diffusion in hydrating cement pastes—Results from NMR studies and perspectives for further research. Cem. Concr. Res. 2007, 37, 398–413. [Google Scholar] [CrossRef]
- Neuman, C. Spin echo of spins diffusing in a bounded medium. J. Chem. Phys. 1974, 60, 4508–4511. [Google Scholar] [CrossRef]
- De Swiet, T.M.; Sen, P.N. Decay of nuclear magnetization by bounded diffusion in a constant field gradient. J. Chem. Phys. 1994, 100, 5597–5604. [Google Scholar] [CrossRef] [Green Version]
- Nestle, N. A Simple Semiempiric Model for NMR Relaxometry Data of Hydrating Cement Pastes. Cem. Concr. Res. 2004, 34, 447–454. [Google Scholar] [CrossRef]
- Papavassiliou, G.; Fardis, M.; Laganas, E.; Leventis, A.; Hassanien, A.; Milia, F.; Papageorgiou, A.; Chaniotakis, E. Role of the surface morphology in cement gel growth dynamics: A combined nuclear magnetic resonance and atomic force microscopy study. J. Appl. Phys. 1997, 82, 449–452. [Google Scholar] [CrossRef]
- Blinc, R.; Dolinsek, J.; Lahajnar, G.; Sepe, A.; Zupančič, I.; Zumer, S.; Milia, F.; Pintar, M.M. Spin-Lattice Relaxation of Water in Cement Gels. Z. Nat. A 1988, 43, 1026–1038. [Google Scholar] [CrossRef]
- Laganas, E.; Papavassiliou, G.; Fardis, M.; Leventis, A.; Milia, F.; Chaniotakis, E.; Meletiou, C. 1H Nuclear Magnetic Resonance Relaxation Measurements in Developing Porous Structures: A Study in Hydrating Cement. J. Appl. Phys. 1995, 77, 3343–3348. [Google Scholar] [CrossRef]
- D’Angelo, R.; Plona, T.J.; Schwartz, L.M.; Coveney, P. Ultrasonic measurements on hydrating cement slurries. Adv. Cem. Based Mater. 1995, 2, 8–14. [Google Scholar] [CrossRef]
- Boumiz, A.; Vernet, C.; Tenoudji, F.C. Mechanical properties of cement pastes and mortars at early ages: Evolution with time and degree of hydration. Adv. Cem. Based Mater. 1996, 3, 94–106. [Google Scholar] [CrossRef]
- Sayers, C.; Dahlin, A. Propagation of ultrasound through hydrating cement pastes at early times. Adv. Cem. Based Mater. 1993, 1, 12–21. [Google Scholar] [CrossRef]
- Keating, J.; Hannant, D.J.; Hibbert, A.P. Comparison of shear modulus and UPV techniques to measure the build-up of structure in fresh cement pastes used in oil well cementing. Cem. Concr. Res. 1989, 19, 554–566. [Google Scholar] [CrossRef]
- Ye, G.; Van Breugel, K.; Fraaij, A.L.A. Experimental study on ultrasonic pulse velocity evaluation of the microstructure of cementitious material at early age. Heron 2001, 46, 161–167. [Google Scholar]
- Jalal, M. Durability enhancement of concrete by incorporating titanium dioxide nanopowder into binder. J. Am. Sci. 2012, 8, 289–294. [Google Scholar]
- Jalal, M.; Fathi, M.; Farza, M. Effects of fly ash and TiO2 nanoparticles on rheological, mechanical, microstructural and thermal properties of high strength self compacting concrete. Mech. Mater. 2013, 61, 11–27. [Google Scholar] [CrossRef]
- Lawrence, P.; Cyr, M.; Ringot, E. Mineral admixtures in mortars-Effect of inert materials on short-term hydration. Cem. Concr. Res. 2003, 33, 1939–1947. [Google Scholar] [CrossRef]
- Jayapalan, A.; Lee, B.; Kurtis, K. Effect of Nano-sized Titanium Dioxide on Early Age Hydration of Portland Cement. In NICOM3; Bittnar, Z., Bartos, P.J.M., Nemecek, J., Smilauer, V., Zeman, J., Eds.; Springer: Prague, Czech Republic, 2009; pp. 267–273. [Google Scholar]
- Folli, A.; Pade, C.; Hansen, T.B.; De Marco, T.; Macphee, D.E. TiO2 photocatalysis in cementitious systems: Insights into self-cleaning and depollution chemistry. Cem. Concr. Res. 2012, 42, 539–548. [Google Scholar] [CrossRef]
- Chen, J.; Kou, S.-C.; Poon, C.-S. Hydration and properties of nano-TiO2 blended cement composites. Cem. Concr. Compos. 2012, 34, 642–649. [Google Scholar] [CrossRef]
- Nazari, A. The effects of curing medium on flexural strength and water permeability of concrete incorporating TiO2 nanoparticles. Mater. Struct. 2011, 44, 773–786. [Google Scholar] [CrossRef]
- Noorvand, H.; Ali, A.A.A.; Demirboga, R.; Farzadnia, N.; Noorvand, H. Incorporation of nano TiO2 in black rice husk ash mortars. Constr. Build. Mater. 2013, 47, 1350–1361. [Google Scholar] [CrossRef]
- Li, H.; Zhang, M.-H.; Ou, J.-P. Abrasion resistance of concrete containing nano-particles for pavement. Wear 2006, 260, 1262–1266. [Google Scholar] [CrossRef]
- Zhang, M.-H.; Li, H. Pore structure and chloride permeability of concrete containing nano-particles for pavement. Constr. Build. Mater. 2011, 25, 608–616. [Google Scholar] [CrossRef]
- Soleymani, F. The filler effects TiO2 nanoparticles on increasing compressive strength of limestone aggregate-based concrete. J. Am. Sci. 2012, 8, 3. [Google Scholar]
- Rashad, A.M. A Synopsis about the Effect of Nano-Titanium Dioxide on Some Properties of Cementitious Materials-a Short Guide for Civil Engineer. Rev. Adv. Mater. Sci. 2015, 40, 72–88. [Google Scholar]
- Meng, T.; Yu, Y.; Qian, X.; Zhan, S.; Qian, K. Effect of nano-TiO2 on the mechanical properties of cement mortar. Constr. Build. Mater. 2012, 29, 241–245. [Google Scholar] [CrossRef]
- Lee, B.Y. Effect of Titanium Dioxide Nanoparticles on Early Age and Long Term Properties of Cementitious Materials. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2012. [Google Scholar]
- Behfarnia, K.; Keivan, A.; Keivan, A. The effects of TiO2 and ZnO nanoparticles on physical and mechanical properties of normal concrete. Asian J. Civ. Eng. 2013, 14, 517–531. [Google Scholar]
- Leslie, J.; Cheesman, W. An ultrasonic method of studying deterioration and cracking in concrete structures. J. Am. Concr. Inst. 1949, 21, 17–36. [Google Scholar]
- Lee, H.K.; Lee, K.M.; Kim, Y.H.; Yim, H.; Bae, D.B. Ultrasonic in-situ monitoring of setting process of high-performance concrete. Cem. Concr. Res. 2004, 34, 631–640. [Google Scholar] [CrossRef]
- Robeyst, N.; Gruyaert, E.; Grosse, C.U.; De Belie, N. Monitoring the setting of concrete containing blast-furnace slag by measuring the ultrasonic p-wave velocity. Cem. Concr. Res. 2008, 38, 1169–1176. [Google Scholar] [CrossRef]
- Gallegos, D.P.; Munn, K.; Smith, D.S.; Stermer, D.L. A NMR Technique for the Analysis of Pore Structure: Application to Materials with Well-Defined Pore Structure. J. Colloid Interface Sci. 1987, 119, 127–140. [Google Scholar] [CrossRef]
- Schreiner, L.J.; MacTavish, J.C.; Miljković, L.; Pintar, M.; Blinc, R.; Lahajnar, G.; Lasic, D.; Reeves, L.W. NMR Line Shape-Spin-Lattice Relaxation Correlation Study of Portland Cement Hydration. J. Am. Ceram. Soc. 1985, 68, 10–16. [Google Scholar] [CrossRef]
- McDonald, P.J.; Korb, J.P.; Mitchell, J.; Monteilhet, L. Surface relaxation and chemical exchange in hydrating cement pastes: A two-dimensional NMR relaxation study. Phys. Rev. E 2005, 72, 011409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hürlimann, M.D. Effective gradients in porous media due to susceptibility differences. J. Magn. Reson. 1998, 131, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Valckenborg, R.M.E. NMR on Technological Porous Materials; Eindhoven University of Technology: Eindhoven, The Netherlands, 2001. [Google Scholar]
- Taylor, H.F. Cement Chemistry; Thomas Telford: London, UK, 1997. [Google Scholar]
- Allen, A.J.; Thomas, J.J.; Jennings, H.M. Composition and density of nanoscale calcium-silicate-hydrate in cement. Nat. Mater. 2007, 6, 311–316. [Google Scholar] [CrossRef] [PubMed]
- EUROPEAN STANDARD NORME196 Part 3, Methods of testing cement. In Determination of Setting Times and Soundness; EU: Brussel, Belgium, 2005.
- Karakosta, E.; Diamantopoulos, G.; Katsiotis, M.S.; Fardis, M.; Papavassiliou, G.; Pipilikaki, P.; Protopapas, M.; Panagiotaras, D. In Situ Monitoring of Cement Gel Growth Dynamics. Use of a Miniaturized Permanent Halbach Magnet for Precise 1H NMR Studies. Ind. Eng. Chem. Res. 2010, 49, 613–622. [Google Scholar] [CrossRef]
- Provencher, S.W. A Constrained Regularization Method for Inverting Data Represented by Linear Algebraic or Integral Equations. Comput. Phys. Commun. 1982, 27, 213–227. [Google Scholar] [CrossRef]
- Parrott, L.J.; Geiker, M.; Gutteridge, W.A.; Killoh, D. Monitoring Portland cement hydration: Comparison of methods. Cem. Concr. Res. 1990, 20, 919–926. [Google Scholar] [CrossRef]
- Tsivilis, S.; Kakali, G.; Chaniotakis, E.; Souvaridou, A. A study on the hydration of Portland limestone cement by means of TG. J. Therm. Anal. Calorim. 1998, 52, 863–870. [Google Scholar] [CrossRef]
- Cioffi, R.; Marroccoli, M.; Santoro, L.; Valenti, G. DTA study of the hydration of systems of interest in the field of building materials manufacture. J. Therm. Anal. Calorim. 1992, 38, 761–770. [Google Scholar] [CrossRef]
- Seki, S.; Kasahara, K.; Kuriyama, T.; Kawasumi, M. Effects of Hydration of cement on compressive strength, modulus of elasticity and creep of concrete. In Proceedings of the Fifth International Symposium on the Chemistry of Cement, Tokyo, Japan, 7–11 October 1968; pp. 175–185. [Google Scholar]
- Ye, G.; Lura, P.; van Breugel, K.; Fraaij, A.L.A. Study on the development of the microstructure in cement-based materials by means of numerical simulation and ultrasonic pulse velocity measurement. Cem. Concr. Res. 2004, 26, 491–497. [Google Scholar] [CrossRef]
- Keating, J.; Hannant, D.J.; Hibbert, A.P. Correlation between cube strength, ultrasonic pulse velocity and volume change for oil well cement slurries. Cem. Concr. Res. 1989, 19, 715–726. [Google Scholar] [CrossRef]
- Gaunaurd, G.; Überall, H. Resonance theory of bubbly liquids. J. Acoust. Soc. Am. 1981, 69, 362–370. [Google Scholar] [CrossRef]
- Feylessoufi, A.; Tenoudji, F.C.; Morin, V.; Richard, P. Early ages shrinkage mechanisms of ultra-high-performance cement-based materials. Cem. Concr. Res. 2001, 31, 1573–1579. [Google Scholar] [CrossRef]
- Bentz, D.P.; Coveney, P.V.; Garboczi, E.J.; Kleyn, M.F.; Stutzman, P.E. Cellular automaton simulations of cement hydration and microstructure development. Model. Simul. Mater. Sci. Eng. 1994, 2, 783. [Google Scholar] [CrossRef]
- Trtnik, G.; Turk, G. Influence of superplasticizers on the evolution of ultrasonic P-wave velocity through cement pastes at early age. Cem. Concr. Res. 2013, 51, 22–31. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, Y.; Jiang, Q.; Sun, G.; Zhang, W. In situ continuously monitoring the early age microstructure evolution of cementitious materials using ultrasonic measurement. Constr. Build. Mater. 2011, 25, 3998–4005. [Google Scholar] [CrossRef]
- Trtnik, G.; Valič, M.I.; Kavčič, F.; Turk, G. Comparison between two ultrasonic methods in their ability to monitor the setting process of cement pastes. Cem. Concr. Res. 2009, 39, 876–882. [Google Scholar] [CrossRef] [Green Version]
- Reinhardt, H.; Grosse, C. Continuous monitoring of setting and hardening of mortar and concrete. Constr. Build. Mater. 2004, 18, 145–154. [Google Scholar] [CrossRef]
- Buchwald, A.; Tatarin, R.; Stephan, D. Reaction progress of alkaline-activated metakaolin-ground granulated blast furnace slag blends. J. Mater. Sci. 2009, 44, 5609–5617. [Google Scholar] [CrossRef]
- Overloop, K.; Gerven, L.V. NMR relaxation in adsorbed water. J. Magn. Reson. 1992, 100, 303–315. [Google Scholar] [CrossRef]
- Blinc, R.; Lahajnar, G.; Zumer, S.; Pintar, M.M. NMR Study of the Time Evolution of the Fractal Geometry of Cement Gels. Phys. Rev. B 1988, 38, 2873–2875. [Google Scholar] [CrossRef] [PubMed]
- Karakosta, E.; Lagkaditi, L.; ElHardalo, S.; Biotaki, A.; Kelessidis, V.C.; Fardis, M.; Papavassiliou, G. Pore structure evolution and strength development of G-type elastic oil well cement. A combined 1 H NMR and ultrasonic study. Cem. Concr. Res. 2015, 72, 90–97. [Google Scholar] [CrossRef]
- Lee, B.Y.; Kurtis, K.E. Influence of TiO2 nanoparticles on early C3S hydration. J. Am. Ceram. Soc. 2010, 93, 3399–3405. [Google Scholar] [CrossRef]
- Bentz, D.P.; Garboczi, E.J. Percolation of phases in a three-dimensional cement paste microstructural model. Cem. Concr. Res. 1991, 21, 325–344. [Google Scholar] [CrossRef]
- Scherer, G.W.; Zhang, J.; Quintanilla, J.A.; Torquato, S. Hydration and percolation at the setting point. Cem. Concr. Res. 2012, 42, 665–672. [Google Scholar] [CrossRef]
- Gussoni, M.; Greco, F.; Bonazzi, F.; Vezzoli, A.; Botta, D.; Dotelli, G.; Sora, I.N.; Pelosato, R.; Zetta, L. 1H NMR spin-spin relaxation and imaging in porous systems: An application to the morphological study of white portland cement during hydration in the presence of organics. Magn. Reson. Imaging 2004, 22, 877–889. [Google Scholar] [CrossRef] [PubMed]



| Sample | Percolation Threshold, pc | Vicat Setting Times (h) | ||
|---|---|---|---|---|
| Ultrasonic/h | NMR/h | Initial | Final | |
| C100 | 4.7 ± 0.08 | 3.6 ± 0.1 | 4.18 ± 0.02 | 4.88 ± 0.02 |
| C97T3 | 4.3 ± 0.1 | 3.3 ± 0.1 | 3.66 ± 0.02 | 4.26 ± 0.02 |
| C93T7 | 3.7 ± 0.2 | 2.8 ± 0.2 | 3.35 ± 0.02 | 3.80 ± 0.02 |
| C85T15 | 3.2 ± 0.4 | 2.2 ± 0.3 | 2.78 ± 0.02 | 3.15 ± 0.02 |
| Samples | C100 | C97T3 | C93T7 | C85T15 | |
|---|---|---|---|---|---|
| NMR | Start of acceleration (h) | 1.63 | 1.57 | 1.20 | 1.08 |
| Formation of “shoulder” (h) | 4.88 | 4.71 | - | - | |
| Start of diffusion (h) | 89.0 | 43.0 | 29.0 | 23.0 | |
| UltraSounic | Initial detection of signal (h) | 2.75 | 2.73 | 2.22 | 2.20 |
| End of acceleration (h) | 8.8 | 6.0 | 4.9 | 3.9 | |
| End of deceleration (h) | 692 | 570 | 490 | 306 | |
| Calorimetry | Start of acceleration (h) | 1.67 | 1.37 | 1.26 | 1.06 |
| End of acceleration/start of deceleration (h) | 9.04 | 6.48 | 5.66 | 4.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diamantopoulos, G.; Katsiotis, M.; Fardis, M.; Karatasios, I.; Alhassan, S.; Karagianni, M.; Papavassiliou, G.; Hassan, J. The Role of Titanium Dioxide on the Hydration of Portland Cement: A Combined NMR and Ultrasonic Study. Molecules 2020, 25, 5364. https://doi.org/10.3390/molecules25225364
Diamantopoulos G, Katsiotis M, Fardis M, Karatasios I, Alhassan S, Karagianni M, Papavassiliou G, Hassan J. The Role of Titanium Dioxide on the Hydration of Portland Cement: A Combined NMR and Ultrasonic Study. Molecules. 2020; 25(22):5364. https://doi.org/10.3390/molecules25225364
Chicago/Turabian StyleDiamantopoulos, George, Marios Katsiotis, Michael Fardis, Ioannis Karatasios, Saeed Alhassan, Marina Karagianni, George Papavassiliou, and Jamal Hassan. 2020. "The Role of Titanium Dioxide on the Hydration of Portland Cement: A Combined NMR and Ultrasonic Study" Molecules 25, no. 22: 5364. https://doi.org/10.3390/molecules25225364






