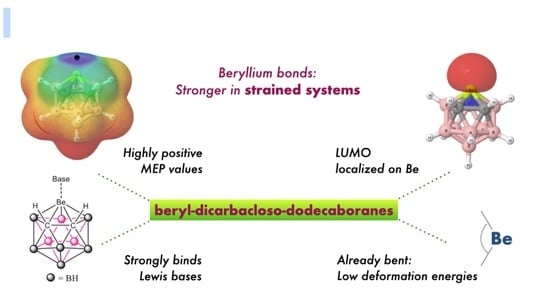
The Importance of Strain (Preorganization) in Beryllium Bonds
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
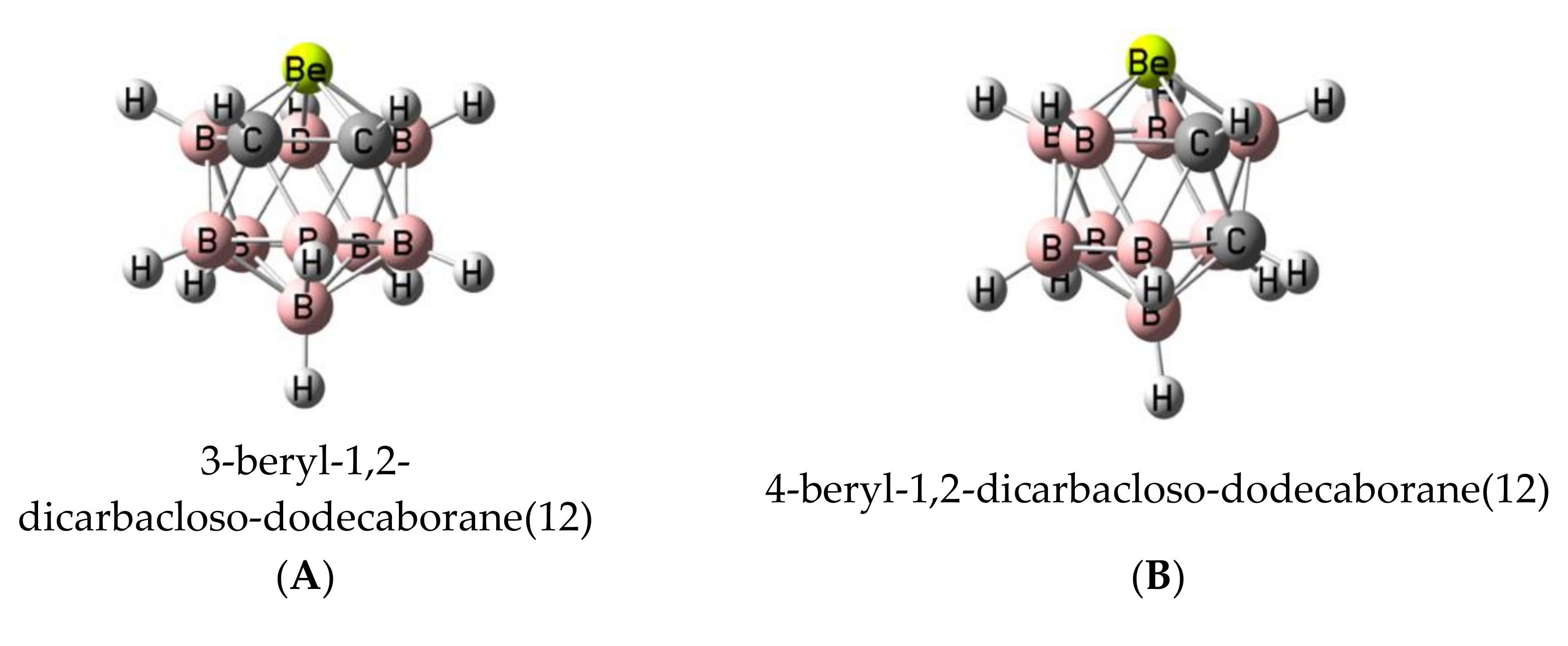
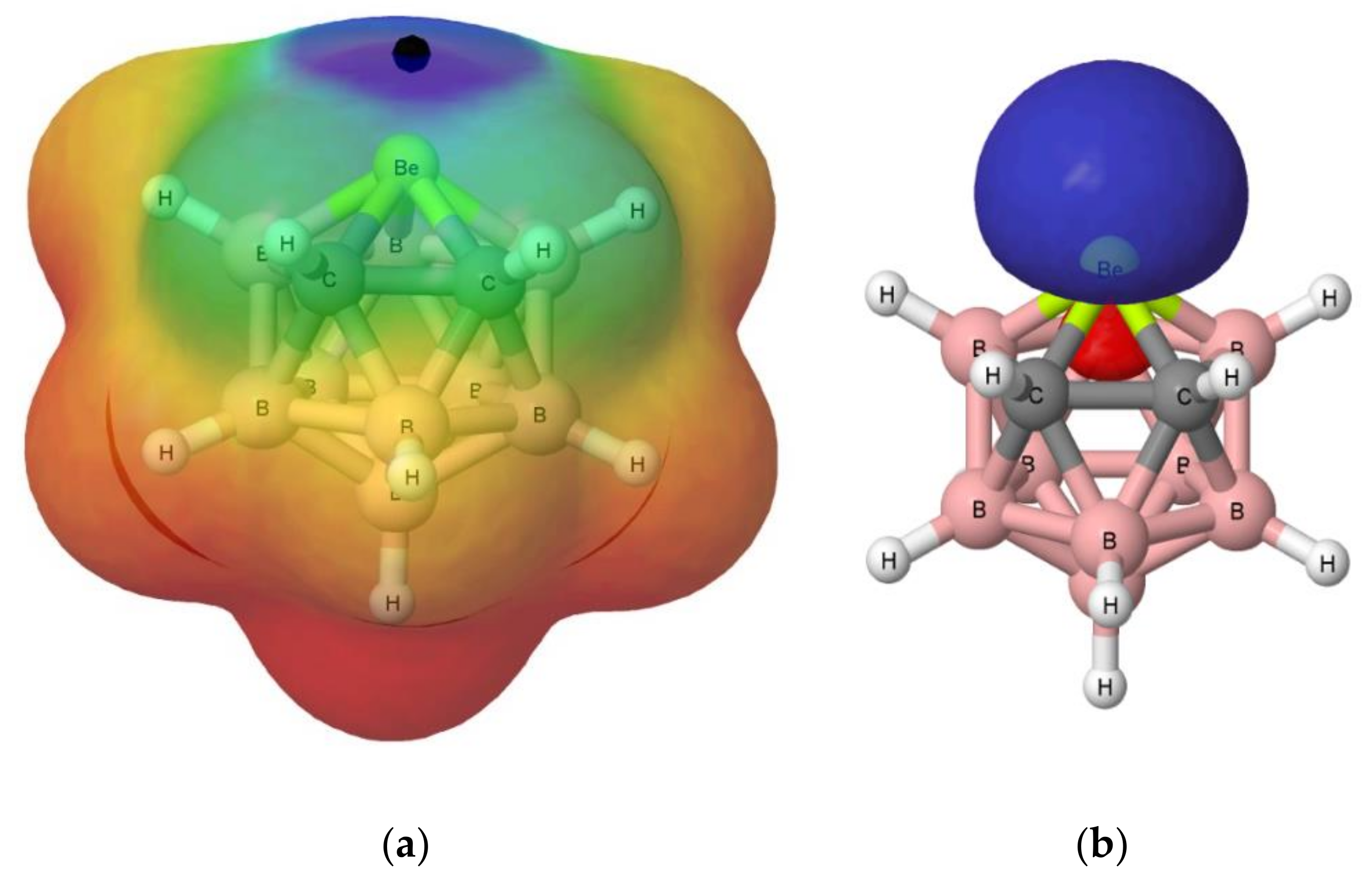
3.1. Isolated Be-Containing Lewis Acids
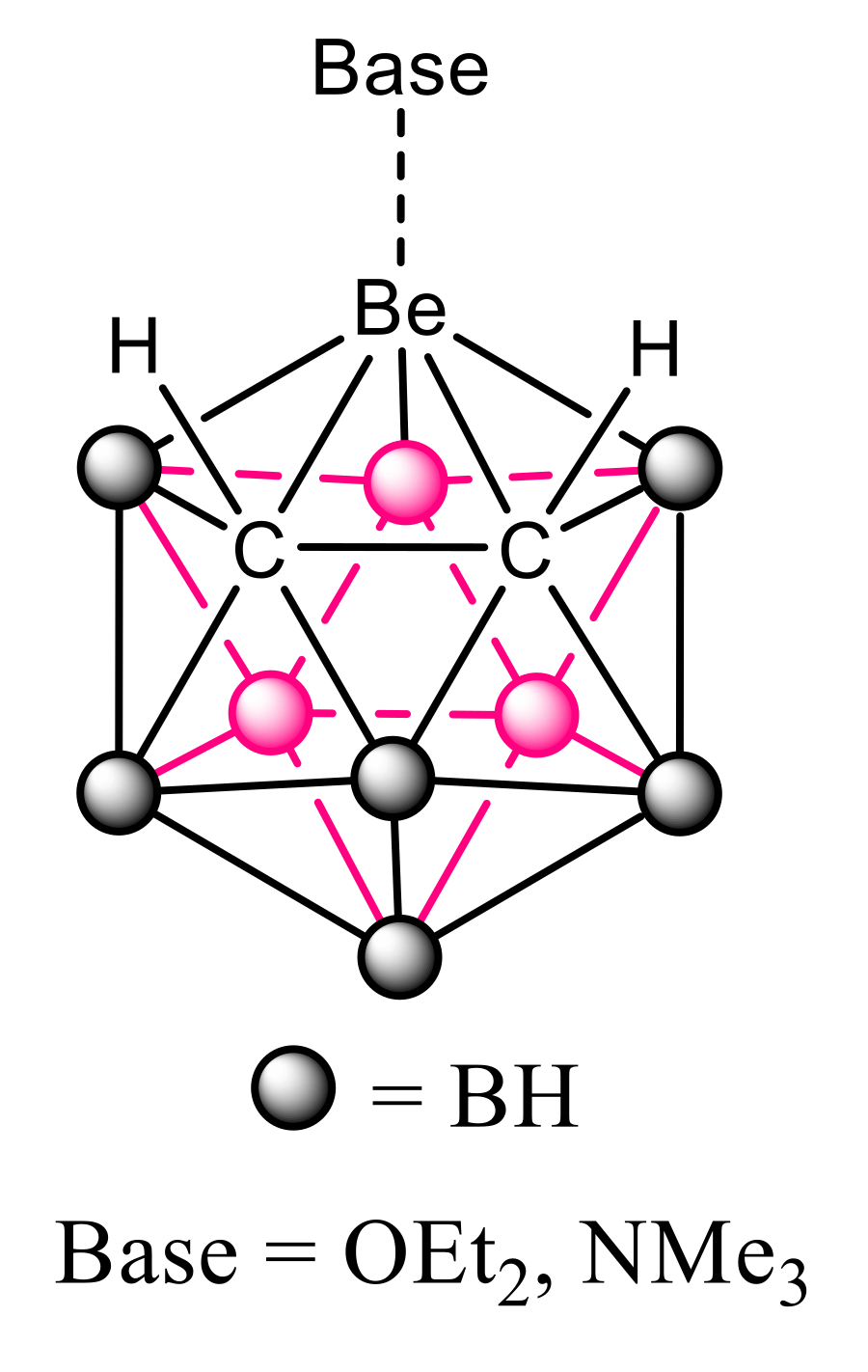
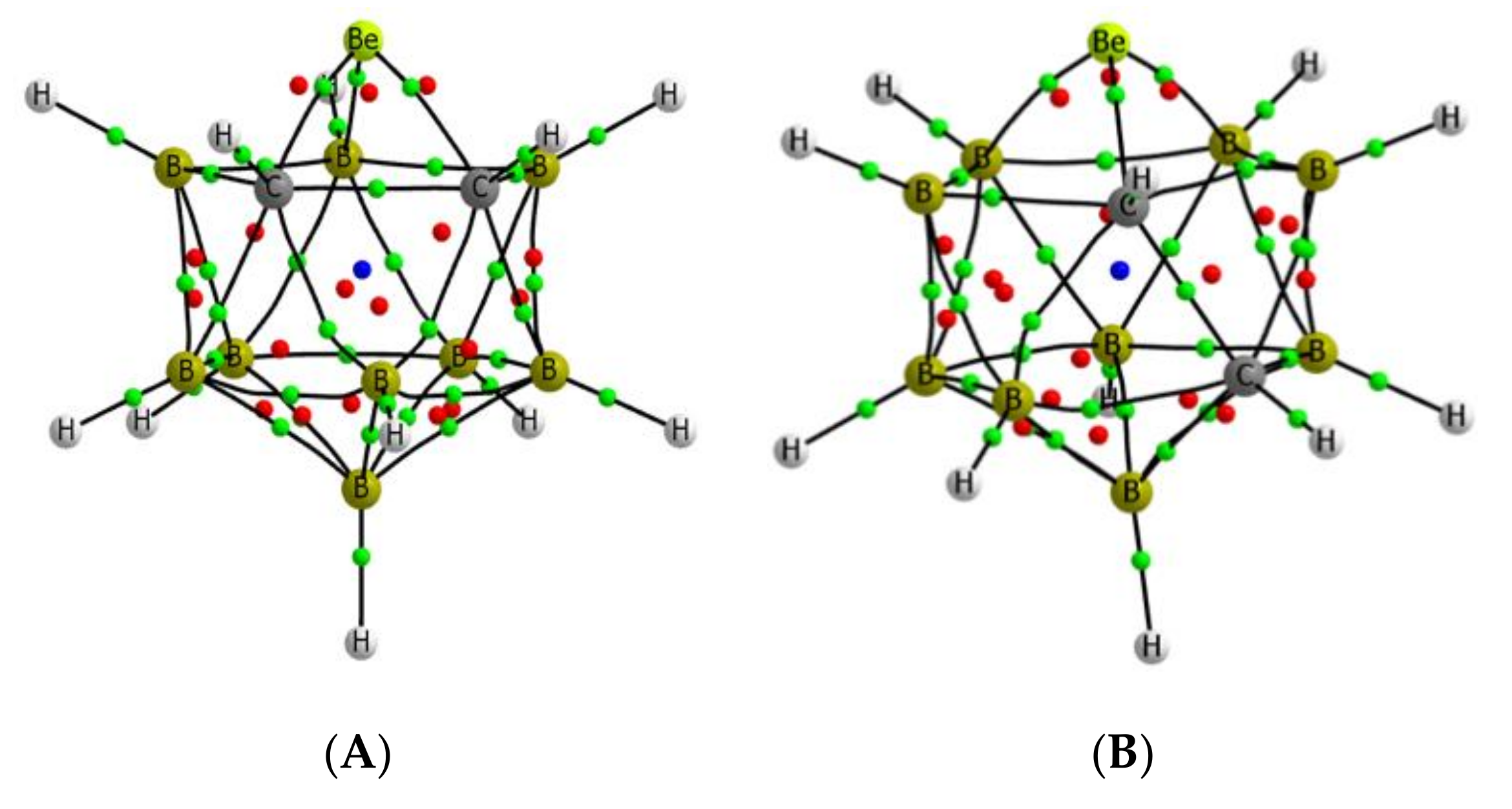
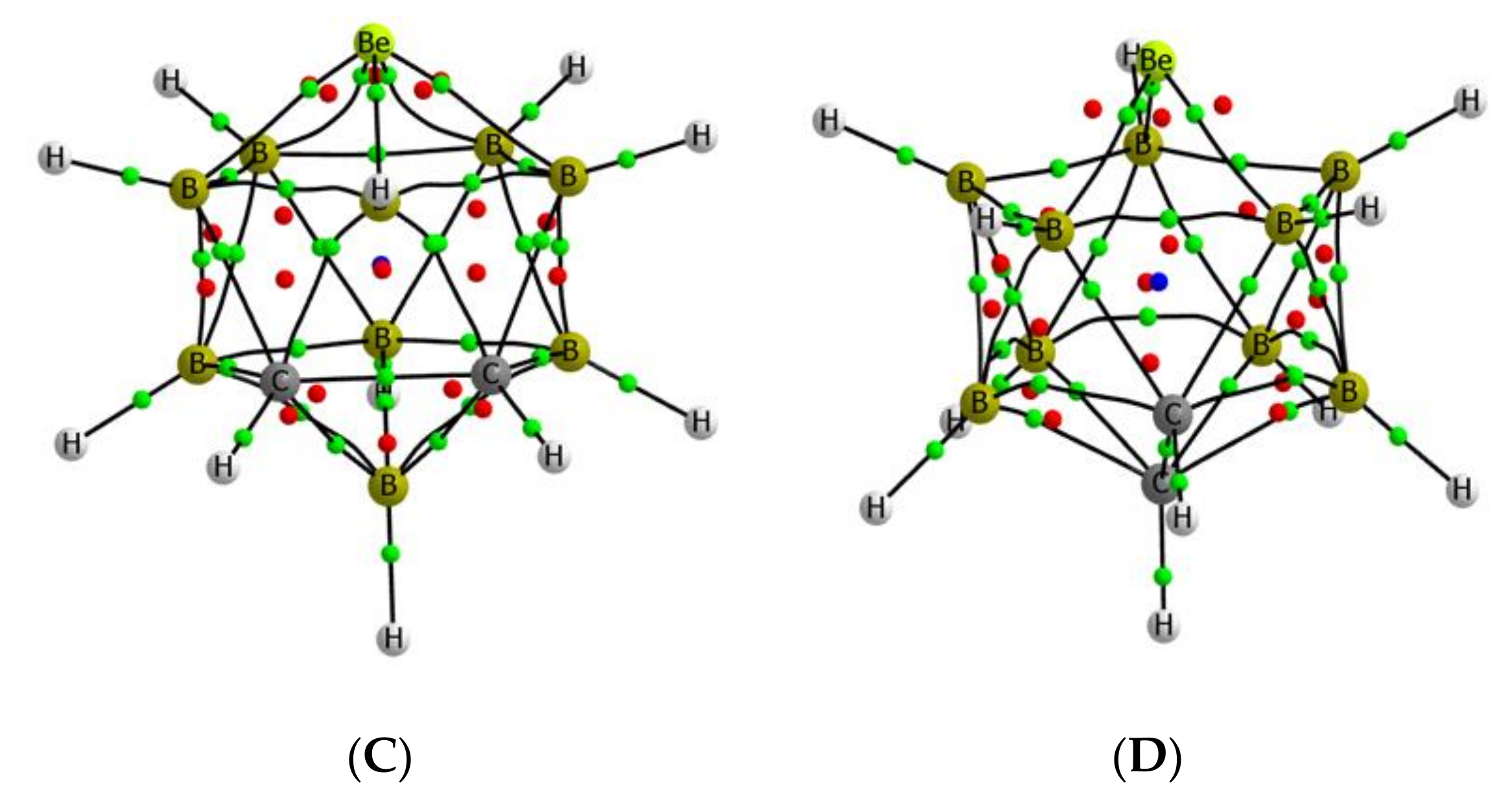
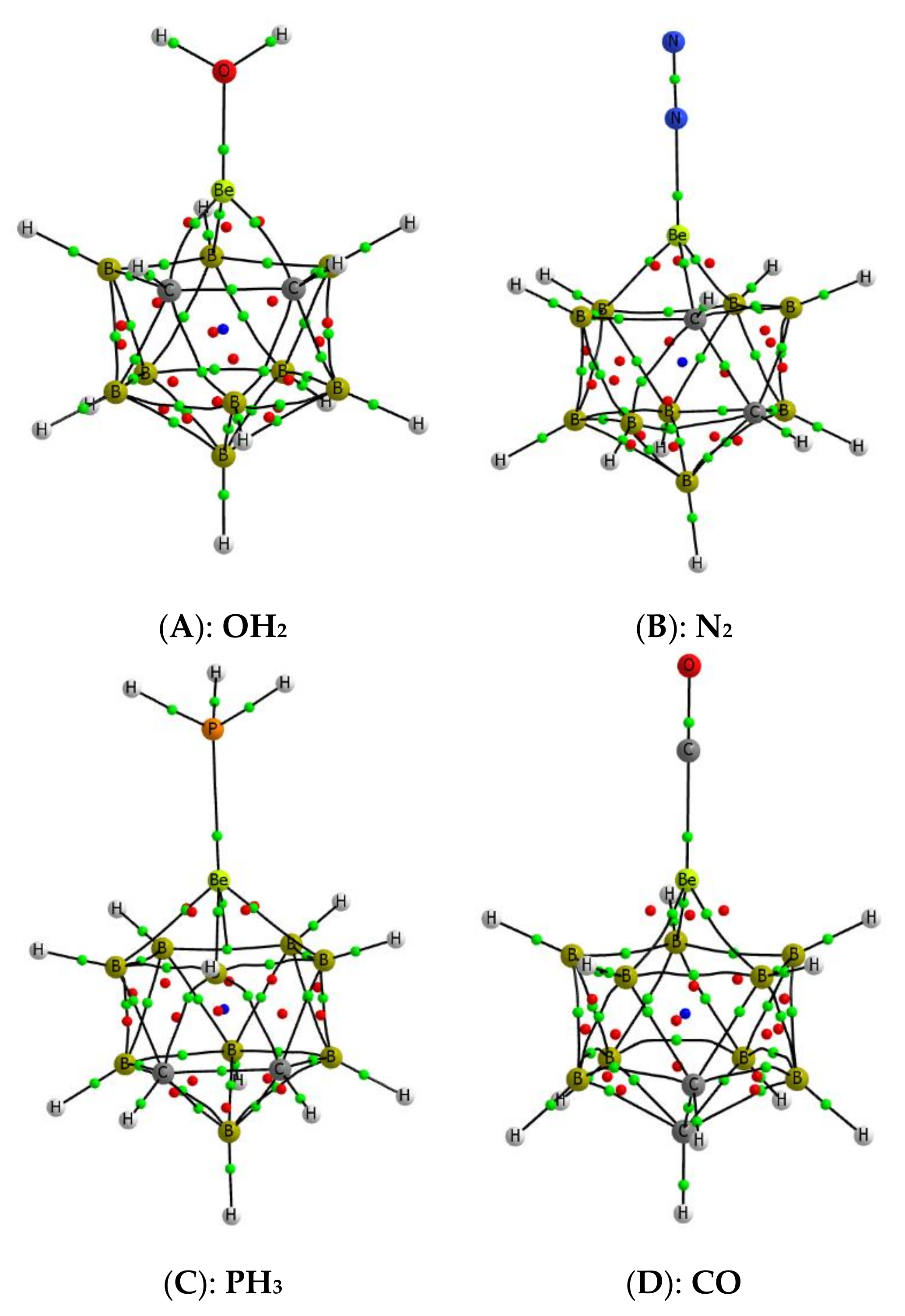
3.2. B9H11C2Be: Lewis Base Complexes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Naming Interactions from the Electrophilic Site. Cryst. Growth Des. 2014, 14, 2697–2702. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A. Aerogen Bonding Interaction: A New Supramolecular Force? Angew. Chem. Int. Ed. 2015, 54, 7340–7343. [Google Scholar] [CrossRef] [PubMed]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711. [Google Scholar] [CrossRef]
- Wang, W.; Ji, B.; Zhang, Y. Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef]
- Sanz, P.; Yáñez, M.; Mó, O. Competition between X···H···Y Intramolecular Hydrogen Bonds and X····Y (X = O, S, and Y = Se, Te) Chalcogen-Chalcogen Interactions. J. Phys. Chem. A 2002, 106, 4661–4668. [Google Scholar] [CrossRef]
- Alkorta, I.; Rozas, I.; Elguero, J. Molecular Complexes between Silicon Derivatives and Electron-Rich Groups. J. Phys. Chem. A 2001, 105, 743–749. [Google Scholar] [CrossRef]
- Aakeroy, C.B.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the chalcogen bond (IUPAC Recommendations 2019). Pure Appl. Chem. 2019, 91, 1889. [Google Scholar] [CrossRef]
- Grabowski, S.J. Tetrel bond–σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Boron and other Triel Lewis Acid Centers: From Hypovalency to Hypervalency. ChemPhysChem 2014, 15, 2985–2993. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Elguero, J.; Del Bene, J.E.; Mó, O.; Yáñez, M. New Insights into Factors Influencing B-N Bonding in X:BH3−nFn and X:BH3−nCln for X = N2, HCN, LiCN, H2CNH, NF3, NH3 and n = 0–3: The Importance of Deformation. Chem. Eur. J. 2010, 16, 11897–11905. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Alkorta, I.; Elguero, J.; Mooibroek, T.J.; Frontera, A. Spodium bonds: Noncovalent interactions involving group 12 of elements. Angew. Chem. Int. Ed. 2020, 59, 17482–17487. [Google Scholar] [CrossRef]
- Legon, A.C.; Walker, N.R. What’s in a name? ‘Coinage-metal’ non-covalent bonds and their definition. Phys. Chem. Chem. Phys. 2018, 20, 19332–19338. [Google Scholar] [CrossRef]
- Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Understanding Regium Bonds and their Competition with Hydrogen Bonds in Au2:HX Complexes. ChemPhysChem 2019, 20, 1572–1580. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Regium bonds between Mn clusters (M = Cu, Ag, Au and n = 2–6) and nucleophiles NH3 and HCN. Phys. Chem. Chem. Phys. 2018, 20, 22498–22509. [Google Scholar] [CrossRef]
- Stenlid, J.H.; Brinck, T. Extending the σ-Hole Concept to Metals: An Electrostatic Interpretation of the Effects of Nanostructure in Gold and Platinum Catalysis. J. Am. Chem. Soc. 2017, 139, 11012–11015. [Google Scholar] [CrossRef]
- Alkorta, I.; Legon, A.C. Non-Covalent Interactions Involving Alkaline-Earth Atoms and Lewis Bases B: An ab Initio Investigation of Beryllium and Magnesium Bonds, B···MR2 (M = Be or Mg, and R = H, F or CH3). Inorganics 2019, 7, 35. [Google Scholar] [CrossRef]
- Mó, O.; Montero-Campillo, M.M.; Alkorta, I.; Elguero, J.; Yáñez, M. Ternary Complexes Stabilized by Chalcogen and Alkaline-Earth Bonds: Crucial Role of Cooperativity and Secondary Noncovalent Interactions. Chem. Eur. J. 2019, 25, 11688–11695. [Google Scholar] [CrossRef]
- Alkorta, I.; Hill, J.G.; Legon, A.C. An ab initio investigation of alkali–metal non-covalent bonds B⋯LiR and B⋯NaR (R = F, H or CH3) formed with simple Lewis bases B: The relative inductive effects of F, H and CH3. Phys. Chem. Chem. Phys. 2020, 22, 16421–16430. [Google Scholar] [CrossRef] [PubMed]
- Yáñez, M.; Sanz, P.; Mó, O.; Alkorta, I.; Elguero, J. Beryllium Bonds, Do They Exist? J. Chem. Theor. Comput. 2009, 5, 2763–2771. [Google Scholar] [CrossRef] [PubMed]
- Montero-Campillo, M.M.; Mó, O.; Yáñez, M.; Alkorta, I.; Elguero, J. Chapter three—The beryllium bond. In Advances in Inorganic Chemistry; van Eldik, R., Puchta, R., Eds.; Academic Press: Cambridge, MA, USA, 2019; Volume 73, pp. 73–121. [Google Scholar]
- Stockmann, P.; Gozzi, M.; Kuhnert, R.; Sárosi, M.B.; Hey-Hawkins, E. New keys for old locks: Carborane-containing drugs as platforms for mechanism-based therapies. Chem. Soc. Rev. 2019, 48, 3497–3512. [Google Scholar] [CrossRef] [PubMed]
- Fisher, S.P.; Tomich, A.W.; Lovera, S.O.; Kleinsasser, J.F.; Guo, J.; Asay, M.J.; Nelson, H.M.; Lavallo, V. Nonclassical Applications of closo-Carborane Anions: From Main Group Chemistry and Catalysis to Energy Storage. Chem. Rev. 2019, 119, 8262–8290. [Google Scholar] [CrossRef]
- Hawthorne, M.F.; Popp, G. 3-Trimethylamino-3-beryl-1,2-dicarba-closo-dodecaborane(12) and related species. Inorg. Chem. 1971, 10, 391–393. [Google Scholar] [CrossRef]
- Alkorta, I.; Campillo, N.; Rozas, I.; Elguero, J. Ring Strain and Hydrogen Bond Acidity. J. Org. Chem. 1998, 63, 7759–7763. [Google Scholar] [CrossRef]
- Mujika, J.I.; Mercero, J.M.; Lopez, X. Water-Promoted Hydrolysis of a Highly Twisted Amide: Rate Acceleration Caused by the Twist of the Amide Bond. J. Am. Chem. Soc. 2005, 127, 4445–4453. [Google Scholar] [CrossRef]
- Alkorta, I.; Montero-Campillo, M.M.; Elguero, J.; Yáñez, M.; Mó, O. Complexes between neutral oxyacid beryllium salts and dihydrogen: A possible way for hydrogen storage? Dalton Trans. 2018, 47, 12516–12520. [Google Scholar] [CrossRef]
- Alkorta, I.; Montero-Campillo, M.M.; Elguero, J.; Yáñez, M.; Mó, O. Complexes between H2 and neutral oxyacid beryllium derivatives. The role of angular strain. Mol. Phys. 2018, 1–9. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Stearns, C.A.; Kohl, F.J. Mass spectrometric determination of the dissociation energies of AlC2, Al2C2, and AlAuC2. J. Phys. Chem. 1973, 77, 136–138. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Popelier, P.L.A. Atoms in Molecules. An introduction; Prentice Hall: Harlow, UK, 2000. [Google Scholar]
- Keith, T.A. AIMAll; Version 17.11.14 B; T.K Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]
- Su, P.; Li, H. Energy decomposition analysis of covalent bonds and intermolecular interactions. J. Chem. Phys. 2009, 131, 014102. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; et al. Gamess; Iowa State University: Ames, IA, USA, 2013. [Google Scholar]
- Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Universal Features of the Electron Density Distribution in Hydrogen-Bonding Regions: A Comprehensive Study Involving H···X (X = H, C, N, O, F, S, Cl, π) Interactions. Chem. Eur. J. 2010, 16, 2442–2452. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Elguero, J. Discrimination of hydrogen-bonded complexes with axial chirality. J. Chem. Phys. 2002, 117, 6463–6468. [Google Scholar] [CrossRef]
- Alkorta, I.; Solimannejad, M.; Provasi, P.; Elguero, J. Theoretical Study of Complexes and Fluoride Cation Transfer between N2F+ and Electron Donors. J. Phys. Chem. A 2007, 111, 7154–7161. [Google Scholar] [CrossRef]
- Legon, A.C.; Millen, D.J. Hydrogen bonding as a probe of electron densities: Limiting gas-phase nucleophilicities and electrophilicities of B and HX. J. Am. Chem. Soc. 1987, 109, 356–358. [Google Scholar] [CrossRef]
- Alkorta, I.; Legon, A.C. Nucleophilicities of Lewis Bases B and Electrophilicities of Lewis Acids A Determined from the Dissociation Energies of Complexes B⋯A Involving Hydrogen Bonds, Tetrel Bonds, Pnictogen Bonds, Chalcogen Bonds and Halogen Bonds. Molecules 2017, 22, 1786. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Yáñez, M.; Mó, O.; Montero-Campillo, M.M. Relativistic Effects on NMR Parameters of Halogen-Bonded Complexes. Molecules 2019, 24, 4399. [Google Scholar] [CrossRef]
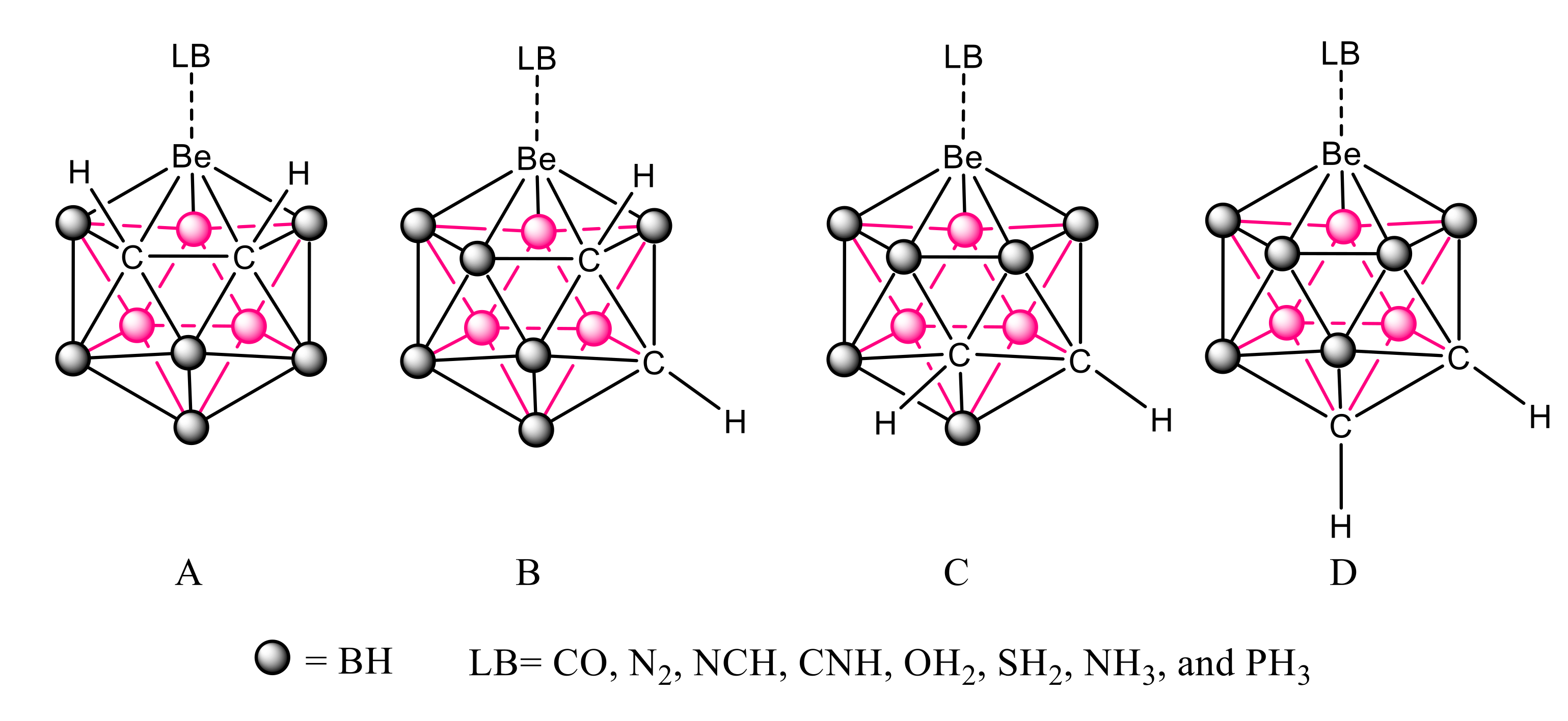


| ΔHrel | Vs, max | |
|---|---|---|
| B9H11C2Be (A) | 17.7 | 669.4 |
| B9H11C2Be (B) | 34.7 | 625.9 |
| B9H11C2Be (C) | 29.2 | 605.0 |
| B9H11C2Be (D) | 0.0 | 575.3 |
| CO3Be | 906.7 | |
| SO4Be | 938.5 | |
| Cl2Be | 141.0 |
| Base\Acid | A | B | C | D | CO3Be | SO4Be | Cl2Be |
|---|---|---|---|---|---|---|---|
| N2 | 1.692 | 1.690 | 1.688 | 1.691 | 1.724 | 1.729 | 1.884 |
| CO | 1.735 | 1.729 | 1.722 | 1.725 | 1.794 | 1.802 | 1.874 |
| SH2 | 2.127 | 2.125 | 2.134 | 2.137 | 2.118 | 2.113 | 2.250 |
| PH3 | 2.140 | 2.138 | 2.137 | 2.140 | 2.167 | 2.164 | 2.278 |
| NCH | 1.660 | 1.661 | 1.663 | 1.665 | 1.671 | 1.670 | 1.730 |
| OH2 | 1.641 | 1.646 | 1.659 | 1.659 | 1.603 | 1.597 | 1.642 |
| CNH | 1.736 | 1.732 | 1.728 | 1.730 | 1.770 | 1.771 | 1.818 |
| NH3 | 1.708 | 1.712 | 1.719 | 1.720 | 1.697 | 1.691 | 1.739 |
| Base\Acid | A | B | C | D | CO3Be | SO4Be | Cl2Be |
|---|---|---|---|---|---|---|---|
| N2 | 111.8 | 108.6 | 83.8 | 57.5 | 93.8 | 103.6 | 6.1 |
| CO | 142.9 | 140.6 | 116.7 | 89.6 | 117.1 | 127.7 | 24.7 |
| SH2 | 160.9 | 154.5 | 124.2 | 96.7 | 146.5 | 160.6 | 45.2 |
| PH3 | 169.6 | 163.4 | 135.3 | 107.6 | 150.0 | 165.3 | 45.2 |
| NCH | 193.3 | 184.0 | 153.0 | 125.3 | 185.1 | 201.0 | 71.1 |
| OH2 | 194.3 | 184.8 | 150.3 | 123.3 | 197.4 | 212.0 | 97.3 |
| CNH | 206.7 | 198.9 | 169.5 | 141.1 | 190.6 | 206.5 | 77.5 |
| NH3 | 241.2 | 231.6 | 199.2 | 171.9 | 238.6 | 256.1 | 124.7 |
| A:LB a | B:LB | C:LB | D:LB | CO3Be:LB | SO4Be:LB | Cl2Be:LB | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | BeD b | LB | BeD | LB | BeD | LB | BeD | LB | BeD | LB | BeD | LB | BeD | LB |
| N2 | 2.3 | 0.0 | 2.4 | 0.0 | 2.3 | 0.0 | 2.5 | 0.0 | 1.9 | 0.1 | 0.2 | 0.1 | 28.4 | 0.1 |
| CO | 3.0 | 0.2 | 3.0 | 0.1 | 2.8 | 0.1 | 3.1 | 0.1 | 2.9 | 0.6 | 0.9 | 0.8 | 34.6 | 0.3 |
| SH2 | 4.2 | 0.3 | 4.2 | 0.3 | 3.9 | 0.2 | 4.2 | 0.2 | 3.2 | 0.5 | 1.9 | 0.5 | 38.4 | 0.4 |
| PH3 | 4.9 | 7.5 | 4.8 | 6.8 | 4.4 | 6.0 | 4.7 | 5.8 | 4.1 | 8.7 | 2.8 | 9.7 | 41.1 | 5.4 |
| NCH | 5.6 | 0.7 | 5.7 | 0.7 | 5.4 | 0.7 | 5.9 | 0.7 | 4.8 | 1.0 | 3.1 | 1.1 | 48.1 | 0.8 |
| OH2 | 4.7 | 1.1 | 4.9 | 1.1 | 4.9 | 0.9 | 5.3 | 1.0 | 3.7 | 2.5 | 2.3 | 2.6 | 45.1 | 3.9 |
| CNH | 5.5 | 1.6 | 5.4 | 1.4 | 5.2 | 1.2 | 5.6 | 1.2 | 5.1 | 2.1 | 3.3 | 2.4 | 48.0 | 1.5 |
| NH3 | 7.1 | 0.0 | 7.2 | 0.0 | 7.0 | 0−.1 | 7.5 | 0−.1 | 5.3 | 0.1 | 4.0 | 0.1 | 54.8 | 0.3 |
| Model 1 | Model 2 | |
|---|---|---|
| All | Without BeCl2 | |
| R2 | 0.96 | 0.98 |
| SD (kJ mol−1) | 9.9 | 5.9 |
| Ea values | ||
| Cl2Be | 5.5 | |
| CO3Be | 13.8 | 13.2 |
| SO4Be | 14.9 | 14.3 |
| A | 14.6 | 14.0 |
| B | 14.1 | 13.5 |
| C | 11.7 | 11.2 |
| D | 9.6 | 9.2 |
| Nb values | ||
| N2 | 7.0 | 7.5 |
| CO | 9.2 | 9.7 |
| SH2 | 10.7 | 11.2 |
| PH3 | 11.2 | 11.8 |
| NCH | 13.2 | 13.8 |
| OH2 | 13.7 | 14.1 |
| CNH | 14.1 | 14.7 |
| NH3 | 17.1 | 17.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
Sample Availability: Samples of the compounds are not available from the authors. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkorta, I.; Elguero, J.; Oliva-Enrich, J.M.; Yáñez, M.; Mó, O.; Montero-Campillo, M.M. The Importance of Strain (Preorganization) in Beryllium Bonds. Molecules 2020, 25, 5876. https://doi.org/10.3390/molecules25245876
Alkorta I, Elguero J, Oliva-Enrich JM, Yáñez M, Mó O, Montero-Campillo MM. The Importance of Strain (Preorganization) in Beryllium Bonds. Molecules. 2020; 25(24):5876. https://doi.org/10.3390/molecules25245876
Chicago/Turabian StyleAlkorta, Ibon, José Elguero, Josep M. Oliva-Enrich, Manuel Yáñez, Otilia Mó, and M. Merced Montero-Campillo. 2020. "The Importance of Strain (Preorganization) in Beryllium Bonds" Molecules 25, no. 24: 5876. https://doi.org/10.3390/molecules25245876
APA StyleAlkorta, I., Elguero, J., Oliva-Enrich, J. M., Yáñez, M., Mó, O., & Montero-Campillo, M. M. (2020). The Importance of Strain (Preorganization) in Beryllium Bonds. Molecules, 25(24), 5876. https://doi.org/10.3390/molecules25245876