Mechanisms of a Cyclobutane-Fused Lactone Hydrolysis in Alkaline and Acidic Conditions
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
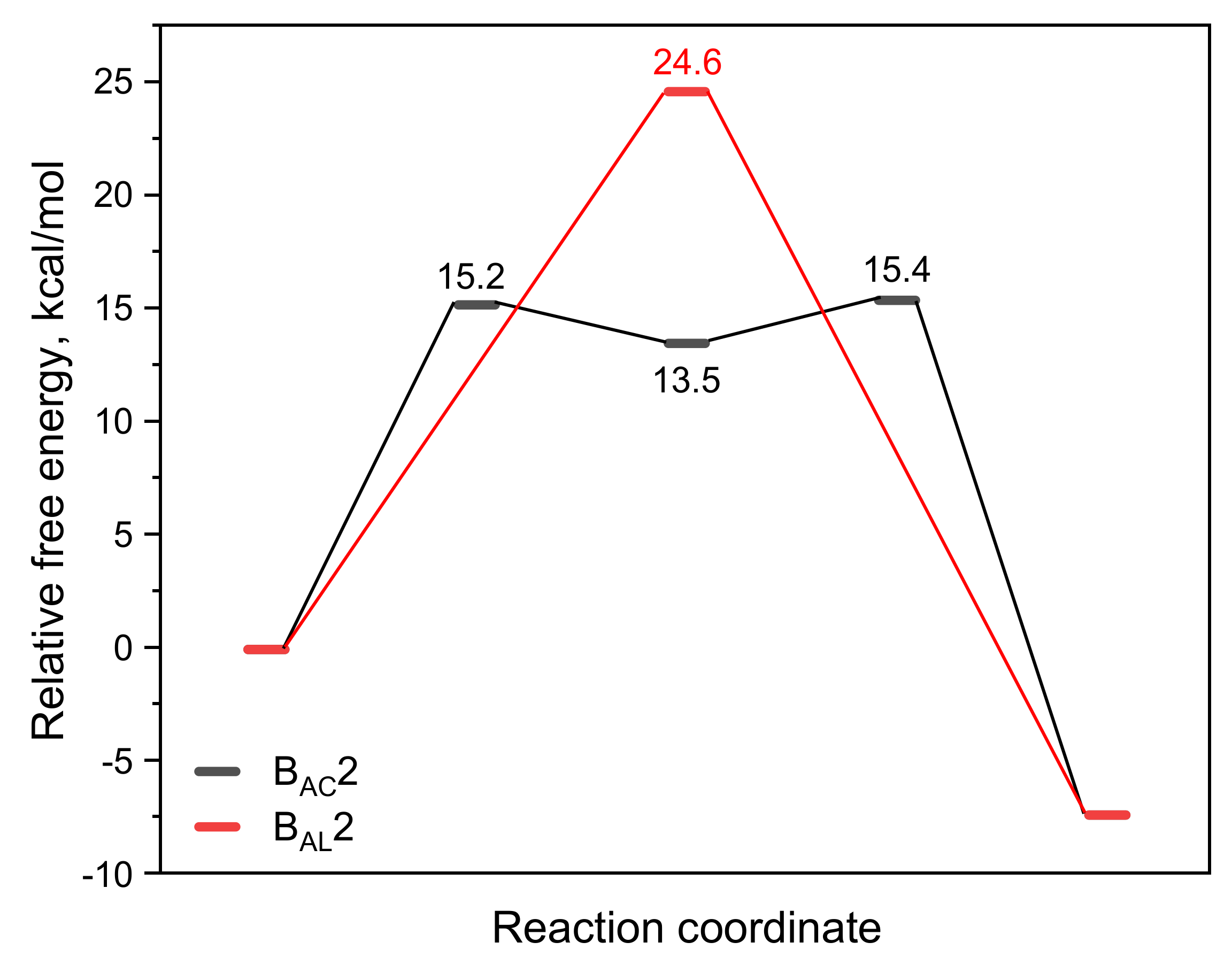
3.1. Alkaline Hydrolysis
3.1.1. The BAC2 Mechanism: Deeper Insight by Explicit Solvent Models
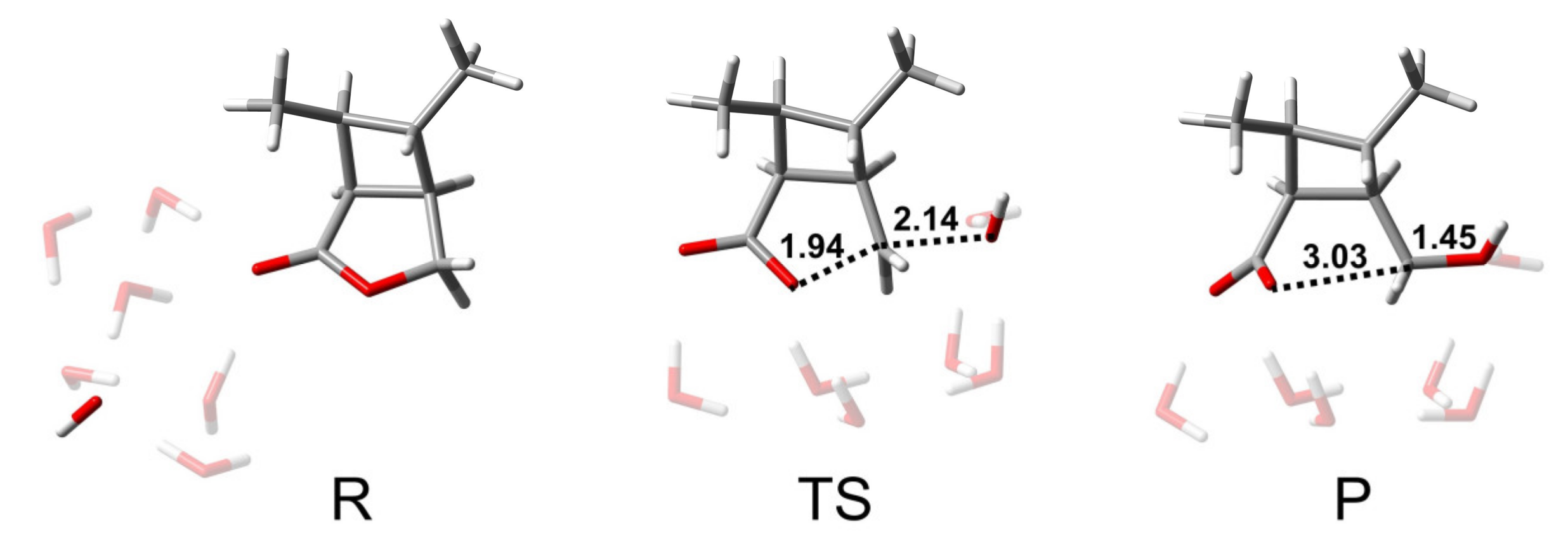
3.1.2. The BAL2 Mechanism
3.2. Acidic Hydrolysis
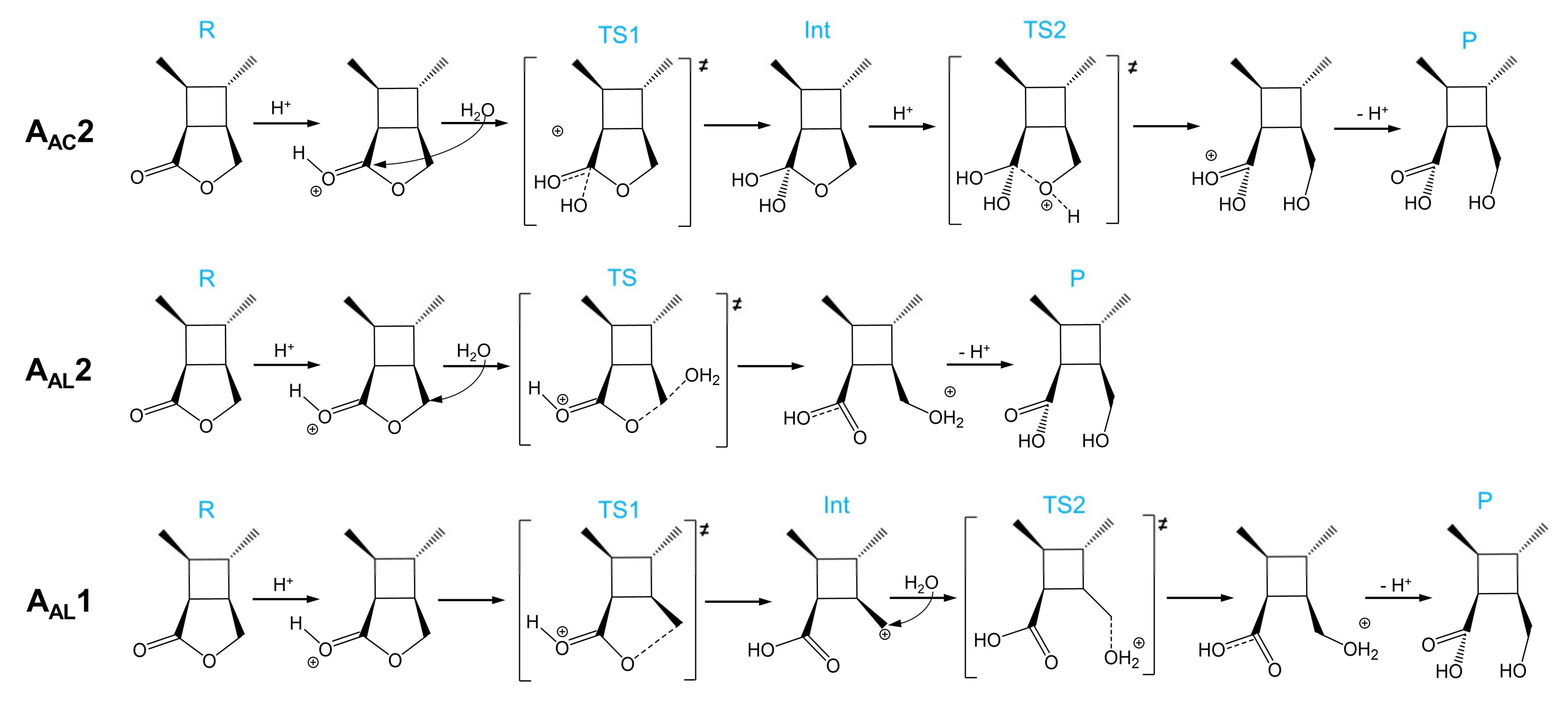
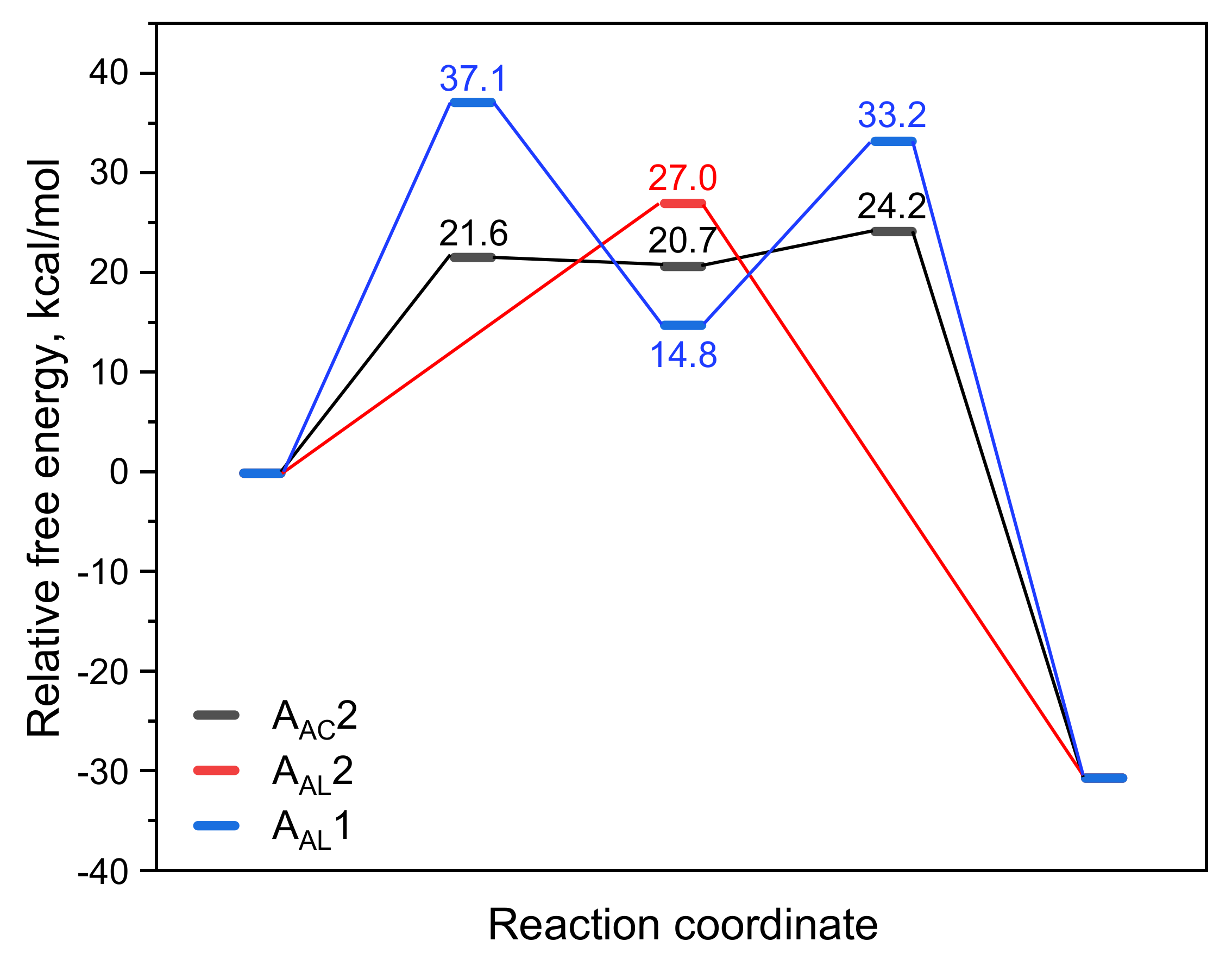
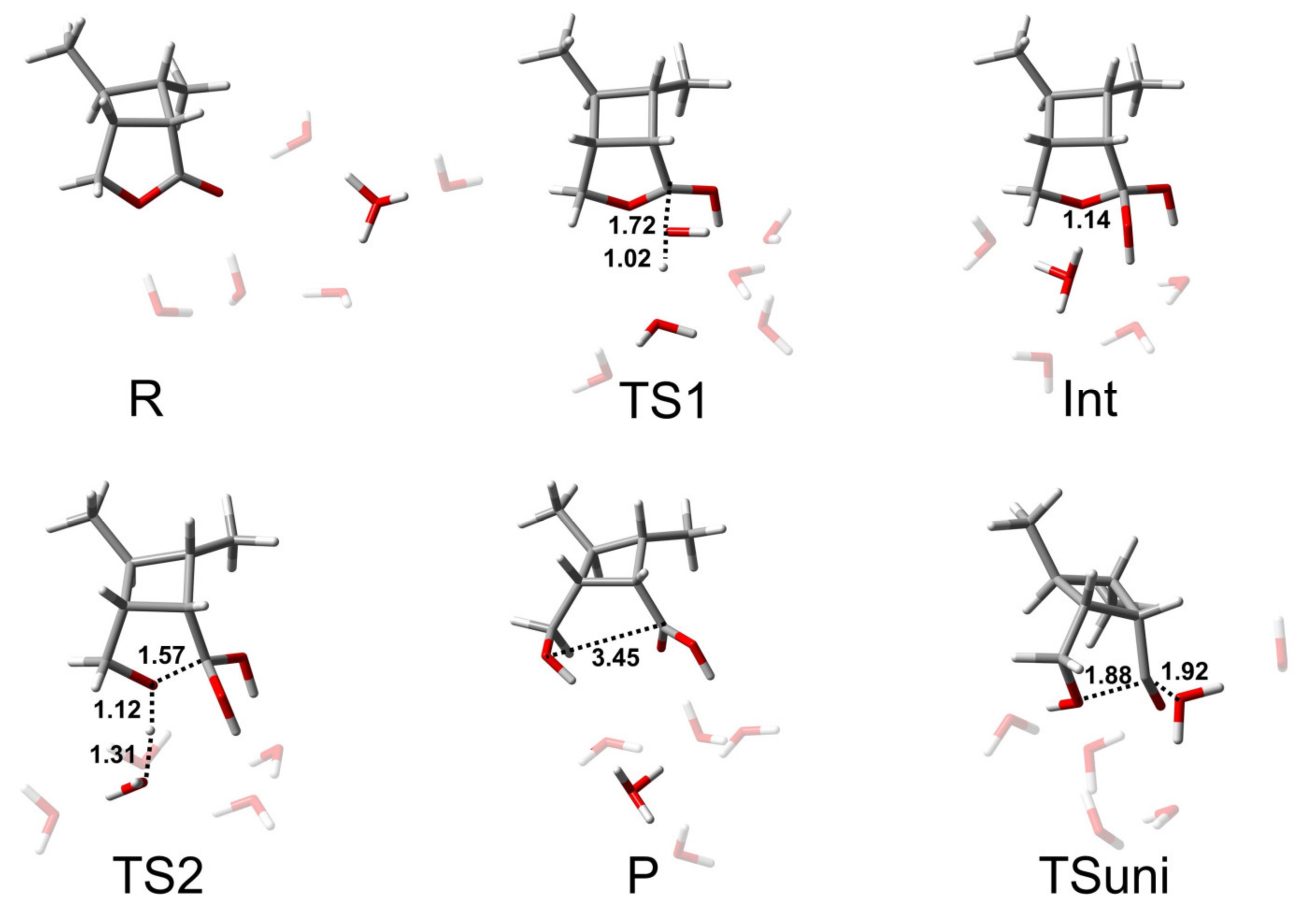
3.2.1. The AAC2 Mechanism
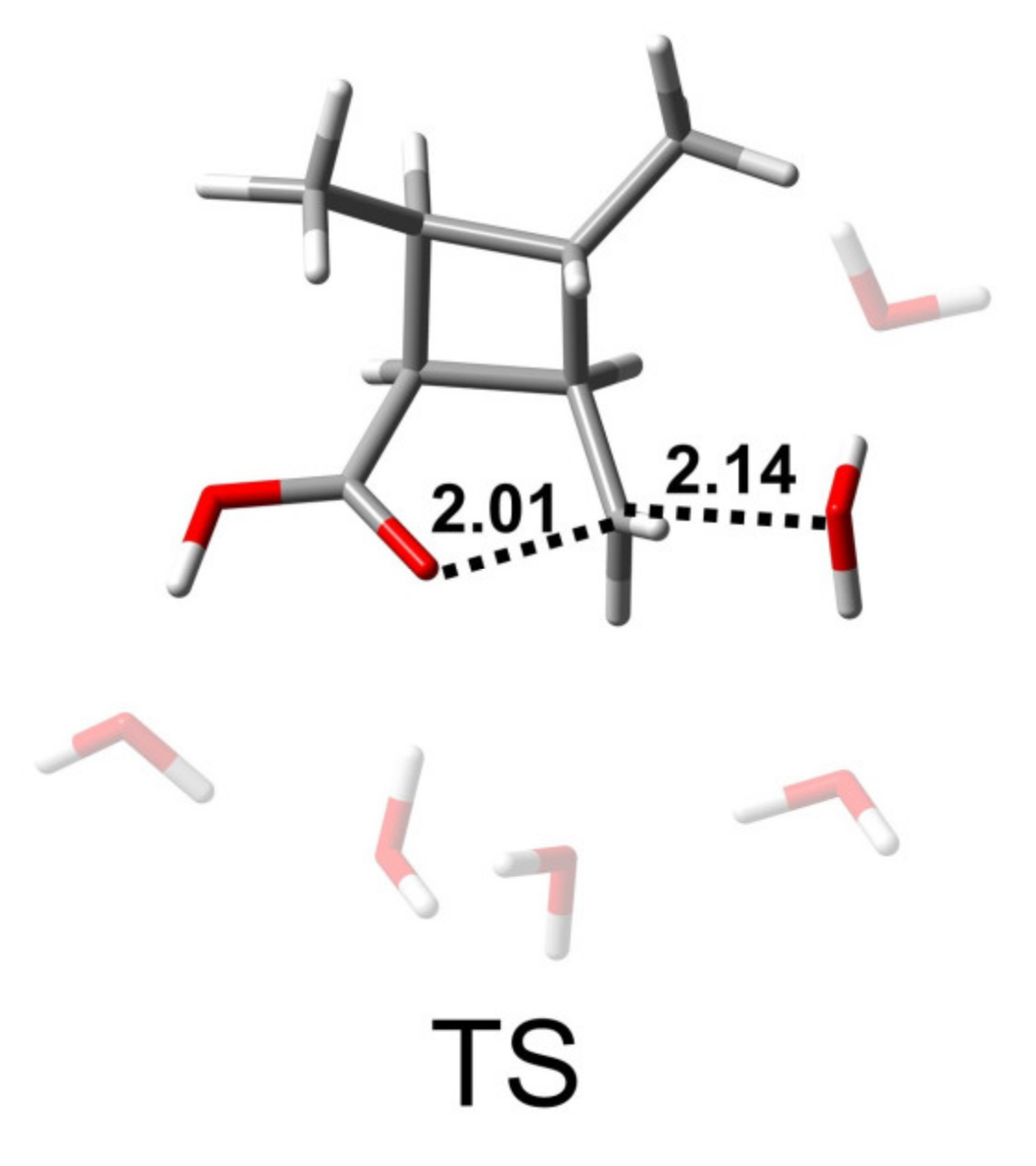
3.2.2. The AAL2 Mechanism
3.2.3. The AAL1 Mechanism
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hsu, T.G.; Zhou, J.; Su, H.W.; Schrage, B.R.; Ziegler, C.J.; Wang, J. A polymer with “locked” degradability: Superior backbone stability and accessible degradability enabled by mechanophore installation. J. Am. Chem. Soc. 2020, 142, 2100–2104. [Google Scholar] [CrossRef] [PubMed]
- Sure, R.; El Mahdali, M.; Plajer, A.; Deglmann, P. Towards a converged strategy for including microsolvation in reaction mechanism calculations. J. Comput. Aided Mol. Des. 2021, 35, 473–492. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Bombarelli, R.; Calle, E.; Casado, J. Mechanisms of lactone hydrolysis in neutral and alkaline conditions. J. Org. Chem. 2013, 78, 6868–6879. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Bombarelli, R.; Calle, E.; Casado, J. Mechanisms of lactone hydrolysis in acidic conditions. J. Org. Chem. 2013, 78, 6880–6889. [Google Scholar] [CrossRef]
- Yan, Z.; Lian, J.; Li, M.; Meng, L.; Zhang, Y.; Ge, C.; Lu, J. Deeper insight into hydrolysis mechanisms of polyester/cotton blended fabrics for separation by explicit solvent models. Int. J. Biol. Macromol. 2020, 154, 596–605. [Google Scholar] [CrossRef]
- Szeler, K.; Williams, N.H.; Hengge, A.C.; Kamerlin, S.C. Modeling the alkaline hydrolysis of diaryl sulfate diesters: A mechanistic study. J. Org. Chem. 2020, 85, 6489–6497. [Google Scholar] [CrossRef]
- Duarte, F.; Åqvist, J.; Williams, N.H.; Kamerlin, S.C. Resolving apparent conflicts between theoretical and experimental models of phosphate monoester hydrolysis. J. Am. Chem. Soc. 2015, 137, 1081–1093. [Google Scholar] [CrossRef]
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; Mourik, T.; Mitchell, J.B.O. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef]
- Dub, P.A.; Ikariya, T. Quantum chemical calculations with the inclusion of nonspecific and specific solvation: Asymmetric transfer hydrogenation with bifunctional ruthenium catalysts. J. Am. Chem. Soc. 2013, 135, 2604–2619. [Google Scholar] [CrossRef]
- Dong, S.; Bi, S. The solvation effect on the rattling behaviour of the hydrated excess proton in water. Phys. Chem. Chem. Phys. 2019, 21, 22385–22389. [Google Scholar] [CrossRef]
- Pliego, J.R.; Riveros, J.M. Hybrid discrete-continuum solvation methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1440. [Google Scholar] [CrossRef]
- Gadre, S.R.; Yeole, S.D.; Sahu, N. Quantum chemical investigations on molecular clusters. Chem. Rev. 2014, 114, 12132–12173. [Google Scholar] [CrossRef]
- Maldonado, A.M.; Hagiwara, S.; Choi, T.H.; Eckert, F.; Schwarz, K.; Sundararaman, R.; Otani, M.; Keith, J.A. Quantifying uncertainties in solvation procedures for modeling aqueous phase reaction mechanisms. J. Phys. Chem. A 2021, 125, 154–164. [Google Scholar] [CrossRef]
- Ingold, C.K. Structure and Mechanism in Organic Chemistry, 2nd ed.; Cornell University Press: Ithaca, NY, USA, 1969; pp. 457–463. [Google Scholar]
- Edenborough, M. Organic Reaction Mechanisms: A Step by Step Approach, 2nd ed.; CRC Press: London, UK, 1998; pp. 168–170. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Akbulatov, S.; Tian, Y.; Kapustin, E.; Boulatov, R. Model studies of the kinetics of ester hydrolysis under stretching force. Angew. Chem. Int. Ed. 2013, 125, 7130–7133. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Tunon, I.; Rinaldi, D.; Ruiz-Ldpez, M.F.; Rivail, J.L. Hydroxide ion in liquid water: Structure, energetics, and proton transfer using a mixed discrete-continuum ab initio model. J. Phys. Chem. 1995, 99, 3798–3805. [Google Scholar] [CrossRef]
- Pliego, J.R.; Riveros, J.M. The cluster-continuum model for the calculation of the solvation free energy of ionic species. J. Phys. Chem. A 2001, 105, 7241–7247. [Google Scholar] [CrossRef]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Adding explicit solvent molecules to continuum solvent calculations for the calculation of aqueous acid dissociation constants. J. Phys. Chem. A 2006, 110, 2493–2499. [Google Scholar] [CrossRef]
- Pliego, J.R. Basic hydrolysis of formamide in aqueous solution: A reliable theoretical calculation of the activation free energy using the cluster-continuum model. Chem. Phys. 2004, 306, 273–280. [Google Scholar] [CrossRef]
- Ślebocka-Tilk, H.; Neverov, A.A.; Brown, R.S. Proton inventory study of the base-catalyzed hydrolysis of formamide. Consideration of the nucleophilic and general base mechanisms. J. Am. Chem. Soc. 2003, 125, 1851–1858. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Zhan, C.G. Theoretical studies of the transition-state structures and free energy barriers for base-catalyzed hydrolysis of amides. J. Phys. Chem. A 2006, 110, 1264–12652. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Cao, Z. Mechanism of acid-catalyzed hydrolysis of formamide from cluster-continuum model calculations: Concerted and stepwise pathway. J. Phys. Chem. A 2010, 114, 12918–12927. [Google Scholar] [CrossRef] [PubMed]
- Catak, S.; Monard, G.; Aviyente, V.; Ruiz-López, M.F. Deamidation of asparagine residues: Direct hydrolysis versus succinimide-mediated deamidation mechanisms. J. Phys. Chem. A 2009, 113, 1111–1120. [Google Scholar] [CrossRef]
- Pan, B.; Ricci, M.S. Molecular mechanism of acid-catalyzed hydrolysis of peptide bonds using a model compound. J. Phys. Chem. B 2010, 114, 4389–4399. [Google Scholar] [CrossRef]
- Kabanda, M.M.; Tran, Q.T.; Ebenso, E.E. A computational study of pyrazinamide: Tautomerism, acid–base properties, micro-solvation effects and acid hydrolysis mechanism. Comput. Theor. Chem. 2014, 1046, 30–41. [Google Scholar] [CrossRef]
- Petrović, D.; Szeler, K.; Kamerlin, S.C.L. Challenges and advances in the computational modeling of biological phosphate hydrolysis. Chem. Commun. 2018, 54, 3077–3089. [Google Scholar] [CrossRef]
- Li, L.; Lelyveld, V.S.; Prywes, N.; Szostak, J.W. Experimental and computational evidence for a loose transition state in phosphoroimidazolide hydrolysis. J. Am. Chem. Soc. 2016, 138, 3986–3989. [Google Scholar] [CrossRef]
- Duarte, F.; Barrozo, A.; Åqvist, J.; Williams, N.H.; Kamerlin, S.C.L. The competing mechanisms of phosphate monoester dianion hydrolysis. J. Am. Chem. Soc. 2016, 138, 10664–10673. [Google Scholar] [CrossRef]
- Mora, J.R.; Kirby, A.J.; Nome, F. Theoretical study of the importance of the spectator groups on the hydrolysis of phosphate triesters. J. Org. Chem. 2012, 77, 7061–7070. [Google Scholar] [CrossRef]
- Kamerlin, S.C.L.; Williams, N.H.; Warshel, A. Dineopentyl phosphate hydrolysis: Evidence for stepwise water attack. J. Org. Chem. 2008, 73, 6960–6969. [Google Scholar] [CrossRef]
- Zhan, C.G.; Landry, D.W.; Ornstein, R.L. Energy barriers for alkaline hydrolysis of carboxylic acid esters in aqueous solution by reaction field calculations. J. Phys. Chem. A 2000, 104, 7672–7678. [Google Scholar] [CrossRef]
- Xie, D.; Zhou, Y.; Xu, D.; Guo, H. Solvent effect on concertedness of the transition state in the hydrolysis of p-nitrophenyl acetate. Org. Lett. 2005, 7, 2093–2095. [Google Scholar] [CrossRef]
- Pliego, J.R.; Riveros, J.M. A theoretical analysis of the free-energy profile of the different pathways in the alkaline hydrolysis of methyl formate in aqueous solution. Chem. Eur. J. 2002, 8, 1945–1953. [Google Scholar] [CrossRef]
- Xu, T.; Chen, J.; Wang, Z.; Tang, W.; Xia, D.; Fu, Z.; Xie, H. Development of prediction models on base-catalyzed hydrolysis kinetics of phthalate esters with density functional theory calculation. Environ. Sci. Technol. 2019, 53, 5828–5837. [Google Scholar] [CrossRef]
- Fukui, K. The path of chemical reactions-the IRC approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Tuñón, I.; Williams, I.H. The transition state and cognate concepts. Adv. Phys. Org. Chem. 2019, 53, 29–68. [Google Scholar]



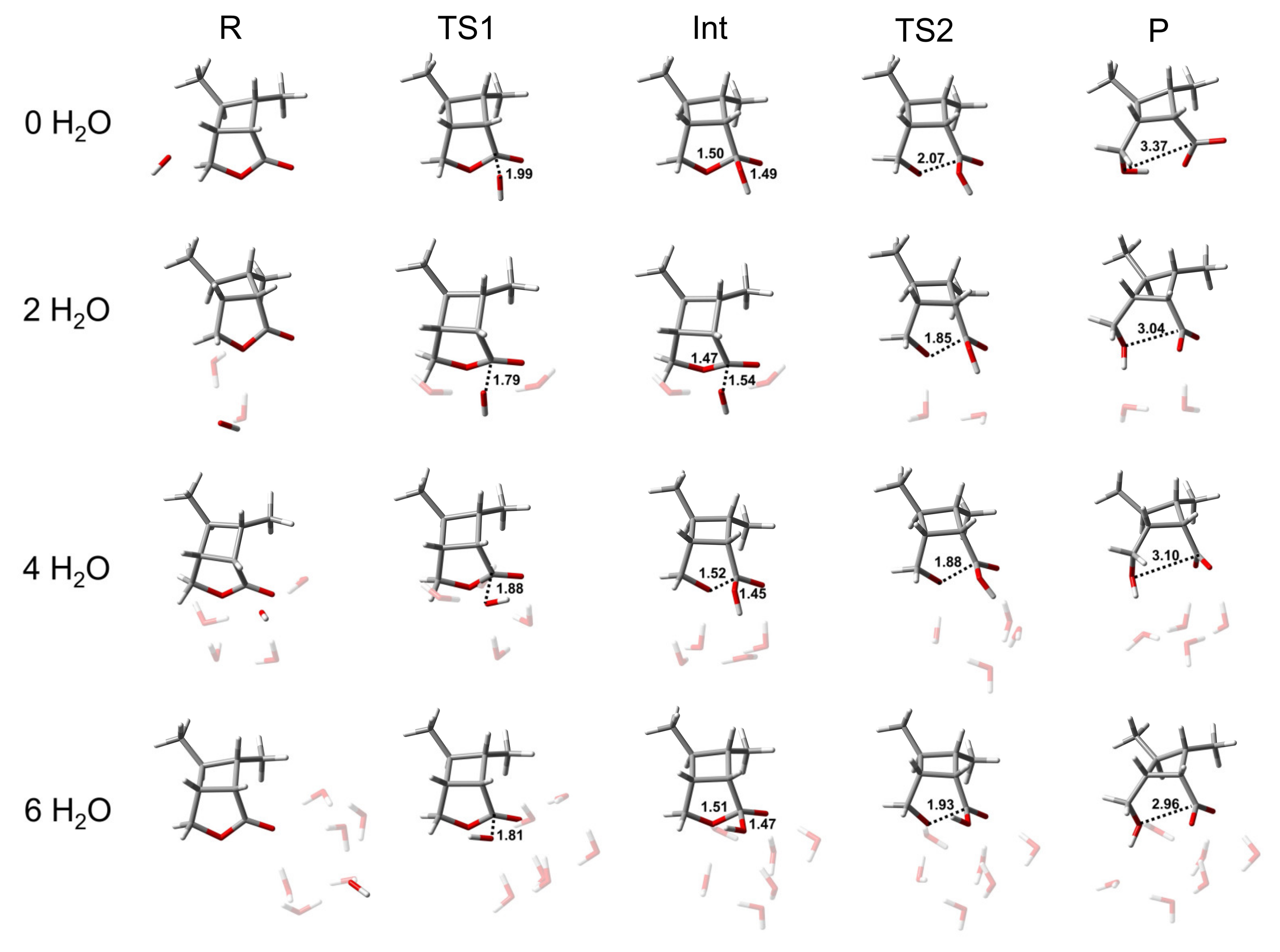
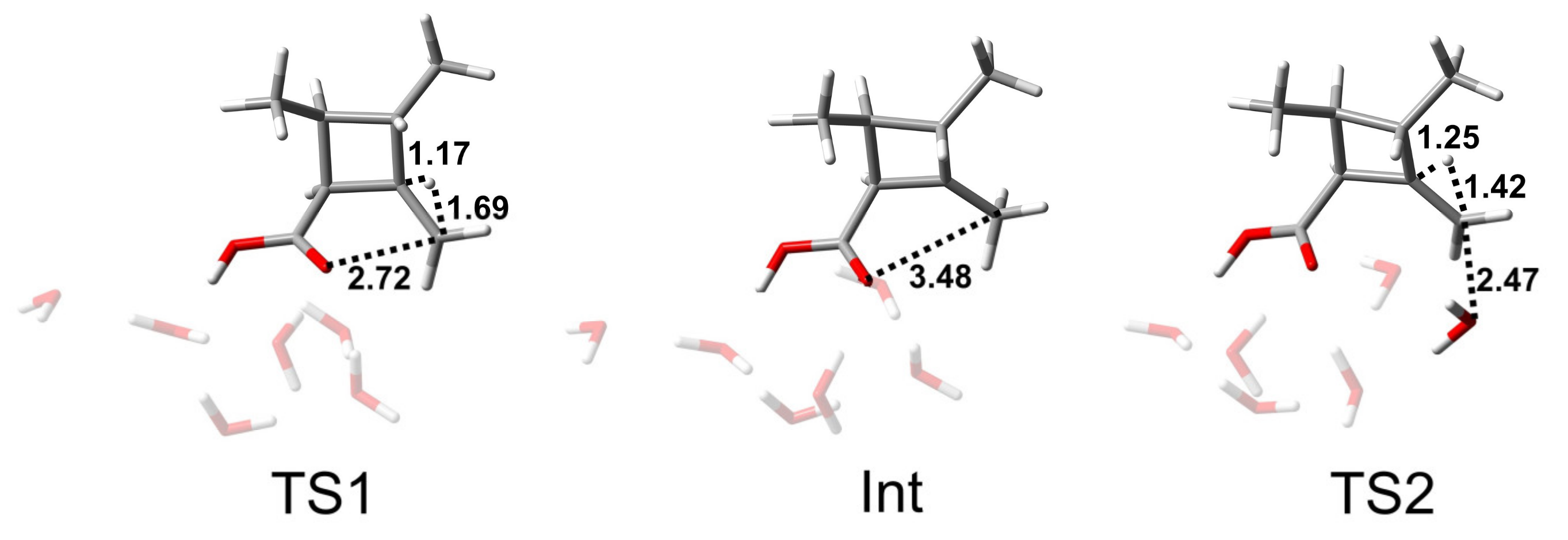
| System | TS1 | Int | TS2 | ΔG≠ |
|---|---|---|---|---|
| 0 H2O | 11.6 | 7.6 | 12.5 | 12.6 |
| 1 H2O | 12.9 | 9.3 | 13.0 | 13.3 |
| 2 H2O | 13.7 | 13.4 | 16.6 | 16.6 |
| 3 H2O | 12.3 | 11.7 | 16.4 | 16.4 |
| 4 H2O | 15.3 | 14.5 | 16.6 | 16.6 |
| 5 H2O | 15.7 | 14.6 | 16.0 | 16.3 |
| 6 H2O | 15.2 | 13.5 | 15.4 | 15.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Ma, H. Mechanisms of a Cyclobutane-Fused Lactone Hydrolysis in Alkaline and Acidic Conditions. Molecules 2021, 26, 3519. https://doi.org/10.3390/molecules26123519
Wang Z, Ma H. Mechanisms of a Cyclobutane-Fused Lactone Hydrolysis in Alkaline and Acidic Conditions. Molecules. 2021; 26(12):3519. https://doi.org/10.3390/molecules26123519
Chicago/Turabian StyleWang, Zhangxia, and Haibo Ma. 2021. "Mechanisms of a Cyclobutane-Fused Lactone Hydrolysis in Alkaline and Acidic Conditions" Molecules 26, no. 12: 3519. https://doi.org/10.3390/molecules26123519
APA StyleWang, Z., & Ma, H. (2021). Mechanisms of a Cyclobutane-Fused Lactone Hydrolysis in Alkaline and Acidic Conditions. Molecules, 26(12), 3519. https://doi.org/10.3390/molecules26123519





